Llectron Le solide cristallin PROPRIETES DES MATERIAUX SOLIDES

























































































































- Slides: 186

L’électron Le solide cristallin PROPRIETES DES MATERIAUX SOLIDES R. Fortunier Électrons dans un solide

L’ELECTRON

L’électron Le solide cristallin description physique PROPRIETES DES MATERIAUX SOLIDES R. Fortunier Électrons dans un solide

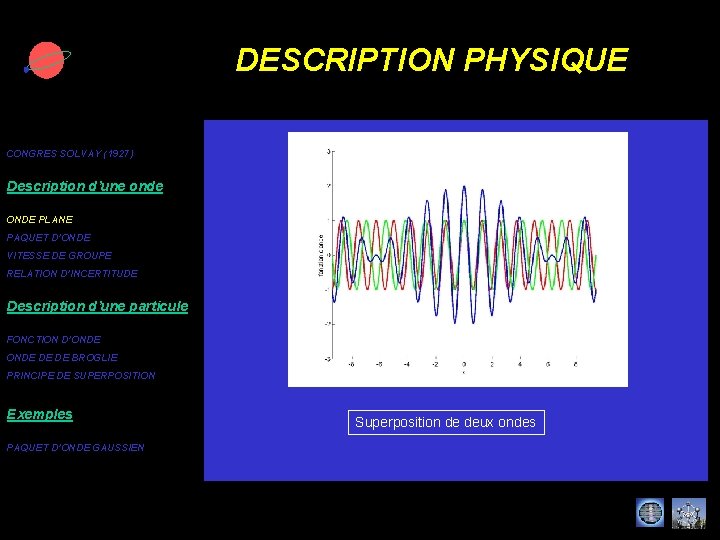
DESCRIPTION PHYSIQUE CONGRES SOLVAY (1927) Description d’une onde ONDE PLANE PAQUET D’ONDE VITESSE DE GROUPE RELATION D’INCERTITUDE Description d’une particule FONCTION D’ONDE DE DE BROGLIE PRINCIPE DE SUPERPOSITION Exemples PAQUET D’ONDE GAUSSIEN

DESCRIPTION PHYSIQUE CONGRES SOLVAY (1927) Description d’une onde ONDE PLANE PAQUET D’ONDE VITESSE DE GROUPE RELATION D’INCERTITUDE Description d’une particule FONCTION D’ONDE DE DE BROGLIE PRINCIPE DE SUPERPOSITION Exemples PAQUET D’ONDE GAUSSIEN A. Piccard, E. Henriot, P. Ehrenfest, E. Herzen, Th. De Donder, E. Schrödinger, F. Verschaffelt, W. Pauli, W. Heisenberg, R. Fowler, L. Brillouin P. Debye, M. Knudsen, W. Bragg, H. Kramers, P. Dirac, A. Compton, L de Broglie, M. Born, N. Bohr I. Langmuir, M. Planck, M. Curie, H. Lorentz, A. Einstein, P. Langevin, Ch. Guye, Ch. Wilson, O. Richardson

DESCRIPTION PHYSIQUE CONGRES SOLVAY (1927) Fonction d’onde Position Temps Description d’une onde ONDE PLANE PAQUET D’ONDE VITESSE DE GROUPE RELATION D’INCERTITUDE Amplitude Vecteur d’onde Pulsation Description d’une particule FONCTION D’ONDE Fréquence (Hz) : Longueur d’onde (m) : ONDE DE DE BROGLIE PRINCIPE DE SUPERPOSITION Exemples PAQUET D’ONDE GAUSSIEN Vitesse de propagation (m/s) : Ondes électromagnétiques (solutions des équations de Maxwell) Ondes de pression (sons, …)

DESCRIPTION PHYSIQUE CONGRES SOLVAY (1927) Description d’une onde ONDE PLANE PAQUET D’ONDE VITESSE DE GROUPE RELATION D’INCERTITUDE Description d’une particule FONCTION D’ONDE DE DE BROGLIE PRINCIPE DE SUPERPOSITION Exemples PAQUET D’ONDE GAUSSIEN Exemples d’ondes électromagnétiques

DESCRIPTION PHYSIQUE CONGRES SOLVAY (1927) Description d’une onde ONDE PLANE PAQUET D’ONDE VITESSE DE GROUPE RELATION D’INCERTITUDE Description d’une particule FONCTION D’ONDE DE DE BROGLIE PRINCIPE DE SUPERPOSITION Exemples PAQUET D’ONDE GAUSSIEN Superposition de deux ondes

DESCRIPTION PHYSIQUE CONGRES SOLVAY (1927) Description d’une onde ONDE PLANE PAQUET D’ONDE VITESSE DE GROUPE RELATION D’INCERTITUDE Description d’une particule FONCTION D’ONDE DE DE BROGLIE PRINCIPE DE SUPERPOSITION Exemples PAQUET D’ONDE GAUSSIEN Superposition de plusieurs ondes y = y 1 + y 2 + y 3 + y 4 + y 5

DESCRIPTION PHYSIQUE CONGRES SOLVAY (1927) Description d’une onde ONDE PLANE PAQUET D’ONDE VITESSE DE GROUPE Distribution du vecteur position au cours du temps (fonction d’onde) RELATION D’INCERTITUDE Description d’une particule FONCTION D’ONDE DE DE BROGLIE PRINCIPE DE SUPERPOSITION Exemples PAQUET D’ONDE GAUSSIEN Distribution du vecteur d’onde au cours du temps

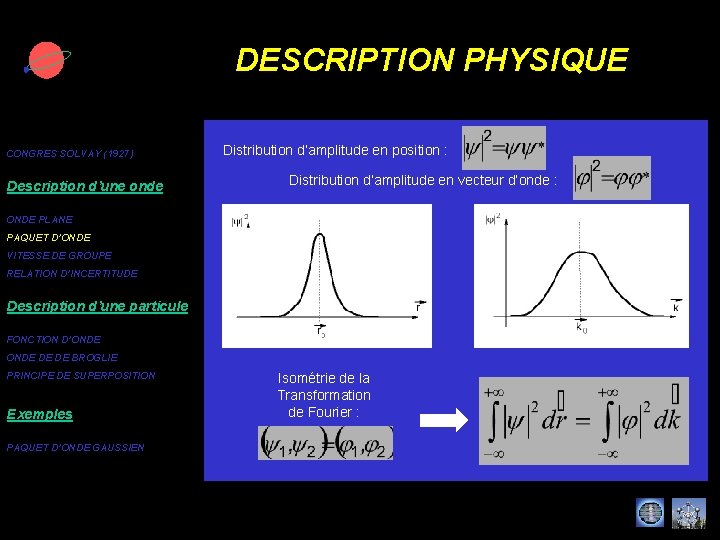
DESCRIPTION PHYSIQUE CONGRES SOLVAY (1927) Description d’une onde Distribution d’amplitude en position : Distribution d’amplitude en vecteur d’onde : ONDE PLANE PAQUET D’ONDE VITESSE DE GROUPE RELATION D’INCERTITUDE Description d’une particule FONCTION D’ONDE DE DE BROGLIE PRINCIPE DE SUPERPOSITION Exemples PAQUET D’ONDE GAUSSIEN Isométrie de la Transformation de Fourier :

DESCRIPTION PHYSIQUE CONGRES SOLVAY (1927) Description d’une onde ONDE PLANE PAQUET D’ONDE VITESSE DE GROUPE RELATION D’INCERTITUDE Description d’une particule FONCTION D’ONDE DE DE BROGLIE PRINCIPE DE SUPERPOSITION Exemples PAQUET D’ONDE GAUSSIEN t t+Dt

DESCRIPTION PHYSIQUE CONGRES SOLVAY (1927) Description d’une onde Dr ONDE PLANE PAQUET D’ONDE VITESSE DE GROUPE RELATION D’INCERTITUDE Description d’une particule FONCTION D’ONDE Dk ONDE DE DE BROGLIE PRINCIPE DE SUPERPOSITION Exemples PAQUET D’ONDE GAUSSIEN Relation d’incertitude : Dk. Dr 1/2

DESCRIPTION PHYSIQUE CONGRES SOLVAY (1927) y(r, t) : fonction d’onde Description d’une onde d. P = |y|2 dr ONDE PLANE PAQUET D’ONDE VITESSE DE GROUPE RELATION D’INCERTITUDE Probabilité de trouver la particule à l’instant t dans un volume dr autour de r Description d’une particule |y|2 : densité de probabilité FONCTION D’ONDE DE DE BROGLIE PRINCIPE DE SUPERPOSITION Exemples PAQUET D’ONDE GAUSSIEN Dr |y|2 dr = 1

DESCRIPTION PHYSIQUE particule CONGRES SOLVAY (1927) Description d’une onde m w v onde k ONDE PLANE PAQUET D’ONDE VITESSE DE GROUPE RELATION D’INCERTITUDE Description d’une particule FONCTION D’ONDE DE DE BROGLIE impulsion : p = mv énergie : E = p. p / 2 m vecteur d’onde : k pulsation : w Postulat de de Broglie Une particule (impulsion p et énergie E) peut être assimilée à une onde (vecteur d’onde k et pulsation w) avec : PRINCIPE DE SUPERPOSITION p = k h E = w h Exemples PAQUET D’ONDE GAUSSIEN Constante de Planck : h = 6, 63 10 -34 Js Constante de Planck « réduite » : = h/2 p = 1, 04 10 h

DESCRIPTION PHYSIQUE CONGRES SOLVAY (1927) Fonction d’onde Position Description d’une onde Temps i i(k. r – (p. r –w. Et) t) h y(r, t) = a e ONDE PLANE PAQUET D’ONDE VITESSE DE GROUPE RELATION D’INCERTITUDE Description d’une particule Densité de probabilité Vecteur impulsion Énergie FONCTION D’ONDE DE DE BROGLIE PRINCIPE DE SUPERPOSITION Exemples PAQUET D’ONDE GAUSSIEN a |y|2 dr 1 !!

DESCRIPTION PHYSIQUE CONGRES SOLVAY (1927) Description d’une onde ONDE PLANE Principe de superposition Une particule est décrite par une superposition d’ondes de de Broglie : un paquet d’onde PAQUET D’ONDE VITESSE DE GROUPE Distribution du vecteur position r au cours du temps (fonction d’onde) RELATION D’INCERTITUDE Description d’une particule 1 y(r, t) = h 3/2 FONCTION D’ONDE DE DE BROGLIE PRINCIPE DE SUPERPOSITION Exemples PAQUET D’ONDE GAUSSIEN + j(p, t) e h i (p. r – Et)dp - Distribution du vecteur impulsion p au cours du temps 1 j(p, t) = h 3/2 + i Et) dr y(r, t) e- (p. r – h -

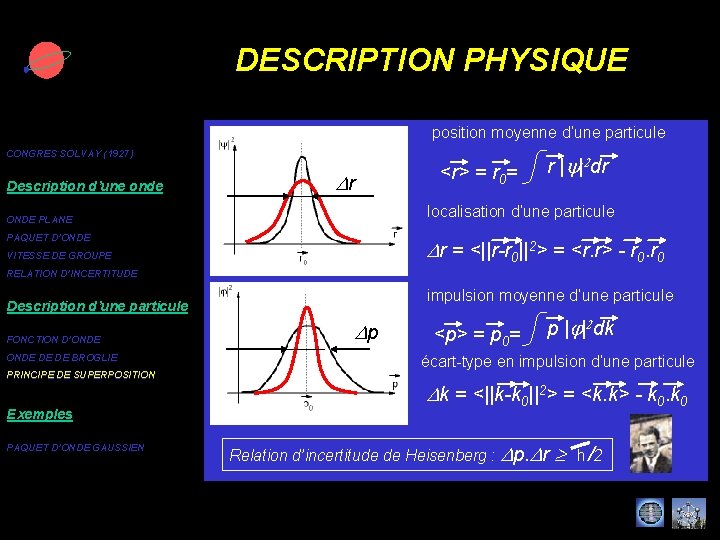
DESCRIPTION PHYSIQUE position moyenne d’une particule CONGRES SOLVAY (1927) Description d’une onde Dr <r> = r 0= r |y|2 dr localisation d’une particule ONDE PLANE PAQUET D’ONDE Dr = <||r-r 0||2> = <r. r> - r 0 VITESSE DE GROUPE RELATION D’INCERTITUDE impulsion moyenne d’une particule Description d’une particule FONCTION D’ONDE DE DE BROGLIE PRINCIPE DE SUPERPOSITION Exemples PAQUET D’ONDE GAUSSIEN Dp <p> = p 0= p |j|2 dk écart-type en impulsion d’une particule Dk = <||k-k 0||2> = <k. k> - k 0 Relation d’incertitude de Heisenberg : h 2 Dp. Dr /

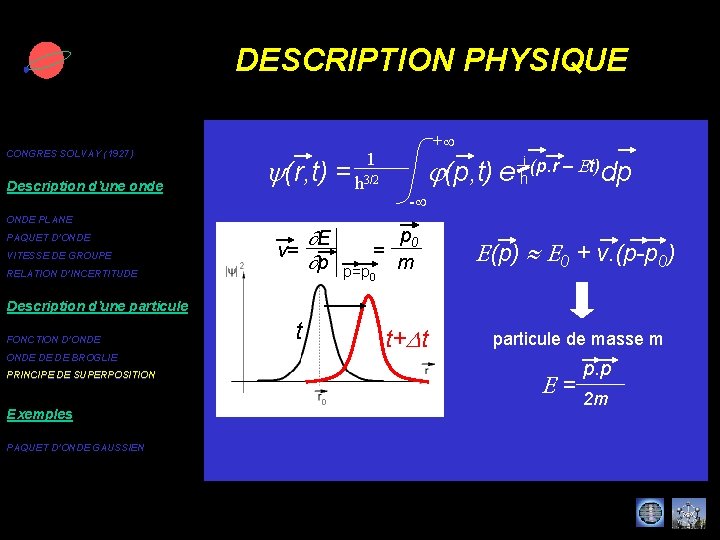
DESCRIPTION PHYSIQUE CONGRES SOLVAY (1927) Description d’une onde ONDE PLANE PAQUET D’ONDE VITESSE DE GROUPE RELATION D’INCERTITUDE + 1 y(r, t) = h 3/2 E v= p j(p, t) e h i (p. r – Et)dp - p 0 = m p=p E(p) E 0 + v. (p-p 0) 0 Description d’une particule FONCTION D’ONDE DE DE BROGLIE PRINCIPE DE SUPERPOSITION Exemples PAQUET D’ONDE GAUSSIEN t t+Dt particule de masse m p. p E = 2 m

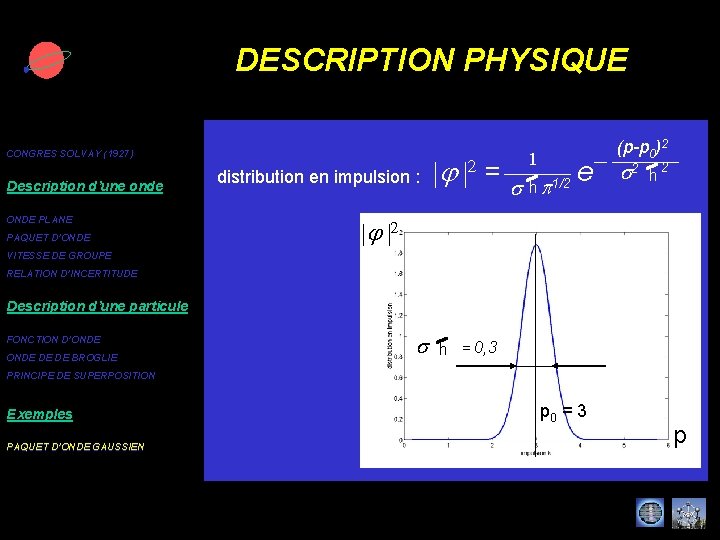
DESCRIPTION PHYSIQUE CONGRES SOLVAY (1927) Description d’une onde ONDE PLANE PAQUET D’ONDE distribution en impulsion : |j |2 =s 1 hp 1/2 e (p-p 0)2 s 2 h 2 |j |2 VITESSE DE GROUPE RELATION D’INCERTITUDE Description d’une particule FONCTION D’ONDE DE DE BROGLIE s h = 0, 3 PRINCIPE DE SUPERPOSITION Exemples PAQUET D’ONDE GAUSSIEN p 0 = 3 p

DESCRIPTION PHYSIQUE CONGRES SOLVAY (1927) Description d’une onde ONDE PLANE PAQUET D’ONDE distribution en position à t=0 : h |y |y |2 s = p 1/2 e -x 2 s 2 |2 VITESSE DE GROUPE RELATION D’INCERTITUDE Description d’une particule FONCTION D’ONDE DE DE BROGLIE 1/s h = 3, 3 PRINCIPE DE SUPERPOSITION Exemples PAQUET D’ONDE GAUSSIEN x 0 = 0 x/ h

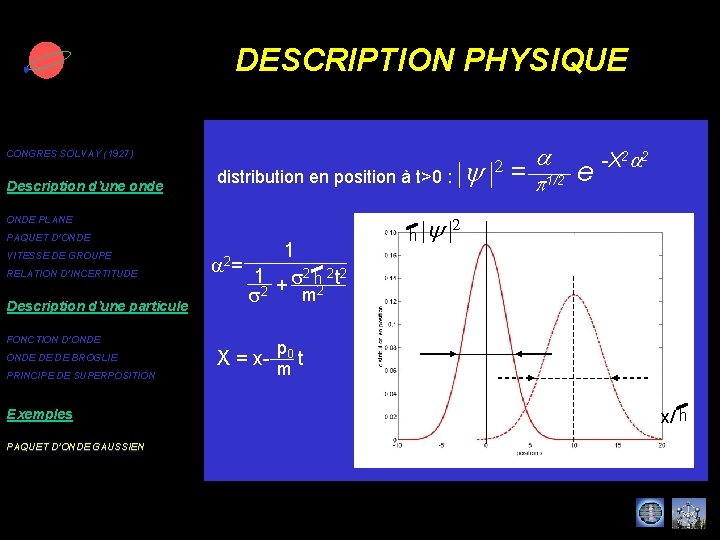
DESCRIPTION PHYSIQUE CONGRES SOLVAY (1927) Description d’une onde distribution en position à t>0 : ONDE PLANE PAQUET D’ONDE VITESSE DE GROUPE RELATION D’INCERTITUDE Description d’une particule FONCTION D’ONDE DE DE BROGLIE PRINCIPE DE SUPERPOSITION Exemples PAQUET D’ONDE GAUSSIEN a 2 = 1 1 + s 2 h 2 t 2 m 2 s 2 h |y |y |2 a = p 1/2 e -X 2 a 2 |2 p m 0 X = x- t x/ h

DESCRIPTION PHYSIQUE CONGRES SOLVAY (1927) Description d’une onde Application numérique 1 Un électron est localisé à t=0 dans un intervalle Dx = 1Å. Où sera-t-il localisé au bout de 1 seconde ? ONDE PLANE PAQUET D’ONDE VITESSE DE GROUPE Dx 600 km !!! RELATION D’INCERTITUDE Description d’une particule FONCTION D’ONDE DE DE BROGLIE Application numérique 2 Quel temps faut-il pour qu’un millimètre cube d’eau double de volume ? PRINCIPE DE SUPERPOSITION Exemples PAQUET D’ONDE GAUSSIEN t 1015 années !!!

DESCRIPTION PHYSIQUE CONGRES SOLVAY (1927) Description d’une onde ONDE PLANE PAQUET D’ONDE VITESSE DE GROUPE RELATION D’INCERTITUDE Description d’une particule FONCTION D’ONDE DE DE BROGLIE PRINCIPE DE SUPERPOSITION Exemples PAQUET D’ONDE GAUSSIEN

L’électron Le solide cristallin équations de mouvement PROPRIETES DES MATERIAUX SOLIDES R. Fortunier Électrons dans un solide

EQUATIONS DE MOUVEMENT Équation de Schrödinger CAS GENERAL ETATS STATIONNAIRES CAS LIMITE DE LA MECANIQUE CLASSIQUE Particule dans un puits de potentiel DESCRIPTION ET RESOLUTION EXEMPLES PARTICULE DANS UNE BOÎTE Oscillateur harmonique DESCRIPTION ET RESOLUTION EXEMPLES

EQUATIONS DE MOUVEMENT Équation de Schrödinger CAS GENERAL ETATS STATIONNAIRES CAS LIMITE DE LA MECANIQUE CLASSIQUE Particule dans un puits de potentiel DESCRIPTION ET RESOLUTION EXEMPLES PARTICULE DANS UNE BOÎTE Oscillateur harmonique DESCRIPTION ET RESOLUTION EXEMPLES onde plane de de Broglie : y(r, t) = a e i h S - action : S = p. r – Et - énergie : E = p. p/2 m + V y h i = E y = (p 2/2 m + V)y t p 2 Dy = div(grady) = div(yp) = - y 2 h 2 m Dy + Vy = i h y t

EQUATIONS DE MOUVEMENT équation de SCHRÖDINGER : Équation de Schrödinger CAS GENERAL 2 h 2 m ETATS STATIONNAIRES CAS LIMITE DE LA MECANIQUE CLASSIQUE Particule dans un puits de potentiel sol. Générale Dy + Vy = i h y t = combinaison linéaire d’ondes planes = paquet d’ondes DESCRIPTION ET RESOLUTION EXEMPLES PARTICULE DANS UNE BOÎTE Oscillateur harmonique DESCRIPTION ET RESOLUTION EXEMPLES y(r, t) = 1 h 3/2 j(p) e - i (p. r – Et) h dp

EQUATIONS DE MOUVEMENT y(r, t) = y(r) W(t) Équation de Schrödinger CAS GENERAL ETATS STATIONNAIRES CAS LIMITE DE LA MECANIQUE CLASSIQUE Particule dans un puits de potentiel DESCRIPTION ET RESOLUTION EXEMPLES PARTICULE DANS UNE BOÎTE Oscillateur harmonique DESCRIPTION ET RESOLUTION EXEMPLES 2 h 2 m Dy + Vy = Ey solutions non triviales (non nulles) pour certaines énergies En : yn(r) -i Et h e ondes stationnaires yn(r, t) -i E tn 2 = yn(r) e h avec |yn| indt du temps superposition d’ondes stationnaires y (r, t) = Sanyn(r, t) et |y|2 fonction du temps n

EQUATIONS DE MOUVEMENT Équation de Schrödinger y(r, t) = a e CAS GENERAL ETATS STATIONNAIRES CAS LIMITE DE LA MECANIQUE CLASSIQUE Particule dans un puits de potentiel DESCRIPTION ET RESOLUTION EXEMPLES PARTICULE DANS UNE BOÎTE 2 h 2 m i h S avec a = a(r, t) et S = S(r, t) Dy + Vy = i h y t 2 1 (a 2) grad. S S h 2 ) = 0 ( + grad. S+V- Da) -i ( +div(a h 2 ma t 2 m m t E h « petit » v Oscillateur harmonique DESCRIPTION ET RESOLUTION EXEMPLES Équation d’Hamilton-Jacobi Équation de continuité

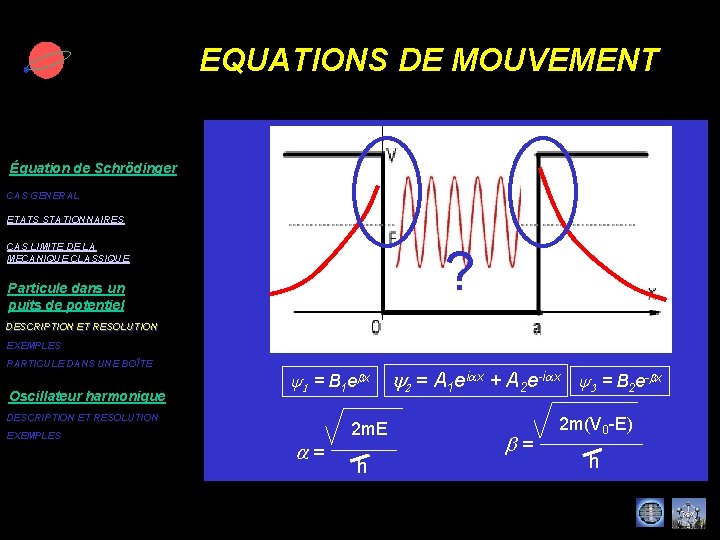
EQUATIONS DE MOUVEMENT Conditions aux limites (x + et x - ) 2 m y’’+ (E-V 2 0)y = 0 Équation de Schrödinger h CAS GENERAL y = B 1 ebx ETATS STATIONNAIRES CAS LIMITE DE LA MECANIQUE CLASSIQUE Particule dans un puits de potentiel b = y = B 2 e-bx 2 m(V 0 -E) b = h DESCRIPTION ET RESOLUTION EXEMPLES PARTICULE DANS UNE BOÎTE Oscillateur harmonique DESCRIPTION ET RESOLUTION EXEMPLES 2 m y’’+ E 2 y = 0 h y = A 1 eiax + A 2 e-iax avec a = 2 m. E h 2 m(V 0 -E) h

EQUATIONS DE MOUVEMENT Équation de Schrödinger CAS GENERAL ETATS STATIONNAIRES CAS LIMITE DE LA MECANIQUE CLASSIQUE ? Particule dans un puits de potentiel DESCRIPTION ET RESOLUTION EXEMPLES PARTICULE DANS UNE BOÎTE Oscillateur harmonique y 1 = B 1 ebx DESCRIPTION ET RESOLUTION EXEMPLES a = 2 m. E h y 2 = A 1 eiax + A 2 e-iax y 3 = B 2 e-bx b = 2 m(V 0 -E) h

EQUATIONS DE MOUVEMENT Équation de Schrödinger CAS GENERAL Conditions de continuité (x =0 et x =a) ETATS STATIONNAIRES CAS LIMITE DE LA MECANIQUE CLASSIQUE Particule dans un puits de potentiel DESCRIPTION ET RESOLUTION EXEMPLES PARTICULE DANS UNE BOÎTE y 1 (0) = y 2 (0) Y 1‘ (0) = y 2‘(0) y 1 = B 1 ebx y 2 = A 1 eiax + A 2 e-iax y 3 = B 2 e-bx y 2 = B 1(cos(ax)+(b/a)sin(ax)) y 2 (a) = y 3 (a) y 3 = B 1(cos(ax)+(b/a)sin(ax))eb(a-x) Y 2‘ (a) = y 3‘(a) B 1(2 cos(aa)-(a 2 -b 2/ab)sin(aa)) = 0 Oscillateur harmonique DESCRIPTION ET RESOLUTION EXEMPLES B 1 = 0 ou tan(aa/2) = b/a ou tan(aa/2 -p/2) = b/a

EQUATIONS DE MOUVEMENT Équation de Schrödinger x = aa/2 h = ba/2 x h 2+ 2 = K 2 = 2 m. V CAS GENERAL ETATS STATIONNAIRES CAS LIMITE DE LA MECANIQUE CLASSIQUE Particule dans un puits de potentiel DESCRIPTION ET RESOLUTION EXEMPLES PARTICULE DANS UNE BOÎTE Oscillateur harmonique DESCRIPTION ET RESOLUTION EXEMPLES a 1, b 1 a 2, b 2 a 3, b 3 a 4, b 4 Plusieurs solutions (energies Ei = h 2 ai 2/m) 0 a 2/ 2 h x tan(x) = h ou x tan(x-p/2) = h

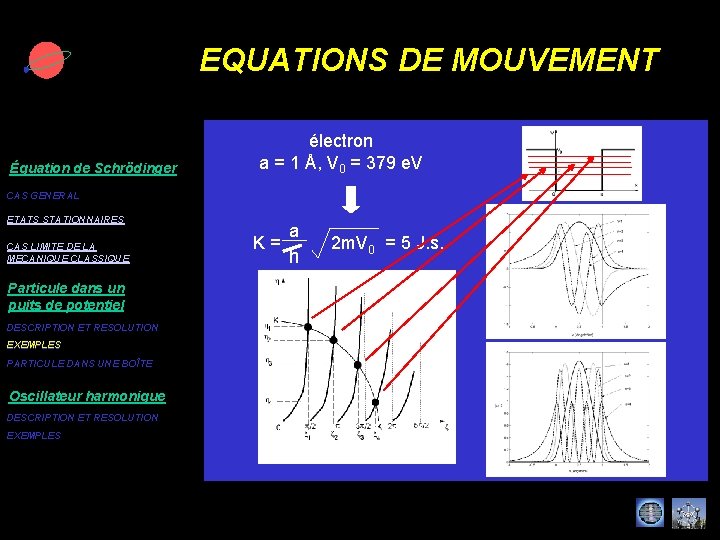
EQUATIONS DE MOUVEMENT Équation de Schrödinger électron a = 1 Å, V 0 = 379 e. V CAS GENERAL ETATS STATIONNAIRES CAS LIMITE DE LA MECANIQUE CLASSIQUE Particule dans un puits de potentiel DESCRIPTION ET RESOLUTION EXEMPLES PARTICULE DANS UNE BOÎTE Oscillateur harmonique DESCRIPTION ET RESOLUTION EXEMPLES a K = = 5 J. s. 2 m. V 0 h

EQUATIONS DE MOUVEMENT Augmentation de K (m plus grande, V 0 plus fort) Équation de Schrödinger CAS GENERAL ETATS STATIONNAIRES CAS LIMITE DE LA MECANIQUE CLASSIQUE Particule dans un puits de potentiel DESCRIPTION ET RESOLUTION EXEMPLES PARTICULE DANS UNE BOÎTE Oscillateur harmonique DESCRIPTION ET RESOLUTION EXEMPLES K = 10 ou 100 J. s. 2 p 2 h n 2 K infini En = 2 m a 2

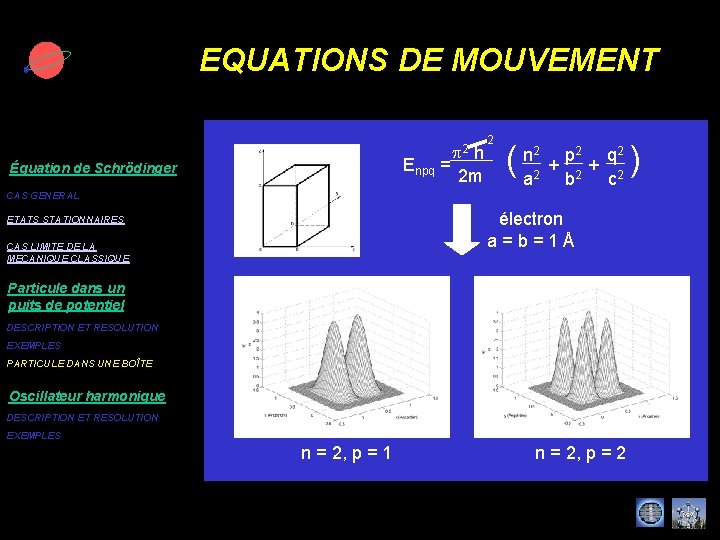
EQUATIONS DE MOUVEMENT p 2 2 ( h n 2 p 2 q 2 Enpq = + + 2 2 m a b 2 c 2 Équation de Schrödinger CAS GENERAL électron a = b = 1 Å ETATS STATIONNAIRES CAS LIMITE DE LA MECANIQUE CLASSIQUE Particule dans un puits de potentiel DESCRIPTION ET RESOLUTION EXEMPLES PARTICULE DANS UNE BOÎTE Oscillateur harmonique DESCRIPTION ET RESOLUTION EXEMPLES n = 2, p = 1 n = 2, p = 2 )

EQUATIONS DE MOUVEMENT Équation de Schrödinger CAS GENERAL ETATS STATIONNAIRES CAS LIMITE DE LA MECANIQUE CLASSIQUE Particule dans un puits de potentiel x DESCRIPTION ET RESOLUTION EXEMPLES 2 m y’’+ (E-V) y = 0 2 PARTICULE DANS UNE BOÎTE h V = ½ mw 2 x 2 Oscillateur harmonique DESCRIPTION ET RESOLUTION EXEMPLES mécanique classique mécanique quantique

EQUATIONS DE MOUVEMENT 2 m y’’+ (E-½m w 2 x 2)y = 0 2 Équation de Schrödinger h x = x (mw/ ) h 1/2 CAS GENERAL ETATS STATIONNAIRES CAS LIMITE DE LA MECANIQUE CLASSIQUE 2 E 2)y (x) = 0 y’’(x) + ( - x w h y(x) = c(x)exp(-x 2/2) Particule dans un puits de potentiel DESCRIPTION ET RESOLUTION EXEMPLES PARTICULE DANS UNE BOÎTE Oscillateur harmonique DESCRIPTION ET RESOLUTION EXEMPLES E 1 c’’ – 2 xc’ + 2( - ) c = 0 w 2 h h w(n+1/2) E = En = c(x) = CHn(x) (polynôme d’Hermite de degré n)

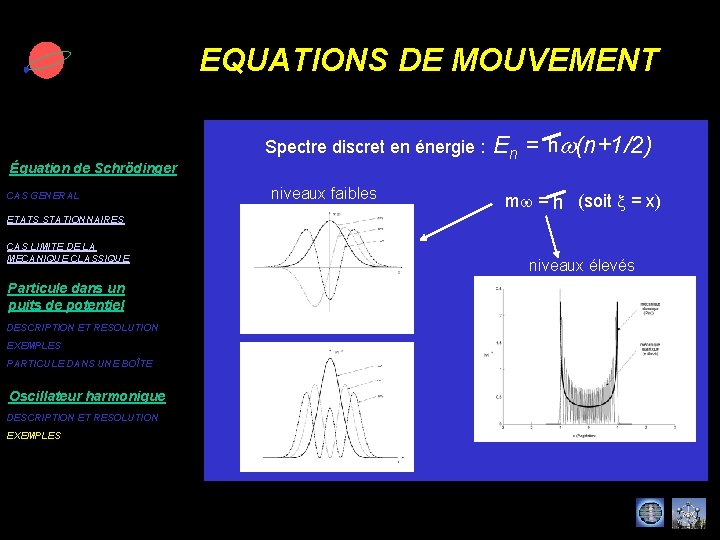
EQUATIONS DE MOUVEMENT Équation de Schrödinger CAS GENERAL hw(n+1/2) Spectre discret en énergie : En = niveaux faibles mw = (soit x = x) h ETATS STATIONNAIRES CAS LIMITE DE LA MECANIQUE CLASSIQUE Particule dans un puits de potentiel DESCRIPTION ET RESOLUTION EXEMPLES PARTICULE DANS UNE BOÎTE Oscillateur harmonique DESCRIPTION ET RESOLUTION EXEMPLES niveaux élevés

EQUATIONS DE MOUVEMENT Équation de Schrödinger CAS GENERAL ETATS STATIONNAIRES CAS LIMITE DE LA MECANIQUE CLASSIQUE Particule dans un puits de potentiel DESCRIPTION ET RESOLUTION EXEMPLES PARTICULE DANS UNE BOÎTE Oscillateur harmonique DESCRIPTION ET RESOLUTION EXEMPLES

L’électron grandeurs physiques Le solide cristallin PROPRIETES DES MATERIAUX SOLIDES R. Fortunier Électrons dans un solide

GRANDEURS PHYSIQUES Opérateurs et observables DEFINITION EXEMPLES Moment cinétique DEFINITION VALEURS PROPRES ET FONCTIONS PROPRES Première description des atomes EQUATION DE SCHRÖDINGER MOMENT CINETIQUE INTRINSEQUE SPIN CLASSIFICATION DES ELEMENTS CHIMIQUES

GRANDEURS PHYSIQUES Opérateurs et observables DEFINITION EXEMPLES f : grandeur physique l’on souhaite mesurer (position, énergie, …) y : fonction d’onde décrivant l’état du système dans lequel on souhaite mesurer f (particule dans un puits de potentiel, …) Moment cinétique y=yn lorsque f=fn DEFINITION VALEURS PROPRES ET FONCTIONS PROPRES fonctions propres de la grandeur physique Première description des atomes EQUATION DE SCHRÖDINGER MOMENT CINETIQUE INTRINSEQUE SPIN CLASSIFICATION DES ELEMENTS CHIMIQUES valeurs propres de la grandeur physique EXEMPLE : énergie d’une particule dans une boîte 1 D A y = yn = (2/A)1/2 sin(npx/A)exp(i. Ent/ ) h 2 p 2 h n 2 lorsque E = En = 2 m A 2

GRANDEURS PHYSIQUES principe de superposition Opérateurs et observables y = S anyn DEFINITION EXEMPLES • Si y = yn, alors an = 1 (les autres sont nuls) et on est sûr de mesurer fn • Si an = 0, alors la valeur propre fn ne peut être observée Moment cinétique DEFINITION VALEURS PROPRES ET FONCTIONS PROPRES Première description des atomes EQUATION DE SCHRÖDINGER MOMENT CINETIQUE INTRINSEQUE SPIN CLASSIFICATION DES ELEMENTS CHIMIQUES |an|2 : probabilité de mesurer fn pour la grandeur physique f • La mesure de f doit donner une des valeurs propres fn avec une probabilité de 1, donc S|an|2 =1 an = (y, yn) an : composante de y dans la base des fonctions propres yn

GRANDEURS PHYSIQUES EXEMPLE : énergie d’une particule dans une boîte 1 D Opérateurs et observables DEFINITION EXEMPLES A |an|2 : probabilité de mesurer une énergie E = En pour la particule Moment cinétique DEFINITION VALEURS PROPRES ET FONCTIONS PROPRES Première description des atomes EQUATION DE SCHRÖDINGER MOMENT CINETIQUE INTRINSEQUE SPIN CLASSIFICATION DES ELEMENTS CHIMIQUES Valeur moyenne de l’énergie : <E> = S En |an|2 CAS GENERAL : valeur moyenne de la grandeur f <f> = S fn |an|2 = S fn an y*yndr = y* S an fn yn dr ^ image de y par l’opérateur f associé à la grandeur physique f

GRANDEURS PHYSIQUES Opérateurs et observables ^ f : opérateur (ou observable) associé à la grandeur physique f DEFINITION EXEMPLES Moment cinétique ^ ^ f : y fy = S a f y n n n DEFINITION VALEURS PROPRES ET FONCTIONS PROPRES Première description des atomes EQUATION DE SCHRÖDINGER MOMENT CINETIQUE INTRINSEQUE SPIN CLASSIFICATION DES ELEMENTS CHIMIQUES Valeur moyenne de f : + ^ <f> = y* f y dr - Valeurs propres et vecteur propres : ^ f yn = fn yn

GRANDEURS PHYSIQUES Opérateurs et observables DEFINITION EXEMPLES Moment cinétique grandeur physique position r impulsion p DEFINITION VALEURS PROPRES ET FONCTIONS PROPRES Première description des atomes énergie cinétique Ec = p 2/2 m énergie potentielle V EQUATION DE SCHRÖDINGER MOMENT CINETIQUE INTRINSEQUE SPIN CLASSIFICATION DES ELEMENTS CHIMIQUES énergie totale E=Ec+V opérateur ou observable ^ r y = r y ^ h p y = grad(y) i 2 ^ h Ec y = - Dy 2 m ^ V y = Vy 2 ^ h H y = - Dy + Vy 2 m

GRANDEURS PHYSIQUES ^ ^ h moment cinétique : opérateur J vérifiant la relation J J = i J Opérateurs et observables DEFINITION EXEMPLES Moment cinétique DEFINITION VALEURS PROPRES ET FONCTIONS PROPRES Première description des atomes EQUATION DE SCHRÖDINGER ^ ^ ^ Exemple 1 : le moment cinétique orbital L = r p mécanique « classique » z L = r p mécanique « quantique » ^ h L y = r grad(y) i L 1 MOMENT CINETIQUE INTRINSEQUE SPIN CLASSIFICATION DES ELEMENTS CHIMIQUES p 2 p 1 r y L 2 ^ ^ ^ L L = i L ? ? h x

GRANDEURS PHYSIQUES Coordonnées sphériques Opérateurs et observables ^ h L y = r grad(y) i DEFINITION EXEMPLES Moment cinétique DEFINITION VALEURS PROPRES ET FONCTIONS PROPRES Première description des atomes h y ^ Lzy = i j ^2 2 y cosq y 2 h [ + L y = - q 2 sinq q 1 2 y + ] sin 2 q j 2 EQUATION DE SCHRÖDINGER MOMENT CINETIQUE INTRINSEQUE SPIN CLASSIFICATION DES ELEMENTS CHIMIQUES 2 y 2 y 1 ^ 2 Dy = + - L y 2 r r r 2 h

GRANDEURS PHYSIQUES Opérateurs et observables DEFINITION EXEMPLES Moment cinétique ^ Exemple 2 : moment cinétique propre d’une particule S n’existe pas en mécanique « classique » est spécifique à un type de particule (électron, proton, …) est difficile à se représenter concrètement DEFINITION VALEURS PROPRES ET FONCTIONS PROPRES Première description des atomes EQUATION DE SCHRÖDINGER MOMENT CINETIQUE INTRINSEQUE SPIN CLASSIFICATION DES ELEMENTS CHIMIQUES trois scientifiques essayent de représenter le moment cinétique propre d’un électron (Argonne, USA)

GRANDEURS PHYSIQUES Opérateurs et observables ^ J moment cinétique ^J 2 et J^ commutent z ^J 2 et J^ ont les mêmes z fonctions propres DEFINITION EXEMPLES Moment cinétique DEFINITION VALEURS PROPRES ET FONCTIONS PROPRES Première description des atomes EQUATION DE SCHRÖDINGER J^2 yj, m = j(j+1) h 2 yj, m J^z yj, m = m y h j, m Les fonctions d’onde yj, m sont les fonctions propres communes deux observables J^z et J^2. étude approfondie de l’opérateur « moment cinétique » MOMENT CINETIQUE INTRINSEQUE SPIN j = 0, 1/2, 1 , 3/2, 2, … CLASSIFICATION DES ELEMENTS CHIMIQUES m = -j, -j+1, …, j-1, j

GRANDEURS PHYSIQUES 2 h 2 m Opérateurs et observables DEFINITION EXEMPLES Moment cinétique DEFINITION VALEURS PROPRES ET FONCTIONS PROPRES Première description des atomes EQUATION DE SCHRÖDINGER MOMENT CINETIQUE INTRINSEQUE SPIN CLASSIFICATION DES ELEMENTS CHIMIQUES Dy + (E-V)y = 0 2 y 2 y 1 ^ 2 + - L y 2 r r r 2 h ^ ^ 2 et L commute avec L z énergie V(r) radial fonctions d’onde dans la base des fonctions propres yl, m 2 h 2 m 2(ryl, m) + (E-Vl(r)) yl, m = 0 2 r l = 0, 1, 2, … m = -l, -l+1, …, l-1, l l(l+1) h 2 Vl(r) = +V(r) 2 mr 2 potentiel central

GRANDEURS PHYSIQUES Opérateurs et observables ul(r) imj fonctions propres : yl, m(r, q, j) = P l, m(cosq)e r fonction normée polynôme de Legendre DEFINITION EXEMPLES Moment cinétique DEFINITION VALEURS PROPRES ET FONCTIONS PROPRES Première description des atomes EQUATION DE SCHRÖDINGER MOMENT CINETIQUE INTRINSEQUE SPIN CLASSIFICATION DES ELEMENTS CHIMIQUES 2 2 h d ul(r) + (E-Vl(r)) ul(r) = 0 2 2 m dr valeurs propres : spectre d’énergie En nombre quantique principal nombre quantique orbital : l = 0, 1, 2, …, n-1 nombre quantique azimutal : m = -l, -l+1, …, l-1, l

GRANDEURS PHYSIQUES Opérateurs et observables ^ S moment cinétique propre d’une particule DEFINITION EXEMPLES Moment cinétique DEFINITION ^ 2 y = j(j+1) S h 2 yj, m (j = 0, 1/2, 1 , 3/2, 2, …) ^ y = s y S h j, m z j, m (s = -j, -j+1, …, 0, …, j-1, j) VALEURS PROPRES ET FONCTIONS PROPRES Première description des atomes EQUATION DE SCHRÖDINGER bosons (photon, particule a, …) nombre quantique de spin fermions (électron, proton, …) MOMENT CINETIQUE INTRINSEQUE SPIN CLASSIFICATION DES ELEMENTS CHIMIQUES électron (j=1/2) : s = 1/2

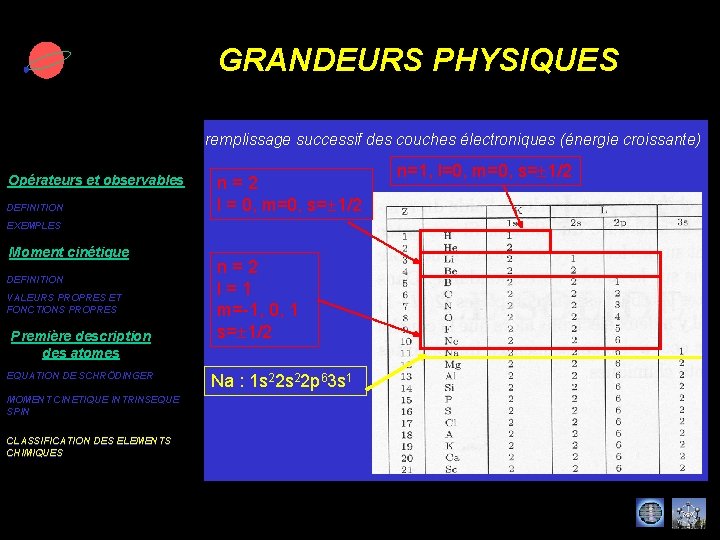
GRANDEURS PHYSIQUES remplissage successif des couches électroniques (énergie croissante) Opérateurs et observables DEFINITION n = 2 l = 0, m=0, s= 1/2 EXEMPLES Moment cinétique DEFINITION VALEURS PROPRES ET FONCTIONS PROPRES Première description des atomes EQUATION DE SCHRÖDINGER MOMENT CINETIQUE INTRINSEQUE SPIN CLASSIFICATION DES ELEMENTS CHIMIQUES n = 2 l = 1 m=-1, 0, 1 s= 1/2 Na : 1 s 22 p 63 s 1 n=1, l=0, m=0, s= 1/2

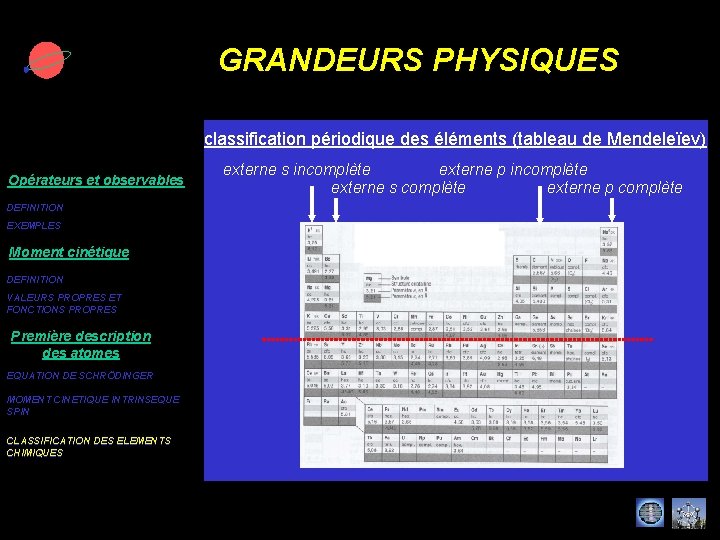
GRANDEURS PHYSIQUES classification périodique des éléments (tableau de Mendeleïev) Opérateurs et observables DEFINITION EXEMPLES Moment cinétique DEFINITION VALEURS PROPRES ET FONCTIONS PROPRES Première description des atomes EQUATION DE SCHRÖDINGER MOMENT CINETIQUE INTRINSEQUE SPIN CLASSIFICATION DES ELEMENTS CHIMIQUES externe s incomplète externe p incomplète externe s complète externe p complète

GRANDEURS PHYSIQUES Opérateurs et observables DEFINITION EXEMPLES Moment cinétique DEFINITION VALEURS PROPRES ET FONCTIONS PROPRES Première description des atomes EQUATION DE SCHRÖDINGER MOMENT CINETIQUE INTRINSEQUE SPIN CLASSIFICATION DES ELEMENTS CHIMIQUES

LE SOLIDE CRISTALLIN

L’électron Le solide cristallin Réseau cristallin PROPRIETES DES MATERIAUX SOLIDES R. Fortunier Électrons dans un solide

LE RESEAU CRISTALLIN Classification des structures RESEAU DE BRAVAIS MOTIF, RANGEES, PLANS ALLOTROPIE STRUCTURES NON CRISTALLINES Structures cristallines usuelles CHLORURE DE SODIUM CHLORURE DE CESIUM CUBIQUE A FACES CENTREES CUBIQUE CENTREE HEXAGONALE COMPACTE DIAMANT

LE RESEAU CRISTALLIN Généré par la translation d’un point M dans trois direction non coplanaires Classification des structures RESEAU DE BRAVAIS MOTIF, RANGEES, PLANS OP = OM + g avec g = u a + v b + w c ALLOTROPIE STRUCTURES NON CRISTALLINES Structures cristallines usuelles CHLORURE DE SODIUM CHLORURE DE CESIUM CUBIQUE A FACES CENTREES CUBIQUE CENTREE HEXAGONALE COMPACTE DIAMANT maille primitive

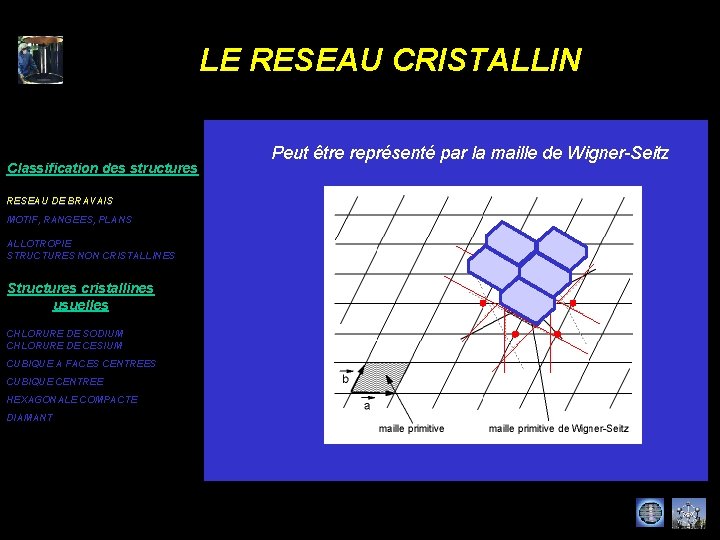
LE RESEAU CRISTALLIN Classification des structures RESEAU DE BRAVAIS MOTIF, RANGEES, PLANS ALLOTROPIE STRUCTURES NON CRISTALLINES Structures cristallines usuelles CHLORURE DE SODIUM CHLORURE DE CESIUM CUBIQUE A FACES CENTREES CUBIQUE CENTREE HEXAGONALE COMPACTE DIAMANT Peut être représenté par la maille de Wigner-Seitz

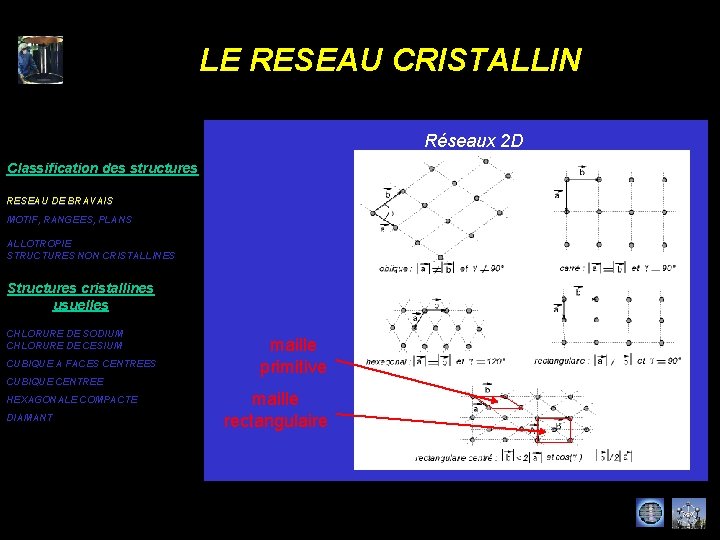
LE RESEAU CRISTALLIN Réseaux 2 D Classification des structures RESEAU DE BRAVAIS MOTIF, RANGEES, PLANS ALLOTROPIE STRUCTURES NON CRISTALLINES Structures cristallines usuelles CHLORURE DE SODIUM CHLORURE DE CESIUM CUBIQUE A FACES CENTREES CUBIQUE CENTREE HEXAGONALE COMPACTE DIAMANT maille primitive maille rectangulaire

LE RESEAU CRISTALLIN Classification des structures RESEAU DE BRAVAIS MOTIF, RANGEES, PLANS ALLOTROPIE STRUCTURES NON CRISTALLINES Structures cristallines usuelles CHLORURE DE SODIUM CHLORURE DE CESIUM CUBIQUE A FACES CENTREES CUBIQUE CENTREE HEXAGONALE COMPACTE DIAMANT Réseaux 3 D

LE RESEAU CRISTALLIN Cristal = réseau + motif Classification des structures RESEAU DE BRAVAIS MOTIF, RANGEES, PLANS ALLOTROPIE STRUCTURES NON CRISTALLINES Structures cristallines usuelles CHLORURE DE SODIUM CHLORURE DE CESIUM CUBIQUE A FACES CENTREES CUBIQUE CENTREE HEXAGONALE COMPACTE DIAMANT réseau motif

LE RESEAU CRISTALLIN Rangées et plans atomiques dans une structure cubique Classification des structures plans (h k l) rangées [u v w] RESEAU DE BRAVAIS MOTIF, RANGEES, PLANS ALLOTROPIE STRUCTURES NON CRISTALLINES Structures cristallines usuelles CHLORURE DE SODIUM CHLORURE DE CESIUM CUBIQUE A FACES CENTREES CUBIQUE CENTREE HEXAGONALE COMPACTE DIAMANT Distance inter-réticulaire dhkl ?

LE RESEAU CRISTALLIN Phases allotropiques Classification des structure cristalline = f(P, T) fera, ferg, ferd RESEAU DE BRAVAIS MOTIF, RANGEES, PLANS ALLOTROPIE STRUCTURES NON CRISTALLINES Structures cristallines usuelles Cristaux liquides nématiques, smectiques, cholestériques CHLORURE DE SODIUM CHLORURE DE CESIUM CUBIQUE A FACES CENTREES CUBIQUE CENTREE HEXAGONALE COMPACTE DIAMANT Matériaux amorphes pas de structure verres, solidification rapide

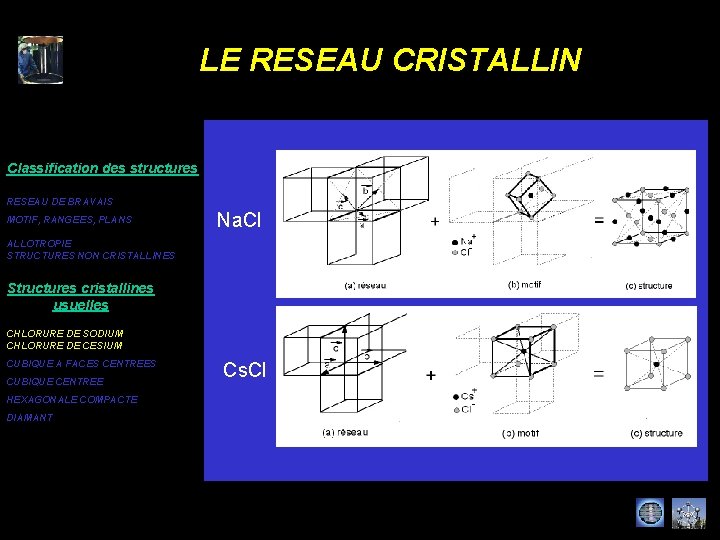
LE RESEAU CRISTALLIN Classification des structures RESEAU DE BRAVAIS MOTIF, RANGEES, PLANS Na. Cl ALLOTROPIE STRUCTURES NON CRISTALLINES Structures cristallines usuelles CHLORURE DE SODIUM CHLORURE DE CESIUM CUBIQUE A FACES CENTREES CUBIQUE CENTREE HEXAGONALE COMPACTE DIAMANT Cs. Cl

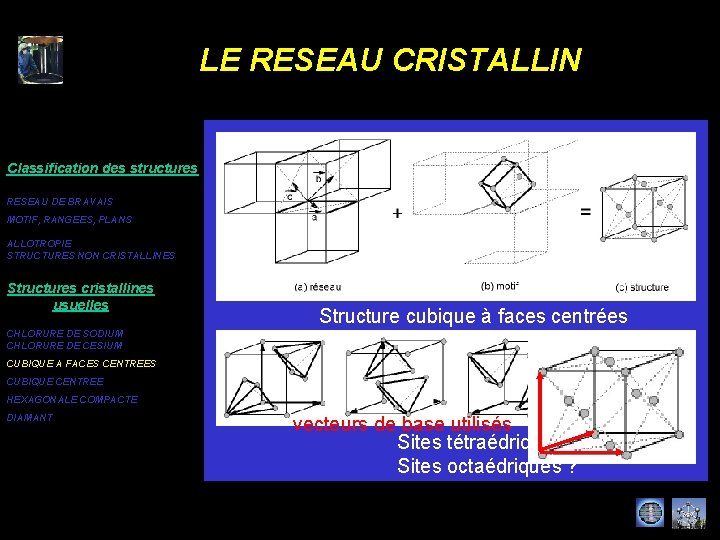
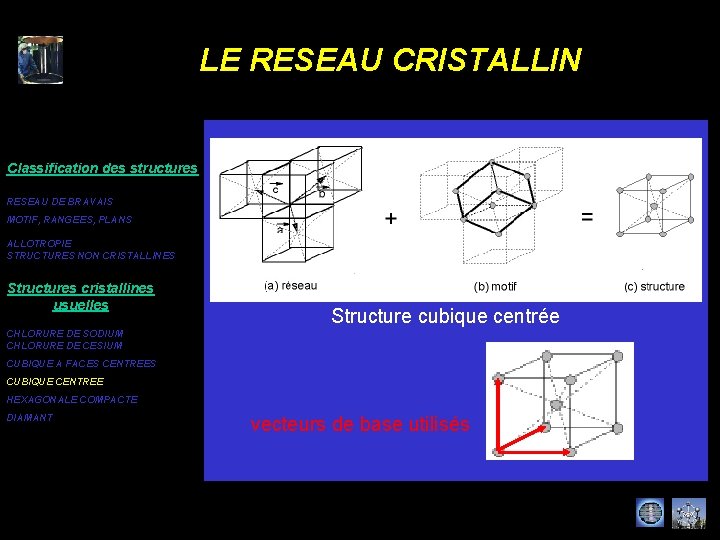
LE RESEAU CRISTALLIN Classification des structures RESEAU DE BRAVAIS MOTIF, RANGEES, PLANS ALLOTROPIE STRUCTURES NON CRISTALLINES Structures cristallines usuelles Structure cubique à faces centrées CHLORURE DE SODIUM CHLORURE DE CESIUM CUBIQUE A FACES CENTREES CUBIQUE CENTREE HEXAGONALE COMPACTE DIAMANT vecteurs de base utilisés Sites tétraédriques Sites octaédriques ?

LE RESEAU CRISTALLIN Classification des structures RESEAU DE BRAVAIS MOTIF, RANGEES, PLANS ALLOTROPIE STRUCTURES NON CRISTALLINES Structures cristallines usuelles Structure cubique centrée CHLORURE DE SODIUM CHLORURE DE CESIUM CUBIQUE A FACES CENTREES CUBIQUE CENTREE HEXAGONALE COMPACTE DIAMANT vecteurs de base utilisés

LE RESEAU CRISTALLIN Classification des structures RESEAU DE BRAVAIS MOTIF, RANGEES, PLANS ALLOTROPIE STRUCTURES NON CRISTALLINES Structures cristallines usuelles Structure hexagonale compacte CHLORURE DE SODIUM CHLORURE DE CESIUM CUBIQUE A FACES CENTREES CUBIQUE CENTREE HEXAGONALE COMPACTE DIAMANT système à quatre indices

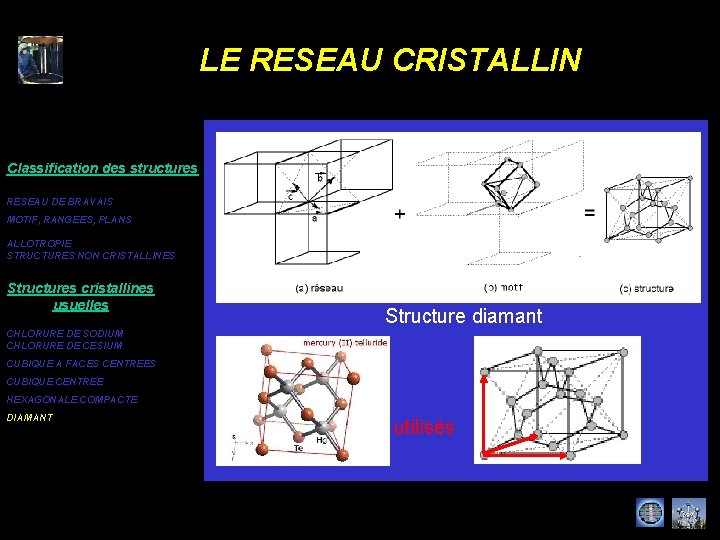
LE RESEAU CRISTALLIN Classification des structures RESEAU DE BRAVAIS MOTIF, RANGEES, PLANS ALLOTROPIE STRUCTURES NON CRISTALLINES Structures cristallines usuelles Structure diamant CHLORURE DE SODIUM CHLORURE DE CESIUM CUBIQUE A FACES CENTREES CUBIQUE CENTREE HEXAGONALE COMPACTE DIAMANT vecteurs de base utilisés

LE RESEAU CRISTALLIN Classification des structures RESEAU DE BRAVAIS MOTIF, RANGEES, PLANS ALLOTROPIE STRUCTURES NON CRISTALLINES Structures cristallines usuelles CHLORURE DE SODIUM CHLORURE DE CESIUM CUBIQUE A FACES CENTREES CUBIQUE CENTREE HEXAGONALE COMPACTE DIAMANT

L’électron Le solide cristallin Interaction onde-réseau PROPRIETES DES MATERIAUX SOLIDES R. Fortunier Électrons dans un solide

INTERACTION ONDE-RESEAU Modélisation de l’interaction LOI DE BRAGG RESEAU RECIPROQUE LOI DE BRAGG GENERALISEE Effets de structure ZONES DE BRILLOUIN FACTEUR DE STRUCTURE

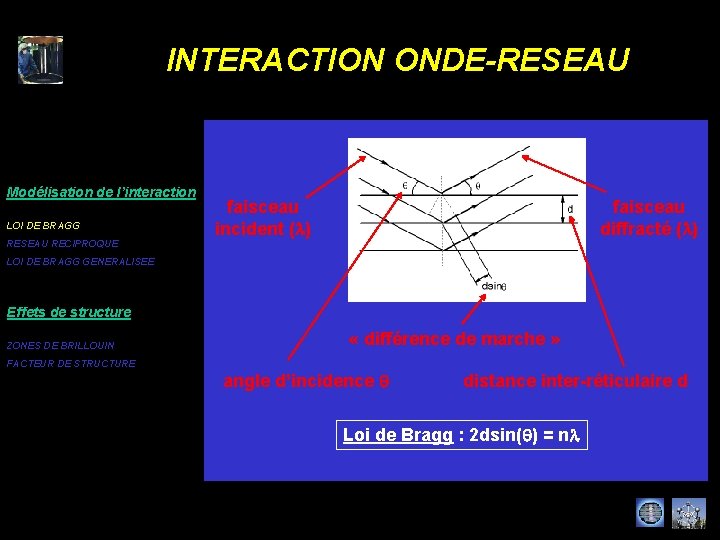
INTERACTION ONDE-RESEAU Modélisation de l’interaction LOI DE BRAGG RESEAU RECIPROQUE faisceau diffracté (l) faisceau incident (l) LOI DE BRAGG GENERALISEE Effets de structure ZONES DE BRILLOUIN « différence de marche » FACTEUR DE STRUCTURE angle d’incidence q distance inter-réticulaire d Loi de Bragg : 2 dsin(q) = nl

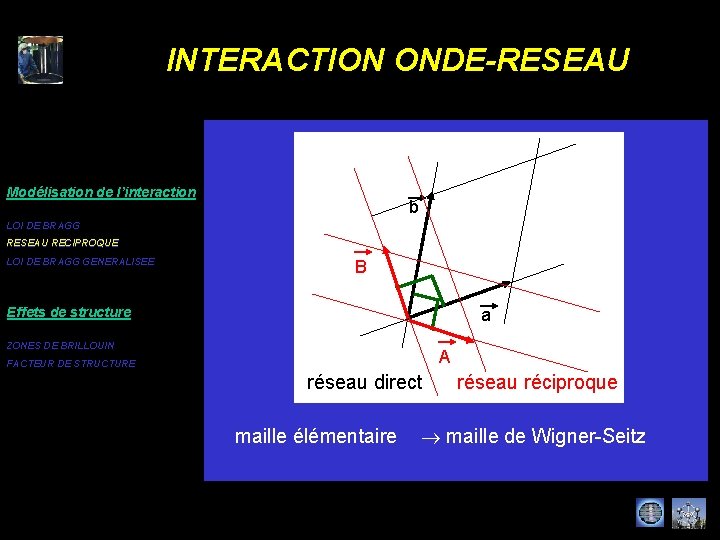
INTERACTION ONDE-RESEAU Modélisation de l’interaction b LOI DE BRAGG RESEAU RECIPROQUE LOI DE BRAGG GENERALISEE B Effets de structure a ZONES DE BRILLOUIN A FACTEUR DE STRUCTURE réseau direct maille élémentaire réseau réciproque maille de Wigner-Seitz

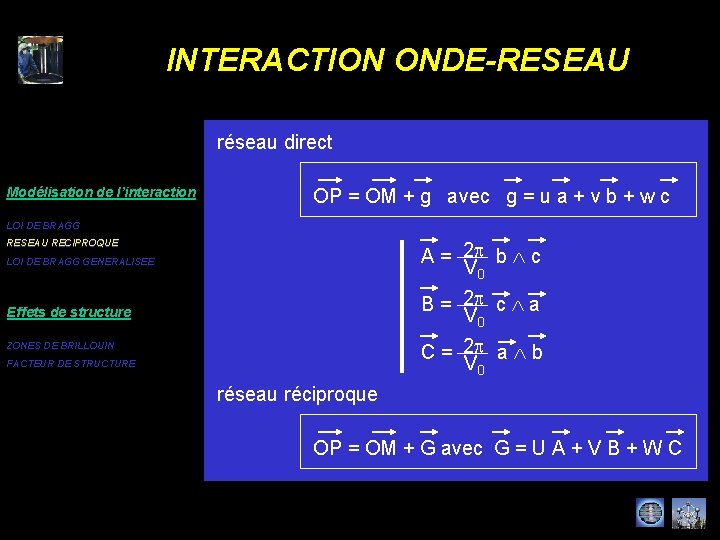
INTERACTION ONDE-RESEAU réseau direct Modélisation de l’interaction OP = OM + g avec g = u a + v b + w c LOI DE BRAGG RESEAU RECIPROQUE LOI DE BRAGG GENERALISEE 2 p A = b c V 0 Effets de structure 2 p B = c a V 0 2 p C = a b V 0 ZONES DE BRILLOUIN FACTEUR DE STRUCTURE réseau réciproque OP = OM + G avec G = U A + V B + W C

INTERACTION ONDE-RESEAU réseau cubique centré Modélisation de l’interaction LOI DE BRAGG RESEAU RECIPROQUE LOI DE BRAGG GENERALISEE Effets de structure ZONES DE BRILLOUIN FACTEUR DE STRUCTURE

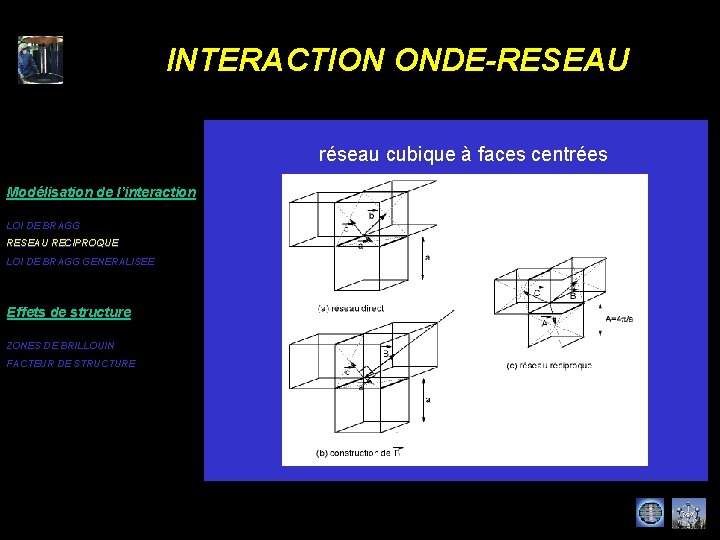
INTERACTION ONDE-RESEAU réseau cubique à faces centrées Modélisation de l’interaction LOI DE BRAGG RESEAU RECIPROQUE LOI DE BRAGG GENERALISEE Effets de structure ZONES DE BRILLOUIN FACTEUR DE STRUCTURE

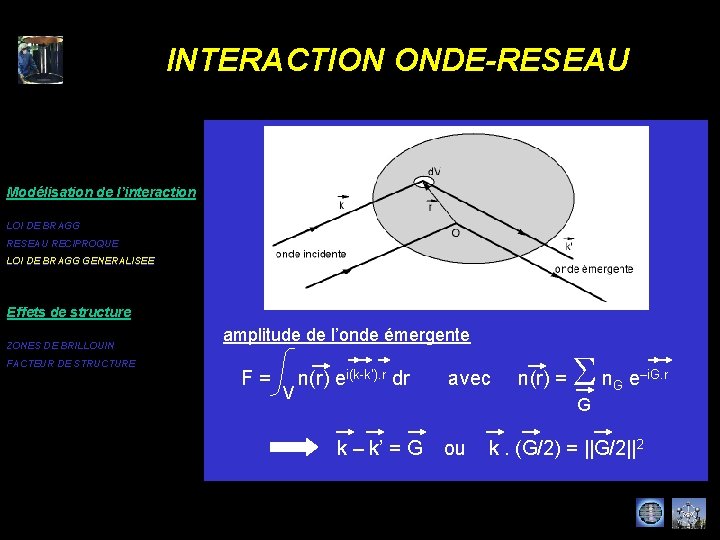
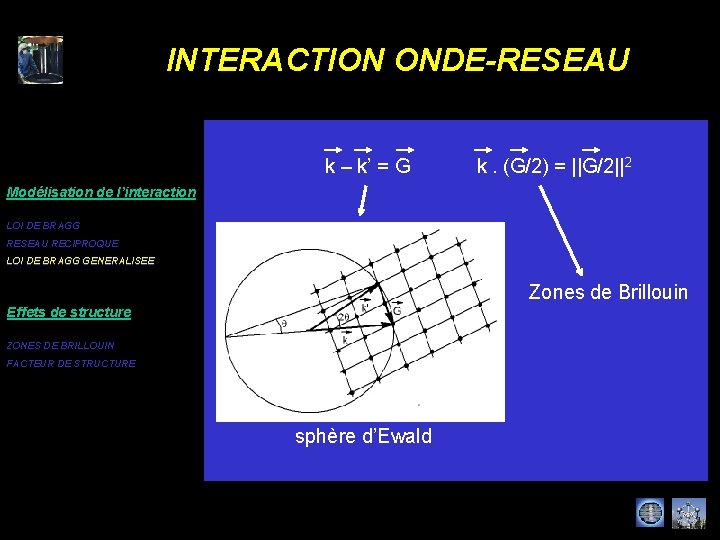
INTERACTION ONDE-RESEAU Modélisation de l’interaction LOI DE BRAGG RESEAU RECIPROQUE LOI DE BRAGG GENERALISEE Effets de structure ZONES DE BRILLOUIN FACTEUR DE STRUCTURE amplitude de l’onde émergente F = n(r) ei(k-k’). r dr avec n(r) = V S n e G –i. G. r G k – k’ = G ou k. (G/2) = ||G/2||2

INTERACTION ONDE-RESEAU k – k’ = G k. (G/2) = ||G/2||2 Modélisation de l’interaction LOI DE BRAGG RESEAU RECIPROQUE LOI DE BRAGG GENERALISEE Zones de Brillouin Effets de structure ZONES DE BRILLOUIN FACTEUR DE STRUCTURE sphère d’Ewald

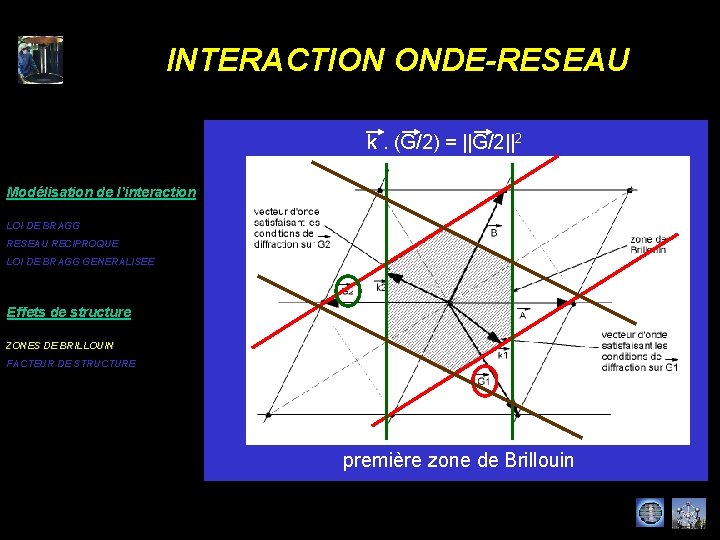
INTERACTION ONDE-RESEAU k. (G/2) = ||G/2||2 Modélisation de l’interaction LOI DE BRAGG RESEAU RECIPROQUE LOI DE BRAGG GENERALISEE Effets de structure ZONES DE BRILLOUIN FACTEUR DE STRUCTURE première zone de Brillouin

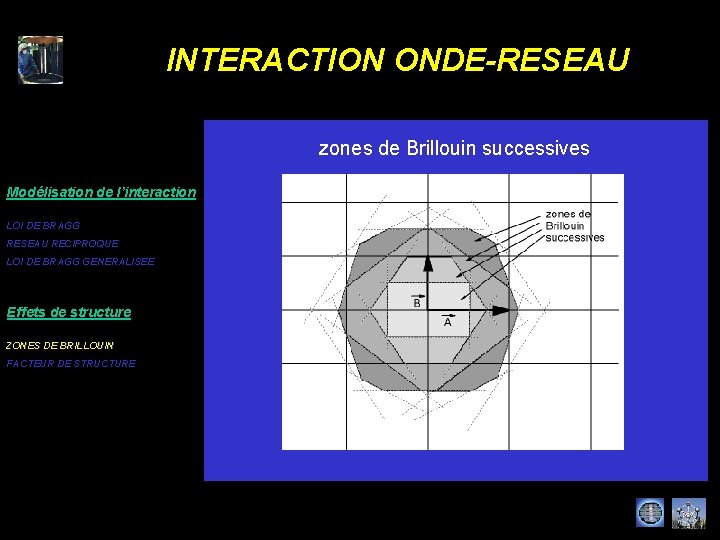
INTERACTION ONDE-RESEAU zones de Brillouin successives Modélisation de l’interaction LOI DE BRAGG RESEAU RECIPROQUE LOI DE BRAGG GENERALISEE Effets de structure ZONES DE BRILLOUIN FACTEUR DE STRUCTURE

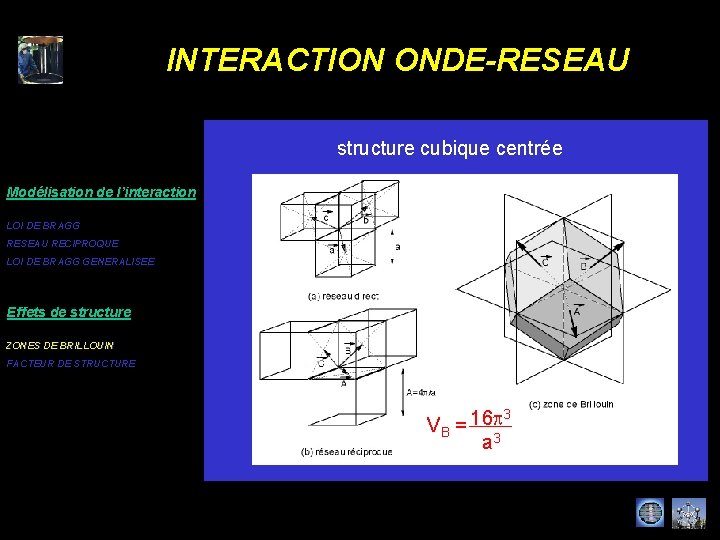
INTERACTION ONDE-RESEAU structure cubique centrée Modélisation de l’interaction LOI DE BRAGG RESEAU RECIPROQUE LOI DE BRAGG GENERALISEE Effets de structure ZONES DE BRILLOUIN FACTEUR DE STRUCTURE VB = 16 p a 3 3

INTERACTION ONDE-RESEAU structure cubique à faces centrées Modélisation de l’interaction LOI DE BRAGG RESEAU RECIPROQUE LOI DE BRAGG GENERALISEE Effets de structure ZONES DE BRILLOUIN FACTEUR DE STRUCTURE VB = 32 p a 3 3

INTERACTION ONDE-RESEAU amplitude de l’onde émergente Modélisation de l’interaction F = n(r) ei. G. r dr = N n(r) ei. G. r dr V V 0 LOI DE BRAGG RESEAU RECIPROQUE facteur de structure LOI DE BRAGG GENERALISEE Effets de structure SG = n(r) ei. G. r dr V 0 ZONES DE BRILLOUIN FACTEUR DE STRUCTURE S(h, k, l) = n(r) = S n (r-r ) j S f exp(i 2 p(hu +kv +lw ) j facteur de forme atomique j j

INTERACTION ONDE-RESEAU atomes identiques dans le motif : Modélisation de l’interaction S(h, k, l) = f S exp(i 2 p(hu +kv +lw ) j j j LOI DE BRAGG RESEAU RECIPROQUE LOI DE BRAGG GENERALISEE Effets de structure ZONES DE BRILLOUIN FACTEUR DE STRUCTURE S(h, k, l) = f (1+eip(h+k+l)) S(h, k, l) = f (1+eip(h+k) +eip(k+l) +eip(h+l))

INTERACTION ONDE-RESEAU Modélisation de l’interaction LOI DE BRAGG RESEAU RECIPROQUE LOI DE BRAGG GENERALISEE Effets de structure ZONES DE BRILLOUIN FACTEUR DE STRUCTURE

L’électron Le solide cristallin Liaisons cristallines PROPRIETES DES MATERIAUX SOLIDES R. Fortunier Électrons dans un solide

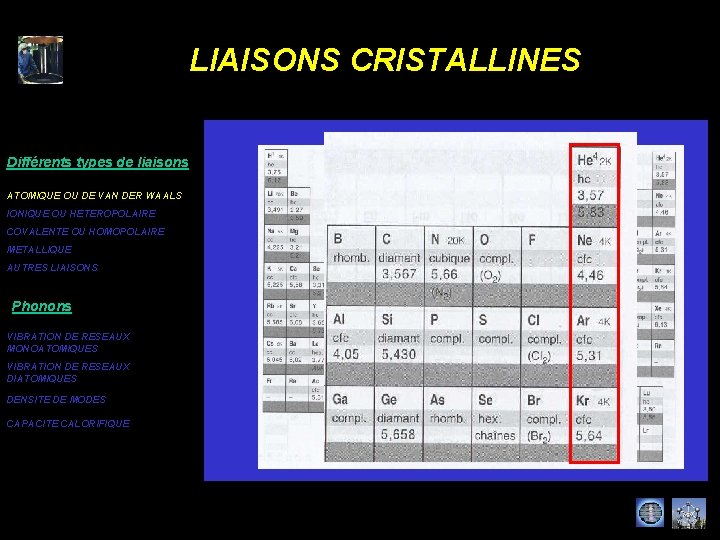
LIAISONS CRISTALLINES Différents types de liaisons ATOMIQUE OU DE VAN DER WAALS IONIQUE OU HETEROPOLAIRE COVALENTE OU HOMOPOLAIRE METALLIQUE AUTRES LIAISONS Phonons VIBRATION DE RESEAUX MONOATOMIQUES VIBRATION DE RESEAUX DIATOMIQUES DENSITE DE MODES CAPACITE CALORIFIQUE

LIAISONS CRISTALLINES Différents types de liaisons ATOMIQUE OU DE VAN DER WAALS atome = dipôle IONIQUE OU HETEROPOLAIRE COVALENTE OU HOMOPOLAIRE METALLIQUE AUTRES LIAISONS Phonons énergie du système sans interaction : ħw 0 énergie du système avec interaction : ħw 0(1 -(e 2/4 Cr 3)2) VIBRATION DE RESEAUX MONOATOMIQUES VIBRATION DE RESEAUX DIATOMIQUES énergie d’attraction de van der Waals : U = -ħw 0(e 2/4 Cr 3)2 DENSITE DE MODES CAPACITE CALORIFIQUE U = -A/r 6

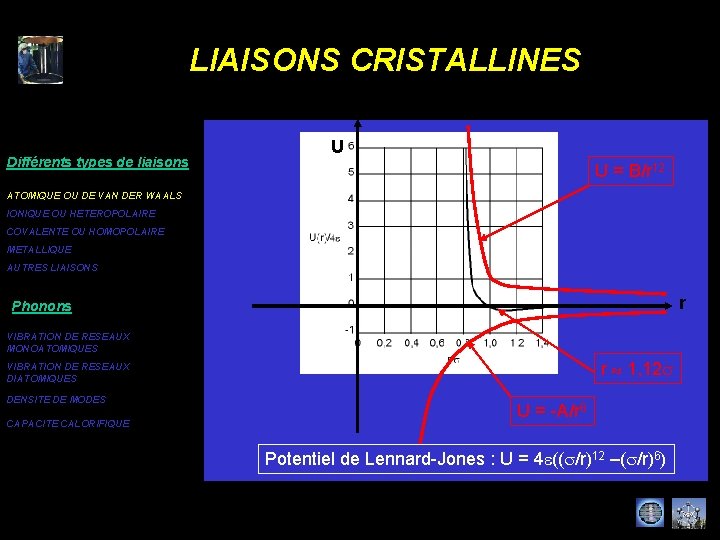
LIAISONS CRISTALLINES Différents types de liaisons U U = B/r 12 ATOMIQUE OU DE VAN DER WAALS IONIQUE OU HETEROPOLAIRE COVALENTE OU HOMOPOLAIRE METALLIQUE AUTRES LIAISONS r Phonons VIBRATION DE RESEAUX MONOATOMIQUES r 1, 12 s VIBRATION DE RESEAUX DIATOMIQUES DENSITE DE MODES CAPACITE CALORIFIQUE U = -A/r 6 Potentiel de Lennard-Jones : U = 4 e((s/r)12 –(s/r)6)

LIAISONS CRISTALLINES Différents types de liaisons ATOMIQUE OU DE VAN DER WAALS IONIQUE OU HETEROPOLAIRE COVALENTE OU HOMOPOLAIRE METALLIQUE AUTRES LIAISONS Phonons VIBRATION DE RESEAUX MONOATOMIQUES VIBRATION DE RESEAUX DIATOMIQUES DENSITE DE MODES CAPACITE CALORIFIQUE

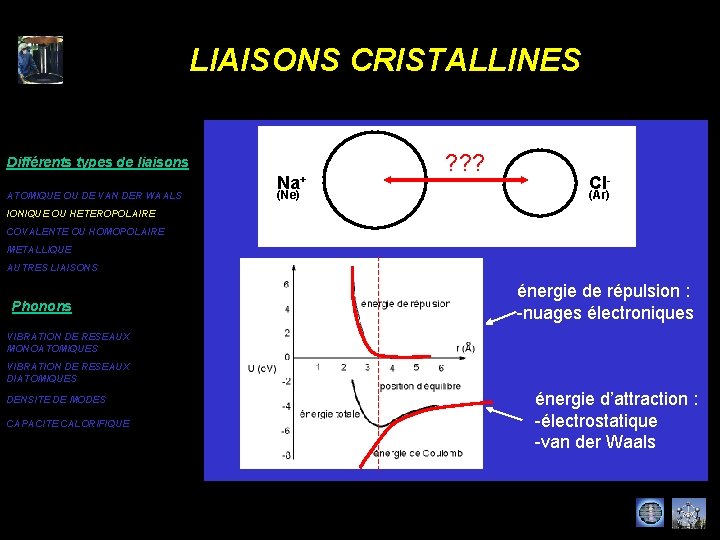
LIAISONS CRISTALLINES Différents types de liaisons ATOMIQUE OU DE VAN DER WAALS Na+ (Ne) ? ? ? Cl(Ar) IONIQUE OU HETEROPOLAIRE COVALENTE OU HOMOPOLAIRE METALLIQUE AUTRES LIAISONS Phonons énergie de répulsion : -nuages électroniques VIBRATION DE RESEAUX MONOATOMIQUES VIBRATION DE RESEAUX DIATOMIQUES DENSITE DE MODES CAPACITE CALORIFIQUE énergie d’attraction : -électrostatique -van der Waals

LIAISONS CRISTALLINES Différents types de liaisons ATOMIQUE OU DE VAN DER WAALS IONIQUE OU HETEROPOLAIRE COVALENTE OU HOMOPOLAIRE METALLIQUE AUTRES LIAISONS Phonons VIBRATION DE RESEAUX MONOATOMIQUES VIBRATION DE RESEAUX DIATOMIQUES DENSITE DE MODES CAPACITE CALORIFIQUE

LIAISONS CRISTALLINES Différents types de liaisons Recouvrement d’orbitales par mise en commun d’électrons : HYBRIDATION ATOMIQUE OU DE VAN DER WAALS IONIQUE OU HETEROPOLAIRE COVALENTE OU HOMOPOLAIRE METALLIQUE grande cohésion, grande stabilité, liaisons directionnelles AUTRES LIAISONS Phonons VIBRATION DE RESEAUX MONOATOMIQUES VIBRATION DE RESEAUX DIATOMIQUES DENSITE DE MODES CAPACITE CALORIFIQUE Molécules (Cl 2, H 2, …) Structures 3 D (Si, C, …) Structures planaires (P, …) Structures filamentaires (Se, Te)

COVALENTE OU HOMOPOLAIRE EN T IONIQUE OU HETEROPOLAIRE VA LE ATOMIQUE OU DE VAN DER WAALS METALLIQUE CAPACITE CALORIFIQUE OV O-C E IQU DENSITE DE MODES ION VIBRATION DE RESEAUX DIATOMIQUES ION VIBRATION DE RESEAUX MONOATOMIQUES Composés III-V AL AUTRES LIAISONS Phonons Type IV CO Différents types de liaisons NT LIAISONS CRISTALLINES Composés II-VI

LIAISONS CRISTALLINES Certains électrons n’appartiennent plus à un atome déterminé, mais sont répartis dans tout le cristal Différents types de liaisons ATOMIQUE OU DE VAN DER WAALS IONIQUE OU HETEROPOLAIRE COVALENTE OU HOMOPOLAIRE METALLIQUE AUTRES LIAISONS électrons délocalisés, servant de transport (charge, chaleur, …) Na+ e- Phonons VIBRATION DE RESEAUX MONOATOMIQUES VIBRATION DE RESEAUX DIATOMIQUES Na+ e- e- e. Na+ ee- DENSITE DE MODES CAPACITE CALORIFIQUE Na+ Na ee+ U(Na+, Na+)+U(e-, e-)+U(Na+, e-)<0 du fait du déplacement libre des électrons GAZ D’ELECTRON Na+ Cas du sodium (Na) propriétés des métaux : -bonne conductivité - pouvoir réflecteur dans le visible - déformations importantes

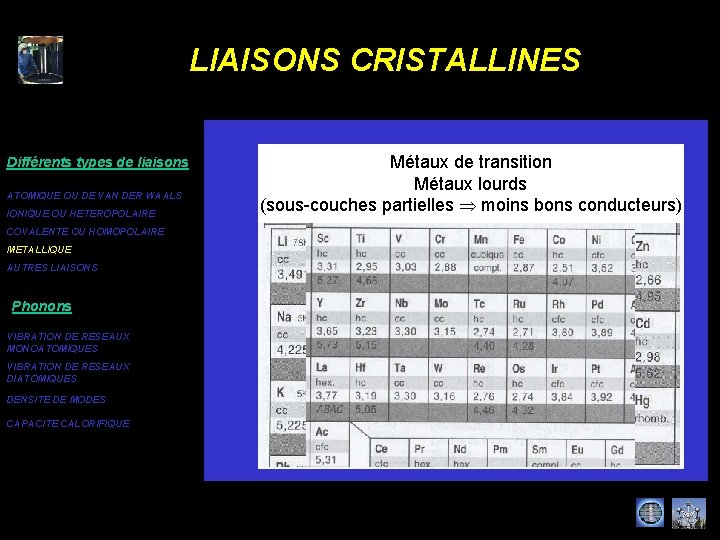
LIAISONS CRISTALLINES Différents types de liaisons ATOMIQUE OU DE VAN DER WAALS IONIQUE OU HETEROPOLAIRE COVALENTE OU HOMOPOLAIRE METALLIQUE AUTRES LIAISONS Phonons VIBRATION DE RESEAUX MONOATOMIQUES VIBRATION DE RESEAUX DIATOMIQUES DENSITE DE MODES CAPACITE CALORIFIQUE Alcalins IA, alcalino-terreux IIA Métaux de transition Métaux nobles IB, métaux IIB Métaux lourds (sous-couches partielles moins bons conducteurs) (électrons très délocalisés bons conducteurs)

LIAISONS CRISTALLINES Différents types de liaisons Nombreux autres types de liaisons (combinaisons de liaisons covalentes, ioniques, …) ATOMIQUE OU DE VAN DER WAALS IONIQUE OU HETEROPOLAIRE COVALENTE OU HOMOPOLAIRE Exemple : la liaison hydrogène METALLIQUE AUTRES LIAISONS H+ Phonons VIBRATION DE RESEAUX MONOATOMIQUES H+ O-- VIBRATION DE RESEAUX DIATOMIQUES DENSITE DE MODES CAPACITE CALORIFIQUE O-- H+ H+

LIAISONS CRISTALLINES Différents types de liaisons ATOMIQUE OU DE VAN DER WAALS IONIQUE OU HETEROPOLAIRE COVALENTE OU HOMOPOLAIRE plans cristallographiques s s+1 m : masse de l’atome du réseau (monoatomique) METALLIQUE AUTRES LIAISONS Phonons VIBRATION DE RESEAUX MONOATOMIQUES VIBRATION DE RESEAUX DIATOMIQUES DENSITE DE MODES force exercée sur le plan s : Fs = - C(us-us-1) + C(us+1 -us) comportement mécanique : Fs = md 2 us/dt 2 = C(us+1 -2 us +us-1) la solution est une onde élastique CAPACITE CALORIFIQUE us = u ei(kd-wt) avec w 2 = 2(C/m) (1 -cos(kd))

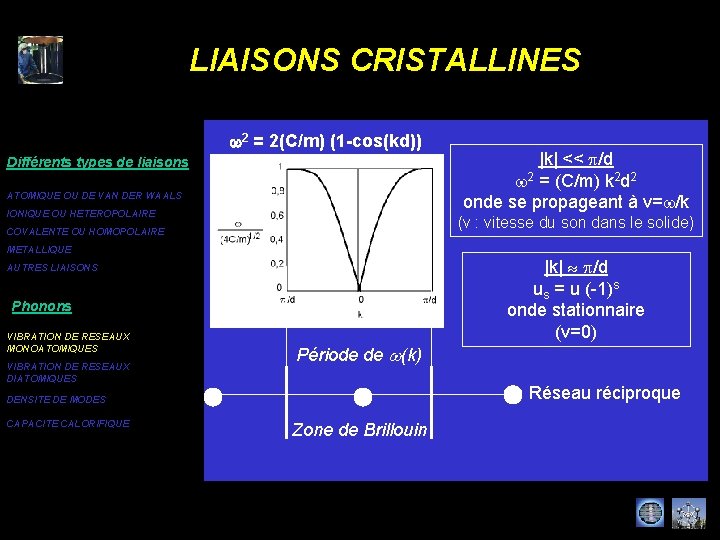
LIAISONS CRISTALLINES w 2 = 2(C/m) (1 -cos(kd)) Différents types de liaisons ATOMIQUE OU DE VAN DER WAALS IONIQUE OU HETEROPOLAIRE |k| << p/d w 2 = (C/m) k 2 d 2 onde se propageant à v=w/k (v : vitesse du son dans le solide) COVALENTE OU HOMOPOLAIRE METALLIQUE |k| p/d us = u (-1)s onde stationnaire (v=0) AUTRES LIAISONS Phonons VIBRATION DE RESEAUX MONOATOMIQUES VIBRATION DE RESEAUX DIATOMIQUES Période de w(k) Réseau réciproque DENSITE DE MODES CAPACITE CALORIFIQUE Zone de Brillouin

LIAISONS CRISTALLINES Différents types de liaisons ATOMIQUE OU DE VAN DER WAALS IONIQUE OU HETEROPOLAIRE COVALENTE OU HOMOPOLAIRE METALLIQUE AUTRES LIAISONS Phonons VIBRATION DE RESEAUX MONOATOMIQUES VIBRATION DE RESEAUX DIATOMIQUES DENSITE DE MODES CAPACITE CALORIFIQUE plans cristallographiques s s+1 m 1 : masse de l’atome 1 du réseau m 2 : masse de l’atome 2 du réseau m 1 d 2 us/dt 2 = C(us+1 -2 us +us-1) m 2 d 2 vs/dt 2 = C(vs+1 – 2 vs +vs-1) les solutions us et vs sont des ondes élastiques us = u ei(kd-wt) et vs = v ei(kd-wt) w 2 = C(1/m 1+1/m 2) [1±(1 -2 m 1 m 2/(m 1+m 2)2(1 -coskd))1/2]

LIAISONS CRISTALLINES Différents types de liaisons ATOMIQUE OU DE VAN DER WAALS IONIQUE OU HETEROPOLAIRE COVALENTE OU HOMOPOLAIRE Bande interdite METALLIQUE AUTRES LIAISONS Na. Cl Si Phonons VIBRATION DE RESEAUX MONOATOMIQUES VIBRATION DE RESEAUX DIATOMIQUES Zone de Brillouin DENSITE DE MODES CAPACITE CALORIFIQUE w 2 = C(1/m 1+1/m 2) [1±(1 -2 m 1 m 2/(m 1+m 2)2(1 -coskd))1/2] RELATIONS DE DISPERSION : w(k)

LIAISONS CRISTALLINES Différents types de liaisons ATOMIQUE OU DE VAN DER WAALS IONIQUE OU HETEROPOLAIRE COVALENTE OU HOMOPOLAIRE METALLIQUE AUTRES LIAISONS Phonons VIBRATION DE RESEAUX MONOATOMIQUES Onde électromagnétique : photon d’énergie E=ħw Onde élastique us = u ei(kd-wt) : phonon d’énergie E= ħw n phonons de fréquence w : énergie En = (n+1/2) ħw (oscillateurs harmoniques) D(w) : nombre de modes de vibration entre w et w+dw N(k) : nombre de modes de vecteur d’onde de norme < k VIBRATION DE RESEAUX DIATOMIQUES DENSITE DE MODES CAPACITE CALORIFIQUE D(w) = d. N/dw = d. N/dk. dk/dw

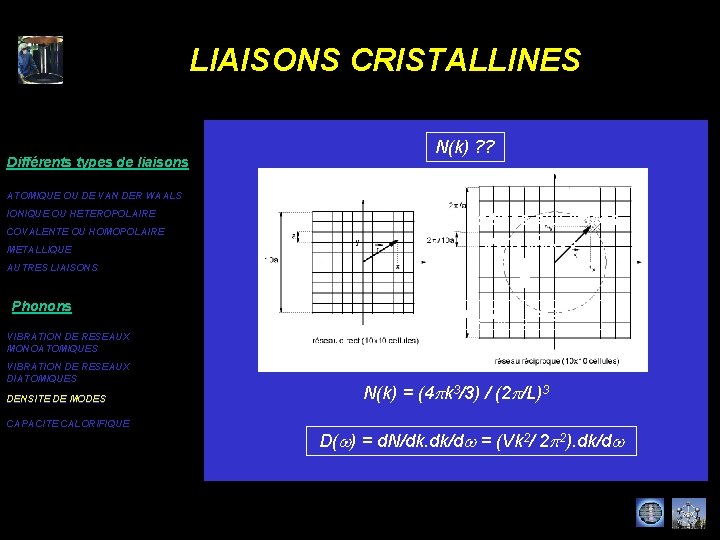
LIAISONS CRISTALLINES Différents types de liaisons N(k) ? ? ATOMIQUE OU DE VAN DER WAALS IONIQUE OU HETEROPOLAIRE COVALENTE OU HOMOPOLAIRE METALLIQUE Conditions aux limites périodiques AUTRES LIAISONS Phonons kx, ky, kz = 2 np/L VIBRATION DE RESEAUX MONOATOMIQUES VIBRATION DE RESEAUX DIATOMIQUES DENSITE DE MODES CAPACITE CALORIFIQUE N(k) = (4 pk 3/3) / (2 p/L)3 D(w) = d. N/dk. dk/dw = (Vk 2/ 2 p 2). dk/dw

LIAISONS CRISTALLINES Différents types de liaisons énergie interne d’un cristal excitée par des phonons : U = 3 ħw n(w) D(w) dw ATOMIQUE OU DE VAN DER WAALS IONIQUE OU HETEROPOLAIRE COVALENTE OU HOMOPOLAIRE METALLIQUE AUTRES LIAISONS Phonons VIBRATION DE RESEAUX MONOATOMIQUES VIBRATION DE RESEAUX DIATOMIQUES DENSITE DE MODES CAPACITE CALORIFIQUE trois directions de vibration énergie d’un phonon nombre quantique moyen des phonons dans un mode densité de modes Capacité calorifique d’un cristal : Cv = ( U / T)V

LIAISONS CRISTALLINES n(w) ? ? ? Différents types de liaisons ATOMIQUE OU DE VAN DER WAALS IONIQUE OU HETEROPOLAIRE COVALENTE OU HOMOPOLAIRE Relation de Boltzmann Le rapport entre le nombre d’oscillateurs dans l’état quantique p+1 et le nombre d’oscillateurs dans l’état quantique p est exp(- ħw/k. BT) METALLIQUE AUTRES LIAISONS Phonons VIBRATION DE RESEAUX MONOATOMIQUES VIBRATION DE RESEAUX DIATOMIQUES DENSITE DE MODES CAPACITE CALORIFIQUE ħw : saut d’énergie entre deux états quantiques successifs nombre relatif d’oscillateurs dans l’état p : ap = exp(-pħw/k. BT) / Sexp(-qħw/k. BT) nombre quantique moyen d’un oscillateur : S n(w) = p ap = … = 1 / (exp(ħw/k. BT) – 1) Distribution de Planck

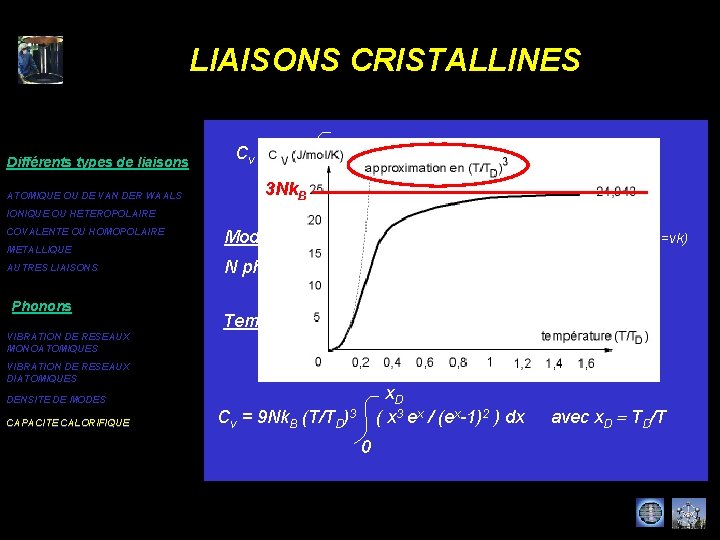
LIAISONS CRISTALLINES Différents types de liaisons Cv = 3 k. B ( t 2 et / (et-1)2 ) D(w) dw avec t = ħw/k. BT ATOMIQUE OU DE VAN DER WAALS D(w) ? ? ? IONIQUE OU HETEROPOLAIRE COVALENTE OU HOMOPOLAIRE METALLIQUE Modèle d’Einstein : D(w) =Ndw (un seul mode w possible) AUTRES LIAISONS Phonons VIBRATION DE RESEAUX MONOATOMIQUES VIBRATION DE RESEAUX DIATOMIQUES DENSITE DE MODES CAPACITE CALORIFIQUE Cv = 3 Nk. B t 2 et / (et-1)2 avec t = ħw/k. BT Plutôt valable à haute température (règle de Dulong et Petit) Cv = 3 Nk. B

LIAISONS CRISTALLINES Différents types de liaisons ATOMIQUE OU DE VAN DER WAALS Cv = 3 k. B ( t 2 et / (et-1)2 ) D(w) dw avec t = ħw/k. BT 3 Nk. B D(w) ? ? ? IONIQUE OU HETEROPOLAIRE COVALENTE OU HOMOPOLAIRE METALLIQUE AUTRES LIAISONS Phonons VIBRATION DE RESEAUX MONOATOMIQUES VIBRATION DE RESEAUX DIATOMIQUES DENSITE DE MODES CAPACITE CALORIFIQUE Modèle de Debye D(w) = Vw 2 / 2 pv 3 (courbe de dispersion w=vk) N phonons acoustiques k k. D=(6 p 2 N/V)1/3 w w. D=v(6 p 2 N/V)1/3 Température de Debye : TD= ħw. D/k. B x. D Cv = 9 Nk. B (T/TD)3 ( x 3 ex / (ex-1)2 ) dx 0 avec x. D = TD/T

LIAISONS CRISTALLINES

L’électron Le solide cristallin Défauts dans les cristaux PROPRIETES DES MATERIAUX SOLIDES R. Fortunier Électrons dans un solide

DEFAUTS DANS LES CRISTAUX Défauts ponctuels ENERGIE DE FORMATION CENTRES F MECANISMES DE DIFFUSION Dislocations LIMITE D’ELASTICITE DES METAUX DIFFERENTS TYPES

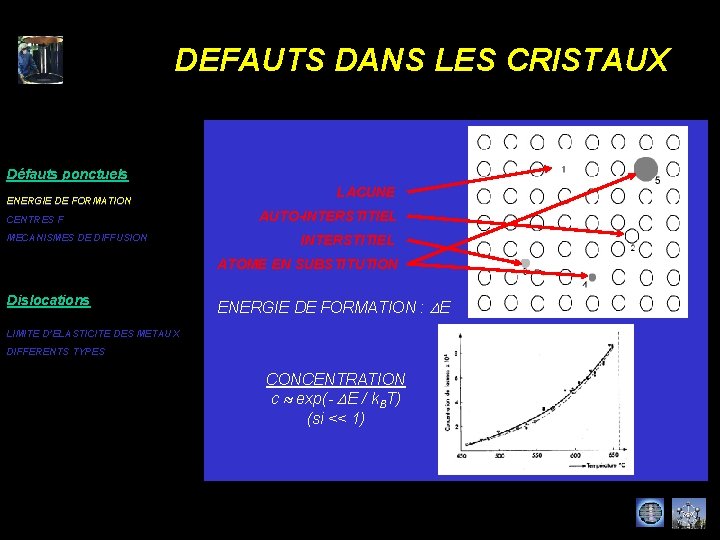
DEFAUTS DANS LES CRISTAUX Défauts ponctuels ENERGIE DE FORMATION CENTRES F MECANISMES DE DIFFUSION LACUNE AUTO-INTERSTITIEL ATOME EN SUBSTITUTION Dislocations ENERGIE DE FORMATION : DE LIMITE D’ELASTICITE DES METAUX DIFFERENTS TYPES CONCENTRATION c exp(- DE / k. BT) (si << 1)

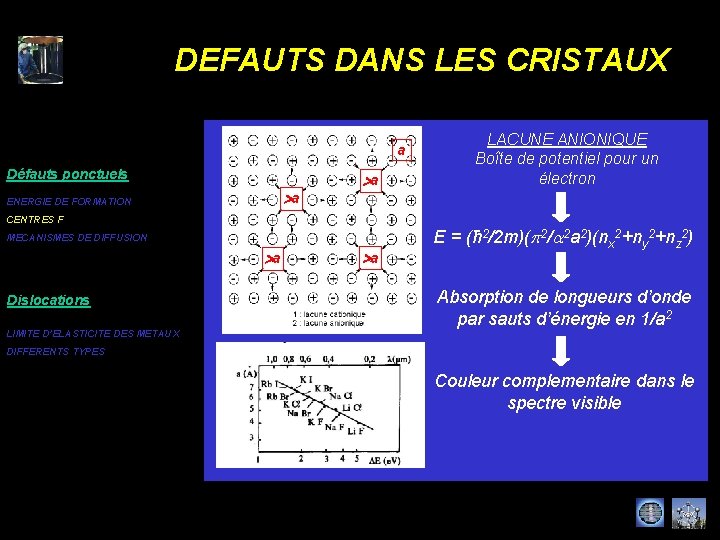
DEFAUTS DANS LES CRISTAUX a Défauts ponctuels >a ENERGIE DE FORMATION >a CENTRES F MECANISMES DE DIFFUSION >a Dislocations LIMITE D’ELASTICITE DES METAUX >a LACUNE ANIONIQUE Boîte de potentiel pour un électron E = (ħ 2/2 m)(p 2/a 2 a 2)(nx 2+ny 2+nz 2) Absorption de longueurs d’onde par sauts d’énergie en 1/a 2 DIFFERENTS TYPES Couleur complementaire dans le spectre visible

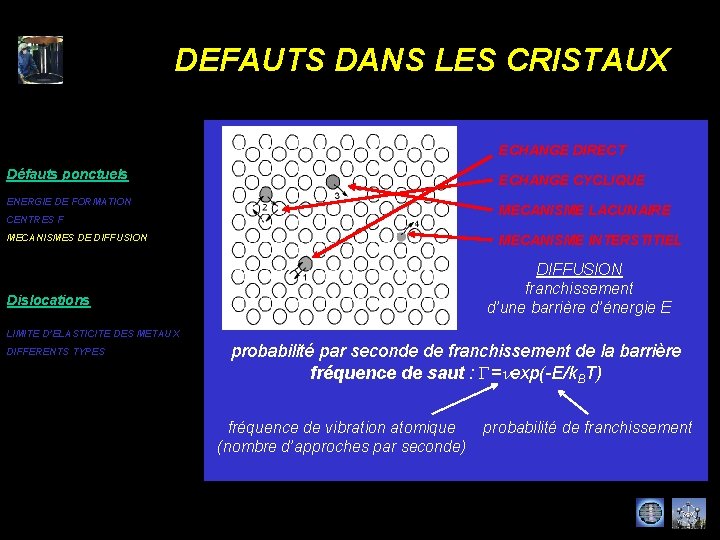
DEFAUTS DANS LES CRISTAUX ECHANGE DIRECT Défauts ponctuels ECHANGE CYCLIQUE ENERGIE DE FORMATION MECANISME LACUNAIRE CENTRES F MECANISMES DE DIFFUSION MECANISME INTERSTITIEL DIFFUSION franchissement d’une barrière d’énergie E Dislocations LIMITE D’ELASTICITE DES METAUX DIFFERENTS TYPES probabilité par seconde de franchissement de la barrière fréquence de saut : G=nexp(-E/k. BT) fréquence de vibration atomique (nombre d’approches par seconde) probabilité de franchissement

DEFAUTS DANS LES CRISTAUX Défauts ponctuels a ENERGIE DE FORMATION x CENTRES F MECANISMES DE DIFFUSION Dislocations LIMITE D’ELASTICITE DES METAUX DIFFERENTS TYPES S atomes d’impureté dans un plan (concentration c=S/a) S + a d. S/dx atomes d’impureté dans le plan suivant - G a d. S/dx atomes passent d’un plan à l’autre par seconde Flux J=- G a 2 dc/dx = -D dc/dx avec D=na 2 exp(-E/k. BT)

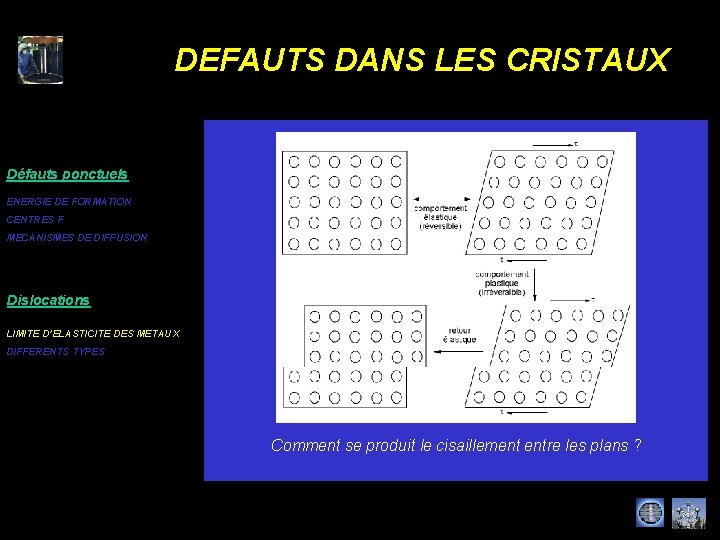
DEFAUTS DANS LES CRISTAUX Défauts ponctuels ENERGIE DE FORMATION CENTRES F MECANISMES DE DIFFUSION Dislocations LIMITE D’ELASTICITE DES METAUX DIFFERENTS TYPES Comment se produit le cisaillement entre les plans ?

DEFAUTS DANS LES CRISTAUX t Défauts ponctuels ENERGIE DE FORMATION CENTRES F MECANISMES DE DIFFUSION t 0 g = u/a t = t 0 sin(2 pu/a) u Dislocations Calcul approché t = mg = mu/a t = t 0 sin(2 pu/a) t 0 = m (u/a) / sin(2 pu/a) t 0 m / 2 p LIMITE D’ELASTICITE DES METAUX DIFFERENTS TYPES Résultats expérimentaux Cuivre m = 48 GPa t 0 = 60 Mpa Alu m = 27 GPa t 0 = 40 MPa ? ? ?

DEFAUTS DANS LES CRISTAUX MECANISME FONDAMENTAL DE GLISSEMENT Défauts ponctuels ENERGIE DE FORMATION CENTRES F MECANISMES DE DIFFUSION Dislocations LIMITE D’ELASTICITE DES METAUX DIFFERENTS TYPES ? ? ?

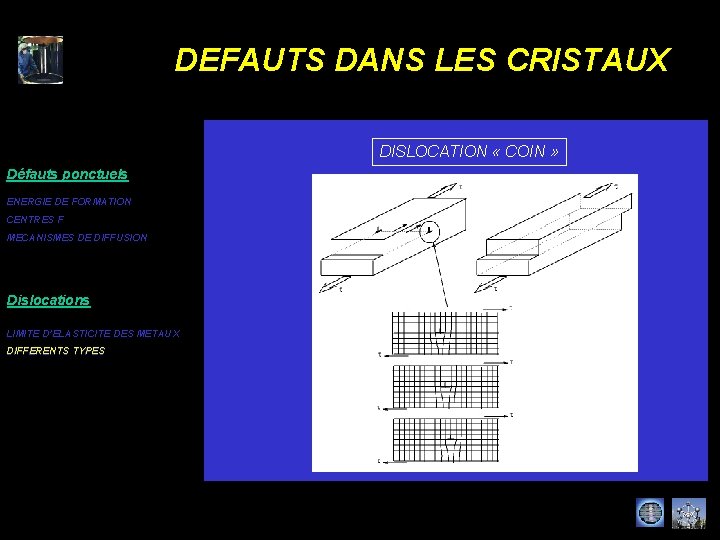
DEFAUTS DANS LES CRISTAUX DISLOCATION « COIN » Défauts ponctuels ENERGIE DE FORMATION CENTRES F MECANISMES DE DIFFUSION Dislocations LIMITE D’ELASTICITE DES METAUX DIFFERENTS TYPES

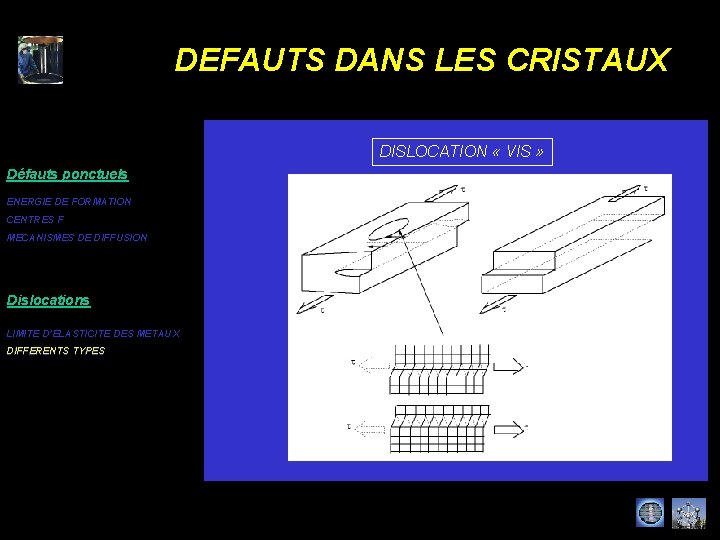
DEFAUTS DANS LES CRISTAUX DISLOCATION « VIS » Défauts ponctuels ENERGIE DE FORMATION CENTRES F MECANISMES DE DIFFUSION Dislocations LIMITE D’ELASTICITE DES METAUX DIFFERENTS TYPES

DEFAUTS DANS LES CRISTAUX DISLOCATIONS « REELLES » Défauts ponctuels ENERGIE DE FORMATION CENTRES F MECANISMES DE DIFFUSION Dislocations Plans (111) d’un cristal d’Al Plutôt « coin » LIMITE D’ELASTICITE DES METAUX DIFFERENTS TYPES Plutôt « vis » Acier inoxydable

DEFAUTS DANS LES CRISTAUX Défauts ponctuels ENERGIE DE FORMATION CENTRES F MECANISMES DE DIFFUSION Dislocations LIMITE D’ELASTICITE DES METAUX DIFFERENTS TYPES

ELECTRONS DANS UN SOLIDE

L’électron Le solide cristallin PROPRIETES DES MATERIAUX SOLIDES R. Fortunier Modèle de DRUDE Électrons dans un solide

MODELE DE DRUDE Description du modèle LE GAZ D’ELECTRONS LES COLLISIONS Quelques propriétés physiques CONDUCTIVITE ELECTRIQUE CONDUCTIVITE THERMIQUE INTERACTION AVEC UN RAYONNEMENT ELECTROMAGNETIQUE

MODELE DE DRUDE mise à disposition de Zc électrons par atome (n. atomique Z) Description du modèle exemples LE GAZ D’ELECTRONS Sodium Na : 1 électron par atome (3 s 1 , couche M) LES COLLISIONS Aluminium Al : 3 électrons par atome (3 s 23 p 1 , couche M) Quelques propriétés physiques CONDUCTIVITE ELECTRIQUE CONDUCTIVITE THERMIQUE INTERACTION AVEC UN RAYONNEMENT ELECTROMAGNETIQUE

MODELE DE DRUDE Description du modèle LE GAZ D’ELECTRONS LES COLLISIONS nombre d’électrons de conduction par unité de volume : n = 6, 022. 1023. r. Zc/A exemples Sodium Na : n = 2, 65. 1022 électrons de conduction par cm 3 Aluminium Al : n = 18, 1. 1022 électrons de conduction par cm 3 Quelques propriétés physiques CONDUCTIVITE ELECTRIQUE CONDUCTIVITE THERMIQUE INTERACTION AVEC UN RAYONNEMENT ELECTROMAGNETIQUE Les électrons de conduction sont dans une boîte de potentiel

MODELE DE DRUDE APROXIMATION DES ELECTRONS INDEPENDANTS Description du modèle LE GAZ D’ELECTRONS LES COLLISIONS Quelques propriétés physiques CONDUCTIVITE ELECTRIQUE Les interactions électron-électron sont négligées APROXIMATION DES ELECTRONS LIBRES Les interactions électron-ion sont négligées Le mouvement des électrons est obtenu en appliquant les lois classiques de la mécanique CONDUCTIVITE THERMIQUE INTERACTION AVEC UN RAYONNEMENT ELECTROMAGNETIQUE quelques résultats aberrants accélération constante des électrons sous l’effet de la force de Laplace vitesse infinie !! force de freinage

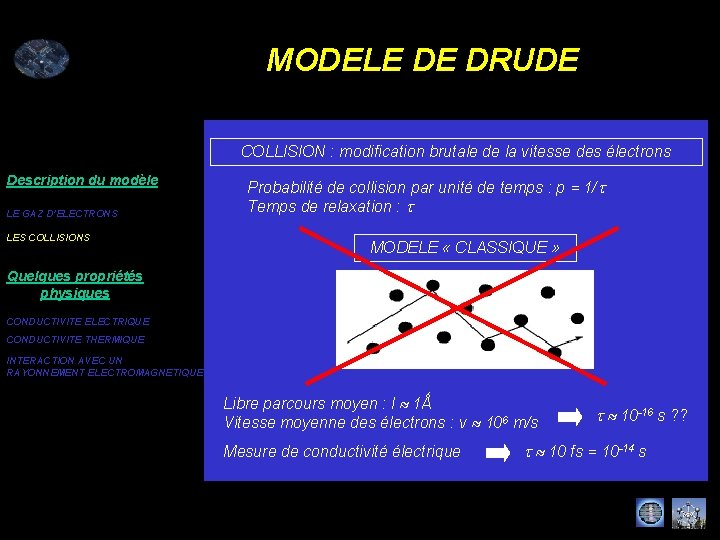
MODELE DE DRUDE COLLISION : modification brutale de la vitesse des électrons Description du modèle LE GAZ D’ELECTRONS LES COLLISIONS Probabilité de collision par unité de temps : p = 1/t Temps de relaxation : t MODELE « CLASSIQUE » Quelques propriétés physiques CONDUCTIVITE ELECTRIQUE CONDUCTIVITE THERMIQUE INTERACTION AVEC UN RAYONNEMENT ELECTROMAGNETIQUE Libre parcours moyen : l 1Ǻ Vitesse moyenne des électrons : v 106 m/s Mesure de conductivité électrique t 10 -16 s ? ? t 10 fs = 10 -14 s

MODELE DE DRUDE COLLISION : modification brutale de la vitesse des électrons Description du modèle LE GAZ D’ELECTRONS LES COLLISIONS Quelques propriétés physiques Moyen de schématiser le ralentissement des électrons Seul mécanisme participant à l’équilibre thermique CAPACITE CALORIFIQUE DES ELECTRONS ? électron direction aléatoire CONDUCTIVITE ELECTRIQUE CONDUCTIVITE THERMIQUE collision INTERACTION AVEC UN RAYONNEMENT ELECTROMAGNETIQUE Théorie cinétique des gaz Vitesse associée À la température locale U = 1/2 mv 2 = 3/2 k. BT Cv = 3/2 N k. B

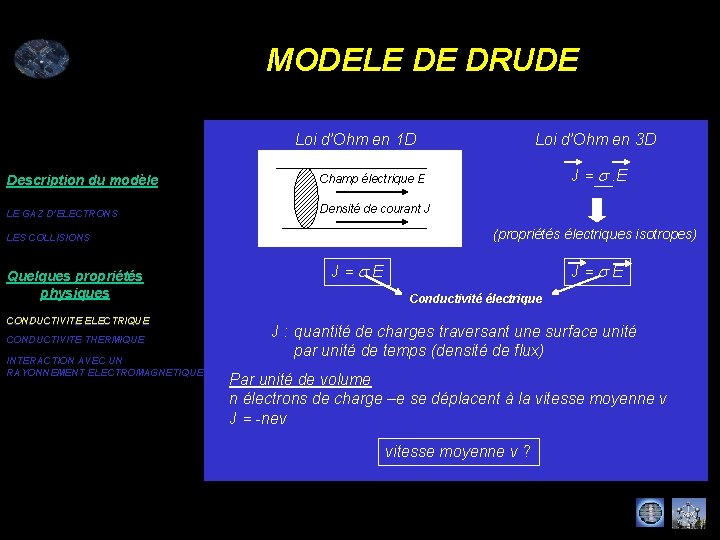
MODELE DE DRUDE Loi d’Ohm en 1 D Description du modèle Champ électrique E LE GAZ D’ELECTRONS Densité de courant J CONDUCTIVITE ELECTRIQUE CONDUCTIVITE THERMIQUE INTERACTION AVEC UN RAYONNEMENT ELECTROMAGNETIQUE J = s. E (propriétés électriques isotropes) LES COLLISIONS Quelques propriétés physiques Loi d’Ohm en 3 D J = s E Conductivité électrique J : quantité de charges traversant une surface unité par unité de temps (densité de flux) Par unité de volume n électrons de charge –e se déplacent à la vitesse moyenne v J = -nev vitesse moyenne v ?

MODELE DE DRUDE Champ électrique E Force de Laplace F = - e E Description du modèle accélération g = - (e/m) E LE GAZ D’ELECTRONS Vitesse moyenne v = - (et/m) E LES COLLISIONS J = - nev Quelques propriétés physiques v = - (et/m) E s = ne 2 t/m r = 1/s = m/ne 2 t CONDUCTIVITE ELECTRIQUE CONDUCTIVITE THERMIQUE INTERACTION AVEC UN RAYONNEMENT ELECTROMAGNETIQUE Exemples Cuivre Cu : r = 1, 56 m. W. cm à 273 K t = 27 fs r = 2, 24 m. W. cm à 373 K t = 19 fs Aluminium Al : r = 2, 45 m. W. cm à 273 K t = 8 fs r = 3, 45 m. W. cm à 373 K t = 5, 5 fs

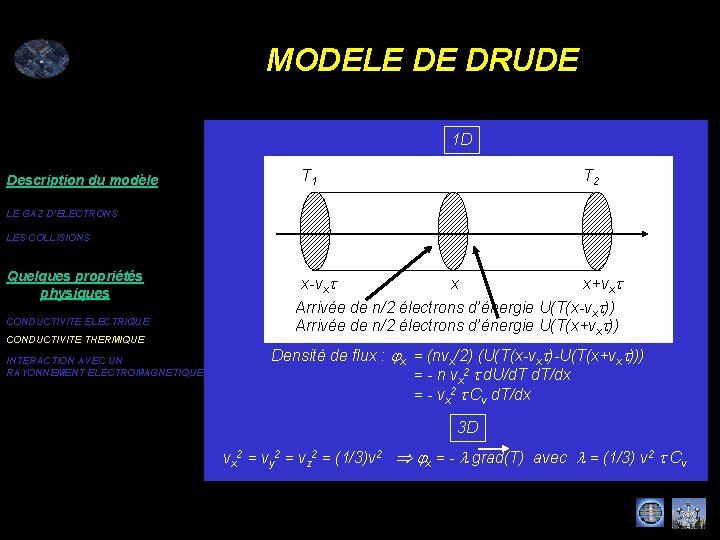
MODELE DE DRUDE 1 D Description du modèle T 2 T 1 LE GAZ D’ELECTRONS LES COLLISIONS Quelques propriétés physiques CONDUCTIVITE ELECTRIQUE CONDUCTIVITE THERMIQUE INTERACTION AVEC UN RAYONNEMENT ELECTROMAGNETIQUE x-vxt x x+vxt Arrivée de n/2 électrons d’énergie U(T(x-vxt)) Arrivée de n/2 électrons d’énergie U(T(x+vxt)) Densité de flux : jx = (nvx/2) (U(T(x-vxt)-U(T(x+vxt))) = - n vx 2 t d. U/d. T/dx = - vx 2 t Cv d. T/dx 3 D vx 2 = vy 2 = vz 2 = (1/3)v 2 jx = - l grad(T) avec l = (1/3) v 2 t Cv

MODELE DE DRUDE Description du modèle LE GAZ D’ELECTRONS LES COLLISIONS Quelques propriétés physiques CONDUCTIVITE ELECTRIQUE CONDUCTIVITE THERMIQUE INTERACTION AVEC UN RAYONNEMENT ELECTROMAGNETIQUE gaz d’électrons de densité n (E, B) Particules de masse m et charge -e Equation de base négligé (v «faible» ) m d 2 x/dt 2 + (m/t) dx/dt + e (E + v B) = 0 Solution stationnaire E = E 0 eiwt x = x 0 eiwt avec x 0 = (et/mw) (1/(i+wt)) E 0 Densité de courant dans le matériau J = - ne dx/dt = J 0 eiwt avec J 0 = (ne 2 t/m) (1/(1 -iwt))E 0 J = sw E avec sw = s / (1 -iwt)

MODELE DE DRUDE l : longueur d’onde du rayonnement (visible entre 10 -7 et 10 -6 m) l = vt : libre parcours moyen des électrons (de l’ordre de 10 -8 m) Description du modèle LE GAZ D’ELECTRONS LES COLLISIONS Quelques propriétés physiques CONDUCTIVITE ELECTRIQUE CONDUCTIVITE THERMIQUE INTERACTION AVEC UN RAYONNEMENT ELECTROMAGNETIQUE l >> l Équations de Maxwell (unités SI, pas de densité de charge) Maxwell – Gauss : div(E) = 0 Biot et Savart : div(B) = 0 Maxwell - Ampère : rot(B) = m 0 J + e 0 m 0 E/ t Maxwell - Faraday : rot(E) = - B/ t solution stationnaire div(grad(E 0)) = - e w 2/c 2 E 0 avec e = 1 – s/(we 0(i+wt)) w : pulsation du rayonnement (visible de l’ordre de 1016 s-1) t : temps de relaxation des électrons (de l’ordre de 10 -14 s) wt >> 1 e = 1 – wp 2/w 2 avec wp = ne 2/e 0 m ou np = wp/2 p ou lp = 2 pc/wp fréquence de plasmon longueur d’onde de plasmon

MODELE DE DRUDE Description du modèle LE GAZ D’ELECTRONS LES COLLISIONS Quelques propriétés physiques CONDUCTIVITE ELECTRIQUE CONDUCTIVITE THERMIQUE INTERACTION AVEC UN RAYONNEMENT ELECTROMAGNETIQUE

L’électron Le solide cristallin PROPRIETES DES MATERIAUX SOLIDES R. Fortunier Modèle de SOMMERFELD Électrons dans un solide

MODELE DE SOMMERFELD Description du modèle APPROXIMATION DES ELECTRONS LIBRES DISTRIBUTION DE FERMI-DIRAC Quelques propriétés physiques CAPACITE CALORIFIQUE DES ELECTRONS CONDUCTIVITE ELECTRIQUE LOI DE WIEDMANN-FRANZ SURFACES LIBRES

MODELE DE SOMMERFELD Élément de volume représentatif du matériau Description du modèle APPROXIMATION DES ELECTRONS LIBRES DISTRIBUTION DE FERMI-DIRAC Quelques propriétés physiques CAPACITE CALORIFIQUE DES ELECTRONS CONDUCTIVITE ELECTRIQUE LOI DE WIEDMANN-FRANZ Conditions aux limites périodiques y(x+L, y, z) = y(x, y, z) y(x, y+L, z) = y(x, y, z) y(x, y, z+L) = y(x, y, z) Equation de Schrödinger -(ħ 2/2 m)Dy = Ey SURFACES LIBRES yn(r) = (1/L 3/2) exp(ikn. r) avec kn = (2 p/L) (nx, ny, nz) En = (ħ 2/2 m) kn. kn = E 0(nx 2+ny 2+nz 2) avec E 0 = (ħ 2/2 m) (2 p/L)2

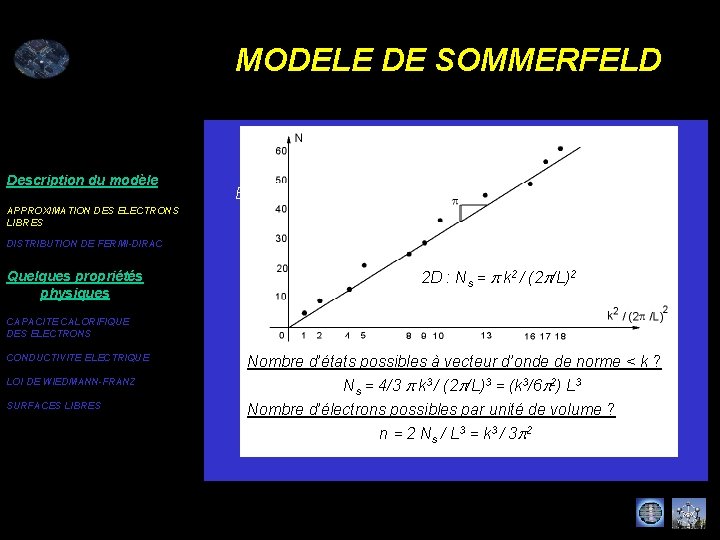
MODELE DE SOMMERFELD Description du modèle APPROXIMATION DES ELECTRONS LIBRES DISTRIBUTION DE FERMI-DIRAC Quelques propriétés physiques Illustration en 2 D yn(r) = (1/L) exp(ikn. r) avec kn = (2 p/L) (nx, ny) En = (ħ 2/2 m) kn. kn = E 0(nx 2+ny 2) avec E 0 = (ħ 2/2 m) (2 p/L)2 Etat (10) : E = E 0 Etat (01) : E = E 0 2 D : Ns = p k 2 / (2 p/L)2 Etat (11) : E = 2 E 0 CAPACITE CALORIFIQUE DES ELECTRONS CONDUCTIVITE ELECTRIQUE LOI DE WIEDMANN-FRANZ SURFACES LIBRES Nombre d’états possibles à vecteur d’onde de norme < k ? Cercle d’iso-énergie 3 3 3 Ns = 4/3 p k / (2 p/L) = (k /6 p 2) L 3 E = (ħ 2/2 m) k. k Nombre d’électrons possibles par unité de volume ? n = 2 Ns / L 3 = k 3 / 3 p 2

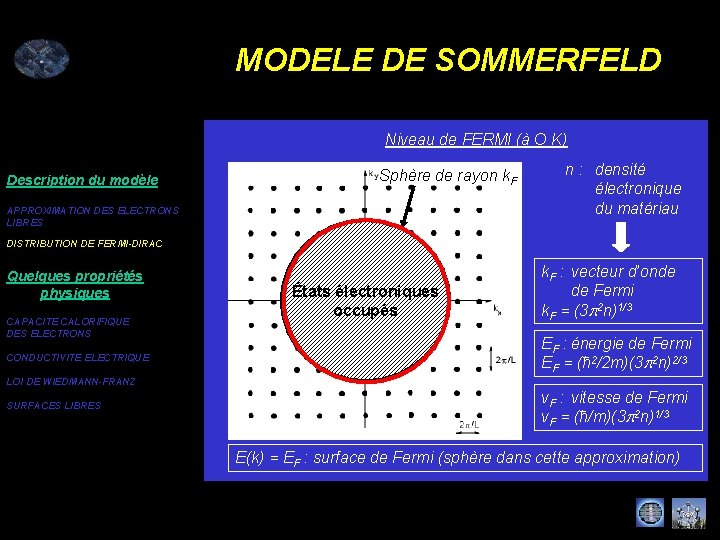
MODELE DE SOMMERFELD Niveau de FERMI (à O K) Description du modèle Sphère de rayon k. F APPROXIMATION DES ELECTRONS LIBRES n : densité électronique du matériau DISTRIBUTION DE FERMI-DIRAC Quelques propriétés physiques CAPACITE CALORIFIQUE DES ELECTRONS CONDUCTIVITE ELECTRIQUE États électroniques occupés k. F : vecteur d’onde de Fermi k. F = (3 p 2 n)1/3 EF : énergie de Fermi EF = (ħ 2/2 m)(3 p 2 n)2/3 LOI DE WIEDMANN-FRANZ SURFACES LIBRES v. F : vitesse de Fermi v. F = (ħ/m)(3 p 2 n)1/3 E(k) = EF : surface de Fermi (sphère dans cette approximation)

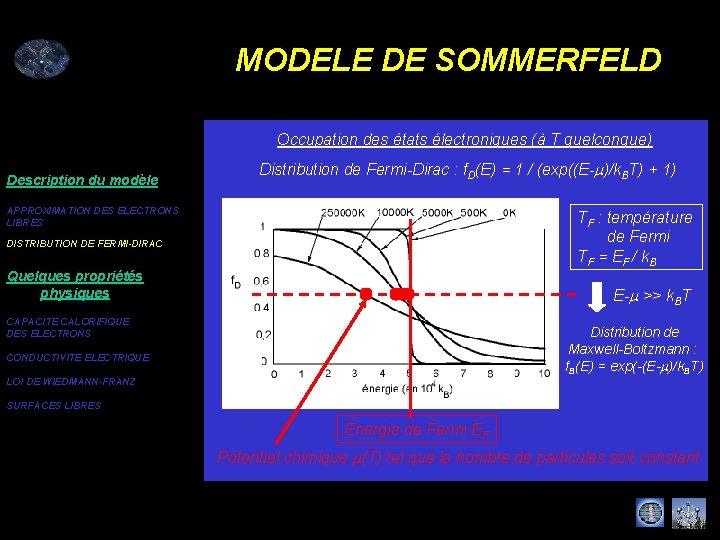
MODELE DE SOMMERFELD Occupation des états électroniques (à T quelconque) Description du modèle Distribution de Fermi-Dirac : f. D(E) = 1 / (exp((E-m)/k. BT) + 1) APPROXIMATION DES ELECTRONS LIBRES TF : température de Fermi TF = EF / k. B DISTRIBUTION DE FERMI-DIRAC Quelques propriétés physiques E-m >> k. BT CAPACITE CALORIFIQUE DES ELECTRONS Distribution de Maxwell-Boltzmann : f. B(E) = exp(-(E-m)/k. BT) CONDUCTIVITE ELECTRIQUE LOI DE WIEDMANN-FRANZ SURFACES LIBRES Énergie de Fermi EF Potentiel chimique m(T) tel que le nombre de particules soit constant

MODELE DE SOMMERFELD contribution électronique à l’ énergie interne d’un cristal : Description du modèle APPROXIMATION DES ELECTRONS LIBRES DISTRIBUTION DE FERMI-DIRAC Quelques propriétés physiques CAPACITE CALORIFIQUE DES ELECTRONS U = E f. D(E) d. E Energie Distribution de Fermi-Dirac Densité d’états ? n =k 3/6 p 2 =1/3 p 2(2 m. E/ħ 2)3/2 CONDUCTIVITE ELECTRIQUE LOI DE WIEDMANN-FRANZ SURFACES LIBRES D(E) =dn/d. E =1/2 p 2(2 m/ħ 2)3/2 E 1/2 = 3 n/2 E

MODELE DE SOMMERFELD U = E f. D(E) d. E Description du modèle APPROXIMATION DES ELECTRONS LIBRES DISTRIBUTION DE FERMI-DIRAC Quelques propriétés physiques CAPACITE CALORIFIQUE DES ELECTRONS CONDUCTIVITE ELECTRIQUE LOI DE WIEDMANN-FRANZ SURFACES LIBRES DU = U(T)–U(0) = f. D(E) E d. E - D(E) E d. E f. D(E) d. E = D(E) d. E DU = f. D(E) (E-EF) d. E - D(E) (E-EF) d. E Cv = d(DU)/d. T = df. D(E)/d. T D(E) (E-EF) d. E EF >> k. BT (T faible) Cv = p 2/2 nk. BT/TF réseau + électrons Cv = a T + g T 3 -électrons libres -électrons indépendants

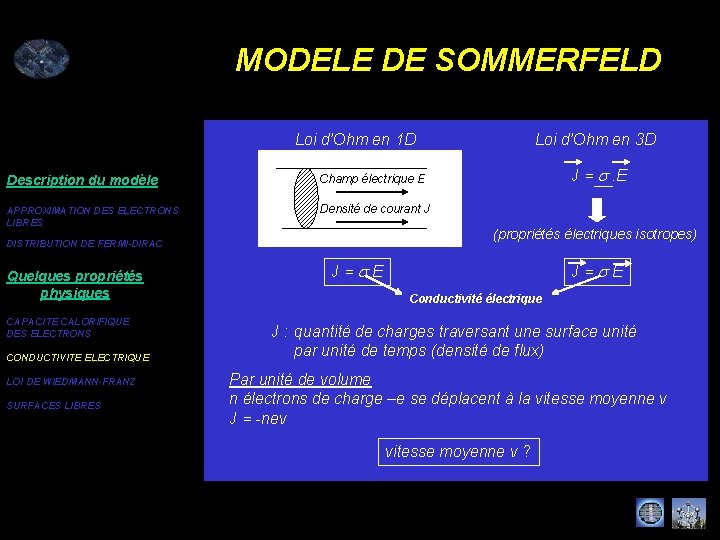
MODELE DE SOMMERFELD Loi d’Ohm en 1 D Description du modèle Champ électrique E APPROXIMATION DES ELECTRONS LIBRES Densité de courant J CAPACITE CALORIFIQUE DES ELECTRONS CONDUCTIVITE ELECTRIQUE LOI DE WIEDMANN-FRANZ SURFACES LIBRES J = s. E (propriétés électriques isotropes) DISTRIBUTION DE FERMI-DIRAC Quelques propriétés physiques Loi d’Ohm en 3 D J = s E Conductivité électrique J : quantité de charges traversant une surface unité par unité de temps (densité de flux) Par unité de volume n électrons de charge –e se déplacent à la vitesse moyenne v J = -nev vitesse moyenne v ?

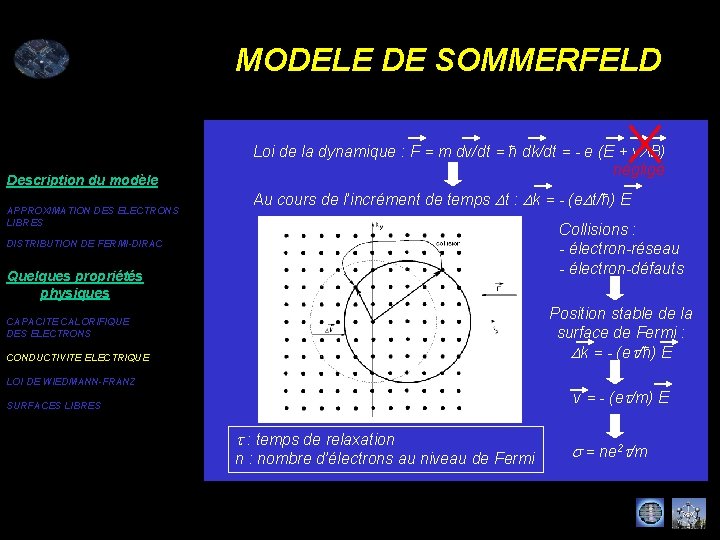
MODELE DE SOMMERFELD Description du modèle APPROXIMATION DES ELECTRONS LIBRES Loi de la dynamique : F = m dv/dt = ħ dk/dt = - e (E + v B) négligé Au cours de l’incrément de temps Dt : Dk = - (e. Dt/ħ) E Collisions : - électron-réseau - électron-défauts DISTRIBUTION DE FERMI-DIRAC Quelques propriétés physiques Position stable de la surface de Fermi : Dk = - (et/ħ) E CAPACITE CALORIFIQUE DES ELECTRONS CONDUCTIVITE ELECTRIQUE LOI DE WIEDMANN-FRANZ v = - (et/m) E SURFACES LIBRES t : temps de relaxation n : nombre d’électrons au niveau de Fermi s = ne 2 t/m

MODELE DE SOMMERFELD Modèles de DRUDE et de SOMMERFELD : Description du modèle APPROXIMATION DES ELECTRONS LIBRES DISTRIBUTION DE FERMI-DIRAC Quelques propriétés physiques l = (1/3) v 2 t. Cv s = ne 2 t/m Modèle de DRUDE : théorie cinétique des gaz E = 1/2 mv 2 = 3/2 k. BT (par électron de conduction) Cv = 3/2 nk. B (pour n électrons de conduction) l/s. T = 3/2 (k. B/e)2 = 1, 12. 10 -8 WW/K 2 CAPACITE CALORIFIQUE DES ELECTRONS CONDUCTIVITE ELECTRIQUE LOI DE WIEDMANN-FRANZ SURFACES LIBRES Modèle de SOMMERFELD : électrons libres de Fermi E = EF = 1/2 mv. F 2 = k. BTF (par électron de Fermi) Cv = p 2/2 nk. B T/TF (pour n électrons de Fermi) l/s. T = p 2/3 (k. B/e)2 = 2, 45. 10 -8 WW/K 2 ?

MODELE DE SOMMERFELD Description du modèle APPROXIMATION DES ELECTRONS LIBRES DISTRIBUTION DE FERMI-DIRAC Quelques propriétés physiques CAPACITE CALORIFIQUE DES ELECTRONS Modèle de DRUDE : l/s. T = 1, 12. 10 -8 WW/K 2 Nombre de Lorentz l/s. T = 2, 45. 10 -8 WW/K 2 Modèle de SOMMERFELD : CONDUCTIVITE ELECTRIQUE LOI DE WIEDMANN-FRANZ SURFACES LIBRES Première validation expérimentale d’un modèle de gaz d’électrons

MODELE DE SOMMERFELD Description du modèle APPROXIMATION DES ELECTRONS LIBRES DISTRIBUTION DE FERMI-DIRAC Quelques propriétés physiques CAPACITE CALORIFIQUE DES ELECTRONS CONDUCTIVITE ELECTRIQUE LOI DE WIEDMANN-FRANZ SURFACES LIBRES Modification de la structure électronique à proximité de la surface Fonction d’onde : y(x, y, z) = 1/L 3/2 exp(i 2 p/L(nxx+nyy)) sin((2 p/L) nzz) pour 0 z L y(x, y, z) = 0 pour z 0 ou z L Les états (nx, ny, 0) ne sont plus possibles (y=0)

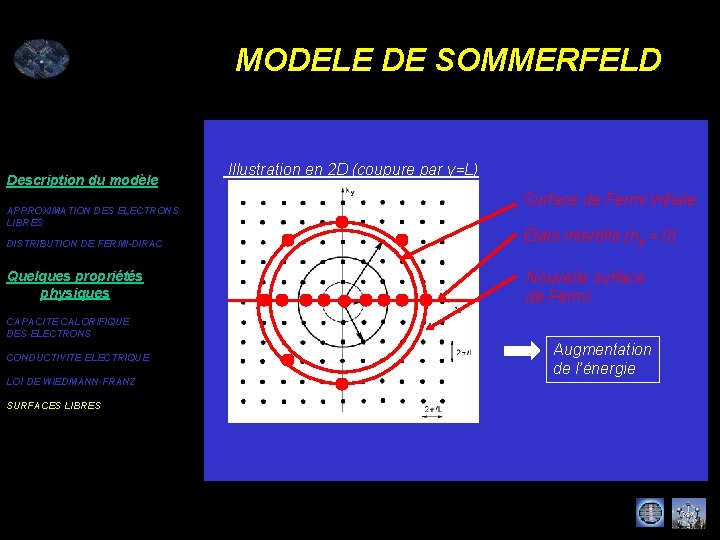
MODELE DE SOMMERFELD Description du modèle APPROXIMATION DES ELECTRONS LIBRES Illustration en 2 D (coupure par y=L) Surface de Fermi initiale DISTRIBUTION DE FERMI-DIRAC États interdits (ny = 0) Quelques propriétés physiques Nouvelle surface de Fermi CAPACITE CALORIFIQUE DES ELECTRONS CONDUCTIVITE ELECTRIQUE LOI DE WIEDMANN-FRANZ SURFACES LIBRES Augmentation de l’énergie

MODELE DE SOMMERFELD Calcul en 3 D (coupure par z=L) Description du modèle APPROXIMATION DES ELECTRONS LIBRES DISTRIBUTION DE FERMI-DIRAC Quelques propriétés physiques CAPACITE CALORIFIQUE DES ELECTRONS CONDUCTIVITE ELECTRIQUE DE = n 0 (EF – E 0) n 0 : nombre d’états interdits (kz=0) n 0 = 2 pk. F 2/(2 p/L)2 = (m. L 2/pħ 2)EF Dans le plan kz=0, la densité d’états est constante k. F E 0 : énergie moyenne des états interdits E 0 = (1/pk. F 2) E(k)2 pkdk 0 E 0 = EF/2 DE = n 0 EF/2 = GS LOI DE WIEDMANN-FRANZ SURFACES LIBRES Énergie de surface G = m. EF 2/4 pħ 2 positive indépendante du plan de coupe

MODELE DE SOMMERFELD Description du modèle APPROXIMATION DES ELECTRONS LIBRES DISTRIBUTION DE FERMI-DIRAC Quelques propriétés physiques CAPACITE CALORIFIQUE DES ELECTRONS CONDUCTIVITE ELECTRIQUE LOI DE WIEDMANN-FRANZ SURFACES LIBRES

L’électron Le solide cristallin PROPRIETES DES MATERIAUX SOLIDES R. Fortunier Bandes d’énergie Électrons dans un solide

BANDES D’ENERGIE Description du modèle ELECTRON DANS UN POTENTIEL PERIODIQUE APPARITION DE BANDES INTERDITES APPROXIMATION DE KRÖNIG-PENNEY Quelques propriétés physiques SURFACE DE FERMI CLASSIFICATION DES MATERIAUX

BANDES D’ENERGIE Le réseau des cristaux présente une périodicité Description du modèle ELECTRON DANS UN POTENTIEL PERIODIQUE APPARITION DE BANDES INTERDITES APPROXIMATION DE KRÖNIG-PENNEY Quelques propriétés physiques SURFACE DE FERMI CLASSIFICATION DES MATERIAUX OP = OM + g avec g = u a + v b + w c Les interactions électron-réseau doivent être représentées par un potentiel présentant la même périodicité V(r+g) = V(r ) si g = u a + v b + w c Le comportement du gaz d’électrons indépendants est régi par l’équation de Schrödinger appliquée à un électron - (ħ 2/2 m) Dy + Vy = Ey Théorème de Bloch : Les fonctions d’onde stationnaires d’un électron dans un potentiel périodique ont la forme d’une onde plane (de de Broglie) multipliée par une fonction possédant la même périodicité

BANDES D’ENERGIE V(r+g) = V(r ) Description du modèle ELECTRON DANS UN POTENTIEL PERIODIQUE APPARITION DE BANDES INTERDITES APPROXIMATION DE KRÖNIG-PENNEY Quelques propriétés physiques SURFACE DE FERMI CLASSIFICATION DES MATERIAUX V(r) = S V exp( -i G. r) G G y(r) = u(r ) exp( i k. r) avec u(r+g) = u(r ) S donnés à déterminer y(r) = u. G exp( i (k-G). r) G Incorporation dans l’équation de Schrödinger Choix convenable d’une origine des potentiels Termes du second ordre négligés (de type u. GVG’ avec G 0) E = (ħ 2/2 m) k. k normalisation u. G = u 0 (m/2ħ 2) VG / ( k. G/2 - ||G/2||2) Approximation valable tant que le vecteur d’onde k n’est pas proche d’une zone de Brillouin

BANDES D’ENERGIE Lorsque le vecteur d’onde est proche d’une zone de Brillouin Description du modèle ELECTRON DANS UN POTENTIEL PERIODIQUE APPARITION DE BANDES INTERDITES APPROXIMATION DE KRÖNIG-PENNEY k = k 0 (1 + e) avec |e| << 1 et k 0. (G/2) = ||G/2||2 Dans la fonction d’onde, les termes prépondérants sont u 0 et u. G y(r) = u 0 exp( i (1+e)k 0. r) + u. G exp( i ((1+e)k 0 -G). r) Incorporation dans l’équation de Schrödinger E = E 0 |VG| + ½(4 E 0 -x)e + (E 0 x 2/8|VG|)e 2 si e 0 ou e 0 électrons libres Quelques propriétés physiques E = (ħ 2/2 m) k. k SURFACE DE FERMI CLASSIFICATION DES MATERIAUX E 0 = (ħ 2/2 m) k 0 bande interdite

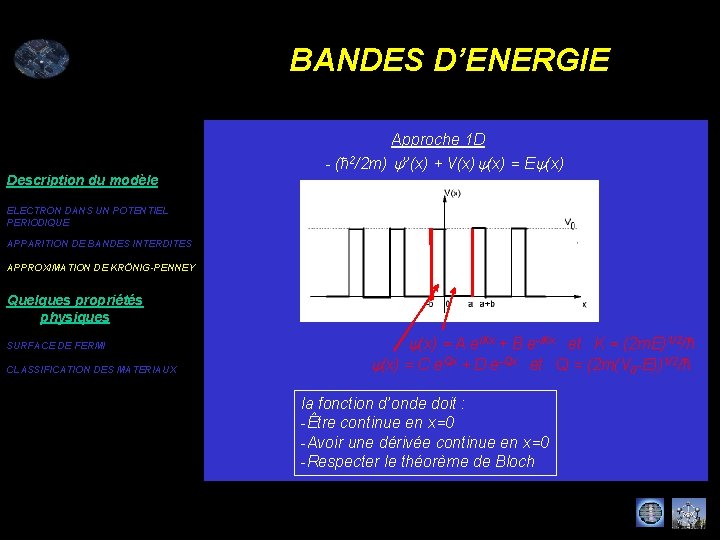
BANDES D’ENERGIE Description du modèle Approche 1 D - (ħ 2/2 m) y’’(x) + V(x)y(x) = Ey(x) ELECTRON DANS UN POTENTIEL PERIODIQUE APPARITION DE BANDES INTERDITES APPROXIMATION DE KRÖNIG-PENNEY Quelques propriétés physiques SURFACE DE FERMI CLASSIFICATION DES MATERIAUX y(x) = A ei. Kx + B e-i. Kx et K = (2 m. E)1/2/ħ y(x) = C e. Qx + D e-Qx et Q = (2 m(V 0 -E))1/2/ħ la fonction d’onde doit : -Être continue en x=0 -Avoir une dérivée continue en x=0 -Respecter le théorème de Bloch

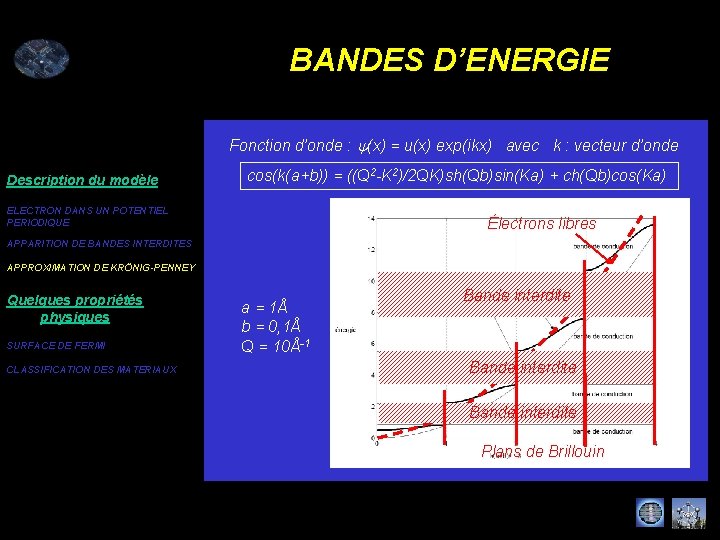
BANDES D’ENERGIE Fonction d’onde : y(x) = u(x) exp(ikx) avec k : vecteur d’onde Description du modèle cos(k(a+b)) = ((Q 2 -K 2)/2 QK)sh(Qb)sin(Ka) + ch(Qb)cos(Ka) ELECTRON DANS UN POTENTIEL PERIODIQUE Électrons libres APPARITION DE BANDES INTERDITES APPROXIMATION DE KRÖNIG-PENNEY Quelques propriétés physiques SURFACE DE FERMI CLASSIFICATION DES MATERIAUX a = 1Å b = 0, 1Å Q = 10Å-1 Bande interdite Plans de Brillouin

BANDES D’ENERGIE espace direct (position r) espace réciproque (vecteur d’onde k) Description du modèle ELECTRON DANS UN POTENTIEL PERIODIQUE APPARITION DE BANDES INTERDITES APPROXIMATION DE KRÖNIG-PENNEY Quelques propriétés physiques SURFACE DE FERMI CLASSIFICATION DES MATERIAUX Deux états électroniques ( ) par vecteur d’onde k 2/(2 p/L)3 = L 3/4 p 2 électrons par unité de volume de l’espace réciproque (L 3/4 p 2)VB électrons dans chaque zone de Brillouin Exemples : cfc 8(L/a)3 électrons dans 4(L/a)3 maille élémentaire cc 4(L/a)3 électrons dans 2(L/a)3 maille élémentaire Chaque zone de Brillouin peut accommoder 2 électrons par maille élémentaire

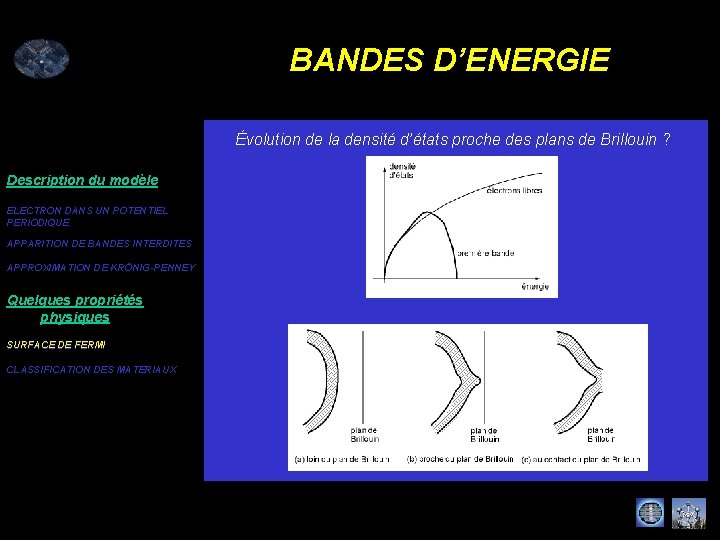
BANDES D’ENERGIE Évolution de la surface de Fermi proche des plans de Brillouin ? Description du modèle ELECTRON DANS UN POTENTIEL PERIODIQUE APPARITION DE BANDES INTERDITES APPROXIMATION DE KRÖNIG-PENNEY Quelques propriétés physiques SURFACE DE FERMI CLASSIFICATION DES MATERIAUX

BANDES D’ENERGIE Évolution de la densité d’états proche des plans de Brillouin ? Description du modèle ELECTRON DANS UN POTENTIEL PERIODIQUE APPARITION DE BANDES INTERDITES APPROXIMATION DE KRÖNIG-PENNEY Quelques propriétés physiques SURFACE DE FERMI CLASSIFICATION DES MATERIAUX

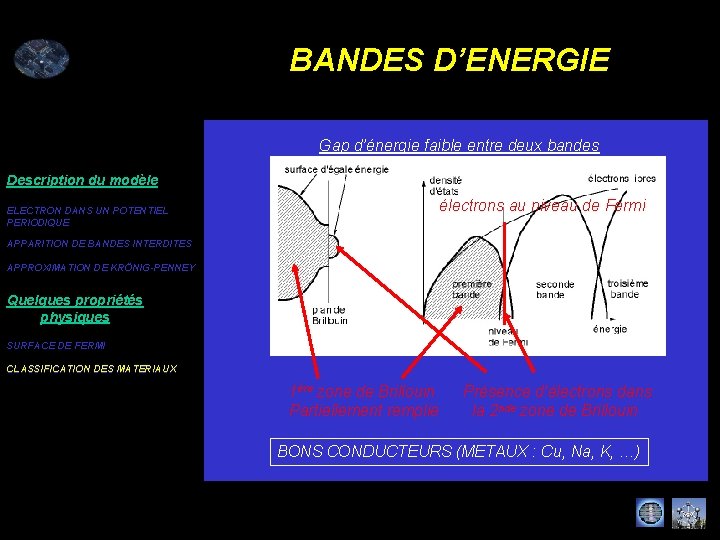
BANDES D’ENERGIE Gap d’énergie faible entre deux bandes Description du modèle ELECTRON DANS UN POTENTIEL PERIODIQUE électrons au niveau de Fermi APPARITION DE BANDES INTERDITES APPROXIMATION DE KRÖNIG-PENNEY Quelques propriétés physiques SURFACE DE FERMI CLASSIFICATION DES MATERIAUX 1ère zone de Brillouin Partiellement remplie Présence d’électrons dans la 2 nde zone de Brillouin BONS CONDUCTEURS (METAUX : Cu, Na, K, …)

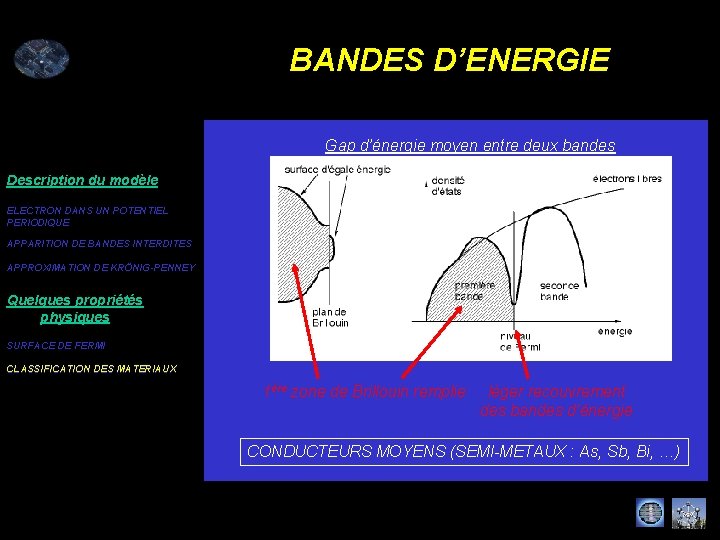
BANDES D’ENERGIE Gap d’énergie moyen entre deux bandes Description du modèle ELECTRON DANS UN POTENTIEL PERIODIQUE APPARITION DE BANDES INTERDITES APPROXIMATION DE KRÖNIG-PENNEY Quelques propriétés physiques SURFACE DE FERMI CLASSIFICATION DES MATERIAUX 1ère zone de Brillouin remplie léger recouvrement des bandes d’énergie CONDUCTEURS MOYENS (SEMI-METAUX : As, Sb, Bi, …)

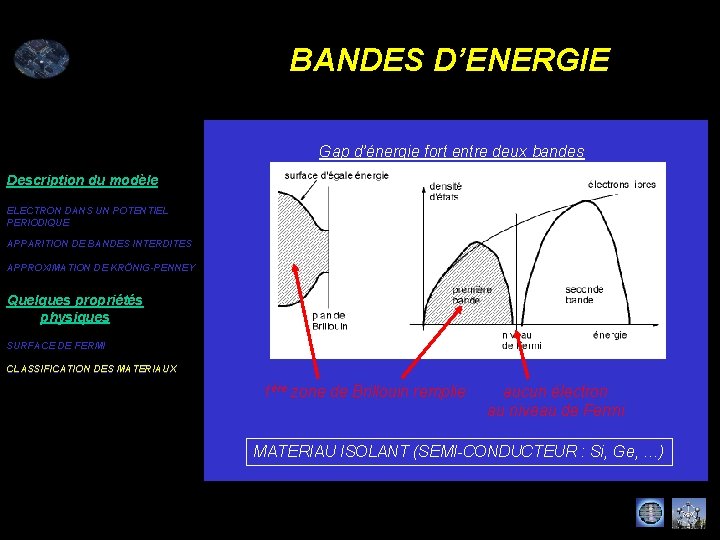
BANDES D’ENERGIE Gap d’énergie fort entre deux bandes Description du modèle ELECTRON DANS UN POTENTIEL PERIODIQUE APPARITION DE BANDES INTERDITES APPROXIMATION DE KRÖNIG-PENNEY Quelques propriétés physiques SURFACE DE FERMI CLASSIFICATION DES MATERIAUX 1ère zone de Brillouin remplie aucun électron au niveau de Fermi MATERIAU ISOLANT (SEMI-CONDUCTEUR : Si, Ge, …)

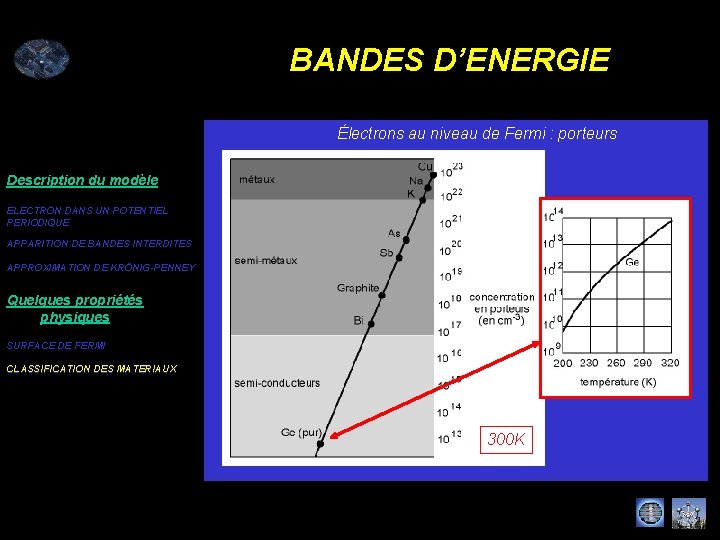
BANDES D’ENERGIE Électrons au niveau de Fermi : porteurs Description du modèle ELECTRON DANS UN POTENTIEL PERIODIQUE APPARITION DE BANDES INTERDITES APPROXIMATION DE KRÖNIG-PENNEY Quelques propriétés physiques SURFACE DE FERMI CLASSIFICATION DES MATERIAUX 300 K

BANDES D’ENERGIE Description du modèle ELECTRON DANS UN POTENTIEL PERIODIQUE APPARITION DE BANDES INTERDITES APPROXIMATION DE KRÖNIG-PENNEY Quelques propriétés physiques SURFACE DE FERMI CLASSIFICATION DES MATERIAUX

L’électron Le solide cristallin PROPRIETES DES MATERIAUX SOLIDES R. Fortunier Cristaux semi-conducteurs Électrons dans un solide

CRISTAUX SEMI-CONDUCTEURS Représentation énergétique DENSITE D’ETATS OCCUPATION DES NIVEAUX Propriétés de conduction SEMI-CONDUCTEUR INTRINSEQUE SEMI-CONDUCTEUR EXTRINSEQUE

CRISTAUX SEMI-CONDUCTEURS Un semi-conducteur est un isolant à 0 K Représentation énergétique Si : 1, 17 e. V Ge : 0, 74 e. V As. Ga : 1, 52 e. V … DENSITE D’ETATS OCCUPATION DES NIVEAUX Propriétés de conduction SEMI-CONDUCTEUR INTRINSEQUE SEMI-CONDUCTEUR EXTRINSEQUE Si : 2 atomes par maille élémentaire 4 électrons de valence par atome 8 électrons de valence par maille élémentaire 4 zones de Brillouin remplies, la 5ème vide Un semi-conducteur est-il conducteur à 300 K ? Métaux: Cu 1023 cm-3 Na 5. 1022 cm-3 Énergie de fluctuation Thermique à 300 K ? E = k. BT 0, 026 e. V

CRISTAUX SEMI-CONDUCTEURS Electrons et Trous Représentation énergétique électrons dans la bande de conduction (charge –e) DENSITE D’ETATS trous dans la bande de valence (charge +e) OCCUPATION DES NIVEAUX Propriétés de conduction SEMI-CONDUCTEUR INTRINSEQUE SEMI-CONDUCTEUR EXTRINSEQUE Masses effectives électrons trous électron = paquet d’onde (impulsion p=ħk, énergie E=ħw) vitesse = vitesse de groupe v = dw/dk = (1/ħ) d. E/dk F = me g me = ħ 2 / d 2 E/dk 2 accélération = g = dv/dt = (1/ħ) d 2 E/dk 2 dk/dt force extérieure = F = dp/dt = ħ dk/dt On traite les électrons et les trous comme des particules de masses effectives me (electrons) et mt (trous) masse effective électrons (bande de conduction) trous (bande de valence) Si 1, 06 m 0, 59 m Ge 0, 55 m 0, 36 m As. Ga 0, 066 m 0, 64 m

CRISTAUX SEMI-CONDUCTEURS Schématisation de la densité d’états proche du gap Représentation énergétique électrons libres D(E) = (1/2 p 2) (2 m/ħ 2)3/2 E 1/2 DENSITE D’ETATS OCCUPATION DES NIVEAUX Propriétés de conduction SEMI-CONDUCTEUR INTRINSEQUE SEMI-CONDUCTEUR EXTRINSEQUE niveau de Fermi bande de conduction : Dc(E) = (1/2 p 2) (2 me/ħ 2)3/2 (E-Ec)1/2 bande de valence : Dv(E) = (1/2 p 2) (2 mt/ħ 2)3/2 (Ev-E)1/2

CRISTAUX SEMI-CONDUCTEURS Concentration en électrons dans la bande de conduction ? Représentation énergétique DENSITE D’ETATS OCCUPATION DES NIVEAUX n = Dc(E) f. D(E) d. E Ec Propriétés de conduction SEMI-CONDUCTEUR INTRINSEQUE SEMI-CONDUCTEUR EXTRINSEQUE n Dc(E) exp((m-E)/k. BT) d. E Ec n nc exp((m-Ec)/k. BT) avec nc = 2(mek. BT/2 pħ 2)3/2

CRISTAUX SEMI-CONDUCTEURS Concentration en trous dans la bande de valence ? Représentation énergétique DENSITE D’ETATS OCCUPATION DES NIVEAUX p = Dv(E) (1 -f. D(E)) d. E Ec Propriétés de conduction SEMI-CONDUCTEUR INTRINSEQUE SEMI-CONDUCTEUR EXTRINSEQUE p Dv(E) exp((E-m)/k. BT) d. E Ec p nv exp((Ev -m)/k. BT) avec nv = 2(mtk. BT/2 pħ 2)3/2

CRISTAUX SEMI-CONDUCTEURS Représentation schématique d’un semi-conducteur Représentation énergétique DENSITE D’ETATS OCCUPATION DES NIVEAUX Concentration en électrons dans la bande de conduction : n nc exp((m-Ec)/k. BT) avec nc = 2(mek. BT/2 pħ 2)3/2 Concentration en trous dans la bande de valence : p nv exp((Ev -m)/k. BT) avec nv = 2(mtk. BT/2 pħ 2)3/2 Propriétés de conduction SEMI-CONDUCTEUR INTRINSEQUE SEMI-CONDUCTEUR EXTRINSEQUE np = nc nv exp(-Eg / k. BT) = 4(k. BT/2 pħ 2)3(memt )3/2 exp (-Eg / k. BT) Eg= Ec - Ev valable si le niveau de Fermi est suffisamment loin des niveaux d’énergie des bandes de valence et de conduction (typiquement distants de 3 k. BT)

CRISTAUX SEMI-CONDUCTEURS Les porteurs de charge ne sont fournis que par les atomes du réseau Représentation énergétique DENSITE D’ETATS OCCUPATION DES NIVEAUX Propriétés de conduction n = p= (np)1/2 = 2(k. BT/2 pħ 2)3/2(memt )3/4 exp (-Eg / 2 k. BT) Conductibilité électrique : s = ne 2 t/m SEMI-CONDUCTEUR INTRINSEQUE SEMI-CONDUCTEUR EXTRINSEQUE s augmente avec la température dans les semi-conducteurs (n ) s diminue avec la température dans les métaux (t )

CRISTAUX SEMI-CONDUCTEURS Position du niveau de Fermi ? Représentation énergétique DENSITE D’ETATS OCCUPATION DES NIVEAUX n = p 2(mek. BT/2 p m-Ec)/k. BT) = 2(mtk. BT/2 pħ 2)3/2 exp((Ev-m)/k. BT) exp(2 m/k. BT) = (mt/me)3/2 exp((Ec+Ev)/k. BT) ħ 2)3/2 exp(( m = (Ec+Ev)/2 + (3 k. BT/4) ln(mt/me) Propriétés de conduction SEMI-CONDUCTEUR INTRINSEQUE SEMI-CONDUCTEUR EXTRINSEQUE Bande de conduction niveau de Fermi Gap Bande de valence

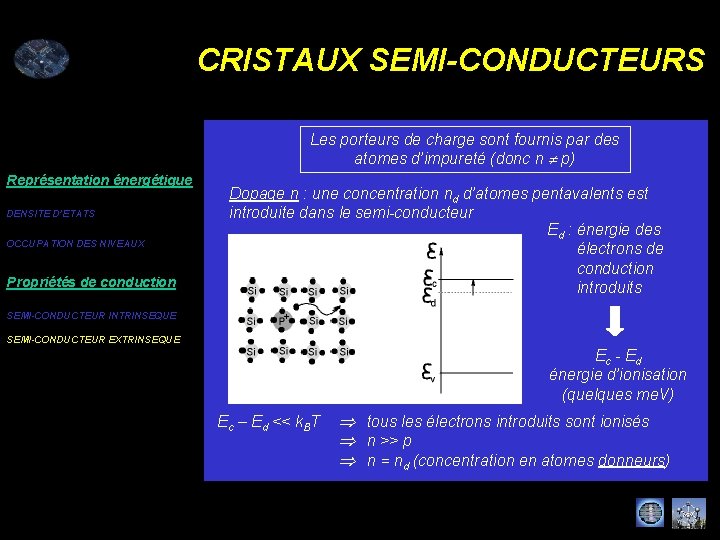
CRISTAUX SEMI-CONDUCTEURS Les porteurs de charge sont fournis par des atomes d’impureté (donc n p) Représentation énergétique DENSITE D’ETATS OCCUPATION DES NIVEAUX Propriétés de conduction Dopage n : une concentration nd d’atomes pentavalents est introduite dans le semi-conducteur Ed : énergie des électrons de conduction introduits SEMI-CONDUCTEUR INTRINSEQUE SEMI-CONDUCTEUR EXTRINSEQUE Ec - Ed énergie d’ionisation (quelques me. V) Ec – Ed << k. BT tous les électrons introduits sont ionisés n >> p n = nd (concentration en atomes donneurs)

CRISTAUX SEMI-CONDUCTEURS Les porteurs de charge sont fournis par des atomes d’impureté (donc n p) Représentation énergétique DENSITE D’ETATS OCCUPATION DES NIVEAUX Propriétés de conduction Dopage p : une concentration na d’atomes trivalents est introduite dans le semi-conducteur Ea : énergie des électrons complétant les ions B- SEMI-CONDUCTEUR INTRINSEQUE SEMI-CONDUCTEUR EXTRINSEQUE Ea - Ev faible (quelques me. V) Ea – Ev << k. BT tous les ions sont complétés p >> n p = na (concentration en atomes accepteurs)

CRISTAUX SEMI-CONDUCTEURS Position des niveaux de Fermi ? Représentation énergétique Dopage n : nd = nc exp((m-Ec)/k. BT) m = Ec – k. BT ln(nc/nd) DENSITE D’ETATS Dopage p : na = p = nv exp(-(m-Ev)/k. BT) m = Ev + k. BT ln(nv/na) OCCUPATION DES NIVEAUX Propriétés de conduction Ec électrons Ed SEMI-CONDUCTEUR INTRINSEQUE EF SEMI-CONDUCTEUR EXTRINSEQUE Ea Ev Si pur Si dopé n électrons Si dopé p

CRISTAUX SEMI-CONDUCTEURS Représentation énergétique DENSITE D’ETATS OCCUPATION DES NIVEAUX Propriétés de conduction SEMI-CONDUCTEUR INTRINSEQUE SEMI-CONDUCTEUR EXTRINSEQUE

FIN
 Volume des liquides et des solides
Volume des liquides et des solides Le volume d'un corps
Le volume d'un corps Espèce chimique naturelle exemple
Espèce chimique naturelle exemple Choix des matériaux indice de performance exercices
Choix des matériaux indice de performance exercices Représentation des 230 groupes d'espace
Représentation des 230 groupes d'espace Distance interréticulaire hexagonal
Distance interréticulaire hexagonal La dilatation des solides
La dilatation des solides Matériaux
Matériaux Introduction sur les matériaux de construction
Introduction sur les matériaux de construction Matériaux conducteurs et isolants
Matériaux conducteurs et isolants Des des des
Des des des Solides compacts et divisés
Solides compacts et divisés Les solides compacts
Les solides compacts La matire
La matire Les solides pulvérisés
Les solides pulvérisés Solide ionique
Solide ionique Flexion du bois
Flexion du bois Tp équilibre d'un solide soumis à trois forces
Tp équilibre d'un solide soumis à trois forces Sinonimo di convesso
Sinonimo di convesso Solide covalent
Solide covalent Dynamique du solide
Dynamique du solide Legge henry
Legge henry Corpurile solide au forma dar nu au volum propriu
Corpurile solide au forma dar nu au volum propriu Paralépipède
Paralépipède Eau solide
Eau solide Valeur absolue propriétés
Valeur absolue propriétés Solide liquide gaz
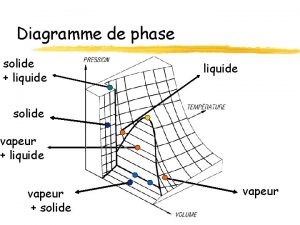
Solide liquide gaz Liaison hydrogéne
Liaison hydrogéne Dilatarea corpurilor solide lichide si gazoase
Dilatarea corpurilor solide lichide si gazoase Galilen
Galilen Rationaliser le dénominateur
Rationaliser le dénominateur Budget des ventes
Budget des ventes Mode verbal
Mode verbal Je t'offrirai des fleurs et des nappes en couleurs
Je t'offrirai des fleurs et des nappes en couleurs Affiche plan marshall ciment de l'europe
Affiche plan marshall ciment de l'europe Robin des bois des alpes
Robin des bois des alpes La diffusion des idées des lumières
La diffusion des idées des lumières Diversification des espaces et des acteurs de la production
Diversification des espaces et des acteurs de la production Des attacks
Des attacks Il existe des personnes qui sont des lumières pour tous
Il existe des personnes qui sont des lumières pour tous Cartographie des flux
Cartographie des flux Définition de l'analyse des pratiques professionnelles
Définition de l'analyse des pratiques professionnelles Gott ist die quelle des lebens
Gott ist die quelle des lebens Milieu de dobell et laidlaw
Milieu de dobell et laidlaw Tu es la plus belle des femmes marie souviens toi
Tu es la plus belle des femmes marie souviens toi Falep bastia
Falep bastia Aufbau des ohres
Aufbau des ohres échelle québécoise des comportements adaptatifs
échelle québécoise des comportements adaptatifs Le temps des cerises montand
Le temps des cerises montand Interest and hobby
Interest and hobby Nicée constantinople
Nicée constantinople Conception des ihm
Conception des ihm Architecture des ordinateurs
Architecture des ordinateurs Hydratation alcyne
Hydratation alcyne Chiasme
Chiasme Cahier des charges intranet
Cahier des charges intranet Abitur bayern 2023 gymnasium
Abitur bayern 2023 gymnasium Personnages manon des sources
Personnages manon des sources Alle sind mitreisende im zug des lebens
Alle sind mitreisende im zug des lebens Les pronoms personnels atones et toniques
Les pronoms personnels atones et toniques Nano puissance de 10
Nano puissance de 10 Ouvrir des chemins d'évangile
Ouvrir des chemins d'évangile Le dernier jour d'un condamné chapitre 49
Le dernier jour d'un condamné chapitre 49 Université de jijel faculté des sciences exactes
Université de jijel faculté des sciences exactes Hept oct non dec
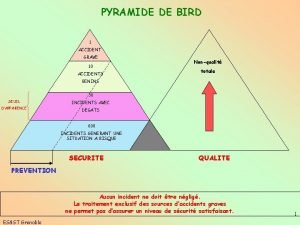
Hept oct non dec Pyramide de bird exemple
Pyramide de bird exemple Nachweis zur begründung des ortswunsches
Nachweis zur begründung des ortswunsches Le chatelier chemie
Le chatelier chemie Préservation des traces et indices
Préservation des traces et indices Claus tieber
Claus tieber Compressibilité des gaz niveau 2
Compressibilité des gaz niveau 2 Tableau de classification des nuages
Tableau de classification des nuages Projection orthogonale dessin technique
Projection orthogonale dessin technique Les racines parfaites
Les racines parfaites Marketing approfondi
Marketing approfondi Anatomie poussin
Anatomie poussin Differentes familles d instruments de musique
Differentes familles d instruments de musique éthique des vertus
éthique des vertus Marché des capitaux
Marché des capitaux Chambre nationale des commissaires aux comptes
Chambre nationale des commissaires aux comptes Slidetodoc.com
Slidetodoc.com Service des inscriptions nanterre
Service des inscriptions nanterre Comparer deux pourcentages
Comparer deux pourcentages Méthode des 5 pourquoi
Méthode des 5 pourquoi Béton bc5
Béton bc5 Karima charmi
Karima charmi Expansion systolique des jugulaires
Expansion systolique des jugulaires Identification des dangers
Identification des dangers Affaire des placards
Affaire des placards Atmungssystem des menschen
Atmungssystem des menschen Bureau de coordination des affaires humanitaires
Bureau de coordination des affaires humanitaires Migration des ions
Migration des ions Les lois de la chimie
Les lois de la chimie Ich bin das brot des lebens
Ich bin das brot des lebens Muscle extenseur des doigts
Muscle extenseur des doigts Des gorman
Des gorman Waldgeist hofheim bembel des todes
Waldgeist hofheim bembel des todes Das stufenalter des menschen
Das stufenalter des menschen Kaufhaus des bundes
Kaufhaus des bundes Exposé sur le dauphin
Exposé sur le dauphin Modes of des
Modes of des Norme prise de courant
Norme prise de courant Regime de neutre it
Regime de neutre it Vocabulaire des fractions
Vocabulaire des fractions Psychosociologie des organisations
Psychosociologie des organisations Aufgaben des betriebsrates
Aufgaben des betriebsrates Structure des fables de la fontaine
Structure des fables de la fontaine Erfinderin des kaffeefilters
Erfinderin des kaffeefilters Collectif autonome des carrefour jeunesse emploi du québec
Collectif autonome des carrefour jeunesse emploi du québec Informatiksteuerungsorgan des bundes
Informatiksteuerungsorgan des bundes Régime des partis
Régime des partis Tomate maladie
Tomate maladie Quantitätsgleichung definition
Quantitätsgleichung definition Phrases avec le subjonctif
Phrases avec le subjonctif Traitement des objections vente
Traitement des objections vente Pose des fourreaux
Pose des fourreaux Loi du 4 mars 2004 transmissions ciblées
Loi du 4 mars 2004 transmissions ciblées Groupe star des basses laurentides
Groupe star des basses laurentides Institut des sciences du mouvement
Institut des sciences du mouvement Loi des mailles exercice
Loi des mailles exercice Démonstration petit théorème de fermat
Démonstration petit théorème de fermat Noir chlorazol
Noir chlorazol Fait des comparaisons avec les adjectifs
Fait des comparaisons avec les adjectifs Menstruatiekalender thuisarts
Menstruatiekalender thuisarts Calepin des nombres mhm
Calepin des nombres mhm Triumph des willens
Triumph des willens Adoration
Adoration Departement des innern st. gallen
Departement des innern st. gallen Ibupofen
Ibupofen Evolution des ponts
Evolution des ponts Ordonnancement tourniquet
Ordonnancement tourniquet Weil verb am ende
Weil verb am ende 1111 invasion des huns
1111 invasion des huns Cartographie processus ressources humaines
Cartographie processus ressources humaines Reizleitungssystem des herzens
Reizleitungssystem des herzens Comprendre la gestion des fichiers
Comprendre la gestion des fichiers Il est des moments dans la vie
Il est des moments dans la vie Terre des hommes alemanha
Terre des hommes alemanha Gott dreieck
Gott dreieck Je ferai de toi un pecheur d'homme
Je ferai de toi un pecheur d'homme Trommsdorff modell
Trommsdorff modell Les amis sont des compagnons de voyage
Les amis sont des compagnons de voyage Les 7 precautions standards d'hygiene
Les 7 precautions standards d'hygiene Avalanche effect in des with example
Avalanche effect in des with example Dilatation des espaces de virchow robin risques
Dilatation des espaces de virchow robin risques Règle des segments inverses exercice
Règle des segments inverses exercice Voyage au pays des nombres
Voyage au pays des nombres Avr bpa entgelttabelle 2021 sachsen
Avr bpa entgelttabelle 2021 sachsen Mouvement classique des précieuses
Mouvement classique des précieuses Taille des mirabelliers
Taille des mirabelliers Exemple remerciements rapport de stage
Exemple remerciements rapport de stage Ti-jacques la guerre des tuques
Ti-jacques la guerre des tuques Confronter des documents
Confronter des documents Le chant des partisans léo ferré
Le chant des partisans léo ferré Spielvermittlungskonzepte
Spielvermittlungskonzepte Physaire
Physaire Phase conceptuelle
Phase conceptuelle Ordre des tubes de prélèvement
Ordre des tubes de prélèvement Processus 4
Processus 4 La lune est large et pale et semble se hater
La lune est large et pale et semble se hater En croyant à des fleurs souvent on les fait naître
En croyant à des fleurs souvent on les fait naître Violette toussaint
Violette toussaint Stade des opérations formelles
Stade des opérations formelles Décloisonnement des activités
Décloisonnement des activités Centralisation des logs
Centralisation des logs Verstärker verlust modell lewinsohn
Verstärker verlust modell lewinsohn Vascularisation glande surrénale
Vascularisation glande surrénale Couleur qui sont des choses
Couleur qui sont des choses Abv des 7
Abv des 7 Abschluss des kaufvertrages alternativen
Abschluss des kaufvertrages alternativen Phobie des hippopotames
Phobie des hippopotames Je sers un sauveur tendre
Je sers un sauveur tendre Aufbau des innenohrs
Aufbau des innenohrs Mapping concurrentiel automobile
Mapping concurrentiel automobile Classification des produits carnés
Classification des produits carnés Comment s'habillent les hommes préhistoriques
Comment s'habillent les hommes préhistoriques Tableau des aliments pauvres en purines
Tableau des aliments pauvres en purines Des conseils pour la vie
Des conseils pour la vie Liste des figures rapport de stage
Liste des figures rapport de stage Exemple carnet de suivi des apprentissages
Exemple carnet de suivi des apprentissages Hotel des mines faymoreau
Hotel des mines faymoreau Musee des beaux arts analysis
Musee des beaux arts analysis échelle d'affirmation de soi de rathus
échelle d'affirmation de soi de rathus Les amis sont des anges qui nous soulèvent
Les amis sont des anges qui nous soulèvent 5 bücher des bgb
5 bücher des bgb Infinitif aller
Infinitif aller Ifsi hus
Ifsi hus