Terminale Si Dynamique 1 Repre Galilen Dfinitions Repre

Terminale Si Dynamique 1

Repère Galiléen Définitions Repère absolu Repère de Copernic ou Repère héliocentrique Repère de Galiléen Repère fixe par rapport à l’univers (? ? ? ) Repère fixe par rapport au système solaire Repère en translation rectiligne uniforme par rapport au repère de Copernic Pour nos études Un repère fixe par rapport à la terre sera supposé galiléen

Dynamique du point Principe fondamental de la dynamique = 2ème loi de Newton Enoncé Soit un point Matériel P, de masse m, en mouvement par rapport à un repère galiléen Rg, alors la somme des efforts extérieurs qui agissent sur la particule est égale à sa masse multipliée par son accélération. Mathématiquement NEWTON Portrait par Enoch Seeman en 1726 « Force » d’inertie Pseudo Pb de statique ! Attention

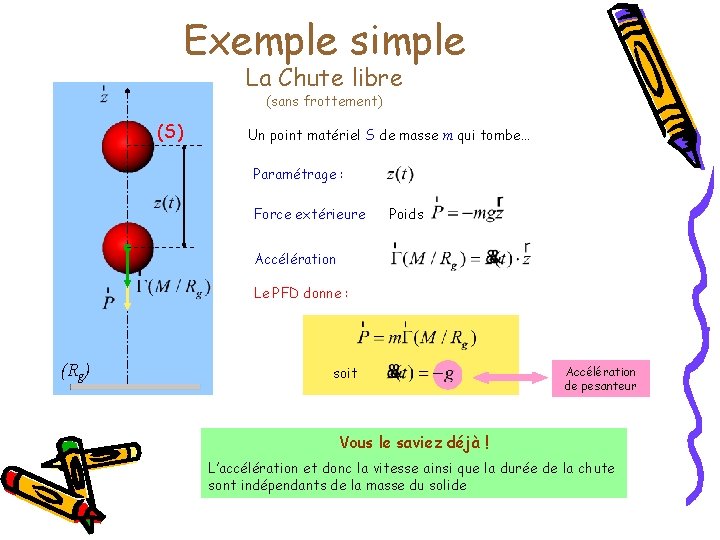
Exemple simple La Chute libre (sans frottement) (S) Un point matériel S de masse m qui tombe… Paramétrage : Force extérieure Poids Accélération Le PFD donne : (Rg) soit Accélération de pesanteur Vous le saviez déjà ! L’accélération et donc la vitesse ainsi que la durée de la chute sont indépendants de la masse du solide

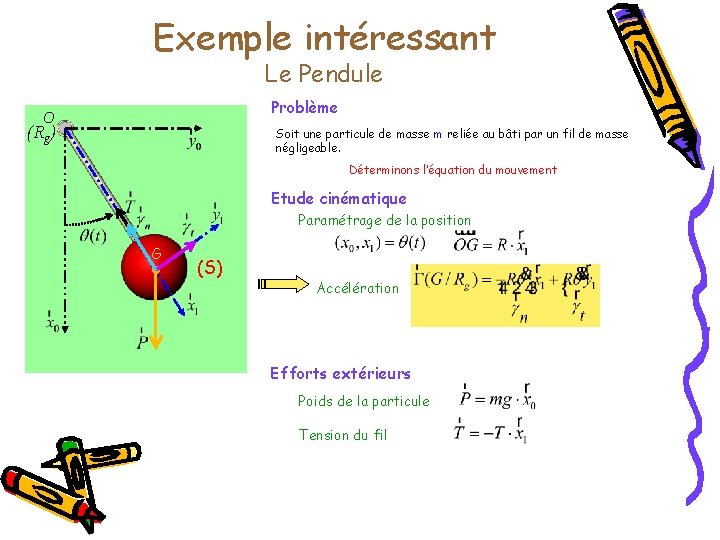
Exemple intéressant Le Pendule Problème O (Rg) Soit une particule de masse m reliée au bâti par un fil de masse négligeable. Déterminons l’équation du mouvement Etude cinématique Paramétrage de la position G (S) Accélération Efforts extérieurs Poids de la particule Tension du fil

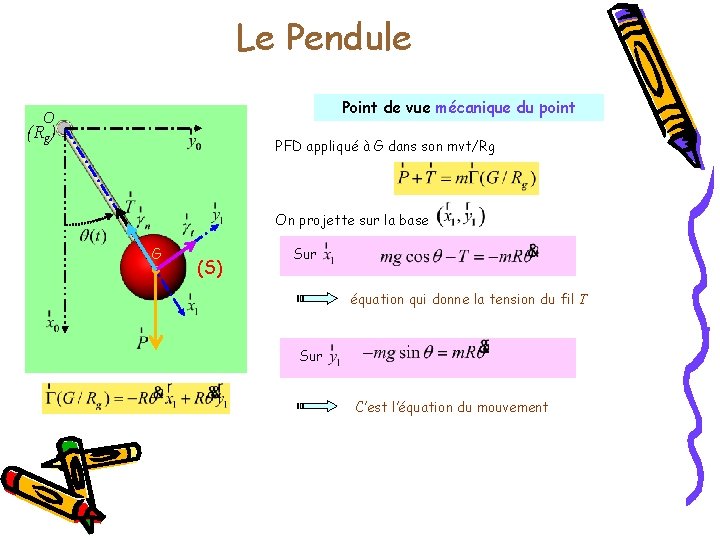
Le Pendule Point de vue mécanique du point O (Rg) PFD appliqué à G dans son mvt/Rg On projette sur la base G (S) Sur équation qui donne la tension du fil T Sur C’est l’équation du mouvement

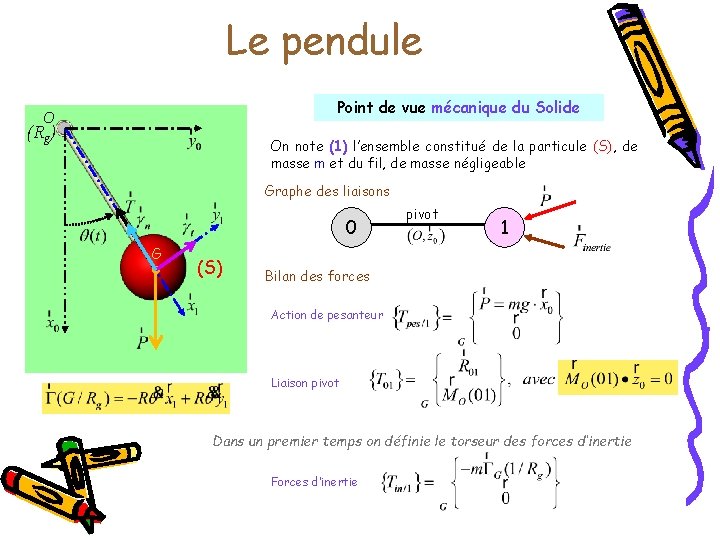
Le pendule Point de vue mécanique du Solide O (Rg) On note (1) l’ensemble constitué de la particule (S), de masse m et du fil, de masse négligeable Graphe des liaisons 0 G (S) pivot 1 Bilan des forces Action de pesanteur Liaison pivot Dans un premier temps on définie le torseur des forces d’inertie Forces d’inertie

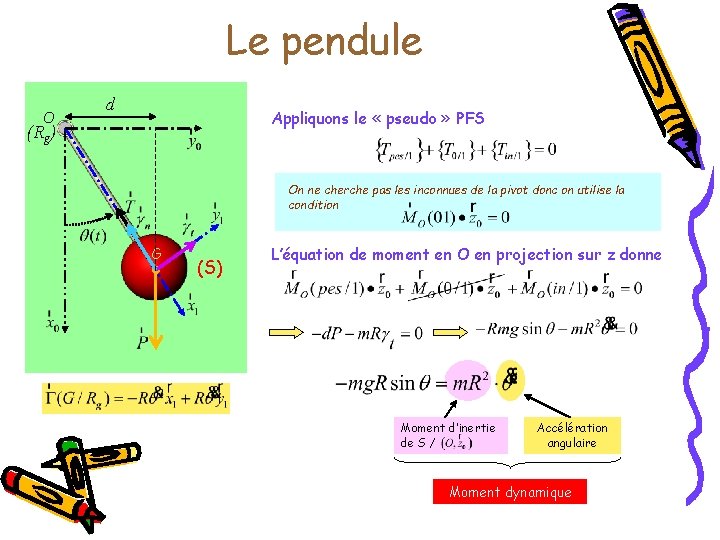
Le pendule O d Appliquons le « pseudo » PFS (Rg) On ne cherche pas les inconnues de la pivot donc on utilise la condition G (S) L’équation de moment en O en projection sur z donne Moment d’inertie de S / Accélération angulaire Moment dynamique

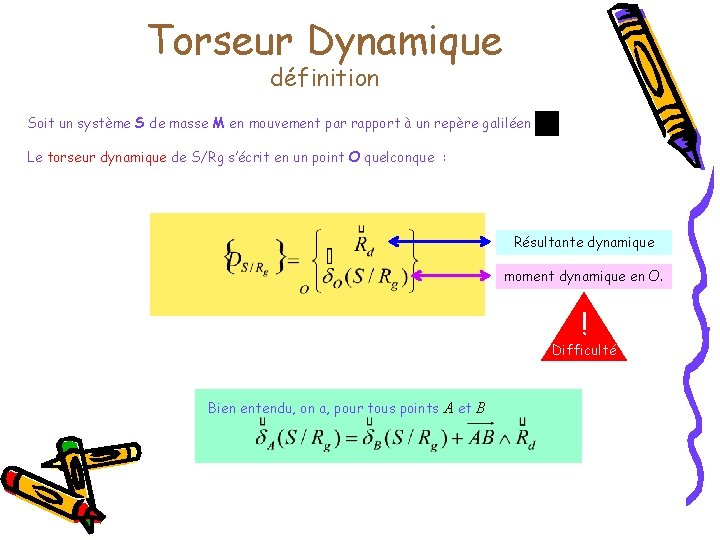
Torseur Dynamique définition Soit un système S de masse M en mouvement par rapport à un repère galiléen Le torseur dynamique de S/Rg s’écrit en un point O quelconque : Résultante dynamique moment dynamique en O. ! Difficulté Bien entendu, on a, pour tous points A et B

Dynamique du solide Principe Fondamental de la Dynamique ( PFD ) Enoncé Soit un Solide (S), de masse M et de centre d’inertie G, en mouvement par rapport à un repère galiléen Rg, alors la somme des torseurs des efforts extérieurs qui agissent sur (S) est égale au torseur dynamique de (S) dans son mouvement par rapport à Rg Mathématiquement Théorème de la Résultante Dynamique – (TRD) Théorème du Moment Dynamique – (TMD)

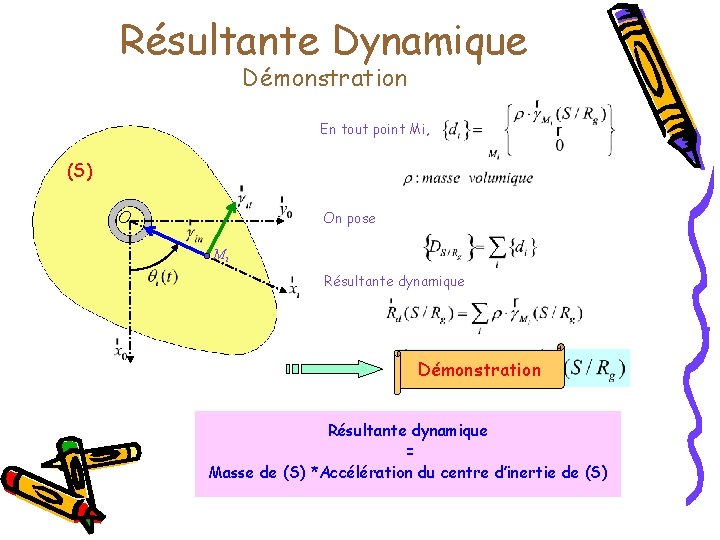
Résultante Dynamique Démonstration En tout point Mi, (S) O On pose Mi Résultante dynamique Démonstration Résultante dynamique = Masse de (S) *Accélération du centre d’inertie de (S)

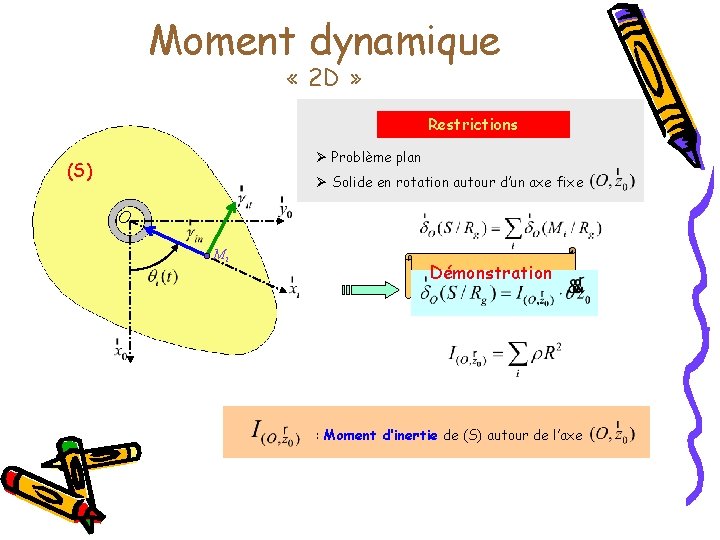
Moment dynamique « 2 D » Restrictions Ø Problème plan (S) Ø Solide en rotation autour d’un axe fixe O Mi Démonstration : Moment d’inertie de (S) autour de l’axe

Moment dynamique « 3 D » Restrictions Ø Solide en rotation autour d’un axe fixe Cj Ø Plan de symétrie de (S) O Modèle : Le solide (S) est un « empilement » de sections Sj On note D’après ce qui précède, on peut écrire, en tout point Cj Gj Cj Démonstration Avec Produit d’inertie

Moment dynamique Analyse du moment d’inertie Cas général d’un solide en rotation autour d’un axe fixe Pour lancer ou arrêter un solide en rotation, il faut lutter sur l’axe de rotation contre un « couple d’inertie » proportionnel q à l’accélération angulaire q au moment d’inertie Moment d’inertie du solide (S) autour de l’axe Représente la répartition de la masse autour de l’axe

Moment dynamique Analyse des produits d’inertie Si la masse est « mal » répartie. = le centre d’inertie de chacune des sections n’est pas sur l’axe de rotation « couples » d’inertie l’axe de rotation. Proportionnel : q à l’accélération angulaire q à la vitesse angulaire q aux produits d’inertie La direction des couples tourne avec le solide VIBRATIONS Si la masse est bien répartie. = le centre d’inertie de chacune des sections est sur l’axe de rotation Pas de couple l’axe de rotation. L’axe est dit principal d’inertie Le solide est équilibré dynamiquement

Paramètres d’inertie Remarques Mécanique du point et Mécanique du solide Masse du solide : M en kg Position du centre d’inertie : G Mécanique du solide Moment d’inertie et Produit d’inertie : en kg. m 2 Un repère étant lié au solide, on peut définir q 3 moments d’inertie : un pour chaque axe q 3 produits d’inertie Car symétrique Ixx Iyy Izz Pxy Pyz Pxz ou Ixy Iyz Izx Ces 6 termes permettent de calculer les moments d’inertie et les produits d’inertie pour n’importe quel autre axe.

Paramètres d’inertie sous MOTIONWORKS Pour chaque corps en mouvement Un repère lié au solide est créé en même temps que la liaison Masse Position du centre d’inertie Produits d’inertie Moments d’inertie

Dynamique à savoir parfaitement Le PFD Solide en translation rectiligne Torseur dynamique définit en G (centre d’inertie) Solide en Rotation Autour d’un axe fixe Torseur dynamique définit en C En un point O quelconque sera une donnée Le solide sera toujours équilibré Et si possible « sentir » la chose