En mcanique quantique llectron nest plus dcrit par

En mécanique quantique, l'électron n'est plus décrit par les vecteurs position et vitesse. Il est décrit par une fonction d'onde, notée E est l ’énergie associée à la fonction d’onde

En mécanique quantique, l'électron n'est plus décrit par les vecteurs position et vitesse. Il est décrit par une fonction d'onde, notée E est l ’énergie associée à la fonction d’onde

En mécanique quantique, l'électron n'est plus décrit par les vecteurs position et vitesse. Il est décrit par une fonction d'onde, notée H est l’hamiltonien, opérateur mathématique qui est caractéristique de l’électron (quantité de mouvement, énergie potentielle) E est l ’énergie associée à la fonction d’onde

En mécanique quantique, l'électron n'est plus décrit par les vecteurs position et vitesse. Il est décrit par une fonction d'onde, notée H est l’hamiltonien, opérateur mathématique qui est caractéristique de l’électron (quantité de mouvement, énergie potentielle) E est l ’énergie associée à la fonction d’onde

La mécanique quantique n’est pas déterministe On ne peut estimer qu’une certaine probabilité de rencontrer l’électron dans une certaine région de l’espace.

d = petit élément de volume d = r 2. sin. dr. d. d

d = petit élément de volume d = r 2. sin. dr. d. d

La mécanique quantique n’est pas déterministe On ne peut estimer qu’une certaine probabilité de rencontrer l’électron dans une certaine région de l’espace. | |2 représente la densité de probabilité de présence de l'électron La probabilité d. P de trouver l'électron dans un volume infinitésimal d centré autour d'un point M 0 de coordonnées (x 0, y 0, z 0) vaut d. P = | |2. d

La mécanique quantique n’est pas déterministe On ne peut estimer qu’une certaine probabilité de rencontrer l’électron dans une certaine région de l’espace. | |2 représente la densité de probabilité de présence de l'électron La probabilité d. P de trouver l'électron dans un volume infinitésimal d centré autour d'un point M 0 de coordonnées (x 0, y 0, z 0) vaut d. P = | |2. d

d. P = | |2. d d = petit élément de volume d = r 2. sin. dr. d. d

La mécanique quantique n’est pas déterministe On ne peut estimer qu’une certaine probabilité de rencontrer l’électron dans une certaine région de l’espace. | |2 représente la densité de probabilité de présence de l'électron La probabilité d. P de trouver l'électron dans un volume infinitésimal d centré autour d'un point M 0 de coordonnées (x 0, y 0, z 0) vaut d. P = | |2. d

L’atome d’hydrogène en mécanique quantique Symétrie sphérique On écrit la fonction d’onde sous lal forme

L’atome d’hydrogène en mécanique quantique On montre que (r, , ) s’écrit sous la forme

L’atome d’hydrogène en mécanique quantique On montre que (r, , ) s’écrit sous la forme R(r ) : fonction de la distance à l’origine = distance de l’électron au noyau

L’atome d’hydrogène en mécanique quantique On montre que (r, , ) s’écrit sous la forme R(r ) : fonction de la distance à l’origine = distance de l’électron au noyau Y( , ) : fonction de la direction dans laquelle on regarde

L’atome d’hydrogène en mécanique quantique On montre que (r, , ) s’écrit sous la forme R(r ) : fonction de la distance à l’origine = distance de l’électron au noyau Y( , ) : fonction de la direction dans laquelle on regarde On montre que (r, , ) dépend de 3 paramètres, ou encore nombres quantiques : n, l, m

L’atome d’hydrogène en mécanique quantique On montre aussi que :

L’atome d’hydrogène en mécanique quantique On montre aussi que : La condition impose que :

L’atome d’hydrogène en mécanique quantique On montre aussi que : La condition impose que :

L’atome d’hydrogène en mécanique quantique On montre aussi que : La condition donc impose que :

L’atome d’hydrogène en mécanique quantique On montre aussi que : La condition donc impose que :

L’atome d’hydrogène en mécanique quantique On montre aussi que : La condition donc Soit encore : impose que :

L’atome d’hydrogène en mécanique quantique Les nombres quantiques n, l, m (ou ml) : n : entier naturel non nul l : entier naturel : 0 ≤ l ≤ n-1 m : entier relatif : - l ≤ m ≤ + l (nombre quantique principal) (nombre quantique secondaire) (nombre quantique magnétique)

L’atome d’hydrogène en mécanique quantique Les nombres quantiques n, l, m (ou ml) : n : entier naturel non nul l : entier naturel : 0 ≤ l ≤ n-1 m : entier relatif : - l ≤ m ≤ + l Rappel : (nombre quantique principal) (nombre quantique secondaire) (nombre quantique magnétique)

L’atome d’hydrogène en mécanique quantique Les nombres quantiques n, l, m (ou ml) : n : entier naturel non nul l : entier naturel : 0 ≤ l ≤ n-1 m : entier relatif : - l ≤ m ≤ + l (nombre quantique principal) (nombre quantique secondaire) (nombre quantique magnétique) Rappel : Pour les atomes polyélectroniques, on a vu que l’énergie dépendait de n et l.

Les orbitales atomiques sont les solutions de l'équation de Schrödinger

Les orbitales atomiques sont les solutions de l'équation de Schrödinger Les orbitales atomiques (OA) dépendent de trois variables il est impossible de les représenter en deux dimensions nécessité d'effectuer des représentations en coupe

Les orbitales atomiques sont les solutions de l'équation de Schrödinger Les orbitales atomiques (OA) dépendent de trois variables il est impossible de les représenter en deux dimensions nécessité d'effectuer des représentations en coupe

Les orbitales atomiques sont les solutions de l'équation de Schrödinger Les orbitales atomiques (OA) dépendent de trois variables il est impossible de les représenter en deux dimensions nécessité d'effectuer des représentations en coupe 2 p-1, 2 p 0 et 2 p+1 sont des fonctions complexes Par combinaisons linéaires, on obtient trois OA réelles : {2 px , 2 py , 2 pz}

Les orbitales atomiques sont les solutions de l'équation de Schrödinger Les orbitales atomiques (OA) dépendent de trois variables il est impossible de les représenter en deux dimensions nécessité d'effectuer des représentations en coupe Les 5 orbitales de type d (n ≥ 3 ; l = 2 ; m = -2, -1, 0, +1, +2) subissent le même traitement, et sont notées sous les labels dz 2, dx 2 -y 2, dxy, dyz et dxz

Expressions des orbitales (n = 1 et 2)

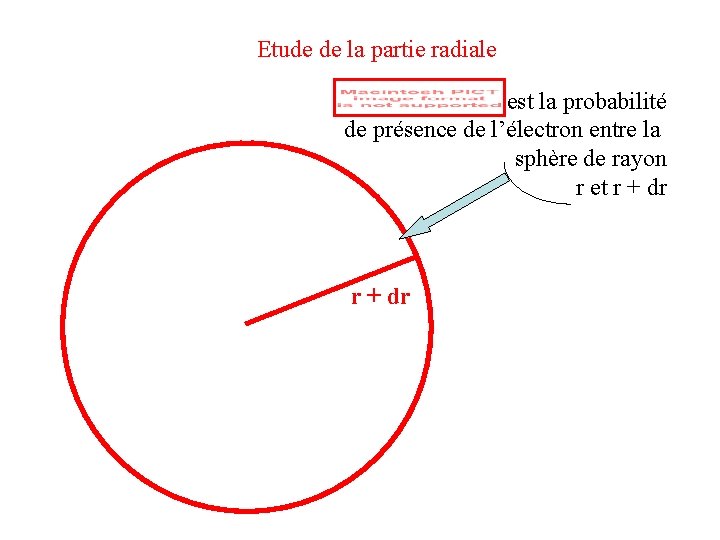
Etude de la partie radiale Notion de densité de probabilité radiale

Etude de la partie radiale Notion de densité de probabilité radiale

Etude de la partie radiale Notion de densité de probabilité radiale | |2 : densité de probabilité de présence de l'électron

Etude de la partie radiale Notion de densité de probabilité radiale | |2 : densité de probabilité de présence de l'électron densité de probabilité de présence radiale de l'électron

Etude de la partie radiale Notion de densité de probabilité radiale | |2 : densité de probabilité de présence de l'électron d. P = | |2. d densité de probabilité de présence radiale de l'électron

Etude de la partie radiale Notion de densité de probabilité radiale | |2 : densité de probabilité de présence de l'électron d. P = | |2. d densité de probabilité de présence radiale de l'électron

Etude de la partie radiale est la probabilité de présence de l’électron entre la sphère de rayon r et r + dr

Etude de la partie radiale Notion de densité de probabilité radiale | |2 : densité de probabilité de présence de l'électron d. P = | |2. d densité de probabilité de présence de l'électron densité de probabilité de présence radiale de l'électron

Etude de la partie radiale Notion de densité de probabilité radiale | |2 : densité de probabilité de présence de l'électron densité de probabilité de présence radiale de l'électron d. P = | |2. d densité de probabilité de présence de l'électron densité de probabilité de présence radiale de l'électron

Densités de probabilité radiale

Densités de probabilité radiale

Densités de probabilité radiale

Etude de la partie radiale Maximum pour la densité de probabilité radiale ◊n=1: ◊n=2: ◊n=3: r = a 0 r ≈ 5 a 0 r ≈ 11 a 0

Etude de la partie radiale Maximum pour la densité de probabilité radiale ◊n=1: ◊n=2: ◊n=3: Définition : r = a 0 r ≈ 5 a 0 r ≈ 11 a 0 le rayon d'une fonction propre est le rayon de maximum de densité de probabilité de présence radiale

Etude de la partie radiale Maximum pour la densité de probabilité radiale ◊n=1: ◊n=2: ◊n=3: Définition : r = a 0 r ≈ 5 a 0 r ≈ 11 a 0 le rayon d'une fonction propre est le rayon de maximum de densité de probabilité de présence radiale Le rayon d'une fonction propre ◊ croît avec n ◊ dépend peu de l Plus les électrons sont sur une couche élevée, plus ils sont loins du noyau

Etude de la partie angulaie La partie radiale R(r) de la fonction propre permettait de visualiser "l'extension" du nuage électronique. La partie angulaire permet de donner une idée des directions priviligiées pour la densité électronique • Yl, m ne dépend pas de n résultats trouvés valables pour tout n. • Yl, m = Yl, m ( , ) nécessité de tracer des fonction en coupe.

Partie angulaire d’une orbitale s

Partie angulaire d’une orbitale s

Partie angulaire d’une orbitale s

Partie angulaire d’une orbitale pz

Partie angulaire d’une orbitale pz

Partie angulaire d’une orbitale pz

Partie angulaire d’une orbitale pz

Partie angulaire d’une orbitale py

Partie angulaire d’une orbitale py

Partie angulaire d’une orbitale py

Partie angulaire d’une orbitale py

Les courbes d’isodensité électronique Idée : avoir accès à l’allure de la densité électronique associée à chaque fonction d’onde

Les courbes d’isodensité électronique Idée : avoir accès à l’allure de la densité électronique associée à chaque fonction d’onde densité de probabilité de présence de l'électron

Les courbes d’isodensité électronique Idée : avoir accès à l’allure de la densité électronique associée à chaque fonction d’onde densité de probabilité de présence de l'électron Définition : Les courbes d'isodensité électronique sont des surfaces pour lesquelles | |2 = k

Courbes d’isodensité électronique d’une orbitale pz (Tracé sur MAPLE)

Les courbes d’isodensité électronique

Les courbes d’isodensité électronique C'est la représentation des courbes d'isodensité qui donne la meilleure idée de l'extension spatiale de la densité électronique pour chaque orbitale

Représentation d’une orbitale

Représentation d’une orbitale

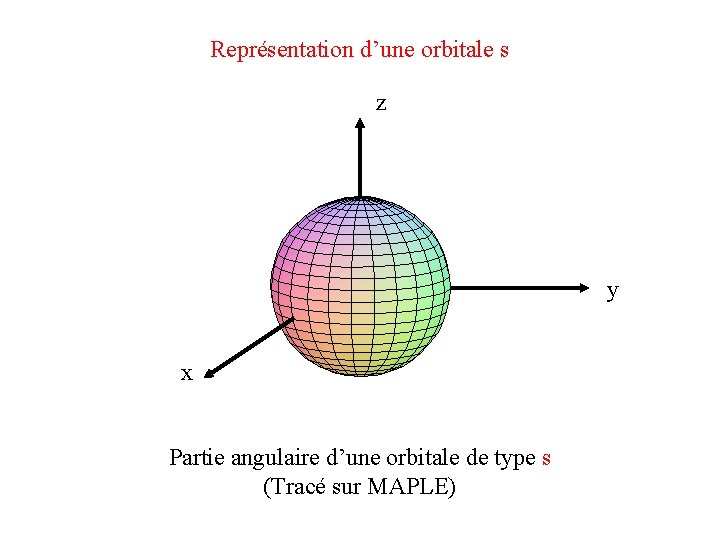
Représentation d’une orbitale s

Représentation d’une orbitale s z y x Partie angulaire d’une orbitale de type s (Tracé sur MAPLE)

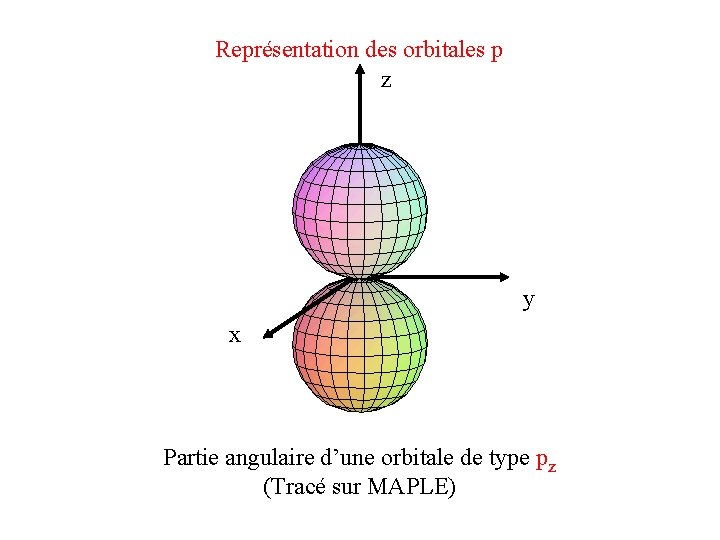
Représentation des orbitales p

Représentation des orbitales p z y x Partie angulaire d’une orbitale de type pz (Tracé sur MAPLE)

Représentation des orbitales d

Représentation des orbitales d z y x Partie angulaire d’une orbitale de type dxy (Tracé sur MAPLE)

Représentation des orbitales d

Représentation des orbitales d

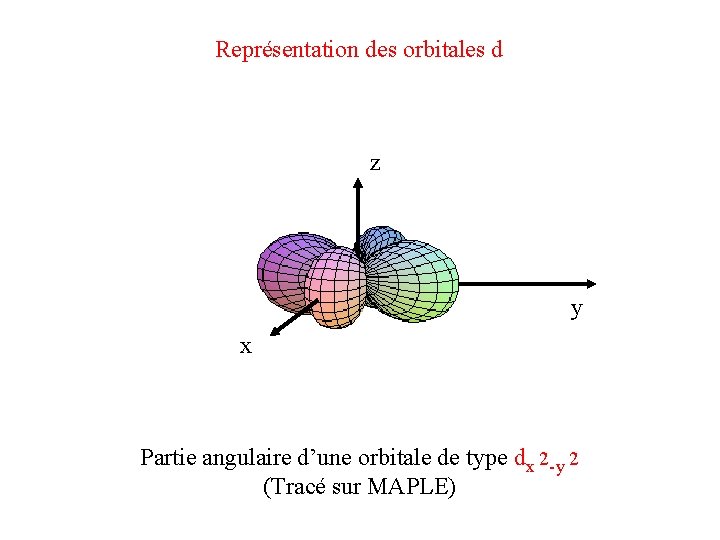
Représentation des orbitales d z y x Partie angulaire d’une orbitale de type dx 2 -y 2 (Tracé sur MAPLE)

Représentation des orbitales d

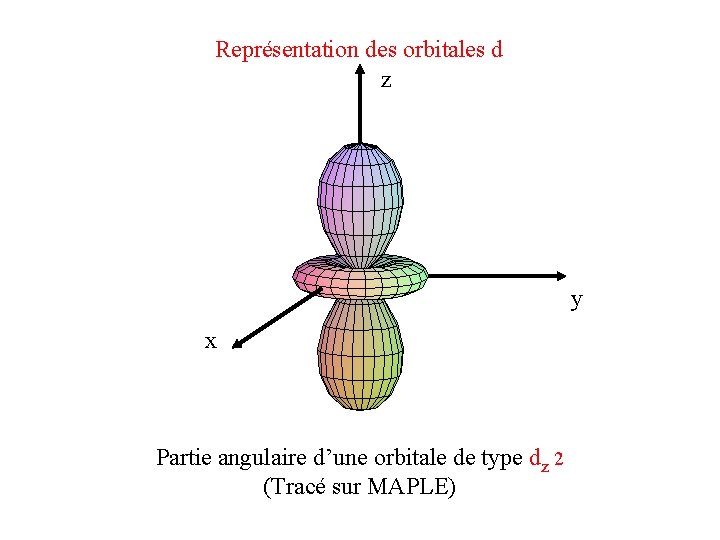
Représentation des orbitales d z y x Partie angulaire d’une orbitale de type dz 2 (Tracé sur MAPLE)

Représentation des orbitales d