Mcanique Quantique I Chapitre VVIVII http dpnc unige








































































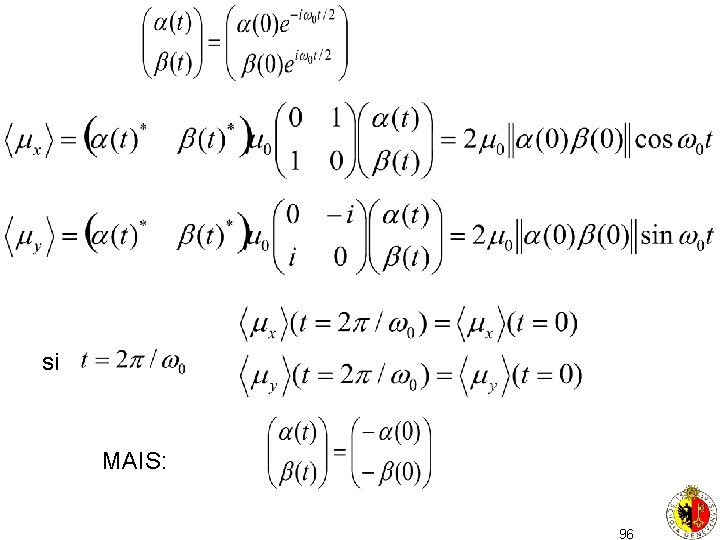












- Slides: 117

Mécanique Quantique I -- Chapitre V-VI-VII http: //dpnc. unige. ch/users/blondel/mecanique-quantique/ cours-VII. pdf 1

à une particule on avait associé une amplitude de probabilité (A. P. ) (ou fonction d’onde) qui est un élément d’un espace de Hilbert (EH =L 2(R 3) , fonctions de carré sommable sur R 3 ) Un Espace de Hilbert est un espace vectoriel sur le corps des complexes, muni d’un produit scalaire Hermitien. On a vu que la donnée de ou de sont équivalentes (transformées de Fourier l’une de l’autre) ce sont deux des représentations possibles d’un même objet mathématique qu’on appelle vecteur d’état Dirac a nommé ces objets kets 2

à une particule on associe une A. P. , ou vecteur d’état ou ket qui est un élément d’un espace de Hilbert Un espace de Hilbert est un espace vectoriel sur le corps des complexes, muni d’un produit scalaire Hermitien le produit scalaire de par est noté il a la symétrie Hermitienne la norme d’un vecteur d’état est par définition (si on parle d’une particule) 3

le produit scalaire de par est noté est appelé bra un bra est un élément de l’espace dual EH* (ensemble des applications linéaires continues définies sur EH ) il y a correspondance bi-univoque entre EH et EH* donc on parle des mêmes objets mathématiques (et ~physiques) 4

exemple I un espace de Hilbert de dimension finie est un espace Hermitien les vecteurs peuvent se représenter comme des matrices colonne de coefficients complexes |ket> = vecteur colonne, <bra| = vecteur ligne des complexes conjugués 5

exemple II EH =L 2(R 3) , fonctions de carré sommable sur R 3 produit scalaire hermitien norme 6

OPERATEURS grandeur physique à mesurer opérateur hermitien opérateur= application linéaire sur l’espace de Hilbert | >= ’> > et ’> EH (dans un espace hermitien c’est une matrice de dimension nxn) on fait souvent l’opération < ( | >)= (< )| >= < | > qui est appelée élement de matrice de entre et valeur moyenne de sur | > : <a> = < | > 7

en notation matricielle: 8

operateur adjoint ou conjugué Hermitique † |u> et |v> EH (transposé et complexe conjugué) un opérateur est auto-adjoint ou Hermitien si = † pour une matrice: Aij= Aji* si = † les valeurs moyennes sont réelles <a> = <u u> = <u † u> = <a>* 9

opérateur position et impulsion EH =L 2(R 3) , fonctions de carré sommable sur R 3 l’opérateur position est donc Hermitien 10

opérateur position et impulsion EH =L 2(R 3) , fonctions de carré sommable sur R 3 on intègre parties l’opérateur impulsion est donc aussi Hermitien le Hamiltonien est aussi un opérateur Hermitien 11

Vecteurs propres et valeurs propres si = † les valeurs propres sont réelles : <A> = < > = = < † >*= * les vecteurs propres correspondant à deux valeurs propres différentes sont orthogonaux < > = < ( >)= < > = (< ) >= < > =0 si 12

Théorème spectral (théorème de Riesz): l’ensemble { , r >} des vecteurs propres orthonormés d’un opérateur Hermitien forme une base Hermitienne de l’espace de Hilbert voir dans le cours l’exemple des états stationnaires de l’oscillateur harmonique qui forment une base de l’expace des fonctions de EH =L 2(R) ceci veut dire que: on peut décomposer tout vecteur de EH comme combinaison linéaire des vecteurs propres d’un opérateur Hermitien 13

projecteur l’opérateur In> <n. I permet de calculer la projection d’un élément de l’espace sur le vecteur In> > = Cn n> <n > = Cn Cn n> = In> <n > = (In> <n ) I > 14

Théorème spectral (théorème de Riesz): soit = † et ses valeurs propres i i=1, …n à chaque valeur propre correspond un sous espace propre (en général ce sous espace propre n’est pas de dimension 1) de dimension n . A cette dimension n on fait correspondre un indice r =1, …n On trouve une base orthonormée du sous espace propre correspondant à la valeur propre dont les vecteurs sont , r > r =1, …n l’ensemble des vecteurs propres de est { i, r i > r i =1, …n i } i=1, …n si l’espace est de dimension finie N, i=1. . n n i =N 15

si on a ainsi défini les vecteurs de base n> on peut écrire tout état sous la forme u> = Cn n> et <u = Cn* <n d’où <u. Iu> = ICn. I 2 l’ensemble des Cn définit complètement l’etat Iu> et constitue une nouvelle représentation de Iu> si Iv> = Dn n> le produit scalaire <v. Iu> s’écrit <v. Iu> = Dn* Cn 16

par exemple l’ensemble des fonctions propres du Hamiltonien de l’oscillateur Harmonique: (revoir cours chap. 4 p. 82) n=0, 1, 2… constitue une base des fonctions de EH =L 2(R 3) , que l’on pourra noter n= In> on peut reprendre les expressions des opérateurs x et px 17

soit on voit que l’application de x ou px fait passer d’un état In> à un mélange de In-1> et In+1> 18

on peut écrire ces récurrences sous forme matricielle 19

exercice: utiliser la relation pour écrire le Hamiltonien et vérifier qu’on retrouve bien 20

Autre exemple: fonctions propres du Hamiltonien d’un puits bords infinis à 3 D qui sont bien des bases des fonctions définies sur un segment et qui s’annulent au bords 21

cette fois la représentation sous forme de bra-kets doit tenir compte de ce qu’on augmente la dimension de l’espace produit tensoriel d’espaces Ex = fonctions de carré sommable sur [0, L] E = fonctions de carré sommable sur [0, Lx]x [0, Ly]x [0, Lz] = Ex Ey Ez pour le Hamiltonien considéré les fonctions propres sont 22

remarquer que si Lx=Ly certaines valeurs de l’énergie correspondent à plusieurs paires de nombres nx et ny (ex. nx=1, ny=2 aura la même énergie que nx=2, ny=1) c’est un exemple de dégénerescence ou l’on doit donner un autre nombre quantique E, soit r dans le cas présent on donnera nx ny, nz ou E, ny, nz pour caractériser un état. 23

Mesure d’une grandeur physique on ne trouvera comme résultat possible que les valeurs propres de pour un état I > = C I > tel que I >= I > la probabilité de mesurer sera P = II< I >II 2 =IIC II 2 Après mesure, si le système existe encore, il sera dans l’état I > les valeurs dépendent de l’opérateur, les probabilités dépendent de l’état du système valeur moyenne des résultats de la mesure <A>=< IAI > = < I A C I > = C * C < I > = IIC II 2 = P 24

Evolution dans le temps Pour un système statique (H ne dépend pas du temps) l’évolution dans le temps de l’amplitude de probabilité d’un système s’obtient en décomposant le vecteur d’état I > sur la base des états propres I n > du Hamiltonien (Etats stationaires) Dans le cas plus général, l’évolution dans le temps s’obtient en appliquant l’équation de Schrödinger 25

Paradoxe! Il semble y avoir deux types d’évolution dans le temps. 1. Celui donné par l’équation de Schrödinger l’évolution est continue, du type 2. l’évolution déterminée par une ‘mesure’, qui est discontinue “Réduction du paquet d’ondes”. Voir la discussion ‘epistémologique’ dans le livre sur les tentatives visant à réconcilier ces deux modes. 26

Avant la mesure, le système évolue mais l’information que l’on a ne change pas. La prédiction du résultat de la prochaine mesure varie de façon continue (et ne varie pas pour un état stationnaire). Après la mesure, une information supplémentaire existe, qui est le résultat de la mesure. Le vecteur d’état est modifié pour tenir en compte cette nouvelle information, et évolue de nouveau de façon continue et réversible. L’interaction physique de l’instrument de mesure avec le système peut contribuer à ce changement, mais pas necessairement. Le passage de ‘avant’ à ‘aprés’ mesure est (quasi) discontinu et généralement irréversible. 27

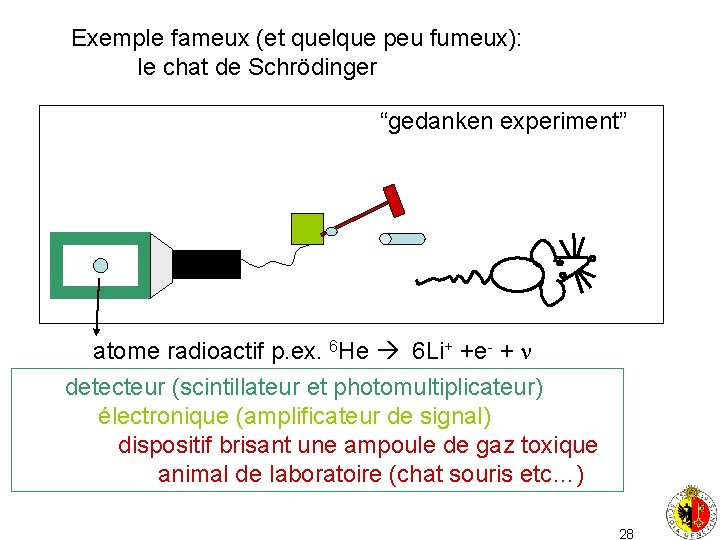
Exemple fameux (et quelque peu fumeux): le chat de Schrödinger “gedanken experiment” atome radioactif p. ex. 6 He 6 Li+ +e- + detecteur (scintillateur et photomultiplicateur) électronique (amplificateur de signal) dispositif brisant une ampoule de gaz toxique animal de laboratoire (chat souris etc…) 28

Comme la boite est fermée il n’y a pas moyen de savoir ce qui se passe. A un certain moment on ouvre la boite et effectue l’observation. la souris peut être “encore vivante” ou “…morte”. Qui tue la souris? -- l’atome qui se désintègre? -- la personne qui ouvre la boite et effectue l’observation? la personne qui a préparé l’epérience. . ? En fait la mécanique quantique ne répond pas à cette question Par contre elle est capable de prédire quelle est la probabilité en fonction du temps que l’observation donne le résultat ‘vivant’ ou ‘mort’ Pmort (t)=1 -exp(-t/ ) ou Pvivant= exp(-t/ ) ou est le temps de vie moyen du 6 He. 29

Chapitre VI Sytèmes à deux états Formalisme et exemples On est dans le cas d’un espace de Hilbert à deux dimensions. Remarques: I. Ceci peut être une approximation (cas de la molécule d’ammoniaque si on se restreint au sous espace des deux niveaux les plus bas) ou un cas plus rigoureux (traitement du spin d’une particule, polarisation de la lumière, système particule-antiparticule (K 0 - K 0, B 0 - B 0) II. le cas de systèmes à trois états (neutrinos), ou à petit nombre d’états molécule de benzène etc. . est similaire. 30

Espace de Hilbert à deux dimensions vecteurs de base: vecteur quelconque: normalisation: opérateur Hermitien général a, b, c, d réels avec 31

Exemple Polarisation de la lumière un faisceau de photons = ensemble de photons indépendants La polarisation de la lumière résulte du spin des photons: ils ‘tournent’ sur eux-mêmes avec un moment cinétique = On peut représenter le spin des photons par un y espace de Hilbert à deux dimensions s p z x lumière polarisée linéairement selon l’axe x, y, lumière polarisée circulairement 32

Polariseur Un polariseur sélectionne la lumière polarisée linéairement selon un axe parallel à l’axe du polariseur. il s’agit bien d’une mesure. L’état de la lumière après le polariseur est Ix>, Iy>, I > pour un polariseur orienté selon x, y, . L’opérateur “polariseur” est représenté par un projecteur = valeurs propres et états propres: 1 <-> I > ; 0 <-> I + /2> La probabilité qu’un photon initialement dans l’état I > ‘passe’ est P= II< I >II 2 = II cos + sin II 2 = cos 2( - ) 33

expériences avec un polariseur on ne peut pas réduire la mécanique quantique à la probabilité des résultats obtenus lors d’une mesure. Le fait que l’état physique résultant est un vecteur propre de l’opérateur correspondant essentiel. 34

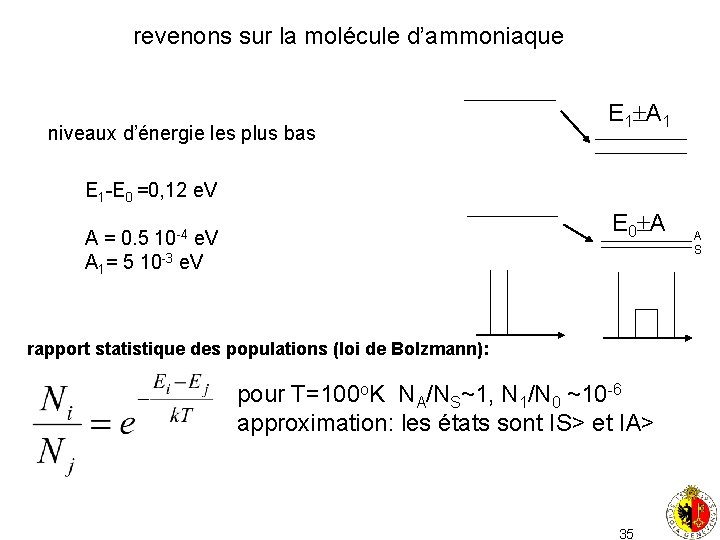
revenons sur la molécule d’ammoniaque niveaux d’énergie les plus bas E 1 A 1 E 1 -E 0 =0, 12 e. V E 0 A 10 -4 A = 0. 5 e. V A 1= 5 10 -3 e. V rapport statistique des populations (loi de Bolzmann): pour T=100 o. K NA/NS~1, N 1/N 0 ~10 -6 approximation: les états sont IS> et IA> 35 A S

Espace de Hilbert à deux dimensions vecteurs de base Hamiltonien vecteur quelconque: Evolution dans le temps: 36

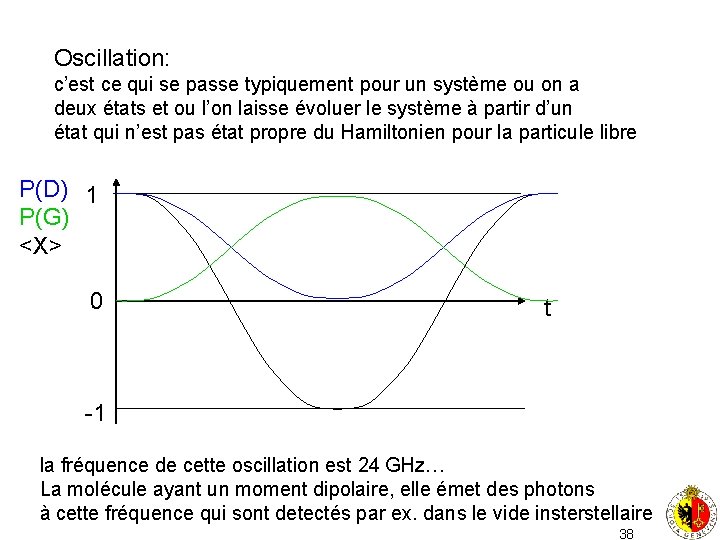
IS> IA> IS> - IA> IS> + IA> IG> et ID> sont les vecteurs propres de 1 pour les valeurs propres -1 et 1. construct observable that is measured to be 1 for ID> and -1 for IG> X= ID> <DI - IG> <GI= ( 01 ) 10 = 1 Evolution dans le temps: supposons qu’on ait comme état initial ID> 37

Oscillation: c’est ce qui se passe typiquement pour un système ou on a deux états et ou l’on laisse évoluer le système à partir d’un état qui n’est pas état propre du Hamiltonien pour la particule libre P(D) 1 P(G) <X> 0 t -1 la fréquence de cette oscillation est 24 GHz… La molécule ayant un moment dipolaire, elle émet des photons à cette fréquence qui sont detectés par ex. dans le vide insterstellaire 38

Molécule dans un champ électrique La molécule d’ammoniaque a un moment électrique dipolaire, la présence d’un champ électrique E donne une énergie potentielle supplémentaire W pour un champ electrique aligné sur ox modification du Hamiltonien H=H 0+W Les valeurs propres sont modifiées, les états propres aussi quelles vont être les conséquences mesurables? 39

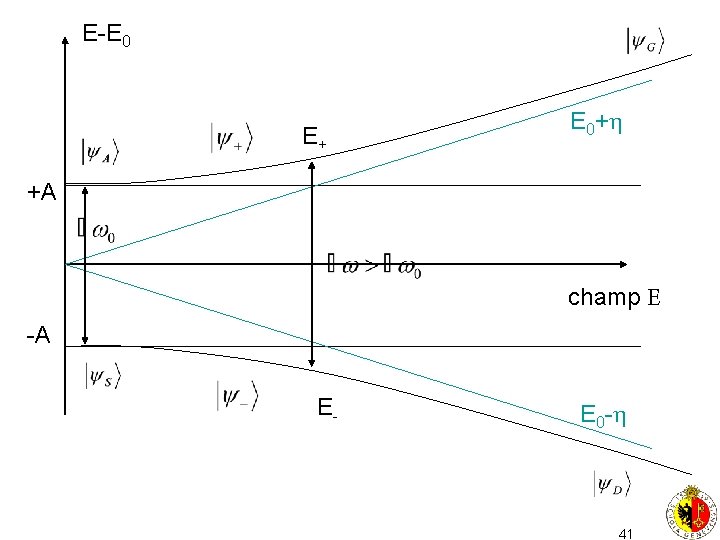
nouvelles valeurs propres v 1+v 2=Trace=2 E 0 v 1. v 2 = determinant= E 02 -A 2 - 2 vecteurs propres: solution 40

E-E 0 E+ E 0+ +A champ -A E- E 0 - 41

Force dans un gradient de champ pour <<A H = E 0 A d 0 2/2 A est semblable à un potentiel cette force est de direction opposée pour les particules dans l’état I -> et I +> séparation des faisceaux! 42

_ + + _ on peut ainsi enrichir le faisceau avec un des deux types de molécules. En particulier on obtient un faisceau enrichi en qui est l’état d’énergie le plus élevé. C’est ce qu’on appelle une inversion de population. La création d’une inversion de population (parfois appelée pompage) est un des préliminaires à l’effet MASER (micowave) ou LASER (Light) Amplification by Stimulated Emission of Radiation 43

Maser à ammoniaque Emission spontanée: très lent ( >= 1 mo) Emission stimulée on soumet les molécules à un champ electromagnétique à une pulsation voisine de 0 : Ceci ajoute au Hamiltonien un terme dans la base , 44

Hamiltonien dépendant du temps! On ne peut pas déterminer la dépendance en temps à partir des états stationnaires: ils n’existent pas. appliquons à soit 45

equations couplées. Poser on verra un exemple soluble exactement avec la résonnance magnétique. On peut résoudre numériquement aussi 46

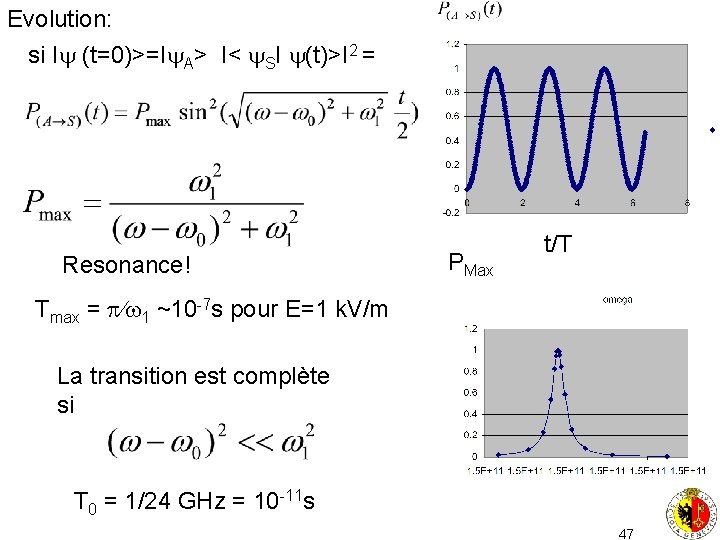
Evolution: si I (t=0)>=I A> I< SI (t)>I 2 = Resonance! PMax t/T Tmax = 1 ~10 -7 s pour E=1 k. V/m La transition est complète si T 0 = 1/24 GHz = 10 -11 s 47

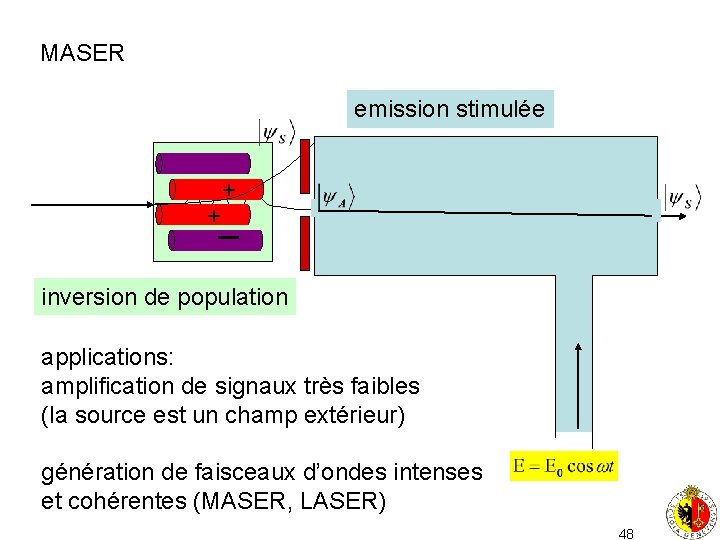
MASER emission stimulée + +_ inversion de population applications: amplification de signaux très faibles (la source est un champ extérieur) génération de faisceaux d’ondes intenses et cohérentes (MASER, LASER) 48

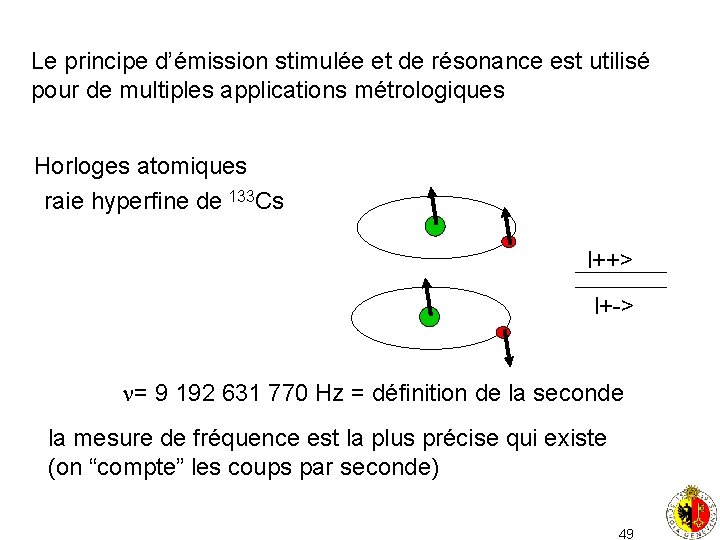
Le principe d’émission stimulée et de résonance est utilisé pour de multiples applications métrologiques Horloges atomiques raie hyperfine de 133 Cs l++> l+-> = 9 192 631 770 Hz = définition de la seconde la mesure de fréquence est la plus précise qui existe (on “compte” les coups par seconde) 49

Observables qui commutent Si deux observables Ô 1 et Ô 2 commutent, il existe un base de EH formée de vecteurs propres communs de Ô 1 et Ô 2 50

exemple: oscillateur harmonique à deux dimensions et commutent est une base commune de et 51

Ensemble complet d’observables qui commutent v 1 v 2 v 3 z 1 } w 2 z 3 { } z 5 { } w 4 } w 5 w 6 { w 3 z 2 z 4 z 6 z 7 note: les valeurs propres w 1 et w 2 sont différentes w 1 et w 3 pas forcément etc… en général le sous espace associé à chaque valeur propre vk a une dimension nk. On a un ensemble COMPLET si l’état propre commun de V, W, Z est unique: Iv, w, z> est de dimension 1. 52

pour --un oscillateur harmonique à une dimension, --un puits fini ou infini à une dimension le Hamiltonien constitue un ECOC à lui tout seul. Pour un Oscillateur Harmonique à 2 dimensions Hx, Hy forment un ECOC. I nx, ny > est unique…bien que son energie ne soit pas unique! L’état I 1, 0 > a la même énergie que l’état I 0, 1 > Un autre base possible de ce même sous espace propre est on va voir qu’ils correspondent à un autre ECOC…. 53

En effet y on peut faire apparaitre le moment cinétique r x fonctions propres de Lz ? 54

contrainte: (r, )= (r, +2 ) qui permet de trouver les valeurs de l’energie (qui seront fonction de l 2 ) un état propre se caractérise par un nombre radial solution de cette equation et un nombre ‘orbital’ l correspondant (Oscillateur harmonique à deux dimensions) 55

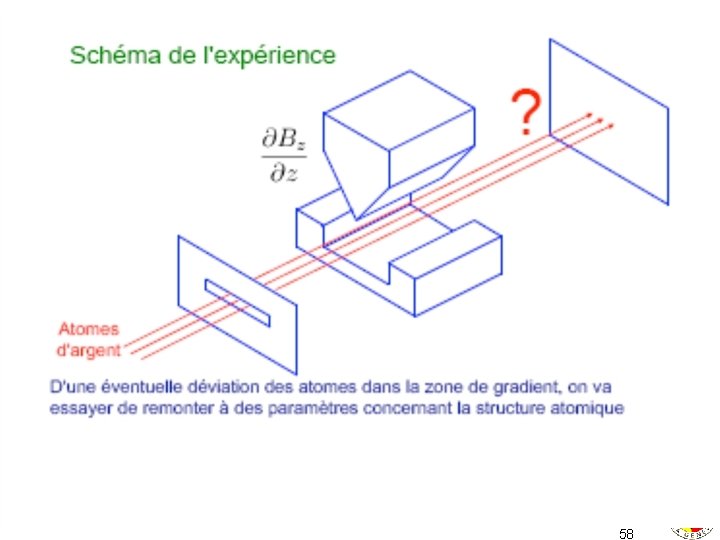
L’expérience de Stern et Gerlach 56

57

58

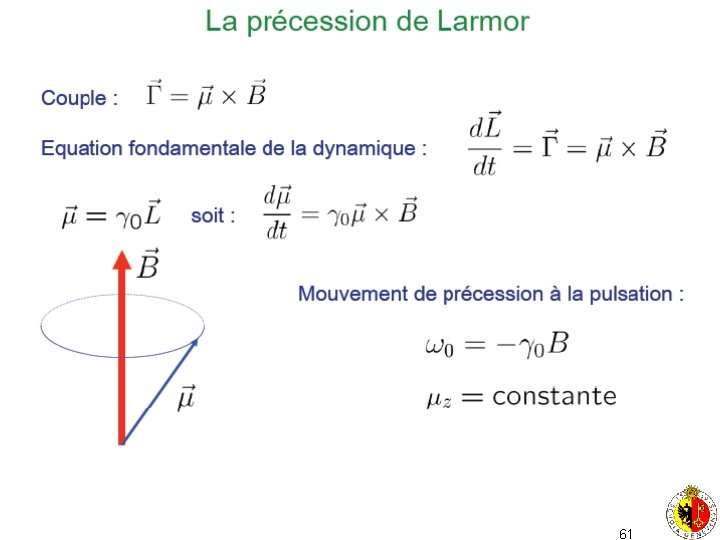
Traitement classique: action d’un champ magnétique sur une particule neutre se fait par son moment dipolaire magnétique B pour un moment magnétique sans friction precession avec friction: il s’aligne sur le champ magnétique (boussole) 59

60

61

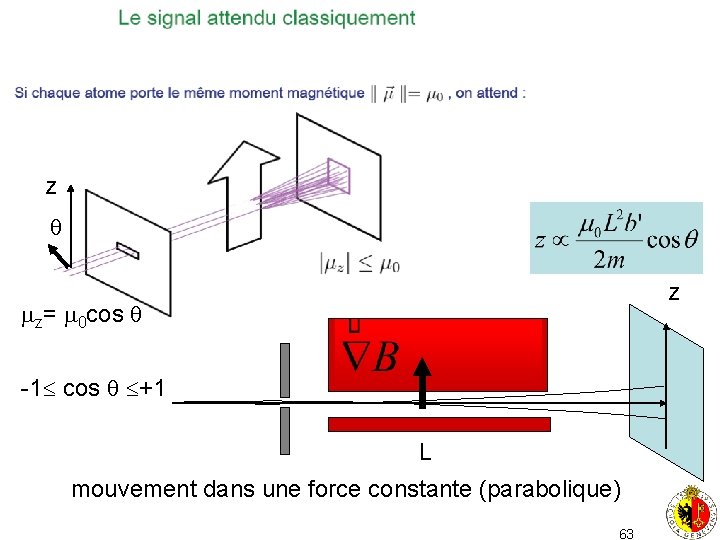
mouvement dans une force constante (parabolique) 62

z z z= 0 cos -1 cos +1 L mouvement dans une force constante (parabolique) 63

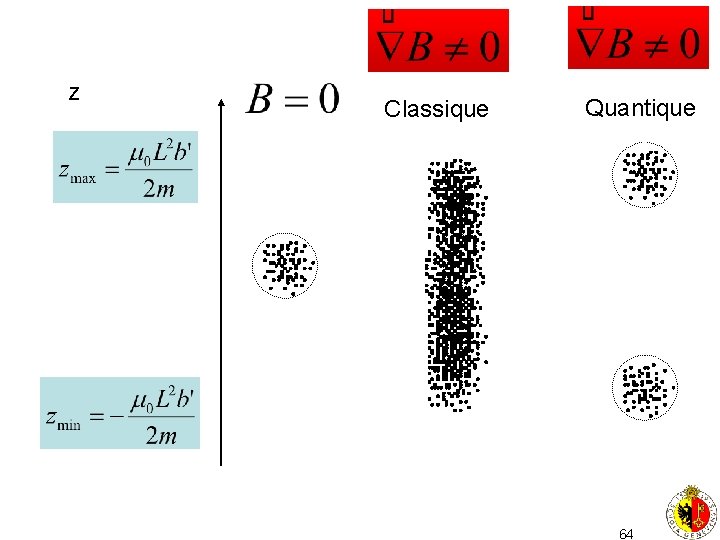
z Classique Quantique 64

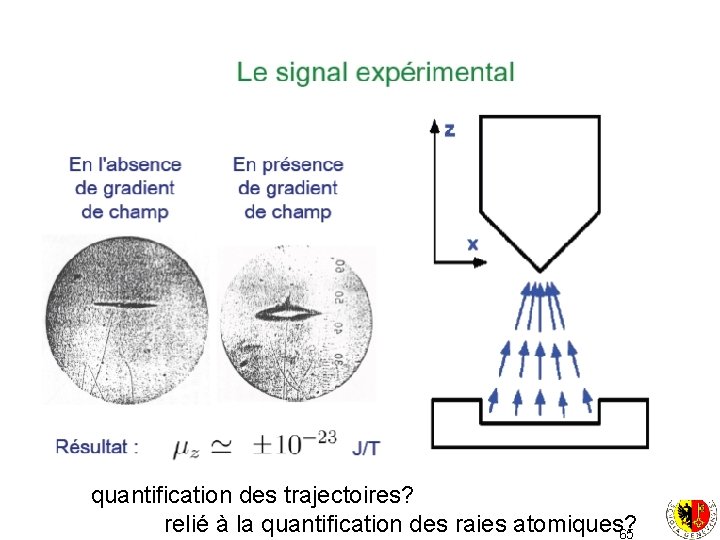
quantification des trajectoires? relié à la quantification des raies atomiques? 65

66

Description quantique Manifestement on doit introduire un degré de liberté interne décrivant le moment magnétique. concentrons nous sur ce degré de liberté interne pour le moment 67

On a trois observables correspondant aux composantes d’un vecteur moment magnétique Chacune a deux résultats de mesure possible nous plaçons donc (au moins) dans un espace à deux dimensions générés par les vecteurs propres de état quelconque on mesurera avec une probabilité 2 68

Espace de Hilbert à deux dimensions vecteurs de base: vecteur quelconque: normalisation: opérateur Hermitien général a, b, c, d réels avec 69

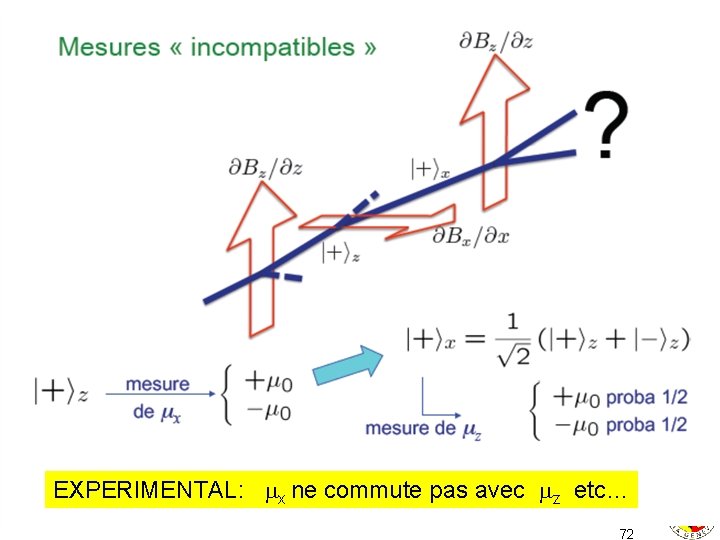
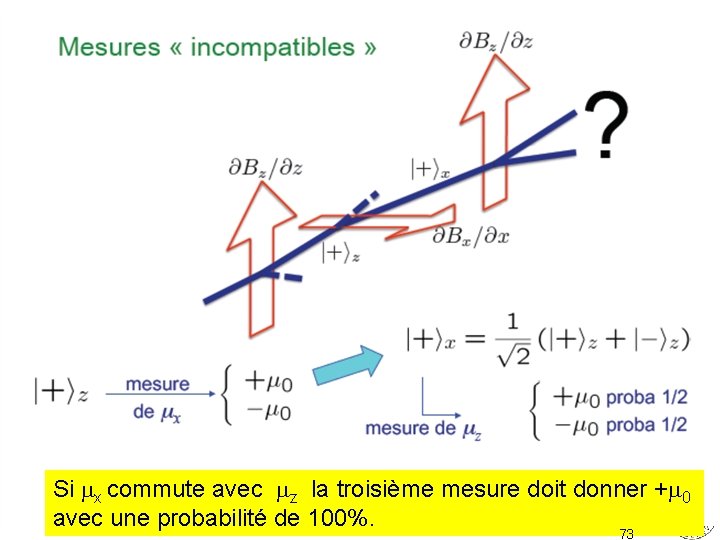
structure de l’espace et règles de commutation: Est-ce que commutent? si oui, on peut trouver une base de vecteurs communs qui pourront s’écrire I x, y, z> (8 vecteurs). Une autre possibilité serait qu’ils ne commutent pas et que l’epace n’ait que deux dimensions. Cette question peut être confrontée à des expériences 70

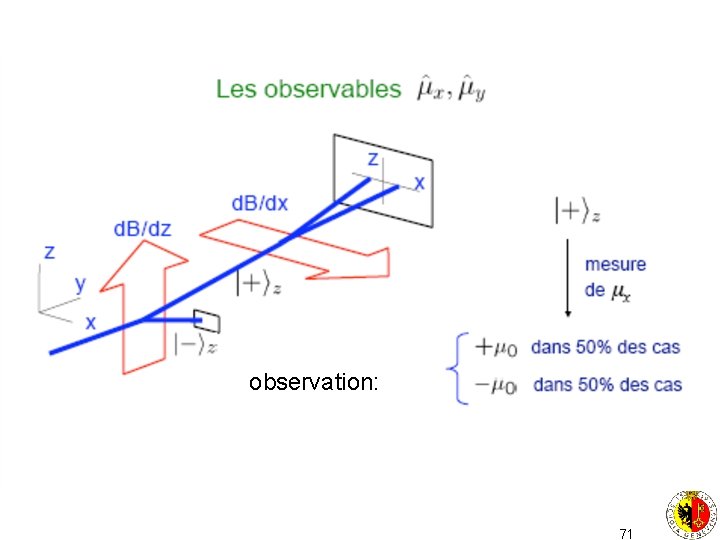
observation: 71

EXPERIMENTAL: x ne commute pas avec z etc… 72

Si x commute avec z la troisième mesure doit donner + 0 avec une probabilité de 100%. 73

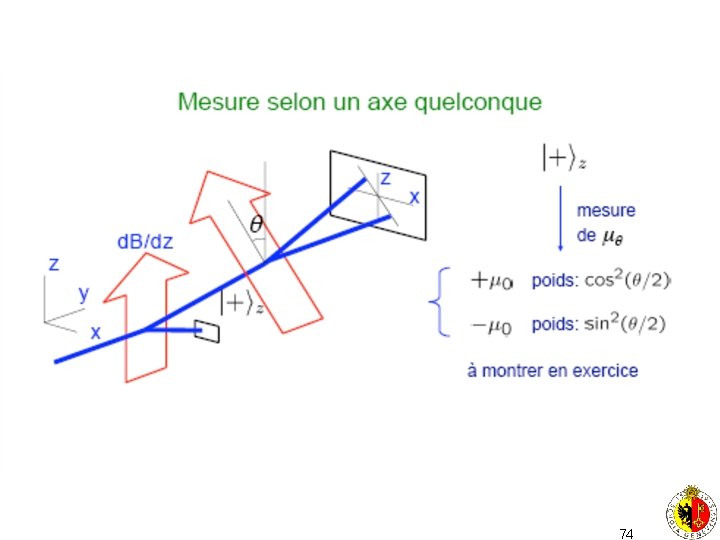
74

toutes les observations sur les moments mahnétiques de l’atome d’argent sont cohérentes avec la non-commutation de et la représentation matricielle suivante: dans la base des états propres de z. 75

76

Description complète du problème 77

78

79

80

81

Evolution d’un moment magnétique dans un champ magnétique uniforme on a des equations indépendantes pour I+> et I-> on sépare donc avec h =2 0 Bz 82

On peut calculer les valeurs moyennes des mesures de on retrouve bien le mouvement de precession – sur les valeurs moyennes! B < > 83

Description théorique de l’expérience de Stern et Gerlach on fait l’approximation que Bz=B+b’z. Ceci ne respecte pas les équations de Maxwell à strictement parler mais est convenable si on se limite au plan x=0. On a vu que < z> reste constante. Appliquons le théorème d’Ehrenfest à <r> car le seul terme qui ne commute pas est p 2 84

de même pour <p>. Le seul terme qui ne commute pas est zzb’ soit On a une force différente pour les deux états. conditions initiales soit en intégrant jusqu’à l’instant t pour les particules dans l’état I+> ou I-> de z resp. 85

On retrouve bien les deux trajectoires possibles. Au bout d’une distance L on a (on a t=L/v ) ou l’expérience n’est significative que si l’effet est plus grand que celui qui résulte de la divergence naturelle du faisceau. 86

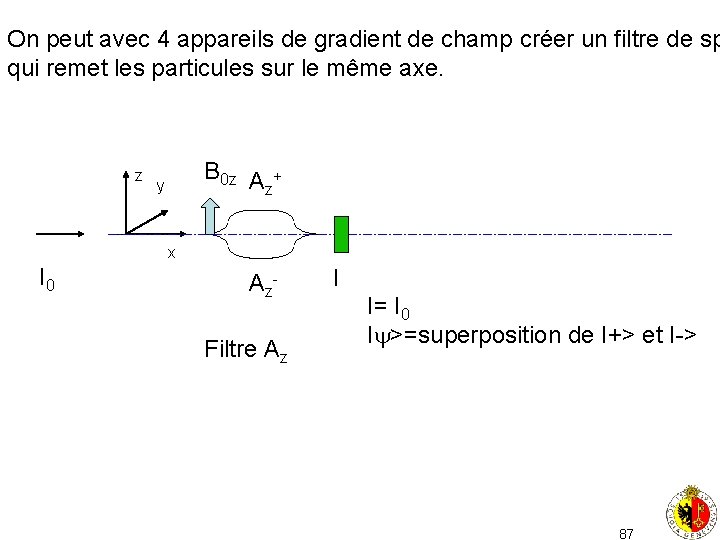
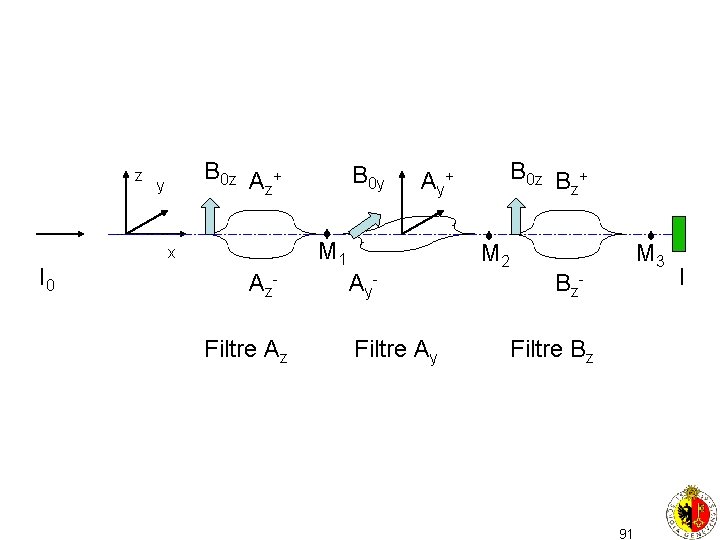
On peut avec 4 appareils de gradient de champ créer un filtre de sp qui remet les particules sur le même axe. z B 0 z A + z y x I 0 A z. Filtre Az I I= I 0 I >=superposition de I+> et I-> 87

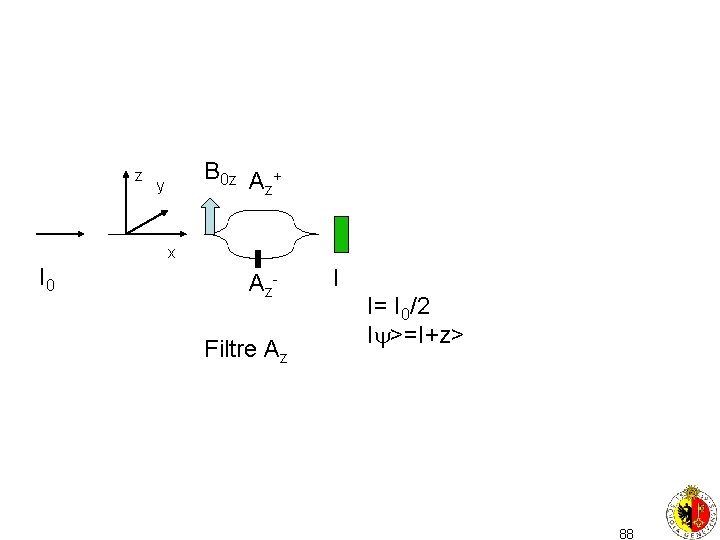
z B 0 z A + z y x I 0 A z. Filtre Az I I= I 0/2 I >=I+z> 88

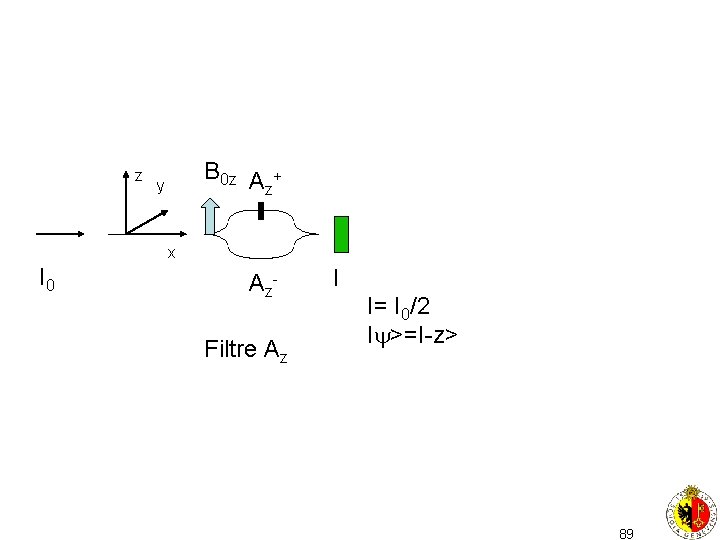
z B 0 z A + z y x I 0 A z. Filtre Az I I= I 0/2 I >=I-z> 89

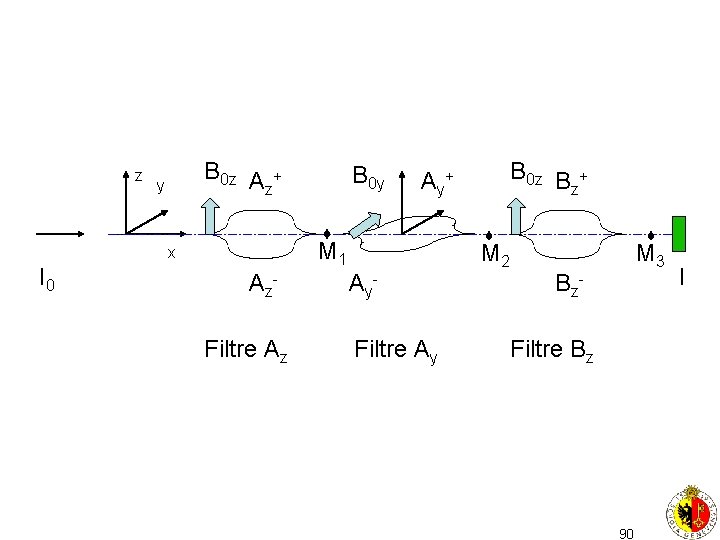
z B 0 z A + z y A y+ M 1 x I 0 B 0 y A z. Filtre Az A y. Filtre Ay B 0 z B + z M 2 M 3 B z- Filtre Bz 90 I

z B 0 z A + z y A y+ M 1 x I 0 B 0 y A z. Filtre Az A y. Filtre Ay B 0 z B + z M 2 M 3 B z- Filtre Bz 91 I

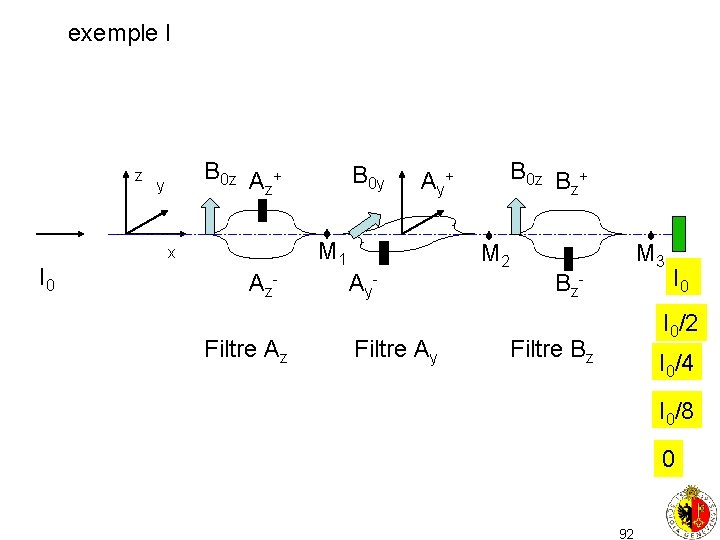
exemple I z B 0 z A + z y A y+ M 1 x I 0 B 0 y A z. Filtre Az A y. Filtre Ay B 0 z B + z M 2 M 3 B z- I 0/2 Filtre Bz I 0/4 I 0/8 0 92

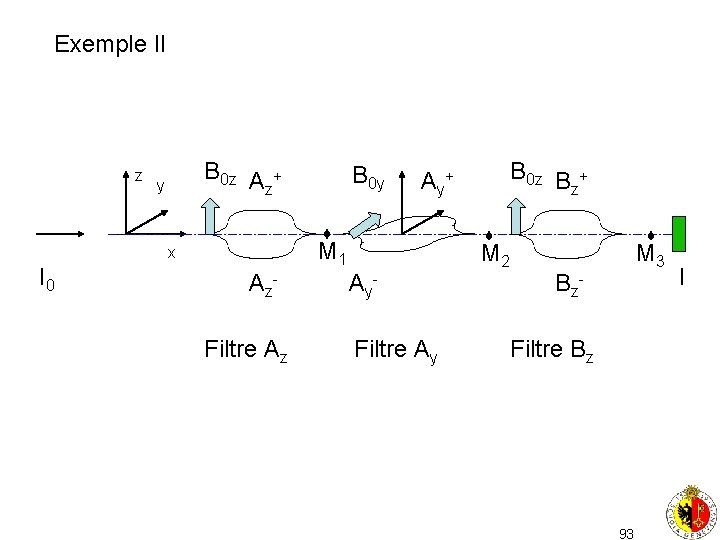
Exemple II z B 0 z A + z y A y+ M 1 x I 0 B 0 y A z. Filtre Az A y. Filtre Ay B 0 z B + z M 2 M 3 B z- Filtre Bz 93 I

Evolution d’un moment magnétique dans un champ magnétique uniforme on a des equations indépendantes pour I+> et I-> on sépare donc avec h =2 0 Bz 94

On peut calculer les valeurs moyennes des mesures de on retrouve bien le mouvement de precession – sur les valeurs moyennes! B < > 95
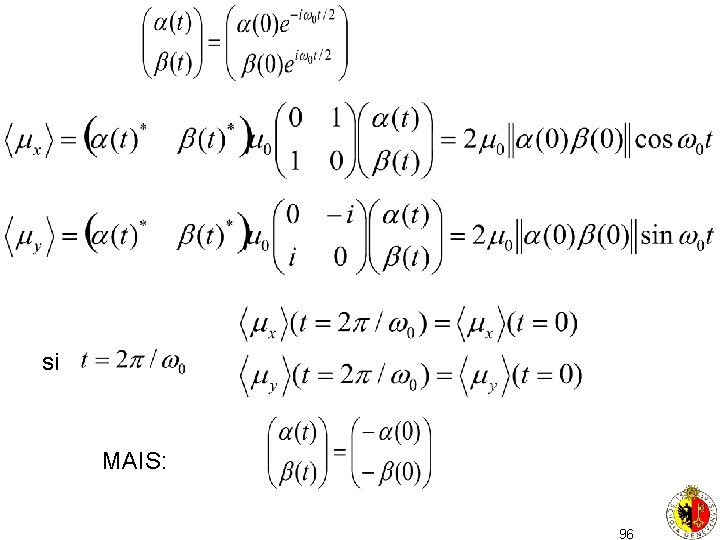
si MAIS: 96

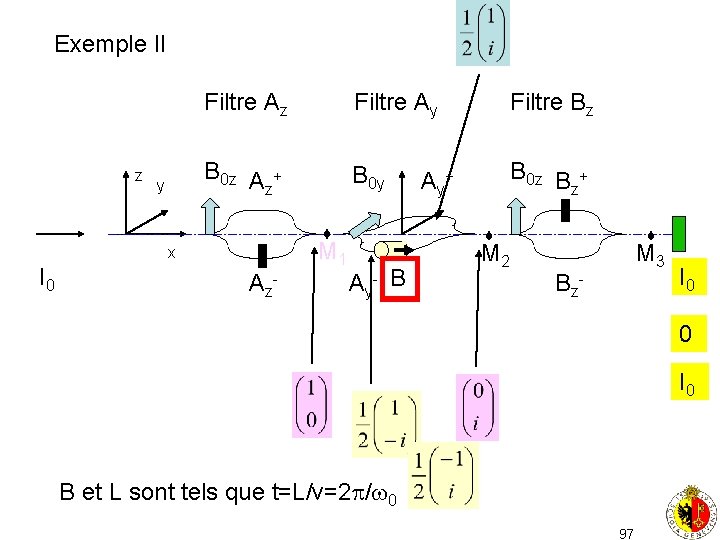
Exemple II z y Filtre Az Filtre Ay Filtre Bz B 0 z A + z B 0 y B 0 z B + z M 1 x I 0 A z- A y- B A y+ M 2 M 3 B z- I 0 0 I 0 B et L sont tels que t=L/v=2 / 0 97

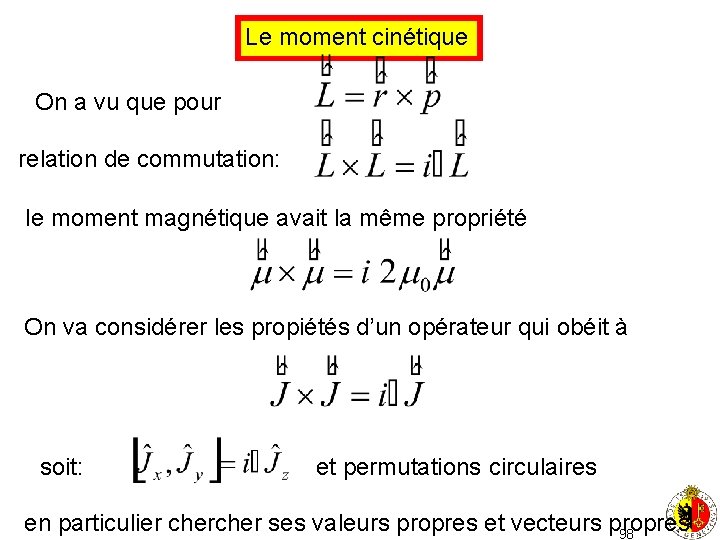
Le moment cinétique On a vu que pour relation de commutation: le moment magnétique avait la même propriété On va considérer les propiétés d’un opérateur qui obéit à soit: et permutations circulaires en particulier cher ses valeurs propres et vecteurs propres 98

99

l’opérateur J 2 on remarque on va donc trouver une base qui diagonalise J 2 et par ex. Jz On vérifiera que la base est unique il s’agit donc d’un ECOC On appellera le vecteur propre de J 2 pour la valeur h 2 j(j+1) et de Jz pour la valeur hm N. B. c’est arbitraire et choisi après connaissance de la solution… mais n’importe quelle valeur de R positive peut s’écrire j(j+1) avec j positif! 100

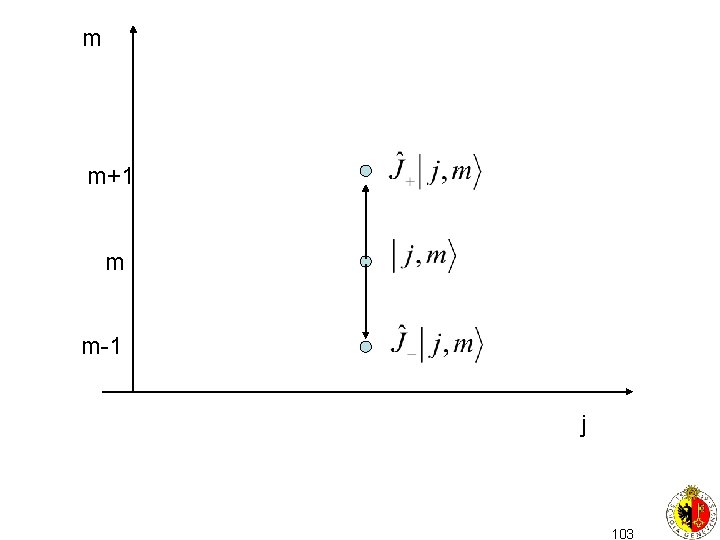
Quelles sont les valeurs de j et m? On introduit des opérateurs J+ et J- de façon semblable aux opérateurs a, a+ pour l’oscillateur harmonique il est évident que J 2 commute avec J+ et J-. Par contre, JZ : étudions l’état 101

étudions l’état est donc un état propre de J 2 pour la valeur j (ou il est nul) est un état propre de Jz pour la valeur m+1 (ou il est nul) de même est un état propre de J 2 pour la valeur j (ou il est nul) est un état propre de Jz pour la valeur m-1 (ou il est nul) 102

m m+1 m m-1 j 103

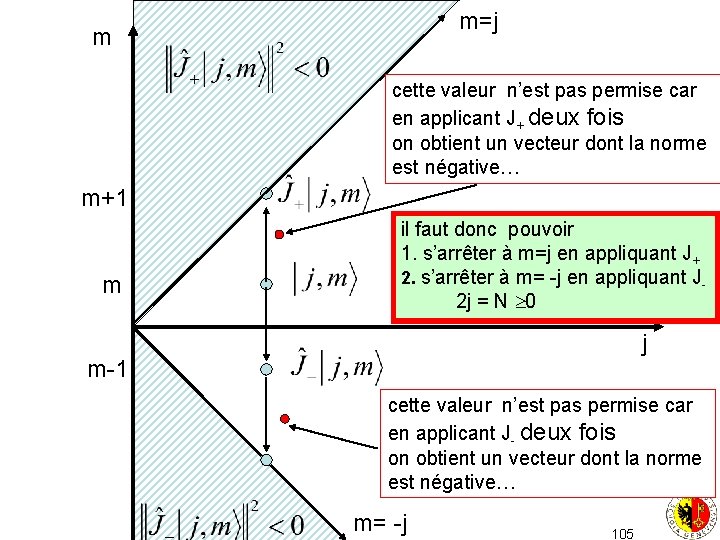
ou nul? calculons le module de pour que ces vecteurs soient non-nuls il faut que -j m j 104

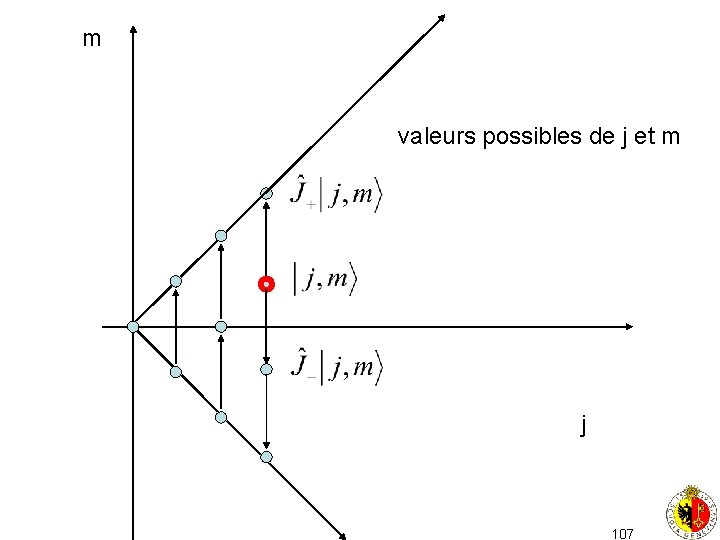
m=j m cette valeur n’est pas permise car en applicant J+ deux fois on obtient un vecteur dont la norme est négative… m+1 m il faut donc pouvoir 1. s’arrêter à m=j en appliquant J+ 2. s’arrêter à m= -j en appliquant J 2 j = N 0 j m-1 cette valeur n’est pas permise car en applicant J- deux fois on obtient un vecteur dont la norme est négative… m= -j 105

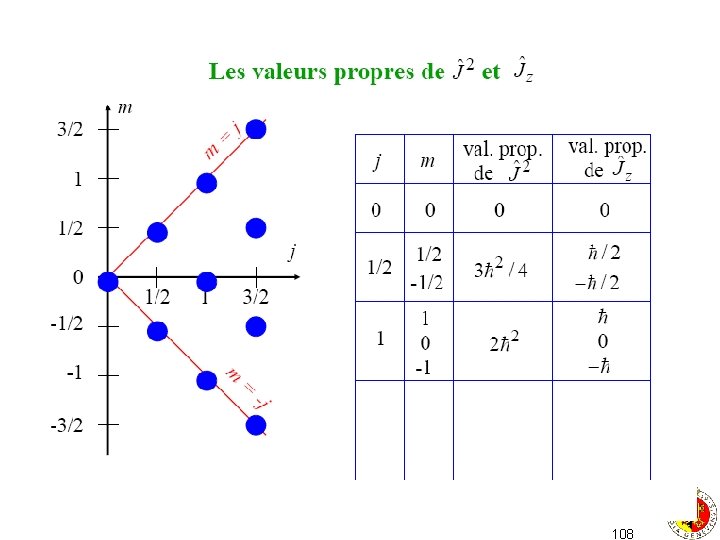
si on applique J+ ou J- à un vecteur Ij, m> on obtient un vecteur Ij, m+1> ou Ij, m-1>. On obtient un vecteur nul si Im. I j. On peut ainsi générer toute une série de N+1>0 vecteurs propres Ij, m> avec -j m j. Soit mmax la plus grande valeur. On a forcément J+ Ij, mmax>=0 ce qui implique mmax=j Cette même série va pouvoir être parcourue en appliquant J-, jusqu’à ce qu’on arrive à une valeur mmin qui, par le même raisonnement sera forcément mmin=-j après un nombre N d’opérations. donc 2 j=N Les valeurs possibles de j sont j=N/2= 0, ½, 1, 3/2, 2 et les valeurs de m sont les valeurs { –j, -j+1, …. . j-1, j} 106

m valeurs possibles de j et m j 107

108

Moment cinétique orbital: 109

Moment cinétique orbital: 110

Moment cinétique orbital: 111

Moment cinétique orbital: 112

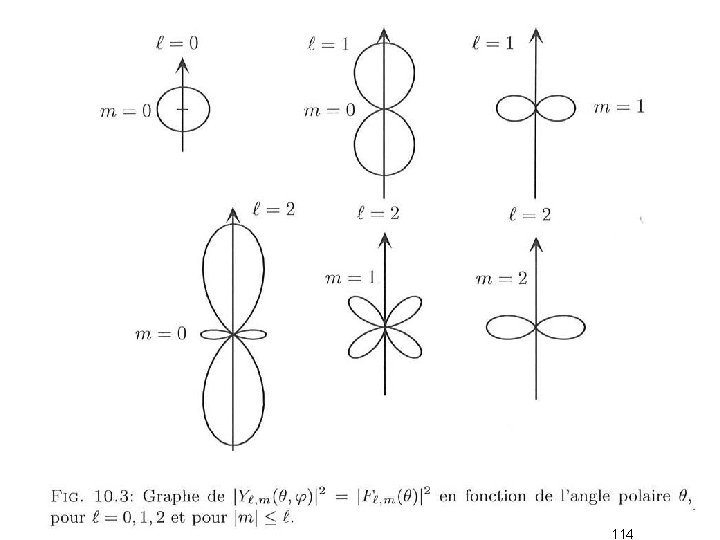
Pour le moment cinétique orbital, 113

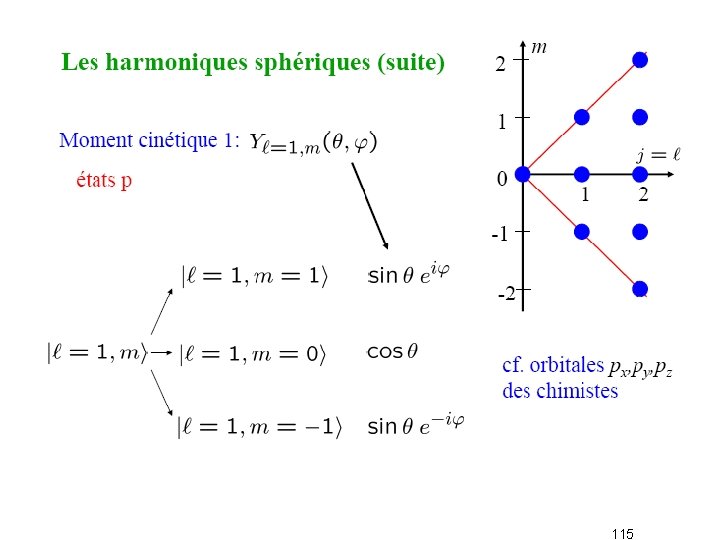
114

115

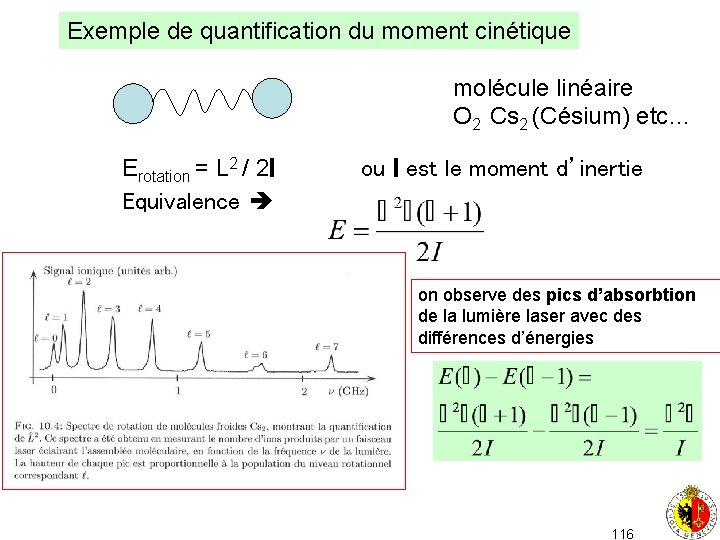
Exemple de quantification du moment cinétique molécule linéaire O 2 Cs 2 (Césium) etc… Erotation = L 2 / 2 I Equivalence ou I est le moment d’inertie on observe des pics d’absorbtion de la lumière laser avec des différences d’énergies 116

Résumé Le moment cinétique est décrit par 2 Observables qui Commutent J 2 et par ex. Jz les vecteurs propres sont notés Les valeurs possibles de j et m sont j=N/2 et m= -j, -j+1. . . j-1, j pour le moment cinétique orbital L=rxp les valeurs propres sont entières! 117