Yield Curves and Rate of Return 1 Yield

Yield Curves and Rate of Return 1

Yield Curves v v v Yield curves measure the level of interest rates across a maturity spectrum (e. g. , overnight to 30 years) Many different types of curves are available v Commercial (Bloomberg, Reuters) and proprietary Accurate yield curves are essential for the pricing, trading, revaluation, and hedging interest-rate sensitive products 2

Yield Measures v v v Current Yield (to Maturity, to Worst) Spread to Benchmark Spread to Yield Curve Example Ø FHLB 4. 25 11/15/2010 Ø Settlement – 2/29/2004 Ø Price – 103. 369 Ø Accrued Interest – 1. 3340 (113 days 113/180 x 2. 125) Ø Full Price – 104. 703 (103. 369+1. 334) 3

Yield Measures – Current Yield v Current Yield FHLB 4. 25 11/15/2010 Flat Price (2/29/2004) = 103. 369 Coupon = 4. 25 v Drawback of Current Yield Ø Ø Ø Does not account for effects of Accretion (movement of the price of a bond towards 100 as it approaches maturity) Discount Bond – Positive Accretion Premium Bond – Negative Accretion 4

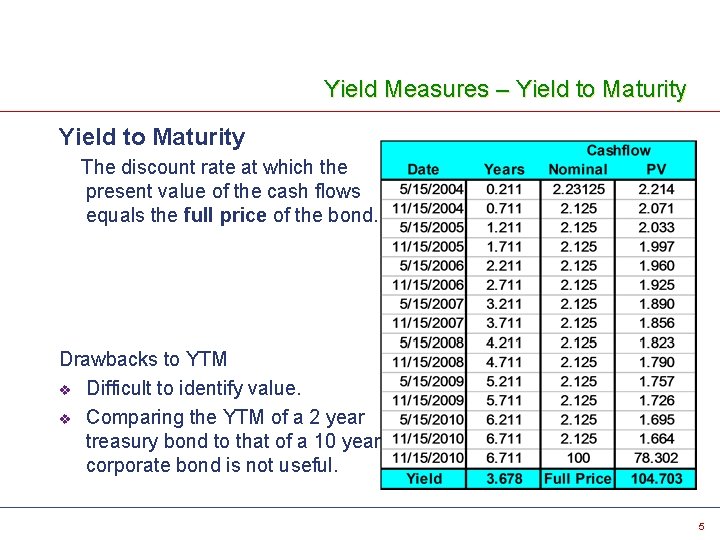
Yield Measures – Yield to Maturity The discount rate at which the present value of the cash flows equals the full price of the bond. Drawbacks to YTM v Difficult to identify value. v Comparing the YTM of a 2 year treasury bond to that of a 10 year corporate bond is not useful. 5

Yield Measures – Spread to Benchmark v v The difference between the yield of a security and the yield of a corresponding benchmark security stated in basis points (1 bp=. 01%) The benchmark is typically an On-the-Run Treasury closest to the maturity of the security (or average life for an amortizing security) Benchmark Security: US 5 2/15/2011 Yield of Bond: 3. 68 Yield of Benchmark Security: 3. 47 Spread to Benchmark: 0. 21 (21 bp) 6

Yield Measures – Spread to Yield Curve v The difference between a security’s yield and the interpolated point on the yield curve corresponding to the security’s average life, stated in basis points (1 bp=. 01%) Ø On-The-Run Treasury Curve Ø Off-The-Run Treasury Model Curve Ø Swap Curve 7

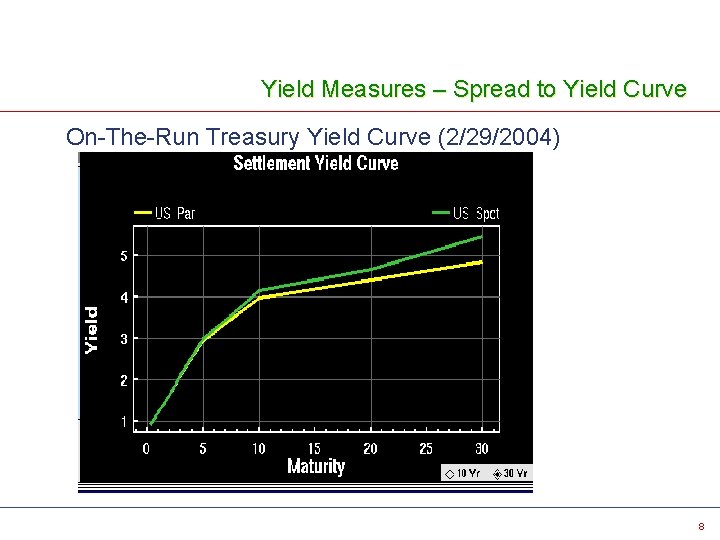
Yield Measures – Spread to Yield Curve On-The-Run Treasury Yield Curve (2/29/2004) 8

Yield Measures – Spread to On the Run Curve v Spread to On-the-Run Treasury Yield Curve Ø Ø Ø v Yield Curve: On-The-Run Tsy (2/29/2004) Average Life of Security: 6. 71 Interpolated Point on Yield Curve: 3. 302 Yield of Security: 3. 678 Spread to Yield Curve: 100 x(3. 68 -3. 30)=38 bp Drawbacks of Spread to OTR Curve Ø Ø OTR Treasuries are lower yielding due to high liquidity Sparse points and curve connects them with a straight line. 9

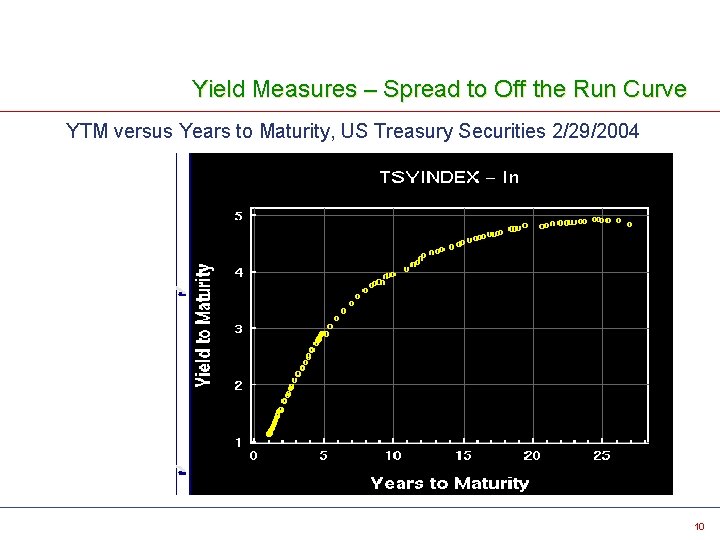
Yield Measures – Spread to Off the Run Curve YTM versus Years to Maturity, US Treasury Securities 2/29/2004 10

Yield Measures – Spread to Off the Run Curve Treasury Off-The-Run Yield Curve v v v Statistically constructed by fitting a curve to YTM versus Years to Maturity data to a universe of Treasury securities Universe includes all Treasury Bills, Notes, and Bonds Ø Excluded - On the Run Treasuries Ø Excluded - Callable Bonds Also referred to as the Treasury Model Curve 11

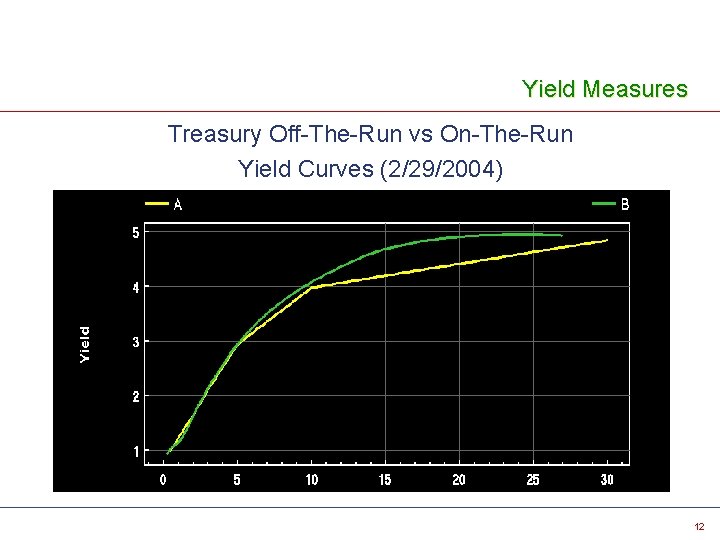
Yield Measures Treasury Off-The-Run vs On-The-Run Yield Curves (2/29/2004) 12

Yield Measures v Spread to Off-the-Run Treasury Yield Curve Ø Ø Ø Yield Curve: Off-The-Run Tsy (2/29/2004) Average Life of Security: 6. 71 Interpolated Point on Yield Curve: 3. 442 Yield of Security: 3. 678 Spread to Yield Curve: 100 x(3. 68 -3. 44)=24 bp 13

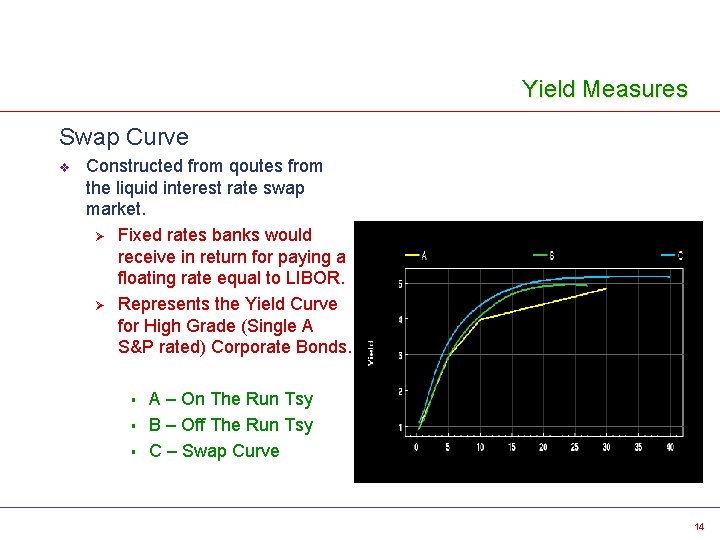
Yield Measures Swap Curve v Constructed from qoutes from the liquid interest rate swap market. Ø Fixed rates banks would receive in return for paying a floating rate equal to LIBOR. Ø Represents the Yield Curve for High Grade (Single A S&P rated) Corporate Bonds. § § § A – On The Run Tsy B – Off The Run Tsy C – Swap Curve 14

Yield Measures v Spread to Swap Yield Curve Ø Ø Ø Yield Curve: Swap (2/29/2004) Average Life of Security: 6. 71 Interpolated Point on Yield Curve: 3. 820 Yield of Security: 3. 678 Spread to Yield Curve: 100 x(3. 68 -3. 82)= -14 bp 15

Yield Curve Shapes – Positive Yield Curve Positive or “Normal” Yield Curve v v A positive yield curve is one where short term rates are lower than longer term rates. This is the “normal” state of the interest rate markets and reflects: Ø An expectation that rates will be higher in the future Ø A liquidity premium for those investing/funding in the long term 16

Drivers of Yield Curve Shapes -Expectations Theory Drivers of Yield Curve Shapes v Expectations Theory Ø Long-term rates reflect the market’s view of rates expected to prevail in the future Ø If investors think that long-term interest rates will rise they will avoid longer-term bonds and invest short term. § Short-term prices rise (rates fall) § Long-term prices fall (rates rise) 17

Liquidity Preference Theory Drivers of Yield Curve Shapes v Liquidity Preference Theory Ø The longer an investor’s horizon, the greater the credit risk Ø Statistically, a borrower is less likely to have credit problems over a shorter period than a longer period. Ø An investor will demand a premium for the extra risk, meaning longer term rates rise above short term rates. 18

Market Segmentation Theory Drivers of Yield Curve Shapes v Market Segmentation Theory Ø The shape of the yield curve is the result of supply and demand for investments in particular segments of the curve. § If an investment fund wants to invest strictly in securities that have maturities between 10 and 15 years that will raise prices (lower yields) in that segment § If demand by short-term investors is exceedingly high, the yield curve will steepen 19

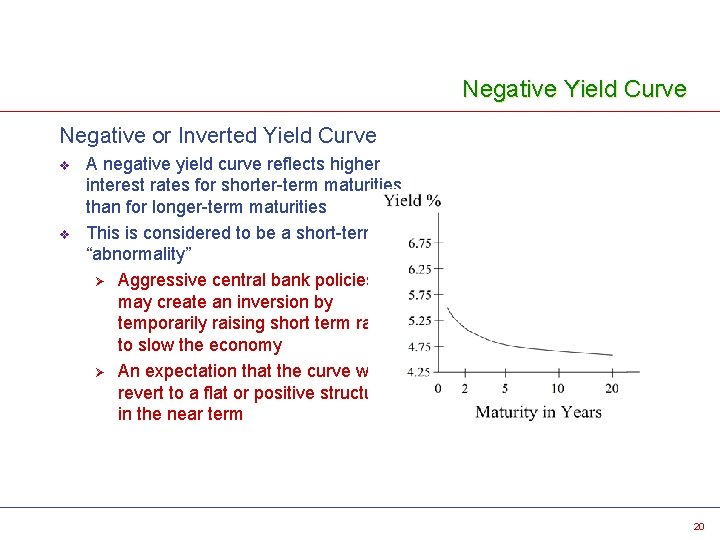
Negative Yield Curve Negative or Inverted Yield Curve v v A negative yield curve reflects higher interest rates for shorter-term maturities than for longer-term maturities This is considered to be a short-term “abnormality” Ø Aggressive central bank policies may create an inversion by temporarily raising short term rates to slow the economy Ø An expectation that the curve will revert to a flat or positive structure in the near term 20

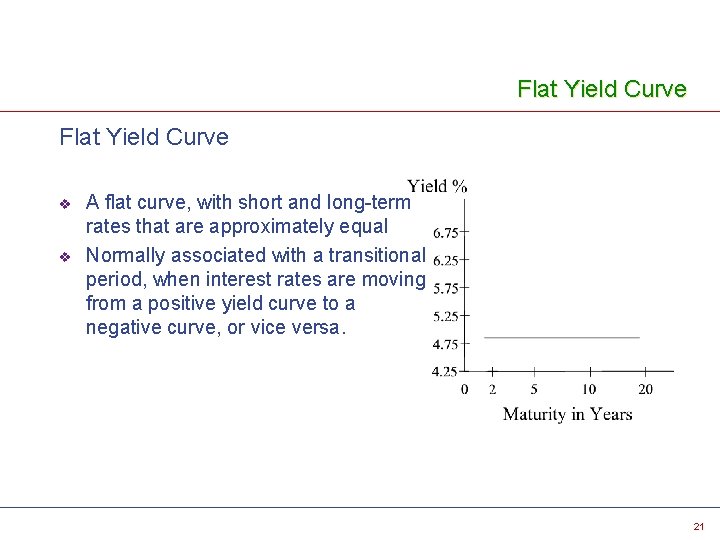
Flat Yield Curve v v A flat curve, with short and long-term rates that are approximately equal Normally associated with a transitional period, when interest rates are moving from a positive yield curve to a negative curve, or vice versa. 21

Spot Yield Curve v v v Par Yield Curves provide a good representation of where market yields are Ø At the beginning of a bond's life Ø Yield is equal (or close) to the coupon rate For deep discount or high premium bonds comparing their yield to the yield of a treasury with a price close to par is not as useful Ø This is particularly true for zero coupon bonds Ø Zero coupon bonds make no payments to the bondholder until the bond's maturity date, when the principal plus interest is paid Zero coupon (spot) rates allow each cash flow to be priced individually using an interest rate relevant to that specific cash flow, rather than one rate for the whole stream of cash flows. 22

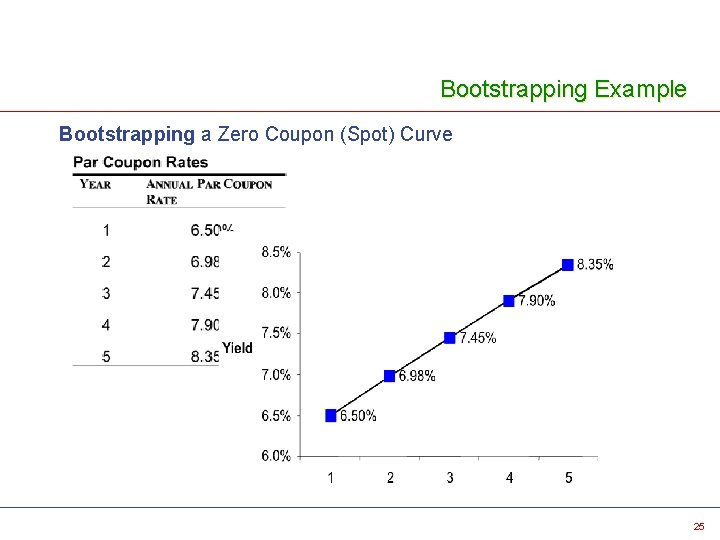
Spot Yield Curve - Bootstrapping a Zero Coupon (Spot) Curve v v To create a zero coupon curve we start with a 1 st period zero coupon rate in order to value the 1 st cash flow. Ø This 1 st year spot rate comes from a 1 -year security which makes only 1 payment (e. g. , Treasury Bill). Ø The 1 -year spot rate is equal to the yield of that security Deriving a spot curve from a par curve involves "stripping" the coupons from the implied par coupon securities and pricing them at the appropriate zero coupon rates. Ø Because the 1 st year coupon must be stripped from a 2 -year security to calculate the 2 -year spot rate, the 1 st year spot rate must be calculated first. Ø Similarly, the year 2 spot rate is needed to calculate the year 3 spot rate 23

Spot Yield Curve - Bootstrapping a Zero Coupon (Spot) Curve v Strip the coupons from a par coupon security and price the coupons using the appropriate zero coupon rates. This pricing is accomplished using the following formula: Where: PVn = present value of the derived zero coupon instrument PCn = par coupon rate in year n Zt = zero coupon rate in year t 24

Bootstrapping Example Bootstrapping a Zero Coupon (Spot) Curve 25

Bootstrapping Example v Example - Bootstrapping a Zero Coupon (Spot) Curve Ø Year 1 par coupon rate = zero coupon rate = 6. 50% Year 2 Step 1. C 2 = 6. 98, : Ø Step 2, PV 2 = 93. 44 Ø Ø Ø 26

Bootstrapping Example v Example - Bootstrapping a Zero Coupon (Spot) Curve (cont’d) Ø Year 3 § Step 1 C 3 = 7. 45, Apply the formula: § Step 2, PV 3 = 86. 50, Apply the formula: 27

Bootstrapping Exercise v Calculate the spot rate in year 4, Z 4 28

Answer to Exercise v Example - Bootstrapping a Zero Coupon (Spot) Curve Ø Year 4 § Step 1 C 4 = 7. 90, Apply the formula: § Step 2, PV 4 = 79. 32, Apply the formula: 29

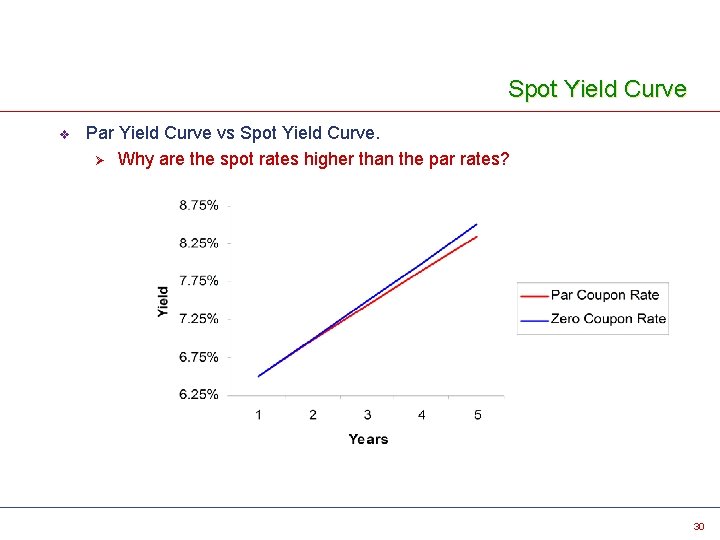
Spot Yield Curve v Par Yield Curve vs Spot Yield Curve. Ø Why are the spot rates higher than the par rates? 30

Forward Rates v v v Par Rate – Rate paid on a par bond (coupon= yield, price=100) Spot Rate – Rate paid on a zero coupon bond. Forward Rate - Rate paid on a forward investment. Ø c 1 = z 1 =f 1 (1+f 2) = (1+z 2)/(1+z 1) In general Ø 31

Total Return Nominal Return v Rate of Return on a security assuming it was purchased on a certain begin (settlement) date and sold on a certain horizon date. v The return calculation takes into account; Ø Settlement full price, Ø Horizon full price Ø Intermediate cash flows from the security (coupon plus any principal payments) Ø Reinvestment of any intermediate cash flow payments to the horizon date. 32

Total Return v Nominal Return Calculation v Annualized Return (semi-annually compounded) v n = number of 6 -month periods from beginning to horizon dates 33

Total Return Example v v On 11/15/2006 you purchase XYZ 6. 00 11/15/2012 at a price of 100. On 5/15/2006 you collect a coupon and reinvest it at 6% yield. On 11/15/2007 you sell the bond at a price of 100 Calculate your nominal and annualized return. Ø Beginning Accrued = 0 Ø Beginning Full Price = 100+0=100 Ø Horizon Accrued = 0 Ø Horizon Full Price = 100+0=100 Ø Reinvestment (1 coupon for half a year)= 3(. 03) =. 09 34

Differences between Annualized ROR and YTM v v YTM is the Internal Rate of Return (IIR) of the bonds cashflows The discount rate at which the sum of the PV of the cashflows equals the Full Price of the bond Ø YTM presumes you hold the bond until maturity Ø YTM ignores reinvestment ROR takes into account Ø Sale of security prior to maturity Ø Reinvestment Rate For ROR = YTM Ø Bond needs to be held to maturity or sold at the same YTM Ø Reinvestment Rate must equal the YTM 35

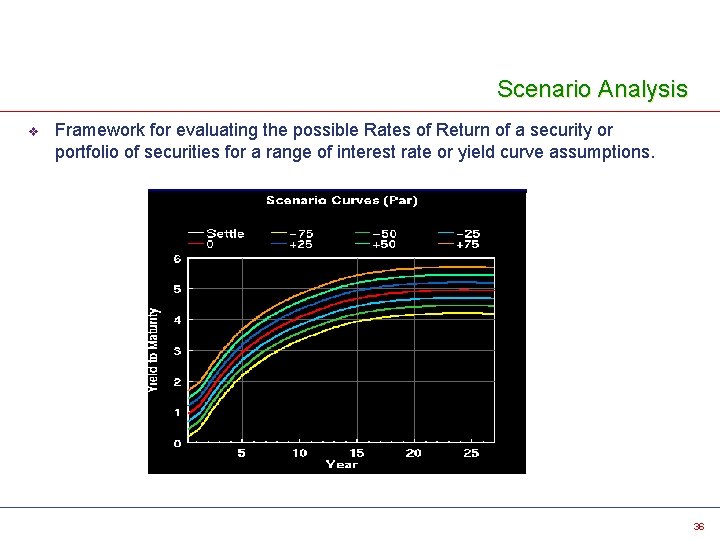
Scenario Analysis v Framework for evaluating the possible Rates of Return of a security or portfolio of securities for a range of interest rate or yield curve assumptions. 36

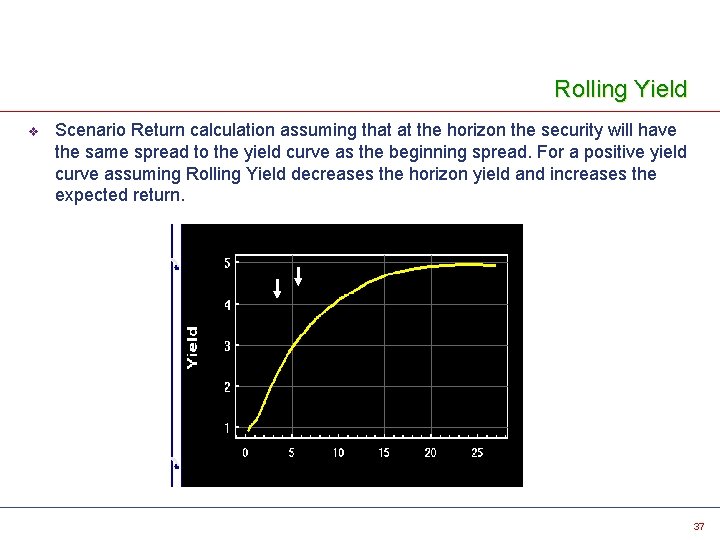
Rolling Yield v Scenario Return calculation assuming that at the horizon the security will have the same spread to the yield curve as the beginning spread. For a positive yield curve assuming Rolling Yield decreases the horizon yield and increases the expected return. 37

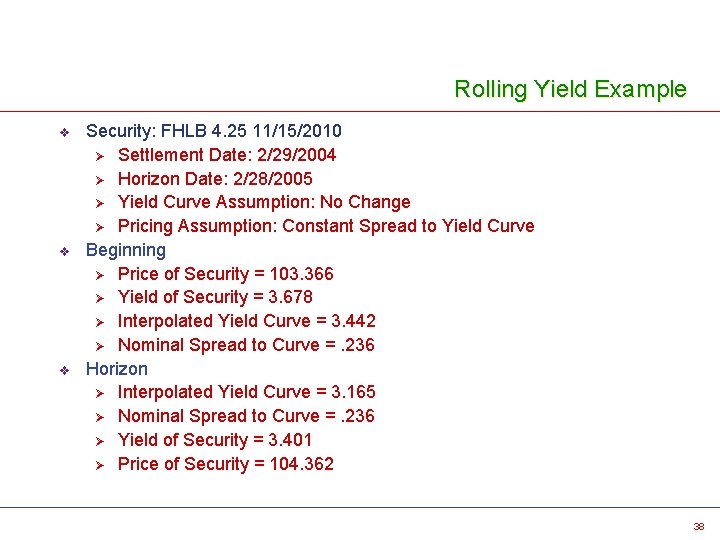
Rolling Yield Example v v v Security: FHLB 4. 25 11/15/2010 Ø Settlement Date: 2/29/2004 Ø Horizon Date: 2/28/2005 Ø Yield Curve Assumption: No Change Ø Pricing Assumption: Constant Spread to Yield Curve Beginning Ø Price of Security = 103. 366 Ø Yield of Security = 3. 678 Ø Interpolated Yield Curve = 3. 442 Ø Nominal Spread to Curve =. 236 Horizon Ø Interpolated Yield Curve = 3. 165 Ø Nominal Spread to Curve =. 236 Ø Yield of Security = 3. 401 Ø Price of Security = 104. 362 38

Rolling Yield Example Beginning Full Price = 103. 366 + 1. 334 = 104. 700 Horizon Full Price = 104. 362 + 1. 216 = 105. 578 Coupon = 2. 231 + 2. 125 = 4. 356 Reinvestment =. 022 39

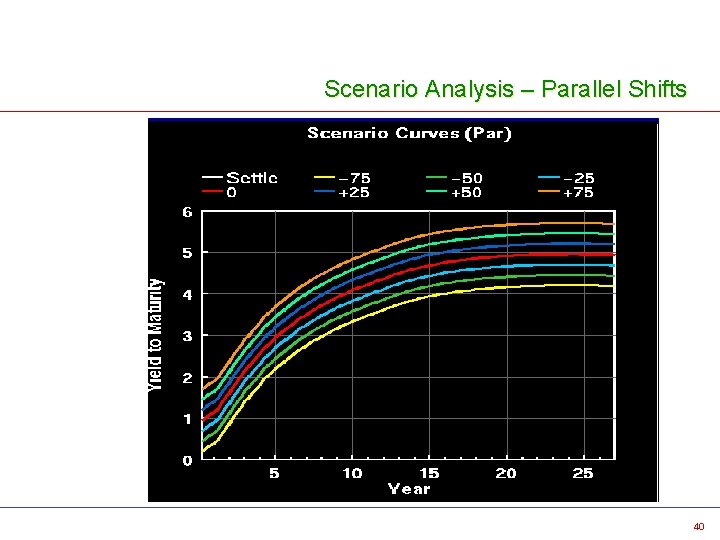
Scenario Analysis – Parallel Shifts 40

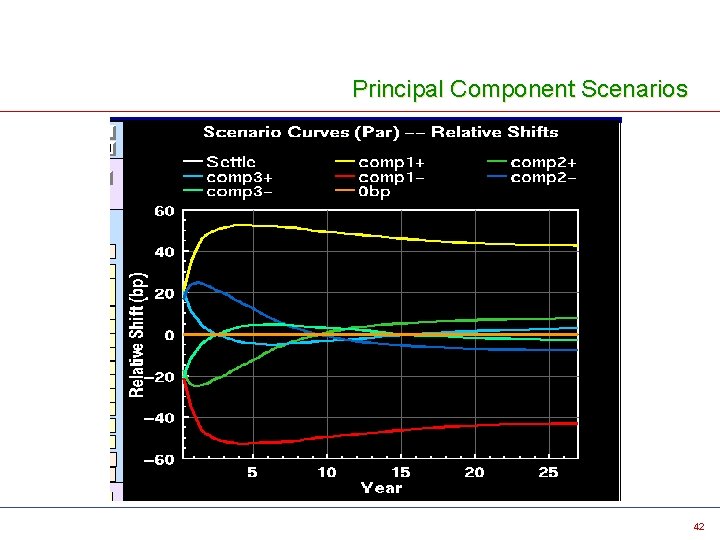
Non Parallel Shifts v v v Principal Component Scenarios Statistically likely re-shapings of the Yield Curve Derived through analysis of 15 years of monthly movements in the Off-the-Run Treasury Yield Curve. These scenarios model 95% of observed movements in the Yield Curve. 95% of the monthly movements over the past 15 years could be represented as a linear combination of the Principal Component Scenarios. 41

Principal Component Scenarios 42