SOLIDI PLATONICI Il termine solido platonico sinonimo di

SOLIDI PLATONICI

Il termine solido platonico è sinonimo di solido regolare e di poliedro convesso regolare e si definisce come poliedro convesso che ha per facce poligoni regolari congruenti

La relazione di Eulero asserisce che F+V= S+ 2 F numero della facce, S numero di spigoli, V numero di vertici.

Moltiplicando il numero L dei lati di ogni faccia per il numero delle facce del poliedro si ottiene il doppio della totalità degli spigoli (ogni spigolo viene contato due volte, una sulla prima faccia ed una sulla faccia attaccata alla prima per quello spigolo): L*F= 2 S/L

Il numero dei vertici V moltiplicati per il numero R di spigoli che si incontrano in essi, equivale alla totalità degli spigoli moltiplicata per due, perché ogni spigolo collega tra loro due vertici: V*R=2 S V = 2 S/R

Dalla relazione di Eulero F+V–S= 2 e le relazioni F = 2 S/L e V =2 S/R 2 S/L + 2 S/R - S = 2 dividendo per 2 S 1/L + 1/R - 1/2 = 1/S > 0

1/L + 1/R - 1/2 = 1/S > 0 L ed R debbono essere maggiori o uguali a 3 poiché un poligono deve avere almeno tre lati ed almeno tre lati devono incontrarsi nel vertice di ciascuno degli angoloidi di un poliedro

1/L + 1/R - 1/2 = 1/S > 0 L ed R non possono essere entrambi uguali a quattro, poiché in tal caso il primo membro dell'equazione sarebbe uguale a 0, mentre 1/S è positivo.

1/L + 1/R - 1/2 = 1/S Se L ed R fossero contemporaneamente maggiori di tre, S dovrebbe essere negativo; questa possibilità è quindi esclusa, ed almeno uno deve essere tre.

1/L + 1/R - 1/2 = 1/S Se L = 3 R può essere uguale solo a 3, 4, oppure 5, 1/3 + 1/R - 1/2 = 1/S R = 3 => S = 6 R = 4 => S = 12 R = 5 => S = 30 F = 2 S/L V = 2 S/R F = 2*6/3 V =2*6/3 F = 2*12/3 V =2*12/4 F = 2*30/3 V =2*30/5 casi che corrispondono rispettivamente al tetraedro, all'ottaedro e all'icosaedro.

Allo stesso modo, se R = 3, allora L può assumere solo i valori 3, 4, oppure 5. Si può scartare 3 perché lo abbiamo considerato nel caso precedente ; 1/L + 1/3 - 1/2 = 1/S L = 4 => S = 12 L = 5 => S = 30 F = 2 S/L V = 2 S/R F = 2*12/4=6 V = 2*12/3=8 F = 2*30/5=12 V =2*30/3=20 corrispondono al cubo e al dodecaedro. Non ci sono altri casi possibili, e quindi esistono al più cinque poliedri regolari.

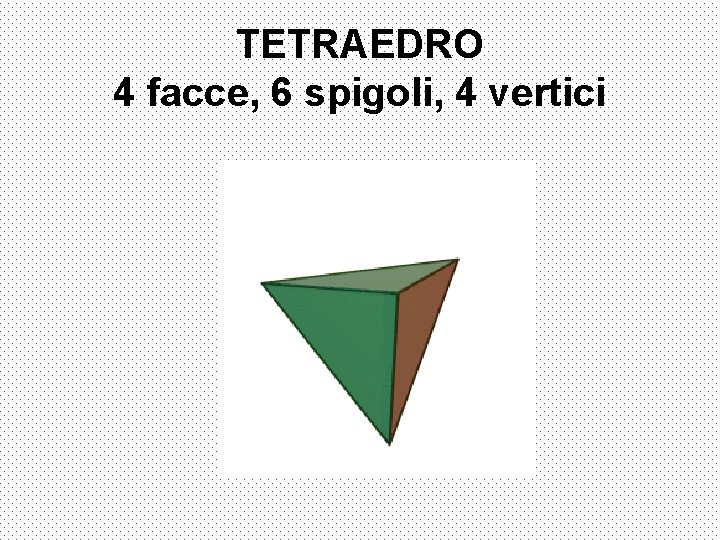
TETRAEDRO 4 facce, 6 spigoli, 4 vertici

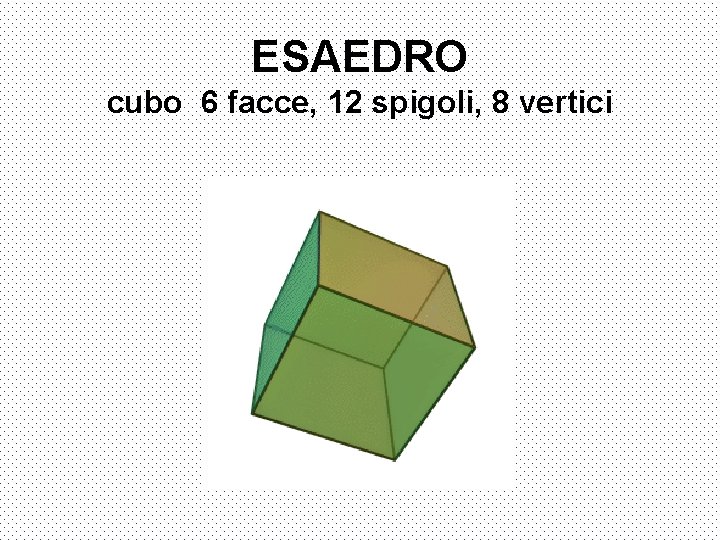
ESAEDRO cubo 6 facce, 12 spigoli, 8 vertici

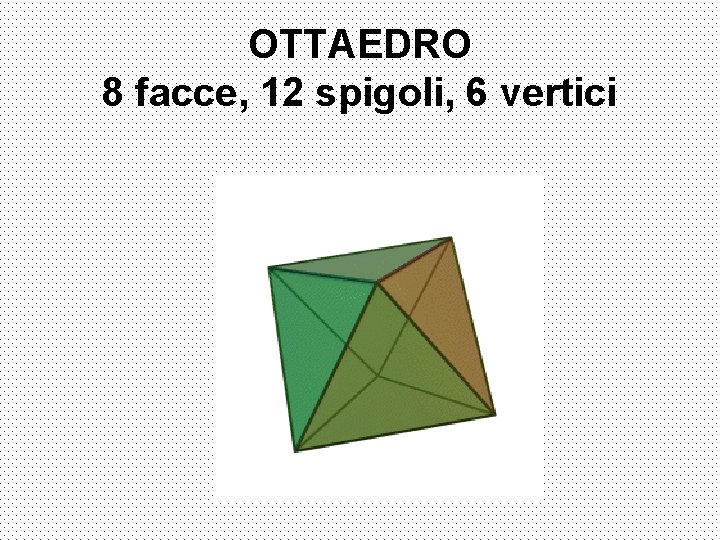
OTTAEDRO 8 facce, 12 spigoli, 6 vertici

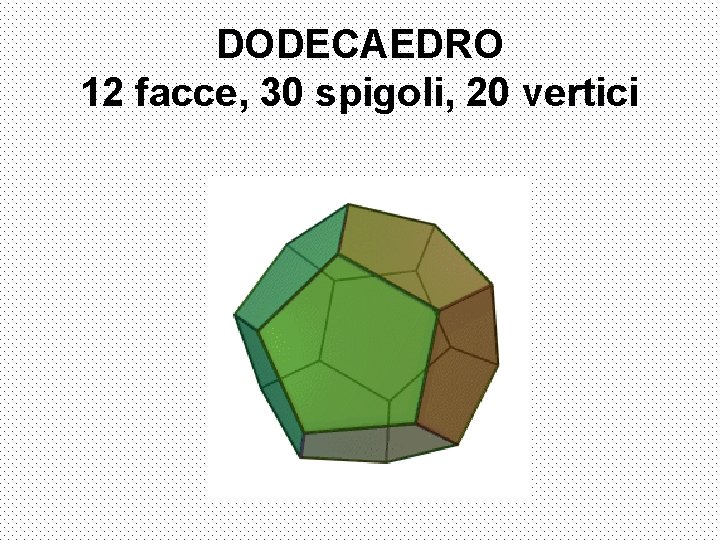
DODECAEDRO 12 facce, 30 spigoli, 20 vertici

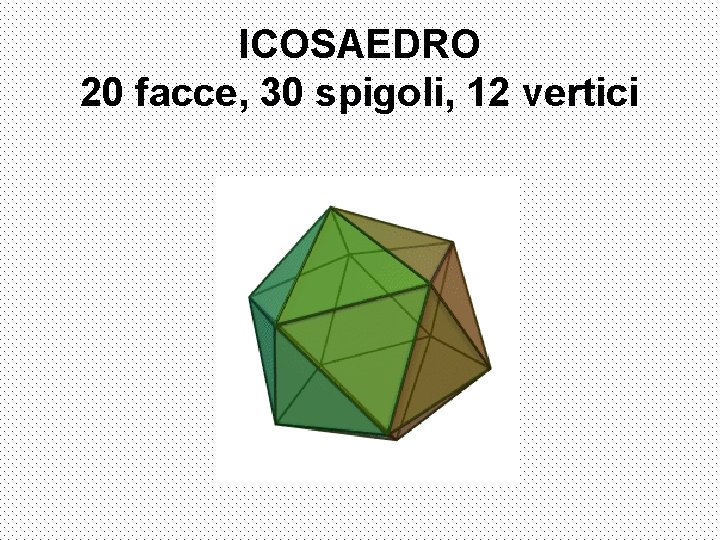
ICOSAEDRO 20 facce, 30 spigoli, 12 vertici