KUKLA DEKENLER Mehmet Vedat PAZARLIOLU Kukla Deiken Nedir











































































































- Slides: 175

KUKLA DEĞİŞKENLER Mehmet Vedat PAZARLIOĞLU

Kukla Değişken Nedir? Cinsiyet, eğitim seviyesi, meslek, din, ırk, bölge, tabiiyet, savaşlar, grevler, siyasi karışıklıklar (=darbeler), iktisat politikasındaki değişiklikler, depremler, yangın ve benzeri nitel değişkenlerin ekonometrik bir modelde ifade edilme şeklidir.

Kukla Değişkenlerin Modelde Kullanımı Kukla Değişken/lerin Modelde bağımsız değişken olarak yer alması Kukla Değişkenin Modelde Bağımlı Değişken olarak yer alması

Bağımsız Kukla Değişkenler • Bir kukla değişkenli modeller (Varyans Analiz Modelleri) • Kukla değişkenlerin ve Sayısal değişkenlerin Birlikte yer aldığı Modeller (Kovaryans Analizi Modeller) • Kukla değişkenlerin karşılıklı olarak birbirini etkilemeleri • Mevsim dalgalanmalarının ölçülmesinde kukla değişkenler • Parçalı Doğrusal Regresyon

Bir kukla değişkenli modeller Yi = a + b Di +ui Yi = Öğretim Üyelerinin Yıllık Maaşları Di = 1 Öğretim Üyesi Erkekse = 0 Diğer Durumlar (yani Kadın Öğretim Üyesi) Varyans Analiz Modelleri (ANOVA) Kadın Öğretim Üyelerinin Ortalama Maaşları: E( Yi|Di = 0 ) = a Erkek Öğretim Üyelerinin Ortalama Maaşları : E ( Yi|Di = 1) = a + b

Bir kukla değişkenli modeller Maaş Cinsiyet 22 1 19 0 18 0 21. 7 18. 5 21 20. 5 17 17. 5 21. 2 1 0 1 1 0 0 1 Yi = 18 + 3. 28 Di (0. 32) (0. 44) t (57. 74)(7. 44) , R 2=0. 8737

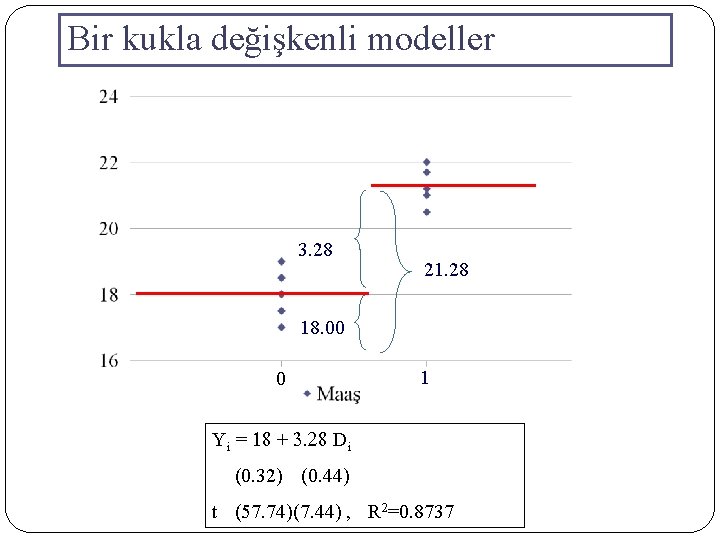
Bir kukla değişkenli modeller Yi = 18 + 3. 28 Di (0. 32) (0. 44) t (57. 74)(7. 44) , R 2=0. 8737 Kadın Öğretim Üyelerinin Ortalama Maaşları: E( Yi|Di = 0 ) = 18 Erkek Öğretim Üyelerinin Ortalama Maaşları : E ( Yi|Di = 1) = 18 + 3. 28 = 21. 28 Erkek ve Kadın Öğretim Üyelerinin Ortalama Maaş Farkı : 3. 28

Bir kukla değişkenli modeller 3. 28 21. 28 18. 00 0 1 Yi = 18 + 3. 28 Di (0. 32) (0. 44) t (57. 74)(7. 44) , R 2=0. 8737

Kukla değişken ve Sayısal Değişkenli Model Yi = a 1 + a 2 Di + b Xi + ui Yi = Öğretim Üyelerinin Yıllık Maaşları Xi = Öğretim Üyesinin Yıl olarak Tecrübesi Di = 1 Öğretim Üyesi Erkekse = 0 Diğer Durumlar (yani Kadın Öğretim Üyesi) Kadın Öğretim Üyelerinin Ortalama Maaşları : E( Yi|Xi, Di = 0 ) = a 1+b. Xi Erkek Öğretim Üyelerinin Ortalama Maaşları : E ( Yi|Xi, Di = 1) = (a 1 + a 2 )+b. Xi

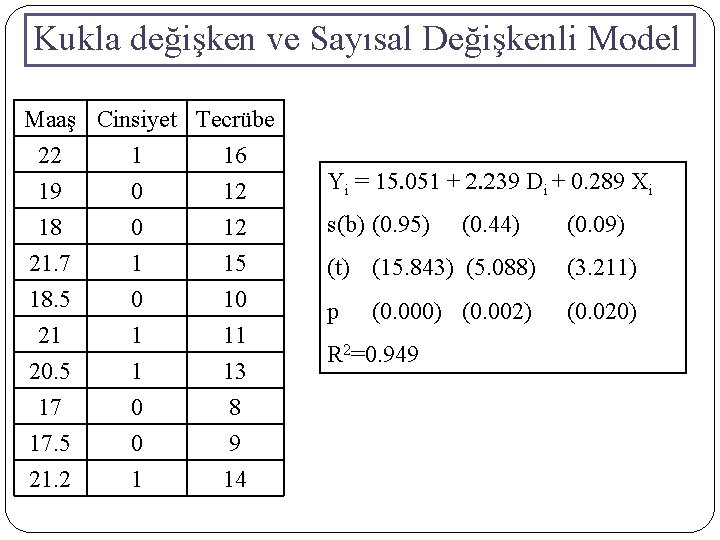
Kukla değişken ve Sayısal Değişkenli Model Maaş Cinsiyet Tecrübe 22 1 16 19 0 12 18 0 12 21. 7 18. 5 21 20. 5 17 17. 5 21. 2 1 0 1 1 0 0 1 15 10 11 13 8 9 14 Yi = 15. 051 + 2. 239 Di + 0. 289 Xi s(b) (0. 95) (0. 44) (0. 09) (t) (15. 843) (5. 088) (3. 211) p (0. 020) (0. 002) R 2=0. 949

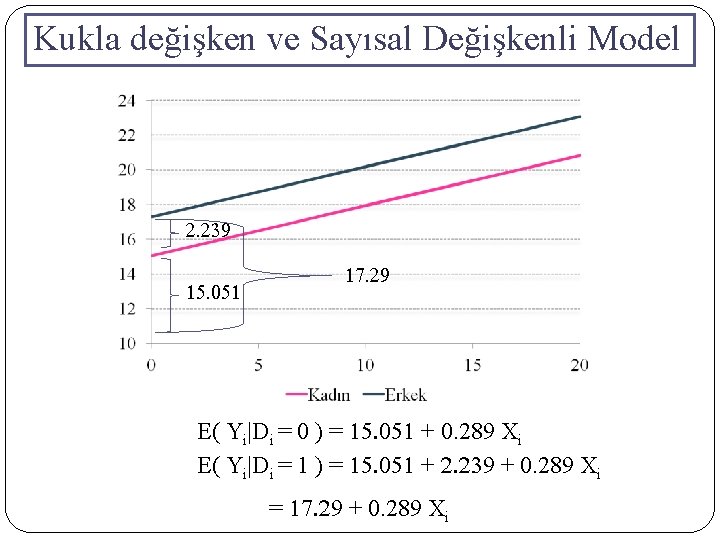
Kukla değişken ve Sayısal Değişkenli Model Yi = 15. 051 + 2. 239 Di + 0. 289 Xi (t) (15. 843) (5. 088) (3. 211) p (0. 020) (0. 002) Kadın Öğretim Üyelerinin Maaş Fonksiyonu: E( Yi|Di = 0 ) = 15. 051 + 0. 289 Xi Erkek Öğretim Üyelerinin Maaş Fonksiyonu: E( Yi|Di = 1 ) = 15. 051 + 2. 239 + 0. 289 Xi = 17. 29 + 0. 289 Xi Erkek ve Kadın Öğretim Üyelerinin Ortalama Maaş Farkı : 2. 239

Kukla değişken ve Sayısal Değişkenli Model 2. 239 15. 051 17. 29 E( Yi|Di = 0 ) = 15. 051 + 0. 289 Xi E( Yi|Di = 1 ) = 15. 051 + 2. 239 + 0. 289 Xi = 17. 29 + 0. 289 Xi

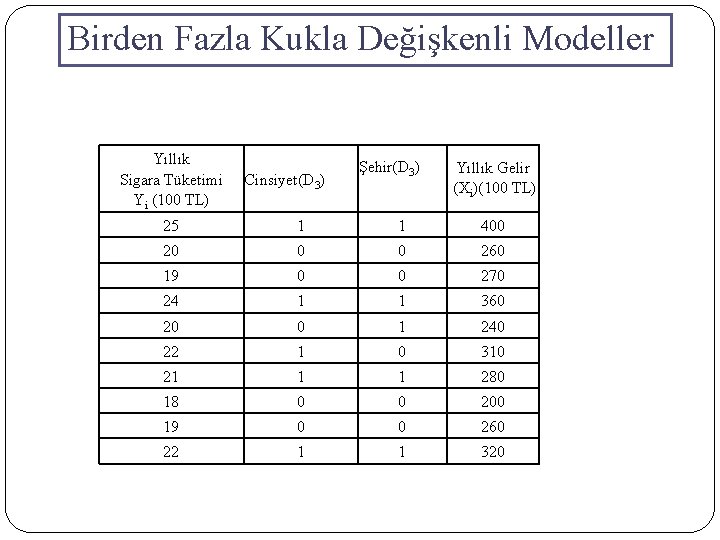
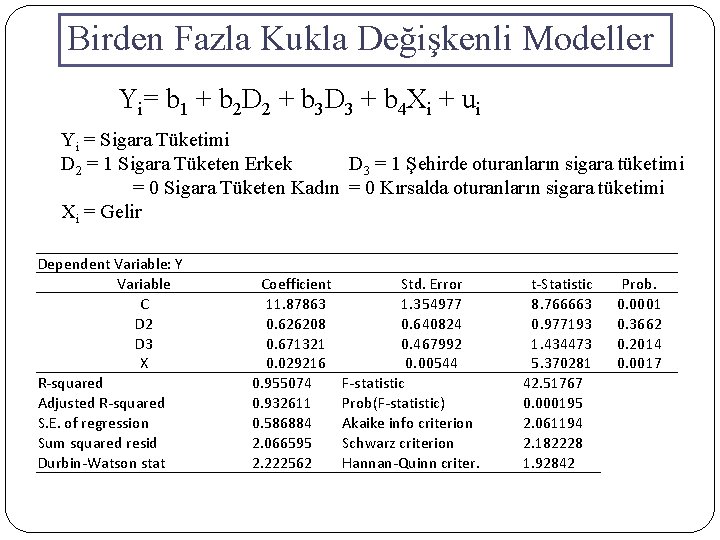
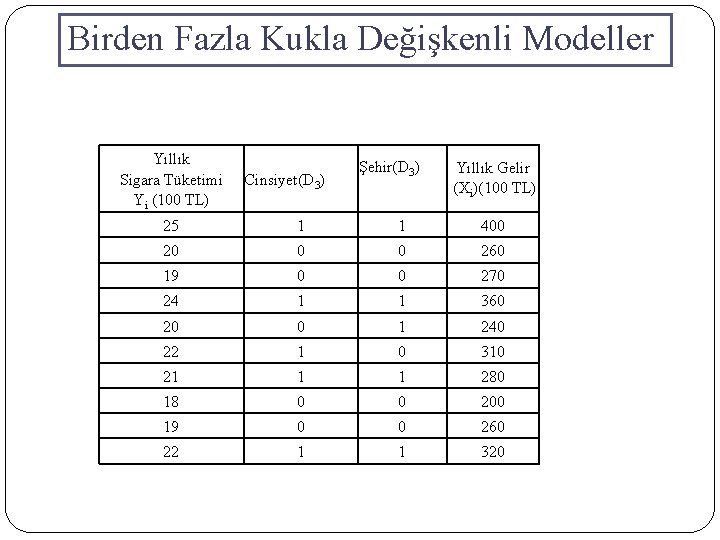
Birden Fazla Kukla Değişkenli Modeller Yi= b 1 + b 2 D 2 + b 3 D 3 + b 4 Xi + ui Yi = Sigara Tüketimi D 2 = 1 Sigara Tüketen Erkek D 3 = 1 Şehirde oturanların sigara tüketimi = 0 Sigara Tüketen Kadın = 0 Kırsalda oturanların sigara tüketimi Xi = Gelir Kırdaki Kadınların Sigara Tüketimi: E( Yi|D 2=0, Yi|D 3=0) = b 1 + b 4 Xi Kırdaki Erkeklerin Sigara Tüketimi : E (Yi|D 2=1, Yi|D 3=0) = b 1 + b 2 D 2 + b 4 Xi Kentteki Kadınların Sigara Tüketimi: E( Yi|D 2=0, Yi|D 3=1 ) = b 1 + b 3 D 3 + b 4 Xi Kentteki Erkeklerin Sigara Tüketimi: E( Yi|D 2=1, Yi|D 3=1 ) = b 1 + b 2 D 2 + b 3 D 3 + b 4 Xi

Birden Fazla Kukla Değişkenli Modeller Yıllık Sigara Tüketimi Yi (100 TL) Cinsiyet(D 3) Şehir(D 3) Yıllık Gelir (Xi)(100 TL) 25 1 1 400 20 0 0 260 19 0 0 270 24 1 1 360 20 0 1 240 22 1 0 310 21 1 1 280 18 0 0 200 19 0 0 260 22 1 1 320

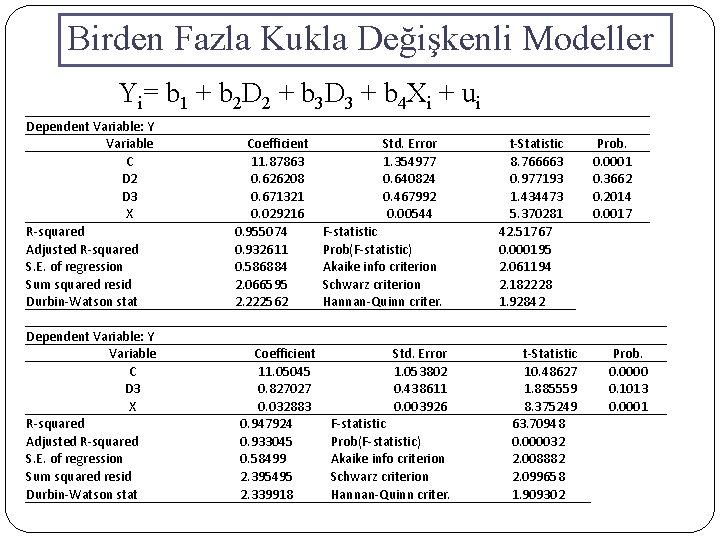
Birden Fazla Kukla Değişkenli Modeller Yi= b 1 + b 2 D 2 + b 3 D 3 + b 4 Xi + ui Yi = Sigara Tüketimi D 2 = 1 Sigara Tüketen Erkek D 3 = 1 Şehirde oturanların sigara tüketimi = 0 Sigara Tüketen Kadın = 0 Kırsalda oturanların sigara tüketimi Xi = Gelir Dependent Variable: Y Variable C D 2 D 3 X R-squared Adjusted R-squared S. E. of regression Sum squared resid Durbin-Watson stat Coefficient 11. 87863 0. 626208 0. 671321 0. 029216 0. 955074 0. 932611 0. 586884 2. 066595 2. 222562 Std. Error 1. 354977 0. 640824 0. 467992 0. 00544 F-statistic Prob(F-statistic) Akaike info criterion Schwarz criterion Hannan-Quinn criter. t-Statistic 8. 766663 0. 977193 1. 434473 5. 370281 42. 51767 0. 000195 2. 061194 2. 182228 1. 92842 Prob. 0. 0001 0. 3662 0. 2014 0. 0017

1. Sabit Terimlerin Farklı Eğimlerin Eşit olması Yi= a 1 + a 2 Di + b. Xi + ui Yi = Sigara Tüketimi Di = 1 Sigara Tüketen Erkek = 0 Xi = Gelir E( Yi|Xi, Di = 0 ) = a 1+b. Xi E ( Yi|Xi, Di = 1) = (a 1 + a 2 )+b. Xi

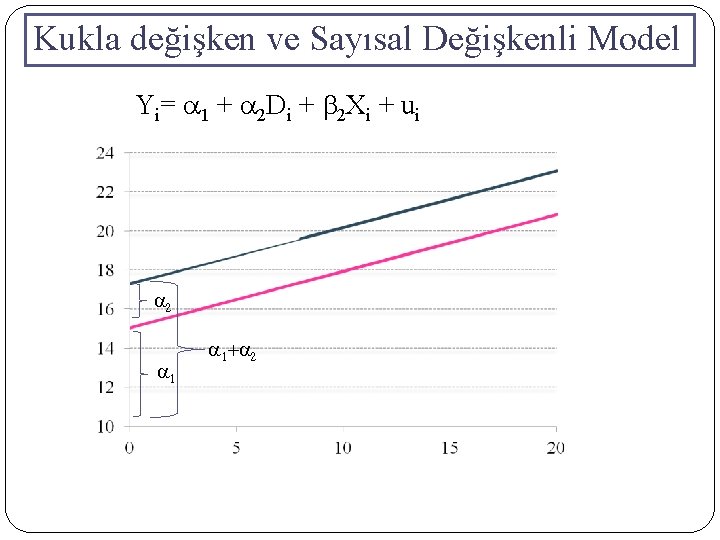
Kukla değişken ve Sayısal Değişkenli Model Yi= a 1 + a 2 Di + b 2 Xi + ui a 2 a 1+a 2

2. Sabit Terimlerin Eşit, Eğimlerin Farklı Olması Hali Yi= a 1 + b 1 Di Xi+ b 2 Xi + ui Yi = Sigara Tüketimi Di = 1 Sigara Tüketen Erkek = 0 Xi = Gelir E( Yi|Xi, Di = 0 ) = a 1+b 2 Xi E ( Yi|Xi, Di = 1) = a 1 + (b 1+b 2)X i

2. Sabit Terimlerin Eşit, Eğimlerin Farklı Olması Hali Yi= a 1 + b 1 Di Xi+ b 2 Xi + ui Yi E ( Yi|Xi, Di = 1) = a 1 + (b 1+b 2)X i ) b 1 + b 2 ) b 2 E( Yi|Xi, Di = 0 ) = a 1+b 2 Xi a 1 Xi 19

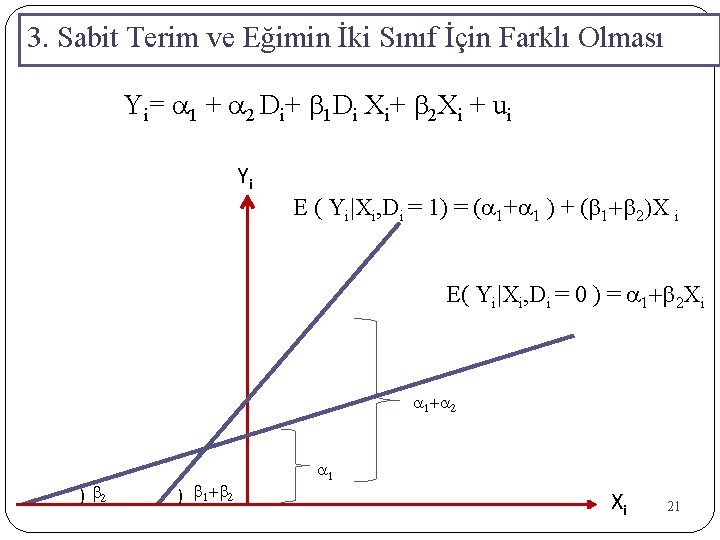
3. Sabit Terim ve Eğimin İki Sınıf İçin Farklı Olması Yi= a 1 + a 2 Di+ b 1 Di Xi+ b 2 Xi + ui Yi = Sigara Tüketimi Di = 1 Sigara Tüketen Erkek = 0 Xi = Gelir E( Yi|Xi, Di = 0 ) = a 1+b 2 Xi E ( Yi|Xi, Di = 1) = (a 1+a 1 ) + (b 1+b 2)X i

3. Sabit Terim ve Eğimin İki Sınıf İçin Farklı Olması Yi= a 1 + a 2 Di+ b 1 Di Xi+ b 2 Xi + ui Yi E ( Yi|Xi, Di = 1) = (a 1+a 1 ) + (b 1+b 2)X i E( Yi|Xi, Di = 0 ) = a 1+b 2 Xi a 1+a 2 ) b 1+b 2 a 1 Xi 21

Modelin t İstatistiklerinin Değerlendirilmesi Yi= a 1 + a 2 Di+ b 1 Di Xi+ b 2 Xi + ui 1. a 2 ve b 1’ün t istatistikleri anlamsızsa iki sınıf sigara tüketim fonksiyonları aynı 2. a 2 ve b 1’ün t istatistikleri anlamlıysa iki sınıf sigara tüketim fonksiyonları farklı (3. durum) 3. a 2 ve b 1’ün t istatistiklerinden a 2 anlamsız ve b 1 anlamlıysa sabit terim aynı eğim farklıdır. (2. durum) 4. a 2 ve b 1’ün t istatistiklerinden a 2 anlamlı ve b 1 anlamsızsa sabit terim farklı eğim aynıdır. (1. durum) 22

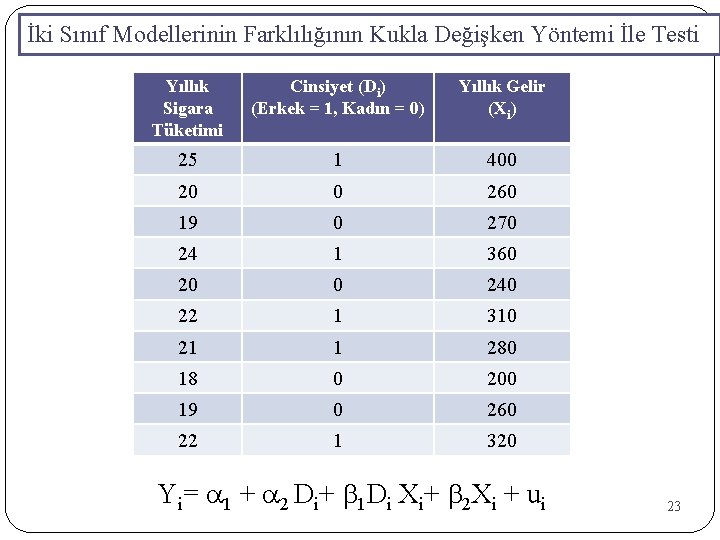
İki Sınıf Modellerinin Farklılığının Kukla Değişken Yöntemi İle Testi Yıllık Sigara Tüketimi Cinsiyet (Di) (Erkek = 1, Kadın = 0) Yıllık Gelir (Xi) 25 1 400 20 0 260 19 0 270 24 1 360 20 0 240 22 1 310 21 1 280 18 0 200 19 0 260 22 1 320 Yi= a 1 + a 2 Di+ b 1 Di Xi+ b 2 Xi + ui 23

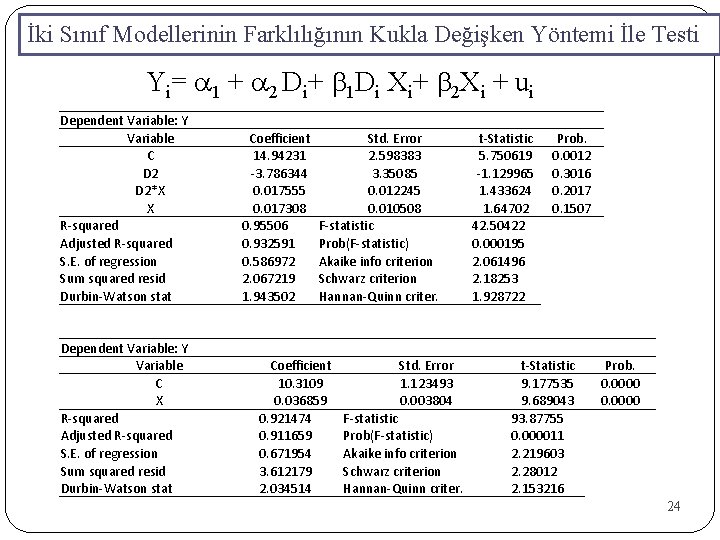
İki Sınıf Modellerinin Farklılığının Kukla Değişken Yöntemi İle Testi Yi= a 1 + a 2 Di+ b 1 Di Xi+ b 2 Xi + ui Dependent Variable: Y Variable C D 2*X X R-squared Adjusted R-squared S. E. of regression Sum squared resid Durbin-Watson stat Dependent Variable: Y Variable C X R-squared Adjusted R-squared S. E. of regression Sum squared resid Durbin-Watson stat Coefficient 14. 94231 -3. 786344 0. 017555 0. 017308 0. 95506 0. 932591 0. 586972 2. 067219 1. 943502 Std. Error 2. 598383 3. 35085 0. 012245 0. 010508 F-statistic Prob(F-statistic) Akaike info criterion Schwarz criterion Hannan-Quinn criter. t-Statistic 5. 750619 -1. 129965 1. 433624 1. 64702 42. 50422 0. 000195 2. 061496 2. 18253 1. 928722 Coefficient 10. 3109 0. 036859 0. 921474 0. 911659 0. 671954 3. 612179 2. 034514 Prob. 0. 0012 0. 3016 0. 2017 0. 1507 Std. Error 1. 123493 0. 003804 F-statistic Prob(F-statistic) Akaike info criterion Schwarz criterion Hannan-Quinn criter. t-Statistic 9. 177535 9. 689043 93. 87755 0. 000011 2. 219603 2. 28012 2. 153216 Prob. 0. 0000 24

2. CHOW testi ile tüketim fonksiyonlarının farklılığının araştırılması Üç grup tüketim fonksiyonu tahmin edilir: H 0: Erkek ve kadınlar için tüketim fonk. aynıdır. H 1: Erkek ve kadınlar için tüketim fonk. farklıdır. 1. Erkek-kadın tüm tüketiciler için tüketim fonksiyonu: HKT=3. 162 2. Erkekler için tüketim fonksiyonu: HKT=0. 2018 3. Kadınlar için tüketim fonksiyonu: HKT=1. 865 Ftest = 2. 243 Ftab= 5. 14 (a=0. 05 f 1=2 f 2=6 sd. lerinde) H 0 kabul 25

Birden Fazla Kukla Değişkenli Modeller Yıllık Sigara Tüketimi Yi (100 TL) Cinsiyet(D 3) Şehir(D 3) Yıllık Gelir (Xi)(100 TL) 25 1 1 400 20 0 0 260 19 0 0 270 24 1 1 360 20 0 1 240 22 1 0 310 21 1 1 280 18 0 0 200 19 0 0 260 22 1 1 320

Birden Fazla Kukla Değişkenli Modeller Yi= b 1 + b 2 D 2 + b 3 D 3 + b 4 Xi + ui Dependent Variable: Y Variable C D 2 D 3 X R-squared Adjusted R-squared S. E. of regression Sum squared resid Durbin-Watson stat Dependent Variable: Y Variable C D 3 X R-squared Adjusted R-squared S. E. of regression Sum squared resid Durbin-Watson stat Coefficient 11. 87863 0. 626208 0. 671321 0. 029216 0. 955074 0. 932611 0. 586884 2. 066595 2. 222562 Coefficient 11. 05045 0. 827027 0. 032883 0. 947924 0. 933045 0. 58499 2. 395495 2. 339918 Std. Error 1. 354977 0. 640824 0. 467992 0. 00544 F-statistic Prob(F-statistic) Akaike info criterion Schwarz criterion Hannan-Quinn criter. t-Statistic 8. 766663 0. 977193 1. 434473 5. 370281 42. 51767 0. 000195 2. 061194 2. 182228 1. 92842 Std. Error 1. 053802 0. 438611 0. 003926 F-statistic Prob(F-statistic) Akaike info criterion Schwarz criterion Hannan-Quinn criter. t-Statistic 10. 48627 1. 885559 8. 375249 63. 70948 0. 000032 2. 008882 2. 099658 1. 909302 Prob. 0. 0001 0. 3662 0. 2014 0. 0017 Prob. 0. 0000 0. 1013 0. 0001

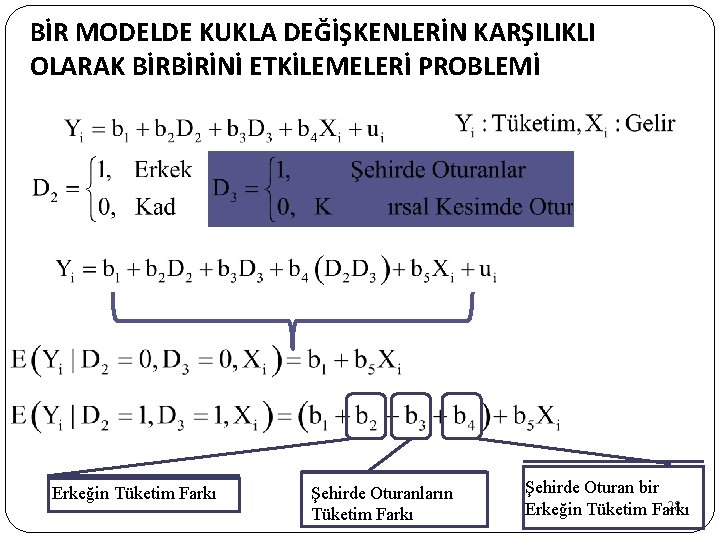
BİR MODELDE KUKLA DEĞİŞKENLERİN KARŞILIKLI OLARAK BİRBİRİNİ ETKİLEMELERİ PROBLEMİ Erkeğin Tüketim Farkı Şehirde Oturanların Tüketim Farkı Şehirde Oturan bir 28 Erkeğin Tüketim Farkı

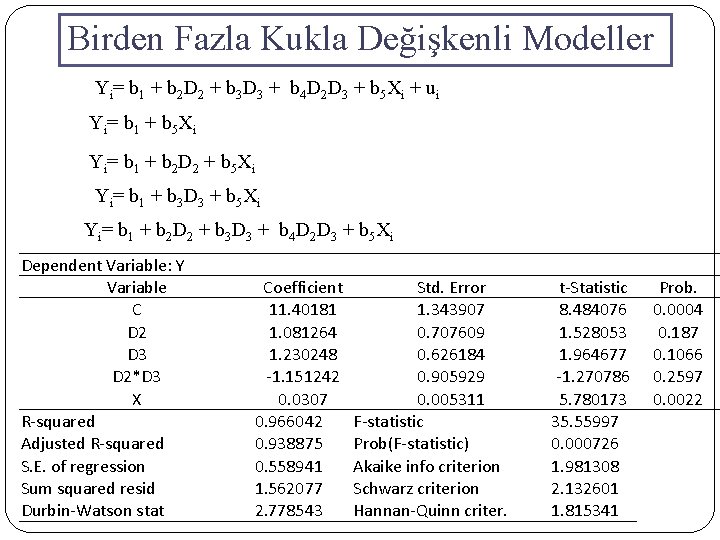
Birden Fazla Kukla Değişkenli Modeller Yi= b 1 + b 2 D 2 + b 3 D 3 + b 4 D 2 D 3 + b 5 Xi + ui Yi= b 1 + b 5 Xi Yi= b 1 + b 2 D 2 + b 5 Xi Yi= b 1 + b 3 D 3 + b 5 Xi Yi= b 1 + b 2 D 2 + b 3 D 3 + b 4 D 2 D 3 + b 5 Xi Dependent Variable: Y Variable C D 2 D 3 D 2*D 3 X R-squared Adjusted R-squared S. E. of regression Sum squared resid Durbin-Watson stat Coefficient 11. 40181 1. 081264 1. 230248 -1. 151242 0. 0307 0. 966042 0. 938875 0. 558941 1. 562077 2. 778543 Std. Error 1. 343907 0. 707609 0. 626184 0. 905929 0. 005311 F-statistic Prob(F-statistic) Akaike info criterion Schwarz criterion Hannan-Quinn criter. t-Statistic 8. 484076 1. 528053 1. 964677 -1. 270786 5. 780173 35. 55997 0. 000726 1. 981308 2. 132601 1. 815341 Prob. 0. 0004 0. 187 0. 1066 0. 2597 0. 0022

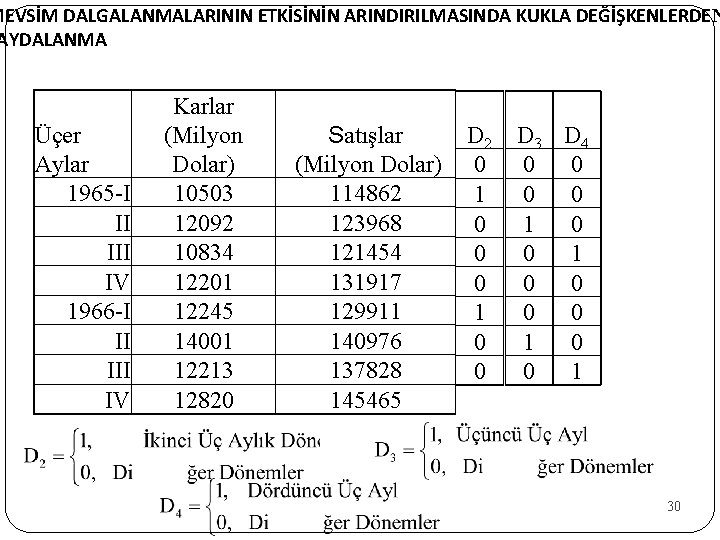
MEVSİM DALGALANMALARININ ETKİSİNİN ARINDIRILMASINDA KUKLA DEĞİŞKENLERDEN AYDALANMA Üçer Aylar 1965 -I II IV 1966 -I II IV Karlar (Milyon Dolar) 10503 12092 10834 12201 12245 14001 12213 12820 Satışlar (Milyon Dolar) 114862 123968 121454 131917 129911 140976 137828 145465 D 2 0 1 0 0 D 3 D 4 0 0 0 0 1 30

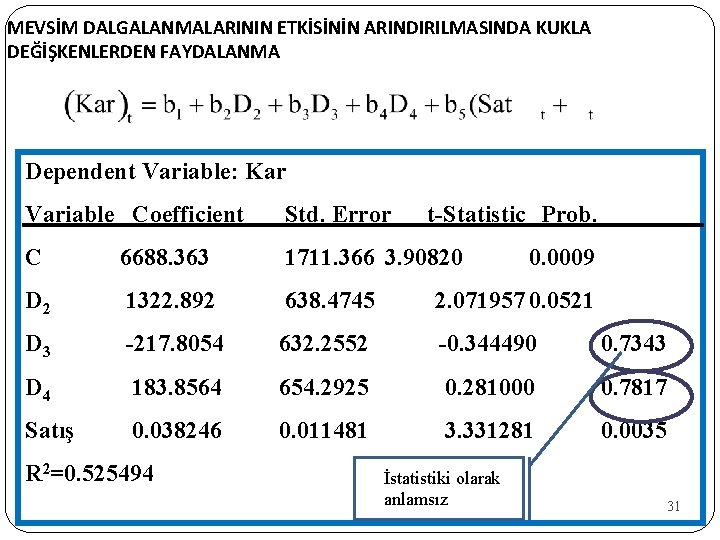
MEVSİM DALGALANMALARININ ETKİSİNİN ARINDIRILMASINDA KUKLA DEĞİŞKENLERDEN FAYDALANMA Dependent Variable: Kar Variable Coefficient Std. Error C 6688. 363 1711. 366 3. 90820 D 2 1322. 892 638. 4745 2. 071957 0. 0521 D 3 -217. 8054 632. 2552 -0. 344490 0. 7343 D 4 183. 8564 654. 2925 0. 281000 0. 7817 Satış 0. 038246 0. 011481 3. 331281 0. 0035 R 2=0. 525494 t-Statistic Prob. İstatistiki olarak anlamsız 0. 0009 31

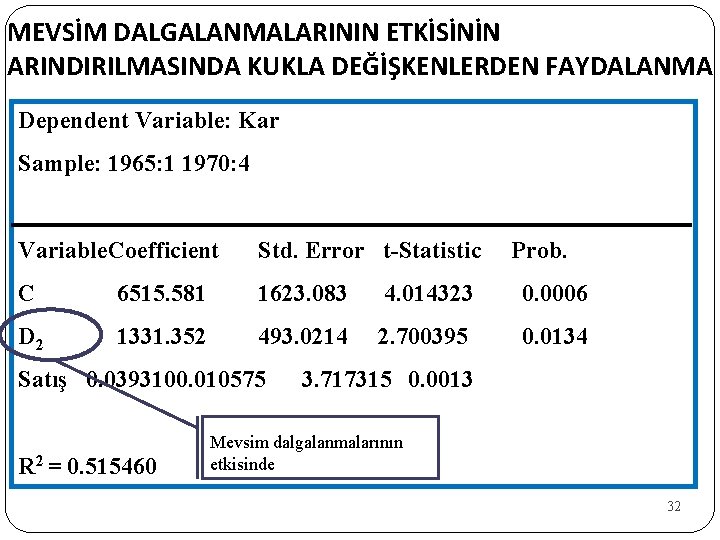
MEVSİM DALGALANMALARININ ETKİSİNİN ARINDIRILMASINDA KUKLA DEĞİŞKENLERDEN FAYDALANMA Dependent Variable: Kar Sample: 1965: 1 1970: 4 Variable. Coefficient Std. Error t-Statistic C 6515. 581 1623. 083 4. 014323 0. 0006 D 2 1331. 352 493. 0214 2. 700395 0. 0134 Satış 0. 0393100. 010575 R 2 = 0. 515460 Prob. 3. 717315 0. 0013 Mevsim dalgalanmalarının etkisinde 32

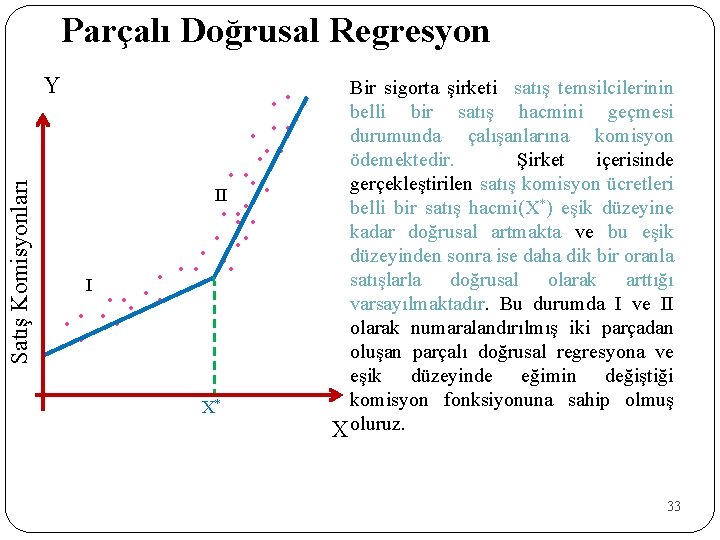
Parçalı Doğrusal Regresyon Satış Komisyonları Y • • • • II • • • • • I • • • X* Bir sigorta şirketi satış temsilcilerinin belli bir satış hacmini geçmesi durumunda çalışanlarına komisyon ödemektedir. Şirket içerisinde gerçekleştirilen satış komisyon ücretleri belli bir satış hacmi(X*) eşik düzeyine kadar doğrusal artmakta ve bu eşik düzeyinden sonra ise daha dik bir oranla satışlarla doğrusal olarak arttığı varsayılmaktadır. Bu durumda I ve II olarak numaralandırılmış iki parçadan oluşan parçalı doğrusal regresyona ve eşik düzeyinde eğimin değiştiği komisyon fonksiyonuna sahip olmuş X oluruz. 33

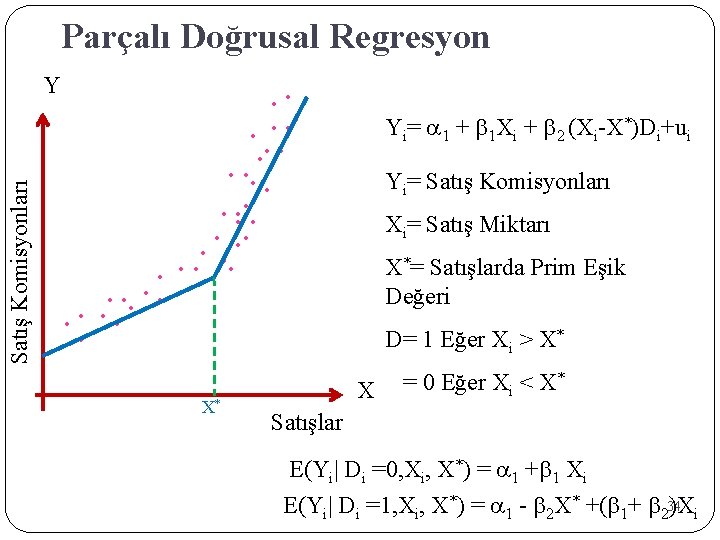
Parçalı Doğrusal Regresyon Satış Komisyonları Y • • • • • • • • • • • X* Yi= a 1 + b 1 Xi + b 2 (Xi-X*)Di+ui Yi= Satış Komisyonları Xi= Satış Miktarı X*= Satışlarda Prim Eşik Değeri D= 1 Eğer Xi > X* * = 0 Eğer X < X i X Satışlar E(Yi| Di =0, Xi, X*) = a 1 +b 1 Xi E(Yi| Di =1, Xi, X*) = a 1 - b 2 X* +(b 1+ b 234 )Xi

Parçalı Doğrusal Regresyon Satış Komisyonları Y b 1+b 2 1 1 b 1 a 1 -b 2 X* X X* Satışlar 35

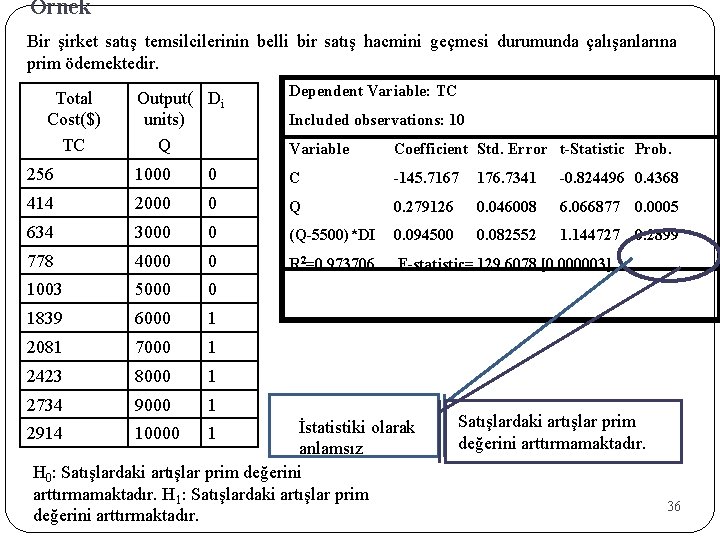
Örnek Bir şirket satış temsilcilerinin belli bir satış hacmini geçmesi durumunda çalışanlarına prim ödemektedir. Output( Di units) Q Dependent Variable: TC Variable Coefficient Std. Error t-Statistic Prob. 256 1000 0 C -145. 7167 176. 7341 -0. 824496 0. 4368 414 2000 0 Q 0. 279126 0. 046008 6. 066877 0. 0005 634 3000 0 (Q-5500)*DI 0. 094500 0. 082552 1. 144727 0. 2899 778 4000 0 R 2=0. 973706 F-statistic= 129. 6078 [0. 000003] 1003 5000 0 1839 6000 1 2081 7000 1 2423 8000 1 2734 9000 1 Total Cost($) TC Included observations: 10 İstatistiki olarak anlamsız H 0: Satışlardaki artışlar prim değerini arttırmamaktadır. H 1: Satışlardaki artışlar prim değerini arttırmaktadır. 2914 10000 1 Satışlardaki artışlar prim değerini arttırmamaktadır. 36

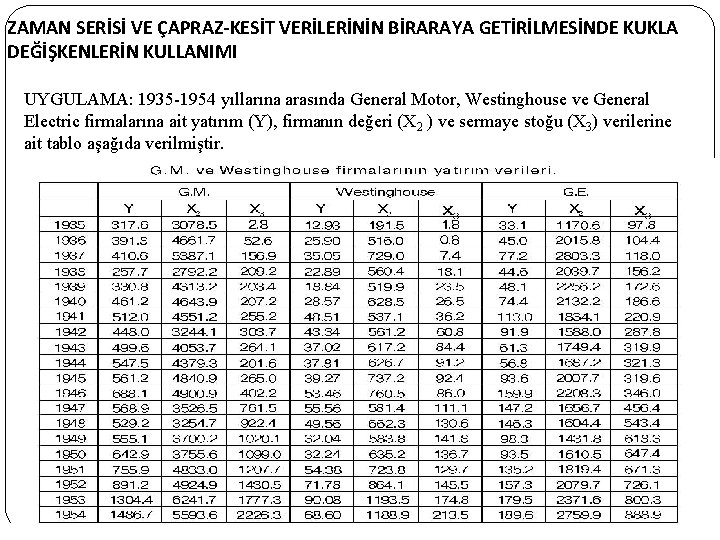
ZAMAN SERİSİ VE ÇAPRAZ-KESİT VERİLERİNİN BİRARAYA GETİRİLMESİNDE KUKLA DEĞİŞKENLERİN KULLANIMI UYGULAMA: 1935 -1954 yıllarına arasında General Motor, Westinghouse ve General Electric firmalarına ait yatırım (Y), firmanın değeri (X 2 ) ve sermaye stoğu (X 3) verilerine ait tablo aşağıda verilmiştir. 37

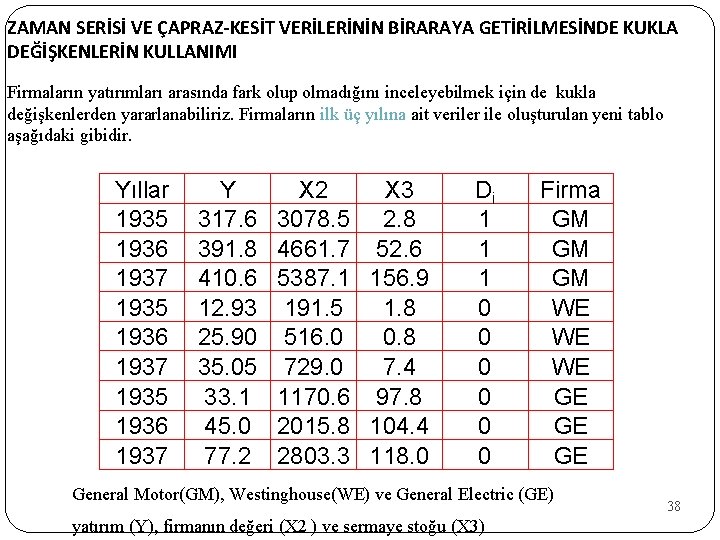
ZAMAN SERİSİ VE ÇAPRAZ-KESİT VERİLERİNİN BİRARAYA GETİRİLMESİNDE KUKLA DEĞİŞKENLERİN KULLANIMI Firmaların yatırımları arasında fark olup olmadığını inceleyebilmek için de kukla değişkenlerden yararlanabiliriz. Firmaların ilk üç yılına ait veriler ile oluşturulan yeni tablo aşağıdaki gibidir. Yıllar 1935 1936 1937 Y 317. 6 391. 8 410. 6 12. 93 25. 90 35. 05 33. 1 45. 0 77. 2 X 3 3078. 5 2. 8 4661. 7 52. 6 5387. 1 156. 9 191. 5 1. 8 516. 0 0. 8 729. 0 7. 4 1170. 6 97. 8 2015. 8 104. 4 2803. 3 118. 0 Di 1 1 1 0 0 0 Firma GM GM GM WE WE WE GE General Motor(GM), Westinghouse(WE) ve General Electric (GE) yatırım (Y), firmanın değeri (X 2 ) ve sermaye stoğu (X 3) 38

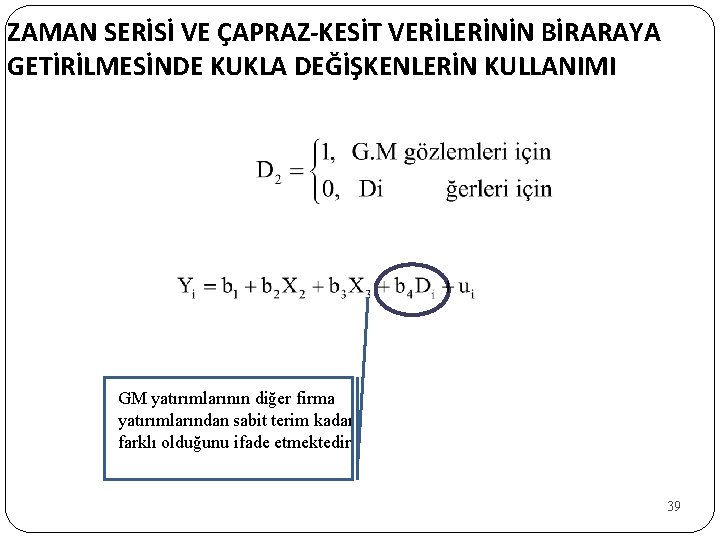
ZAMAN SERİSİ VE ÇAPRAZ-KESİT VERİLERİNİN BİRARAYA GETİRİLMESİNDE KUKLA DEĞİŞKENLERİN KULLANIMI GM yatırımlarının diğer firma yatırımlarından sabit terim kadar farklı olduğunu ifade etmektedir. 39

ZAMAN SERİSİ VE ÇAPRAZ-KESİT VERİLERİNİN BİRARAYA GETİRİLMESİNDE KUKLA DEĞİŞKENLERİN KULLANIMI Dependent Variable: Y Method: Least Squares Included observations: 60 Variable C X 2 X 3 DI Coefficient Std. Errort-Statistic Prob. -61. 80754 23. 79039 -2. 598004 0. 038311 0. 016752 2. 286884 0. 0260 0. 347303 0. 032048 10. 83683 0. 0000 278. 5911 51. 74338 5. 384091 0. 0000 0. 0120 R-squared 0. 924866 Mean dependent var 251. 067 Adjusted R-squared 0. 920841 S. D. dependent var 311. 6501 S. E. of regression 87. 68352 Akaike info criterion 11. 84969 Sum squared resid 430550. 4 Schwarz criterion 11. 9893 Log likelihood -351. 4906 F-statistic 229. 7778 Durbin-Watson stat 0. 502776 Prob(F-statistic) 0. 000000 İstatistiksel olarak anlamlı 40

ÖRNEKLER 41

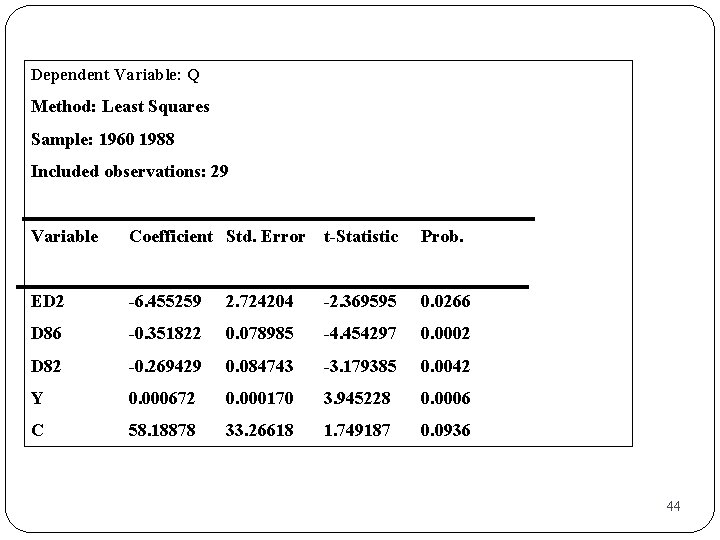
DATA 7 -19 1960 -1988 yılları arasında Türkiye’deki Sigara Tüketimi Q Yetişkinlerin sigara tüketim miktarı(kg), Range 1. 86 - 2. 723. Y GNP(1968) TL, Range 2560 - 5723. P Türkiye’deki sigara fiyatları Range 1. 361 - 3. 968. ED 1 Kayıtlı ortaokul ve lise mezunu nüfus oranı(12 -17 yaş) Range 0. 112 - 0. 451. ED 2 Kayıtlı üniversite mezunu oranı (20 -24) Range 0. 026 - 0. 095. D 82 = 1 , 1982 ve sonrası D 86 = 1 , 1986 ve sonrası 42

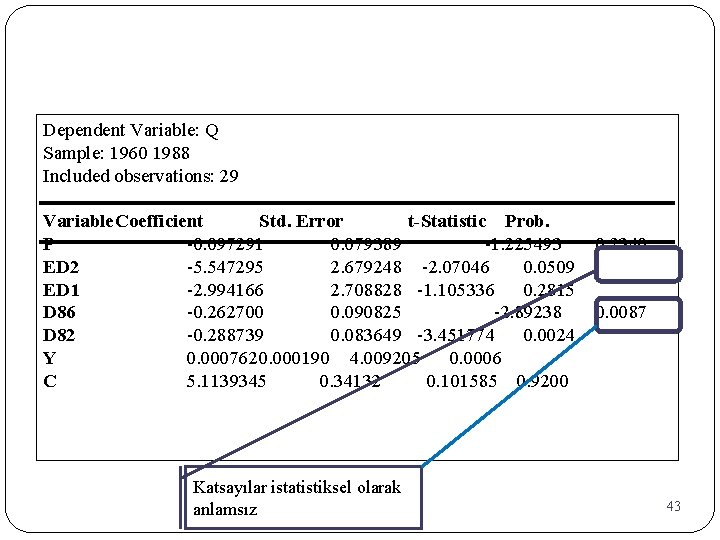
Dependent Variable: Q Sample: 1960 1988 Included observations: 29 Variable. Coefficient Std. Error t-Statistic Prob. P -0. 097291 0. 079389 -1. 225493 0. 2340 ED 2 -5. 547295 2. 679248 -2. 07046 0. 0509 ED 1 -2. 994166 2. 708828 -1. 105336 0. 2815 D 86 -0. 262700 0. 090825 -2. 89238 0. 0087 D 82 -0. 288739 0. 083649 -3. 451774 0. 0024 Y 0. 0007620. 000190 4. 009205 0. 0006 C 5. 1139345 0. 34132 0. 101585 0. 9200 Katsayılar istatistiksel olarak anlamsız 43

Dependent Variable: Q Method: Least Squares Sample: 1960 1988 Included observations: 29 Variable Coefficient Std. Error t-Statistic Prob. ED 2 -6. 455259 2. 724204 -2. 369595 0. 0266 D 86 -0. 351822 0. 078985 -4. 454297 0. 0002 D 82 -0. 269429 0. 084743 -3. 179385 0. 0042 Y 0. 000672 0. 000170 3. 945228 0. 0006 C 58. 18878 33. 26618 1. 749187 0. 0936 44

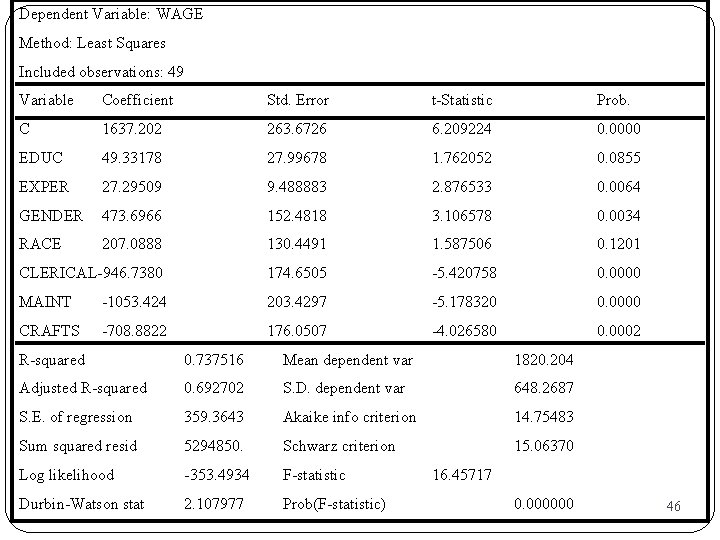
DATA 7 -2 Belirli bir şirkette çalışan 49 kişinin istihdam durumu ve ücretleri WAGE = Aylık Ücret (Range 981 - 3833) EDUC = 8 yıllık eğitimden sonraki sahip olunan eğitim seviyesi(Range 1 - 11) EXPER =Şirkette çalışma süresi(Range 1 - 23) AGE = Yaş (25 - 64) GENDER = 1, Erkek ise; 0 kadın ise RACE = 1, beyaz ise; 0 diğerleri CLERICAL = 1 büro memuru ise, 0 diğerleri MAINT = 1 bakım işlerinde çalışıyor ise; 0 diğerleri CRAFTS =1, usta ise; 0 diğerleri Temel sınıf Profesyonel meslek grupları. 45

Dependent Variable: WAGE Method: Least Squares Included observations: 49 Variable Coefficient Std. Error t-Statistic Prob. C 1637. 202 263. 6726 6. 209224 0. 0000 EDUC 49. 33178 27. 99678 1. 762052 0. 0855 EXPER 27. 29509 9. 488883 2. 876533 0. 0064 GENDER 473. 6966 152. 4818 3. 106578 0. 0034 RACE 207. 0888 130. 4491 1. 587506 0. 1201 CLERICAL-946. 7380 174. 6505 -5. 420758 0. 0000 MAINT -1053. 424 203. 4297 -5. 178320 0. 0000 CRAFTS -708. 8822 176. 0507 -4. 026580 0. 0002 R-squared 0. 737516 Mean dependent var 1820. 204 Adjusted R-squared 0. 692702 S. D. dependent var 648. 2687 S. E. of regression 359. 3643 Akaike info criterion 14. 75483 Sum squared resid 5294850. Schwarz criterion 15. 06370 Log likelihood -353. 4934 F-statistic Durbin-Watson stat 2. 107977 Prob(F-statistic) 16. 45717 0. 000000 46

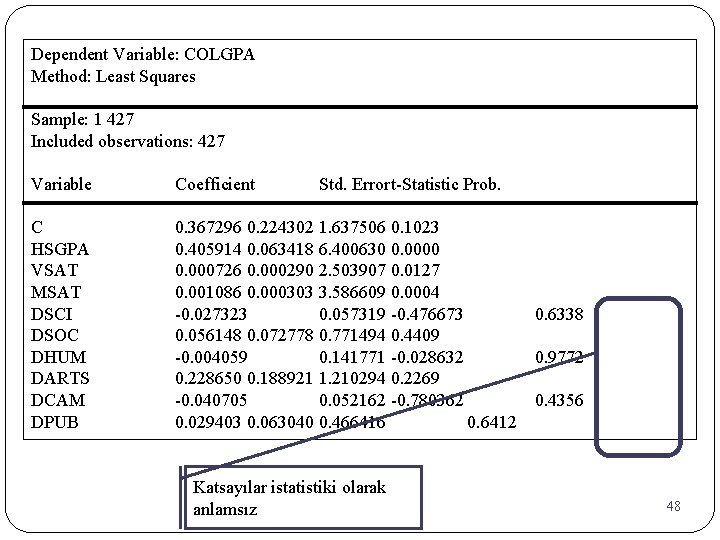
DATA 7 -9 1985 yılında koleje giriş yapan öğrencilerin ilk yıl başarılarını göstermekte colgpa = 1986 sonbaharındaki ortalamaları (Range 0. 85 - 3. 97) hsgpa = Lise GPA (Range 2. 29 - 4. 5) vsat = Sözel derecesi (Range 200 - 700) msat = Sayısal derecesi (Range 330 - 770) dsci = 1 Bilim dalı için, 0 diğerleri dsoc = 1 Sosyal bilim dallı için, 0 diğerleri dhum = 1 Beşeri bilimdalı için 0 diğerleri darts = 1 Sanat dalı için, 0 diğerleri dcam = 1 Öğrenci kampüste yaşıyorsa, 0 diğerleri dpub = 1 Genel lise mezunu ise, 0 diğerleri 47

Dependent Variable: COLGPA Method: Least Squares Sample: 1 427 Included observations: 427 Variable C HSGPA VSAT MSAT DSCI DSOC DHUM DARTS DCAM DPUB Coefficient Std. Errort-Statistic Prob. 0. 367296 0. 224302 1. 637506 0. 1023 0. 405914 0. 063418 6. 400630 0. 000726 0. 000290 2. 503907 0. 0127 0. 001086 0. 000303 3. 586609 0. 0004 -0. 027323 0. 057319 -0. 476673 0. 6338 0. 056148 0. 072778 0. 771494 0. 4409 -0. 004059 0. 141771 -0. 028632 0. 9772 0. 228650 0. 188921 1. 210294 0. 2269 -0. 040705 0. 052162 -0. 780362 0. 4356 0. 029403 0. 063040 0. 466416 0. 6412 Katsayılar istatistiki olarak anlamsız 48

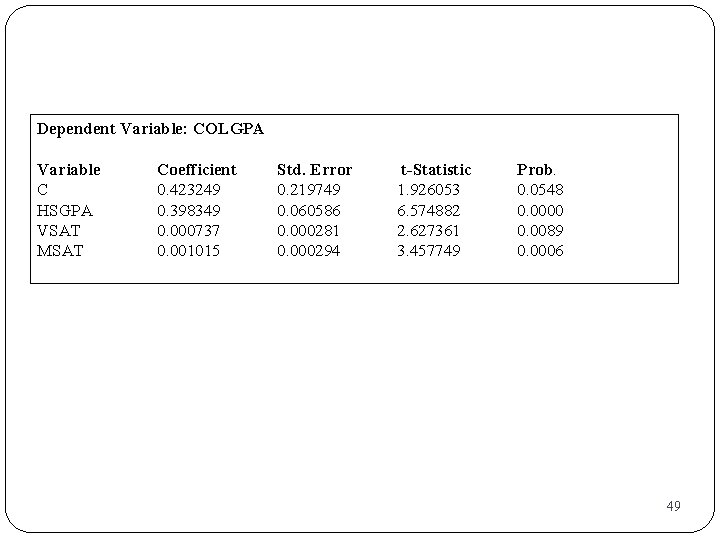
Dependent Variable: COLGPA Variable C HSGPA VSAT MSAT Coefficient 0. 423249 0. 398349 0. 000737 0. 001015 Std. Error 0. 219749 0. 060586 0. 000281 0. 000294 t-Statistic 1. 926053 6. 574882 2. 627361 3. 457749 Prob. 0. 0548 0. 0000 0. 0089 0. 0006 49

Bağımlı Kukla Değişkenler Bağımlı değişken özünde iki değer alabiliyorsa yani bir özelliğin varlığı ya da yokluğu söz konusu ise bu durumda bağımlı kukla değişkenler söz konusudur. • Bu durumdaki modelleri tahmin etmek için dört yaklaşım vardır: -Doğrusal Olasılık Modeli -Logit Modeli -Probit Modeli -Tobit Modeli

Doğrusal Olasılık Modeli Yi = b 1 + b 2 Xi +ui Yi= 1 0 Eğer i. Birey istenen özelliğe sahipse Diğer Durumlarda Xi= Bağımsız değişken Bu modele olasılıklı model denmesinin nedeni, Y’nin X için şartlı beklenen değerinin, Y’nin X için şartlı olasılığına eşit olmasıdır. E(Yi|Xi)= Pr(Yi=1| Xi)

Doğrusal Olasılık Modeli Yi = b 1 + b 2 Xi +ui E(ui) = 0 E(Yi |Xi)= b 1 + b 2 Xi Yi değişkeninin olasılık dağılımı: Yi Olasılık 0 1 -Pi 1 Pi Toplam 1 E(Yi |Xi) = Yi. Pi = 0. (1 -Pi) + 1. (Pi) = Pi E(Yi |Xi)= b 1 + b 2 Xi 0 E(Yi |Xi) 1

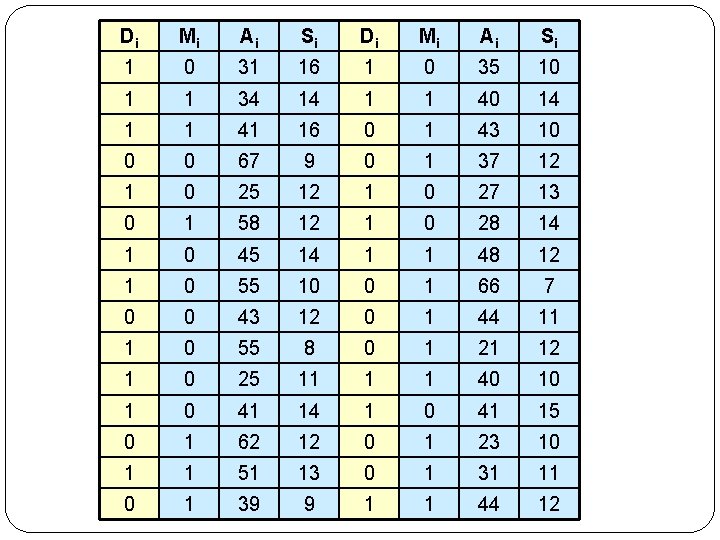
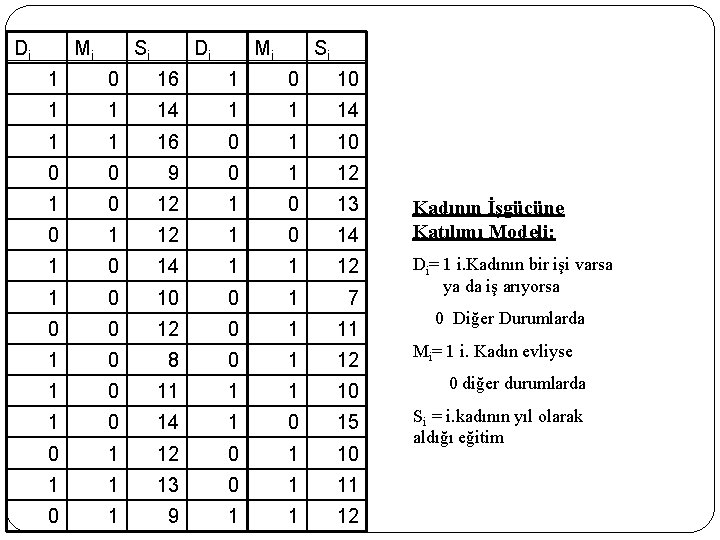
Doğrusal Olasılık Modeli Di = b 1 + b 2 Medenii +b 3 Egitimi +ui Di= 1 Eğer i. Kadının bir işi varsa ya da iş arıyorsa 0 Diğer Durumlarda Medenii= 1 Eğer i. Kadın evliyse diğer durumlarda 0 Eğitimi = i. kadının yıl olarak aldığı eğitim Yaşi = i. Kadının Yaşı

Di Mi Ai Si 1 0 31 16 1 0 35 10 1 1 34 14 1 1 40 14 1 1 41 16 0 1 43 10 0 0 67 9 0 1 37 12 1 0 25 12 1 0 27 13 0 1 58 12 1 0 28 14 1 0 45 14 1 1 48 12 1 0 55 10 0 1 66 7 0 0 43 12 0 1 44 11 1 0 55 8 0 1 21 12 1 0 25 11 1 1 40 10 1 0 41 14 1 0 41 15 0 1 62 12 0 1 23 10 1 1 51 13 0 1 31 11 0 1 39 9 1 1 44 12

Kadının İşgücüne Katılımı Modeli Di = b 1 + b 2 Medenii +b 3 Egitimi Dependent Variable: DI Included observations: 30 Variable C MEDENI EGITIM R-squared Adjusted R-squared S. E. of regression Sum squared resid Durbin-Watson stat Coefficient -0. 284 -0. 382 0. 093 0. 363 0. 316 0. 412 4. 583 2. 551 Std. Error 0. 436 0. 153 0. 035 F-statistic Prob(F-statistic) Akaike info criterion Schwarz criterion Hannan-Quinn criter. t-Statistic -0. 652 -2. 494 2. 688 7. 708 0. 002 1. 159 1. 299 1. 204 Prob. 0. 520 0. 019 0. 012

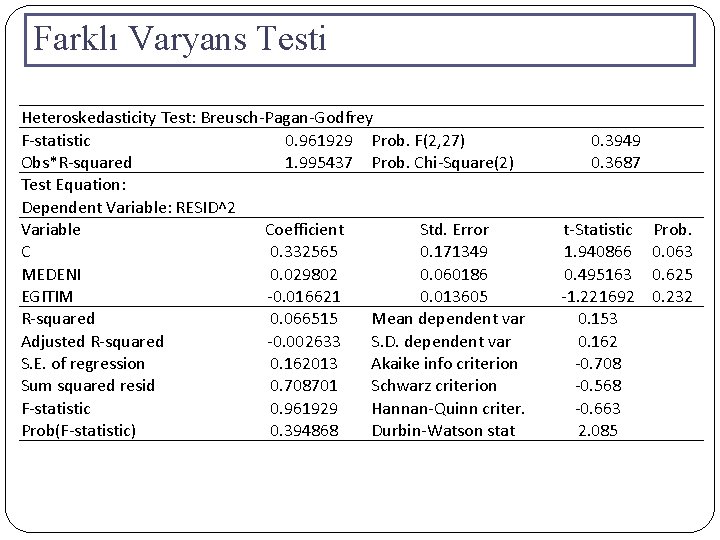
Farklı Varyans Testi Heteroskedasticity Test: Breusch-Pagan-Godfrey F-statistic 0. 961929 Prob. F(2, 27) Obs*R-squared 1. 995437 Prob. Chi-Square(2) Test Equation: Dependent Variable: RESID^2 Variable Coefficient Std. Error C 0. 332565 0. 171349 MEDENI 0. 029802 0. 060186 EGITIM -0. 016621 0. 013605 R-squared 0. 066515 Mean dependent var Adjusted R-squared -0. 002633 S. D. dependent var S. E. of regression 0. 162013 Akaike info criterion Sum squared resid 0. 708701 Schwarz criterion F-statistic 0. 961929 Hannan-Quinn criter. Prob(F-statistic) 0. 394868 Durbin-Watson stat 0. 3949 0. 3687 t-Statistic Prob. 1. 940866 0. 063 0. 495163 0. 625 -1. 221692 0. 232 0. 153 0. 162 -0. 708 -0. 568 -0. 663 2. 085

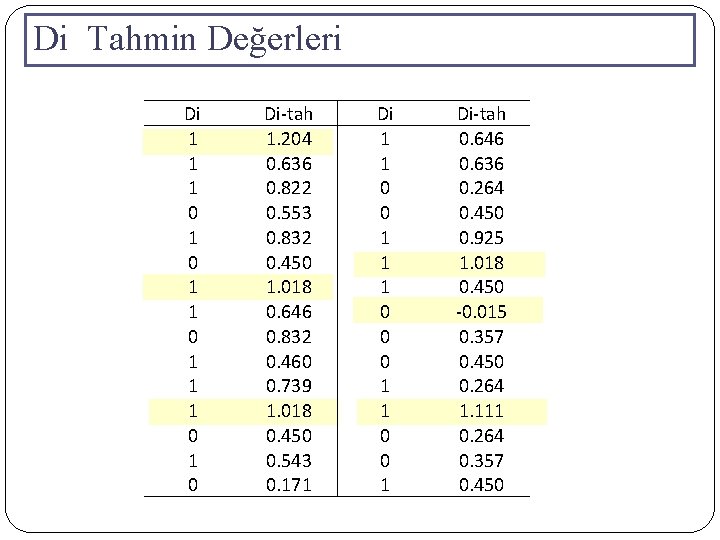
Di Tahmin Değerleri Di 1 1 1 0 1 0 Di-tah 1. 204 0. 636 0. 822 0. 553 0. 832 0. 450 1. 018 0. 646 0. 832 0. 460 0. 739 1. 018 0. 450 0. 543 0. 171 Di 1 1 0 0 1 1 1 0 0 0 1 1 0 0 1 Di-tah 0. 646 0. 636 0. 264 0. 450 0. 925 1. 018 0. 450 -0. 015 0. 357 0. 450 0. 264 1. 111 0. 264 0. 357 0. 450

DOM Tahminindeki Sorunlar ui hata teriminin normal dağılmaması ui hata teriminin Binom Dağılımlı Olması ui hata teriminin değişen varyanslı olması 0 E(Yi |Xi) 1 varsayımının yerine gelmeyişi

ui hata teriminin normal dağılmaması • Normallik varsayımının sağlanmaması durumunda tahmin ediciler sapmasızlıklarını korurlar. • Nokta tahminde normallik varsayımı gözardı edilir. • Örnek hacmi sonsuza giderken EKK tahmincileri çoğunlukla normal dağılıma uyarlar. • DOM ile yapılan istatistiksel çıkarsamalar normallik varsayımı altındaki EKK sürecine uyarlar.

ui hata teriminin Binom Dağılımlı Olması DOM’de u’lar normal dağılmaz, binom dağılımı gösterir: Y 1 ve 0 değerini aldığında Yi =1 için Yi =0 için u’lar normal değildir. İki değerli binom dağılımlıdır. Ancak büyük örneklerde DOM güven aralıkları ve hipotez testleri geçerlidir ve EKKY normal dağılım varsayımının sağlandığı kabul edilmektedir.

ui hata teriminin değişen varyanslı olması kesikli bir Y değişkeni varyansından hareketle Y yerine u alınarak Yi 0 1 ui -b 1 -b 2 X İhtimal=P(ui) (1 -Pi) Pi u’nun varyansı farklıdır. u’nun varyansı Y’nin X için şartlı beklenen değerine bağlıdır ve sonuçta u’nun varyansı X’in değerine bağlı olacak ve eşit olmayacaktır.

ui hata teriminin değişen varyanslı olması Var(ui) = Pi(1 -Pi) DOM’nin EKKY ile tahmininde ortaya çıkan farklı varyans problemine aşağıdaki dönüşümlü modeli tahmin ederek çözüm getirmek mümkündür: ler bilinmediğinden bunun yerine örnek tahmini değerleri hesaplanarak konarak ler kullanılır. ifadesinde yerine

0 E(Yi |Xi) 1 varsayımının yerine gelmeyişi DOM’de Y’nin şartlı olasılığını gösteren E(Y|X) nın 0 ila 1 arasında bulunması şarttır. Y; 0 ve 1 değerini almaktadır. Bu şart anakütle için geçerlidir. Anakütlenin tahmincisi için geçerli olmayabilir. Tahmini şartlı olasılıklar 0 ile 1 olmayabilir:

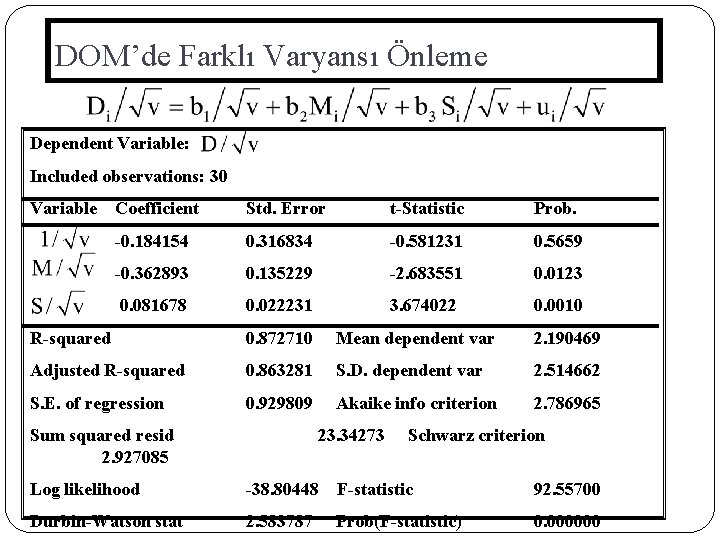
0 E(Yi |Xi) 1 0 ile 1 arasında mıdır? DOM”, EKKY ile elde edildikten sonra Bunlardan bir kısmı 0 dan küçük, negatif değerli ise, bunlar için 0 değerini alır. 1’den büyük değerli ise bunlar için nin 1’e eşit olduğu kabul edilir. Dönüştürmeden sonra EKKY tekrar uygulanır ve farklı varyansın kalktığı görülebilir. eşit varyanslıdır. Bu yöntem TEKKY’dir.

DOM’de Farklı Varyansı Önleme Dependent Variable: Included observations: 30 Variable Coefficient Std. Error t-Statistic Prob. -0. 184154 0. 316834 -0. 581231 0. 5659 -0. 362893 0. 135229 -2. 683551 0. 0123 0. 081678 0. 022231 3. 674022 0. 0010 R-squared 0. 872710 Mean dependent var 2. 190469 Adjusted R-squared 0. 863281 S. D. dependent var 2. 514662 S. E. of regression 0. 929809 Akaike info criterion 2. 786965 Sum squared resid 2. 927085 23. 34273 Schwarz criterion Log likelihood -38. 80448 F-statistic 92. 55700 Durbin-Watson stat 2. 583787 Prob(F-statistic) 0. 000000

DOM’e Alternatif Model Arama • DOM ile ilgili sayılan sorunların hepsi bir şekilde aşılabilir • Ancak, DOM, Pi=E(Y=1|X) olasılığının X’le doğrusal olarak arttığını varsayar. Yani X’deki marjinal veya küçük bir artış hep sabittir. Gerçek hayatta ise bu beklenen bir durum değildir. • DOM ile ilgili sorunlar şu iki özellik sayesinde aşılabilir: 1. Xi arttıkça Pi=E(Y=1|X)’de artar ancak 0 ile 1 aralığının dışına çıkmaması gerekmektedir. 2. Pi ile Xi arasındaki ilişkinin doğrusal olmaması gerekmektedir. 66

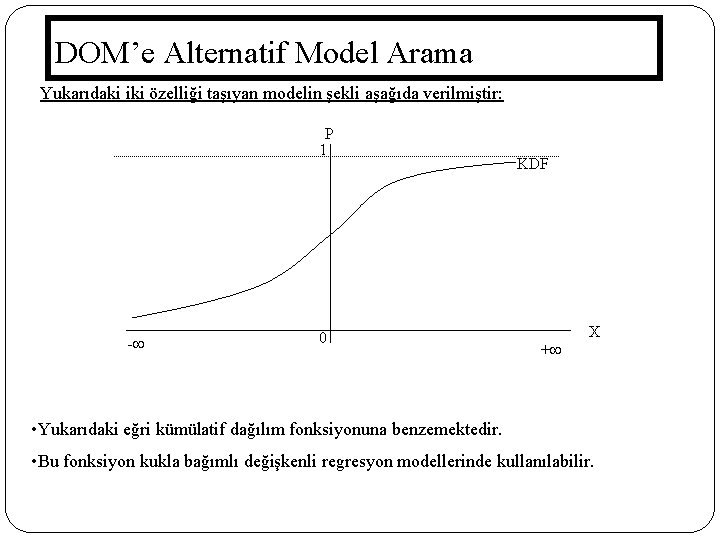
DOM’e Alternatif Model Arama Yukarıdaki iki özelliği taşıyan modelin şekli aşağıda verilmiştir: P 1 - 0 KDF X + • Yukarıdaki eğri kümülatif dağılım fonksiyonuna benzemektedir. • Bu fonksiyon kukla bağımlı değişkenli regresyon modellerinde kullanılabilir. 67

Logit Model Logistik Dağılım Fonksiyonu kümülatif lojistik dağılım fonksiyonudur. Bahis yada olabilirlik oranı Bu orana ev sahibi olma lehine fark oranı denir. Lojistik modelin her iki tarafının doğal log. alındığında Li fark oranı logaritması olup hem X, hem parametrelere göre doğrusaldır. Z değişkeni - dan + a değişirken, P 0 ile 1 arasında değişir. 68

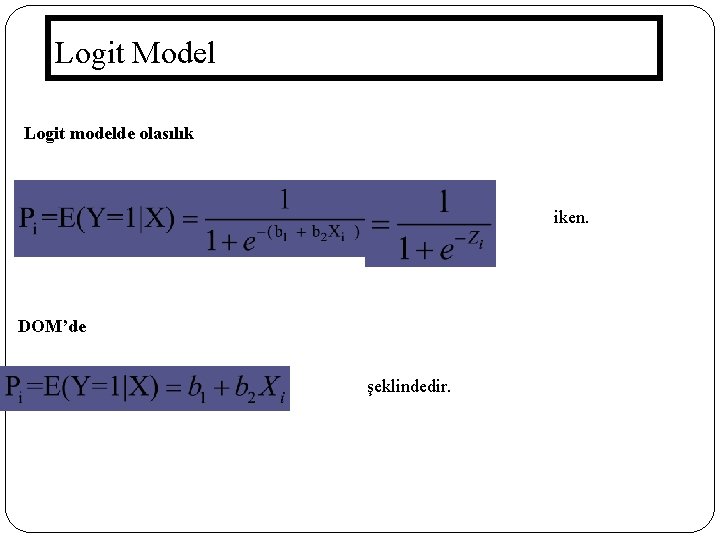
Logit Model Logit modelde olasılık iken. DOM’de şeklindedir. 69

Logit Model • Zi, - ile + arasında değerler alırken Pi’nin aldığı değerler ise 0 ile 1 arasında değişmektedir. • Zi ile Pi arasındaki ilişki doğrusal değildir. 70

Logit Modelin Özellikleri 1. Pi, 0’dan 1’e kadar değer aldığında, Logitte - ile + arasında değer alır. Pi=1 = + Pi=0 = - 2. Logit, X’e göre doğrusal iken olasılıklara göre değildir. 3. Logit modelin b 2 katsayısı şu şekilde yorumlanır: Bağımsız değişkendeki birimlik değişme karşısında logitteki değişmeyi gösterir. 4. Logit model tahmin edildikten sonra, X bağımsız değişkeninin belirli bir değeri için logitin gerçekleşme olasılığı hesaplanabilir. 71

Logit Modelin EKKY İle Tahmini 1. Adım: İhtimalleri hesaplanır. 2. Adım: fark oranı logaritmaları hesaplanır. 3. Adım: Orijinal lojistik modeli tahminlenir. Farklı varyans durumu söz konusu ise; orijinal lojistik modelin her iki tarafı da ile çarpılarak dönüşümlü lojistik model elde edilir.

Logit Modelin EKKY İle Tahmini Farklı varyans durumu söz konusu ise; orijinal lojistik modelin her iki tarafı da ile çarpılarak dönüşümlü lojistik model elde edilir. Dönüşümlü veya Tartılı EKK Lojistik Modeli 73

Logistik Model Uygulaması 300 aileden oluşan küçük bir kasabada ailelerin, yıllık gelirleri (Xi) ve ev sahibi olanların sayısı (ni) aşağıdaki tabloda gösterilmiştir. X Aile Sayısı= Ev Sahibi Nispi Milyon TL) Ni Olan Aile Frekanslar Sayısı=ni Pi=ni/Ni 74 12 20 5 0. 25 16 25 6 0. 24 20 35 10 0. 28 26 45 15 0. 33 30 50 25 0. 50 40 34 18 0. 53 50 30 20 0. 66 60 26 16 0. 61 70 20 15 0. 75 80 15 10 0. 67 Ni = 300 ni = 140

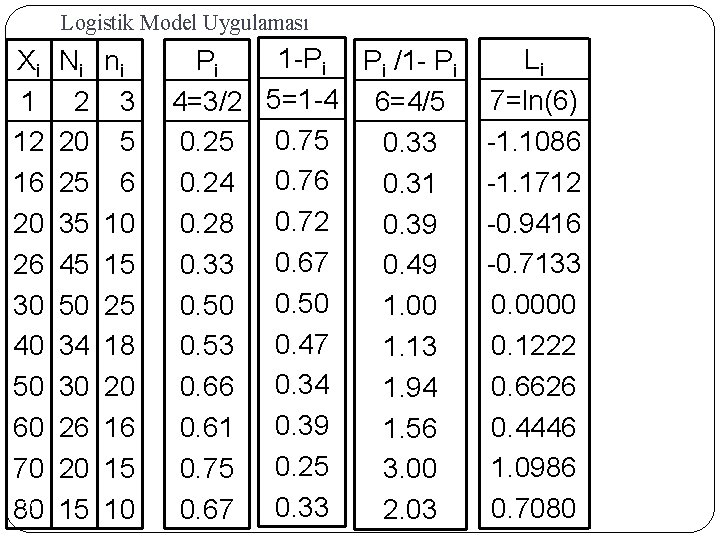
Logistik Model Uygulaması Xi 1 12 16 20 26 30 40 50 60 70 75 80 Ni 2 20 25 35 45 50 34 30 26 20 15 ni 3 5 6 10 15 25 18 20 16 15 10 1 -Pi Pi /1 - Pi Pi 4=3/2 5=1 -4 6=4/5 0. 25 0. 75 0. 33 0. 24 0. 76 0. 31 0. 28 0. 72 0. 39 0. 33 0. 67 0. 49 0. 50 1. 00 0. 53 0. 47 1. 13 0. 66 0. 34 1. 94 0. 61 0. 39 1. 56 0. 75 0. 25 3. 00 0. 67 0. 33 2. 03 Li 7=ln(6) -1. 1086 -1. 1712 -0. 9416 -0. 7133 0. 0000 0. 1222 0. 6626 0. 4446 1. 0986 0. 7080

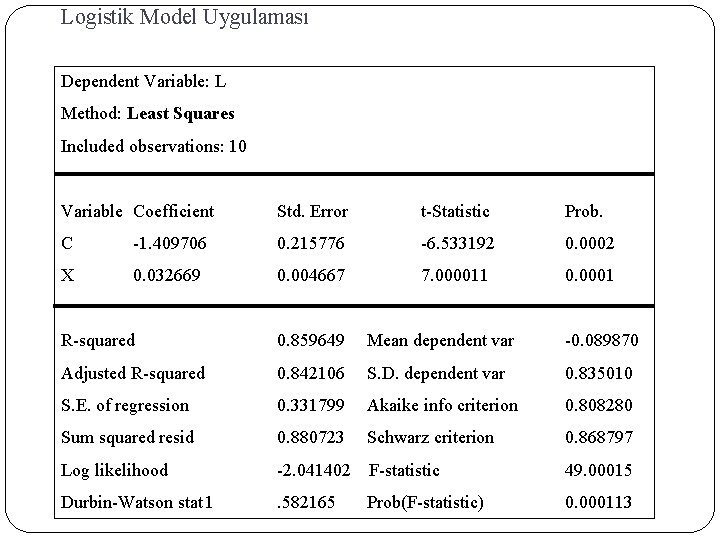
Logistik Model Uygulaması Dependent Variable: L Method: Least Squares Included observations: 10 76 Variable Coefficient Std. Error t-Statistic Prob. C -1. 409706 0. 215776 -6. 533192 0. 0002 X 0. 032669 0. 004667 7. 000011 0. 0001 R-squared 0. 859649 Mean dependent var -0. 089870 Adjusted R-squared 0. 842106 S. D. dependent var 0. 835010 S. E. of regression 0. 331799 Akaike info criterion 0. 808280 Sum squared resid 0. 880723 Schwarz criterion 0. 868797 Log likelihood -2. 041402 F-statistic 49. 00015 Durbin-Watson stat 1 . 582165 Prob(F-statistic) 0. 000113

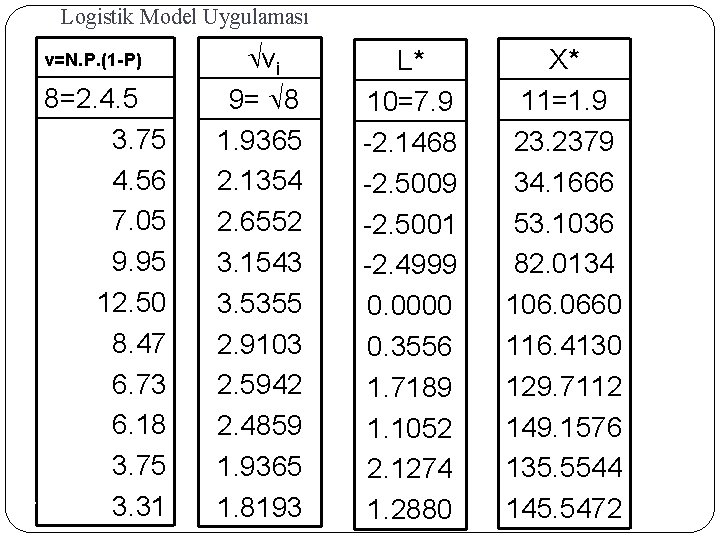
Logistik Model Uygulaması v=N. P. (1 -P) 8=2. 4. 5 3. 75 4. 56 7. 05 9. 95 12. 50 8. 47 6. 73 6. 18 3. 75 77 3. 31 vi 9= 8 1. 9365 2. 1354 2. 6552 3. 1543 3. 5355 2. 9103 2. 5942 2. 4859 1. 9365 1. 8193 L* 10=7. 9 -2. 1468 -2. 5009 -2. 5001 -2. 4999 0. 0000 0. 3556 1. 7189 1. 1052 2. 1274 1. 2880 X* 11=1. 9 23. 2379 34. 1666 53. 1036 82. 0134 106. 0660 116. 4130 129. 7112 149. 1576 135. 5544 145. 5472

Logistik Model Uygulaması Li*= -1. 38056 vi + 0. 03363 Xi*, s= 0. 8421 s(bi): (0. 2315) (0. 00556) , t= (6. 0424) , (-5. 9617) R 2= 0. 80 d= 1. 649, F= 36. 95 Gelir birim arttığında, ev sahibi olma lehine fark oranının logaritması 0. 033 artmaktadır. Bu fark oranına göre belli bir gelir seviyesinde ev sahibi olma olasılığı hesaplanabilir: X=40 iken değerleri yukarıdaki denklemde yerine konduğunda L*=-0. 10288 bulunur. olabilirlik oranı 78

40 birim gelirli bir ailenin ev sahibi olma olasılığı %47. 43’dür. Lojistik modelden, belli bir gelir seviyesinde gelirdeki birimlik artışın ev sahibi olma olasılığını ne ölçüde arttıracağı tahmin edilebilir: formülünden yararlanılır. X=40 iken gelir 1 birim arttığında ev sahibi olma olasılığı [0. 03363(1 -0. 4743)0. 4743]=0. 00838(%0. 8) 79

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION p m L m This sequence introduces the principle of maximum likelihood estimation and illustrates it with some simple examples. 1

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION p m L m Suppose that you have a normally-distributed random variable X with unknown population mean m and standard deviation s, and that you have a sample of two observations, 4 and 6. For the time being, we will assume that s is equal to 1. 2

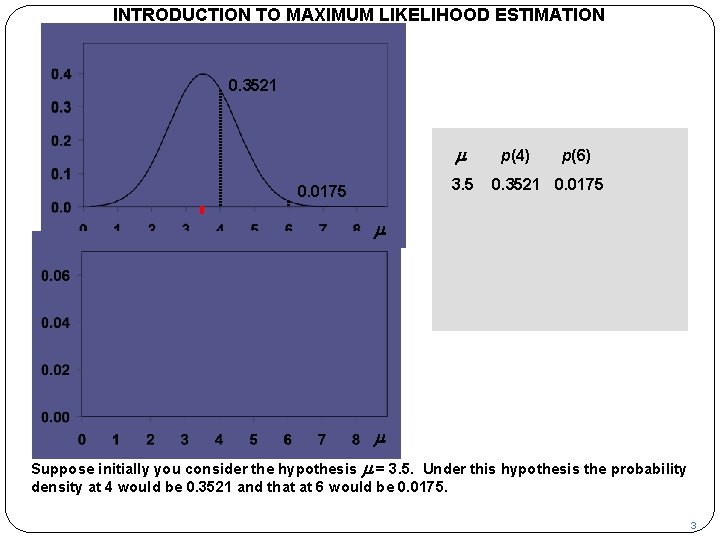
INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION p 0. 3521 m 3. 5 0. 0175 p(4) p(6) 0. 3521 0. 0175 m L m Suppose initially you consider the hypothesis m = 3. 5. Under this hypothesis the probability density at 4 would be 0. 3521 and that at 6 would be 0. 0175. 3

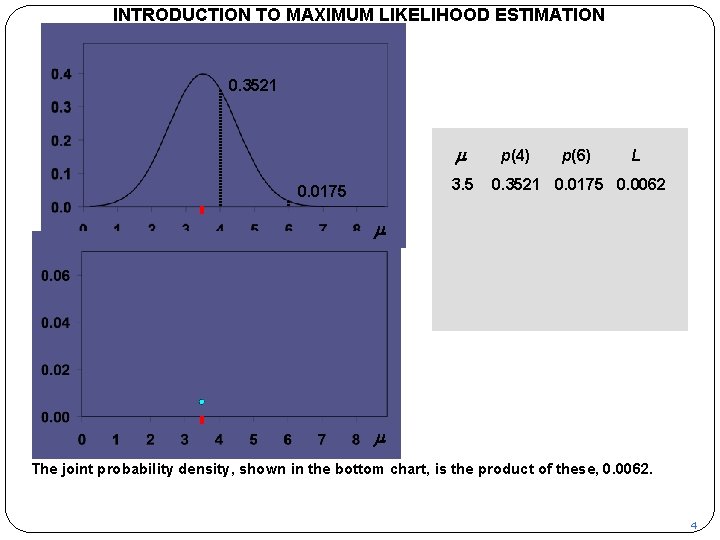
INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION p 0. 3521 m 3. 5 0. 0175 p(4) p(6) L 0. 3521 0. 0175 0. 0062 m L m The joint probability density, shown in the bottom chart, is the product of these, 0. 0062. 4

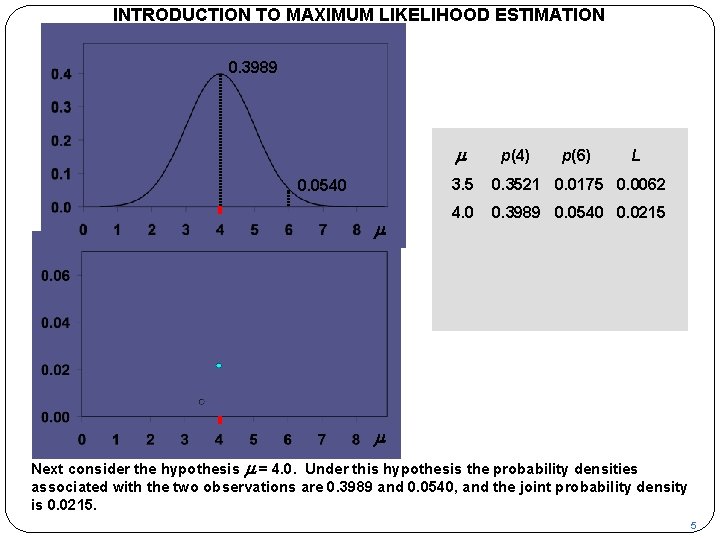
INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION p 0. 3989 m 0. 0540 m p(4) p(6) L 3. 5 0. 3521 0. 0175 0. 0062 4. 0 0. 3989 0. 0540 0. 0215 L m Next consider the hypothesis m = 4. 0. Under this hypothesis the probability densities associated with the two observations are 0. 3989 and 0. 0540, and the joint probability density is 0. 0215. 5

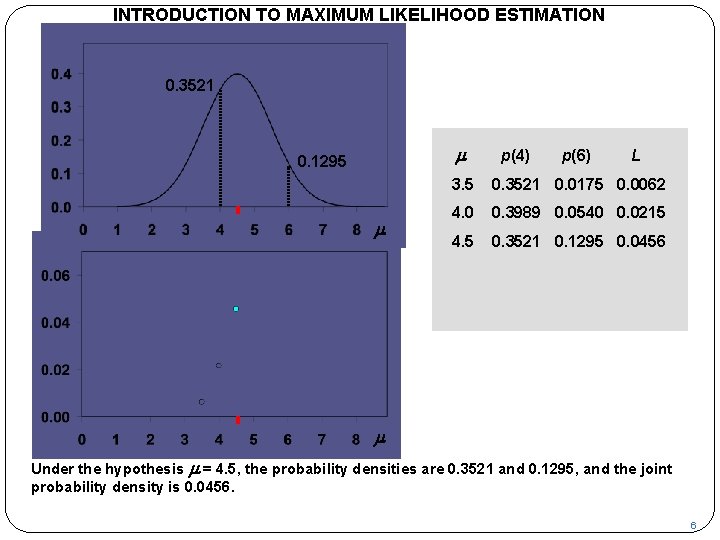
INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION p 0. 3521 m 0. 1295 m L p(4) p(6) L 3. 5 0. 3521 0. 0175 0. 0062 4. 0 0. 3989 0. 0540 0. 0215 4. 5 0. 3521 0. 1295 0. 0456 m Under the hypothesis m = 4. 5, the probability densities are 0. 3521 and 0. 1295, and the joint probability density is 0. 0456. 6

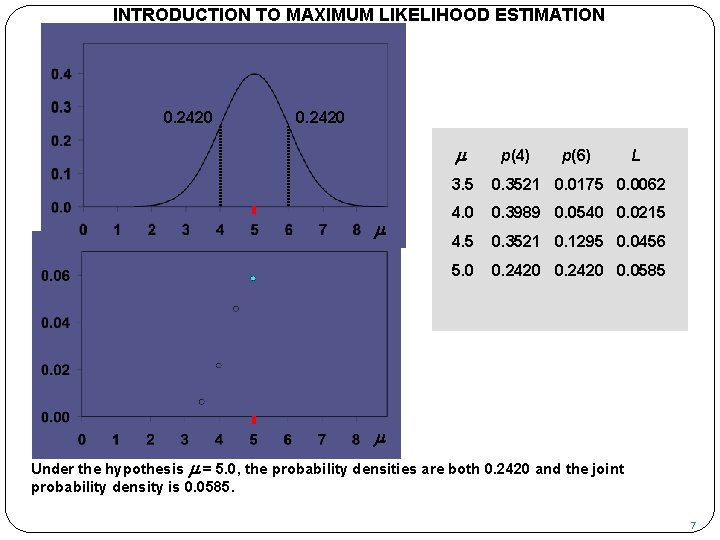
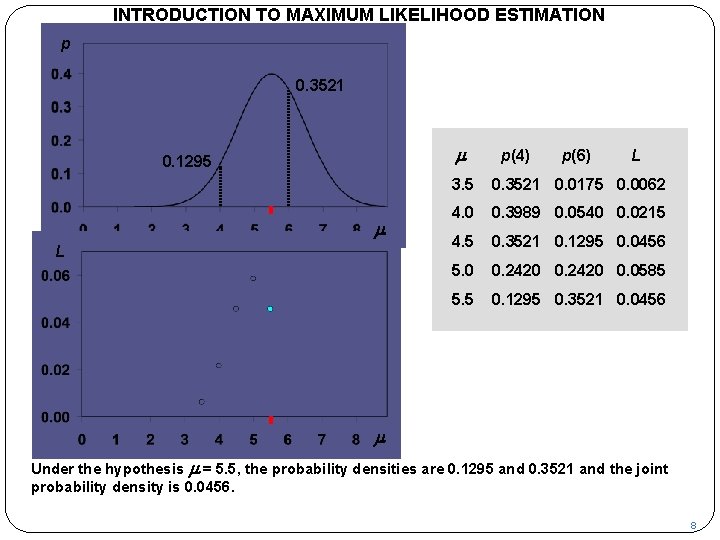
INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION p 0. 2420 m m L p(4) p(6) L 3. 5 0. 3521 0. 0175 0. 0062 4. 0 0. 3989 0. 0540 0. 0215 4. 5 0. 3521 0. 1295 0. 0456 5. 0 0. 2420 0. 0585 m Under the hypothesis m = 5. 0, the probability densities are both 0. 2420 and the joint probability density is 0. 0585. 7

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION p 0. 3521 m 0. 1295 m L p(4) p(6) L 3. 5 0. 3521 0. 0175 0. 0062 4. 0 0. 3989 0. 0540 0. 0215 4. 5 0. 3521 0. 1295 0. 0456 5. 0 0. 2420 0. 0585 5. 5 0. 1295 0. 3521 0. 0456 m Under the hypothesis m = 5. 5, the probability densities are 0. 1295 and 0. 3521 and the joint probability density is 0. 0456. 8

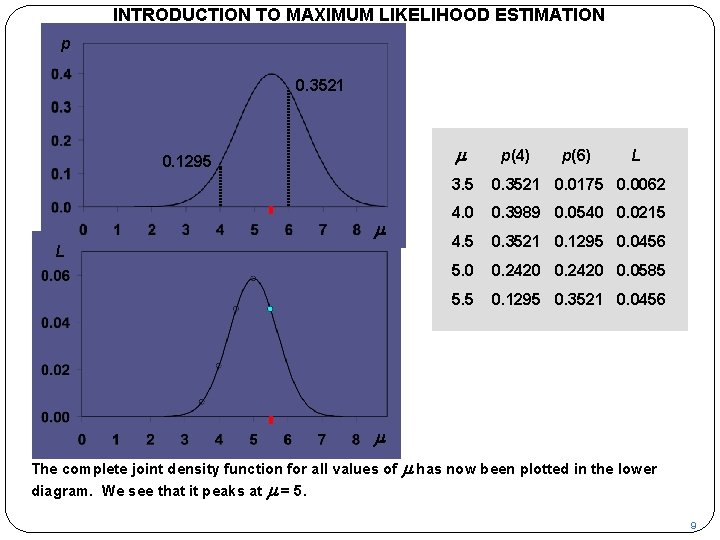
INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION p 0. 3521 m 0. 1295 m L p(4) p(6) L 3. 5 0. 3521 0. 0175 0. 0062 4. 0 0. 3989 0. 0540 0. 0215 4. 5 0. 3521 0. 1295 0. 0456 5. 0 0. 2420 0. 0585 5. 5 0. 1295 0. 3521 0. 0456 m The complete joint density function for all values of diagram. We see that it peaks at m = 5. m has now been plotted in the lower 9

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION Now we will look at the mathematics of the example. If X is normally distributed with mean m and standard deviation s, its density function is as shown. 10

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION For the time being, we are assuming s is equal to 1, so the density function simplifies to the second expression. 11

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION Hence we obtain the probability densities for the observations where X = 4 and X = 6. 12

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION The joint probability density for the two observations in the sample is just the product of their individual densities. 13

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION In maximum likelihood estimation we choose as our estimate of m the value that gives us the greatest joint density for the observations in our sample. This value is associated with the greatest probability, or maximum likelihood, of obtaining the observations in the sample. 14

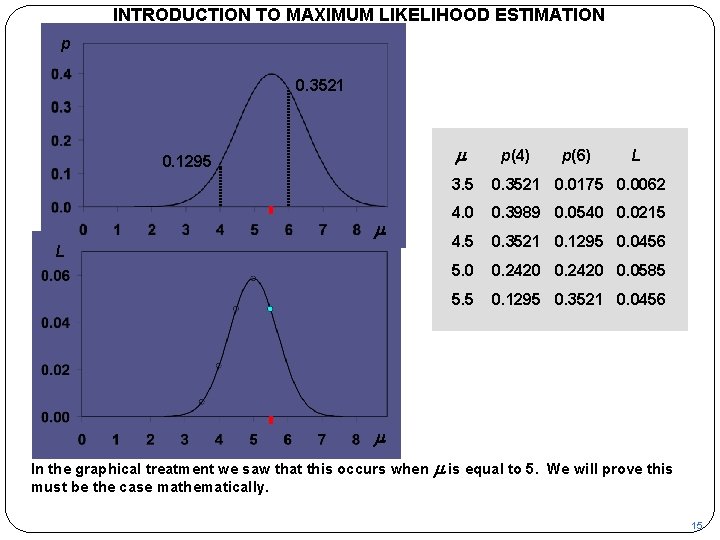
INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION p 0. 3521 m 0. 1295 m L p(4) p(6) L 3. 5 0. 3521 0. 0175 0. 0062 4. 0 0. 3989 0. 0540 0. 0215 4. 5 0. 3521 0. 1295 0. 0456 5. 0 0. 2420 0. 0585 5. 5 0. 1295 0. 3521 0. 0456 m In the graphical treatment we saw that this occurs when must be the case mathematically. m is equal to 5. We will prove this 15

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION To do this, we treat the sample values X = 4 and X = 6 as given and we use the calculus to determine the value of m that maximizes the expression. 16

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION When it is regarded in this way, the expression is called the likelihood function for the sample observations 4 and 6. This is the meaning of L(m | 4, 6). m, given 17

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION To maximize the expression, we could differentiate with respect to m and set the result equal to 0. This would be a little laborious. Fortunately, we can simplify the problem with a trick. 18

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION log L is a monotonically increasing function of L (meaning that log L increases if L increases and decreases if L decreases). 19

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION It follows that the value of m which maximizes log L is the same as the one that maximizes L. As it so happens, it is easier to maximize log L with respect to m than it is to maximize L. 20

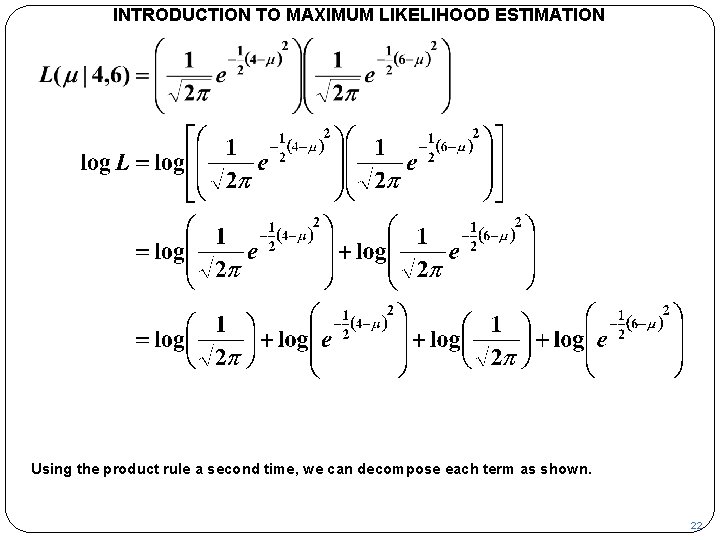
INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION The logarithm of the product of the density functions can be decomposed as the sum of their logarithms. 21

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION Using the product rule a second time, we can decompose each term as shown. 22

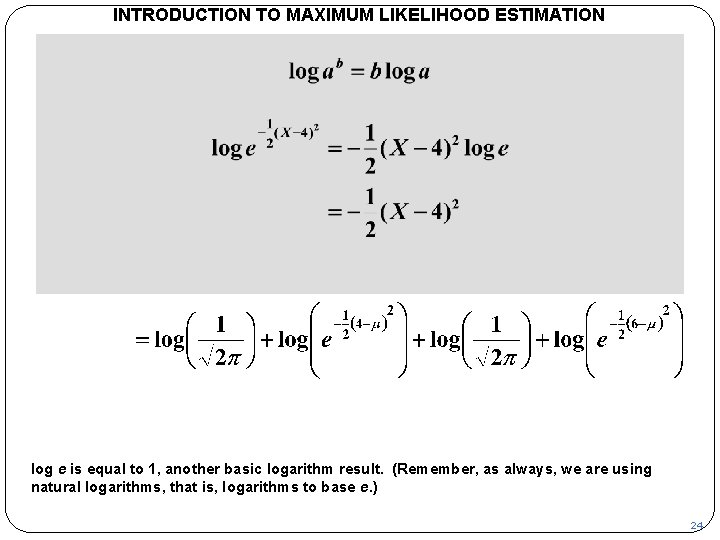
INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION Now one of the basic rules for manipulating logarithms allows us to rewrite the second term as shown. 23

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION log e is equal to 1, another basic logarithm result. (Remember, as always, we are using natural logarithms, that is, logarithms to base e. ) 24

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION Hence the second term reduces to a simple quadratic in X. And so does the fourth. 25

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION We will now choose m so as to maximize this expression. 26

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION Quadratic terms of the type in the expression can be expanded as shown. 27

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION Thus we obtain the differential of the quadratic term. 28

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION Applying this result, we obtain the differential of log L with respect to m. (The first term in the expression for log L disappears completely since it is not a function of m. ) 29

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION Thus from the first order condition we confirm that 5 is the value of -likelihood function, and hence the likelihood function. m that maximizes the log 30

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION Note that a caret mark has been placed over m, because we are now talking about an estimate of m, not its true value. 31

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION Note also that the second differential of log L with respect to m is -2. Since this is negative, we have found a maximum, not a minimum. 32

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION We will generalize this result to a sample of n observations X 1, . . . , Xn. The probability density for Xi is given by the first line. 33

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION The joint density function for a sample of n observations is the product of their individual densities. 34

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION Now treating the sample values as fixed, we can re-interpret the joint density function as the likelihood function for m, given this sample. We will find the value of m that maximizes it. 35

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION We will do this indirectly, as before, by maximizing log L with respect to m. The logarithm decomposes as shown. 36

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION We differentiate log L with respect to m. 37

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION The first order condition for a minimum is that the differential be equal to zero. 38

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION Thus we have demonstrated that the maximum likelihood estimator of m is the sample mean. The second differential, -n, is negative, confirming that we have maximized log L. 39

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION So far we have assumed that s, the standard deviation of the distribution of X, is equal to 1. We will now relax this assumption and find the maximum likelihood estimator of it. 40

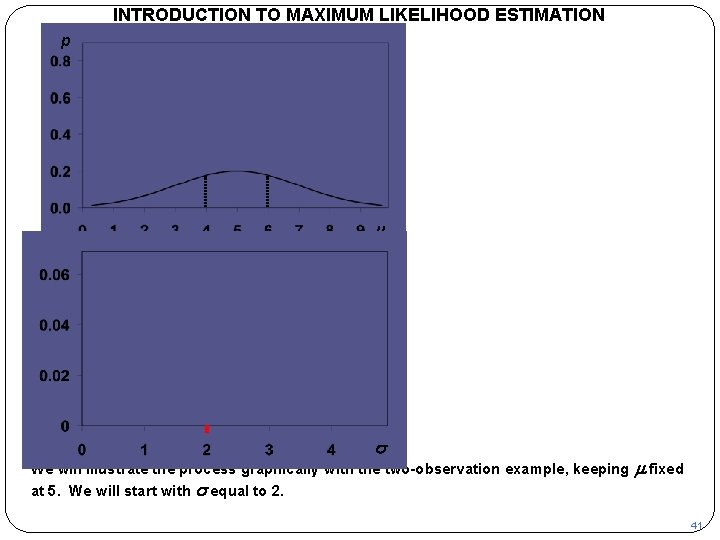
INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION p m L s We will illustrate the process graphically with the two-observation example, keeping at 5. We will start with s equal to 2. m fixed 41

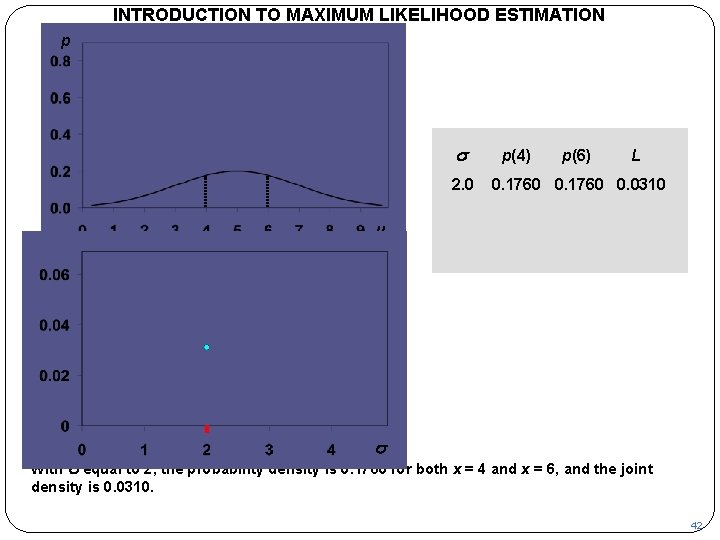
INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION p s 2. 0 p(4) p(6) L 0. 1760 0. 0310 m L s With s equal to 2, the probability density is 0. 1760 for both x = 4 and x = 6, and the joint density is 0. 0310. 42

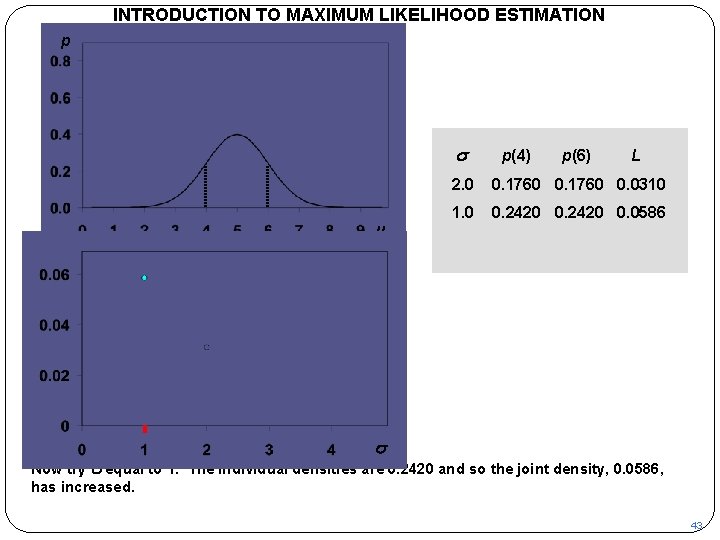
INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION p s m p(4) p(6) L 2. 0 0. 1760 0. 0310 1. 0 0. 2420 0. 0586 L s Now try s equal to 1. The individual densities are 0. 2420 and so the joint density, 0. 0586, has increased. 43

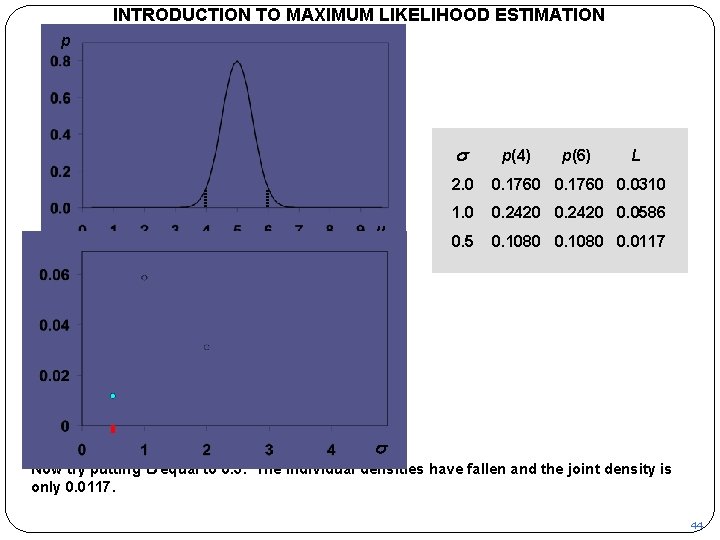
INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION p s m L p(4) p(6) L 2. 0 0. 1760 0. 0310 1. 0 0. 2420 0. 0586 0. 5 0. 1080 0. 0117 s Now try putting s equal to 0. 5. The individual densities have fallen and the joint density is only 0. 0117. 44

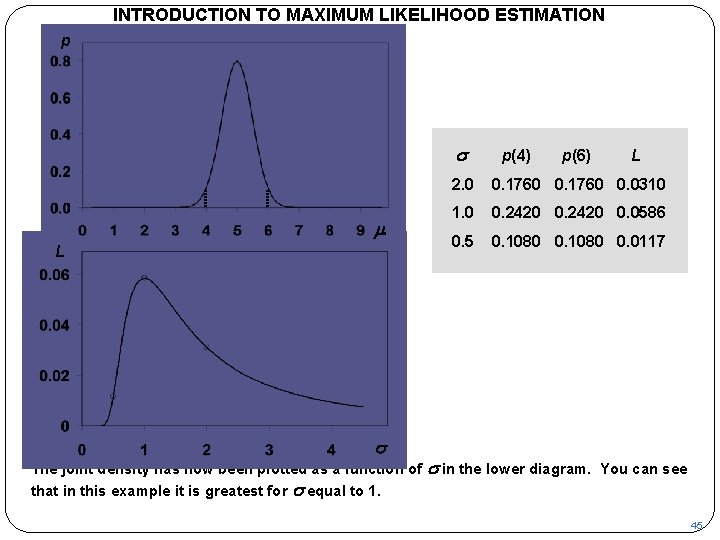
INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION p s m L s The joint density has now been plotted as a function of that in this example it is greatest for s equal to 1. p(4) p(6) L 2. 0 0. 1760 0. 0310 1. 0 0. 2420 0. 0586 0. 5 0. 1080 0. 0117 s in the lower diagram. You can see 45

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION We will now look at this mathematically, starting with the probability density function for x given m and s. 46

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION The joint density function for the sample of n observations is given by the second line. 47

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION As before, we can re-interpret this function as the likelihood function for sample of observations. m and s, given the 48

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION We will find the values of m and s that maximize this function. We will do this indirectly by maximizing log L. 49

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION We can decompose the logarithm as shown. To maximize it, we will set the partial derivatives with respect to m and s equal to zero. 50

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION When differentiating with respect to m, the first two terms disappear. We have already seen how to differentiate the other terms. 51

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION Setting the first differential equal to 0, the maximum likelihood estimate of mean, as before. m is the sample 52

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION Next, we take the partial differential of the log-likelihood function with respect to s. 53

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION Before doing so, it is convenient to rewrite the equation. 54

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION The derivative of log s with respect to s is 1/s. The derivative of s--2 is -2 s--3. 55

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION Setting the first derivative of log L to zero gives us a condition that must be satisfied by the maximum likelihood estimator. 56

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION We have already demonstrated that the maximum likelihood estimator of mean. m is the sample 57

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION Hence the maximum likelihood estimator of the population variance is the sample variance. 58

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION Note that it is biased. The unbiased estimator is obtained by dividing by (n - 1), not n. 59

INTRODUCTION TO MAXIMUM LIKELIHOOD ESTIMATION However it can be shown that the maximum likelihood estimator is asymptotically efficient, in the sense of having a smaller mean square error than the unbiased estimator in large samples. 60

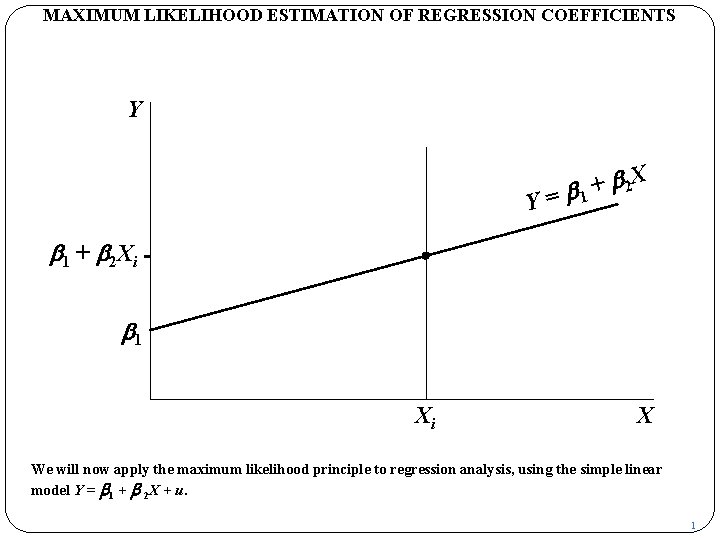
MAXIMUM LIKELIHOOD ESTIMATION OF REGRESSION COEFFICIENTS Y Y b 2 X + = b 1 + b 2 Xi b 1 Xi X We will now apply the maximum likelihood principle to regression analysis, using the simple linear model Y = b 1 + b 2 X + u. 1

MAXIMUM LIKELIHOOD ESTIMATION OF REGRESSION COEFFICIENTS Y Y b 2 X + = b 1 + b 2 Xi b 1 Xi X The black marker shows the value that Y would have if X were equal to Xi and if there were no disturbance term. 2

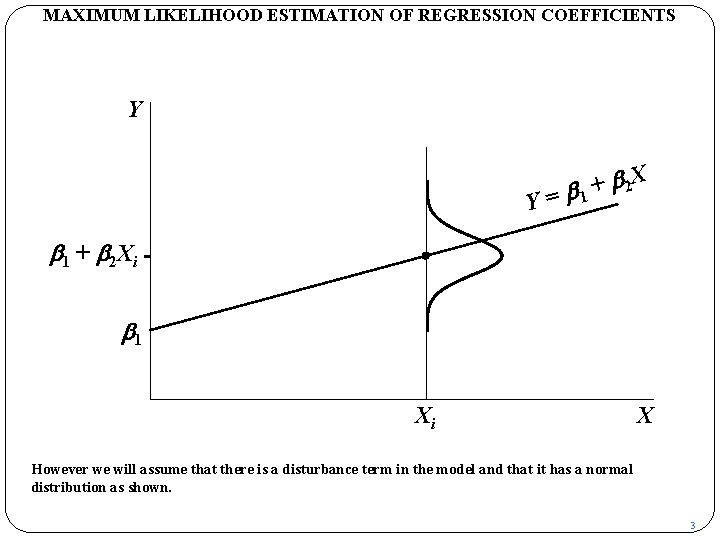
MAXIMUM LIKELIHOOD ESTIMATION OF REGRESSION COEFFICIENTS Y Y b 2 X + = b 1 + b 2 Xi b 1 Xi X However we will assume that there is a disturbance term in the model and that it has a normal distribution as shown. 3

MAXIMUM LIKELIHOOD ESTIMATION OF REGRESSION COEFFICIENTS Y Y b 2 X + = b 1 + b 2 Xi b 1 Xi X Relative to the black marker, the curve represents the ex ante distribution for u, that is, its potential distribution before the observation is generated. Ex post, of course, it is fixed at some specific value. 4

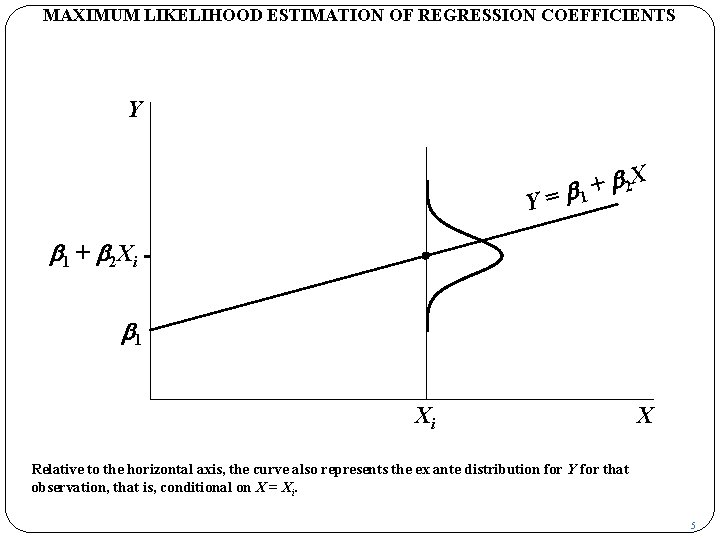
MAXIMUM LIKELIHOOD ESTIMATION OF REGRESSION COEFFICIENTS Y Y b 2 X + = b 1 + b 2 Xi b 1 Xi X Relative to the horizontal axis, the curve also represents the ex ante distribution for Y for that observation, that is, conditional on X = Xi. 5

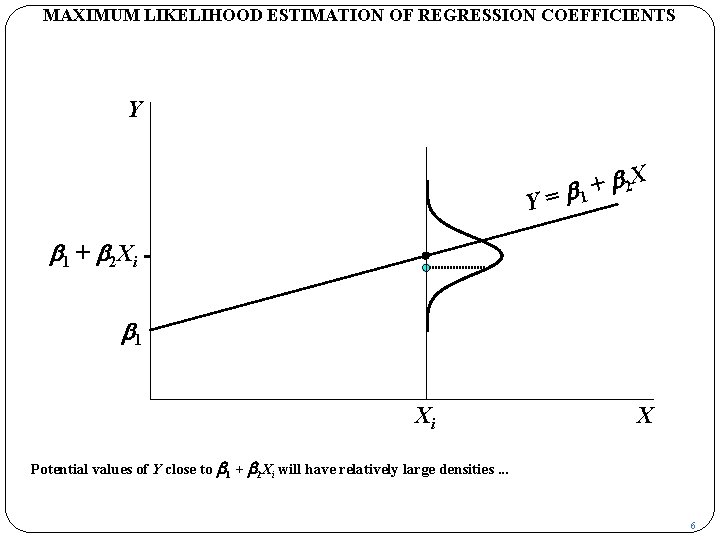
MAXIMUM LIKELIHOOD ESTIMATION OF REGRESSION COEFFICIENTS Y Y b 2 X + = b 1 + b 2 Xi b 1 Xi X Potential values of Y close to b 1 + b 2 Xi will have relatively large densities. . . 6

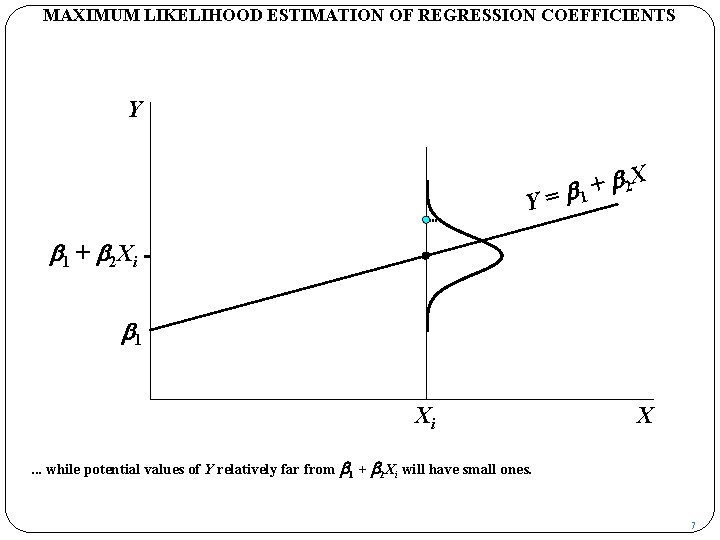
MAXIMUM LIKELIHOOD ESTIMATION OF REGRESSION COEFFICIENTS Y Y b 2 X + = b 1 + b 2 Xi b 1 Xi X . . . while potential values of Y relatively far from b 1 + b 2 Xi will have small ones. 7

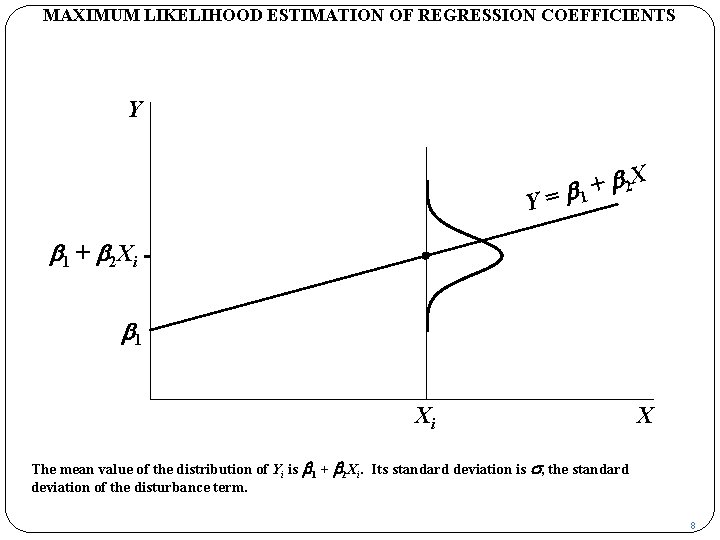
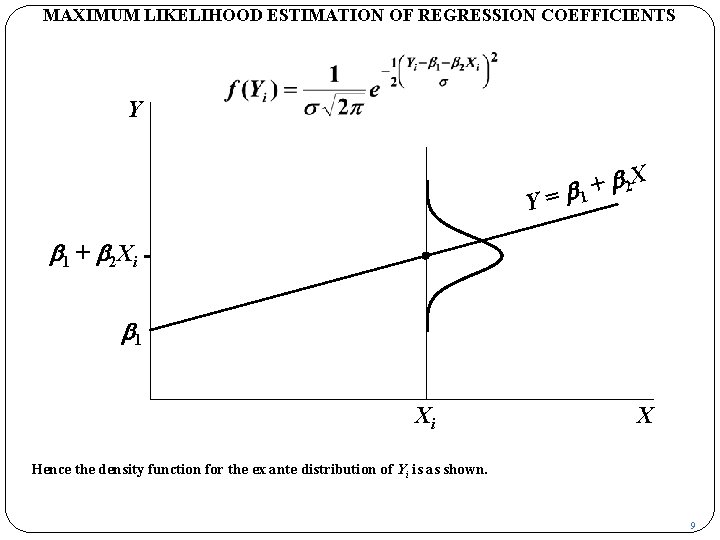
MAXIMUM LIKELIHOOD ESTIMATION OF REGRESSION COEFFICIENTS Y Y b 2 X + = b 1 + b 2 Xi b 1 Xi X The mean value of the distribution of Yi is b 1 + b 2 Xi. Its standard deviation is s, the standard deviation of the disturbance term. 8

MAXIMUM LIKELIHOOD ESTIMATION OF REGRESSION COEFFICIENTS Y Y b 2 X + = b 1 + b 2 Xi b 1 Xi X Hence the density function for the ex ante distribution of Yi is as shown. 9

MAXIMUM LIKELIHOOD ESTIMATION OF REGRESSION COEFFICIENTS The joint density function for the observations on Y is the product of their individual densities. 10

MAXIMUM LIKELIHOOD ESTIMATION OF REGRESSION COEFFICIENTS Now , taking b 1, b 2 and s as our choice variables, and taking the data on Y and X as given, we can reinterpret this function as the likelihood function for b 1, b 2, and s. 11

MAXIMUM LIKELIHOOD ESTIMATION OF REGRESSION COEFFICIENTS We will choose b 1, b 2, and s so as to maximize the likelihood, given the data on Y and X. As usual, it is easier to do this indirectly, maximizing the log-likelihood instead. 12

MAXIMUM LIKELIHOOD ESTIMATION OF REGRESSION COEFFICIENTS As usual, the first step is to decompose the expression as the sum of the logarithms of the factors. 13

MAXIMUM LIKELIHOOD ESTIMATION OF REGRESSION COEFFICIENTS Then we split the logarithm of each factor into two components. The first component is the same in each case. 14

MAXIMUM LIKELIHOOD ESTIMATION OF REGRESSION COEFFICIENTS Hence the log-likelihood simplifies as shown. 15

MAXIMUM LIKELIHOOD ESTIMATION OF REGRESSION COEFFICIENTS To maximize the log-likelihood, we need to minimize Z. But choosing estimators of b 1 and b 2 to minimize Z is exactly what we did when we derived the least squares regression coefficients. 16

MAXIMUM LIKELIHOOD ESTIMATION OF REGRESSION COEFFICIENTS Thus, for this regression model, the maximum likelihood estimators are identical to the least squares estimators. The estimator of s will, however, be slightly different. 17

Copyright Christopher Dougherty 2000 -2002. This slideshow may be freely copied for personal use. 22. 02

Probit Model Bağımlı kukla değişkenli modellerden kümülatif lojistik fonksiyonundan farklı olarak, normal kümülatif dağılım fonksiyonunu kullanan PROBİT(NORMAL) vardır. P R O B İ T (NORMAL) MODEL F(z)= Probit modeli şu şekilde tanımlayabiliriz: Herhangi bir i hanesinin ev sahibi olma veya olmama kararının gözlenemeyen bir fayda indeksi Ii’ye bağlı olduğunu varsayalım. 158

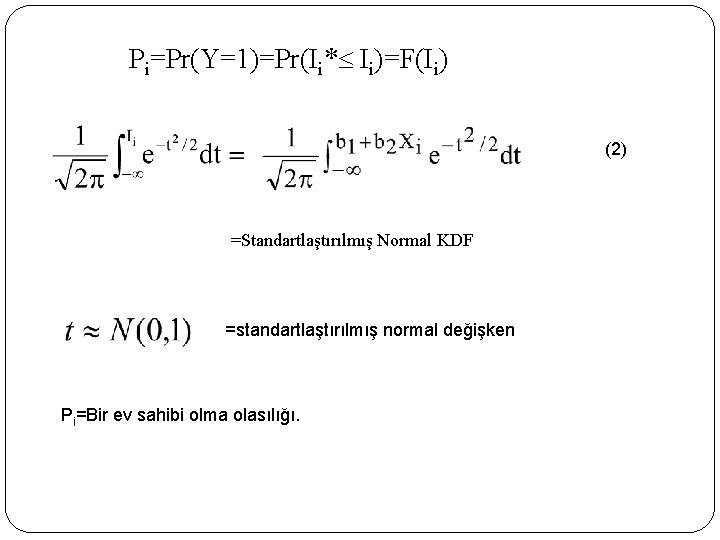
Ii, bağımsız değişkenlere bağlıdır. Örneğin Xi (gelir)değişkeni. Ii= b 1 + b 2 Xi Y=1 hane ev sahibi (1) Y=0 hane ev sahibi değil. Her hane için Ii’nın belli bir değerinden itibaren ev sahibi olma durumu söz konusudur. Ii değeri, Ii* değerini aştığı zaman hane, ev sahibi olacak aksi durumda olmayacaktır. Ii* Ii ifadesi faydanın belli bir eşik değerinden sonra söz konusu olabileceğini gösterir. Ii* başlangıç değeri de Ii gibi gözlenemez. Ancak, aynı ortalama ve varyanslı normal dağıldığı varsayılarak Ii değerleri yukarıdaki regresyon denkleminden tahmin edilir. Tahminciler bulunur. Normal dağılım varsayımıyla Ii* ın Ii den küçük veya eşit olma olasılığı aşağıdaki standartlaştırılmış normal KDF ile hesaplanabilir: 159

Pi=Pr(Y=1)=Pr(Ii* Ii)=F(Ii) (2) =Standartlaştırılmış Normal KDF =standartlaştırılmış normal değişken Pi=Bir ev sahibi olma olasılığı. 160

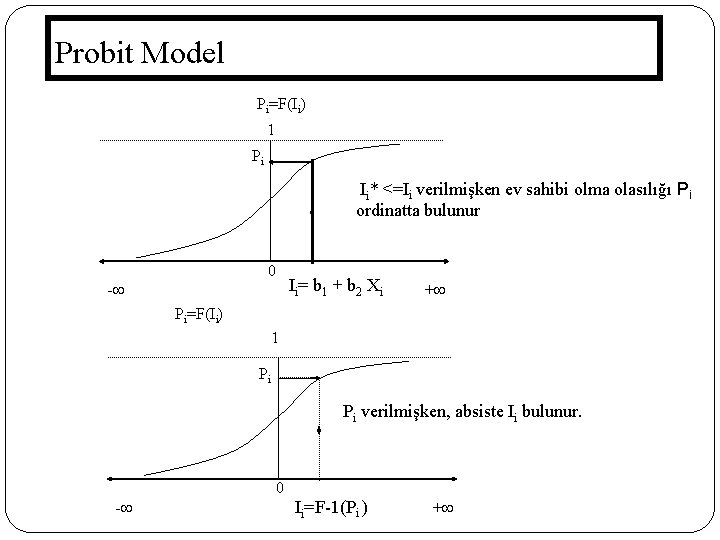
Probit Model Pi=F(Ii) 1 Pi Ii* <=Ii verilmişken ev sahibi olma olasılığı Pi ordinatta bulunur 0 - Ii= b 1 + b 2 Xi + Pi=F(Ii) 1 Pi Pi verilmişken, absiste Ii bulunur. 0 161 - Ii=F-1(Pi ) +

Ii’yı bulabilmek için 2 no’lu ifadenin tersi alınmalıdır. Ii = (Ii)= (Pi)=b 1+b 2 Xi =Probit model : normal kümülatif dağılım fonksiyonunun tersi. 162

Probit Modelin Tahmin Aşamaları 1. Pi= ni/Ni hesaplanır. 2. Ii = (Pi)= normal eşdeğer sapma bulunur. 3. Ii = b 1 + b 2 Xi + ui EKK ile tahmin edilir. 4. İstenirse, Ii yerine, (Ii + 5)=probit değerleri alınarak, EKKY ile (13. 19) tahmin edilir. 5. modelinin hata terimi ui farklı varyanslıdır. Bu sebepten dönüşümlü değerler alınarak TEKKY uygulanabilir: = 163

fi= (Pi) ifadesine eşit standart normal yoğunluk fonksiyonudur. 6. Büyük örnekler için bi'lerin güven aralıkları ve hipotez testleri uygulanarak, anakütlede durumun geçerliliği araştırılabilir. 7. Belirlilik katsayısı R 2, modelin fonksiyonel biçiminin iyi seçilip seçilmediği konusunda bize fikir vermez. 164

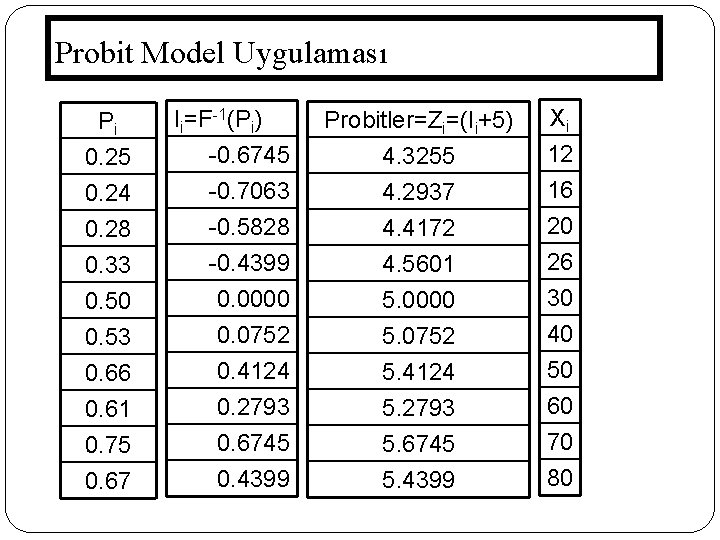
Probit Model Uygulaması 165 Pi 0. 25 0. 24 0. 28 Ii=F-1(Pi) -0. 6745 -0. 7063 -0. 5828 0. 33 0. 50 0. 53 0. 66 0. 61 0. 75 0. 67 -0. 4399 0. 0000 0. 0752 0. 4124 0. 2793 0. 6745 0. 4399 Probitler=Zi=(Ii+5) 4. 3255 4. 2937 4. 4172 Xi 12 16 20 4. 5601 5. 0000 5. 0752 5. 4124 5. 2793 5. 6745 5. 4399 26 30 40 50 60 70 80

Probit Model Uygulaması Ii= -0. 8587 + 0. 0200 Xi , r 2= 0. 8628 s(bi) (0. 0028) s= 0. 2 t= (7. 094) d= 1. 59 Zi= 4. 1324 + 0. 0201 Xi , r 2= 0. 8621 s(bi) (0. 0028) s= 0. 2 t= (7. 071) 166 r= 0. 9289 d= 1. 5637 r= 0. 9285

Wooldridge Example 17. 1 inlf kidslt 6 kidsge 6 age educ exper nwifeinc expersq Obs: 753 1. inlf =1 işgücüne katılıyorsa 2. kidslt 6 6 < yaşında küçük çocuk sayısı 3. kidsge 6 6 -18 yaşları arasındaki çocuk sayısı 4. age kadının yaşı 5. educ eğitim yılı 6. exper deneyim 7. nwifeinc (ailegeliri – ücret*saat)/1000 8. expersq deneyimkare 167

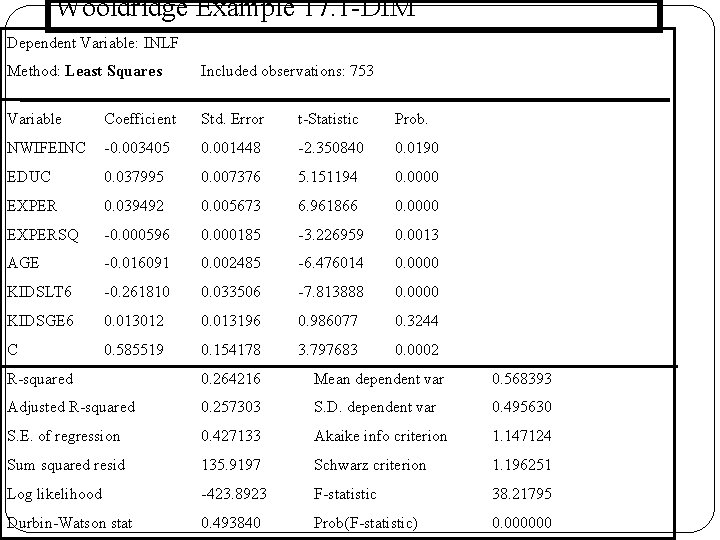
Wooldridge Example 17. 1 -DİM Dependent Variable: INLF Method: Least Squares Included observations: 753 Variable Coefficient Std. Error t-Statistic Prob. NWIFEINC -0. 003405 0. 001448 -2. 350840 0. 0190 EDUC 0. 037995 0. 007376 5. 151194 0. 0000 EXPER 0. 039492 0. 005673 6. 961866 0. 0000 EXPERSQ -0. 000596 0. 000185 -3. 226959 0. 0013 AGE -0. 016091 0. 002485 -6. 476014 0. 0000 KIDSLT 6 -0. 261810 0. 033506 -7. 813888 0. 0000 KIDSGE 6 0. 013012 0. 013196 0. 986077 0. 3244 C 0. 585519 0. 154178 3. 797683 0. 0002 R-squared 0. 264216 Mean dependent var 0. 568393 Adjusted R-squared 0. 257303 S. D. dependent var 0. 495630 S. E. of regression 0. 427133 Akaike info criterion 1. 147124 Sum squared resid 135. 9197 Schwarz criterion 1. 196251 Log likelihood -423. 8923 F-statistic 38. 21795 Durbin-Watson stat 0. 493840 Prob(F-statistic) 0. 000000 168

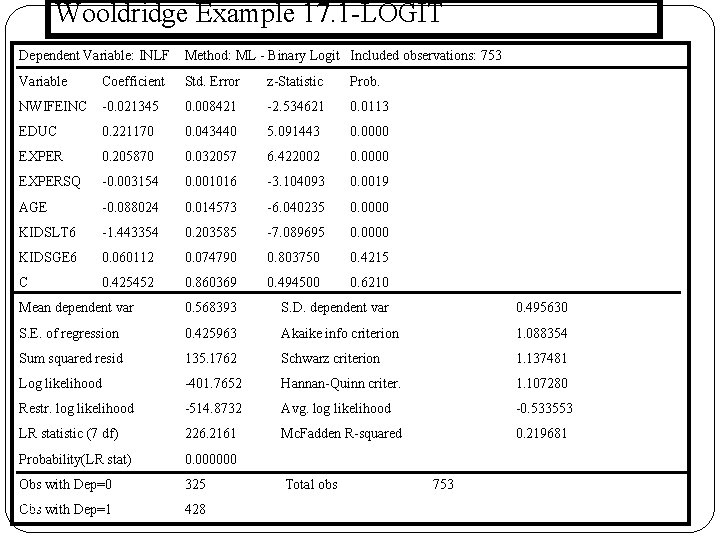
Wooldridge Example 17. 1 -LOGİT Dependent Variable: INLF Method: ML - Binary Logit Included observations: 753 Variable Coefficient Std. Error z-Statistic Prob. NWIFEINC -0. 021345 0. 008421 -2. 534621 0. 0113 EDUC 0. 221170 0. 043440 5. 091443 0. 0000 EXPER 0. 205870 0. 032057 6. 422002 0. 0000 EXPERSQ -0. 003154 0. 001016 -3. 104093 0. 0019 AGE -0. 088024 0. 014573 -6. 040235 0. 0000 KIDSLT 6 -1. 443354 0. 203585 -7. 089695 0. 0000 KIDSGE 6 0. 060112 0. 074790 0. 803750 0. 4215 C 0. 425452 0. 860369 0. 494500 0. 6210 Mean dependent var 0. 568393 S. D. dependent var 0. 495630 S. E. of regression 0. 425963 Akaike info criterion 1. 088354 Sum squared resid 135. 1762 Schwarz criterion 1. 137481 Log likelihood -401. 7652 Hannan-Quinn criter. 1. 107280 Restr. log likelihood -514. 8732 Avg. log likelihood -0. 533553 LR statistic (7 df) 226. 2161 Mc. Fadden R-squared 0. 219681 Probability(LR stat) 0. 000000 Obs with Dep=0 325 169 Obs with Dep=1 428 Total obs 753

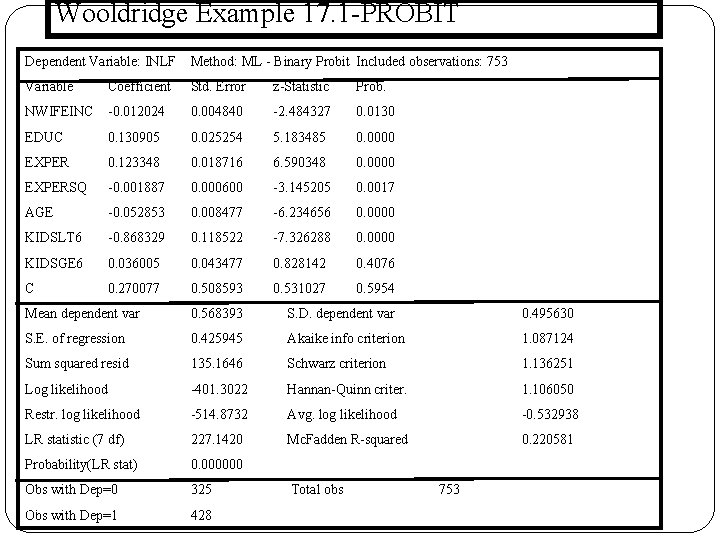
Wooldridge Example 17. 1 -PROBİT Dependent Variable: INLF Method: ML - Binary Probit Included observations: 753 Variable Coefficient Std. Error z-Statistic Prob. NWIFEINC -0. 012024 0. 004840 -2. 484327 0. 0130 EDUC 0. 130905 0. 025254 5. 183485 0. 0000 EXPER 0. 123348 0. 018716 6. 590348 0. 0000 EXPERSQ -0. 001887 0. 000600 -3. 145205 0. 0017 AGE -0. 052853 0. 008477 -6. 234656 0. 0000 KIDSLT 6 -0. 868329 0. 118522 -7. 326288 0. 0000 KIDSGE 6 0. 036005 0. 043477 0. 828142 0. 4076 C 0. 270077 0. 508593 0. 531027 0. 5954 Mean dependent var 0. 568393 S. D. dependent var 0. 495630 S. E. of regression 0. 425945 Akaike info criterion 1. 087124 Sum squared resid 135. 1646 Schwarz criterion 1. 136251 Log likelihood -401. 3022 Hannan-Quinn criter. 1. 106050 Restr. log likelihood -514. 8732 Avg. log likelihood -0. 532938 LR statistic (7 df) 227. 1420 Mc. Fadden R-squared 0. 220581 Probability(LR stat) 0. 000000 Obs with Dep=0 170 Obs with Dep=1 325 428 Total obs 753

UYGULAMA: Aşağıda bir okulun eğitimi ile ilgili verileri kullanarak Probit denklemini çıkartınız. GRADE: Yeni bir tekniğin uygulanması sonucu öğrencilerin başarısı PSI: Yeni Bir Ekonomi Öğretme Yöntemi GPA: Ortalama Derece TUCE: Sınav Öncesi Konu ile ilgili Bilgi SKoru 171

Dependent Variable: GRADE Method: ML - Binary Probit Included observations: 32 Convergence achieved after 5 iterations Variable Coefficient Std. Errorz-Statistic. Prob. C -7. 452320 2. 542472 -2. 931131 GPA 1. 625810 0. 693882 2. 343063 0. 0191 PSI 1. 426332 0. 595038 2. 397045 0. 0165 TUCE 0. 051729 0. 083890 0. 616626 0. 5375 172 0. 0034

Dependent Variable: GRADE Method: ML - Binary Logit Sample: 1 32 Variable Coefficient Std. Errorz-Statistic. Prob. C -13. 02135 4. 931317 -2. 640541 GPA 2. 826113 1. 262940 2. 237726 0. 0252 PSI 2. 378688 1. 064563 2. 234426 0. 0255 TUCE 0. 095158 0. 141554 0. 672235 0. 5014 173 0. 0083

Di 174 Mi Si Di Mi Si 1 0 16 1 0 10 1 1 14 1 1 16 0 1 10 0 0 9 0 1 12 1 0 13 0 1 12 1 0 14 1 1 12 1 0 10 0 1 7 0 0 12 0 1 11 1 0 8 0 1 12 Mi= 1 i. Kadın evliyse 1 0 11 1 1 10 0 diğer durumlarda 1 0 14 1 0 15 0 1 12 0 1 10 Si = i. kadının yıl olarak aldığı eğitim 1 1 13 0 1 11 0 1 9 1 1 12 Kadının İşgücüne Katılımı Modeli: Di= 1 i. Kadının bir işi varsa ya da iş arıyorsa 0 Diğer Durumlarda

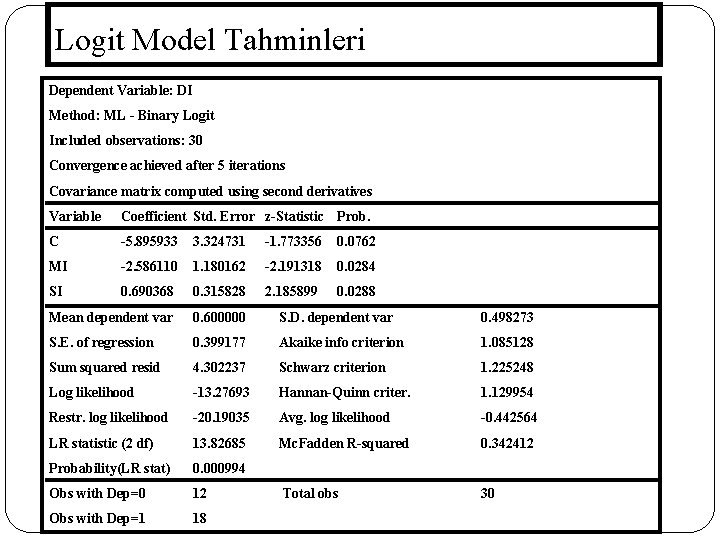
Logit Model Tahminleri Dependent Variable: DI Method: ML - Binary Logit Included observations: 30 Convergence achieved after 5 iterations Covariance matrix computed using second derivatives 175 Variable Coefficient Std. Error z-Statistic Prob. C -5. 895933 3. 324731 -1. 773356 0. 0762 MI -2. 586110 1. 180162 -2. 191318 0. 0284 SI 0. 690368 0. 315828 2. 185899 0. 0288 Mean dependent var 0. 600000 S. D. dependent var 0. 498273 S. E. of regression 0. 399177 Akaike info criterion 1. 085128 Sum squared resid 4. 302237 Schwarz criterion 1. 225248 Log likelihood -13. 27693 Hannan-Quinn criter. 1. 129954 Restr. log likelihood -20. 19035 Avg. log likelihood -0. 442564 LR statistic (2 df) 13. 82685 Mc. Fadden R-squared 0. 342412 Probability(LR stat) 0. 000994 Obs with Dep=0 12 Total obs 30 Obs with Dep=1 18
 Kukla gözü refleksi
Kukla gözü refleksi Vedat kunt
Vedat kunt System dynamics
System dynamics Doğrusal olmayan programlama örnekleri
Doğrusal olmayan programlama örnekleri Kukla değişken
Kukla değişken Vedat pazarlıoğlu
Vedat pazarlıoğlu Vedat balkan
Vedat balkan Ekonometrist maaşları
Ekonometrist maaşları Komik kukla metinleri
Komik kukla metinleri Landau refleksi
Landau refleksi Kukla çağrıştıran kelimeler
Kukla çağrıştıran kelimeler Kukla değişken
Kukla değişken Kukla motýla
Kukla motýla Lišaj dubový
Lišaj dubový Kısa kukla konuşmaları
Kısa kukla konuşmaları Hacivat karagöz metni
Hacivat karagöz metni Mehmet nurullah budak
Mehmet nurullah budak Serkan yurttutan
Serkan yurttutan Mehmet nacar 001
Mehmet nacar 001 Sorgunmehmetakifersoyoo
Sorgunmehmetakifersoyoo Mehmet morali
Mehmet morali Pasinler mehmet akif ersoy ortaokulu
Pasinler mehmet akif ersoy ortaokulu 4.mehmet
4.mehmet Prof dr mehmet yılmazer
Prof dr mehmet yılmazer Kaerc
Kaerc Mehmet akif inan anadolu lisesi obp
Mehmet akif inan anadolu lisesi obp Malign hipertermi nedir
Malign hipertermi nedir Mehmet ali uysal
Mehmet ali uysal Mehmet ali lahur
Mehmet ali lahur Hakan kutucu
Hakan kutucu Mehmet emre cihangir
Mehmet emre cihangir Mehmet akif baytar
Mehmet akif baytar Mehmet serkan gür kimdir
Mehmet serkan gür kimdir Mehmet aktekin
Mehmet aktekin 0-10 enlemleri
0-10 enlemleri Mehmet erdoğan anadolu lisesi
Mehmet erdoğan anadolu lisesi Mehmet serdar güzel
Mehmet serdar güzel Mehmet serdar güzel
Mehmet serdar güzel Mehmet erem
Mehmet erem Mehmet emre vural
Mehmet emre vural Mehmet yumru
Mehmet yumru Turkcell arge
Turkcell arge Strateji tuvali
Strateji tuvali Mehmet nurullah kurutkan
Mehmet nurullah kurutkan şehzade mehmet orhan
şehzade mehmet orhan Necmettin cengiz
Necmettin cengiz Ruhum sana aşık sana hayrandır efendim mehmet emin ay
Ruhum sana aşık sana hayrandır efendim mehmet emin ay Mehmet emin yurdakul slayt
Mehmet emin yurdakul slayt Mehmet behzat ekinci
Mehmet behzat ekinci Ymm mehmet erkan
Ymm mehmet erkan Kaymakam mehmet tahir imam hatip ortaokulu
Kaymakam mehmet tahir imam hatip ortaokulu Mehmet ali kaynar
Mehmet ali kaynar Mehmet emre arı
Mehmet emre arı Mehmet uludoğan detaylı ultrason
Mehmet uludoğan detaylı ultrason Mehmet sinan bilgili
Mehmet sinan bilgili Dr inanch mehmet
Dr inanch mehmet Mehmet engin tozal
Mehmet engin tozal Yb mehmet alkan
Yb mehmet alkan Prof dr mehmet ada
Prof dr mehmet ada Gevher hatun anaokulu
Gevher hatun anaokulu Likisi
Likisi Mehmet akif ersoy un edebi kişiliği
Mehmet akif ersoy un edebi kişiliği Mehmet emre yurttutan
Mehmet emre yurttutan Paul bunnel testi
Paul bunnel testi 2. mehmet çok programlı anadolu lisesi
2. mehmet çok programlı anadolu lisesi Mehmet sakinci
Mehmet sakinci Mehmet tombakoğlu
Mehmet tombakoğlu Prof dr mehmet baykara
Prof dr mehmet baykara Mehmet zahid esgilli
Mehmet zahid esgilli Mehmet dorak
Mehmet dorak Mehmet dorak
Mehmet dorak Mehmet emre yılmaz
Mehmet emre yılmaz Bulmaca buldurmaca mehmet
Bulmaca buldurmaca mehmet Mehmet ali habeşoğlu
Mehmet ali habeşoğlu Mehmet fırat baran
Mehmet fırat baran Mehmet mutlu gen
Mehmet mutlu gen Mehmet rıfat evyap mesleki ve teknik anadolu lisesi
Mehmet rıfat evyap mesleki ve teknik anadolu lisesi Akdeniz üniversitesi üroloji mehmet baykara
Akdeniz üniversitesi üroloji mehmet baykara Mehmet aktekin
Mehmet aktekin Mehmet ko
Mehmet ko Mehmet
Mehmet Prof dr mehmet kıyan
Prof dr mehmet kıyan Mehmet candas
Mehmet candas Emin korkut
Emin korkut Mehmet
Mehmet şehit polis mehmet çelik ortaokulu
şehit polis mehmet çelik ortaokulu Mehmet baykara
Mehmet baykara Mehmet bakir
Mehmet bakir Prof dr mehmet demirhan
Prof dr mehmet demirhan Mehmet sinan atkın
Mehmet sinan atkın Arif ahmet denizolgun ayşe gülderen kuriş
Arif ahmet denizolgun ayşe gülderen kuriş Saldırıya yönelik pazarlama stratejileri
Saldırıya yönelik pazarlama stratejileri Masa tenisi vuruş teknikleri
Masa tenisi vuruş teknikleri Mehmet tombul
Mehmet tombul Mehmet sinan koraltan
Mehmet sinan koraltan Dr inanch mehmet
Dr inanch mehmet Mehmet ali ercan sunu
Mehmet ali ercan sunu Mehmet official
Mehmet official Magil forsepsi
Magil forsepsi Karışımların özkütlesi
Karışımların özkütlesi Ankilostomiasis nedir
Ankilostomiasis nedir Primordial koruma
Primordial koruma Izhar kelime i vahide
Izhar kelime i vahide özerkliğe saygı ilkesi
özerkliğe saygı ilkesi Iyon derişimi
Iyon derişimi Derişik çözelti nedir
Derişik çözelti nedir Hızlı tur tekniği
Hızlı tur tekniği Müellefi kulub
Müellefi kulub Zehra karhan
Zehra karhan Vecize nedir
Vecize nedir Pekiştirilmiş zarf örnekleri
Pekiştirilmiş zarf örnekleri Tekrar grubu nedir örnek
Tekrar grubu nedir örnek Durum zarfı
Durum zarfı Dromotrop nedir
Dromotrop nedir Zarar vermeme
Zarar vermeme Koruyucu rezin restorasyon tipleri
Koruyucu rezin restorasyon tipleri Plazmon nedir
Plazmon nedir Sürelerine göre planlar
Sürelerine göre planlar Modern örgüt modelleri
Modern örgüt modelleri Allostaz
Allostaz Kısa dönemli amaç örnekleri
Kısa dönemli amaç örnekleri şekil uzay yeteneği nedir
şekil uzay yeteneği nedir Magmanın yeryüzüne çıktığı yere ne denir
Magmanın yeryüzüne çıktığı yere ne denir Etwinning net
Etwinning net Hiperoksi testi
Hiperoksi testi Van soest analiz yöntemleri
Van soest analiz yöntemleri Kontrollü yazma ve güdümlü yazma arasındaki fark
Kontrollü yazma ve güdümlü yazma arasındaki fark Bakakalırım nasıl yazılır
Bakakalırım nasıl yazılır Zenit açısı nedir
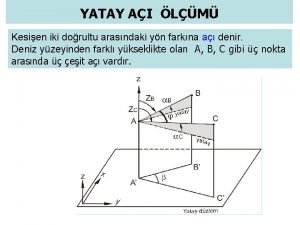
Zenit açısı nedir Yataa
Yataa Rol koridoru ve bilinç koridoru farkı
Rol koridoru ve bilinç koridoru farkı Scamper nedir
Scamper nedir öğrenme halkası nedir
öğrenme halkası nedir Geleneksel ve yapılandırmacı yaklaşım
Geleneksel ve yapılandırmacı yaklaşım Kompasite
Kompasite Weka nedir
Weka nedir Hedef uyaran nedir
Hedef uyaran nedir Yanal düşünme yöntemi nedir
Yanal düşünme yöntemi nedir Monarşik yönetim nedir
Monarşik yönetim nedir Yahudilik 10 emir
Yahudilik 10 emir Ekzosistem nedir
Ekzosistem nedir Modüler programlama yaklaşımı
Modüler programlama yaklaşımı Muhteşem üçlü kuralı
Muhteşem üçlü kuralı öndeyi sağlama nedir
öndeyi sağlama nedir Inidb
Inidb Lvsı nedir tıp
Lvsı nedir tıp Egzema herpetikum nedir
Egzema herpetikum nedir William morgan voleybol
William morgan voleybol Ganglion cervicale superius lezyonu
Ganglion cervicale superius lezyonu Verilerin kodlanması
Verilerin kodlanması Betimsel istatistik nedir
Betimsel istatistik nedir Vektörel büyüklükler
Vektörel büyüklükler Türkiye mahkemeler şeması
Türkiye mahkemeler şeması Discriminant validity
Discriminant validity Vakfı kabih nedir
Vakfı kabih nedir Selman solhan
Selman solhan Berkson yanılgısı nedir
Berkson yanılgısı nedir Kuldoplasti ne demek
Kuldoplasti ne demek Cm m basamakları
Cm m basamakları Kortikal asosiyasyon alanları
Kortikal asosiyasyon alanları Uzaktan algılama ders notları
Uzaktan algılama ders notları Taşisistol nedir
Taşisistol nedir Uossm gaziantep
Uossm gaziantep Geosentrizm
Geosentrizm Uyds giris
Uyds giris Eksenel kompresörler
Eksenel kompresörler Predictive criterion validity
Predictive criterion validity Round character nedir
Round character nedir Tek yönlü varyans analizi örnek
Tek yönlü varyans analizi örnek Twin board nedir etwinning
Twin board nedir etwinning Sezin cansın perçin
Sezin cansın perçin Pazarlama fonksiyonu
Pazarlama fonksiyonu Maha nedir tıp
Maha nedir tıp Ttp pentad
Ttp pentad Metimazol etki mekanizması
Metimazol etki mekanizması Kara hakimiyet teorisi nedir
Kara hakimiyet teorisi nedir