DORUSAL OLMAYAN PROGRAMLAMA DOP PROF DR VEDAT CEYHAN

DOĞRUSAL OLMAYAN PROGRAMLAMA (DOP) PROF. DR. VEDAT CEYHAN

Ø Doğrusal olmayan programlamanın diğer programlarla farkları ve benzerlikleri Ø Doğrusal olmayan programlama modelinin özellikleri Ø Doğrusal olmayan programlama modelleri üTek Değişkenli DOP üÇok Değişkenli DOP üKısıtsız DOP üKısıtlı DOP Ø Temel kavramlar Ø Örnek uygulamalar 2

Diğer Programlarla Farklar ve Benzerlikler • Doğrusal Programlama (LP) – Doğrusal amaç fonksiyonu + doğrusal kısıtlar (tümü) – Sürekli değişkenler • Tam Sayılı Programlama (IP) – Doğrusal amaç fonksiyonu + doğrusal kısıtlar (tümü) – Sürekli olmayan değişkenler • Doğrusal Olmayan Programlama (NLP) – Doğrusal olmayan amaç fonksiyonu veya doğrusal olmayan kısıtlar 3

Doğrusal Olmayan Programlama Modelinin Özellikleri (NLP) üÇözümü zordur üOptimal çözümlerin köşe noktalarda olması gerekli değildir üÇözüm başlangıç noktasına bağlı olabilir. üBaşlangıç noktası genellikle keyfidir. 4

• Problem aşağıdaki formları içerir: – Amaç fonksiyonu doğrusal olmayabilir – Kısıtlar doğrusal olmayabilir – Veya, doğrusal olmayan amaç ve kısıtlar fonksiyonu – Uygun bir algoritma seçiminde problem tipinin belirlenmesi önemlidir. Bazı algoritmalar bazı sorunların türü için daha hızlı gerçekleştirilebilir. 5

• Bir karar probleminin optimizasyonunun yapılabilmesi için matematiksel modelinin kurulması gerekir. Matematiksel model, probleme ilişkin parametrelerin, değişkenlerin ve bunlar arasındaki fonksiyonel ilişkilerin belirlenmesi aşamasından sonra oluşturulabilir. • Genel olarak bir matematiksel modelin üç öğesi vardır: – Karar vericinin amacını ifade eden amaç fonksiyonu, – karar verme sürecinde etkili olan kısıtlayıcı fonksiyonlar ve – değişkenler üzerindeki işaret (negatif olmama) kısıtıdır. 6

• Doğrusal, tamsayı ve hedef programlama, bir problemin amaç fonksiyonunun ve kısıtlarının doğrusal olduğunu varsayarlar. • Yani , 1/X 2, log X 3 veya 5 X 1 X 2 gibi doğrusal olmayan terimleri içermezler. • Doğrusal programlama yöntemlerinin aksine, birçok doğrusal olmayan programlama (NLP) problemlerin çözümü için hesaplama prosedürleri her zaman en uygun çözümü sağlamazlar (Render ve ark, 2012). 7

Doğrusal olmayan programlama problemlerinde amaç; • gi(x) ≤ bi kısıtları altında • z = f(x) fonksiyonunu en iyileyen (optimal yapan) x= (x 1, x 2, …, xn) vektörünün bulunmasıdır. 8

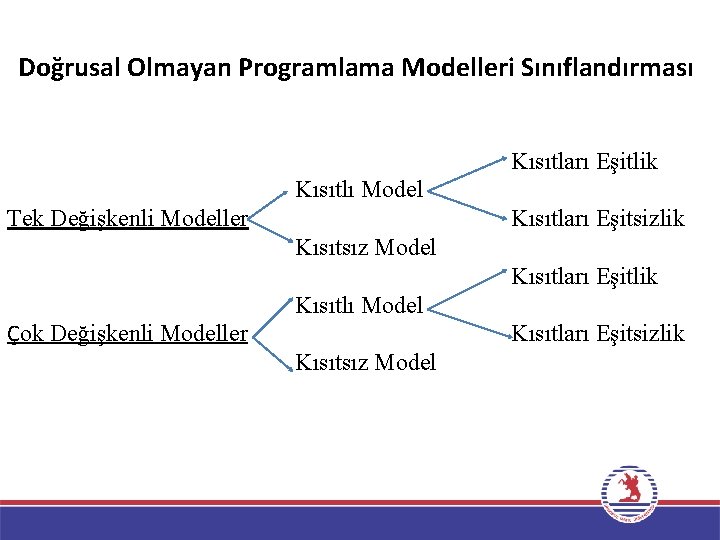
Doğrusal olmayan programlama modelleri; • Değişken sayısına bağlı olarak; – tek ve çok değişkenli, – kısıtlayıcıların varlığına bağlı olarak; kısıtlı ve kısıtsız, – eğer kısıtlayıcılar var ise; tüm kısıtlayıcıları eşitlik ve eşitlik biçiminde olmayan modeller olarak sınıflandırılabilir. Bu durum şematik olarak Şekil 1’deki gibi gösterilebilir. 9

Doğrusal Olmayan Programlama Modelleri Sınıflandırması Kısıtları Eşitlik Kısıtlı Model Tek Değişkenli Modeller Kısıtları Eşitsizlik Kısıtsız Model Kısıtları Eşitlik Kısıtlı Model Çok Değişkenli Modeller Kısıtları Eşitsizlik Kısıtsız Model 10

ü Bir doğrusal olmayan programlama modelinin x=(x 1, …, xn) optimum çözümü; tüm kısıtlayıcıları sağlayan ve amaç fonksiyonunu en iyi yapan x(x 1, x 2, …, xn) değerlerinin bulunmasını gerektirir. ü Her tür doğrusal olmayan programlama probleminin çözümüne uygulanacak tek bir çözüm yöntemi mevcut değildir. ü Dolayısıyla seçilecek çözüm yöntemi problemin yapısına bağlı olarak değişecektir. 11

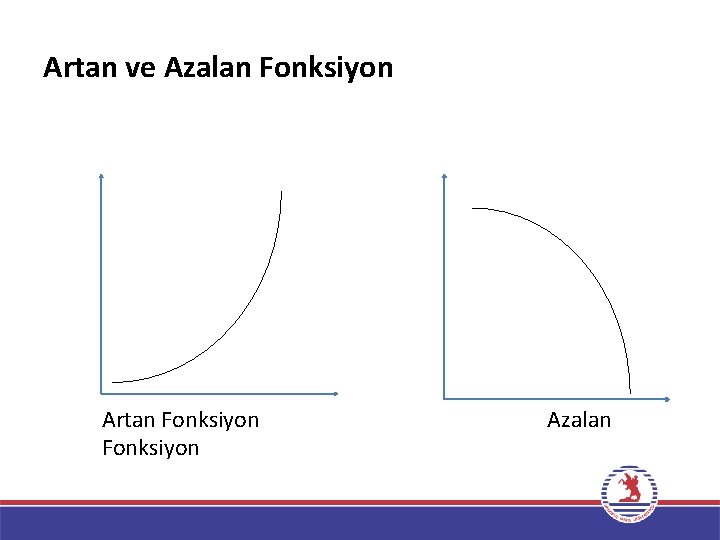
TEMEL KAVRAMLAR • Artan ve Azalan Fonksiyon y=f(x)’in tanımlı olduğu bir alt aralığa ilişkin herhangi iki değer x 1 ve x 2 olsun. Eğer x 1<x 2 olduğu zaman f(x 1)<f(x 2) oluyorsa f(x) fonksiyonuna bu aralıkta artan fonksiyon denir. Eğer x 1<x 2 için f(x 1)>f(x 2) oluyorsa f(x) fonksiyonuna ilgili aralıkta azalan fonksiyon denir. 12

Artan ve Azalan Fonksiyon Artan Fonksiyon Azalan 13

– Yerel Maksimum ve Minimum Bir f(x) fonksiyonu için x’in herhangi bir komşuluğunda f(x’’), f(x)’den büyük/küçük ise x=x’’ noktası bir yerel (lokal) maksimum/minimum noktadır (Doğan, 1995). – Bir Fonksiyon Gradiantı Z=f(x 1, x 2, …, xn) fonksiyonunun gradiantı, fonksiyonun bağımsız değişkenlere bağlı birinci dereceden türev vektörüdür. 14

Hessian Matris • Bir f(x 1, x 2, …, xn) fonksiyonunun ikinci kısmi türevlerinden oluşan nxn boyutlu matrise “hessian matris” denir. 15

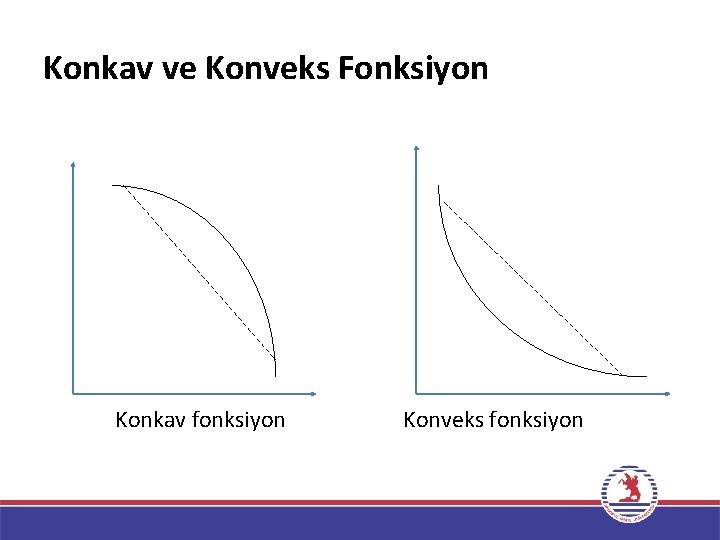
Konkavlık (İçbükey) ve Konvekslik (Dışbükey) • f(x)’e karşılık gelen eğri üzerindeki herhangi iki noktayı birleştiren doğru, eğrinin altına düşmüyorsa (eğri bir kayığı andırıyorsa) fonksiyon konvekstir. • Konveks fonksiyonların aksine, eğri üzerindeki iki noktayı birleştiren doğru parçası, eğrinin üzerine çıkmıyorsa (eğri bir şemsiyeyi andırıyorsa) fonksiyon konkavdır. • Konveks bir eğri üzerinde ya da konkav bir eğri altında kalan, belirli bir aralıktaki noktaların oluşturduğu kümeye “konveks küme” denir (Daellenbach, 1983). 16

ü Doğrusal programlama problemlerinde kabul edilebilir çözüm bölgesi daima bir konveks kümedir ve optimal çözüm konveks kümenin uç noktalarından birinde çıkar. ü Oysa, doğrusal olmayan programlamada, optimal çözümün uç noktada olma zorunluluğu yoktur. 17

Konkav ve Konveks Fonksiyon Konkav fonksiyon Konveks fonksiyon 18

Örnekler: 1) f(x)= √x fonksiyonu [S= 0, ∞) aralığında konveks midir konkav mıdır? İnceleyelim. f(x)=√x Konkav fonksiyon ü Şekilden de görüldüğü gibi, fonksiyonun eğrisi üzerindeki herhangi iki noktayı birleştiren doğru parçası eğrinin altında kaldığından bu fonksiyon konkavdır. 19

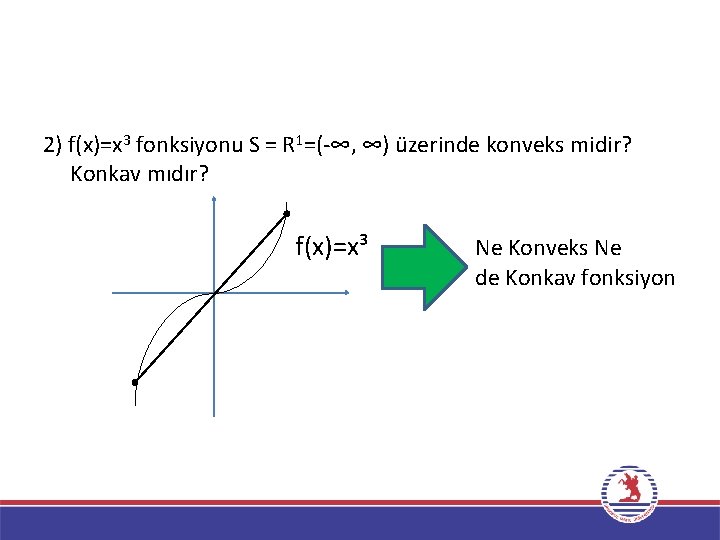
2) f(x)=x 3 fonksiyonu S = R 1=(-∞, ∞) üzerinde konveks midir? Konkav mıdır? f(x)=x³ Ne Konveks Ne de Konkav fonksiyon 20

• Şekil incelendiğinde eğri üzerindeki herhangi iki noktayı birleştiren doğrunun(-∞, 0] aralığında büküm noktasının altında, [0, ∞) aralığında büküm noktasının üzerinde kaldığı görülür. Buradan fonksiyonun (-∞, 0] aralığında konkav, [0, ∞ ) aralığında konveks olduğunu söyleyebiliriz. Ancak (-∞, ∞) aralığında ne konveks ne de konkavdır. 21

3) f(x)=3 x-3 fonksiyonu S = R 1= (-∞, ∞) üzerinde konveks midir konkav mıdır? f(x)=3 x-3 1 Hem Konveks Hem De Konkav Fonksiyon -3 ü Şekilden de görüldüğü gibi fonksiyonun eğrisi büküm noktası bulunmayan bir doğrudur. Doğru üzerindeki herhangi iki noktayı birleştiren doğru parçası bu doğru ile çakıştığından f(x) hem konveks hem de konkavdır. 22

üDoğrusal olmayan programlamada amaç fonksiyonu ve kısıtlayıcı fonksiyonların konvekslik ve konkavlıkları çok önemlidir. üKarşılabilecek farklı fonksiyon tipleri için geliştirilmiş birçok algoritma vardır. 23

Bu amaçla kullanılan bazı temel özellikler vardır: f(x) in tanımlı olduğu S kümesi içinde x 0’ın komşuluğu A olsun. O halde, • Eğer f(x), x 0 da yerel en küçük değerini alıyorsa, f(x 0) A kümesinde konvekstir. • Eğer f(x), x 0 da yerel en büyük değerini alıyorsa, f(x 0) A kümesinde konkavdır. 24

Tek Değişkenli Kısıtsız Doğrusal Olmayan Programlama • Bu tür programlamalar herhangi bir kısıt olmaksızın, tek değişkenli bir fonksiyonun maksimum ya da minimum değerinin bulunmasıyla ilgilenen doğrusal olmayan programlamadır (Bal, 1992). 25

Çok Değişkenli Kısıtsız Doğrusal Olmayan Programlama • Herhangi bir kısıt olmaksızın, çok değişkenli bir amaç fonksiyonunu f(x 1, x 2, …, xn) maksimize ya da minimize edecek optimum noktayı (x 1*, x 2*, …, xn*) araştıran doğrusal olmayan programlamadır. • Bu programlamaya, malın fiyatı, tüketicilerin satın alma gücü, zevk ve alışkanlıkları gibi çok sayıda değişkenle açıklanan bir talep fonksiyonunun optimizasyonu örnek olarak gösterilebilir. 26

Çok Değişkenli Kısıtsız Doğrusal Olmayan Programlama • Uygulamada karşılan problemlerin pek çoğu çok değişkenli ilişkilerle açıklanabilecek niteliktedir. Örneğin, bir malın talebinde(d); – – – malın sunum miktarı (s), satış fiyatı (f), tüketicinin gelir düzeyi (g), zevk ve alışkanlıkları (z), nüfus artış hızı (h) ve zaman etkili (t) olduğu düşünülüyorsa, talep fonksiyonu, tüm bu faktörlerin bir fonksiyonu olarak d=f(s, f, g, z, h, t) şeklinde açıklanır. Böyle bir fonksiyona çok değişkenli fonksiyon denir. 27

Kısıtlı Doğrusal Olmayan Programlama • Şimdiye kadar kısıtlayıcı fonksiyon içermeyen problemler üzerinde durulmuştur. Uygulamada, amaç fonksiyonunun bir dizi fonksiyonun kısıtlayıcı koşulları altında en iyi sonucu türündeki problemlerle karşılaşmak daha yaygındır. Burada, çok değişkenli f(x 1, x 2, ……, xn) fonksiyonundaki x 1, x 2, ……, xn değişkenlerinin bir ya da birden çok eşitlik ile bağlantılı olmaları durumu incelenecektir. Bunun için, • • f(x 1, x 2, ……, xn) fonksiyonunun, • g 1(x 1, x 2, ……, xn) = b 1 • g 2(x 1, x 2, ……, xn) =b 2 • gm(x 1, x 2, ……, xn) =bm • biçimindeki kısıtlayıcıların sınırlayıcı koşulları altında en büyük (veya en küçük) değerine ulaştığı noktanın belirlenmek istendiğini varsayalım. 28

• Bu sorunun çözülmesi için Lagrange yöntemi denilen bir matematiksel yönteme başvurulur. Bu yöntem, yukarıda genel gösterimi sunulan problemin en iyi çözümünün hesaplanmasında kısıtlayıcı fonksiyonların her biri için bir tane olmak üzere kısıtlayıcı sayısı kadar yani m tane yeni değişken tanımlanması ile, • L(x 1, x 2, ……………. xn, λ 1, λ 2, ………. λm)= f(x 1, x 2, ……. . xn) + i[ bi- gi (x 1, x 2, ………xn)] olarak ifade edilen yeni bir fonksiyon oluşturulur. Bu fonksiyona Lagrange Fonksiyonu , I’ye Lagrange Çarpanı denir. 29

• Lagrange fonksiyonuna dayanan Lagrange yönteminin esası, Lagrange fonksiyonu için en büyük veya en küçük gösteren (x 1*, x 2*, ……………. xn*, λ 1*, λ 2*, ………. λm*) noktasının belirlenmesidir. • Lagrange fonksiyonu için en iyi çözüm olma özelliğine sahip bu nokta aynı zamanda, esas fonksiyonun da en büyük değerinin ortaya çıktığı (x 1*, x 2*, ……………. xn*, λ 1*, λ 2*, ………. λm*) noktasında, • =bi –gi(x 1, x 2, ……, xn) =0 olur. 30

Örnek 31

Doğrusal Olmayan Amaç Fonksiyonu ve Doğrusal Kısıtlar 32

1. Doğrusal olmayan bir amaç fonksiyonu-doğrusal kısıtlar örneği; Ø Great Western Appliance Şirketi Mikrotoaster (X 1) ve Self. Clean Toaster Oven (X 2) iki model tost makinesi satmaktadır. Firma satılan sayısına bakılmaksızın her Mikrotoaster için 28 $ kar elde etmektedir. Self-Clean modeli için kar, ancak, daha fazla birim olarak artması sabit genel üretim nedeniyle satılmaktadır. Bu modelde kar 21 X 2+0, 25 olarak ifade edilebilir. Ø Burada firmanın amaç fonksiyonu doğrusal değildir: Ø Maksimum kar=28 X 1+21 X 2+0, 25 Ø Great Western’nin karında, mevcut satış zamanı ve üretim kapasitesi olarak iki doğrusal kısıt söz konusudur. Ø X 1+X 2 ≤ 1, 000 (üretim kapasitesinin birimleri) Ø 0. 5 X 1+0. 4 X 2 ≤ 500 (mevcut satış süresinin saatleri) Ø X 1, X 2 ≥ 0 (Kaynak: Render ve ark. , 2012) 33

2. Quadratik programlama amaç fonksiyonunda kareli terimler içerir; Ø Amaç fonksiyonu kareli terimler içerdiğinde (0, 25 gibi) ve problemin kısıtları doğrusal olduğunda buna quadratik programlama problemi denir. Ø Quadratik programlar simplex yöntemi değiştirilmiş bir yöntemle çözülebilir. (Kaynak: Render ve ark. , 2012) 34

ÖRNEKLER 35

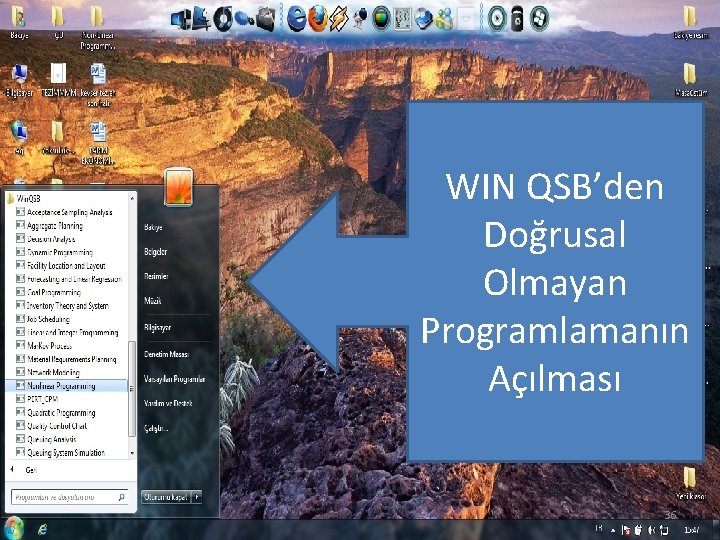
WIN QSB’den Doğrusal Olmayan Programlamanın Açılması 36

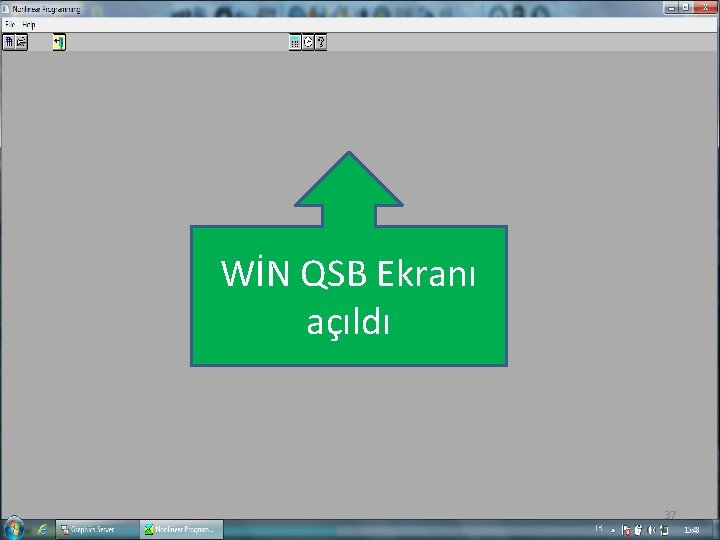
WİN QSB Ekranı açıldı 37

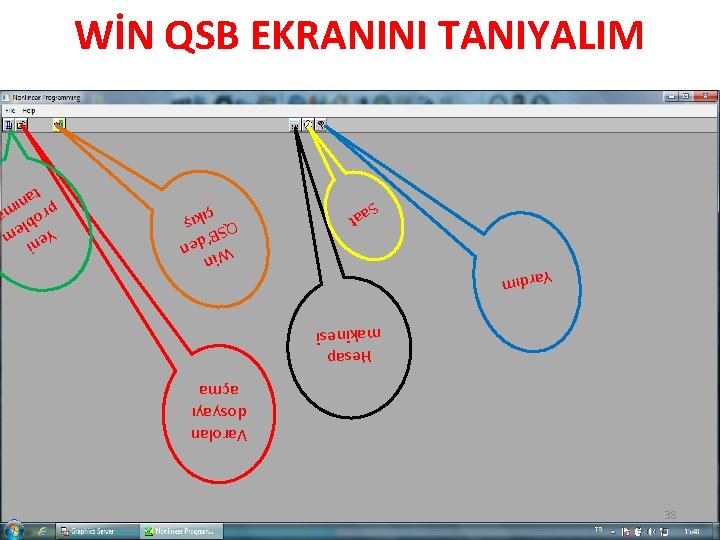
38 Varolan dosyayı açma Hesap makinesi Yardım at Sa Win en ’d QSB ş çıkı ni Ye m ble pro ım tan WİN QSB EKRANINI TANIYALIM

Kısıtsız Doğrusal Olmayan Programlama Örneği • minimum x(sin(3. 14159 x)) • 0 <= x <= 6 • Amaç fonksiyonunu minimum yapmak için sadece bir tane doğrusal olmayan x terimine sahibiz (sin(3. 14159 x) 39

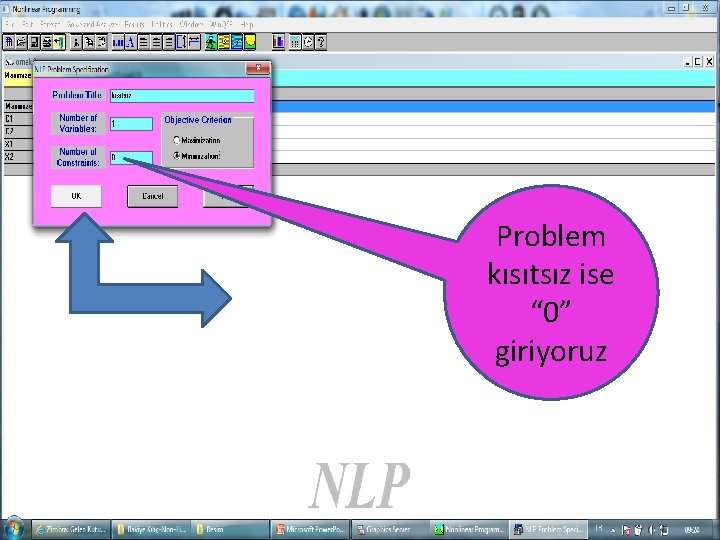
Problem kısıtsız ise “ 0” giriyoruz 40

Kısıtsız Doğrusal Olmayan Programlama Örneği 41

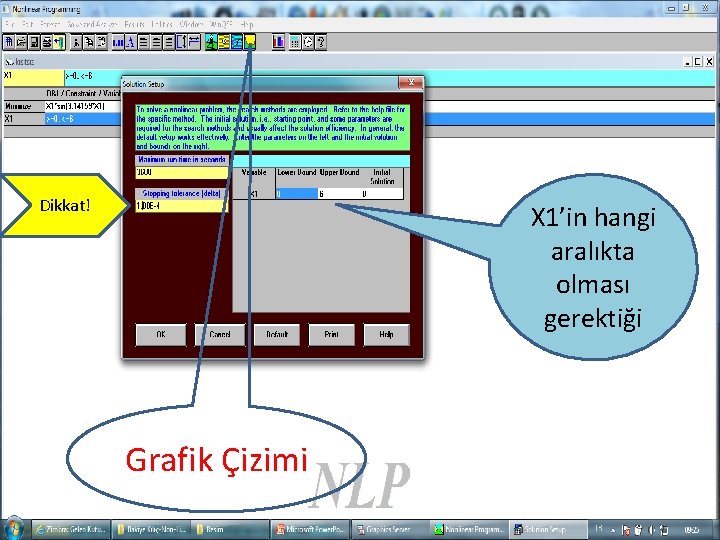
Dikkat! X 1’in hangi aralıkta olması gerektiği Grafik Çizimi 42

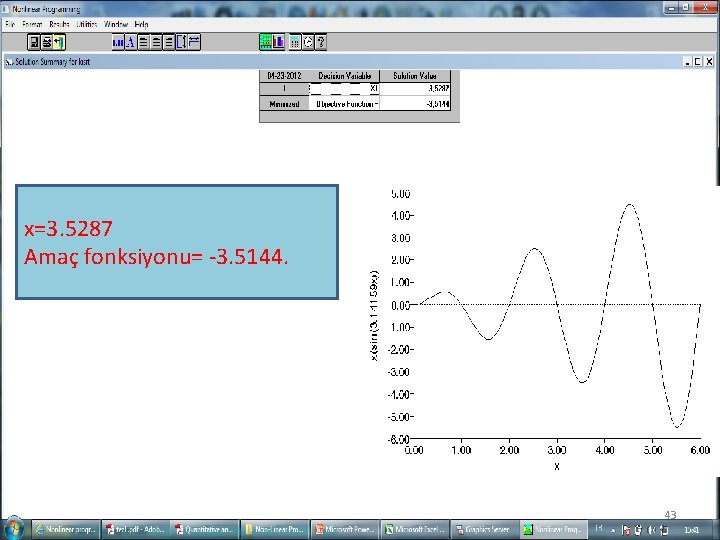
x=3. 5287 Amaç fonksiyonu= -3. 5144. 43

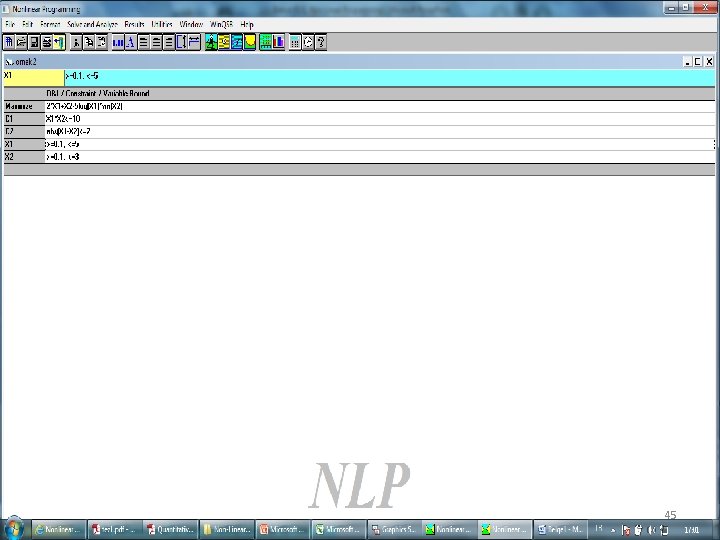
Örnek 2: Amaç Fonksiyonu: maximum 2 x 1 + x 2 - 5 loge(x 1)sin(x 2) Kısıtlar x 1 x 2 <= 10 | x 1 - x 2 | <= 2 0. 1 <= x 1 <= 5 0. 1 <= x 2 <= 3 44

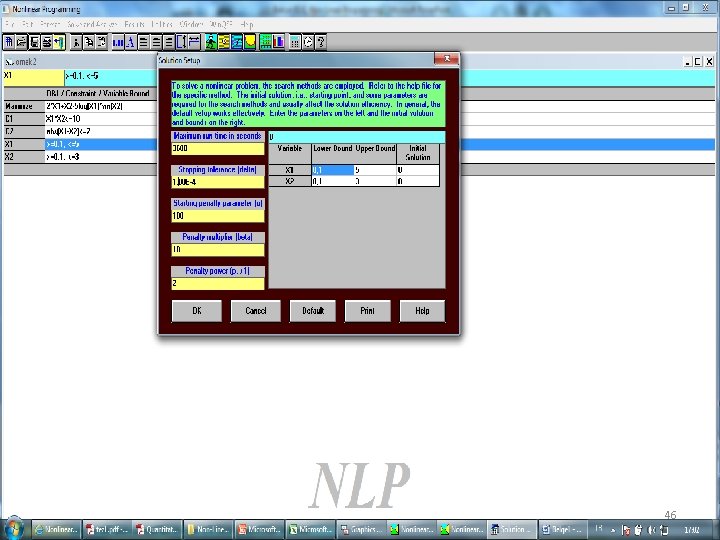
45

46

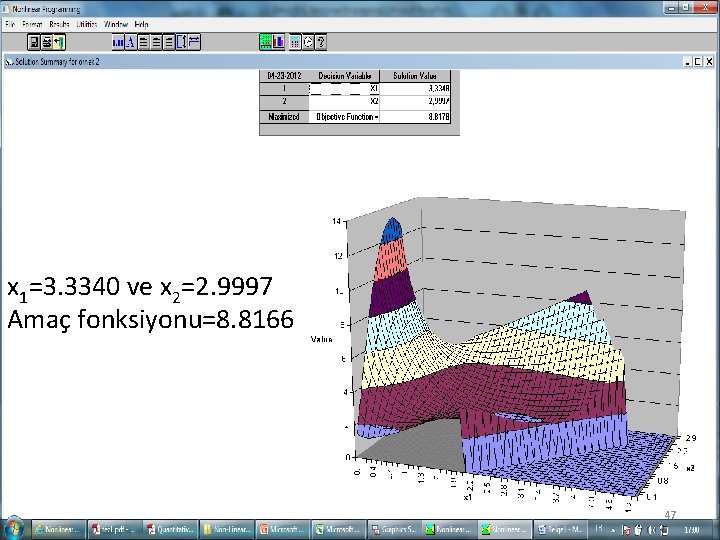
x 1=3. 3340 ve x 2=2. 9997 Amaç fonksiyonu=8. 8166 47

Hem Doğrusal Olmayan Amaç Fonksiyonu Hem De Doğrusal Olmayan Kısıtlar 48

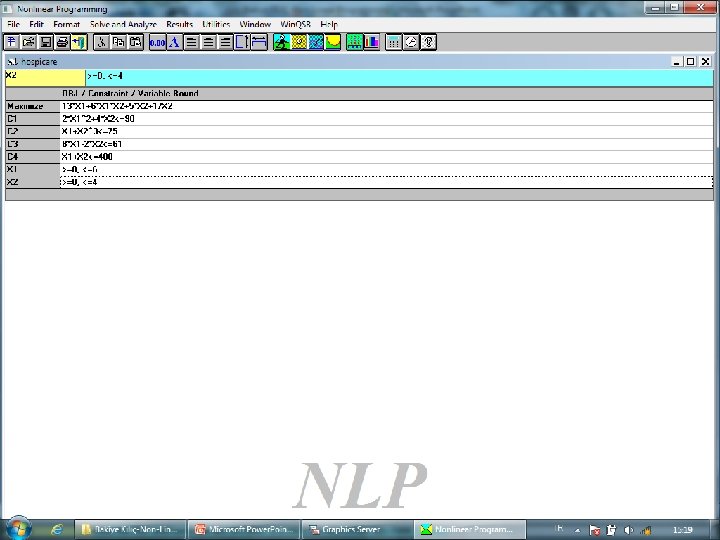
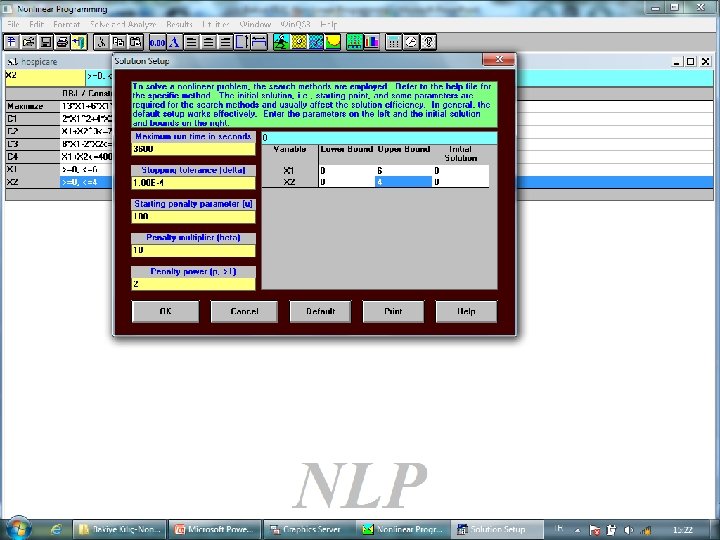
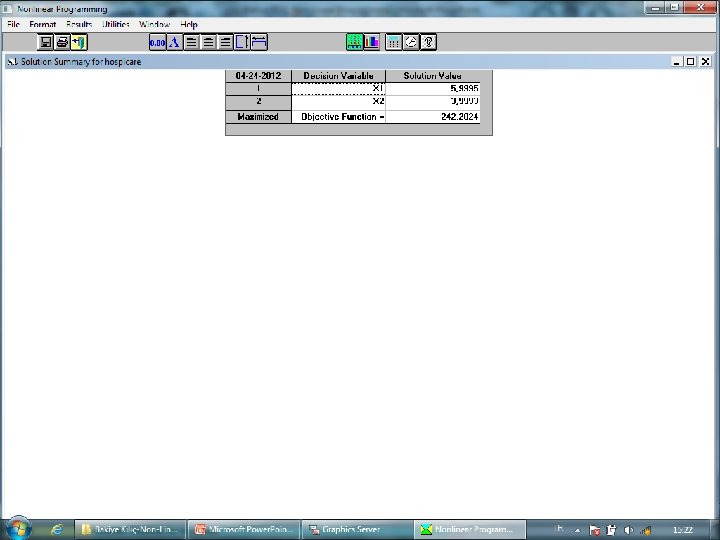
• Orta ölçekli bir (200 -400 yataklı) Hospicare Corporation’a ait hastanede yıllık kar, başvuran tıbbi hasta (X 1) ve başvuran cerrahi hasta sayısına (X 2) bağlıdır. • Hospicare için doğrusal olmayan amaç fonksiyonu: $13 X 1 + $6 X 1 X 2 + $5 X 2 + $1/X 2 Kısıtlar; • • • 2 X 12+4 X 2≤ 90 (hemşire kapasitesi) X 1+X 23≤ 75 (X-Işını kapasitesi) 8 X 1 -2 X 2≤ 61 (pazarlama bütçesi) 49

50

51

52

Örnek: Pickens Memorial Hastanesi ü Hasta talebi hastanenin kapasitesini aşıyor Amaç: Maximum kar 53

Karar Değişkenleri M =Kabul edilen tıbbi hasta sayısı S = Kabul edilen cerrahi hasta sayısı P = Kabul edilen çocuk hastalıkları hasta sayısı Kar Fonksiyonu Hastaların sayısı arttıkça kar artar (yani doğrusal olmayan kar fonksiyonu) 54

Kısıtlayıcılar • Hastane kapasitesi: Toplam 200 hasta • X-ray kapasitesi: haftada 560 x-rays • Pazarlama bütçesi: haftada $1000 • Laboratuar kapasitesi: haftada 140 saat 55

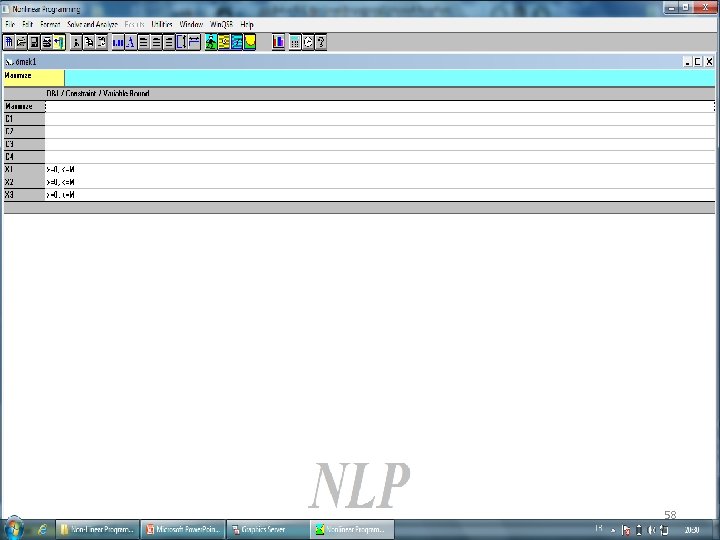
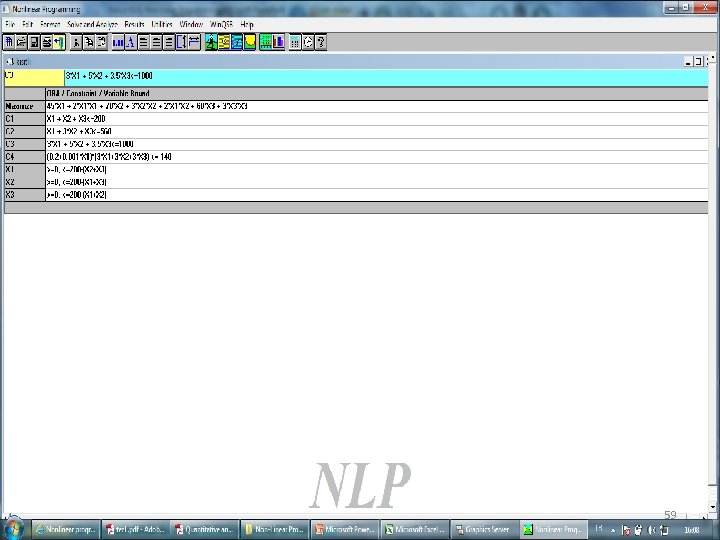
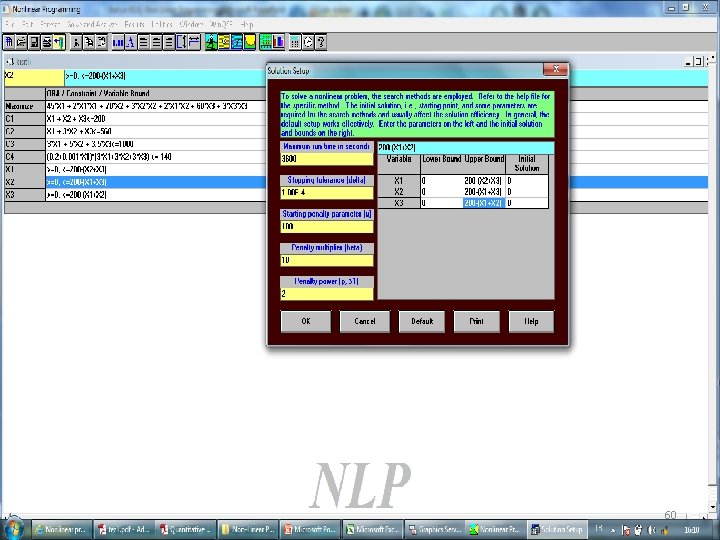
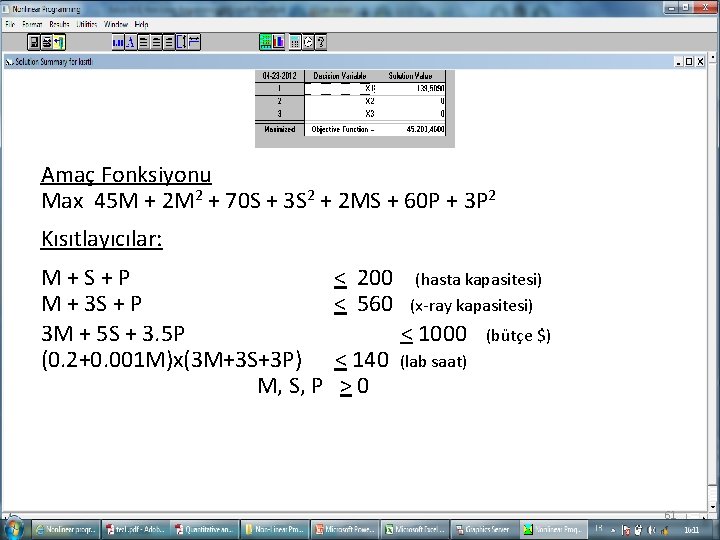
Amaç Fonksiyonu Max 45 M + 2 M 2 + 70 S + 3 S 2 + 2 MS + 60 P + 3 P 2 Kısıtlayıcılar: M + S + P < 200 (hasta kapasitesi) M + 3 S + P < 560 (x-ray kapasitesi) 3 M + 5 S + 3. 5 P < 1000 (bütçe $) (0. 2+0. 001 M)x(3 M+3 S+3 P) < 140 (lab saat) M, S, P > 0 56

57

58

59

60

Amaç Fonksiyonu Max 45 M + 2 M 2 + 70 S + 3 S 2 + 2 MS + 60 P + 3 P 2 Kısıtlayıcılar: M + S + P < 200 (hasta kapasitesi) M + 3 S + P < 560 (x-ray kapasitesi) 3 M + 5 S + 3. 5 P < 1000 (bütçe $) (0. 2+0. 001 M)x(3 M+3 S+3 P) < 140 (lab saat) M, S, P > 0 61