Algorithms for the Linear Case Algorithmic Game Theory



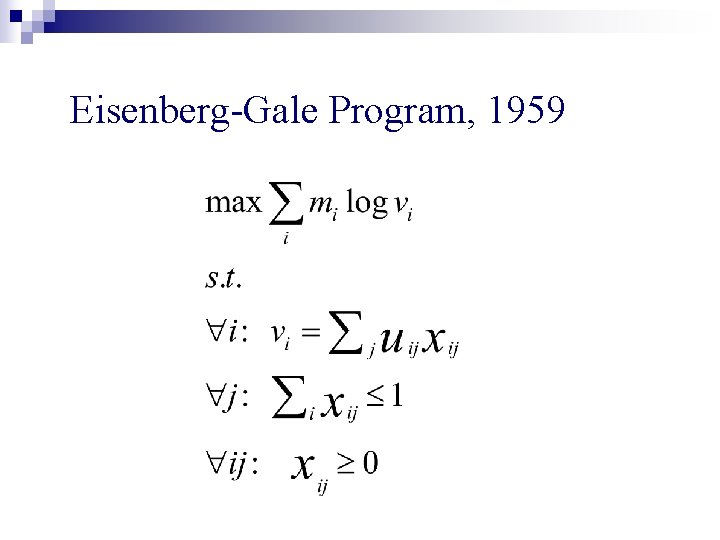
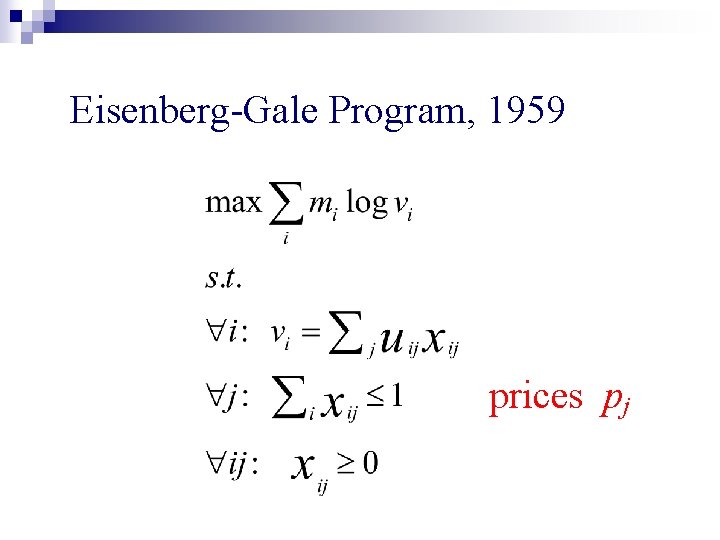








































































- Slides: 106

Algorithms for the Linear Case, Algorithmic Game Theory and Beyond … and Internet Computing Vijay V. Vazirani Georgia Tech

Irving Fisher, 1891 n Defined a fundamental market model n Special case of Walras’ model

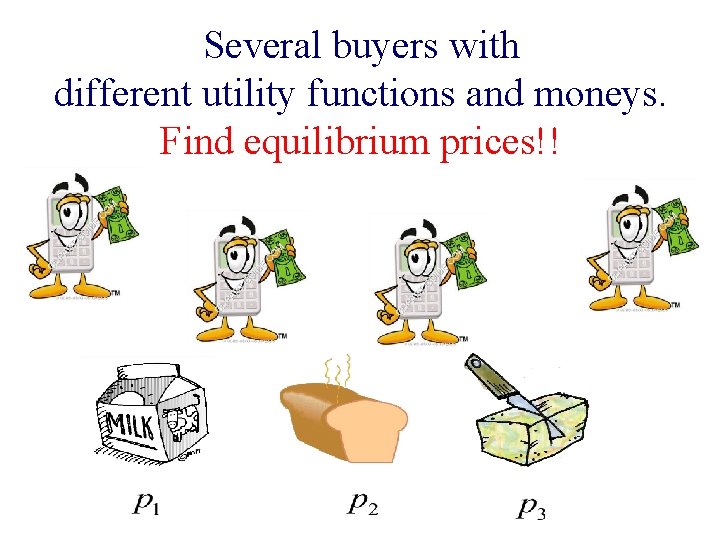
Several buyers with different utility functions and moneys. Find equilibrium prices!!

Linear Fisher Market n Assume: ¨ Buyer i’s total utility, mi : money of buyer i. ¨ One unit of each good j. ¨ n Find market clearing prices!
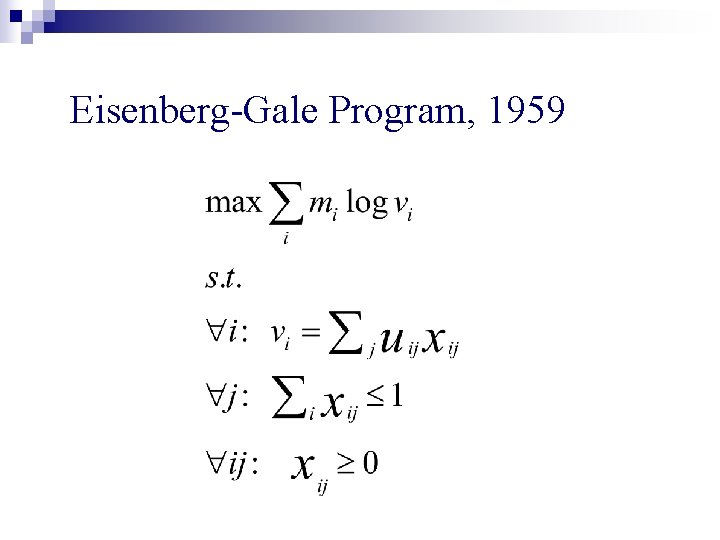
Eisenberg-Gale Program, 1959
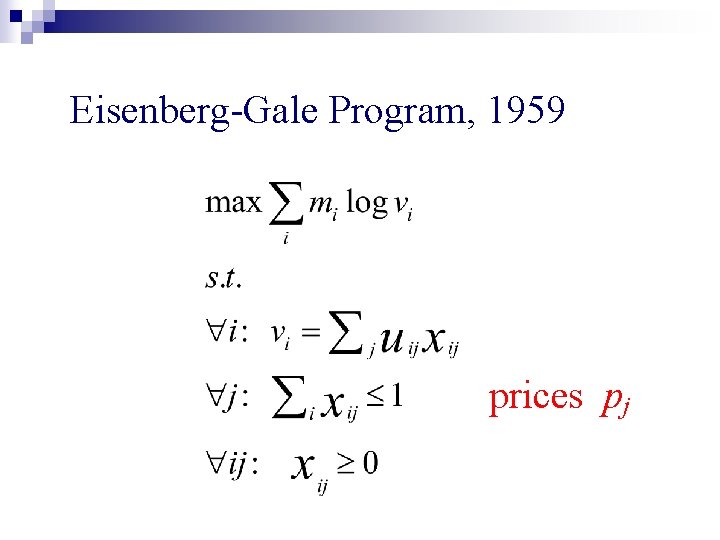
Eisenberg-Gale Program, 1959 prices pj

Convex programs that capture market equilibria n Underly all “efficient” markets (so far). n Rational convex programs for many markets! n Algorithms: combinatorial, for rational (primal-dual) ¨ continuous (ellipsoid/interior point) ¨

Combinatorial algorithms for rational convex programs n Natural extension of field of combinatorial optimization!

Combinatorial algorithms for rational convex programs n Natural extension of field of combinatorial optimization! n Central aspect of C. O. – efficient algorithms for solving integral LP’s, e. g. matching, flow.

Combinatorial Algorithm for Linear Case of Fisher’s Model n Devanur, Papadimitriou, Saberi & V. , 2002 By extending the primal-dual paradigm to the setting of convex programs & KKT conditions

Combinatorial algorithms n Yield deep structural insights. n Preferable for applications.

Auction for Google’s TV ads N. Nisan et. al, 2009: n Used market equilibrium based approach. n Combinatorial algorithms for linear case provided “inspiration”.

Primal-Dual Paradigm n Highly successful algorithm design technique from exact and approximation algorithms

Exact Algorithms for Cornerstone Problems in P: n n n Matching (general graph) Network flow Shortest paths Minimum spanning tree Minimum branching

Approximation Algorithms set cover Steiner tree Steiner network k-MST scheduling. . . facility location k-median multicut feedback vertex set



Yin & Yang

An easier question n Given prices p, are they equilibrium prices? n If so, find equilibrium allocations.

An easier question n Given prices p, are they equilibrium prices? n If so, find equilibrium allocations. n Equilibrium prices are unique!

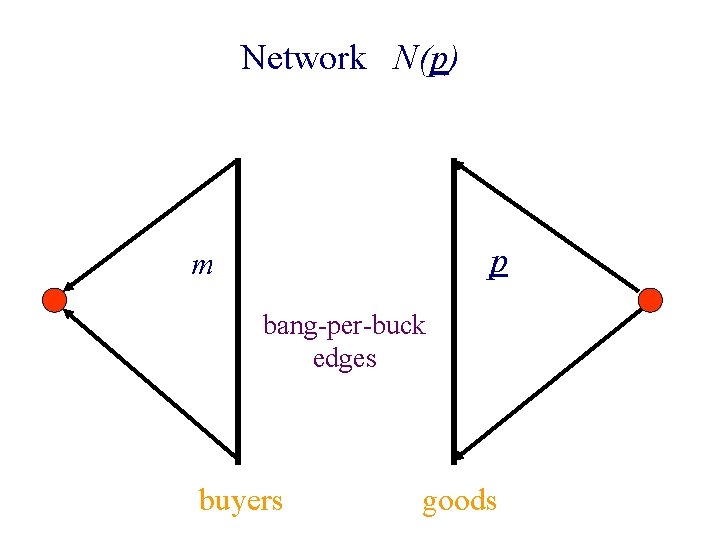
Bang-per-buck n At prices p, buyer i’s most desirable goods, Si = n Any goods from Si worth m(i) constitute i’s optimal bundle

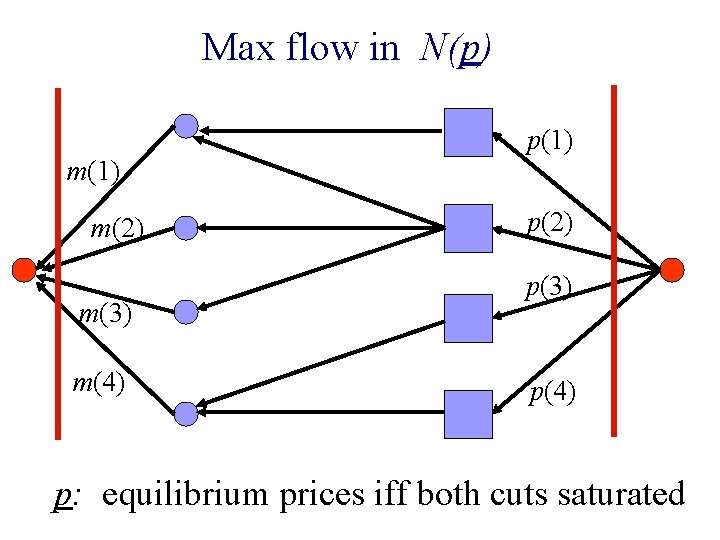
For each buyer, most desirable goods, i. e. m(1) p(1) m(2) p(2) m(3) p(3) m(4) p(4)

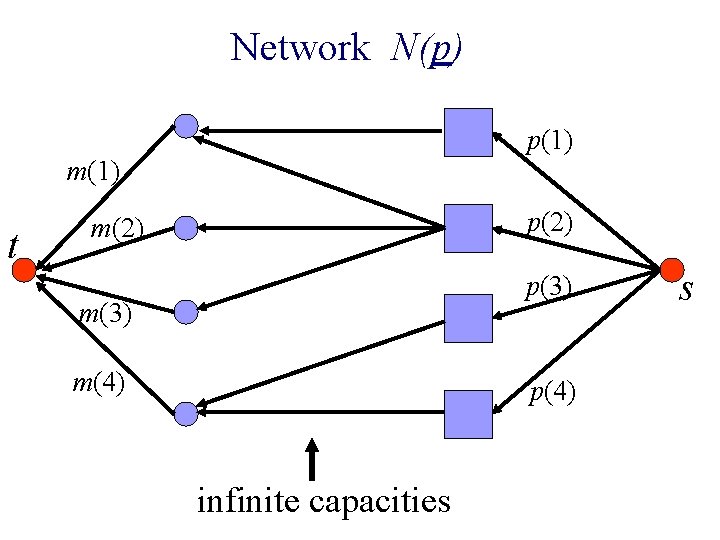
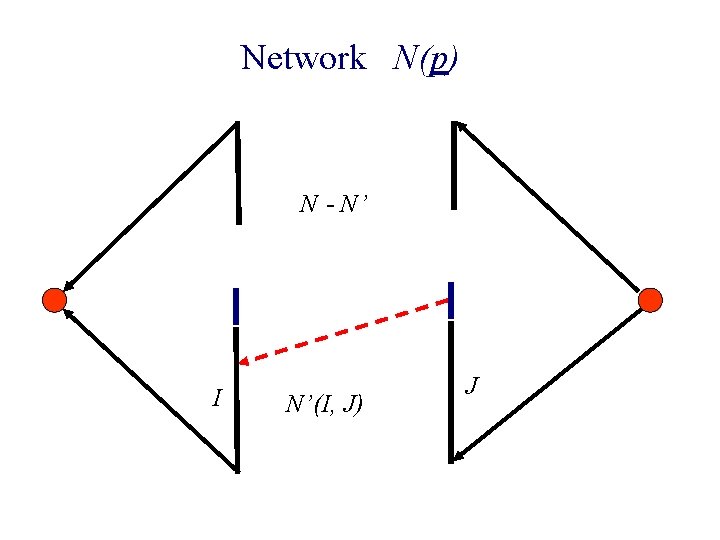
Network N(p) p(1) m(1) t p(2) m(2) p(3) m(4) p(4) infinite capacities s

Max flow in N(p) m(1) m(2) m(3) m(4) p(1) p(2) p(3) p(4) p: equilibrium prices iff both cuts saturated

Idea of algorithm n “primal” variables: allocations n “dual” variables: prices of goods n Approach equilibrium prices from below: ¨ start with very low prices; buyers have surplus money ¨ iteratively keep raising prices and decreasing surplus

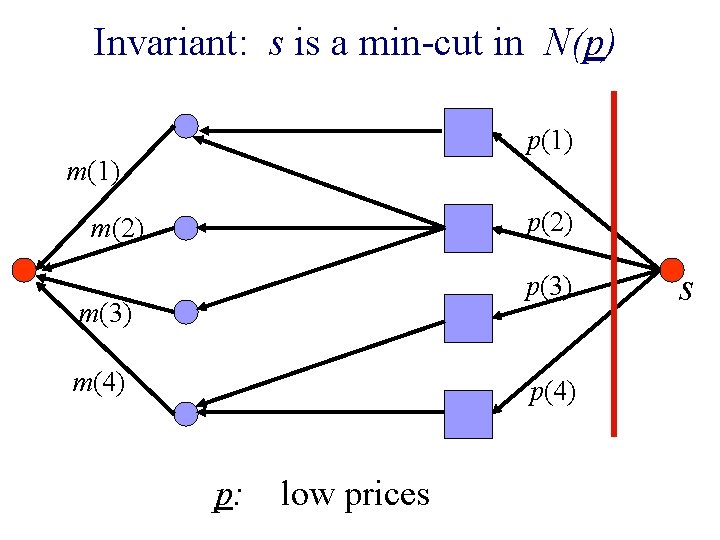
An important consideration n The price of a good never exceeds its equilibrium price ¨ Invariant: s is a min-cut

Invariant: s is a min-cut in N(p) p(1) m(1) p(2) m(2) p(3) m(4) p: low prices s

Idea of algorithm n Iterations: execute primal & dual improvements Allocations Prices

How is primal-dual paradigm adapted to nonlinear setting?

Fundamental difference between LP’s and convex programs n Complementary slackness conditions: involve primal or dual variables, not both. n KKT conditions: involve primal and dual variables simultaneously.

KKT conditions

KKT conditions

Primal-dual algorithms so far (i. e. , LP-based) n Raise dual variables greedily. (Lot of effort spent on designing more sophisticated dual processes. )

Primal-dual algorithms so far n Raise dual variables greedily. (Lot of effort spent on designing more sophisticated dual processes. ) ¨ Only exception: Edmonds, 1965: algorithm for max weight matching.

Primal-dual algorithms so far n Raise dual variables greedily. (Lot of effort spent on designing more sophisticated dual processes. ) ¨ Only n exception: Edmonds, 1965: algorithm for max weight matching. Otherwise primal objects go tight and loose. Difficult to account for these reversals -in the running time.

Our algorithm n Dual variables (prices) are raised greedily n Yet, primal objects go tight and loose ¨ Because of enhanced KKT conditions

Our algorithm n Dual variables (prices) are raised greedily n Yet, primal objects go tight and loose ¨ Because n of enhanced KKT conditions New algorithmic ideas needed!

Key Algorithmic Idea n Dual variables (prices) are raised greedily n Yet, primal objects go tight and loose ¨ Because n of enhanced KKT conditions Balanced Flows: For limiting no. of such events

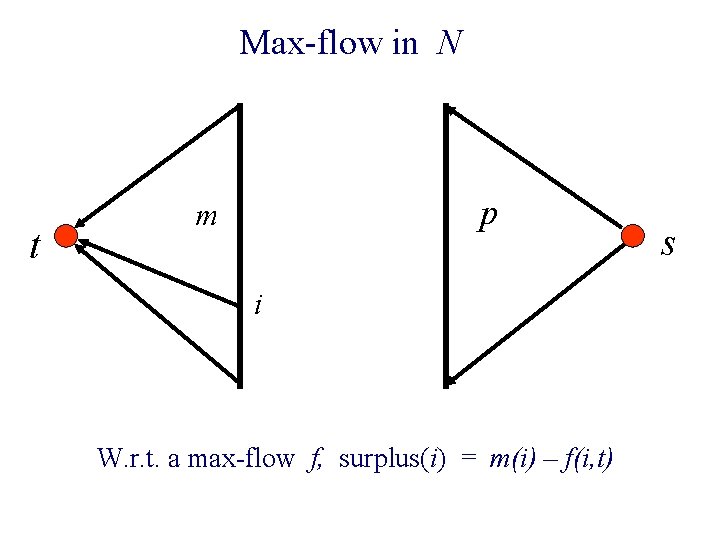
Max-flow in N t p m i W. r. t. a max-flow f, surplus(i) = m(i) – f(i, t) s

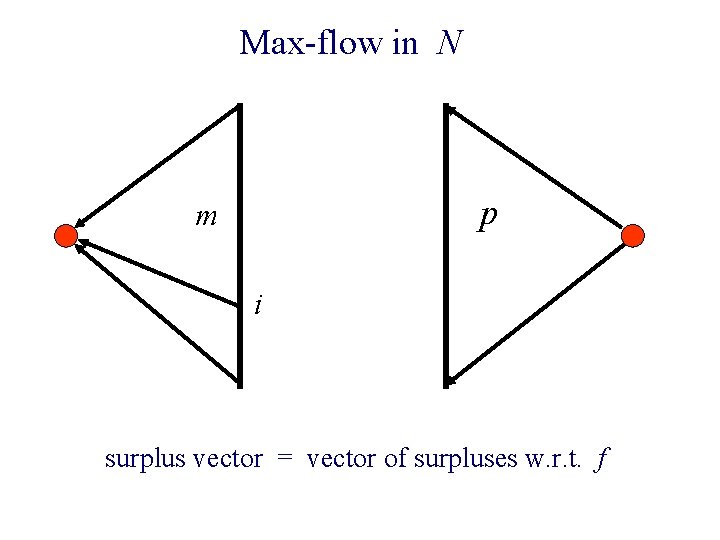
Max-flow in N p m i surplus vector = vector of surpluses w. r. t. f

Obvious potential function n Total surplus money = l 1 norm of surplus vector n Reduce l 1 norm of surplus vector by inverse polynomial fraction in each iteration

Balanced flow n A max-flow that minimizes l 2 norm of surplus vector. n Makes surpluses as equal as possible.

Balanced flow n A max-flow that minimizes l 2 norm of surplus vector. n Makes surpluses as equal as possible. n All balanced flows have same surplus vector.

Our algorithm n Reduces l 2 norm of surplus vector by inverse polynomial fraction in each iteration.


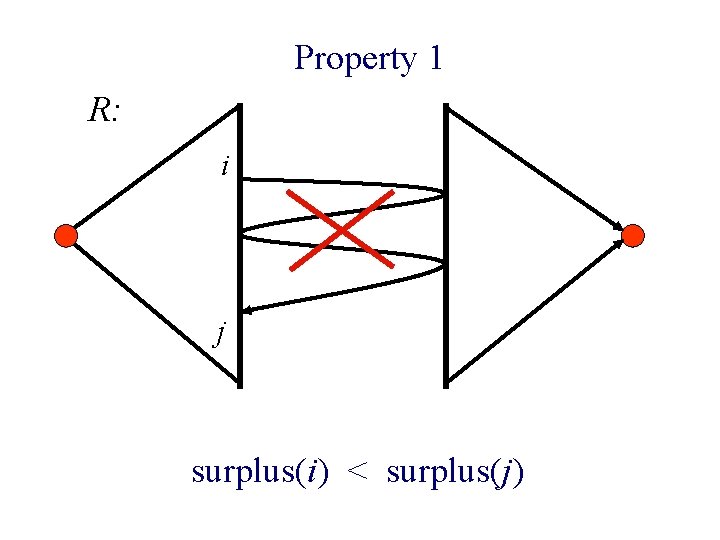
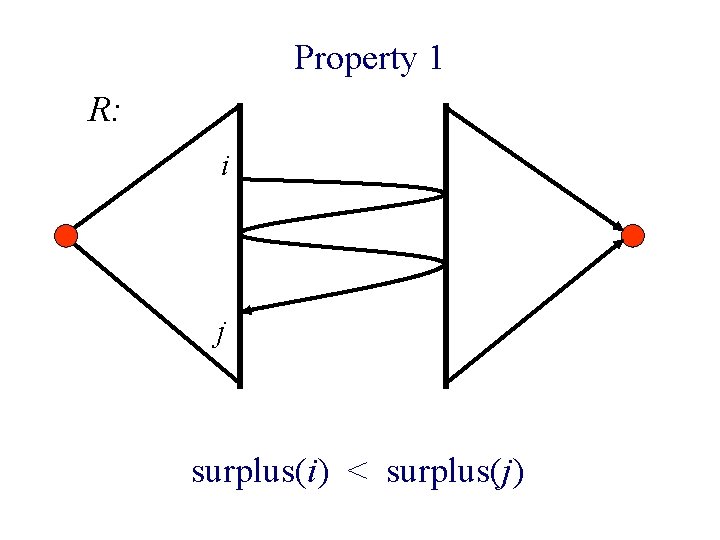
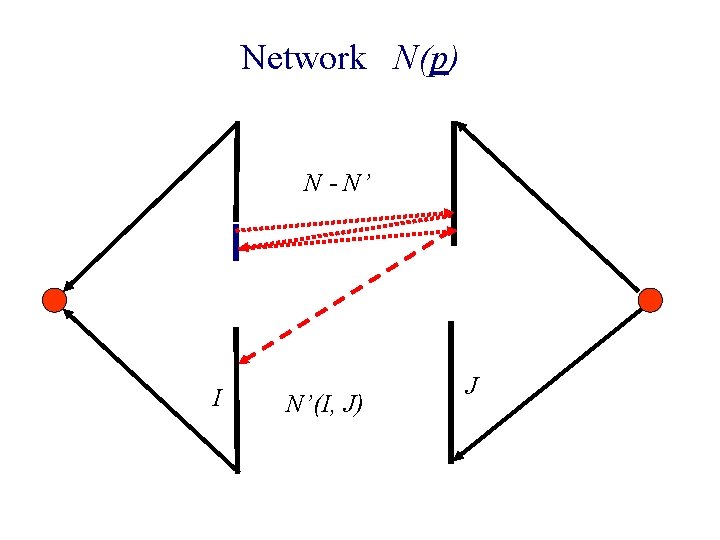
Property 1 n f: max-flow in N. n R: residual graph w. r. t. f. n If surplus (i) < surplus(j) then there is no path from i to j in R.

Property 1 R: i j surplus(i) < surplus(j)

Property 1 R: i j surplus(i) < surplus(j)

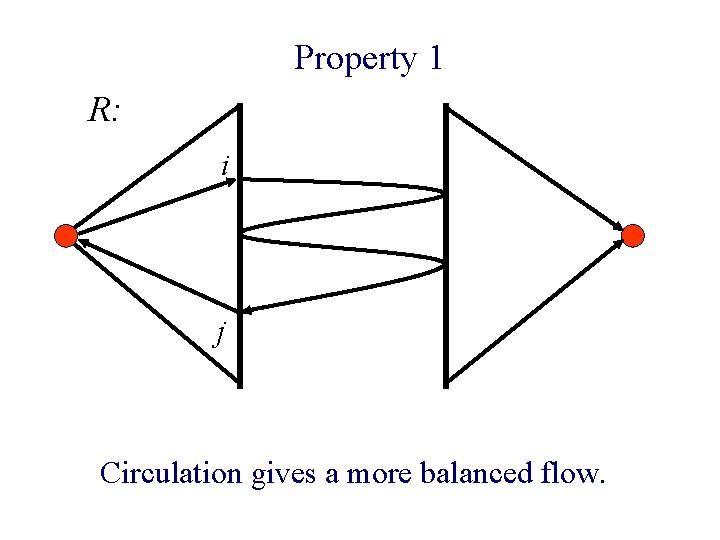
Property 1 R: i j Circulation gives a more balanced flow.

Property 1 n Theorem: A max-flow is balanced iff it satisfies Property 1.

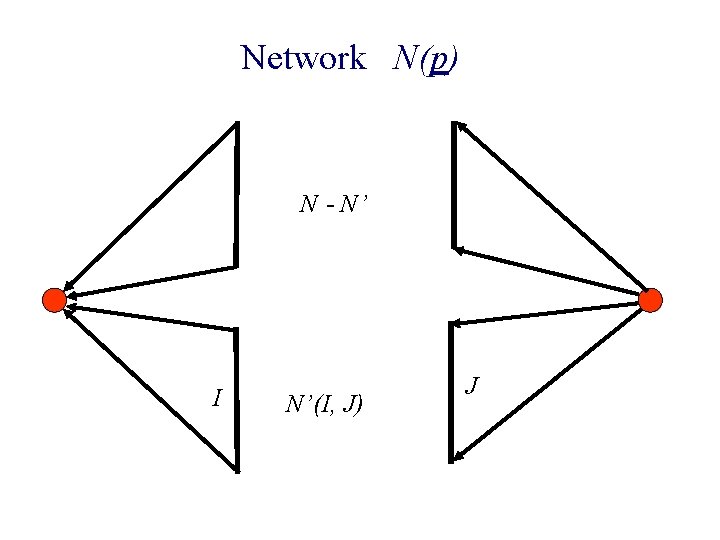
Algorithm for an iteration n Construct N’(I, J) n Raise prices in J n New edge enters N n Stop when Invariant is threatened

Network N(p) p m bang-per-buck edges buyers goods

n Construct N’(I, J) ¨ Find a balanced flow in N(p) Let d = max surplus w. r. t. balanced flow ¨ I = buyers with surplus d ¨ J = goods desired by I n Raise prices in J n New edge enters N n Stop when Invariant is threatened

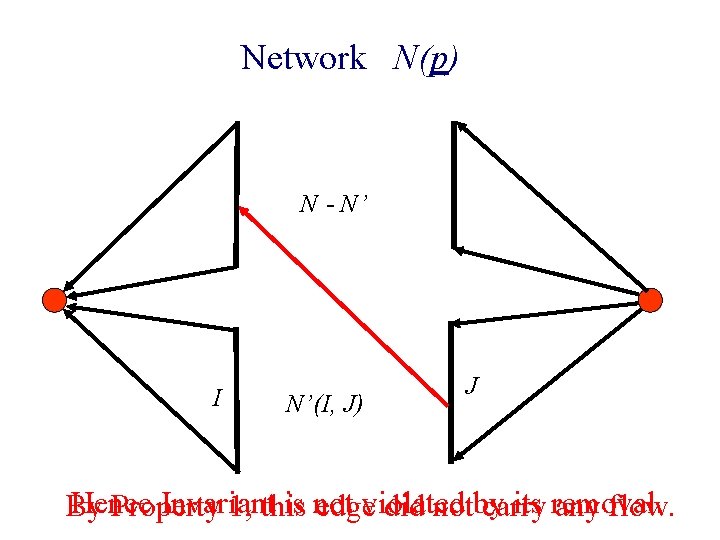
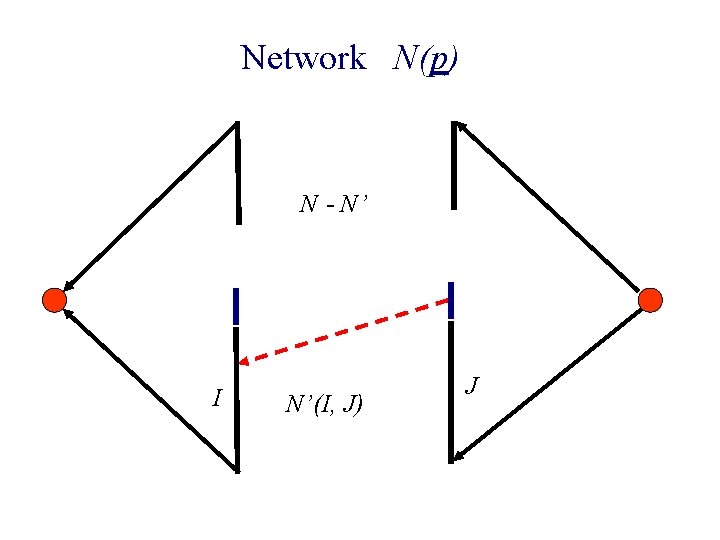
Network N(p) N - N’ I N’(I, J) J

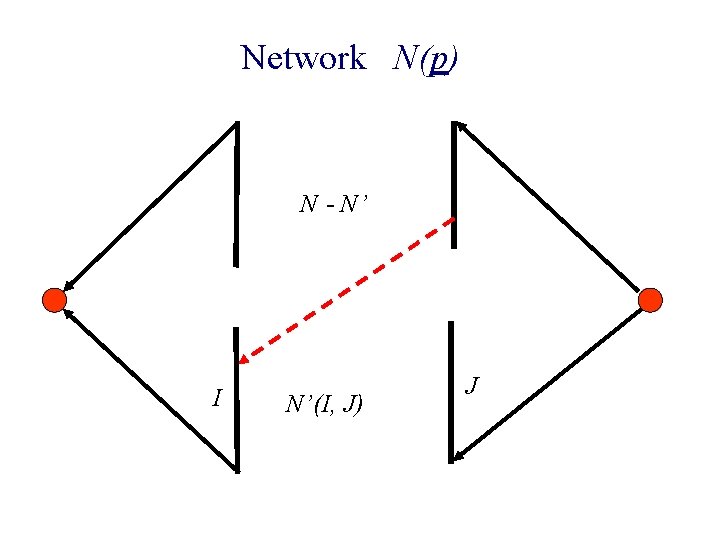
Network N(p) N - N’ I N’(I, J) J

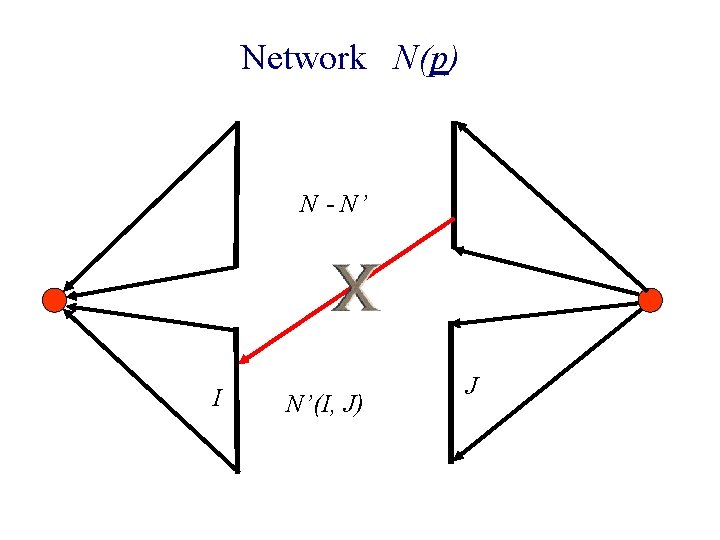
n Construct N’(I, J) n Raise prices in J ¨ N’ is decoupled from N - N’ n New edge enters N n Stop when Invariant is threatened

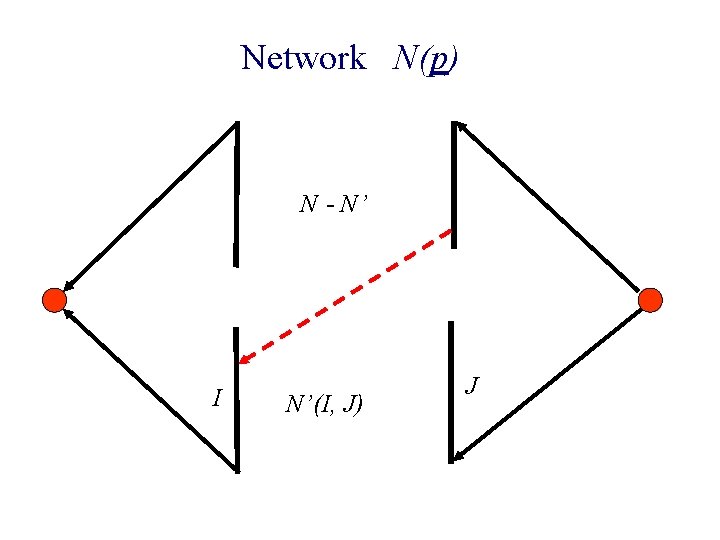
Network N(p) N - N’ I N’(I, J) J

Network N(p) N - N’ I N’(I, J) J Hence Invariant is not its removal. By Property 1, this edgeviolated did notby carry any flow.

Raise prices in J n n proportionately, so that edges in N’ don’t change. p. x, for each p in J initialize x = 1 ¨ raise x ¨

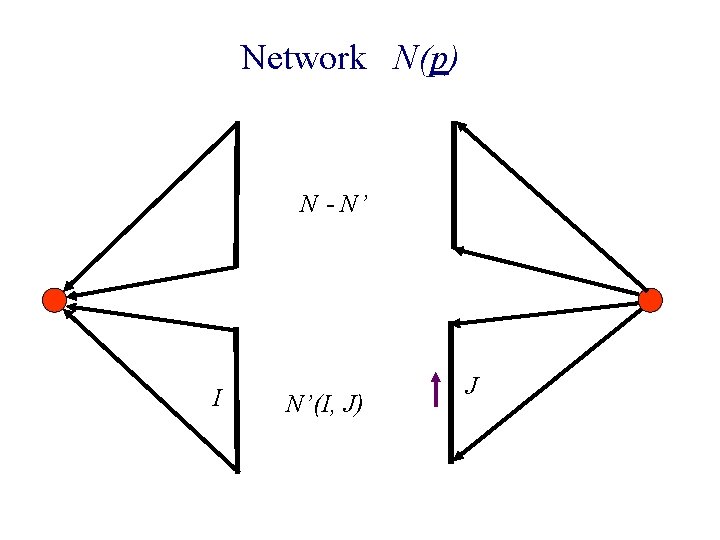
n Construct N’(I, J) n Raise prices in J n New edge enters N n Stop when Invariant is threatened

Network N(p) N - N’ I N’(I, J) J

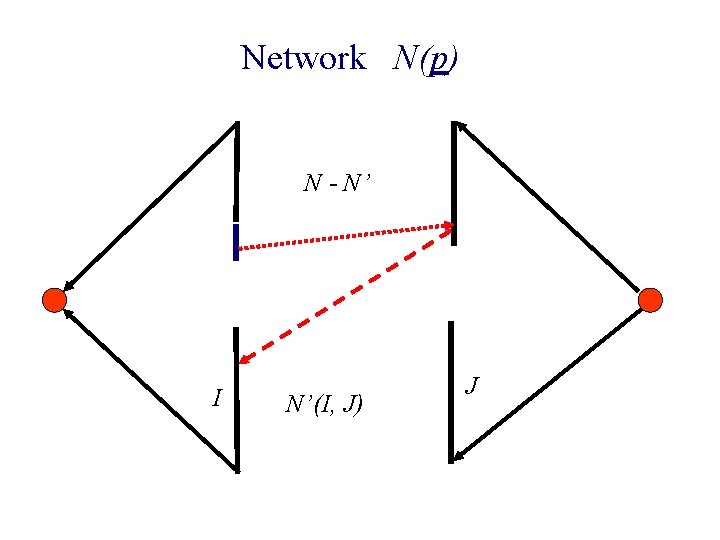
n Construct N’(I, J) n Raise prices in J n New edge enters N ¨ Recompute balanced flow ¨ Buyers in N - N’ having residual paths to N’ Move to N’ n Stop when Invariant is threatened

Network N(p) N - N’ I N’(I, J) J

Network N(p) N - N’ I N’(I, J) J

Network N(p) N - N’ I N’(I, J) J

n Construct N’(I, J) n Raise prices in J n New edge enters N ¨ Recompute balanced flow ¨ Buyers moved to N’ will have sufficiently large surplus n Stop when Invariant is threatened

Algorithm for an iteration n Construct N’(I, J) n Raise prices in J n New edge enters N n Stop when Invariant is threatened

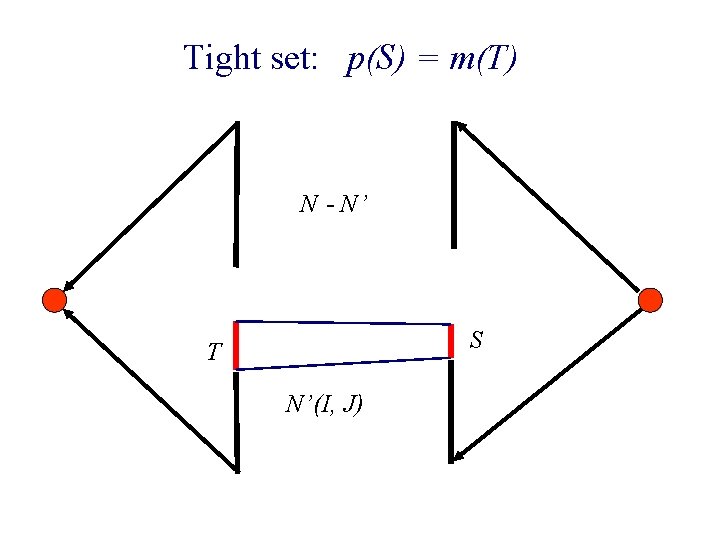
Tight set: p(S) = m(T) N - N’ S T N’(I, J)

n Surplus of buyers in T drops to 0

n Surplus of buyers in T drops to 0 n l 1 norm of surplus vector drops by 1/n fraction after the iteration.

n Assume k sub-iterations. n Let d 0 = d. At the end of lth sub-iteration, dl = min {surplus(i) | i is in I}. So, dk = 0.

Network N(p) N - N’ I N’(I, J) J

n Some i in old I will achieve minimum. Its surplus must drop by at least (dl-1 – dl). n Therefore, decrease in l 1 norm in sub-iteration l is at least (dl-1 – dl) n Therefore, decrease in iteration is at least d

Network N(p) N - N’ I N’(I, J) J

n Assume k sub-iterations. n Let d 0 = d. At the end of lth sub-iteration, dl = min {surplus(i) | i is in I}. So, dk = 0. n Decrease in l 1 norm in sub-iteration l is at least (dl-1 – dl) n Decrease in l 22 norm in sub-iteration l is at least (dl-1 – dl)2

Our algorithm n Reduces l 2 norm of surplus vector by 1/n 2 fraction in each iteration

Open question n Can define balanced flow without l 2 norm ¨ Balanced n flow = lexicographically smallest flow Q: Can we dispense with l 2 norm in proof?

Open question n Can define balanced flow without l 2 norm ¨ Balanced flow = lexicographically smallest flow n Q: Can we dispense with l 2 norm in proof? n V, 2008: Family of examples s. t. l 1 norm of surplus vector decreases by inverse exponential fraction in an iteration!


KKT conditions were relaxed n n e(i): money currently spent by i w. r. t. a balanced flow in N surplus money of i

Relaxed KKT conditions e(i)

Potential function Algorithm drops potential by an inverse polynomial factor in each iteration (strongly polynomial time).

Potential function Algorithm drops potential by an inverse polynomial factor in each iteration (strongly polynomial time).

Second point of departure KKT conditions are satisfied via a continuous process n Normally: in discrete steps n


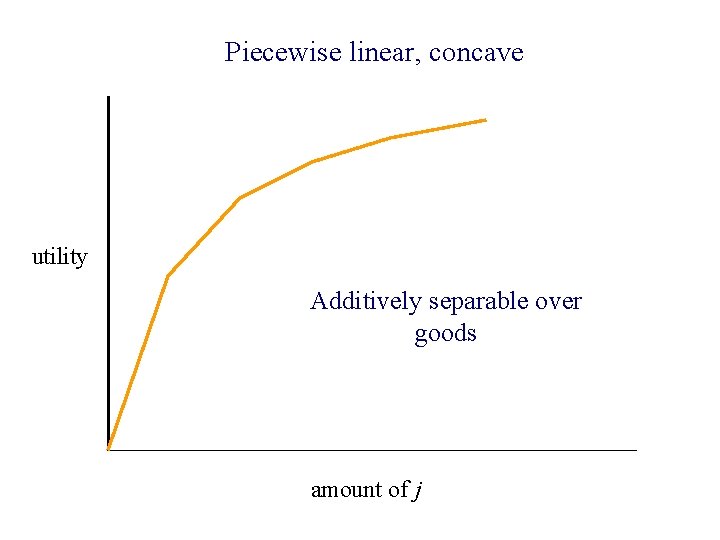
Piecewise linear, concave utility Additively separable over goods amount of j

Long-standing open problem n Complexity of finding an equilibrium for Fisher and Arrow-Debreu models under separable, plc utilities?

How do we build on solution to the linear case?

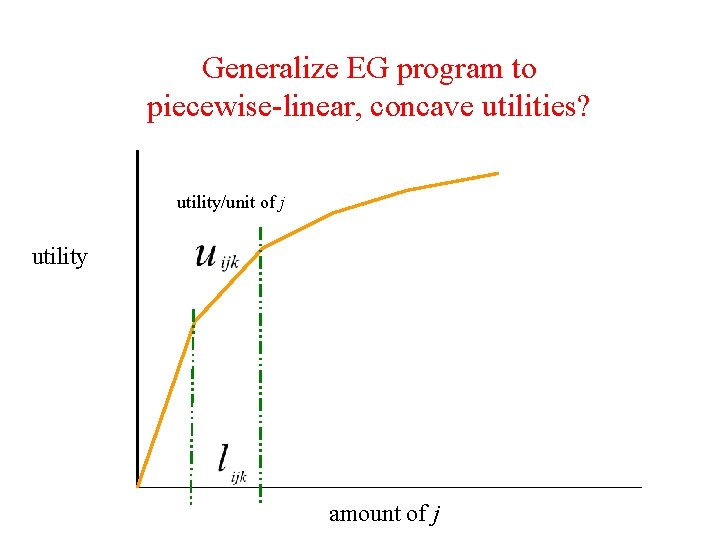
Generalize EG program to piecewise-linear, concave utilities? utility/unit of j utility amount of j

Generalization of EG program

Generalization of EG program

Build on combinatorial insights n V. & Yannakakis, 2007: Equilibrium is rational for Fisher and Arrow-Debreu models under separable, plc utilities. n Given prices p, are they equilibrium prices?

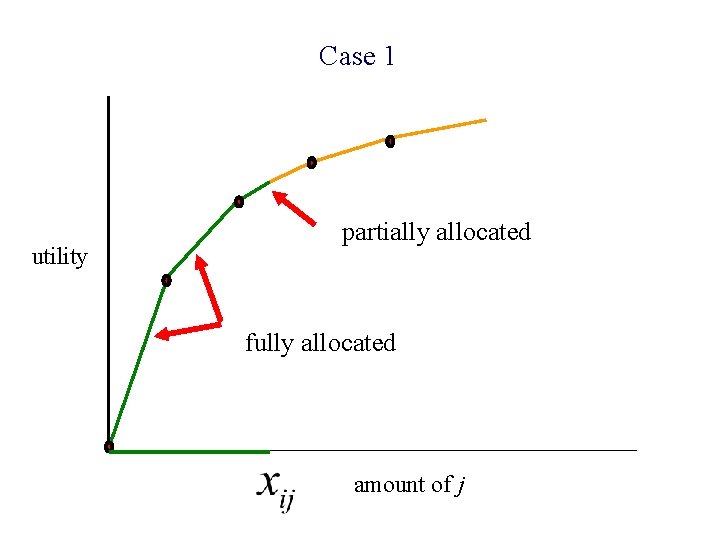
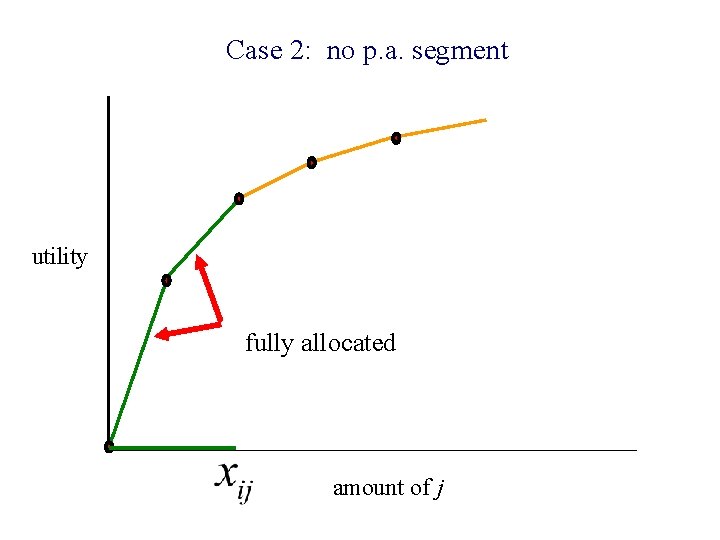
Case 1 utility partially allocated fully allocated amount of j

Case 2: no p. a. segment utility fully allocated amount of j

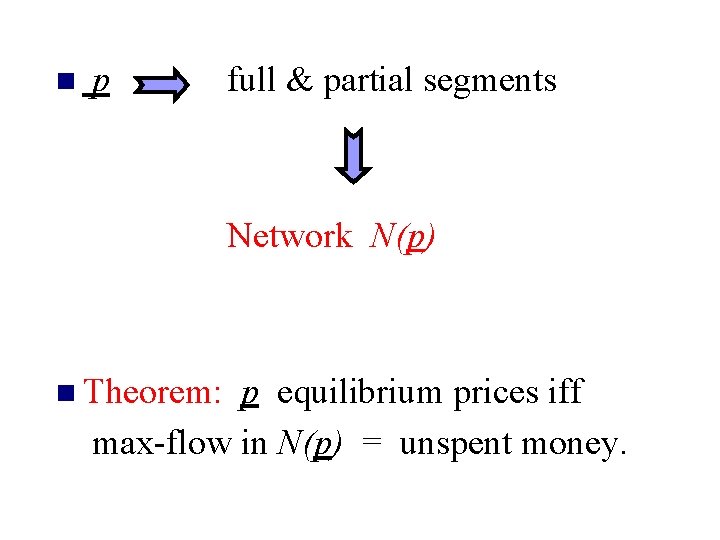
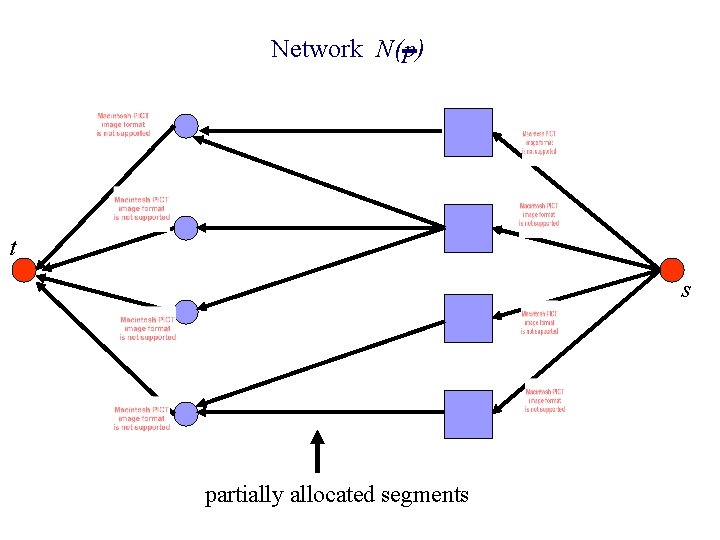
n p full & partial segments Network N(p) n Theorem: p equilibrium prices iff max-flow in N(p) = unspent money.

Network N(p) t s partially allocated segments

n LP for max-flow in N(p); variables = fe’s n Next, let p be variables! n “Guess” full & partial segments – gives N(p) n Write max-flow LP -- it is still linear! ¨ variables = fe’s & pj’s

Rationality proof n If “guess” is correct, at optimality, pj’s are equilibrium prices. n Hence rational!

Rationality proof n If “guess” is correct, at optimality, pj’s are equilibrium prices. n n Hence rational! In P? ?

NP-hardness does not apply n Megiddo, 1988: ¨ Equilibrium n NP-hard => NP = co-NP Papadimitriou, 1991: PPAD ¨ 2 -player Nash equilibrium is PPAD-complete ¨ Rational n Etessami & Yannakakis, 2007: FIXP ¨ 3 -player Nash equilibrium is FIXP-complete ¨ Irrational

Markets with piecewise-linear, concave utilities n Chen, Dai, Du, Teng, 2009: ¨ PPAD-hardness for Arrow-Debreu model

Markets with piecewise-linear, concave utilities n Chen, Dai, Du, Teng, 2009: ¨ PPAD-hardness n Chen & Teng, 2009: ¨ PPAD-hardness n for Arrow-Debreu model for Fisher’s model V. & Yannakakis, 2009: ¨ PPAD-hardness for Fisher’s model

Markets with piecewise-linear, concave utilities V, & Yannakakis, 2009: n Membership in PPAD for both models,

Algorithmic ratification of the “invisible hand of the market” How do we salvage the situation? ?

Is PPAD really hard? ? What is the “right” model? ?

Open Can Fisher’s linear case be captured via an LP?