CHNG 4 CC CH TIU THNG K MC

CHƯƠNG 4 CÁC CHỈ TIÊU THỐNG KÊ MỨC ĐỘ KHỐI LƯỢNG CỦA HIỆN TƯỢNG KINH TẾ - XÃ HỘI VÀ KINH DOANH SẢN XUẤT - DỊCH VỤ

NỘI DUNG 4. 1. Chỉ tiêu mức độ khối lượng tuyệt đối trong thống kê 4. 2. Chỉ tiêu mức độ khối lượng bình quân trong thống kê 4. 3. Chỉ tiêu mức độ khối lượng tăng giảm 4. 4. Chỉ tiêu mức độ biến thiên của tiêu thức

4. 1. Chỉ tiêu mức độ khối lượng tuyệt đối trong thống kê 4. 1. 1. Khái niệm, đặc điểm, ý nghĩa tác dụng v Khái niệm: § Số tuyệt đối trong thống kê là loại chỉ tiêu biểu hiện quy mô, khối lượng, kích thước… của hiện tượng kinh tế - xã hội trong điều kiện thời gian và địa điểm cụ thể. Ví dụ: Tổng số tiền lương của DN thương mại X trong tháng 02/2019 là 255 triệu đồng. Số lao động của đơn vị là 15. 000 người. => Con số 255 triệu đồng là con số tuyệt đối. § Số tuyệt đối còn nói lên: + Số đơn vị của tổng thể. Ví dụ: Số doanh nghiệp, số máy móc thiết bị…

I. Chỉ tiêu mức độ khối lượng tuyệt đối trong thống kê 4. 1. 1 Khái niệm, đặc điểm, ý nghĩa tác dụng v Khái niệm: § + Hoặc: Tổng số các trị số biểu hiện một tiêu thức nào đó. Ví dụ: Số sản phẩm sản xuất được trong 1 tháng hoặc trong 1 quý của 1 đơn vị sản xuất.

4. 1. Chỉ tiêu mức độ khối lượng tuyệt đối trong thống kê(tt) v Ý nghĩa, tác dụng § Số tuyệt đối có ý nghĩa rất quan trọng: Giúp ta nhận thức được một cách cụ thể về quy mô, khối lượng của hiện tượng nghiên cứu, thấy rõ được cụ thể các kết quả đạt được về phát triển KT-XH của đất nước, tiềm năng của nền kinh tế quốc dân. Số tuyệt đối chính xác là chân lý khách quan có sức thuyết phục rất lớn.

4. 1. Chỉ tiêu mức độ khối lượng tuyệt đối trong thống kê(tt) v Ý nghĩa: § Số tuyệt đối là cơ sở đầu tiên để tiến hành phân tích thống kê đồng thời là cơ sở để tính ra số tương đối và số bình quân. Ví dụ: với số liệu ở ví dụ trên (Tổng số tiền lương của DN thương mại X trong tháng 02/2019 là 255 triệu đồng, Số lao động của đơn vị là 15. 000 người): ta có thể tính được tiền lương bình quân cho 1 người lao động trong tháng 02. § Số tuyệt đối trong thống kê còn là căn cứ không thể thiếu được trong công việc xây dựng các chương trình dự án, kế hoạch phát triển KT-XH và tổ chức chỉ đạo thực hiện chúng.

4. 1. Chỉ tiêu mức độ khối lượng tuyệt đối trong thống kê(tt) v Ý nghĩa: • Thể hiện tình hình biến động vốn đầu tư • Thể hiện một cách cụ thể về qui mô, số lượng • Là cơ sở để tiến hành phân tích thống kê v Đặc điểm • Đơn vị tính là hiện vật tự nhiên, hiện vật qui đổi, giá trị • Phản ánh qui mô khối lượng kết quả hoạt động • Các số tuyệt đối có mối quan hệ mật thiết với nhau • Dùng làm cơ sở để xác định các chỉ tiêu chất lượng khác

4. 1. Chỉ tiêu mức độ khối lượng tuyệt đối trong thống kê (tt) v Đặc điểm q. Mỗi số tuyệt đối trong thống kê đều bao hàm một nội dung kinh tế cụ thể gắn liền với thời gian và địa điểm nhất định. § Ví dụ: Dân số Việt Nam lúc 0 h ngày 01/04/2018 là 76. 324. 753 người. • Các số tuyệt đối trong thống kê không phải là con số lựa chọn tùy tiện mà phải thông qua điều tra thực tế và tổng hợp các tài liệu điều tra mới có (PP Thu thập, tính toán)

4. 1. Chỉ tiêu mức độ khối lượng tuyệt đối trong thống kê (tt) 4. 1. 2 Đơn vị tính toán: -Đơn vị hiện vật: tự nhiên (người, cái, con, …), qui ước (kg, tạ, lít, …), qui đổi (1 kg thóc=2 kg bắp hạt), giá trị (tiền, …) tự nhiên (người, cái, con, …), qui ước (kg, tạ, lít, …) => Phản ánh chính xác theo giá trị sử dụng của sản phẩm nhưng không tổng hợp được các sản phẩm khác loại và có tính chất dịch vụ v Qui đổi (1 kg thóc=2 kg bắp hạt) § Ưu điểm: tổng hợp được các sản phẩm cùng loại nhưng có quy cách, phẩm chất khác nhau. § Nhược điểm: không thể tổng hợp được tất cả các loại sản phẩm khác tên; và phản ánh giá trị sử dụng là tương đương chứ không phải là giá trị thực tế § => Nó có tính trừu tượng, giảm tính cụ thể của đơn vị hiện vật tự nhiên.

4. 1. Chỉ tiêu mức độ khối lượng tuyệt đối trong thống kê (tt) - Đơn vị thời gian lao động: giờ công, ngày công, giây, phút, tháng, quí, năm - Các phương pháp tính chỉ tiêu tuyệt đối: + Phương pháp kiểm kê: + Phương pháp cân đối: VD: Doanh thu = giá bán * số lượng bán

4. 1. Chỉ tiêu mức độ khối lượng tuyệt đối trong thống kê (tt) 4. 1. 2. Đơn vị tính toán (tt): -Đơn vị hiện vật: v Giá trị (tiền, …) VN đồng, đô la, rúp… => Như vậy do giá cả hàng hóa luôn thay đổi nên đơn vị tiền tệ không có tính chất so sánh được qua thời gian. Vì vậy chúng ta thường sử dụng giá so sánh hay giá cố định. Tuy nhiên, hiện nay có xu hướng bỏ giá cố định và thay bằng việc tính chỉ số lạm phát giá cả để loại trừ ảnh hưởng của giá. -Đơn vị thời gian lao động: v Đơn vị thời gian hao phí sản xuất sản phẩm: giây, phút, ngày, tháng. . v Đo lường lao động hao phí: giờ - công, ngày - công

4. 1. Chỉ tiêu mức độ khối lượng tuyệt đối trong thống kê (tt) 4. 1. 2. Đơn vị tính toán: -Các phương pháp tính chỉ tiêu tuyệt đối: + Phương pháp kiểm kê: + Phương pháp cân đối: VD: doanh thu = giá bán * số lượng bán

4. 1. Chỉ tiêu mức độ khối lượng tuyệt đối trong thống kê (tt) 4. 1. 3. Các loại chỉ tiêu mức độ khối lượng tuyệt đối a- Chỉ tiêu mức độ khối lượng tuyệt đối thời điểm: § Khái niệm: Là loại số biểu hiện quy mô, khối lượng của hiện tượng nghiên cứu tại một thời điểm nhất định. -Ý nghĩa: Phản ánh qui mô, số lượng, thực trạng của hiện tượng tại một thời điểm xác định trong kỳ nghiên cứu. -Đặc điểm: Các số tuyệt đối thời điểm không cộng dồn được vì trước và sau thời điểm nghiên cứu trạng thái của hiện tượng có thể khác. ví dụ: Bảng cân đối kế toán

4. 1. Chỉ tiêu mức độ khối lượng tuyệt đối trong thống kê (tt) b- Chỉ tiêu mức độ khối lượng tuyệt đối thời kỳ § Khái niệm: Là biểu hiện quy mô, khối lượng của hiện tượng trong từng khoảng thời gian nhất định. Ví dụ: Doanh thu của công ty X quý I năm 2019 là 550 triệu đồng. -Ý nghĩa: Phản ánh qui mô số lượng, kết quả trong từng thời kỳ nhất định. § Đặc điểm: Nó hình thành do sự tích lũy về mặt lượng của hiện tượng qua thời gian khác nhau. Phản ánh quá trình tích lũy của hiện tượng, các số tuyệt đối cùng đơn vị có thể cộng trực tiếp được với nhau. Ví dụ: Chỉ tiêu 6 thánh đầu năm có thể cộng được với 6 tháng cuối năm. Ví dụ: Báo cáo kết quả HĐKD

4. 2. Chỉ tiêu mức độ khối lượng bình quân trong thống kê 4. 2. 1. Khái niệm, ý nghĩa, đặc điểm của chỉ tiêu - Khái niệm: Trong thống kê, các chỉ tiêu dùng để biểu hiện mức độ đại biểu theo một tiêu thức, có mặt lượng là số bình quân. Ví dụ: Điểm bình quân các môn học của từng học sinh - Ý nghĩa: + Biểu hiện mức độ điển hình, đặc điểm chung + So sánh các hiện tượng không cùng quy mô VD: Mức tiền lương bình quân 1 lao động của DN A cao hơn của DN B, có thể rút ra kết luận mức sống của người lao động của DN A cao hơn của DN B + Sự biến động của số bình quân theo thời gian có thể cho thấy xu hướng phát triển cơ bản của hiện tượng số lớn. + Đóng một vai trò quan trọng trong nhiều phương pháp phân tích thống kê

4. 2. Chỉ tiêu mức độ khối lượng bình quân trong thống kê 4. 2. 1. Khái niệm, ý nghĩa, đặc điểm của chỉ tiêu - Đặc điểm: + Chỉ được tính từ tiêu thức số lượng + Có tính chất tổng hợp và tính khái quát cao biểu hiện: § Chỉ bằng 1 trị số nhất định, số bình quân nêu lên mức độ chung nhất, phổ biến nhất, có tính đại biểu nhất của tiêu thức nghiên cứu, không kể đến sự chênh lệch thực tế giữa các đơn vị. § Số bình quân san bằng mọi chênh lệch giữa các đơn vị về trị số của tiêu thức nghiên cứu. § Là một số trừu tượng chứ không phải số cụ thể, nó đại diện chung cho cả tổng thể.

4. 2. Chỉ tiêu mức độ khối lượng bình quân trong thống kê 4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định a- Chỉ tiêu mức độ khối lượng bình quân trong một thời kỳ -Số bình quân cộng giản đơn: Phạm vi áp dụng: Tính cho tài liệu không phân tổ, ứng với mỗi lượng biến chỉ có 1 đơn vị tổng thể. Công thức: Số bình quân cộng = tổng lượng biến của tiêu thức/số đvị t thể hay:

4. 2. Chỉ tiêu mức độ khối lượng bình quân trong thống kê 4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định a- Chỉ tiêu mức độ khối lượng bình quân trong một thời kỳ Trong đó: + : Số bình quân. xi: mức độ của trị số i (i=1, 2, 3, …, n) n: tổng số đơn vị của tổng thể.

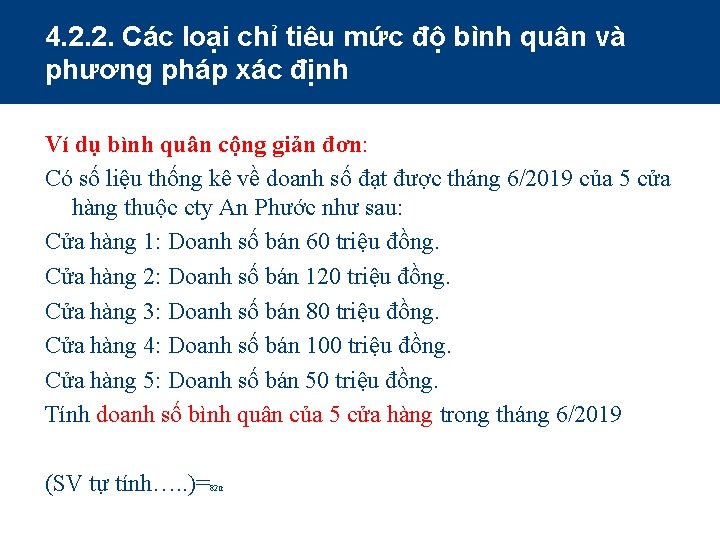
4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định Ví dụ bình quân cộng giản đơn: Có số liệu thống kê về doanh số đạt được tháng 6/2019 của 5 cửa hàng thuộc cty An Phước như sau: Cửa hàng 1: Doanh số bán 60 triệu đồng. Cửa hàng 2: Doanh số bán 120 triệu đồng. Cửa hàng 3: Doanh số bán 80 triệu đồng. Cửa hàng 4: Doanh số bán 100 triệu đồng. Cửa hàng 5: Doanh số bán 50 triệu đồng. Tính doanh số bình quân của 5 cửa hàng trong tháng 6/2019 (SV tự tính…. . )= 82 tr

4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định -Số bình quân cộng gia quyền: Phạm vi áp dụng: Tính cho tài liệu được phân tổ, nghĩa là khi mỗi lượng biến có nhiều đơn vị tổng thể(tần số). • Tích của lượng biến với tần số của lượng biến đó gọi là gia quyền(xifi). • Tần số trong trường hợp này còn được gọi là quyền số hay trọng số Công thức: hay: fi: là các tần số (i = 1, 2, . . . , n) xi: trị số i của các lượng biến (i=1, 2, 3, …, n) : Tổng trị số các lượng biến của tiêu thức

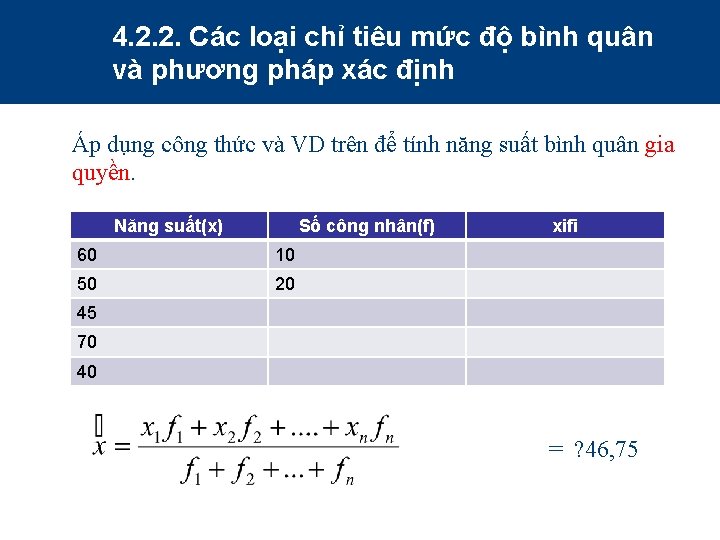
4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định +Trường hợp phân tổ đơn giản: VÍ DỤ: Khảo sát năng suất lao động/ngày của 100 công nhân doanh nghiệp X cho thấy: 10 công nhân có mức năng suất là 60 sp/ngày/người 20 công nhân có mức năng suất là 50 sp/ngày/người 25 công nhân có mức năng suất là 45 sp/ngày/người 5 công nhân có mức năng suất là 70 sp/ngày/người 40 công nhân có mức năng suất là 40 sp/ngày/người Gợi ý: Như vậy lượng biến 60 sp có tần số (f) là 10, lượng biến 50 sp có…… (SV tự tính…. ) VD khác bậc lương (xi); số Công nhân (fi)

4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định Áp dụng công thức và VD trên để tính năng suất bình quân gia quyền. Năng suất(x) Số công nhân(f) 60 10 50 20 xifi 45 70 40 = ? 46, 75

4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định +Trường hợp phân tổ có khoảng cách tổ khép kín: trị số x được thay bởi x’ của từng tổ với cách tính như sau: Trong đó và là giới hạn trên và dưới của mỗi tổ Công thức tính số bình quân được viết như sau: thay x bang x’ hay

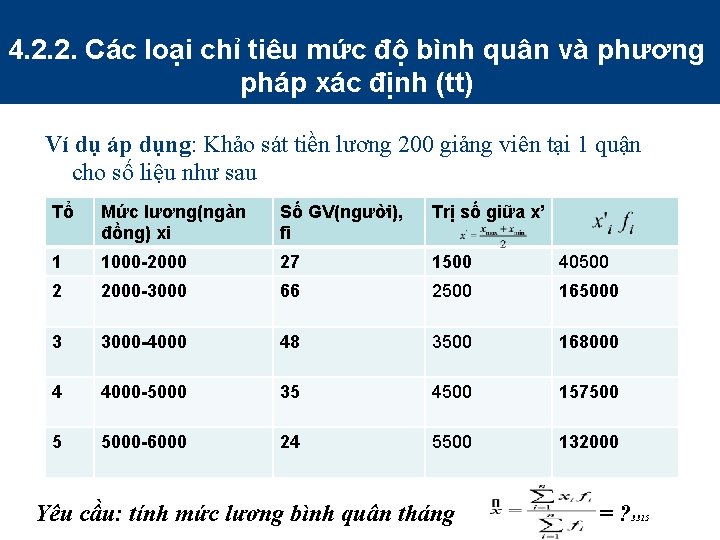
4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định (tt) Ví dụ áp dụng: Khảo sát tiền lương 200 giảng viên tại 1 quận cho số liệu như sau Tổ Mức lương(ngàn đồng) xi Số GV(người), fi Trị số giữa x’ 1 1000 -2000 27 1500 40500 2 2000 -3000 66 2500 165000 3 3000 -4000 48 3500 168000 4 4000 -5000 35 4500 157500 5 5000 -6000 24 5500 132000 Yêu cầu: tính mức lương bình quân tháng =? 3315

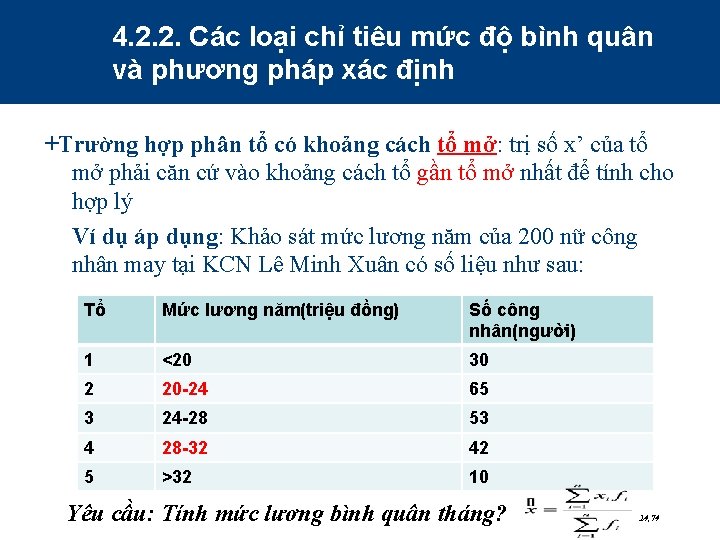
4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định +Trường hợp phân tổ có khoảng cách tổ mở: trị số x’ của tổ mở phải căn cứ vào khoảng cách tổ gần tổ mở nhất để tính cho hợp lý Ví dụ áp dụng: Khảo sát mức lương năm của 200 nữ công nhân may tại KCN Lê Minh Xuân có số liệu như sau: Tổ Mức lương năm(triệu đồng) Số công nhân(người) 1 <20 30 2 20 -24 65 3 24 -28 53 4 28 -32 42 5 >32 10 Yêu cầu: Tính mức lương bình quân tháng? 24, 74

4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định b- Chỉ tiêu mức độ khối lượng bình quân trong thời kỳ nghiên cứu dài: Là mức độ bình quân theo thời gian -Chỉ tiêu mức độ bình quân theo thời gian của dãy số mức độ khối lượng thời kỳ. Công thức: : mức độ bình quân của dãy số mức độ thời kỳ : tổng trị số của các mức độ thời kỳ n : tổng số hạng các mức độ trong dãy số

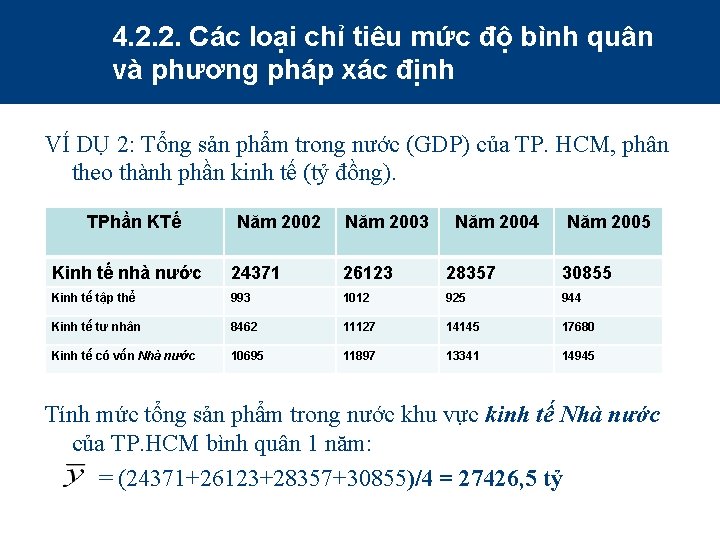
4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định VÍ DỤ 2: Tổng sản phẩm trong nước (GDP) của TP. HCM, phân theo thành phần kinh tế (tỷ đồng). TPhần KTế Năm 2002 Năm 2003 Năm 2004 Năm 2005 Kinh tế nhà nước 24371 26123 28357 30855 Kinh tế tập thể 993 1012 925 944 Kinh tế tư nhân 8462 11127 14145 17680 Kinh tế có vốn Nhà nước 10695 11897 13341 14945 Tính mức tổng sản phẩm trong nước khu vực kinh tế Nhà nước của TP. HCM bình quân 1 năm: = (24371+26123+28357+30855)/4 = 27426, 5 tỷ

4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định -Chỉ tiêu mức độ bình quân theo thời gian của dãy số mức độ khối lượng thời điểm: áp dụng khoảng cách bằng nhau Công thức:

4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định VÍ DỤ: (Các dãy số khối lượng tuyệt đối thời điểm có khoảng cách giữa các thời điểm bằng nhau). Số liệu lao động như sau: Chỉ tiêu Đơn vị Thời điểm 1/1 Thời điểm 1/2 Thời điểm 1/3 Thời điểm 1/4 Số lao động Người 200 218 222 KL vật tư B tồn kho kg 800 820 900 980 - Tính số lao động bình quân 1 tháng: áp dụng c thức trên số Lđbq = ? 213 người - Tính KL vật tư B tồn kho bình quân 1 tháng: số vật tư B bình quân = ? 870 kg

4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định -Chỉ tiêu mức độ bình quân theo thời gian của dãy số mức độ khối lượng thời điểm: áp dụng khoảng cách không bằng nhau Công thức: n å i i Yt Y= i=1 n åt i i =1 Ví dụ: (Tài liệu trang 37) Có tình hình công ty tháng 04/2003: Ngày 1 10 15 21 Số công nhân viên 4. 000 4. 050 4. 080 4. 060

4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định c- Chỉ tiêu mức độ tập trung, phổ biến nhất về lượng biến của hiện tượng nghiên cứu: Chỉ tiêu mốt - Khái niệm: Mốt là lượng biến của một tiêu thức được gặp nhiều nhất trong 1 tổng thể hay trong một dãy số phân phối. - Xác định mốt: +Đối với dãy số lượng biến rời rạc: Mốt là lượng biến có tần số lớn nhất. - Ý nghĩa: -Mốt có khả năng nêu lên mức độ điển hình, tập trung của hiện tượng. -Mốt được sử dụng rộng rãi trong thực tế, như dùng để điều tra thị hiếu tiêu dùng của người dân, mặt hảng sản phẩm được ưa chuộng nhất, mặt hảng sản phẩm được tiêu thụ nhiều nhất

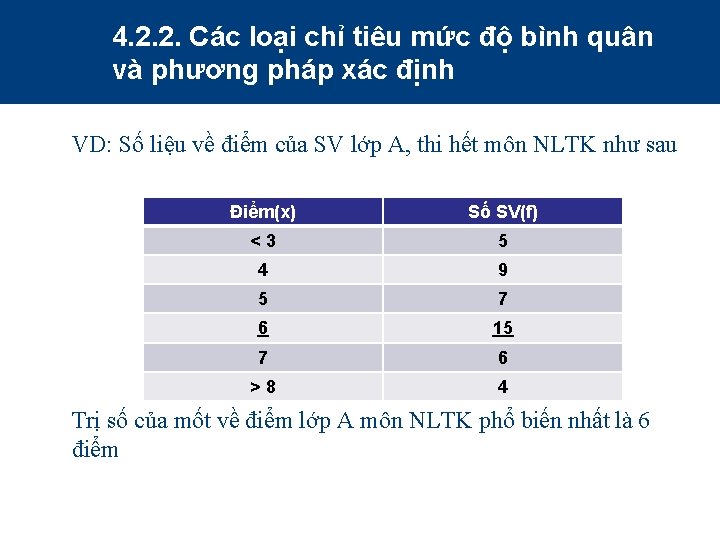
4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định VD: Số liệu về điểm của SV lớp A, thi hết môn NLTK như sau Điểm(x) Số SV(f) < 3 5 4 9 5 7 6 15 7 6 > 8 4 Trị số của mốt về điểm lớp A môn NLTK phổ biến nhất là 6 điểm

4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định +Đối với dãy số lượng biến có khoảng cách tổ: (đều nhau) • Xác định tổ có chứa mốt; là tổ có mật độ phân phối lớn nhất. Trong đó: • CT: Mật độ phân phối • CT: Tính trị số Mốt: : Mật đpp tổ chứa Mo f: tần số d: trị số khoảng cách tổ i: 1, 2, 3, . . , n XMo(min): g. hạn dưới Mo

4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định § § § XMo (min): Giới hạn dưới của tổ chứa Mo d. Mo: Trị số khoảng cách tổ chứa Mo FMo: Tần số của tổ chứa Mo FMo-1: Tần số của tổ đứng trước liền kề tổ chứa Mo FMo+1: Tần số của tổ đứng sau liền kề tổ chứa Mo

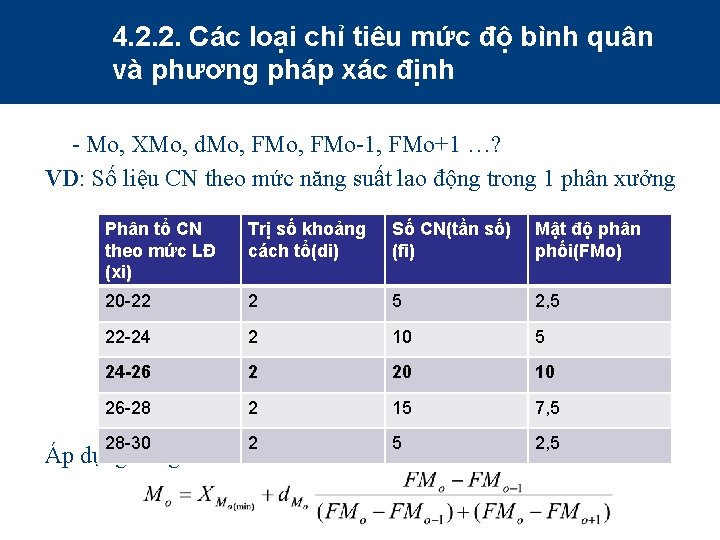
4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định - Mo, XMo, d. Mo, FMo-1, FMo+1 …? VD: Số liệu CN theo mức năng suất lao động trong 1 phân xưởng Phân tổ CN theo mức LĐ (xi) Trị số khoảng cách tổ(di) Số CN(tần số) (fi) Mật độ phân phối(FMo) 20 -22 2 5 2, 5 22 -24 2 10 5 24 -26 2 20 10 26 -28 2 15 7, 5 28 -30 2 5 Áp dụng công thức trên tính mốt: Mo = ? 2, 5 25, 33

4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định § Mo = 25, 33 nghĩa là số công nhân có mức năng suất lao động phổ biến nhất trong 1 phân xưởng

4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định d-Chỉ tiêu mức độ của đơn vị trung tâm: Số trung vị - KN: số trung vị là trị số lượng biến của đơn vị đứng ở giữa trong dãy phân phối lượng biến. -Đặc điểm: số trung vị phân chia dãy số lượng biến thành hai phần, mỗi phần có số đơn vị tổng thể bằng nhau. - Trình tự xác định trung vị: Ø Xác định vị trí của số trung vị: Xác định tổ lượng biến có chứa số trung vị Ø Xác định trị số gần đúng của số trung vị thep phương pháp phù hợp với trường hợp cụ thể sắp xếp thứ tự và phân tổ các lượng biến.

4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định d-Chỉ tiêu mức độ của đơn vị trung tâm: Số trung vị (tt) - Ý nghĩa số trung vị: Trong thống kê, nếu dữ liệu tương đồng nhau, sử dụng giá trị trung bình cho bạn kết quả phân tích chính xác nhất, nhưng nếu dữ liệu bị phân tán, có một vài giá trị mà chúng ta gọi là giá trị nhiễu, giá trị ngoại biên thì sử dụng số trung vị sẽ cho bạn kết quả chính xác nhất bởi số trung vị không phụ thuộc vào giá trị nhiễu. VD: Xác định xây dựng trạm đổ xe buýt, trạm điện thoại di động, cửa hàng, khu vui chơi, …

4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định Muốn đánh giá mức thu nhập bình quân của 5 hộ gia đình ở xóm Hót, giả sử 5 hộ gia đình đều có mức thu nhập là 10 triệu/1 tháng, tức là mức thu nhập của nhà ai cũng như nhau, vậy tính mức thu nhập bình quân của xóm Hót bằng giá trị trung bình không những quá dễ mà còn khá chính xác nữa: (10 + 10) / 5 = 10 triệu/tháng. § Nhưng trong 5 hộ gia đình này có 1 hộ gia đình là nhà của anh A rất giàu có, mức thu nhập khủng 1 tỉ/tháng, 4 hộ còn lại chỉ có 10 triệu/tháng. Oke, vậy khi tính mức thu nhập bình quân của xóm Hót, nếu chúng ta sử dụng giá trị trung bình để tính: (10 triệu + 1 tỉ) / 5 = 208 triệu/tháng. § quá sai, chỉ có 1 nhà giàu có thôi, 4 nhà còn lại nghèo lắm, nhưng nếu chúng ta sử dụng số trung vị để tính mức thu nhập bình quân, tức là chọn lấy số ở giữa nhất = 10 triệu/tháng.

4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định d-Chỉ tiêu mức độ của đơn vị trung tâm: Số trung vị (tt) - Trình tự xác định trung vị: Ø Xác định vị trí của số trung vị: Xác định tổ lượng biến có chứa số trung vị Ø Xác định trị số gần đúng của số trung vị (Trị số trung vị ) theo phương pháp phù hợp với trường hợp cụ thể sắp xếp thứ tự và phân tổ các lượng biến. + Đối với dãy số lượng biến rời rạc (Không có khoảng cách tổ, theo trình tự từ nhỏ đến lớn) • Trường hợp số đơn vị tổng thể lẻ (n=2 m+1) ün: số đơn vị tổng thể Số trung vị sẽ là lượng biến ở đơn vị thứ: m+1 Ký hiệu số trung vị: Me =Xm+1

4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định VD Trường hợp số đơn vị tổng thể lẻ : mức năng suất lao động của 5 CN trong 1 tổ: 20, 22, 25, 27, 29 tạ/người vậy số trung vị là mức năng suất lao động của người thứ 3 : 25 tạ/người. • Trường hợp số đơn vị tổng thể chẳn(n=2 m) Số trung vị sẽ là lượng biến ở vị trí giữa biến m và m+1 Me=(Xm+Xm+1)/2 VD: năng suất lao động của 6 CN trong 1 tổ: 20, 22, 25, 27, 29, 30 tạ/người Xác định vị trí của số trung vị: n là 6, m =3 : Tức là số trung vị ở giữa vị trí thứ 3 và thứ 4 vậy Xác định trị số gần đúng của số trung vị là: Me=(25+27)/2=26 tạ/người

4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định §

4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định § § § +Đối với dãy số lượng biến có khoảng cách tổ • Me, XMe(min), h. Me, S(Me-1), f. Me, …. ? XMe (min): Giới hạn dưới của tổ chứa Me h. Me: Trị số khoảng cách tổ chứa Me FMe: Tần số của tổ chứa Me S(Me-1): Tần số tích lũy của tổ đứng trước f. Me: Tần số có chứa số trung vị Me : Tổng các tần số

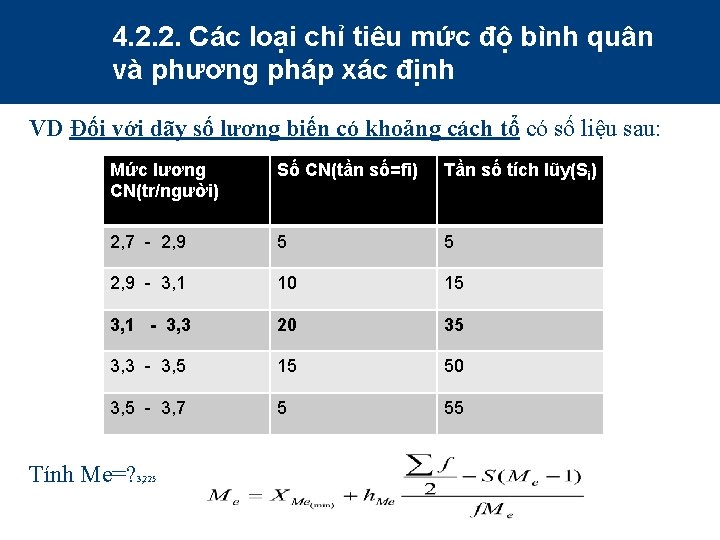
4. 2. 2. Các loại chỉ tiêu mức độ bình quân và phương pháp xác định VD Đối với dãy số lượng biến có khoảng cách tổ có số liệu sau: Mức lương CN(tr/người) Số CN(tần số=fi) Tần số tích lũy(Si) 2, 7 - 2, 9 5 5 2, 9 - 3, 1 10 15 3, 1 - 3, 3 20 35 3, 3 - 3, 5 15 50 3, 5 - 3, 7 5 55 Tính Me=? 3, 225

Ghi chú: § Lượng biến (xi): là các trị số nói lên biểu hiện cụ thể của tiêu thức số lượng § Tần số (fi): là số lần xuất hiện của các lượng biến § Tần suất (di): tỉ trọng số đơn vị của từng tổ trong tổng thể, tính bằng đơn vị lần hay % di =f 1/ ∑fi Ý nghĩa: Cho biết số đơn vị mỗi tổ chiếm bao nhiêu % trong toàn bộ tổng thể. § Tần số tích lũy (Si): là tần số cộng dồn từ trên xuống § Mật độ phân phối :

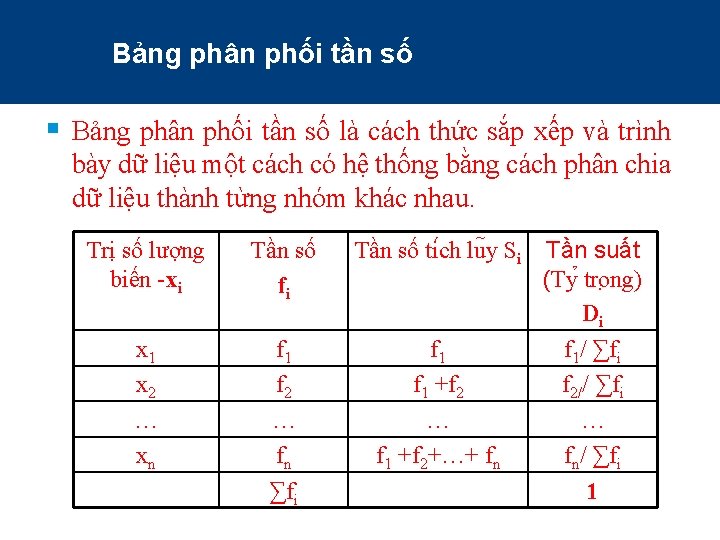
Bảng phân phối tần số § Bảng phân phối tần số là cách thức sắp xếp và trình bày dữ liệu một cách có hệ thống bằng cách phân chia dữ liệu thành từng nhóm khác nhau. Trị số lượng biến -xi Tần số fi Tần số ti ch lu y Si x 1 x 2 … xn f 1 f 2 … fn ∑fi f 1 +f 2 … f 1 +f 2+…+ fn Tần suất (Ty tro ng) Di f 1/ ∑fi f 2// ∑fi … fn/ ∑fi 1

4. 3. Chỉ tiêu mức độ khối lượng tăng - giảm 4. 3. 1 Chỉ tiêu mức độ khối lượng tăng - giảm tuyệt đối 4. 3. 1. 1 Chỉ tiêu mức độ khối lượng tuyệt đối tăng, giảm giữa 2 kỳ nghiên cứu: Là mức độ chênh lệch về khối lượng giữa kỳ báo cáo so với kỳ gốc biểu hiện bằng số tuyệt đối. + CT: Trong đó: y 1: mức độ KL tuyệt đối kỳ báo cáo yo: mức độ KL tuyệt đối kỳ gốc mức độ KL tuyệt đối tăng, giảm

4. 3. Chỉ tiêu mức độ khối lượng tăng - giảm 4. 3. 1. 1 Chỉ tiêu mức độ khối lượng tăng - giảm tuyệt đối +VD: Tổng sản phẩm trong nước (GDP) của TP HCM 2019 (năm nghiên cứu) là: 89. 000 tỷ, năm 2018 (năm gốc) là: 60. 000 tỷ. Tính mức độ tăng giảm tổng sản phẩm quốc nội qua 2 năm 2019 so với 2018: 89. 000 tỷ - 60. 000 tỷ = 29. 000 tỷ Vậy mức tăng trưởng GDP TP. HCM 2019 so với 2018 là: 29. 000 tỷ

4. 3. Chỉ tiêu mức độ khối lượng tăng - giảm 4. 3. 1. 2 Chỉ tiêu mức độ khối lượng tuyệt đối tăng, giảm trong kỳ nghiên cứu dài: 4. 3. 1. 2. 1 Chỉ tiêu mức độ KL tuyệt đối tăng, giảm liên hoàn: là mức độ khối lượng tăng giảm theo gốc so sánh liên hoàn (so sánh mức độ giữa 2 kỳ liền nhau) CT: trong đó: yi, yi-1…. ?

4. 3. Chỉ tiêu mức độ khối lượng tăng - giảm 4. 3. 1. 2 Chỉ tiêu mức độ khối lượng tuyệt đối tăng, giảm trong kỳ nghiên cứu dài: 4. 3. 1. 2. 1 Chỉ tiêu mức độ KL tuyệt đối tăng, giảm liên hoàn: Trong đó: : mức độ KL tuyệt đối kỳ nghiên cứu : mức độ KL tuyệt đối đứng trước liền kề với kỳ nghiên cứu (gốc so sánh liên hoàn) : mức độ KL tuyệt đối tăng, giảm

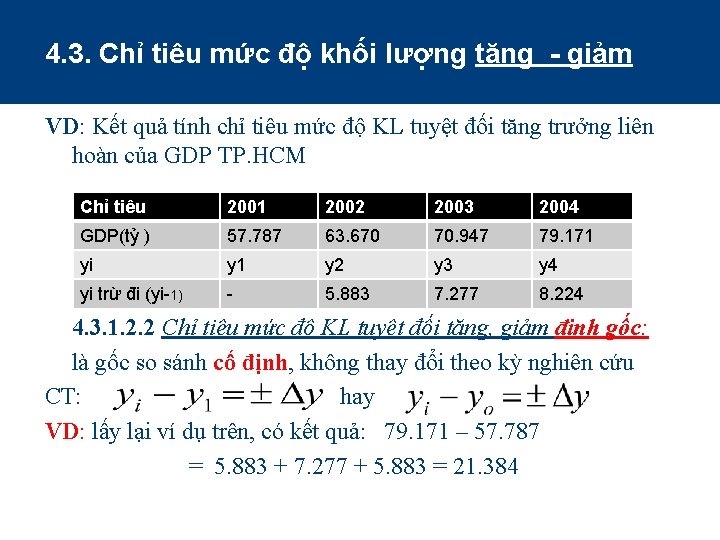
4. 3. Chỉ tiêu mức độ khối lượng tăng - giảm VD: Kết quả tính chỉ tiêu mức độ KL tuyệt đối tăng trưởng liên hoàn của GDP TP. HCM Chỉ tiêu 2001 2002 2003 2004 GDP(tỷ ) 57. 787 63. 670 70. 947 79. 171 yi y 1 y 2 y 3 y 4 yi trừ đi (yi-1) - 5. 883 7. 277 8. 224 4. 3. 1. 2. 2 Chỉ tiêu mức độ KL tuyệt đối tăng, giảm định gốc: là gốc so sánh cố định, không thay đổi theo kỳ nghiên cứu CT: hay VD: lấy lại ví dụ trên, có kết quả: 79. 171 – 57. 787 = 5. 883 + 7. 277 + 5. 883 = 21. 384

4. 3. 2. Chỉ tiêu mức độ khối lượng tăng, giảm bình quân 4. 3. 1. 2. 1 Chỉ tiêu mức độ khối lượng tăng giảm bình quân Là mức bình quân của các mức độ KL tuyệt đối tăng giảm liên hoàn (từng kỳ) của các dãy mức độ KL tuyệt đối liên hoàn (từng kỳ). CT: hay trong đó: m, n, y 1…? VD: theo số liệu và kết quả của ví dụ trên ta có: = (5883+7277+8224) / 3= 7. 128 tỷ =21. 384/3

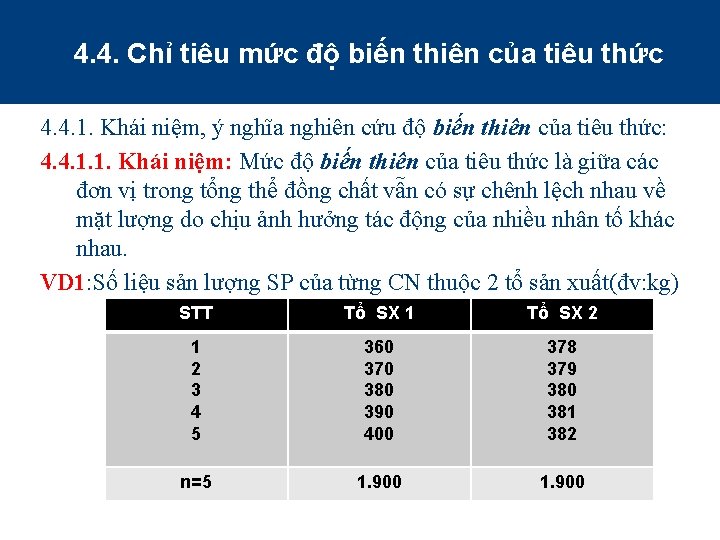
4. 4. Chỉ tiêu mức độ biến thiên của tiêu thức 4. 4. 1. Khái niệm, ý nghĩa nghiên cứu độ biến thiên của tiêu thức: 4. 4. 1. 1. Khái niệm: Mức độ biến thiên của tiêu thức là giữa các đơn vị trong tổng thể đồng chất vẫn có sự chênh lệch nhau về mặt lượng do chịu ảnh hưởng tác động của nhiều nhân tố khác nhau. VD 1: Số liệu sản lượng SP của từng CN thuộc 2 tổ sản xuất(đv: kg) STT Tổ SX 1 Tổ SX 2 1 2 3 4 5 360 370 380 390 400 378 379 380 381 382 n=5 1. 900

4. 4. Chỉ tiêu mức độ biến thiên của tiêu thức Áp dụng phương pháp số học giản đơn: +Tổ 1: = (360+370+380+390+400)/5=380 kg +Tồ 2: = (378+379+380+381+382)/5=380 kg Qua ví dụ trên cho thấy được mức độ biến thiên của tiêu thức. Nhận xét sự biến thiên của sản lượng SP: Tổ 1: 10 -40 kg……. bquân: 10 -20 kg Tổ 2: 1 -4 kg………. . bquân: 1 -2 kg

4. 4. Chỉ tiêu mức độ biến thiên của tiêu thức 4. 4. 1. 2. Ý nghĩa nghiên cứu mức độ biến thiên của tiêu thức: + Hạn chế của số bình quân chỉ nêu lên đặc điểm điển hình, tiêu biểu nhất của tổng thể nghiên cứu, không chú ý đến mức độ chênh lệch thực tế về lượng giữa các đơn vị cá biệt trong tổng thể hiện tượng nghiên cứu. + Nhận thức, đánh giá được tính chất đồng đều của việc phân phối lượng biến giữa các đơn vị bộ phận trong tổng thể hiện tượng nghiên cứu. + Nhận thấy được đặc trưng kết cấu của tổng thể + Được áp dụng nhiều trong công tác đánh giá chất lượng của kế hoạch.

4. 4. Chỉ tiêu mức độ biến thiên của tiêu thức 4. 4. 2. Các chỉ tiêu biểu hiện độ biến thiên của tiêu thức: 4. 4. 2. 1. Chỉ tiêu khoảng biến thiên (R) Là mức độ chênh lệch giữa lượng biến lớn nhất (Xmax) và lượng biến nhỏ nhất (Xmin) của tiêu thức nghiên cứu. R = Xmax – Xmin + Áp dụng tính theo ví dụ 1 ta có: R 1 = 400 – 360 = 40 kg R 2 = 382 - 378 = 4 kg à R 1 > R 2 + Nhận xét: . Sự biến động về số lượng SP của tổ 2 ít hơn tổ 1. Trình độ tay nghề CN tổ 2 đều hơn tổ 1

4. 4. Chỉ tiêu mức độ biến thiên của tiêu thức 4. 4. 2. 2. Chỉ tiêu độ lệch tuyệt đối bình quân ( ) Là số bình quân tính theo phương pháp số học của các độ lệch tuyệt đối giữa các lượng biến(xi) với số bình quân tính theo phương pháp số học từ các lượng biến đó( ) + C. Thức: . Trường hợp giản đơn, không có quyền số (1): . Trường hợp gia quyền, có quyền số (2): , n, fi, ……?

4. 4. Chỉ tiêu mức độ biến thiên của tiêu thức 4. 4. 2. 2. Chỉ tiêu độ lệch tuyệt đối bình quân ( ) n: Số đơn vị trong tổng thể fi: Tần số của lượng biến (số đơn vị của từng lượng biến) : Độ lệch tuyệt đối giữa các lượng biến với số bình quân : Độ lệch tuyệt đối bình quân : Số bình quân

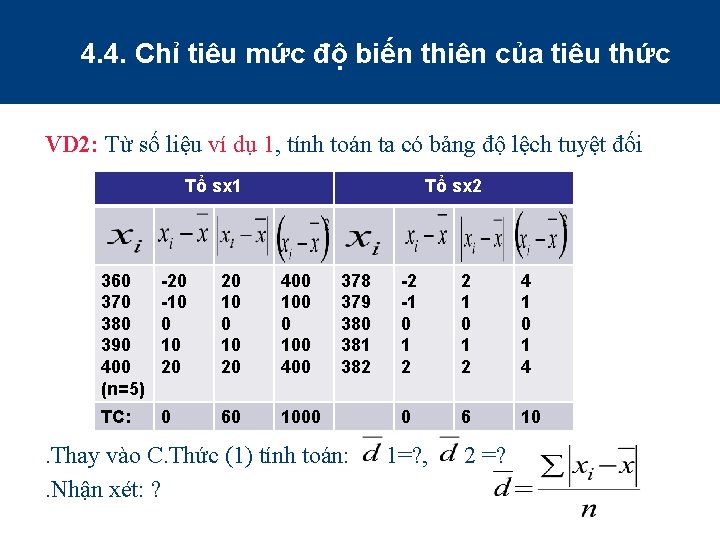
4. 4. Chỉ tiêu mức độ biến thiên của tiêu thức VD 2: Từ số liệu ví dụ 1, tính toán ta có bảng độ lệch tuyệt đối Tổ sx 1 Tổ sx 2 360 370 380 390 400 (n=5) -20 -10 0 10 20 20 10 20 400 100 400 TC: 0 60 1000 378 379 380 381 382 -2 -1 0 1 2 2 1 0 1 2 4 1 0 1 4 0 6 10 . Thay vào C. Thức (1) tính toán: 1=? , 2 =? . Nhận xét: ?

4. 4. Chỉ tiêu mức độ biến thiên của tiêu thức VD 2: Từ số liệu ví dụ 1, tính toán ta có bảng độ lệch tuyệt đối . Thay vào C. Thức (1) tính toán: 1=? , 2 =? . Nhận xét: Chỉ tiêu mức độ tuyệt đối phản ảnh mức độ biến thiên của tiêu thức bình quân được chặt chẽ hơn Chỉ tiêu khoảng biến thiên (R)

4. 4. Chỉ tiêu mức độ biến thiên của tiêu thức 4. 4. 2. 3. Chỉ tiêu phương sai: ( ) + Là chỉ tiêu bình phương các độ lệch giữa các lượng biến (xi) với số bình quân từ các lượng biến đó( ): + Cthức: . Trường hợp đơn giản, không có quyền số(1): . Trường hợp gia quyền, có quyền số(2): + Áp dụng: Từ số liệu ví dụ 2, C. thức(1)ta có kết quả: , =? + Nhận xét: ……?

4. 4. Chỉ tiêu mức độ biến thiên của tiêu thức 4. 4. 2. 3. Chỉ tiêu phương sai: ( ) + Áp dụng: Từ số liệu ví dụ 2, C. thức (1) ta có kết quả: , =? + Nhận xét: Chỉ tiêu phương sai: ( ) là kết quả tính được tạo nên mức độ chênh lệch quá lớn giữa các tổ nên có nhiều khó khăn khi đưa ra nhận xét chính xác.

4. 4. Chỉ tiêu mức độ biến thiên của tiêu thức 4. 4. 2. 4. Chỉ tiêu độ lệch chuẩn ( ) + Còn gọi là chỉ tiêu độ lệch quân phương hay chỉ tiêu sai lệch điển hình, là căn bậc 2 của phương sai. + C. Thức: . Trường hợp đơn giản, không có quyền số(1): . Trường hợp gia quyền, có quyền số(2): + Áp dụng: Từ số liệu ví dụ 2, C. thức(1)ta có kết quả: , = ? + Nhận xét: ……?

4. 4. Chỉ tiêu mức độ biến thiên của tiêu thức 4. 4. 2. 4. Chỉ tiêu độ lệch chuẩn ( ) + Áp dụng: Từ số liệu ví dụ 2, C. thức (1) ta có kết quả: > + Nhận xét: Chỉ tiêu độ lệch chuẩn là chỉ tiêu biểu hiện mức độ biến thiên của tiêu thức hoàn thiện nhất, đưa ra nhận xét chính xác hơn vì nó khắc phục những hạn chế của 3 chỉ tiêu trên.

4. 4. Chỉ tiêu mức độ biến thiên của tiêu thức 4. 4. 2. 5 Chỉ tiêu hệ số biến thiên (v): + Là chỉ tiêu so sánh độ biến thiên tiêu thức của các hiện tượng KT-XH cùng loại hoặc khác loại có mức độ bình quân không bằng nhau + C. thức: . Trường hợp tính theo chỉ tiêu mức độ lệch tuyệt đối bình quân: . Trường hợp tính theo chỉ tiêu độ lệch tiêu chuẩn: + Áp dụng: Từ số liệu ví dụ 2, tính toán ta có kết quả: , = ? + Nhận xét: cái nào lớn, nhỏ = ?