An Improved Liar Game Strategy From a Deterministic

An Improved Liar Game Strategy From a Deterministic Random Walk Robert Ellis February 22 nd, 2010 Peled Workshop, UIC Joint work with Joshua Cooper, University of South Carolina

Outline § Diffusion processes on Z – Simple random walk (linear machine) – Liar machine – Pathological liar game, alternating question strategy § Improved pathological liar game bound – Reduction to liar machine – Discrepancy analysis of liar machine versus linear machine § Concluding remarks 2

3 Linear Machine on Z 11 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9

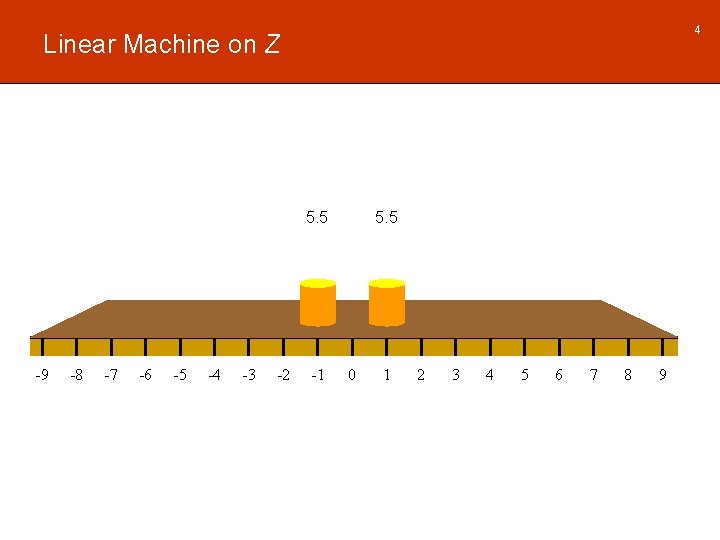
4 Linear Machine on Z 5. 5 -9 -8 -7 -6 -5 -4 -3 -2 -1 5. 5 0 1 2 3 4 5 6 7 8 9

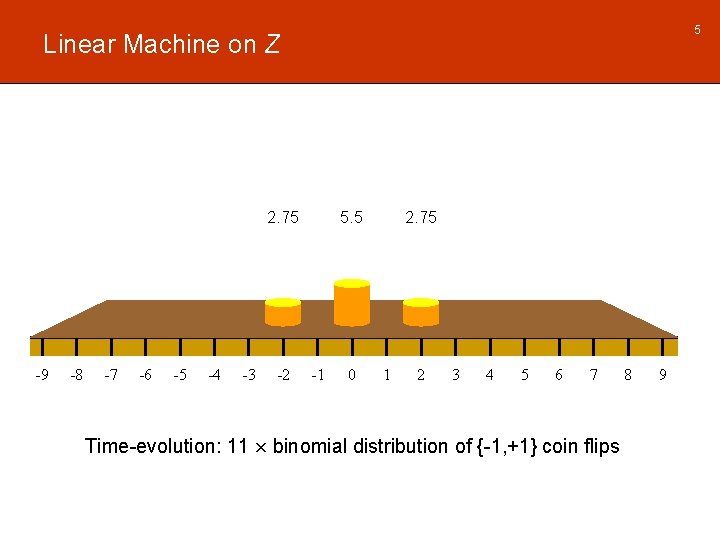
5 Linear Machine on Z 2. 75 -9 -8 -7 -6 -5 -4 -3 -2 5. 5 -1 0 2. 75 1 2 3 4 5 6 7 Time-evolution: 11 £ binomial distribution of {-1, +1} coin flips 8 9

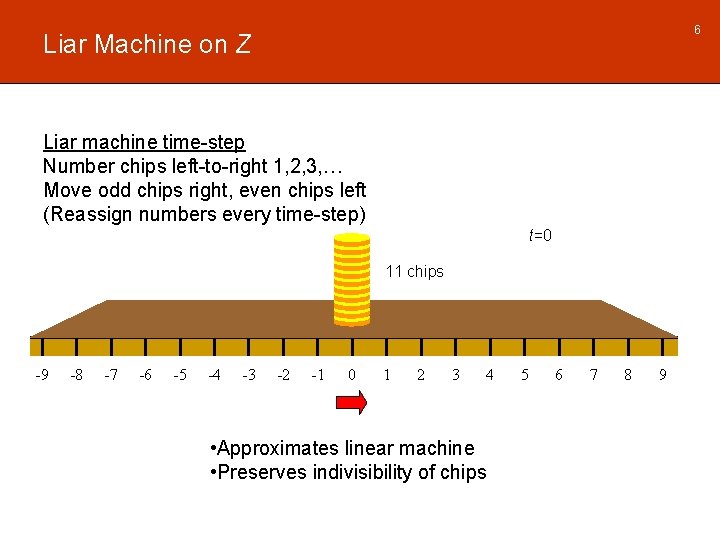
6 Liar Machine on Z Liar machine time-step Number chips left-to-right 1, 2, 3, … Move odd chips right, even chips left (Reassign numbers every time-step) t=0 11 chips -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 • Approximates linear machine • Preserves indivisibility of chips 5 6 7 8 9

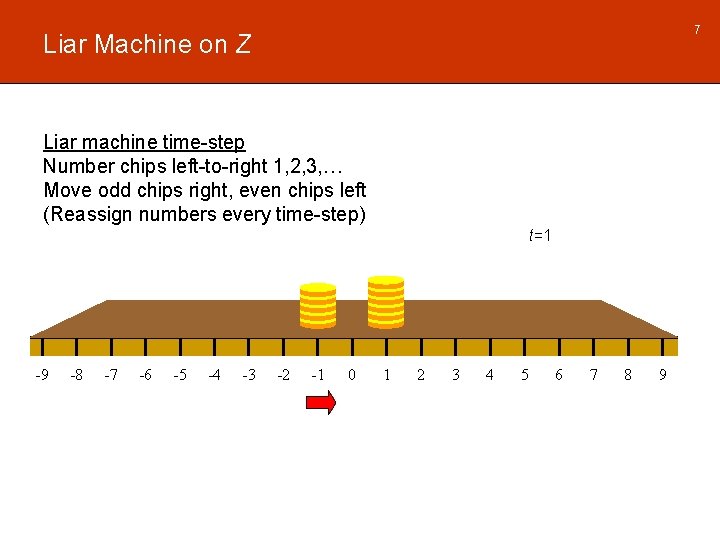
7 Liar Machine on Z Liar machine time-step Number chips left-to-right 1, 2, 3, … Move odd chips right, even chips left (Reassign numbers every time-step) t=1 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9

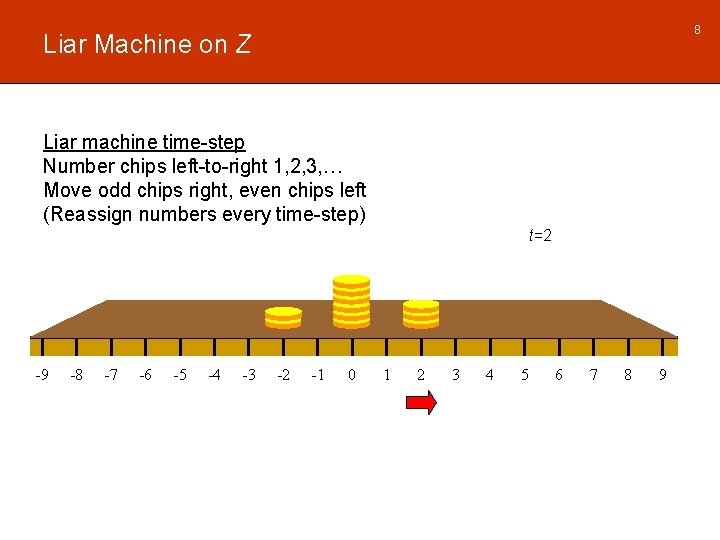
8 Liar Machine on Z Liar machine time-step Number chips left-to-right 1, 2, 3, … Move odd chips right, even chips left (Reassign numbers every time-step) t=2 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9

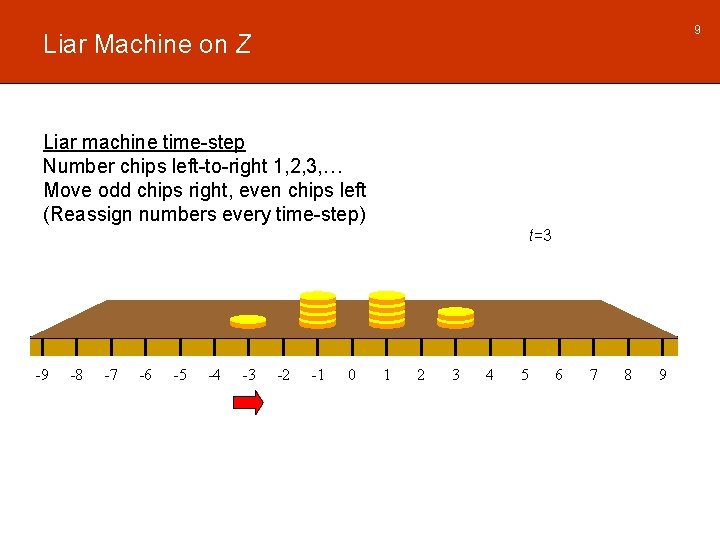
9 Liar Machine on Z Liar machine time-step Number chips left-to-right 1, 2, 3, … Move odd chips right, even chips left (Reassign numbers every time-step) t=3 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9

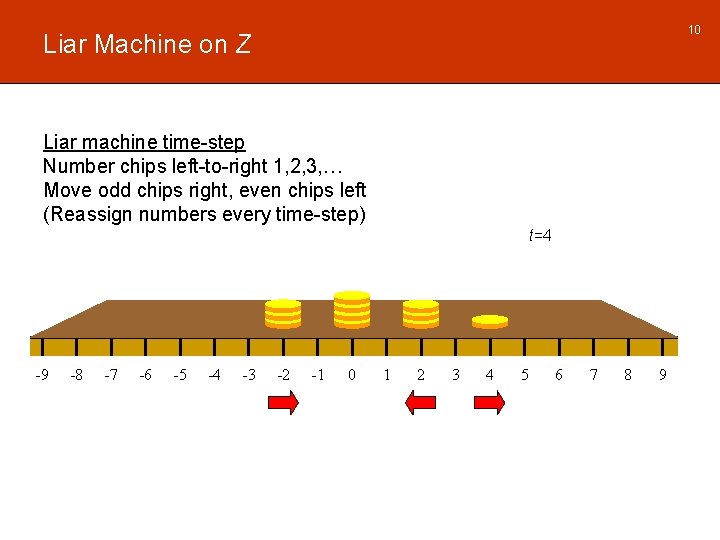
10 Liar Machine on Z Liar machine time-step Number chips left-to-right 1, 2, 3, … Move odd chips right, even chips left (Reassign numbers every time-step) t=4 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9

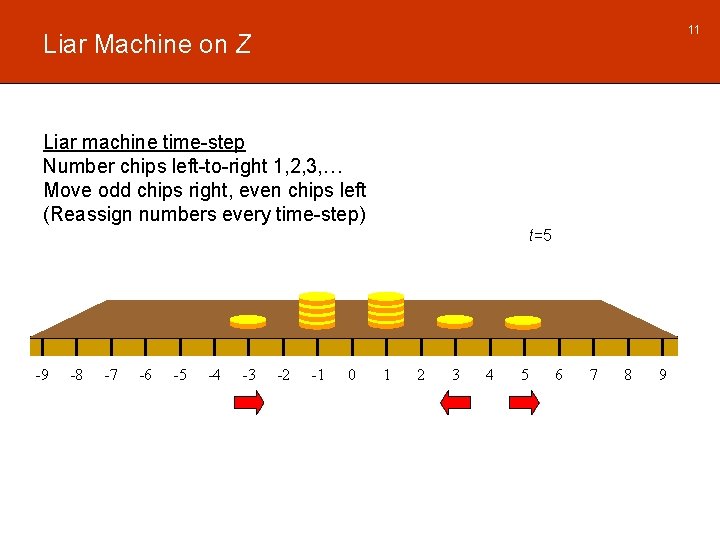
11 Liar Machine on Z Liar machine time-step Number chips left-to-right 1, 2, 3, … Move odd chips right, even chips left (Reassign numbers every time-step) t=5 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9

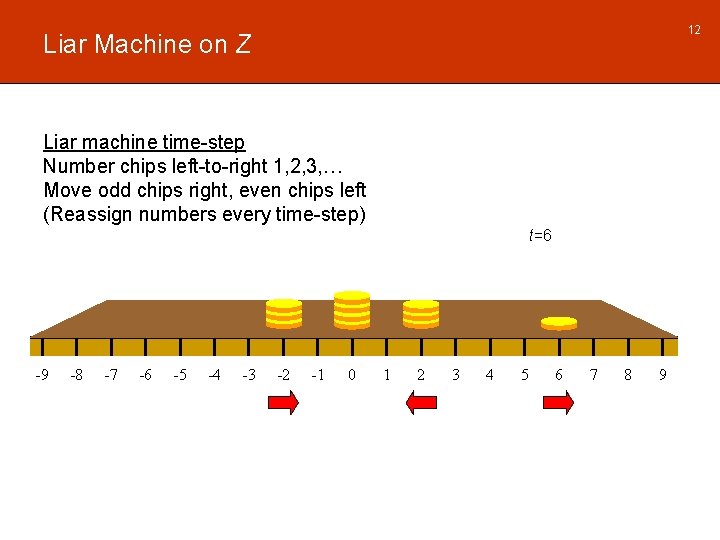
12 Liar Machine on Z Liar machine time-step Number chips left-to-right 1, 2, 3, … Move odd chips right, even chips left (Reassign numbers every time-step) t=6 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9

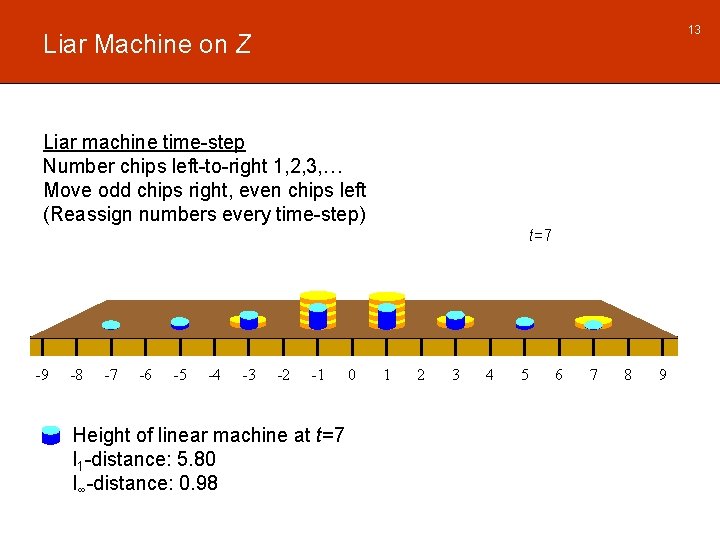
13 Liar Machine on Z Liar machine time-step Number chips left-to-right 1, 2, 3, … Move odd chips right, even chips left (Reassign numbers every time-step) t=7 -9 -8 -7 -6 -5 -4 -3 -2 -1 Height of linear machine at t=7 l 1 -distance: 5. 80 l∞-distance: 0. 98 0 1 2 3 4 5 6 7 8 9

Discrepancy for Two Discretizations Liar machine: round-offs spatially balanced Rotor-router model/Propp machine: round-offs temporally balanced The liar machine has poorer discrepancy… but provides bounds to a certain liar game. 14

Proof of Liar Machine Pointwise Discrepancy 15

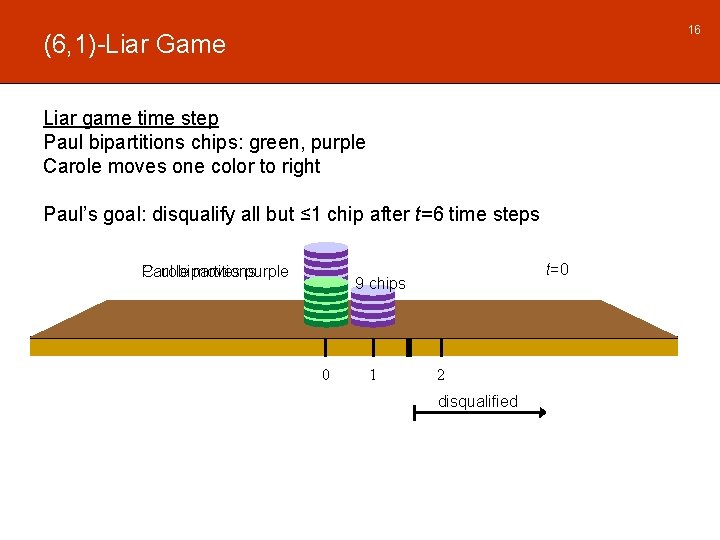
16 (6, 1)-Liar Game Liar game time step Paul bipartitions chips: green, purple Carole moves one color to right Paul’s goal: disqualify all but ≤ 1 chip after t=6 time steps Paul bipartitions Carole moves purple t=0 9 chips 0 1 2 disqualified

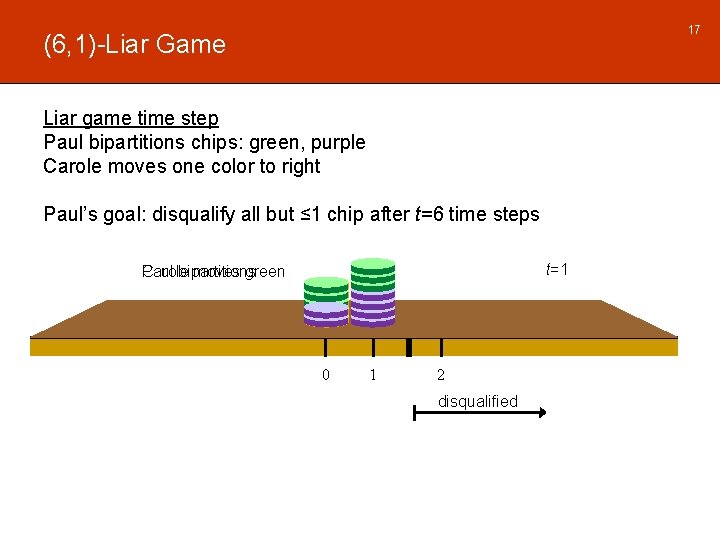
17 (6, 1)-Liar Game Liar game time step Paul bipartitions chips: green, purple Carole moves one color to right Paul’s goal: disqualify all but ≤ 1 chip after t=6 time steps t=1 Paul bipartitions Carole moves green 0 1 2 disqualified

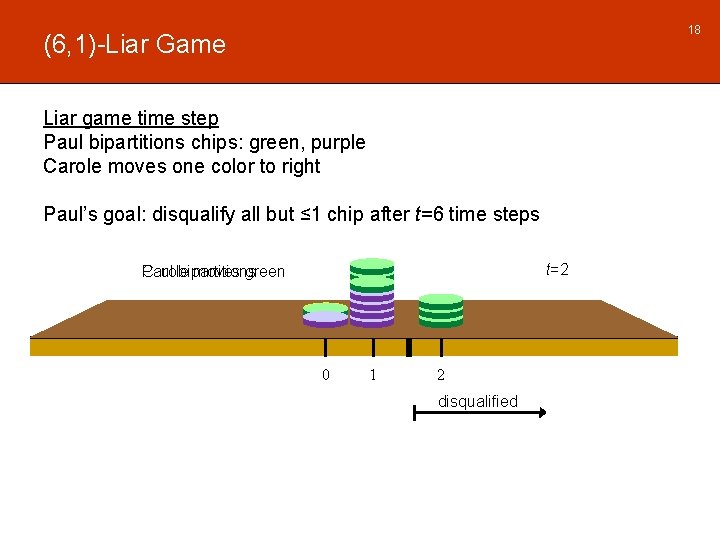
18 (6, 1)-Liar Game Liar game time step Paul bipartitions chips: green, purple Carole moves one color to right Paul’s goal: disqualify all but ≤ 1 chip after t=6 time steps t=2 Paul bipartitions Carole moves green 0 1 2 disqualified

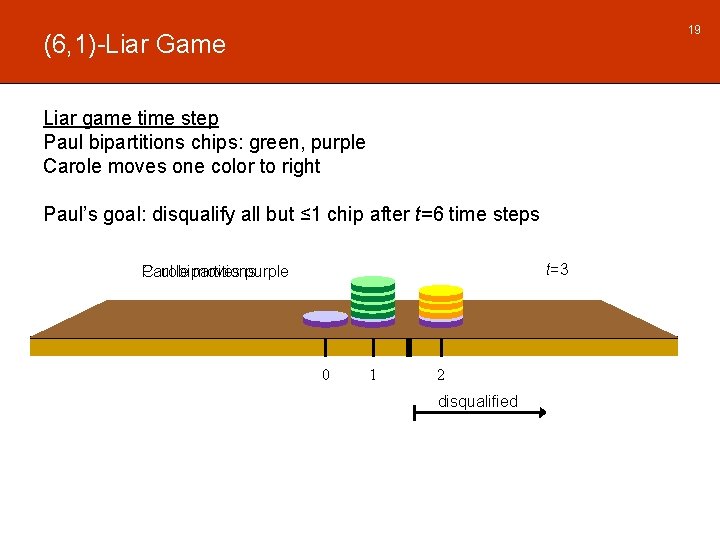
19 (6, 1)-Liar Game Liar game time step Paul bipartitions chips: green, purple Carole moves one color to right Paul’s goal: disqualify all but ≤ 1 chip after t=6 time steps t=3 Paul bipartitions Carole moves purple 0 1 2 disqualified

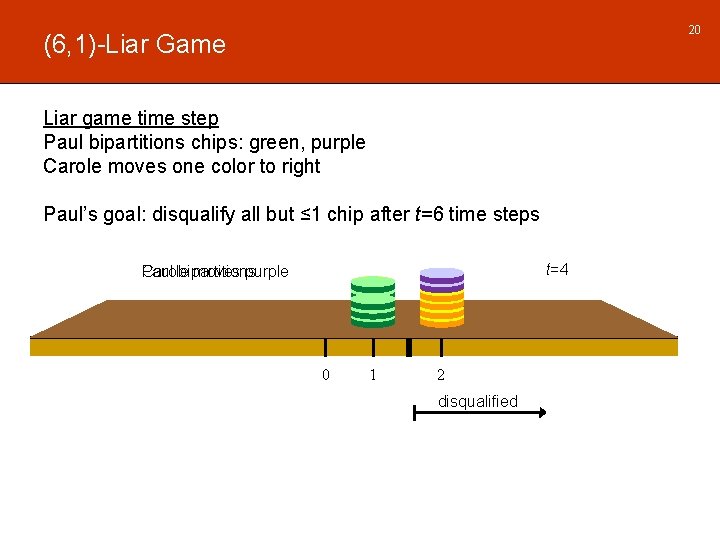
20 (6, 1)-Liar Game Liar game time step Paul bipartitions chips: green, purple Carole moves one color to right Paul’s goal: disqualify all but ≤ 1 chip after t=6 time steps t=4 Carole Paul bipartitions moves purple 0 1 2 disqualified

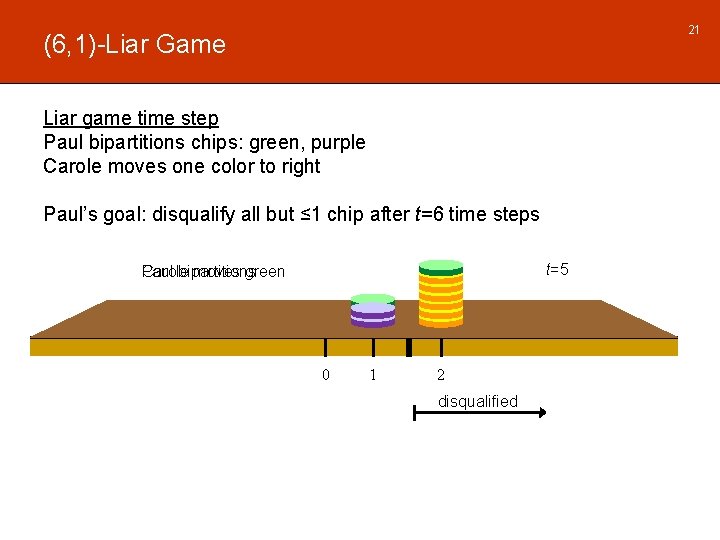
21 (6, 1)-Liar Game Liar game time step Paul bipartitions chips: green, purple Carole moves one color to right Paul’s goal: disqualify all but ≤ 1 chip after t=6 time steps t=5 Carole Paul bipartitions moves green 0 1 2 disqualified

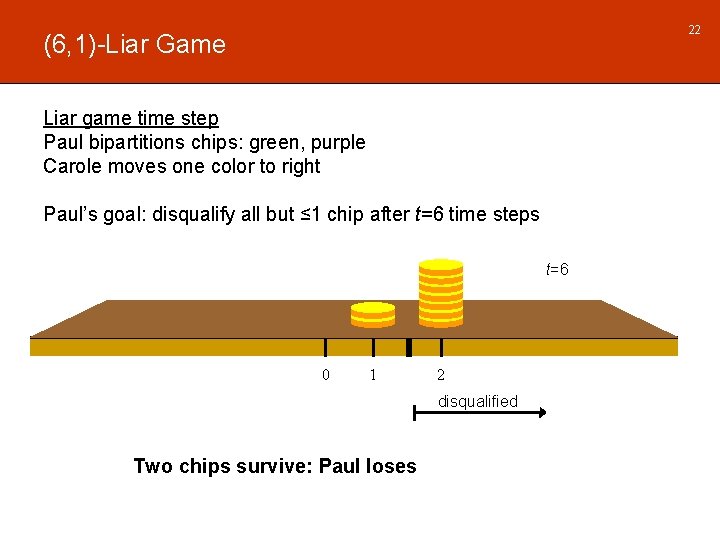
22 (6, 1)-Liar Game Liar game time step Paul bipartitions chips: green, purple Carole moves one color to right Paul’s goal: disqualify all but ≤ 1 chip after t=6 time steps t=6 0 1 2 disqualified Two chips survive: Paul loses

A Liar Game Strategy for Carole § Weight function for n rounds left; xi = #chips with i lies: § Lemma (Berlekamp) § Refined sphere bound Liar game. Carole keeps half of weight every step. Initial weight > 2 n ) Final weight >1 ) Carole wins. Pathological variant. Carole reduces half of weight every step. Initial weight < 2 n ) Final weight <1 ) Carole wins. 23

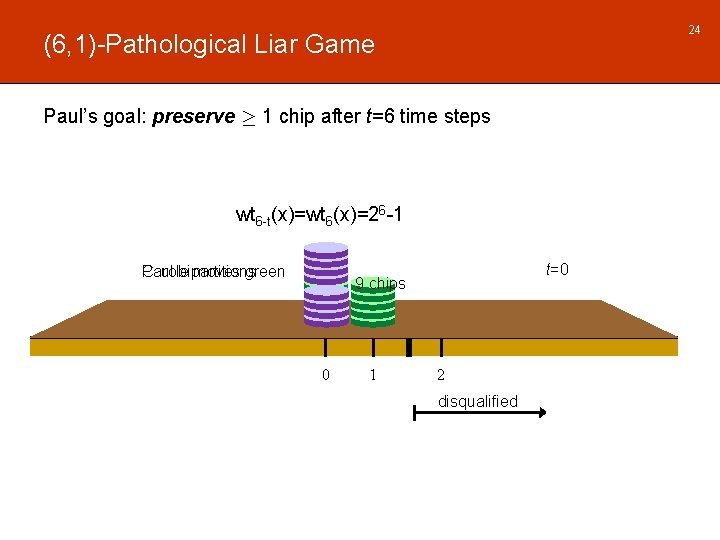
24 (6, 1)-Pathological Liar Game Paul’s goal: preserve ¸ 1 chip after t=6 time steps wt 6 -t(x)=wt 6(x)=26 -1 Paul bipartitions Carole moves green t=0 9 chips 0 1 2 disqualified

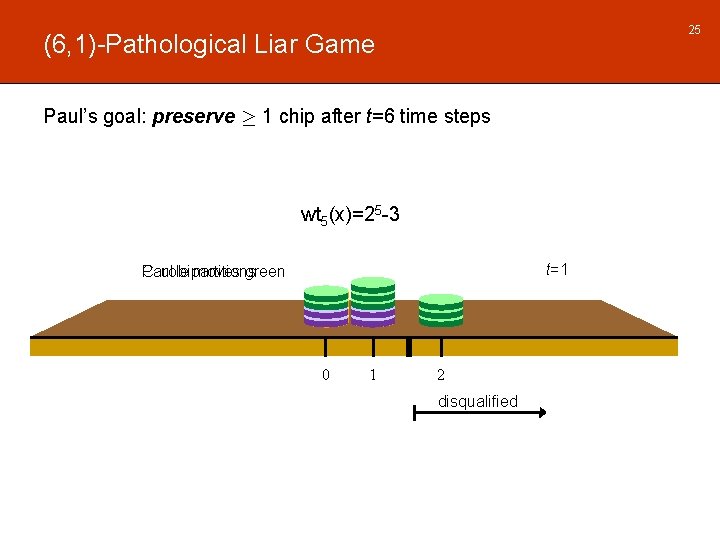
25 (6, 1)-Pathological Liar Game Paul’s goal: preserve ¸ 1 chip after t=6 time steps wt 5(x)=25 -3 t=1 Paul bipartitions Carole moves green 0 1 2 disqualified

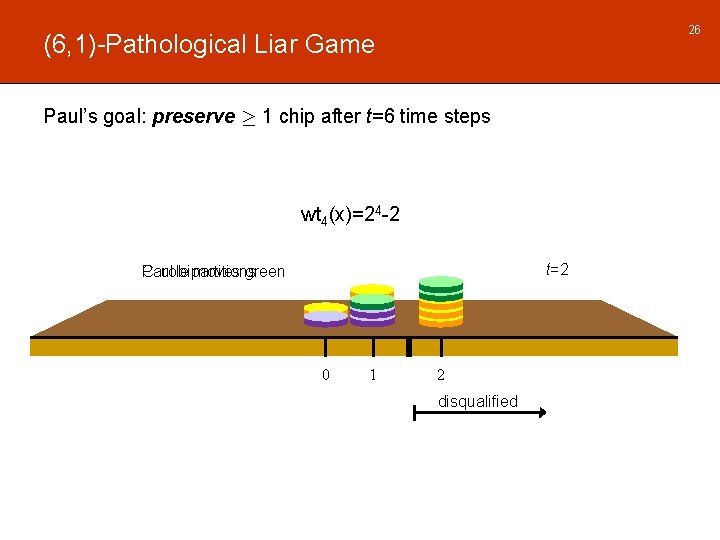
26 (6, 1)-Pathological Liar Game Paul’s goal: preserve ¸ 1 chip after t=6 time steps wt 4(x)=24 -2 t=2 Paul bipartitions Carole moves green 0 1 2 disqualified

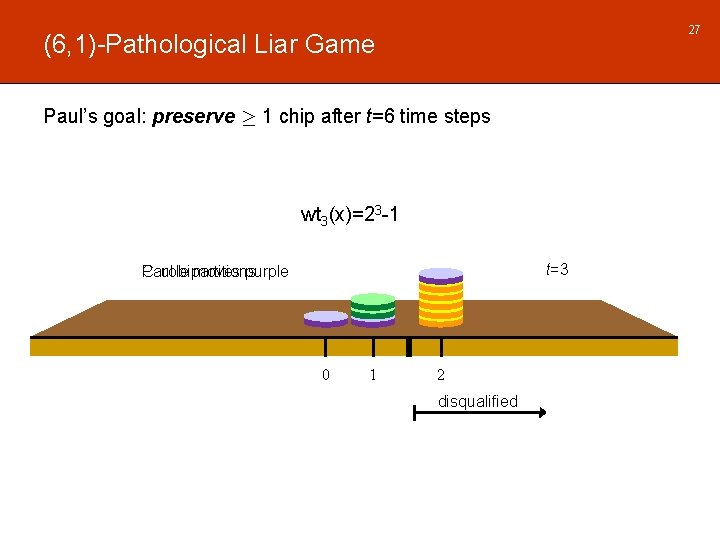
27 (6, 1)-Pathological Liar Game Paul’s goal: preserve ¸ 1 chip after t=6 time steps wt 3(x)=23 -1 t=3 Paul bipartitions Carole moves purple 0 1 2 disqualified

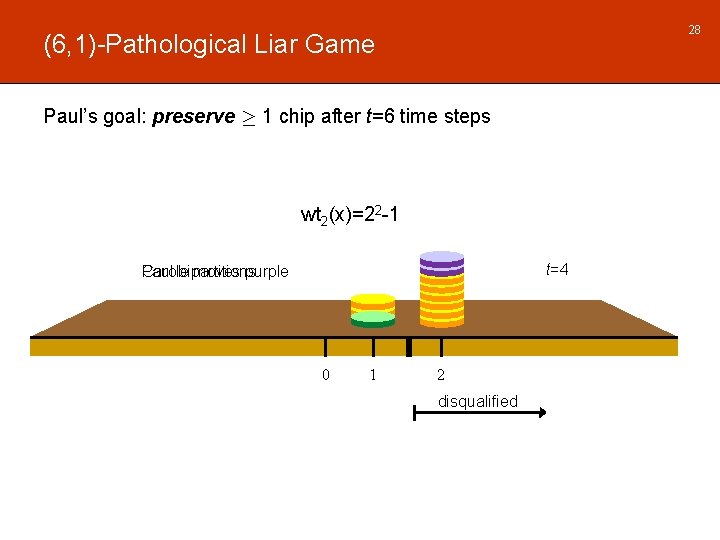
28 (6, 1)-Pathological Liar Game Paul’s goal: preserve ¸ 1 chip after t=6 time steps wt 2(x)=22 -1 t=4 Carole moves purple Paul bipartitions 0 1 2 disqualified

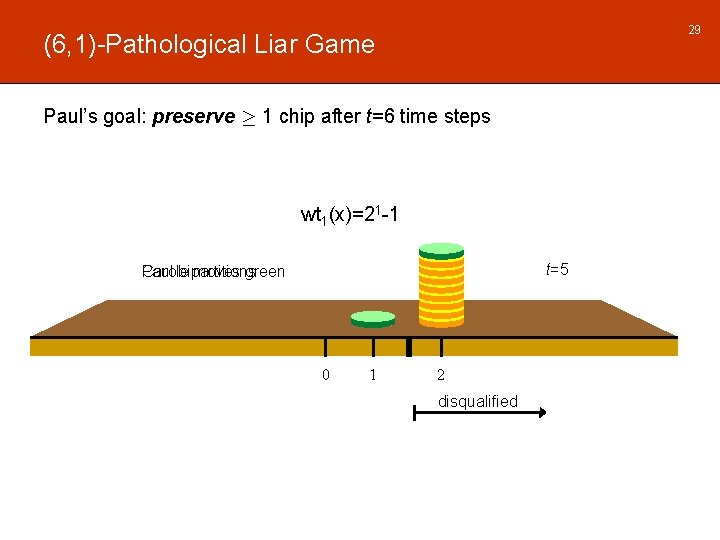
29 (6, 1)-Pathological Liar Game Paul’s goal: preserve ¸ 1 chip after t=6 time steps wt 1(x)=21 -1 t=5 Carole moves green Paul bipartitions 0 1 2 disqualified

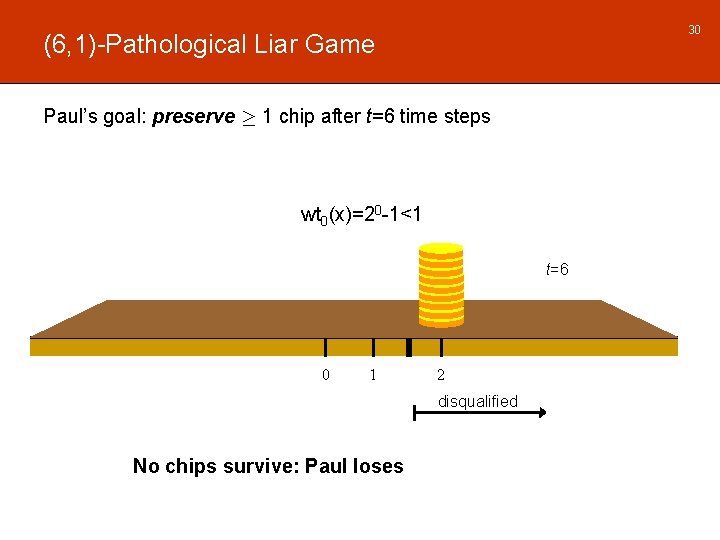
30 (6, 1)-Pathological Liar Game Paul’s goal: preserve ¸ 1 chip after t=6 time steps wt 0(x)=20 -1<1 t=6 0 1 2 disqualified No chips survive: Paul loses

31 Optimal (6, 1)-Codes Code type Optimal #chips (6, 1)-Liar game 8 Linear machine 9 1/7 (6, 1)-Pathological liar game 10

New Approach to the Pathological Liar Game Spencer and Winkler (`92) reduced the liar game to the liar machine, a discrete diffusion process on the integer line. Ellis and Yan (`04) introduced the pathological liar game. Cooper and Spencer (`06) use discrepancy analysis to compare the Propp-machine to simple random walk on Zd. Here: (1) We reduce the pathological liar game to the liar machine, (2) Use discrepancy analysis to compare the liar machine to simple random walk on Z, and thereby (3) Improve the best known pathological liar game strategy when the number of lies is a constant fraction of the number of rounds. 32

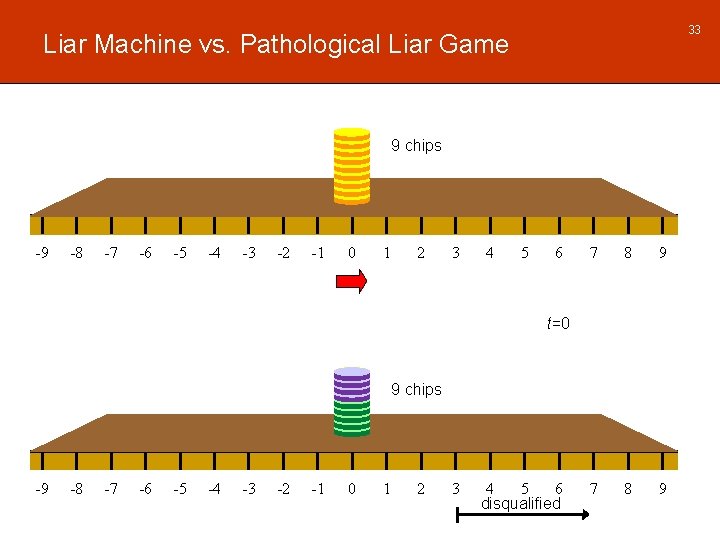
33 Liar Machine vs. Pathological Liar Game 9 chips -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 t=0 9 chips -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 disqualified

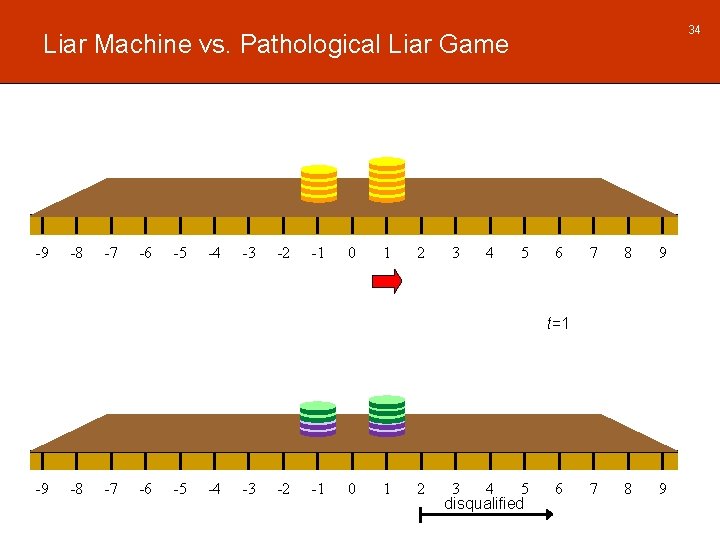
34 Liar Machine vs. Pathological Liar Game -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 t=1 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 disqualified 6

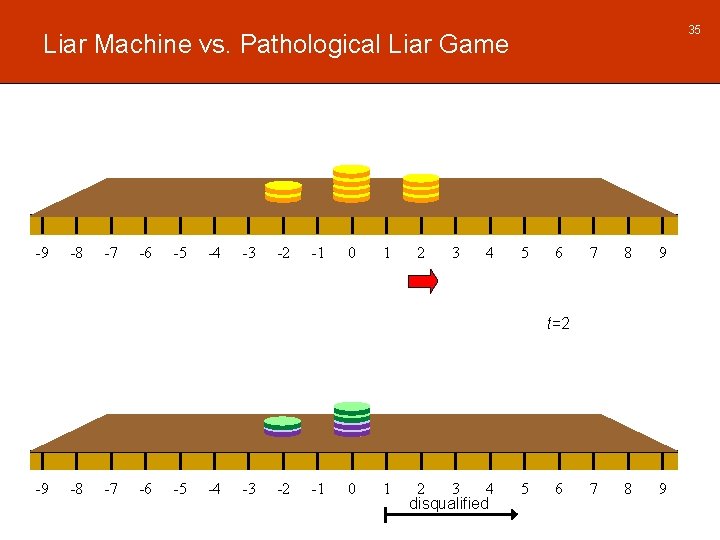
35 Liar Machine vs. Pathological Liar Game -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 t=2 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 disqualified 5 6

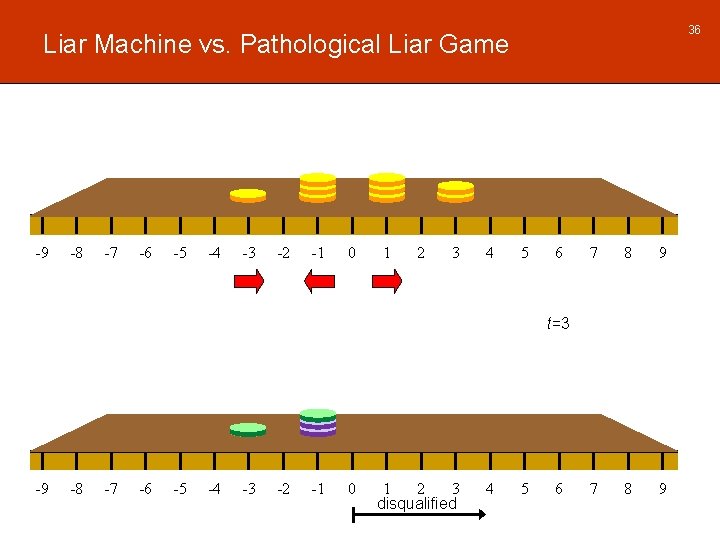
36 Liar Machine vs. Pathological Liar Game -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 t=3 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 disqualified 4 5 6

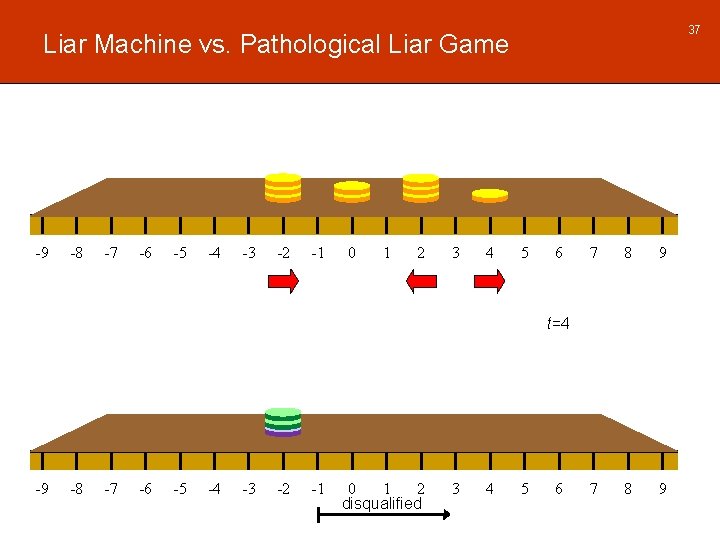
37 Liar Machine vs. Pathological Liar Game -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 t=4 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 disqualified 3 4 5 6

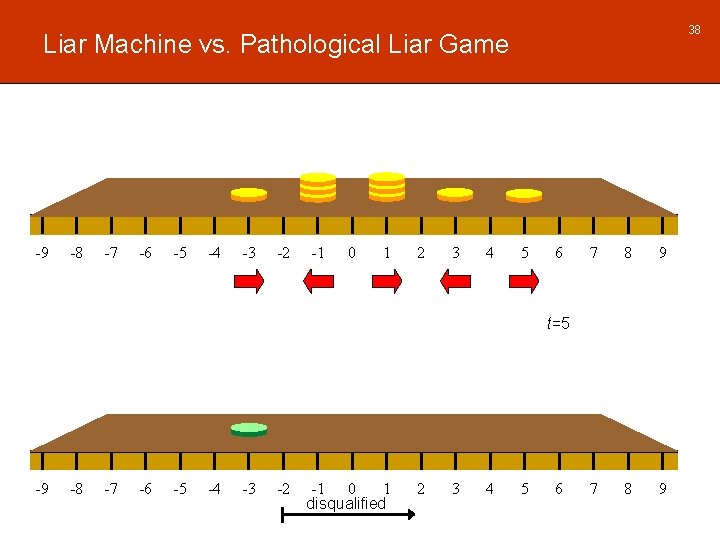
38 Liar Machine vs. Pathological Liar Game -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 t=5 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 disqualified 2 3 4 5 6

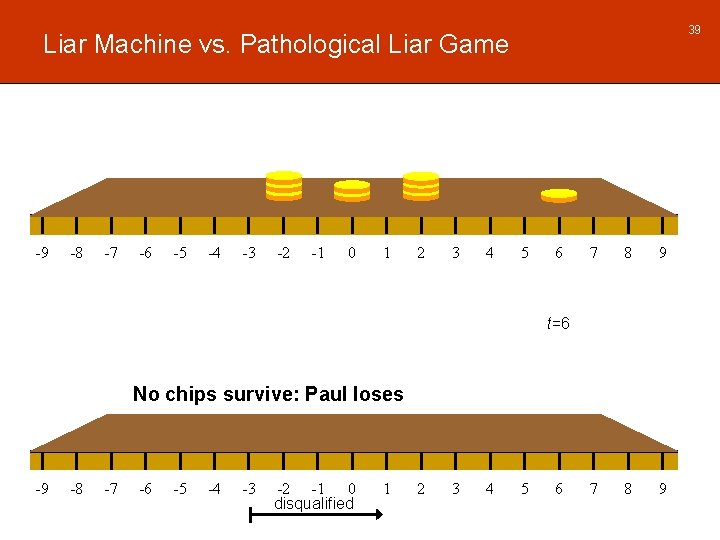
39 Liar Machine vs. Pathological Liar Game -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 t=6 No chips survive: Paul loses -9 -8 -7 -6 -5 -4 -3 -2 -1 0 disqualified 1 2 3 4 5 6

(6, 1)-Pathological Liar Game, Liar Machine Code type Optimal #chips Linear machine 9 1/7 (6, 1)-Pathological liar game 10 (6, 1)-Liar machine 12 -8 -7 -6 -5 -4 optimum: -3 -2 -1 0 1 Minimum 2 3 4 5 6 number 7 8 9 of (6, 1)-liar-9 machine initial chips for ¸ 1 chip disqualified to be at position · -4 when t=6 (6, 1)-Liar machine started with 12 chips after 6 rounds 40

Reduction: Pathological Liar Game ! Liar Machine 41

Reduction to Liar Machine 42

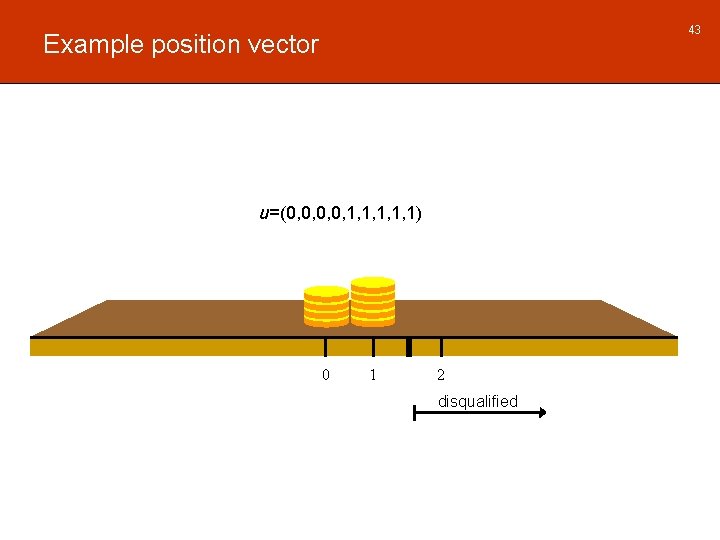
43 Example position vector u=(0, 0, 1, 1, 1) 0 1 2 disqualified

Liar Machine Versus Linear Machine 44

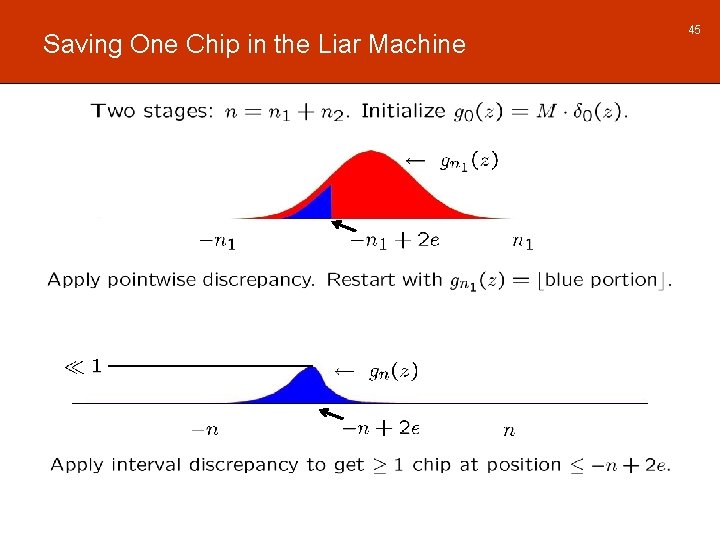
Saving One Chip in the Liar Machine 45

Pathological Liar Game Theorem 46

Further Exploration § Tighten the discrepancy analysis for the special case of initial chip configuration f 0(z)=M 0(z). § Generalize from binary questions to q-ary questions, q ¸ 2. § Improve analysis of the original liar game from Spencer and Winkler `92. § Prove general pointwise and interval discrepancy theorems for various discretizations of random walks. 47

Reading List § This paper: Linearly bounded liars, adaptive covering codes, and deterministic random walks, preprint (see homepage). § The liar machine – Joel Spencer and Peter Winkler. Three thresholds for a liar. Combin. Probab. Comput. , 1(1): 81 -93, 1992. § The pathological liar game – Robert Ellis, Vadim Ponomarenko, and Catherine Yan. The Renyi-Ulam pathological liar game with a fixed number of lies. J. Combin. Theory Ser. A, 112(2): 328 -336, 2005. § Discrepancy of deterministic random walks – Joshua Cooper and Joel Spencer, Simulating a Random Walk with Constant Error, Combinatorics, Probability, and Computing, 15 (2006), no. 06, 815 -822. – Joshua Cooper, Benjamin Doerr, Joel Spencer, and Gabor Tardos. Deterministic random walks on the integers. European J. Combin. , 28(8): 2072 -2090, 2007. 48