An Improved Liar Game Strategy From a Deterministic

An Improved Liar Game Strategy From a Deterministic Random Walk Robert Ellis April 9 th, 2010 San Diego State University Joint work with Joshua Cooper, University of South Carolina

Outline of Talk § Coding theory overview – Packing (error-correcting) & covering codes – Coding as a 2 -player game – Liar game and pathological liar game § Diffusion processes on Z – Simple random walk (linear machine) – Liar machine – Pathological liar game, alternating question strategy § Improved pathological liar game bound – Reduction to liar machine – Discrepancy analysis of liar machine versus linear machine § Concluding remarks 2

Coding Theory Overview § Codewords: fixed-length strings from a finite alphabet § Primary uses: Error-correction for transmission in the presence of noise Compression of data with or without loss § Viewpoints: Packings and coverings of Hamming balls in the hypercube 2 -player perfect information games § Applications: Cell phones, compact disks, deep-space communication 3

4 Coding Theory: (n, e)-Codes § Transmit blocks of length n § Noise changes ≤ e bits per block (|| ||1 ≤ e) x 1…xn (x 1+ 1)…(xn+ n) Richard Hamming § Repetition code 111, 000 – length: n = 3 – e=1 – information rate: 1/3 Received: 110 000 101 blockwise majority vote Decoded: 111 000 111

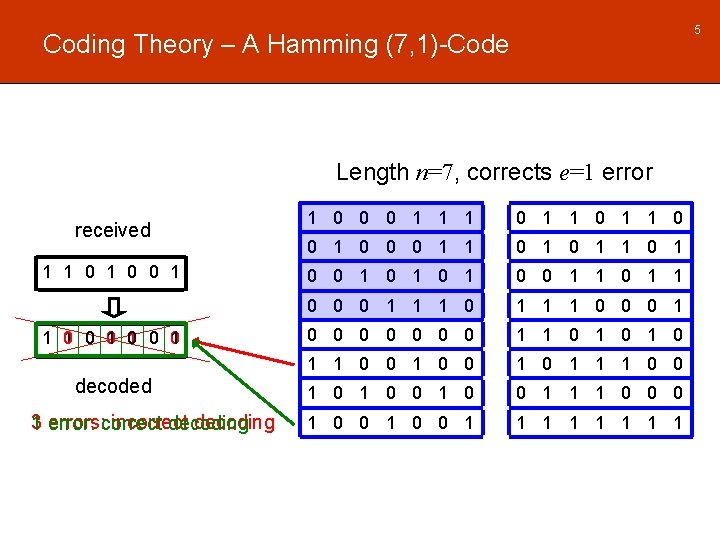
5 Coding Theory – A Hamming (7, 1)-Code Length n=7, corrects e=1 error received 1 1 0 0 1 1 0 1 0 decoded 3 error: errors: correct incorrect decoding 1 0 0 0 1 1 1 0 0 0 1 1 0 1 0 0 1 1 0 0 0 1 0 0 0 0 1 1 0 1 0 1 1 0 0 1 0 1 1 1 0 0 1 1 1 0 0 0 1 1 1 1

6 A Repetition Code as a Packing § (3, 1)-code: 111, 000 § Pairwise distance = 3 1 error can be corrected § The M codewords of an (n, e)-code correspond to a packing of Hamming balls of radius e in the n-cube 111 110 101 011 100 010 001 000 A packing of 2 radius-1 Hamming balls in the 3 -cube

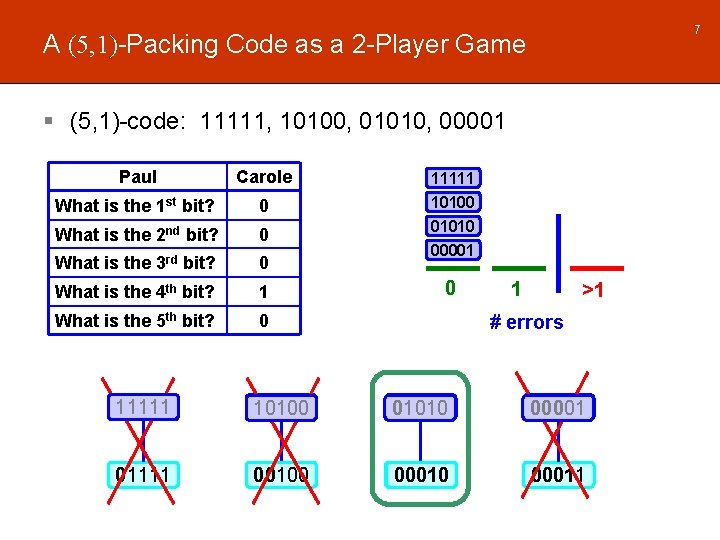
7 A (5, 1)-Packing Code as a 2 -Player Game § (5, 1)-code: 11111, 10100, 01010, 00001 Paul Carole What is the 1 st bit? 0 What is the 2 nd bit? 0 What is the 3 rd bit? 0 What is the 4 th bit? 1 What is the 5 th bit? 0 11111 10100 01010 00001 0 1 >1 # errors 11111 10100 01010 00001 01111 00100 00011

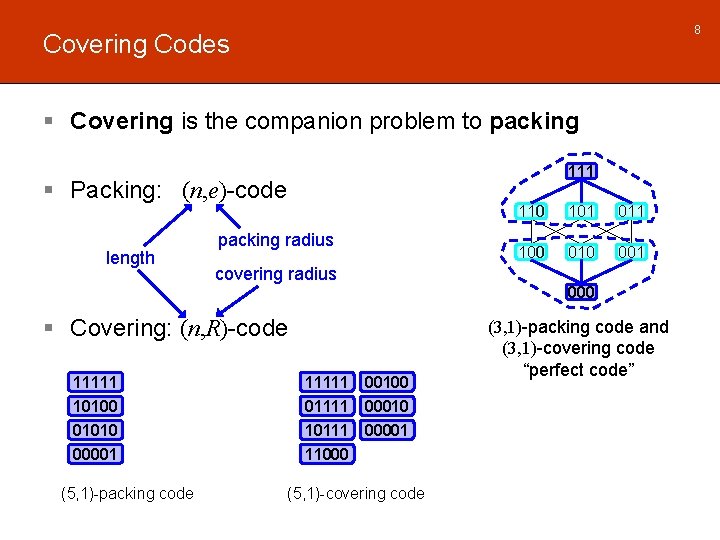
8 Covering Codes § Covering is the companion problem to packing 111 § Packing: (n, e)-code length packing radius covering radius § Covering: (n, R)-code 11111 10100 01010 00001 (5, 1)-packing code 11111 00100 01111 00010 10111 00001 11000 (5, 1)-covering code 110 101 011 100 010 001 000 (3, 1)-packing code and (3, 1)-covering code “perfect code”

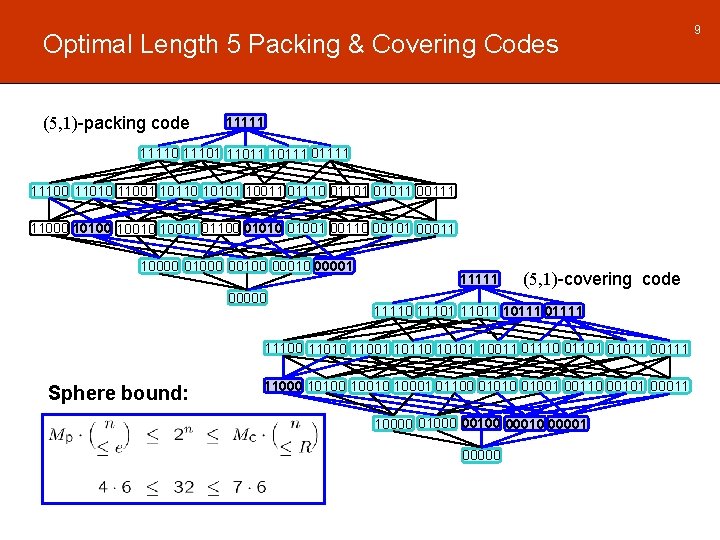
Optimal Length 5 Packing & Covering Codes (5, 1)-packing code 111110 111011 101111 11100 11010 11001 10110 10101 10011 01110 01101 01011 00111 11000 10100 10010 10001 01100 01010 01001 00110 00101 00011 10000 01000 00100 00010 00001 00000 11111 (5, 1)-covering code 111101 110111 01111 11100 11010 11001 10110 10101 10011 01110 01101 01011 00111 Sphere bound: 11000 10100 10010 10001 01100 01010 01001 00110 00101 00011 10000 01000 00100 00010 00001 00000 9

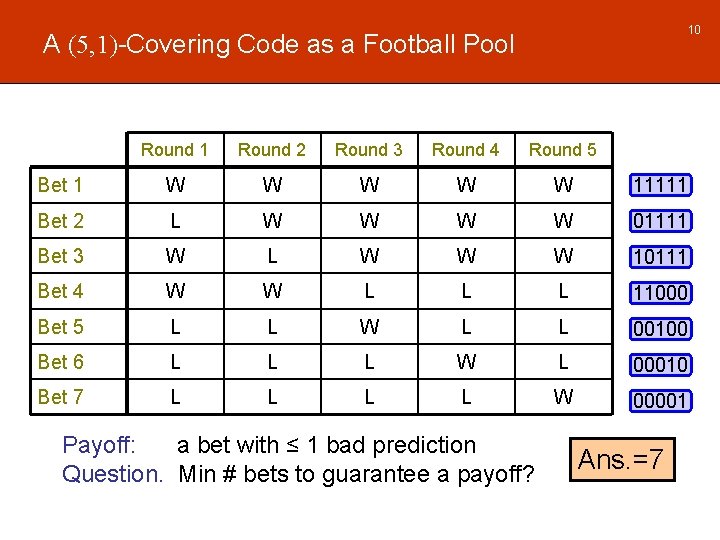
10 A (5, 1)-Covering Code as a Football Pool Round 1 Round 2 Round 3 Round 4 Round 5 Bet 1 W W W 11111 Bet 2 L W W 01111 Bet 3 W L W W W 10111 Bet 4 W W L L L 11000 Bet 5 L L W L L 00100 Bet 6 L L L W L 00010 Bet 7 L L W 00001 Payoff: a bet with ≤ 1 bad prediction Question. Min # bets to guarantee a payoff? Ans. =7

11 Codes with Feedback (Adaptive Codes) § Feedback Noiseless, delay-less report of actual received bits § Improves the number of decodable messages E. g. , from 20 to 28 messages for an (8, 1)-code sender 1, 0, 1, 1, 0 receiver Noise 1, 1, 0 Noiseless Feedback Elwyn Berlekamp

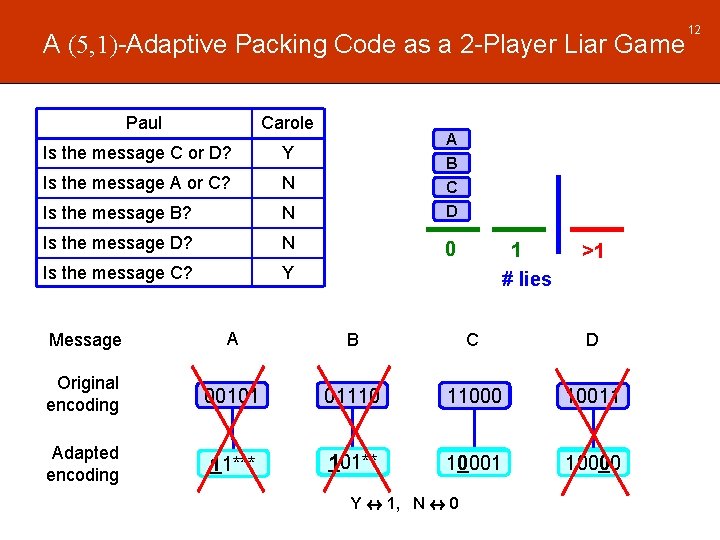
A (5, 1)-Adaptive Packing Code as a 2 -Player Liar Game Paul Carole Is the message C or D? Y Is the message A or C? N Is the message B? N A B C D Is the message D? N 0 Is the message C? Y 1 # lies >1 Message A B C D Original encoding 00101 01110 01010 11000 10011 Adapted encoding 1**** 11*** 101** 1**** 100** 10*** 10001 1000* 10000 Y $ 1, N $ 0 12

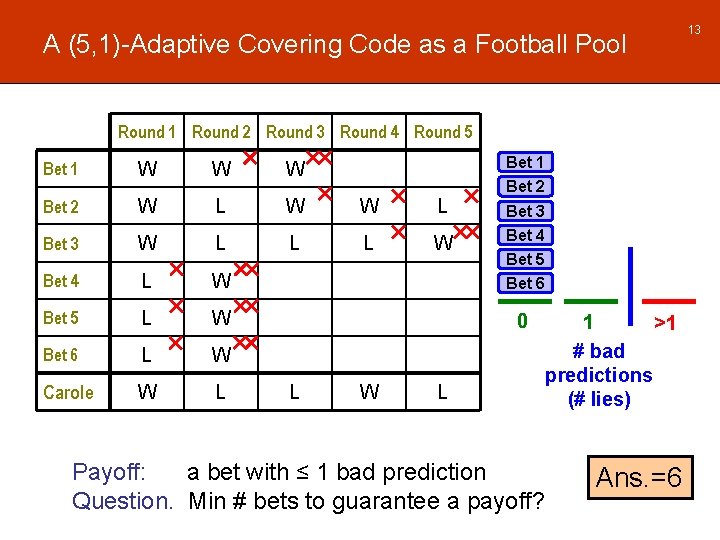
A (5, 1)-Adaptive Covering Code as a Football Pool Round 1 Round 2 Round 3 Round 4 Round 5 Bet 1 W W W Bet 2 W L W W L Bet 3 W L L L W Bet 4 L W Bet 3 Bet 4 Bet 5 Bet 6 Bet 5 L W 0 Bet 6 L W Carole W L L W Bet 2 L Payoff: a bet with ≤ 1 bad prediction Question. Min # bets to guarantee a payoff? 1 >1 # bad predictions (# lies) Ans. =6 13

14 Optimal (5, 1)-Codes Code type Optimal size (5, 1)-code 4 (5, 1)-adaptive code 4 Sphere bound 5 1/3 (= 25/(5+1) ) (5, 1)-adaptive covering code 6 (5, 1)-covering code 7

Adaptive Codes: Results and Questions Sizes of optimal adaptive packing codes • Binary, fixed e ≥ sphere bound - ce (Spencer `92) • Binary, e=1, 2, 3 =sphere bound - O(1), exact solutions (Pelc; Guzicki; Deppe) • Q-ary, e=1 =sphere bound - c(q, e), exact solution (Aigner `96) • Q-ary, e linear unknown if rate meets Hamming bound for all e. (Ahlswede, C. Deppe, and V. Lebedev) Sizes of optimal adaptive covering codes • Binary, fixed e · sphere bound + Ce Binary, e=1, 2 =sphere bound + O(1), exact solution (Ellis, Ponomarenko, Yan `05) Near-perfect adaptive codes • Q-ary, symmetric or “balanced”, e=1 exact solution (Ellis `04+) • General channel, fixed e asymptotic first term (Ellis, Nyman `09) 15

Outline of Talk § Coding theory overview – Packing (error-correcting) & covering codes – Coding as a 2 -player game – Liar game and pathological liar game § Diffusion processes on Z – Simple random walk (linear machine) – Liar machine – Pathological liar game, alternating question strategy § Improved pathological liar game bound – Reduction to liar machine – Discrepancy analysis of liar machine versus linear machine § Concluding remarks 16

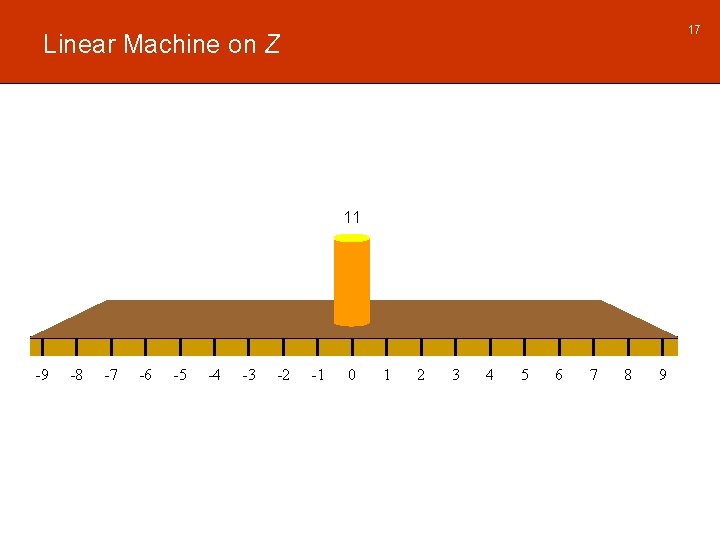
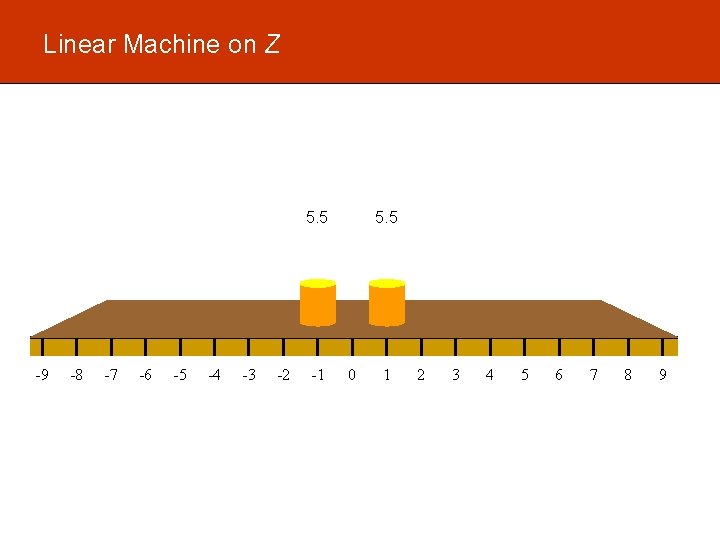
17 Linear Machine on Z 11 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9

Linear Machine on Z 5. 5 -9 -8 -7 -6 -5 -4 -3 -2 -1 5. 5 0 1 2 3 4 5 6 7 8 9

Linear Machine on Z 2. 75 -9 -8 -7 -6 -5 -4 -3 -2 5. 5 -1 0 2. 75 1 2 3 4 5 6 7 Time-evolution: 11 £ binomial distribution of {-1, +1} coin flips 8 9

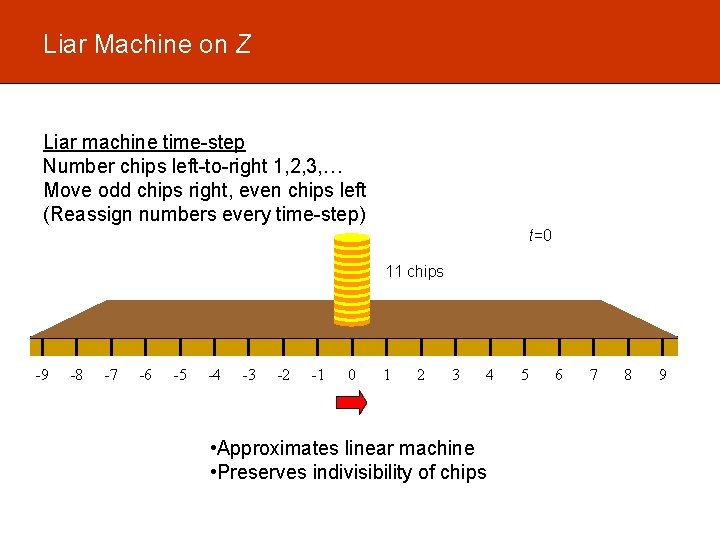
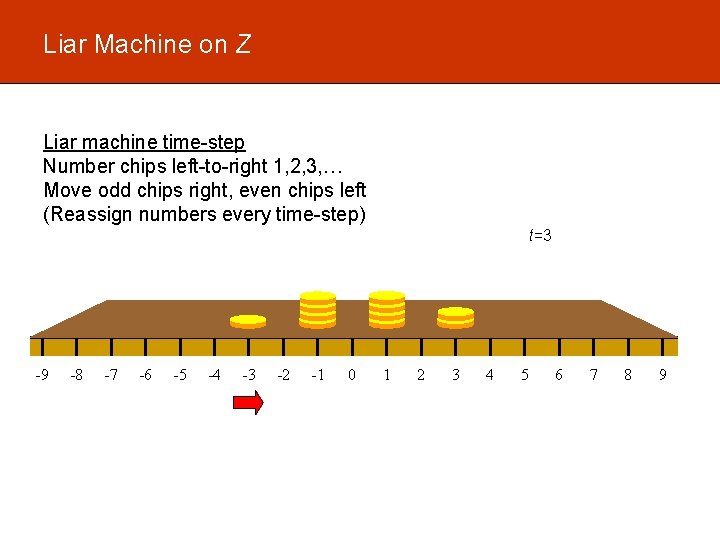
Liar Machine on Z Liar machine time-step Number chips left-to-right 1, 2, 3, … Move odd chips right, even chips left (Reassign numbers every time-step) t=0 11 chips -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 • Approximates linear machine • Preserves indivisibility of chips 5 6 7 8 9

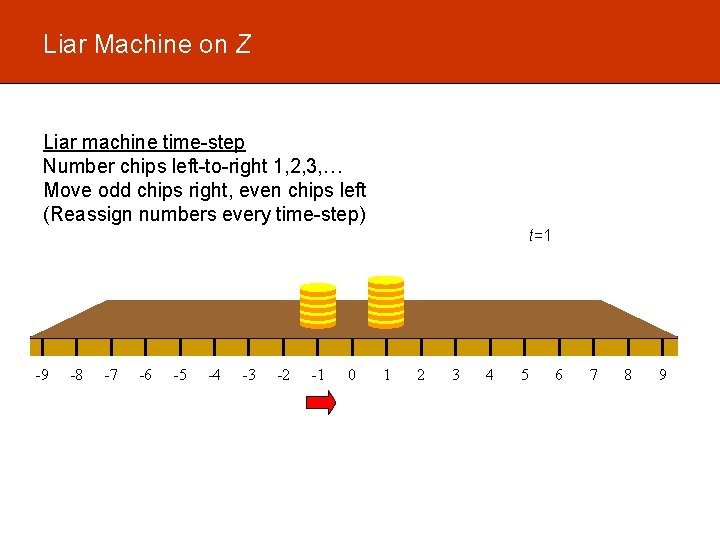
Liar Machine on Z Liar machine time-step Number chips left-to-right 1, 2, 3, … Move odd chips right, even chips left (Reassign numbers every time-step) t=1 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9

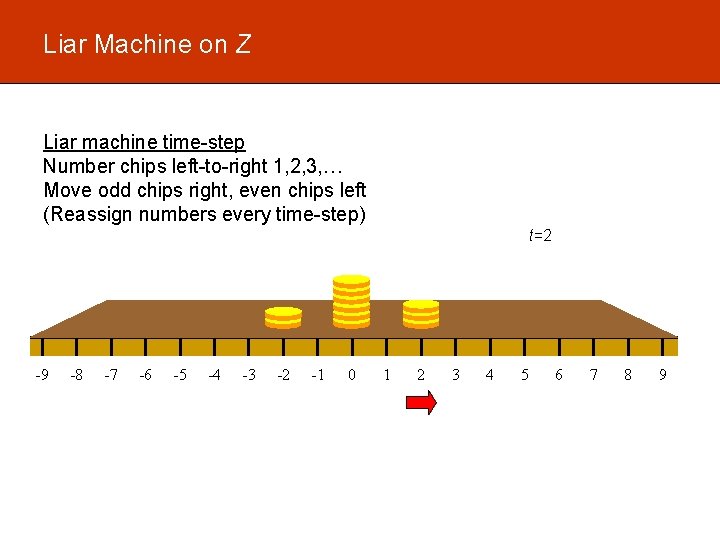
Liar Machine on Z Liar machine time-step Number chips left-to-right 1, 2, 3, … Move odd chips right, even chips left (Reassign numbers every time-step) t=2 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9

Liar Machine on Z Liar machine time-step Number chips left-to-right 1, 2, 3, … Move odd chips right, even chips left (Reassign numbers every time-step) t=3 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9

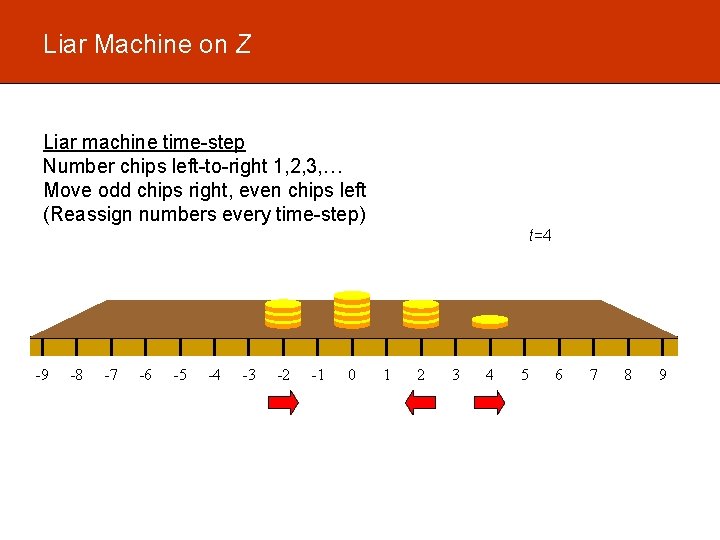
Liar Machine on Z Liar machine time-step Number chips left-to-right 1, 2, 3, … Move odd chips right, even chips left (Reassign numbers every time-step) t=4 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9

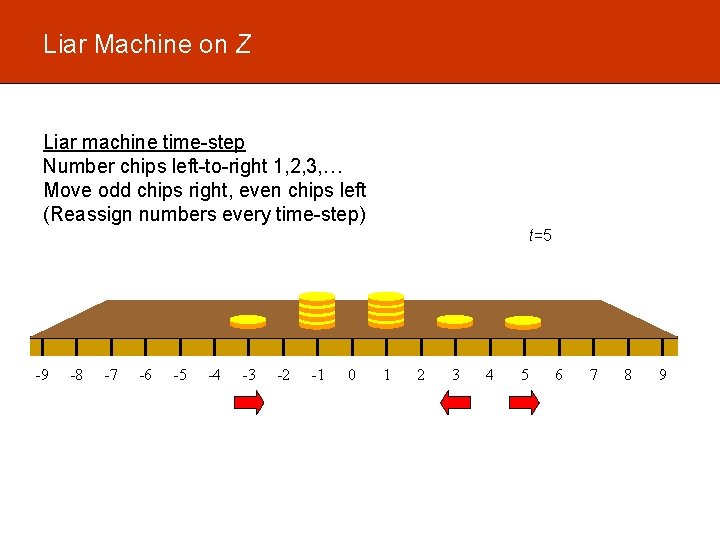
Liar Machine on Z Liar machine time-step Number chips left-to-right 1, 2, 3, … Move odd chips right, even chips left (Reassign numbers every time-step) t=5 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9

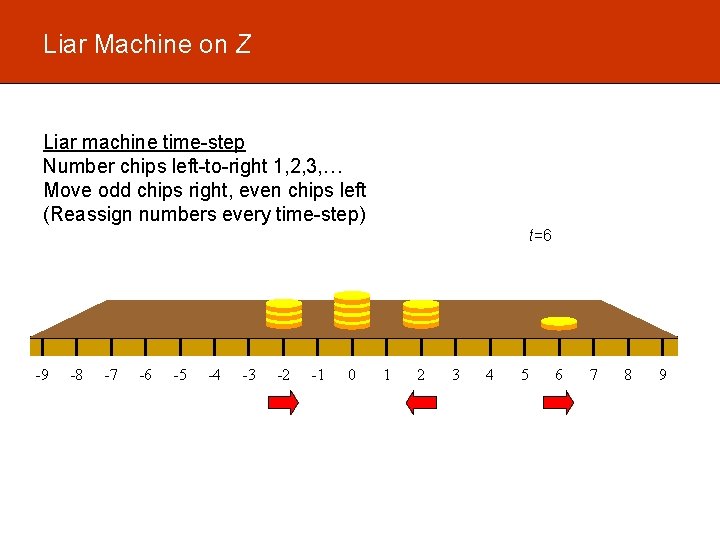
Liar Machine on Z Liar machine time-step Number chips left-to-right 1, 2, 3, … Move odd chips right, even chips left (Reassign numbers every time-step) t=6 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9

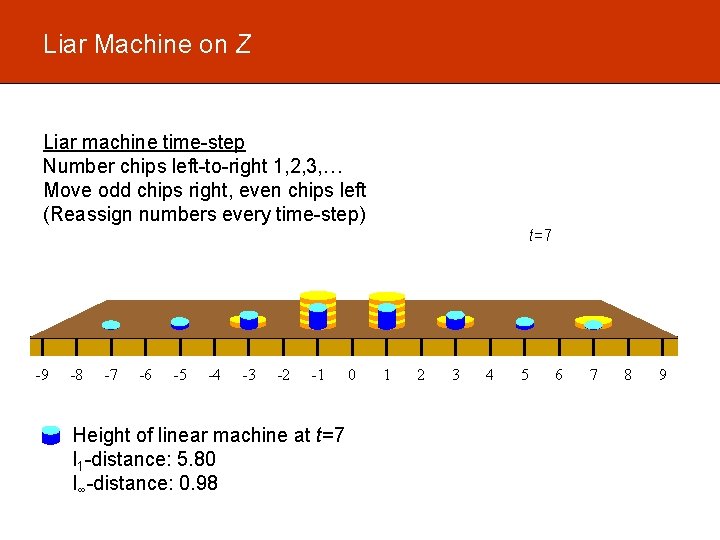
Liar Machine on Z Liar machine time-step Number chips left-to-right 1, 2, 3, … Move odd chips right, even chips left (Reassign numbers every time-step) t=7 -9 -8 -7 -6 -5 -4 -3 -2 -1 Height of linear machine at t=7 l 1 -distance: 5. 80 l∞-distance: 0. 98 0 1 2 3 4 5 6 7 8 9

Discrepancy for Two Discretizations Liar machine: round-offs spatially balanced Rotor-router model/Propp machine: round-offs temporally balanced The liar machine has poorer discrepancy… but provides bounds to the pathological liar game.

Proof of Liar Machine Pointwise Discrepancy

The Liar Game as a Diffusion Process A priori: M=#chips, n=#rounds, e=max #lies Initial configuration: f 0 = M ¢ 0 Each round, obtain ft+1 from ft by: (1) Paul 2 -colors the chips (2) Carole moves one color class left, the other right Final configuration: fn Winning conditions Original variant (Berlekamp, Rényi, Ulam) Pathological variant (Ellis, Yan)

Pathological Liar Game Bounds Fix n, e. Define M*(n, e) = minimum M such that Paul can win the pathological liar game with parameters M, n, e. Sphere Bound (E, P, Y `05) For fixed e, M*(n, e) · sphere bound + Ce (Delsarte, Piret `86) For e/n 2 (0, 1/2), M*(n, e) · sphere bound ¢ n ln 2. (C, E `09+) For e/n 2 (0, 1/2), using the liar machine, M*(n, e) = sphere bound ¢.

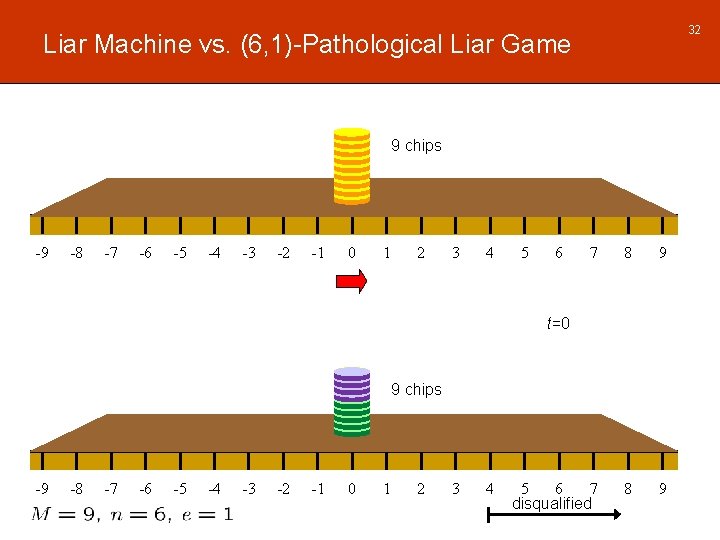
32 Liar Machine vs. (6, 1)-Pathological Liar Game 9 chips -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 5 6 7 disqualified 8 9 t=0 9 chips -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4

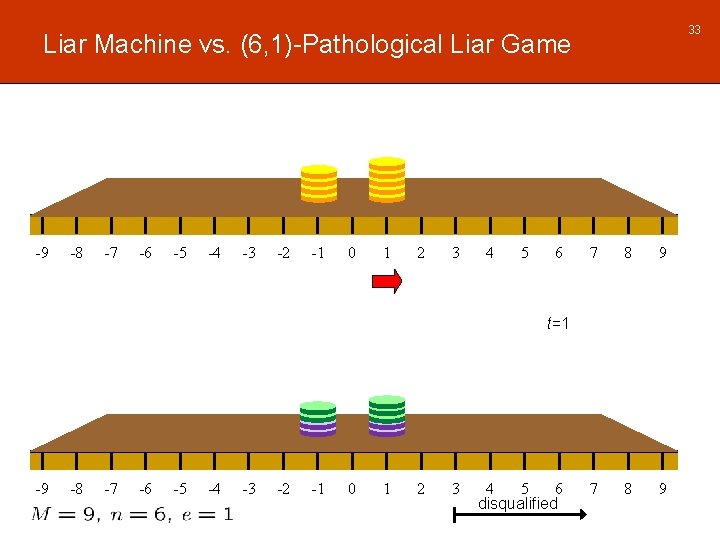
33 Liar Machine vs. (6, 1)-Pathological Liar Game -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 t=1 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 disqualified

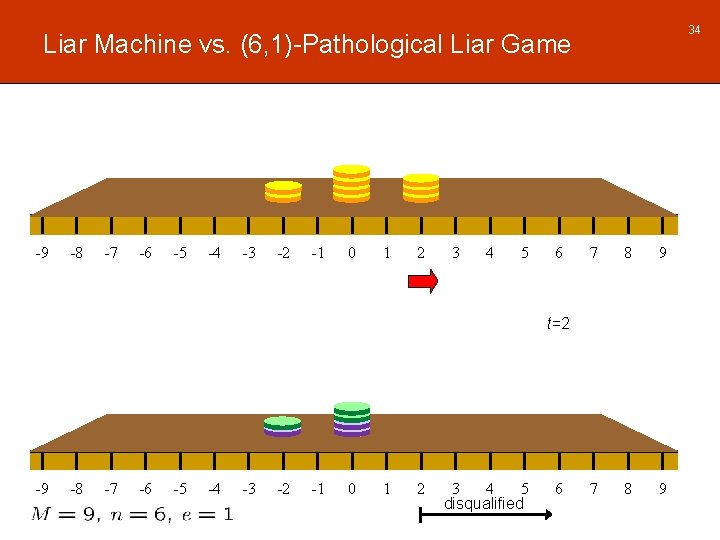
34 Liar Machine vs. (6, 1)-Pathological Liar Game -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 t=2 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 disqualified 6

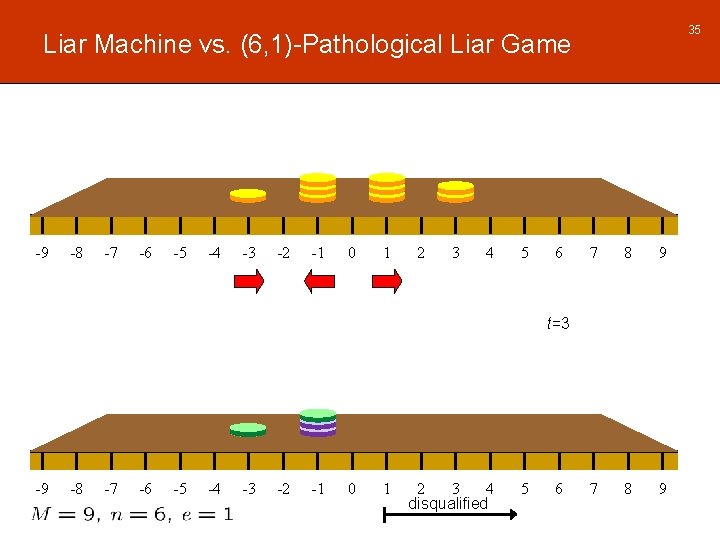
35 Liar Machine vs. (6, 1)-Pathological Liar Game -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 t=3 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 disqualified 5 6

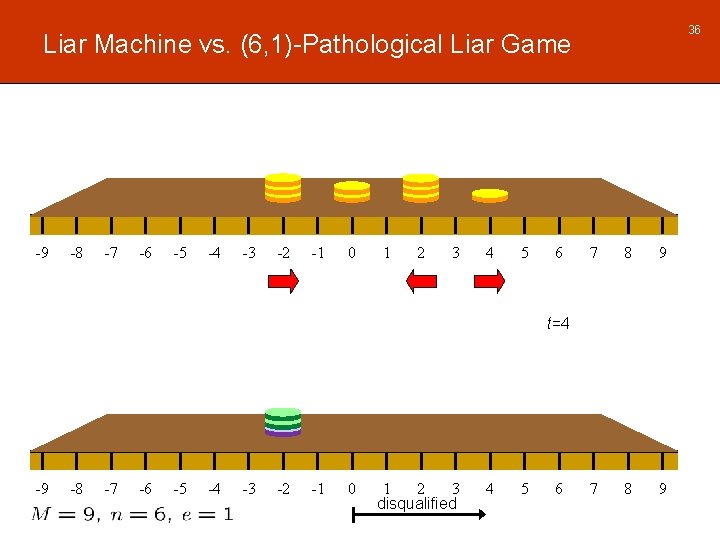
36 Liar Machine vs. (6, 1)-Pathological Liar Game -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 t=4 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 disqualified 4 5 6

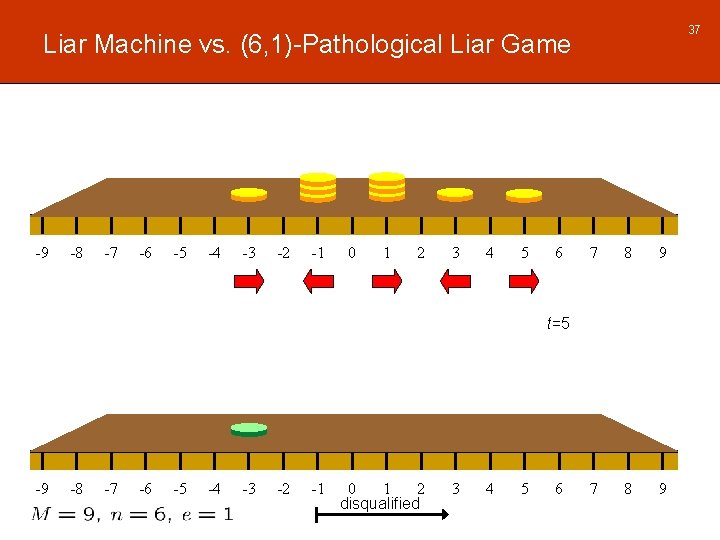
37 Liar Machine vs. (6, 1)-Pathological Liar Game -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 t=5 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 disqualified 3 4 5 6

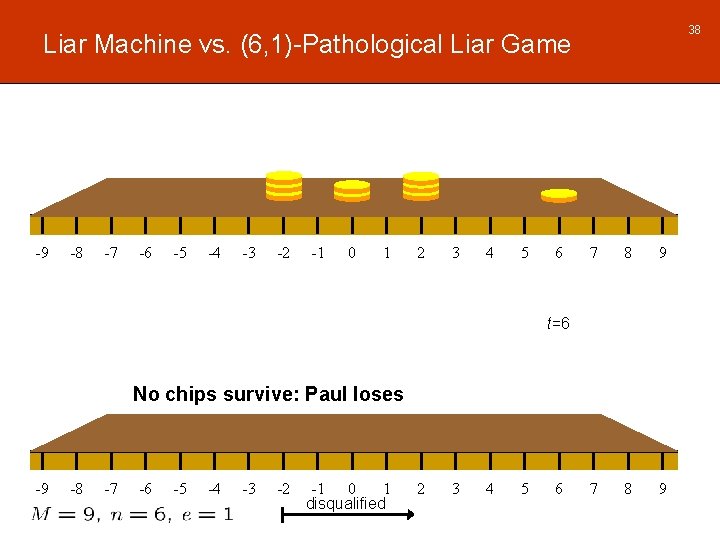
38 Liar Machine vs. (6, 1)-Pathological Liar Game -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 t=6 No chips survive: Paul loses -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 disqualified 2 3 4 5 6

39 Comparison of Processes Process Optimal #chips Linear machine 9 1/7 (6, 1)-Pathological liar game 10 (6, 1)-Liar machine 12 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 disqualified (6, 1)-Liar machine started with 12 chips after 6 rounds

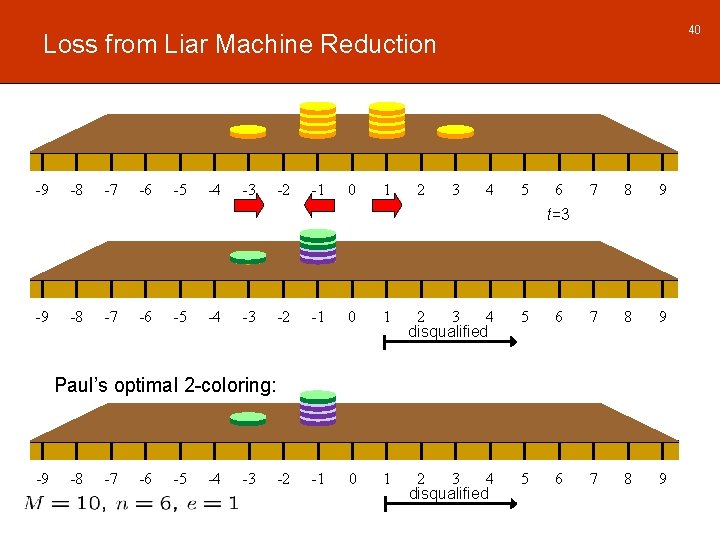
40 Loss from Liar Machine Reduction -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 t=3 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 disqualified 5 6 7 8 9 Paul’s optimal 2 -coloring: -9 -8 -7 -6 -5 -4 -3 -2

Reduction to Liar Machine

Saving One Chip in the Liar Machine 42

Summary: Pathological Liar Game Theorem

Further Exploration § Tighten the discrepancy analysis for the special case of initial chip configuration f 0=M 0. § Generalize from binary questions to q-ary questions, q ¸ 2. § Improve analysis of the original liar game from Spencer and Winkler `92; solve the optimal rate of q-ary adaptive block codes for all fractional error rates. § Prove general pointwise and interval discrepancy theorems for various discretizations of random walks. 44

Reading List § This paper: Linearly bounded liars, adaptive covering codes, and deterministic random walks, preprint (see homepage). § The liar machine – Joel Spencer and Peter Winkler. Three thresholds for a liar. Combin. Probab. Comput. 1(1): 81 -93, 1992. § The pathological liar game – Robert Ellis, Vadim Ponomarenko, and Catherine Yan. The Renyi-Ulam pathological liar game with a fixed number of lies. J. Combin. Theory Ser. A 112(2): 328 -336, 2005. § Discrepancy of deterministic random walks – Joshua Cooper and Joel Spencer, Simulating a Random Walk with Constant Error, Combin. Probab. Comput. 15 (2006), no. 06, 815 -822. – Joshua Cooper, Benjamin Doerr, Joel Spencer, and Gabor Tardos. Deterministic random walks on the integers. European J. Combin. , 28(8): 2072 -2090, 2007. 45