Game Programming Algorithms and Techniques Chapter 3 Linear

Game Programming Algorithms and Techniques Chapter 3 Linear Algebra for Games

Chapter 3 Objectives § Vectors – Learn the fundamentals of vectors – Learn the two products (dot and cross) and their uses – Apply them to sample problems – Learn about different coordinate systems § Matrices – Learn how to multiply matrices – Transforming vectors by matrices

Vector Definition § Represents a magnitude and direction in n-dimensional space, with one real number per dimension: – For games, usually 2 D or 3 D vectors, though sometimes we use 4 D in 3 D games. § Expressed as: § No concept of position!

Vectors: No Position § § Where we draw a vector does not change its magnitude or direction, so it doesn't change the vector. These vectors all have the same value: Vector field where all the vectors are equivalent

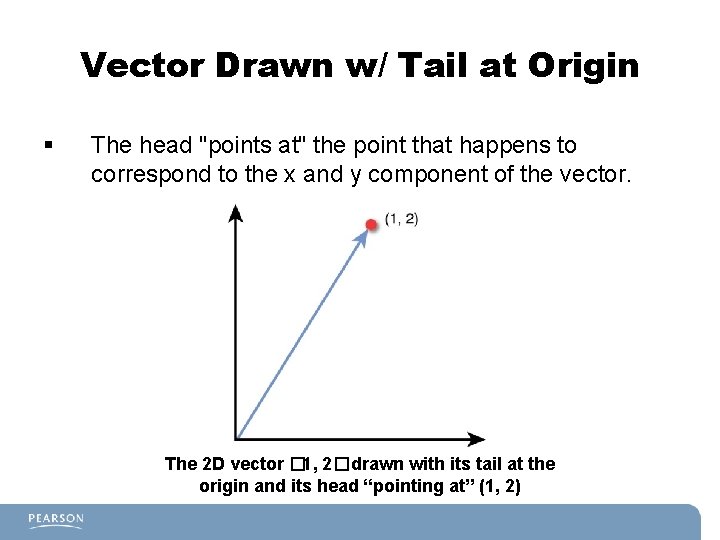
Vector Terms § Tail: where the vector starts. § Head: what the arrow is "pointing at. " § Although where a vector is drawn doesn't change its value, it's helpful to draw with the tail starting at the origin.

Vector Drawn w/ Tail at Origin § The head "points at" the point that happens to correspond to the x and y component of the vector. The 2 D vector � 1, 2�drawn with its tail at the origin and its head “pointing at” (1, 2)

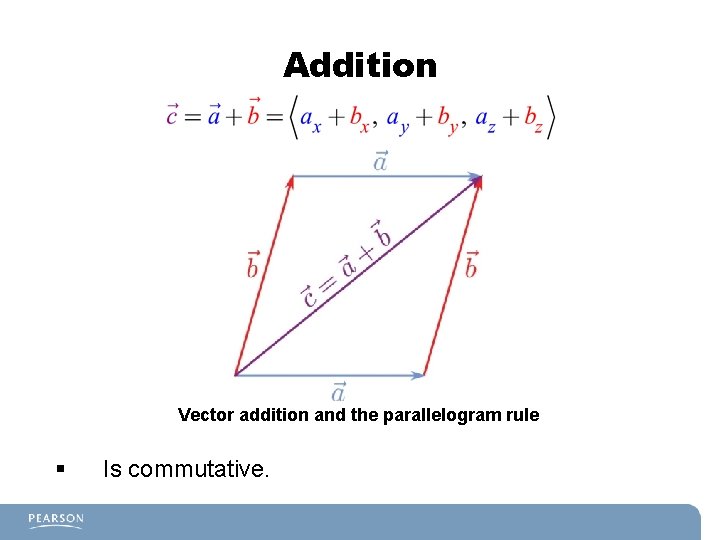
Addition Vector addition and the parallelogram rule § Is commutative.

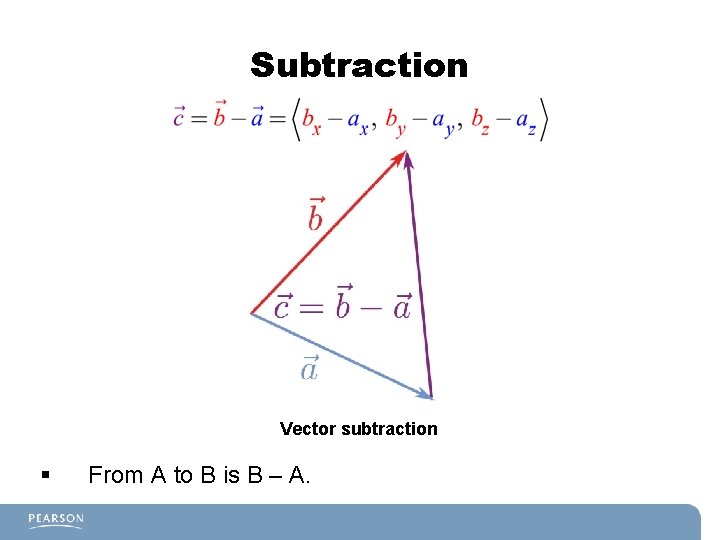
Subtraction Vector subtraction § From A to B is B – A.

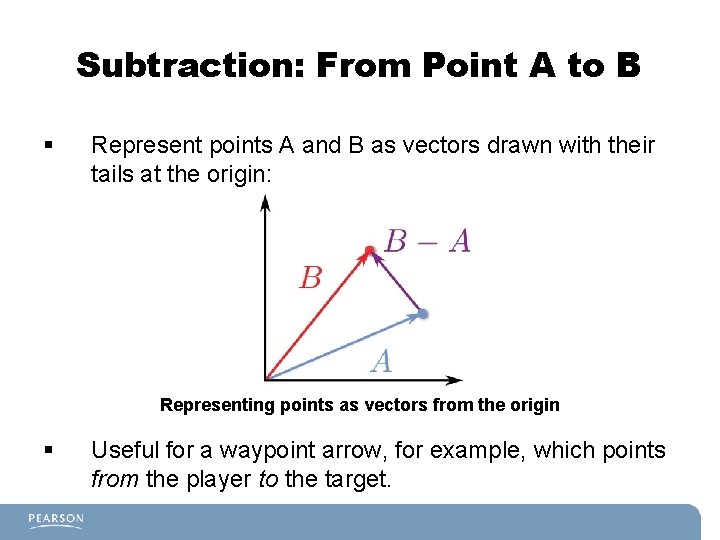
Subtraction: From Point A to B § Represent points A and B as vectors drawn with their tails at the origin: Representing points as vectors from the origin § Useful for a waypoint arrow, for example, which points from the player to the target.

Length and Length Squared § To calculate the length (or magnitude) of a vector: § If we just need a comparison between the length of two vectors, avoid the square root by using length squared:

Unit Vectors and Normalization § § Unit vectors have a length of 1. Drawn with a hat, like To convert a non-unit vector to a unit one, normalize the vector: Normalizing loses magnitude: – If you care about magnitude, don't normalize. – If you only care about direction, do normalize.

Scalar Multiplication Scalar multiplication

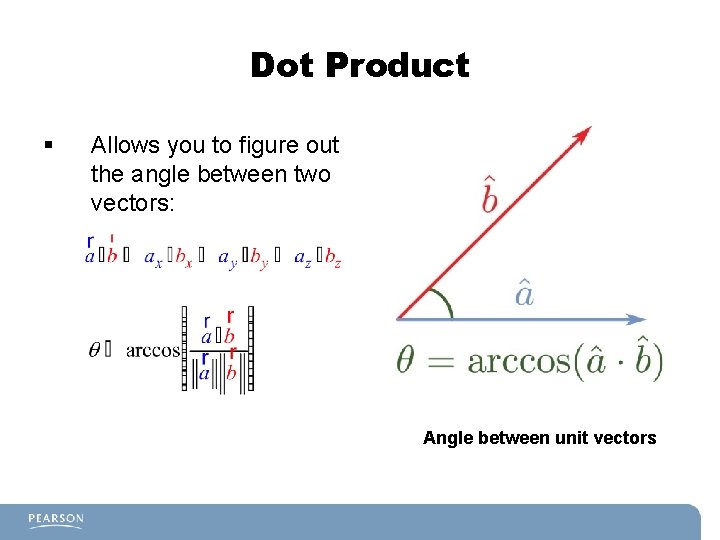
Dot Product § Allows you to figure out the angle between two vectors: Angle between unit vectors

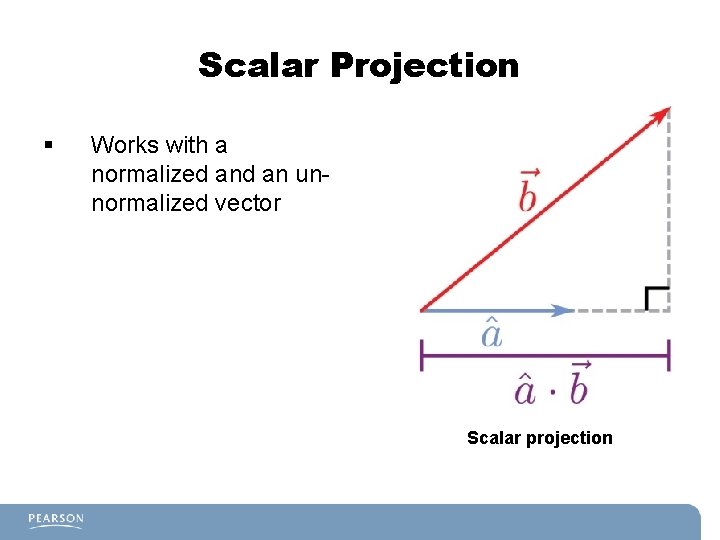
Scalar Projection § Works with a normalized an unnormalized vector Scalar projection

Dot Product Special Cases (For Normalized Vectors) § 0 = Two vectors are perpendicular. § 1 = Two vectors are parallel and facing in the same direction. § -1 = Two vectors are parallel and facing in the opposite direction.

Dot Product Properties § Commutative, distributed over addition, and associative: § Length squared is the same thing as dot product with self:

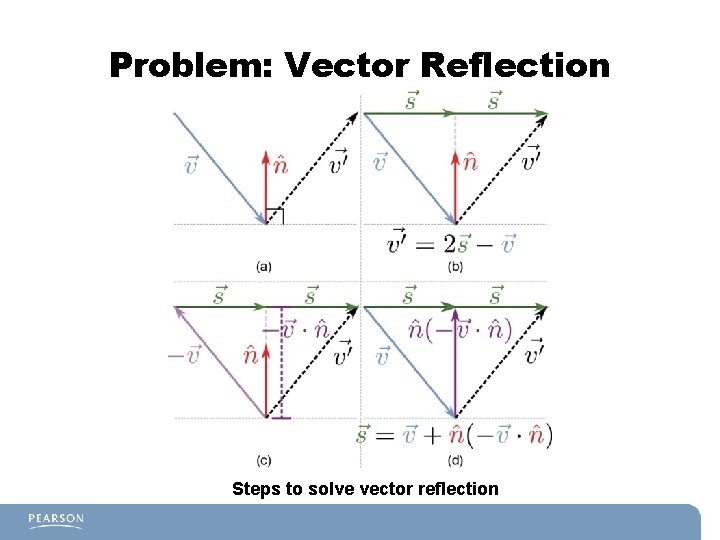
Problem: Vector Reflection Steps to solve vector reflection

Vector Reflection Solution

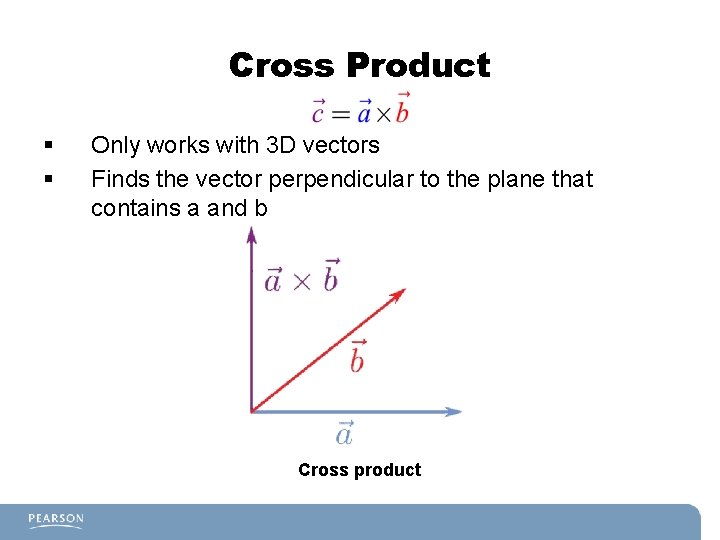
Cross Product § § Only works with 3 D vectors Finds the vector perpendicular to the plane that contains a and b Cross product

"xyzzy" Mnemonic § Tells the subscripts of the first row: § Then rotate components in the order x -> y -> z -> x to get the next two rows:

Cross Product Properties § Is anti-commutative: § If the result of the cross product has 0 for every component, it means the two vectors are parallel.

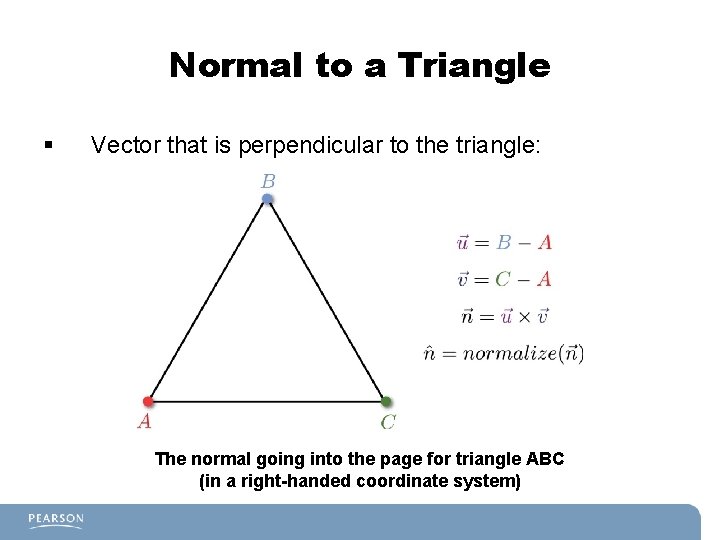
Normal to a Triangle § Vector that is perpendicular to the triangle: The normal going into the page for triangle ABC (in a right-handed coordinate system)

Problem: Rotating a 2 D Character § How do you know if you turn clockwise or counterclockwise? The player needs to rotate to face the explosion.

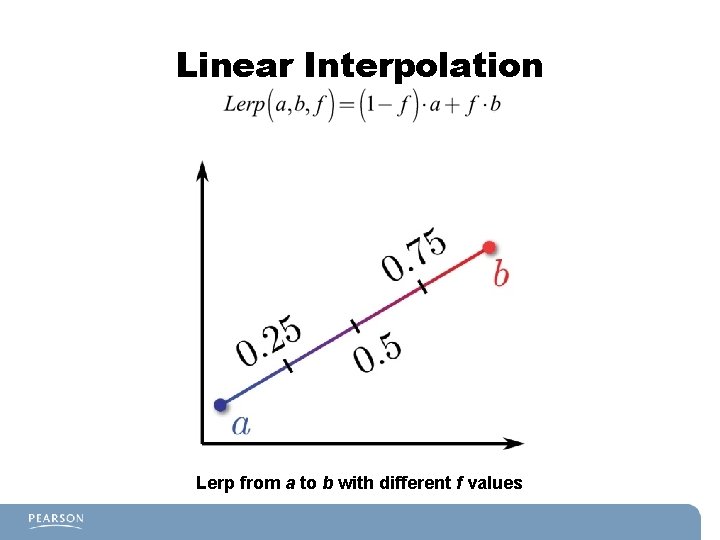
Linear Interpolation Lerp from a to b with different f values

Coordinate Systems § Which coordinate system you choose is arbitrary, but must be consistent! Sample right-handed (a) and left-handed (b) coordinate systems

Matrices § A matrix is a grid of real numbers with m rows and n columns. § For games, 3 x 3 or 4 x 4 matrices are the most common.

Matrix Multiplication § Matrices A and B can be multiplied if the number of columns in A are equal to the number of rows in B:

Identity Matrix § Multiplying a matrix by the identity matrix does not change its value: § Number of rows/columns in I is equal to the number of columns in A: § If a matrix is multiplied by its inverse, the result is identity:

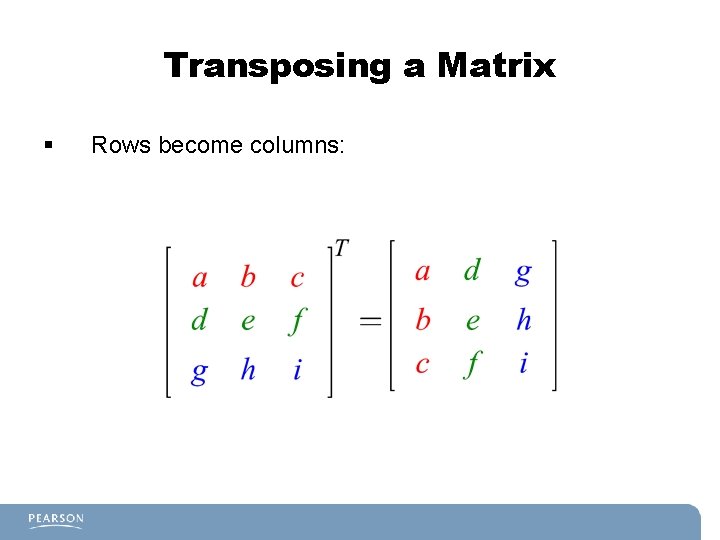
Transposing a Matrix § Rows become columns:

Representing a Vector as a Matrix § § § You can use either row-major or column-major. It doesn't matter which you select, but be consistent (most engines use row-major). Row-major: § Column-major:

Multiply a Vector by a Matrix § If you change from row-major to column-major (or vice versa), you must transpose the matrix: