LINEAR PROGRAMMING Linear Programming Linear programming is a

LINEAR PROGRAMMING

Linear Programming Linear programming is a mathematical technique. This technique is applied for choosing the best alternative from a set of feasible alternatives. This technique is designed to help managers in planning, decision making and to allocate the resources.

Definitions “The analysis of problems in which a linear function of a number of variables is to be maximised (or minimised) when these variables are subject to number of restraints in the form of linear inequalities. ” - Samuelson & Slow

In the words of LOOMBA : “LP is only one aspect of what has been called a system approach to management where in all programmes are designed and evaluated in the terms of their ultimate affects in the realization of business objectives. ”

Terminology & Requirements n n n n Objective Function Presence of constraints or restrictions Alternative course of action Non-negativity Constraints Linearity Finite number of variables Certainty

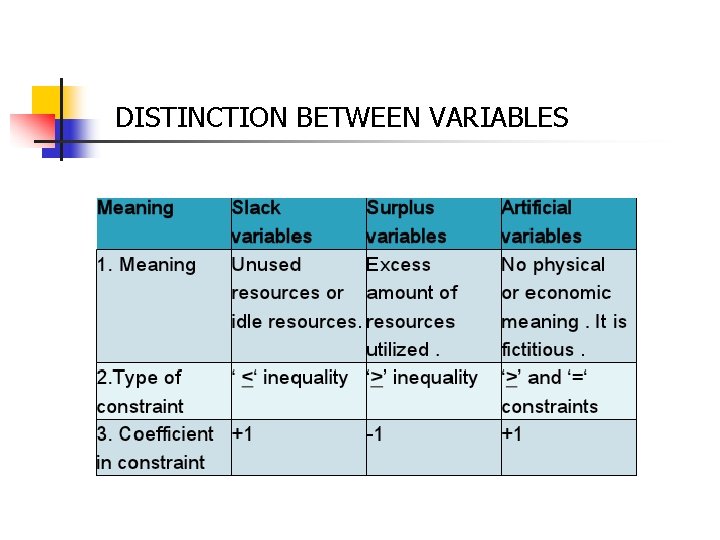
§ § § § Additivity Divisibility Decision Variables Basic Variables Slack Variables Surplus Variables Artificial Variables Optimum Solution

DISTINCTION BETWEEN VARIABLES

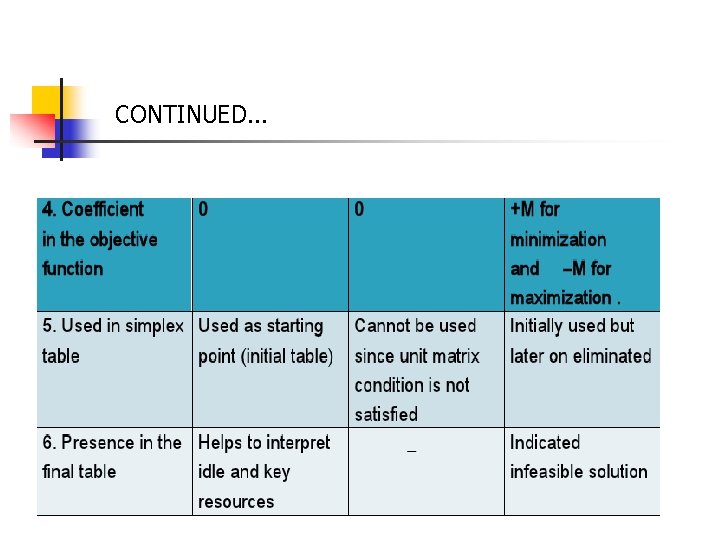
CONTINUED. . .

General Form of LPP (Max. / Min. ) Z = a 1 x 1+a 2 x 2+. . . +anxn (objective function) Subject to constraints : a 11 x 1+a 12 x 2<, =, > b 1 ; a 21 x 1+a 22 x 2<, =, > b 2 ; & x 1, x 2 are not equal to 0 (non-negativity constraint)

Applications Linear programming is a technique for optimizing or making most effective use of given conditions. During the last 40 years applications of the technique in a number of areas have been developed. Some important situations where it is very popular are discussed further.

1. Product Mix : Most popular application of linear programming is product mix decisions i. e. On deciding how much quantity of each product should be made to maximise profit or minimise cost which making best use of the given production facility or considering the limited availability of men, material, machines, money, markets etc. 2. Diet Problem: The diet problem arises whenever the manager is to determine that optimal combination of diet of feed mix which will satisfy specified nutritional requirements and minimize and maximize the total cost of purchasing the diet.

3. The portfolio selection problem : A portfolio selection problem arises whenever a given amount of money is to be allocated among served investment opportunities the portfolio selection problem is quite general in the sense that is can exist for individual fund managers or opportunities. The components of the portfolio can be bonds savings certificates. 4. Media Selections : Lpp has also been used in advertisements field as a decision aid in selecting the effective media. Media helps the marketing managers in allocations a fixed budget across various advertising media like newspaper, magazines, radio and televisions etc. in most of these cases the objective is taken to be the maximization of audience of exposure.

5. Blending Problems : The manufacturing process involves mixing of three various types of materials in specific quantity. Supply of raw materials and these specification are the constraints in obtaining the minimum raw materials cost. Our solution indicates the number of units of each raw materials which are to be blended in one unit of product. 6. Transportation problems : Physical movement of goods from plants to warehouses to wholesalers, wholesalers to retailers, and at last retailers to customers. solutions of the transportation models requires the determinations of how many units should be transported from each supply origin to each demand destinations in order to satisfy all the destinations demands while minimizing the total associated cost of transportations

Administrative Applications • • Linear programming can be used for administrative applications. Administrative Applications of LPP are concerned with optimal usage of resources like men, machine and material. Linear programming helps an administrative incharge in the best possible manner to utilize his resources.

n n Linear programming can be used to make decisions for departmental staff requirements for given period of time. It can be used for work distribution among staff members according to their efficiency, so as to obtain optimum result.

Solution Procedure of LPP For the solution of LPP mathematical model is developed. The mathematical model serves as a basis for initial solution and is improved step by step, till an optimal solution is obtained. There are three stages of solution: n Feasible solution n Basic Feasible solution n Optimal solution

FORMULATION OF LINEAR PROGRAMMING PROBLEM

Problem 1. Problem: A diet for a sick person must contain at least 4000 units of vitamins, 50 units of minerals and 1400 calories. Two foods A and B are available at a cost of Rs. 4 and Rs. 3 per unit respectively. If one unit of food B contains 100 units of vitamins, 2 units of minerals and 40 calories, find by graphical method, what combination of food be used to have least cost?

Solution The mathematical formulation of the problem is as under: Min: Z= 4 x 1 + 3 x 2 (objective function) Subject to: 200 x 1 + 100 x 2 > 4000 x 1 + 2 x 2 > 50 40 x 1 + 40 x 2 > 1400 } } constraints } Where x 1, x 2> 0 (non-negativity constraint)

The above constraints can be simplified as under: 2 x 1+x 2> 40 x 1+x 2 > 35 Now converting the inequalities of the above constraints to equalities in order to plot the constraints on the graph, we get 2 w 1+x 2=40……. (i) x 1+2 x 2=50……. . (ii) x 1+x 2=35……. . (iii)

Problem 2. The Manager of an oil refinery must decide on the optimal mix of 2 possible blending processes of which the inputs and outputs per production run as follows: The maximum availability crude A & B are 250 units and 200 units respectively. The market requirement shows that at least 150 units of gasoline X and 130 units of gasoline Y must be produced. The profit per production run from process 1&2 are Rs. 40 and Rs. 50 respectively. Formulate the problem for maximising the profit.

Solution • Step-1 Let x , y designate the number of production of the two processes respectively. � Step-2 The constraints of the problem are: 6 x + 5 y ≤ 250 3 x+ 6 y ≤ 200 6 x+ 5 y ≤ 150 9 x+ 5 y ≤ 130 � Step-3 The objective is to maximise the total profit. Z = 40 x + 50 y

Step-4 The feasible alternatives are: xᶟ 0 , yᶟ 0 So, the formulated problem is Max. Z = 40 x + 50 y Subject to 6 x 3 x 6 x 9 x + + 5 y 6 y 5 y 5 y ≤ ≤ 250 200 150 130 Where as x, y ᶟ 0

Merits of LPP n n 1. The linear programming technique helps to make the best possible use of available productive resources (such as time, labour, machines etc. ) 2. In a production process, bottle necks may occur. For example, in a factory some machines may be in great demand while others may lie idle for some time. A significant advantage of linear programming is highlighting of such bottle necks.

§ 3. Linear programming helps in studying the information of an organization in such a way that it depicts clear picture of a problem. This scientific approach is very valuable. § 4. Linear programming helps the manager to plan and execute the policies of top management in such a way that cost involved are minimum. It helps to make use of limited resources. § 5. Linear programming highlights the various bottlenecks in problem process and it helps to remove such bottlenecks. § 6. Linear programming is one of the best technique to be used under changing circumstances. It has flexibility to adjust in changing conditions.

Limitations of LPP • Linear Relationship: - One of the basic assumptions of L. P. P is the relationship between variables. But in actual practice many objective functions can be expressed linearly. • Time Effect: - L. P Models do not consider the effect of time. The solution to the problems are good in case of static situation not in case of dynamic situation. • Conflicting multiple goals: - LPP also fails to give a solution if the management has conflicting multiple goals. In LP models there is always one goal which is expressed in the objective function.

• Divisibility of resources : - We have assumed that L. P models are based on perfect divisibility of resources. It means all solution variables should have any value, but in certain situation like in a product mix problem, it can be fractional units. • Complexity: - If there are large number of variables and constraints, then the formulated mathematical model become complex. • Single objective: - L. P deals with the single objective where in real life situation we may come across more than one objective.