1 PEMROGRAMAN LINEAR BULAT Integer Linear Programming ILP

1

PEMROGRAMAN LINEAR BULAT (Integer Linear Programming - ILP) Apa yang dimaksud dengan Pemrograman Bulat ? METODE SIMPLEKS Solusi yang didapat optimal, tetapi mungkin tidak integer. 2

Integer Linear Programming Misalnya saja kita ingin menentukan solusi optimal dari satu lini perakitan televisi, yang memproduksi beberapa tipe televisi. Mengganggu batasan Pembulatan matematis ? ILP 3

Integer Linear Programming ¡ ¡ ¡ Jika model mengharapkan semua variabel basis bernilai integer (bulat positif atau nol), dinamakan pure integer programming. Jika model hanya mengharapkan variabel-variabel tertentu bernilai integer, dinamakan mixed integer programming. Jika model hanya mengharapkan nilai nol atau satu untuk variabelnya, dinamakan zero one integer programming. 4

SOLUSI INTEGER PROGRAMMING PENDEKATAN PEMBULATAN ¡ ¡ ¡ Pendekatan ini mudah dan praktis dalam hal usaha, waktu dan biaya. Pendekatan pembulatan dapat merupakan cara yang sangat efektif untuk masalah integer programming yang besar dimana biaya-biaya hitungan sangat tinggi atau untuk masalah nilai-nilai solusi variabel keputusan sangat besar. Contohnya, pembulatan nilai solusi jumlah pensil yang harus diproduksi dari 14. 250, 2 menjadi 14. 250, 0 semestinya dapat diterima. Sebab utama kegagalan pendekatan ini adalah bahwa solusi yang diperoleh mungkin bukan solusi integer optimum yang sesungguhnya. Solusi pembulatan dapat lebih jelek dibanding solusi integer optimum yang sesungguhnya atau mungkin merupakan solusi tak layak. 5

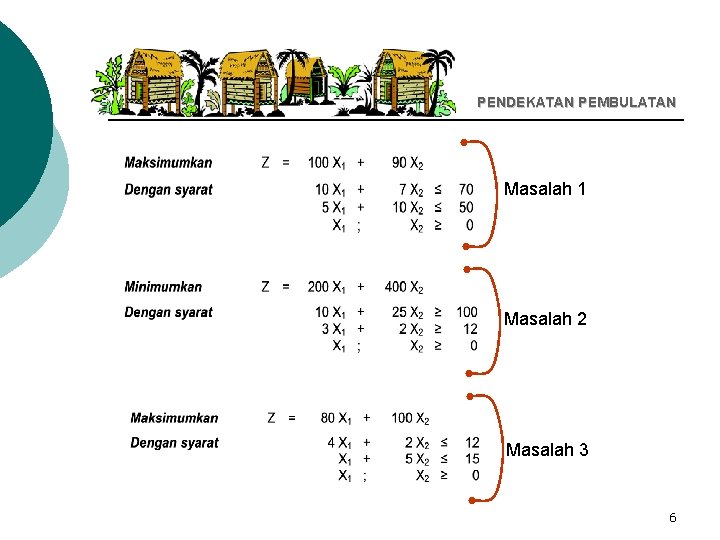
PENDEKATAN PEMBULATAN Masalah 1 Masalah 2 Masalah 3 6

Perbandingan antara solusi dengan metode simpleks tanpa pembatasan bilangan bulat, pembulatan ke bilangan bulat terdekat dan solusi integer optimum yang sesungguhnya untuk ketiga masalah diatas adalah : 7

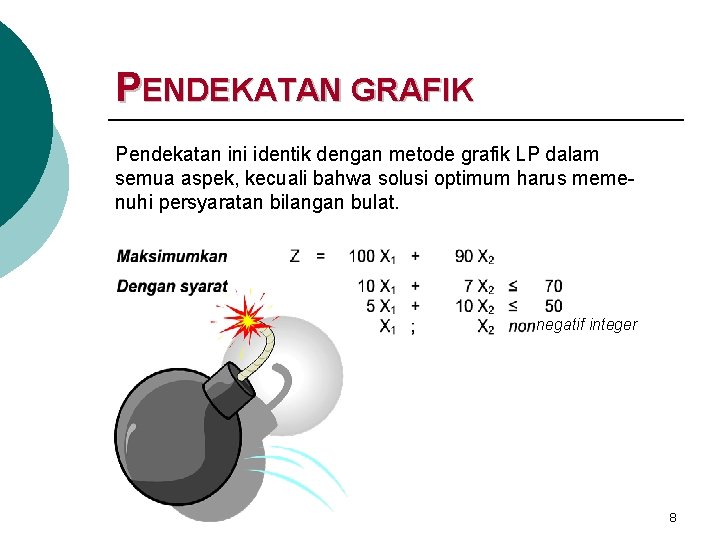
PENDEKATAN GRAFIK Pendekatan ini identik dengan metode grafik LP dalam semua aspek, kecuali bahwa solusi optimum harus memenuhi persyaratan bilangan bulat. negatif integer 8

PENDEKATAN GRAFIK ¡ Model ini serupa dengan model LP biasa. Perbedaanya hanya pada kendala terakhir yang mengharapkan bahwa variabel terjadi pada nilai non negatif integer. ¡ Solusi grafik masalah ini ditunjukkan pada gambar dibawah ini. Ruang solusi layak adalah OABC. Solusi optimum masalah LP ditunjukkan pada titik B, dengan X 1 = 5, 38 dan X 2 = 2, 31 serta Z = 746, 15. Untuk mencari solusi integer optimum masalah ini, garis Z (slope = -9/10) digeser secara sejajar dari titik B menuju titik asal. ¡ Solusi integer optimum adalah titik integer pertama yang bersinggungan dengan garis Z. Titik itu adalah A, dengan X 1 = 7 dan X 2 = 0 serta Z = 700. 9

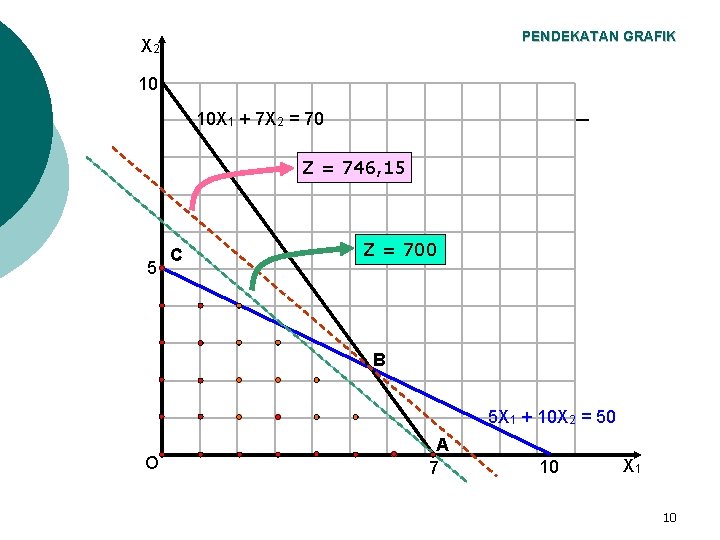
PENDEKATAN GRAFIK X 2 10 10 X 1 + 7 X 2 = 70 Z = 746, 15 5 C Z = 700 B 5 X 1 + 10 X 2 = 50 O A 7 10 X 1 10

PENDEKATAN GOMORY (CUTTING PLANE ALGORITHM) Langkah-langkah prosedur Gomory diringkas seperti berikut : Selesaikan masalah integer programming dengan meng-gunakan metode simpleks. Jika masalah sederhana, ia dapat diselesaikan dengan pendekatan grafik, sehingga pendekatan Gomory kurang efisien. 2. Periksa solusi optimum. Jika semua variabel basis memi -liki nilai integer, solusi optimum integer telah diperoleh dan proses solusi telah berakhir. Jika satu atau lebih variabel basis masih memiliki nilai pecah, teruskan ke tahap 3. 3. Buatlah suatu skala Gomory (suatu bidang pemotong atau cutting plane) dan cari solusi optimum melalui prosedur dual simpleks. Kembali ke tahap 2. 1. 11

KENDALA GOMORY DALAM PURE INTEGER PROGRAMMING Tabel optimum masalah LP dibawah ini merupakan tabel solusi optimum kontinyu. 12

KENDALA GOMORY DALAM PURE INTEGER PROGRAMMING ¡ ¡ Variabel Xi (i =1, …, m) menunjukkan variabel basis. Variabel Xj (j = 1, . . . , n) adalah variabel non basis. Perhatikan persamaan ke i dimana variabel Xi diasumsikan bernilai non integer. Xi = bi – Σ aij Wj , dimana b non integer Kemudian pisahkan bi dan aij menjadi bagian yang bulat dan bagian pecah non negatif seperti berikut : bi = bi + f i jadi f i = bi - bi , dimana 0 ≤ f i ≤ 1 aij = aij + f i jadi f i = aij - aij , dimana 0 ≤ f ij ≤ 1 13

KENDALA GOMORY DALAM PURE INTEGER PROGRAMMING ¡ ¡ ¡ Kendala Gomory yang diinginkan adalah : Sg - f ij Wj = - f i , Sg adalah variabel slack Gomory ke g. Pada umumnya, persamaan kendala yang berhubungan dengan solusi pecah dipilih untuk menghasilkan suatu kendala Gomory. Namun, sebagai aturan main biasanya dipilih persamaan yang memiliki fi, maksimum. 14

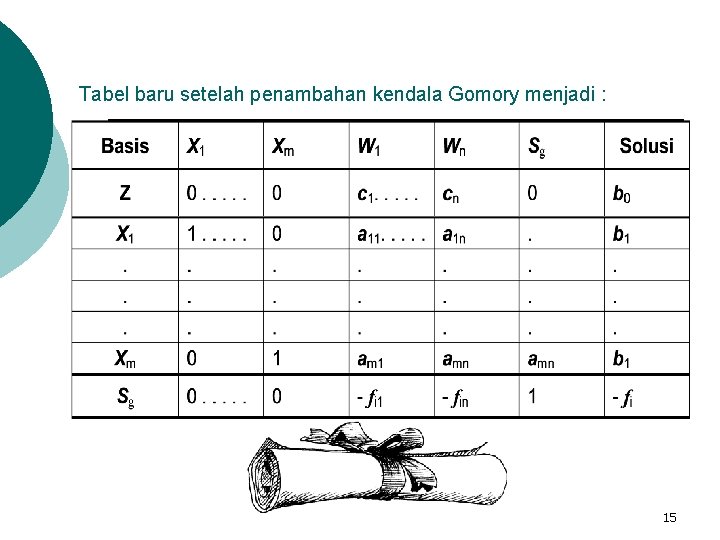
Tabel baru setelah penambahan kendala Gomory menjadi : 15

KENDALA GOMORY DALAM PURE INTEGER PROGRAMMING ¡ Jika diperoleh solusi primal optimum tetapi tidak layak maka digunakan metode dual simpleks. ¡ Proses pembentukan kendala Gomory berakhir jika solusi baru semua berupa bilangan bulat. ¡ Jika tidak, suatu kendala Gomory baru dibuat lagi dari tabel yang dihasilkan dan metode dual simpleks digunakan lagi untuk mengatasi ketidak layakan. ¡ Jika pada setiap iterasi metode dual simpleks menunjukkan bahwa tidak ada solusi layak, berarti masalah itu tidak memiliki solusi integer yang layak. 16

KENDALA GOMORY DALAM PURE INTEGER PROGRAMMING negatif integer Solusi kontinyu optimumnya diperoleh dalam tabel berikut : 17

KENDALA GOMORY DALAM PURE INTEGER PROGRAMMING ¡ Karena solusi tidak bulat, suatu kendala Gomory ditambahkan pada tabel itu. Kedua persamaan (X 1 dan X 2) pada masalah ini memiliki nilai f i yang sama, yaitu f 1 = f 2 = ½ , sehingga salah satu dapat digunakan, misalkan digunakan persamaan X 2 , ini menghasilkan : l l ¡ X 2 + 7/22 S 1 + 1/22 S 2 = 7/2 atau X 2 + (0 + 7/22) S 1 + (0 + 1/22) S 2 = (3 + ½) Sehingga kendala Gomorynya adalah : l Sg 1 - 7/22 S 1 – 1/22 S 2 = - ½ 18

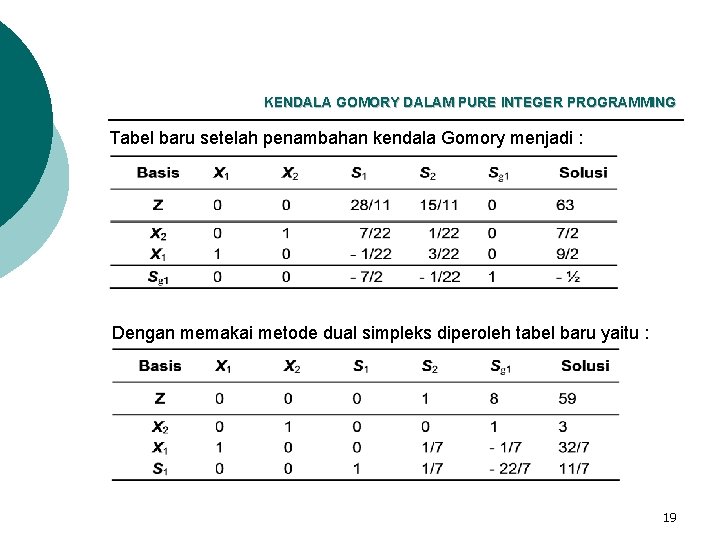
KENDALA GOMORY DALAM PURE INTEGER PROGRAMMING Tabel baru setelah penambahan kendala Gomory menjadi : Dengan memakai metode dual simpleks diperoleh tabel baru yaitu : 19

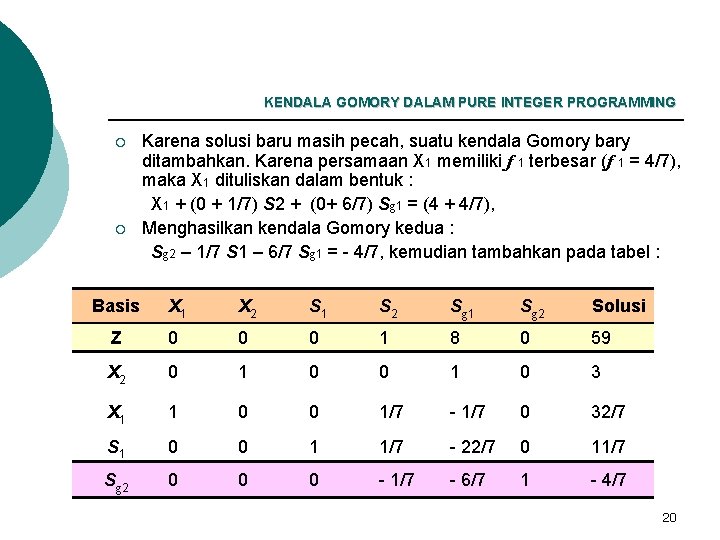
KENDALA GOMORY DALAM PURE INTEGER PROGRAMMING ¡ ¡ Karena solusi baru masih pecah, suatu kendala Gomory bary ditambahkan. Karena persamaan X 1 memiliki f 1 terbesar (f 1 = 4/7), maka X 1 dituliskan dalam bentuk : X 1 + (0 + 1/7) S 2 + (0+ 6/7) Sg 1 = (4 + 4/7), Menghasilkan kendala Gomory kedua : Sg 2 – 1/7 S 1 – 6/7 Sg 1 = - 4/7, kemudian tambahkan pada tabel : Basis X 1 X 2 S 1 S 2 Sg 1 Sg 2 Solusi Z 0 0 0 1 8 0 59 X 2 0 1 0 3 X 1 1 0 0 1/7 - 1/7 0 32/7 S 1 0 0 1 1/7 - 22/7 0 11/7 Sg 2 0 0 0 - 1/7 - 6/7 1 - 4/7 20

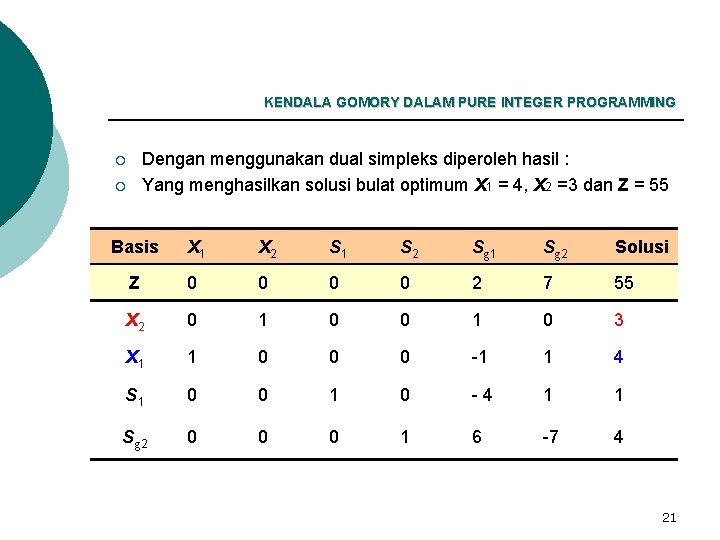
KENDALA GOMORY DALAM PURE INTEGER PROGRAMMING Dengan menggunakan dual simpleks diperoleh hasil : Yang menghasilkan solusi bulat optimum X 1 = 4, X 2 =3 dan Z = 55 ¡ ¡ Basis X 1 X 2 S 1 S 2 Sg 1 Sg 2 Solusi Z 0 0 2 7 55 X 2 0 1 0 3 X 1 1 0 0 0 -1 1 4 S 1 0 0 1 0 -4 1 1 Sg 2 0 0 0 1 6 -7 4 21

METODE BRANCH DAN BOUND Metode Branch dan Bound telah menjadi kode komputer standar untuk integer programming, dan penerapan- penerapan dalam praktek tampaknya menyarankan bahwa metode ini lebih efisien dibanding dengan pendekatan Gomory. Teknik ini dapat diterapkan baik untuk masalah pure programming maupun mixed integer programming. 22

Langkah-langkah metode Branch dan Bound untuk masalah maksimasi dapat dilakukan seperti berikut : 1. Selesaikan LP dengan metode simpleks biasa 2. Teliti solusi optimumnya. Jika variabel basis yang diharapkan bulat adalah bulat, solusi optimum bulat telah tercapai. 3. Nilai solusi pecah yang layak dicabangkan ke dalam sub-sub masalah. Tujuannya adalah untuk menghilangkan solusi kontinyu yang tidak memenuhi persyaratan bulat dalam masalah itu. 4. Untuk setiap sub-masalah, nilai solusi optimum kontinyu fungsi tujuan ditetapkan sebagai batas. Solusi bulat terbaik menjadi batas bawah (pada awalnya, ini adalah solusi kontinyu yang dibulatkan ke bawah). Sub-sub masalah yang memiliki batas kurang dari batas bawah yang ada, tidak diikut sertakan pada analisa selanjutnya. Suatu solusi bulat layak adalah sama baik atau lebih baik dari batas untuk setiap sub masalah yang dicari. Jika solusi yang demikian terjadi, suatu sub masalah dengan batas terbaik dipilih untuk dicabangkan. Kembali ke langkah 3. 23

METODE BRANCH DAN BOUND ¡ Untuk memperoleh gambaran yang lebih jelas tentang metode Branch dan Bound, perhatikan contoh masalah berikut : negatif integer ¡ Solusi optimum kontinyu masalah ini adalah X 1 = 8, X 2 = 2, 26 dan Z = 35, 25. ¡ Solusi ini menunjukkan batas awal. 24

METODE BRANCH DAN BOUND ¡ ¡ ¡ Batas bawah adalah solusi yang dibulatkan ke bawah X 1 = 8, X 2 = 2 dan Z = 34. Dalam metode Branch dan Bound, masalah itu dibagi ke dalam dua bagian untuk mencari nilai solusi bulat yang mungkin bagi X 1 dan X 2. Variabel dengan nilai solusi pecah terbesar dipilih. Karena pada solusi ini hanya X 2 yang memiliki bagian pecah, ia dipilih. Untuk menghilangkan bagian pecah dari nilai X 2 = 2, 25, dua kendala baru dibuat. Kendala-kendala ini mewakili dua bagian baru dari masalah itu. Dua nilai bulat terdekat terhadap 2, 25 adalah 2 dan 3. Sehingga diperoleh dua masalah baru melalui dua kendala mutually exclusive, X 2 ≤ 2 dan X 2 ≥ 3, yang akan diuraikan berikut ini sebagai bagian A dan B. Kendala-kendala ini secara efektif menghilangkan semua nilai pecah yang mungkin bagi X 2, antara 2 dan 3. Pengaruhnya mereka mengurangi ruang solusi layak sehingga angka solusi bulat yang dievaluasi pada masalah ini makin sedikit 25

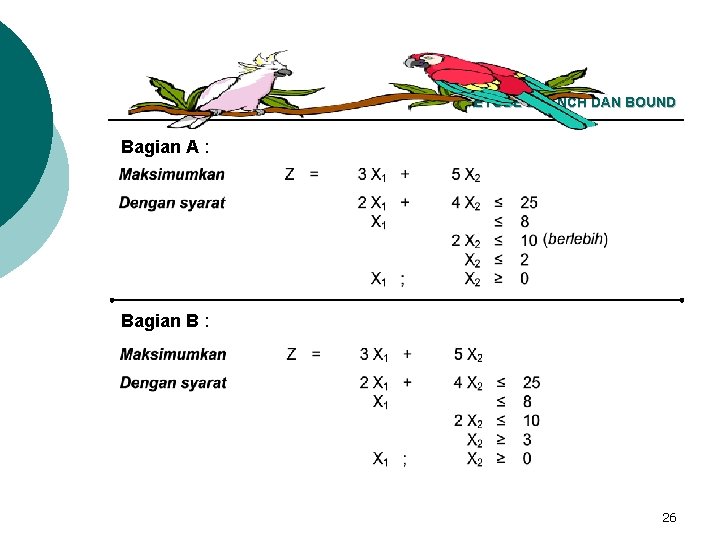
METODE BRANCH DAN BOUND Bagian A : Bagian B : 26

METODE BRANCH DAN BOUND ¡ Bagian A dan B diselesaikan tanpa pembatasan bilangan bulat dengan metode simpleks. Solusi simpleksnya adalah : l l Bagian A : X 1 = 8, X 2 = 2 dan Z = 34 Bagian B : X 1 = 6, 5, X 2 = 3 dan Z = 34, 5 ¡ Bagian A menghasilkan suatu solusi yang semuanya bulat. Untuk bagian A batas dan bawah adalah Z = 34. Solusi pecah bagian B membenarkan pencarian lebih lanjut karena menghasilkan nilai fungsi tujuan yang lebih besar dari batas bagian A. Sangat mungkin bahwa pencarian lebih lanjut dapat menghasilkan suatu solusi yang semuanya bulat dengan nilai fungsi tujuan melebihi batas bagian A = 34. ¡ Bagian B dicabangkan ke dalam dua sub bagian, B 1 dan B 2, pertama dengan kendala X 1 ≤ 6 dan yang lain dengan X 2 ≥ 7. 27

METODE BRANCH DAN BOUND Sub Bagian B 1 : (berlebih) Sub Bagian B 2 : 28

METODE BRANCH DAN BOUND ¡ Solusi simpleksnya adalah : l l ¡ Sub-bagian B 1 : X 1 = 6, X 2 = 3, 25 dan Z = 34, 25 Sub-bagian B 2 : tidak layak. Karena sub-bagian B 1 menghasilkan nilai fungsi tujuan yang lebih besar dari 34 (batas bagian A), maka harus dicabangkan lagi ke dalam dua sub masalah, dengan kendala X 2 ≤ 3 dan X 2 ≥ 4. Kedua kendala sub masalah diberi nama bagian B 1 a dan B 2 b. 29

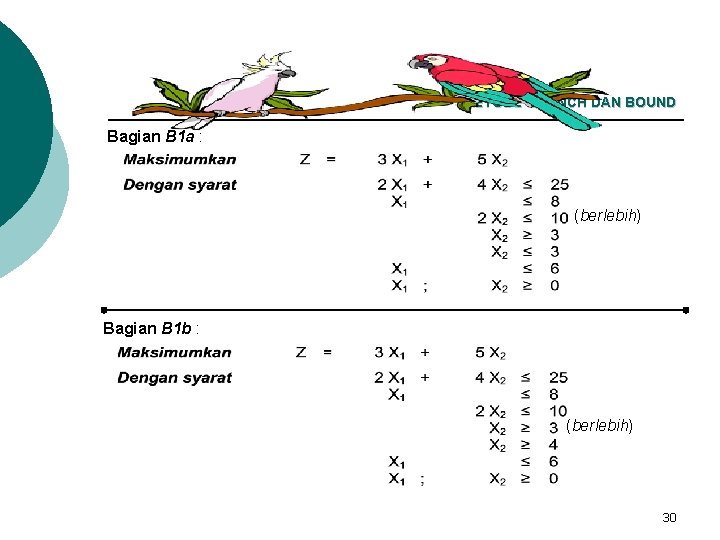
METODE BRANCH DAN BOUND Bagian B 1 a : (berlebih) Bagian B 1 b : (berlebih) 30

METODE BRANCH DAN BOUND ¡ Solusi optimum dengan metode simpleks adalah : l l Sub-bagian B 1 a : X 1 = 6, X 2 = 3 dan Z = 33 Sub-bagian B 1 b : X 1 = 4, 25, X 2 = 4 dan Z = 33, 5 ¡ Kedua solusi itu memiliki batas ( Z = 33 dan Z = 33, 5) yang lebih buruk dibanding dengan solusi yang dihasilkan oleh bagian A. Karena itu, solusi bulat optimum adalah X 1 = 8, X 2 = 2 dan Z = 34 yang dihasilkan oleh bagian A. ¡ Jika pencarian telah diselesaikan, solusi bulat dengan fungsi tujuan tertinggi (dalam masalah maksimasi) dipilih sebagai solusi optimum. 31

METODE BRANCH DAN BOUND ¡ Kelemahan dasar dari metode ini adalah bahwa diperlukan pemecahan masalah LP untuk setiap pencabangan. Dalam masalah yang besar dapat memakan banyak waktu. Karena itu dalam prosedur pencabangan dan pencarian, analisa selanjutnya dihentikan jika : 1. Hasil dari sub-problem lebih jelek dibanding dengan batas yang sudah diidentifikasi 2. Pencabangan selanjutnya menghasilkan solusi tak layak. 32

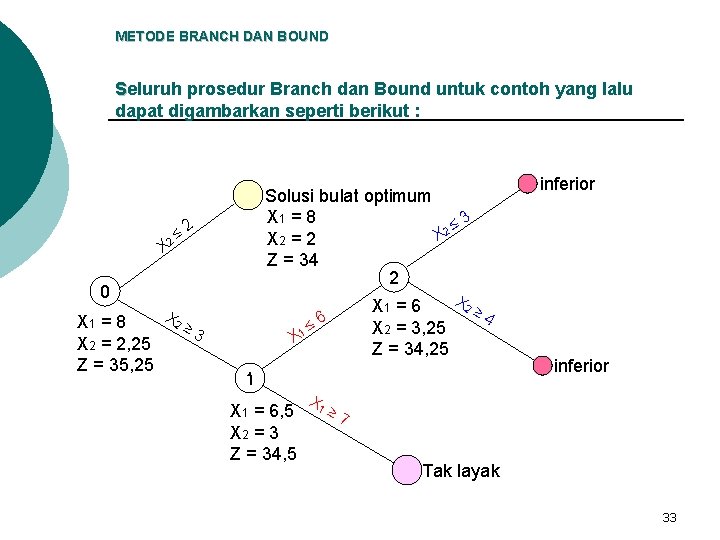
METODE BRANCH DAN BOUND Seluruh prosedur Branch dan Bound untuk contoh yang lalu dapat digambarkan seperti berikut : X 2 ≤ Solusi bulat optimum X 1 = 8 3 2≤ X X 2 = 2 Z = 34 2 2 0 X 2 X 1 = 8 ≥ 3 X 2 = 2, 25 Z = 35, 25 X 1 ≤ 6 X 2 X 1 = 6 ≥ 4 X 2 = 3, 25 Z = 34, 25 1 X 1 = 6, 5 X 2 = 3 Z = 34, 5 X 1 inferior ≥ 7 Tak layak 33