Grundlagen der Algorithmen und Datenstrukturen Kapitel 5 Prof

Grundlagen der Algorithmen und Datenstrukturen Kapitel 5 Prof. Dr. Christian Scheideler (Stv: Stefan Schmid) SS 2008 6/10/2021 Kapitel 5 1

Ein paar Infos vorweg. . . - Kapitel 0 -4 sind relevant für Klausur (also inkl. Hashing)! - Notenbonus der Uebungen gilt nicht, falls Prüfung nicht bestanden. - Gesamtnote = 50% Mid + 50% End - Probeprüfung auf Web (Lösung? ) - Mitnehmen: Handschriftliches DIN A 4 Blatt 6/10/2021 Kapitel 5 2

6/10/2021 Kapitel 5 3

Wörterbuch S: Menge von Elementen Jedes Element e identifiziert über key(e). Operationen: • S. insert(e: Element): S: =S [ {e} • S. remove(k: Key): S: =Sn{e}, wobei e das Element ist mit key(e)=k • S. find(k: Key): Falls es ein e 2 S gibt mit key(e)=k, dann gib e aus, sonst gib ? aus 6/10/2021 Kapitel 5 4

Statisches Wörterbuch Lösungsmöglichkeiten: 1 • Perfektes Hashing – Vorteil: Suche in konstanter Zeit – Nachteil: keine Ordnung auf Elementen, d. h. Bereichsanfragen (alle Namen, die mit A anfangen) teuer 3 14 5 5 10 14 19 3 19 1 10 • Speicherung der Daten in sortiertem Feld 1 3 5 10 14 19 Wie geht das? – Vorteil: Bereichsanfragen möglich – Nachteil: Suche teurer (logarithmische Zeit) 6/10/2021 Kapitel 5 5

Wieso Sortieren? • Telefonbuch ohne Sortierung nach Namen? • Beispiel aus dem Skript: Statistik bei Volkszählung – Bei der US Volkzählung 1880 benötigten 1500 Leute 7 Jahre um die Daten zu zählen und ordnen – Herman Hollerith baute darauf hin Sortiermaschinen, welche die Bearbeitungszeit der nächsten Zählung trotz grösserer Population auf 1 Jahr reduzierte. – Ursprung von IBM – Sortieren (Pre-processing) hilft vielerlei Fragen effizient zu beantworten: e. g. , finde alle Personen zw. 20 und 30 die auf einem Bauernhof leben 6/10/2021 Kapitel 5 6

Sortierproblem • Eingabe: Sequenz s = <e 1, …, en> mit Ordnung <= auf den Schlüsseln key(ei) (Beispiel: 5 10 19 1 14 3 ) • Ausgabe: Sequenz s´ = <e´ 1, …, e´n>, so dass key(ei)<=key(ei+1) für alle 1<=i<n und s´ eine Permutation von s ist (Beispiel: 1 3 5 10 14 19 ) 6/10/2021 Kapitel 5 7

Ordnungen • Ordnung auf Zahlen: klar • Ordnung auf Vektoren: z. B. Länge des Vektors • Ordnung auf Namen: lexikographische Ordnung (erst alle Namen, die mit A beginnen, dann B, usw. ) 6/10/2021 Kapitel 5 8

Einfache Sortierverfahren Selection Sort: nimm wiederholt das kleinste Element aus der Eingabesequenz, lösche es, und hänge es an das Ende der Ausgabesequenz an. Beispiel: 6/10/2021 <4, 7, 1, 1> | <> ! <4, 7, 1> | <1> ! <4, 7> | <1, 1> ! <7> | <1, 1, 4> ! <> | <1, 1, 4, 7> Kapitel 5 9

Einfache Sortierverfahren Selection Sort: nimm wiederholt das kleinste Element aus der Eingabesequenz, lösche es, und hänge es an das Ende der Ausgabesequenz an. Zeitaufwand (worst case): • Minimumsuche in Feld der Größe i: (i) • Gesamtzeit: i=1. . n (i) = (n 2) 6/10/2021 Kapitel 5 10

Selection Sort Procedure Selection. Sort(a: Array [1. . n] of Element) for i: =1 to n-1 do // bewege min{a[i], …, a[n]} nach a[i] for j: =i+1 to n do if a[i]>a[j] then a[i] $ a[j] Vorteil: sehr einfach zu implementieren (1 Array reicht!), also gut für kurze Sequenzen Nachteil: kann für lange Sequenzen lange dauern 6/10/2021 Kapitel 5 11

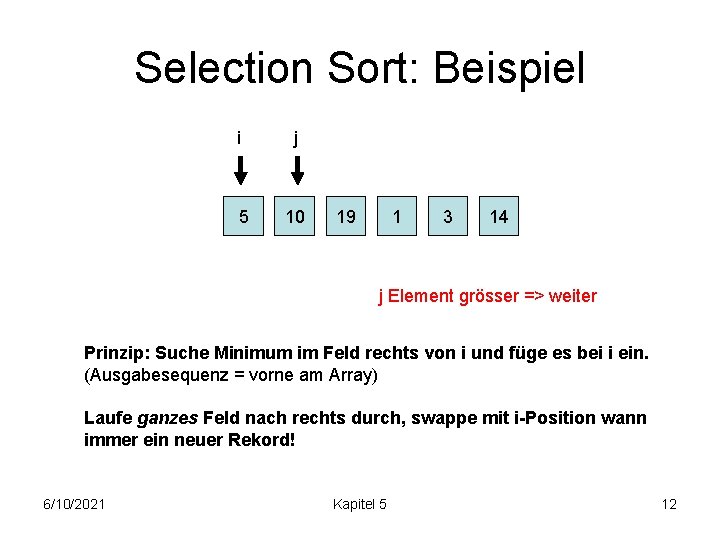
Selection Sort: Beispiel i j 5 10 19 1 3 14 j Element grösser => weiter Prinzip: Suche Minimum im Feld rechts von i und füge es bei i ein. (Ausgabesequenz = vorne am Array) Laufe ganzes Feld nach rechts durch, swappe mit i-Position wann immer ein neuer Rekord! 6/10/2021 Kapitel 5 12

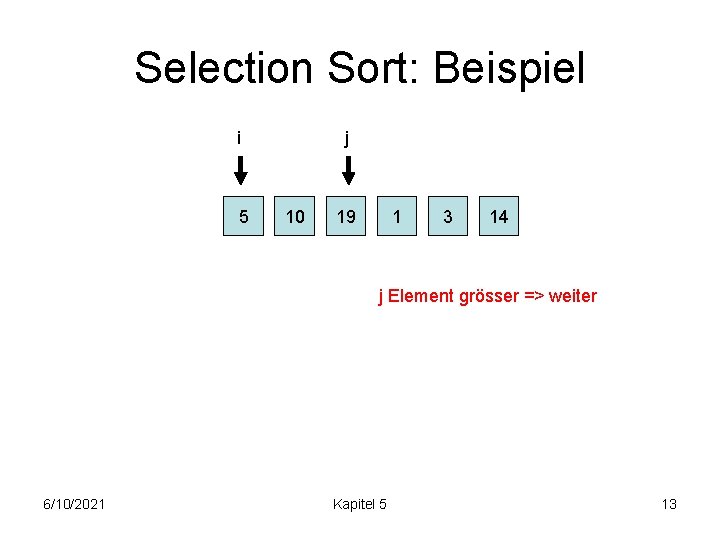
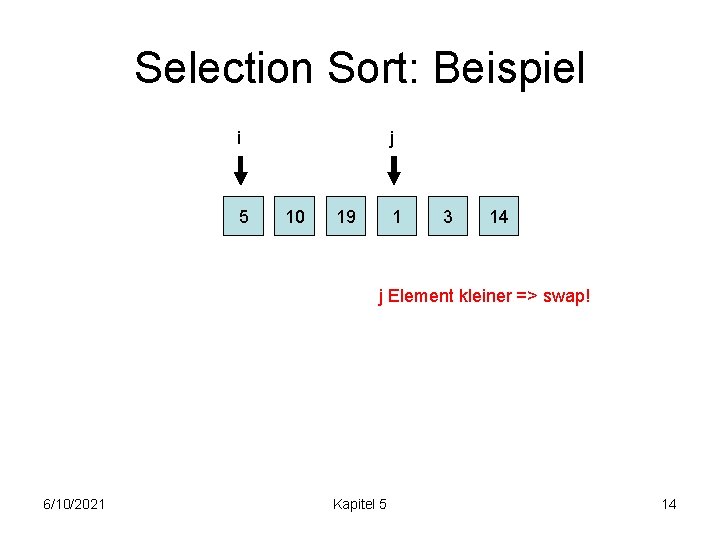
Selection Sort: Beispiel i 5 j 10 19 1 3 14 j Element grösser => weiter 6/10/2021 Kapitel 5 13

Selection Sort: Beispiel i 5 j 10 19 1 3 14 j Element kleiner => swap! 6/10/2021 Kapitel 5 14

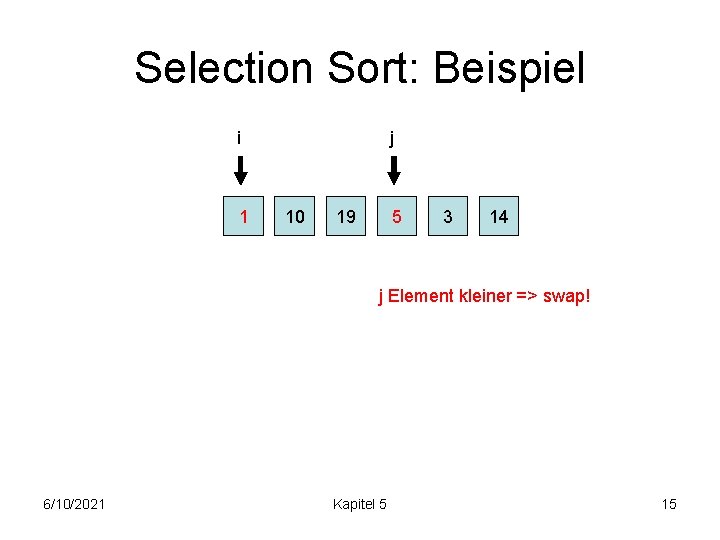
Selection Sort: Beispiel i 1 j 10 19 5 3 14 j Element kleiner => swap! 6/10/2021 Kapitel 5 15

Selection Sort: Beispiel i 1 j 10 19 5 3 14 j Element grösser => weiter! 6/10/2021 Kapitel 5 16

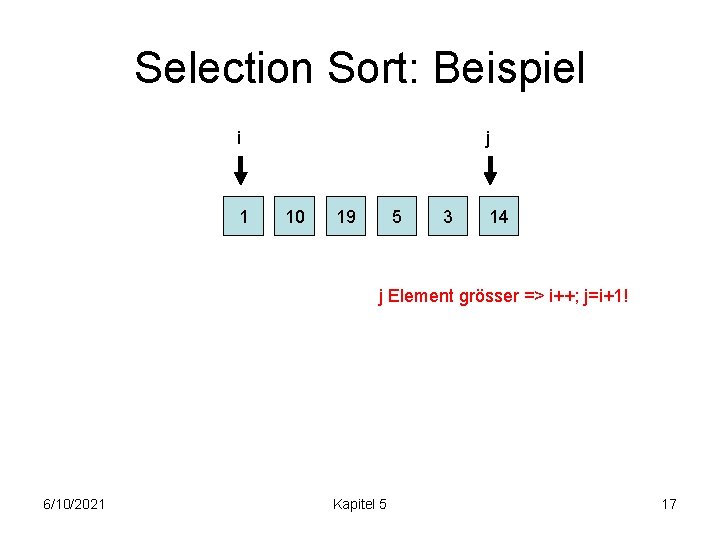
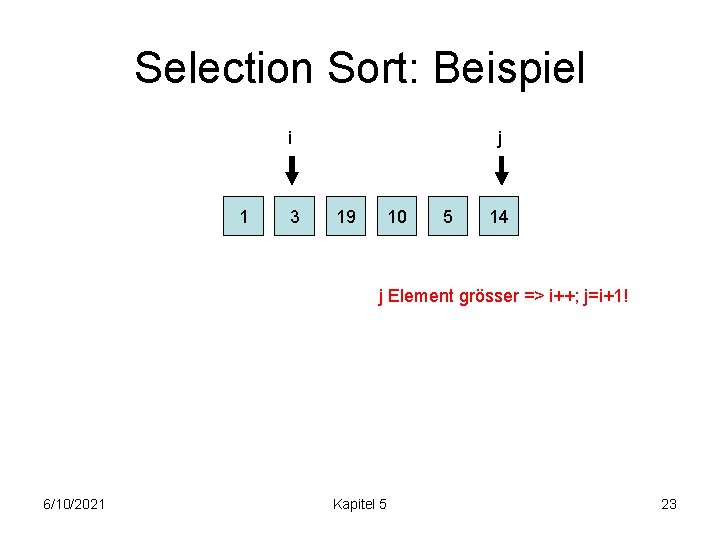
Selection Sort: Beispiel i 1 j 10 19 5 3 14 j Element grösser => i++; j=i+1! 6/10/2021 Kapitel 5 17

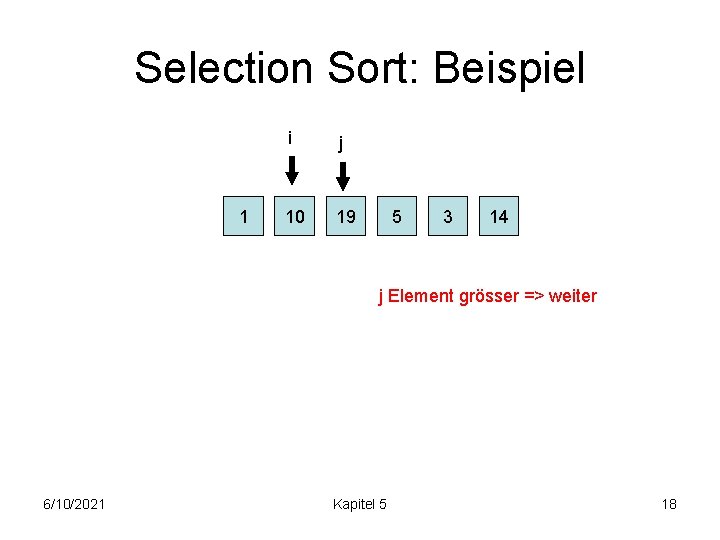
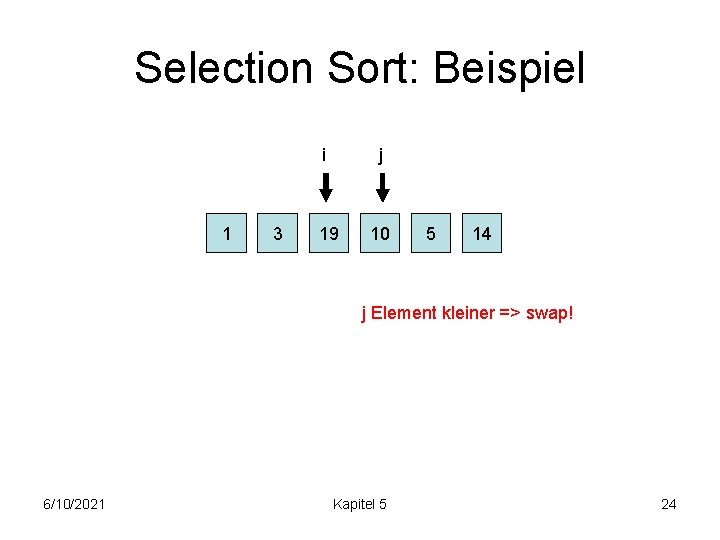
Selection Sort: Beispiel 1 i j 10 19 5 3 14 j Element grösser => weiter 6/10/2021 Kapitel 5 18

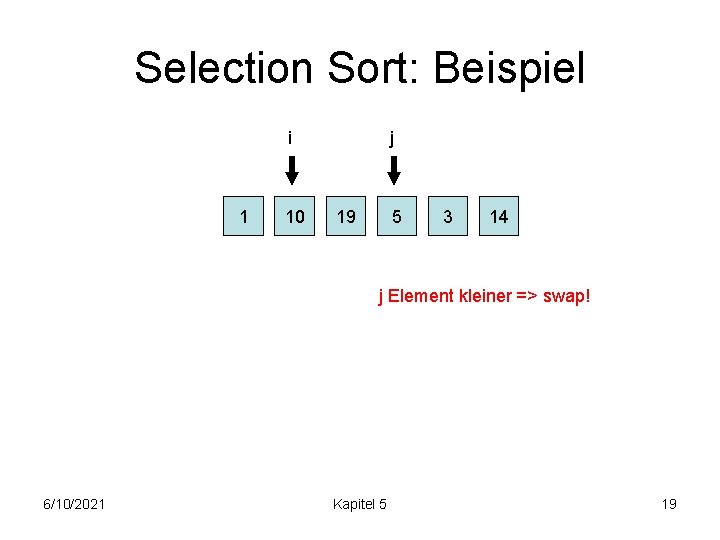
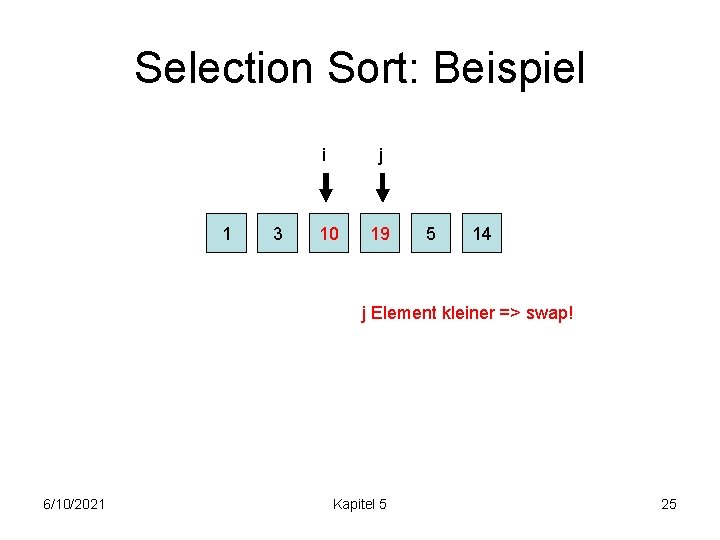
Selection Sort: Beispiel i 1 10 j 19 5 3 14 j Element kleiner => swap! 6/10/2021 Kapitel 5 19

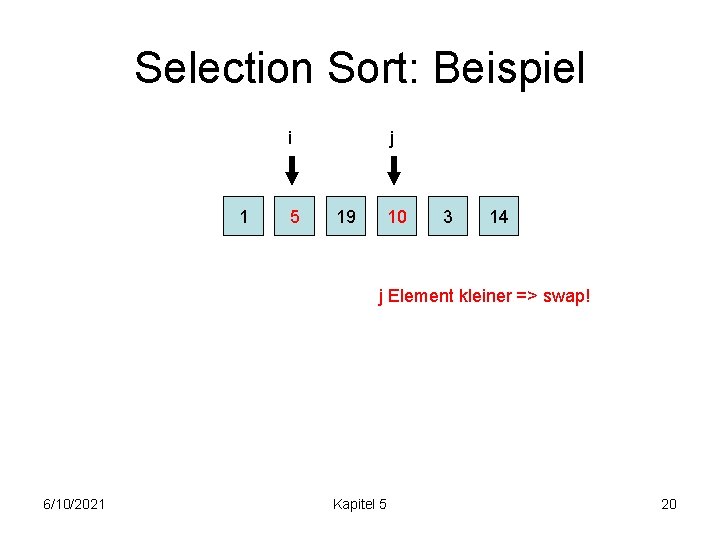
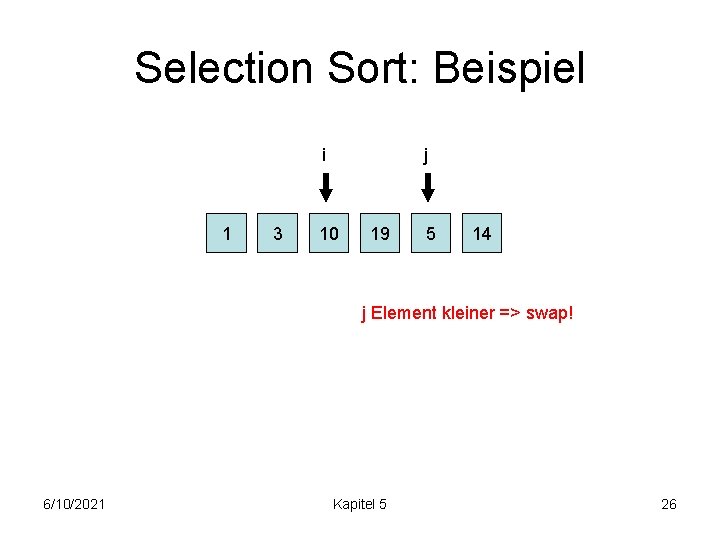
Selection Sort: Beispiel i 1 5 j 19 10 3 14 j Element kleiner => swap! 6/10/2021 Kapitel 5 20

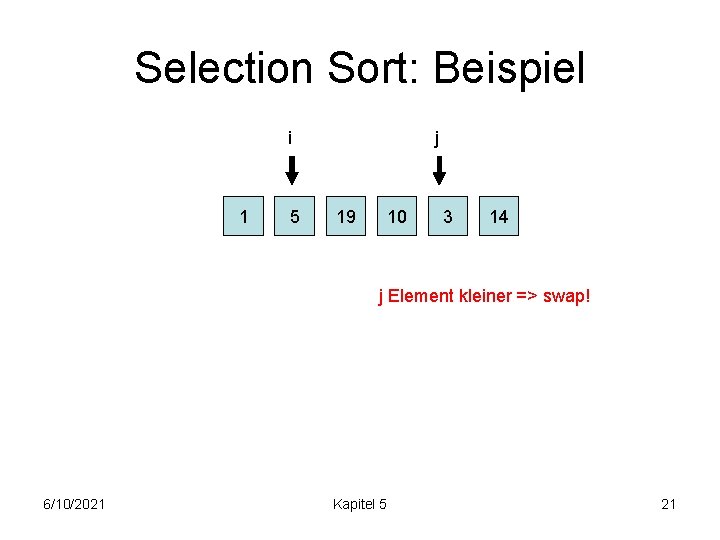
Selection Sort: Beispiel i 1 5 j 19 10 3 14 j Element kleiner => swap! 6/10/2021 Kapitel 5 21

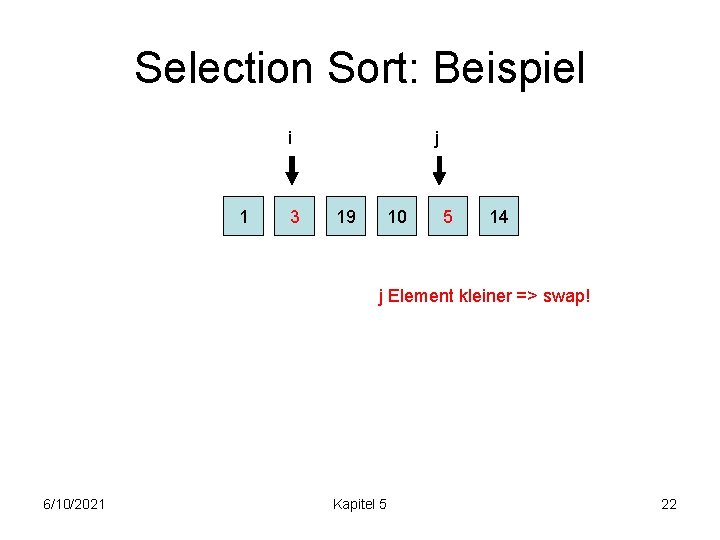
Selection Sort: Beispiel i 1 3 j 19 10 5 14 j Element kleiner => swap! 6/10/2021 Kapitel 5 22

Selection Sort: Beispiel i 1 3 j 19 10 5 14 j Element grösser => i++; j=i+1! 6/10/2021 Kapitel 5 23

Selection Sort: Beispiel 1 3 i j 19 10 5 14 j Element kleiner => swap! 6/10/2021 Kapitel 5 24

Selection Sort: Beispiel 1 3 i j 10 19 5 14 j Element kleiner => swap! 6/10/2021 Kapitel 5 25

Selection Sort: Beispiel i 1 3 j 10 19 5 14 j Element kleiner => swap! 6/10/2021 Kapitel 5 26

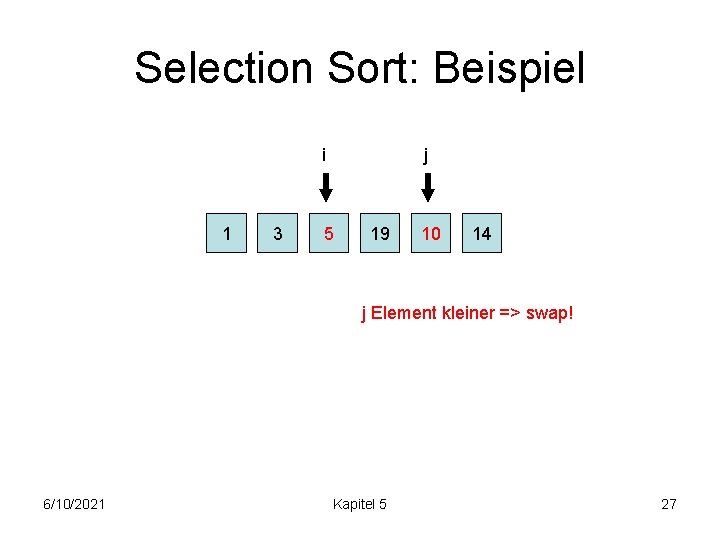
Selection Sort: Beispiel i 1 3 j 5 19 10 14 j Element kleiner => swap! 6/10/2021 Kapitel 5 27

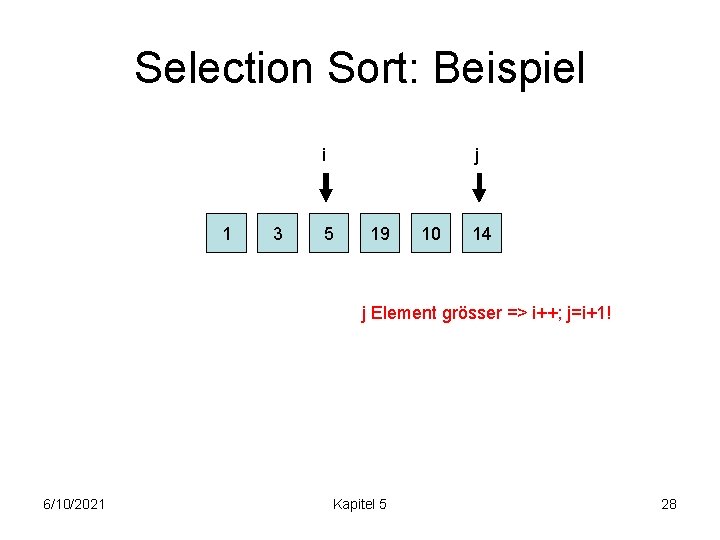
Selection Sort: Beispiel i 1 3 j 5 19 10 14 j Element grösser => i++; j=i+1! 6/10/2021 Kapitel 5 28

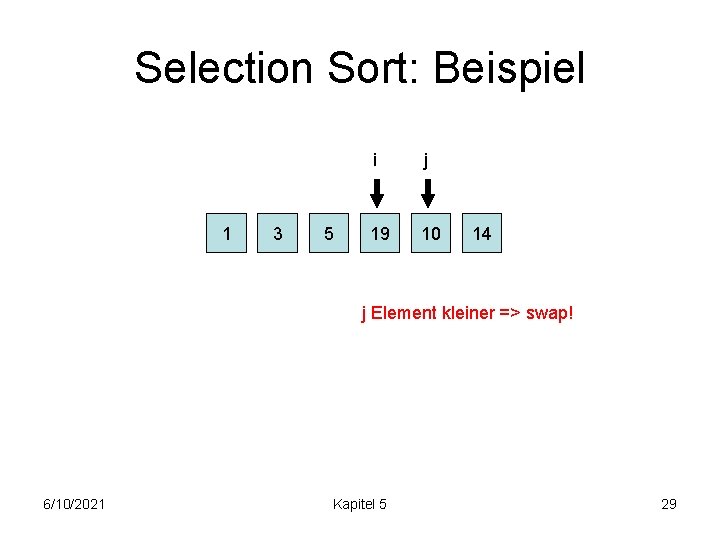
Selection Sort: Beispiel 1 3 5 i j 19 10 14 j Element kleiner => swap! 6/10/2021 Kapitel 5 29

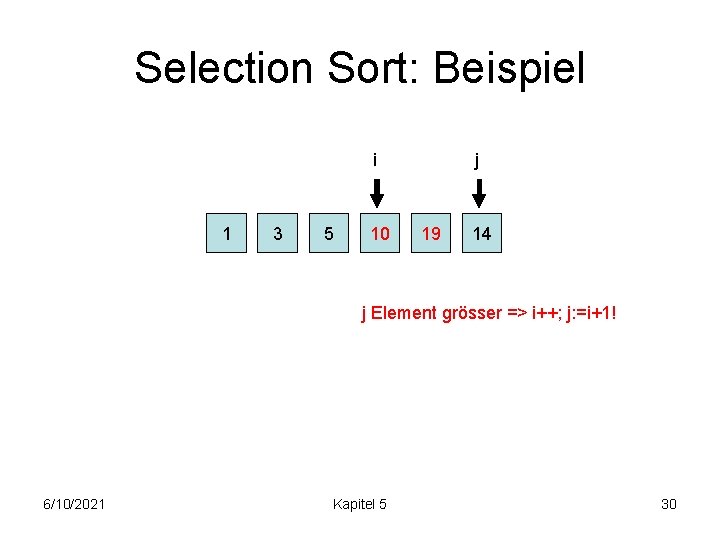
Selection Sort: Beispiel i 1 3 5 10 j 19 14 j Element grösser => i++; j: =i+1! 6/10/2021 Kapitel 5 30

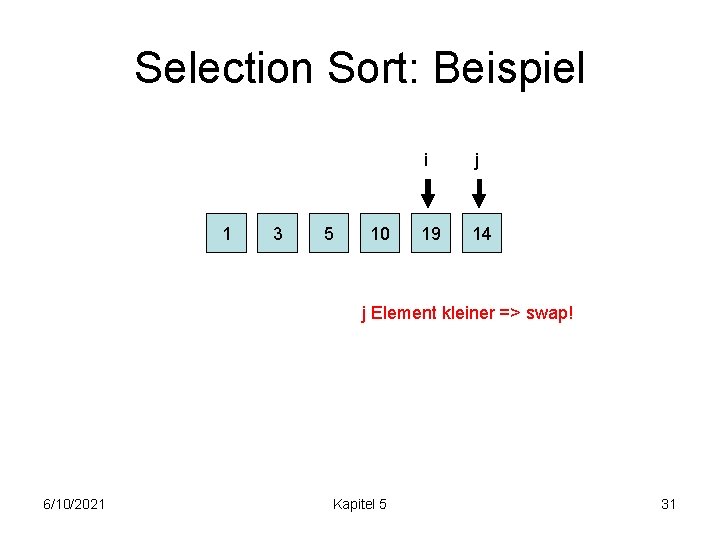
Selection Sort: Beispiel 1 3 5 10 i j 19 14 j Element kleiner => swap! 6/10/2021 Kapitel 5 31

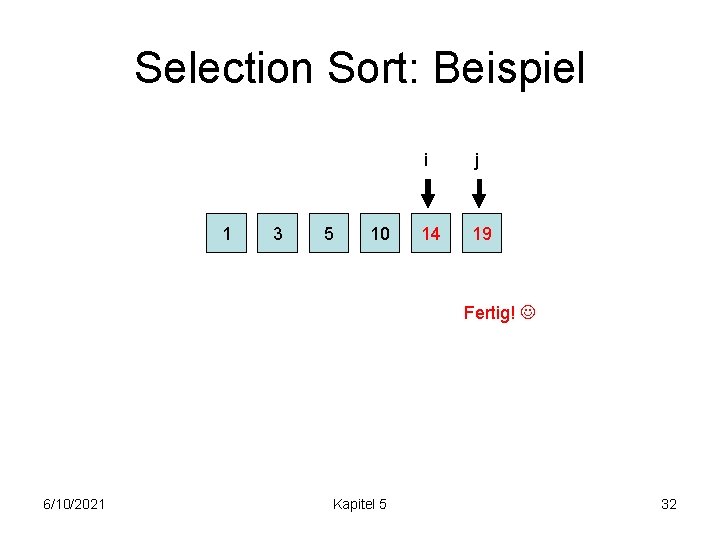
Selection Sort: Beispiel 1 3 5 10 i j 14 19 Fertig! 6/10/2021 Kapitel 5 32

Einfache Sortierverfahren Insertion Sort: nimm Element für Element aus der Eingabesequenz und füge es in der richtigen Position der Ausgabesequenz ein Beispiel: 6/10/2021 <4, 7, 1, 1> | <> ! <7, 1, 1> | <4> ! <1, 1> | <4, 7> ! <1> | <1, 4, 7> ! <> | <1, 1, 4, 7> Kapitel 5 33

Einfache Sortierverfahren Insertion Sort: nimm Element für Element aus der Eingabesequenz und füge es in der richtigen Position der Ausgabesequenz ein Zeitaufwand (worst case): • Einfügung an richtiger Stelle beim i-ten Element: O(i) (wegen Verschiebungen) • Gesamtaufwand: i=1. . n O(i) = O(n 2) Wieso O()? 6/10/2021 Kapitel 5 34

Insertion Sort Procedure Insertion. Sort(a: Array [1. . n] of Element) for i: =2 to n do // bewege a[i] zum richtigen Platz „runterblubbern“ for j: =i-1 downto 1 do if a[j]>a[j+1] then a[j] $ a[j+1] Vorteil: sehr einfach zu implementieren (1 Array genügt auch hier), also gut für kurze Sequenzen Nachteil: kann für lange Sequenzen lange dauern 6/10/2021 Kapitel 5 35

Beispiel (Wikipedia. . . ) 6/10/2021 Kapitel 5 36

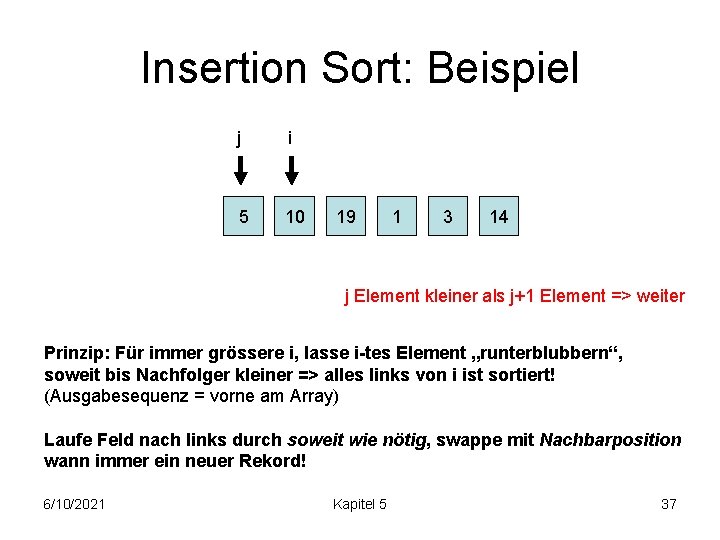
Insertion Sort: Beispiel j i 5 10 19 1 3 14 j Element kleiner als j+1 Element => weiter Prinzip: Für immer grössere i, lasse i-tes Element „runterblubbern“, soweit bis Nachfolger kleiner => alles links von i ist sortiert! (Ausgabesequenz = vorne am Array) Laufe Feld nach links durch soweit wie nötig, swappe mit Nachbarposition wann immer ein neuer Rekord! 6/10/2021 Kapitel 5 37

Insertion Sort: Beispiel 5 j i 10 19 1 3 14 j Element kleiner als j+1 Element => weiter 6/10/2021 Kapitel 5 38

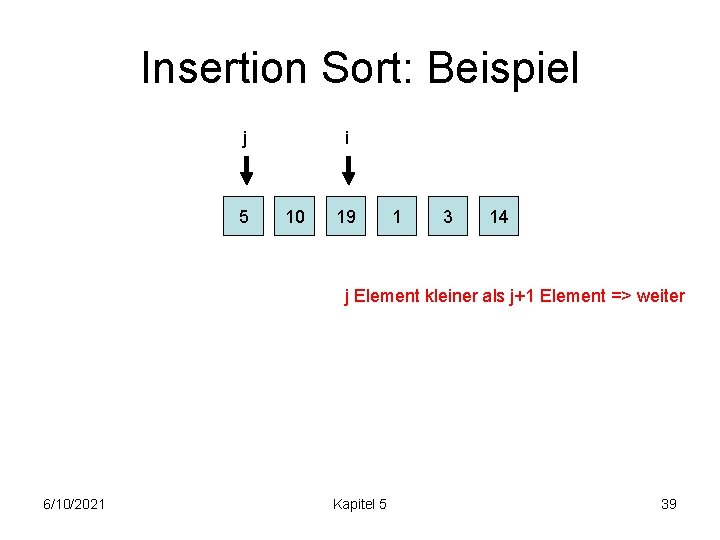
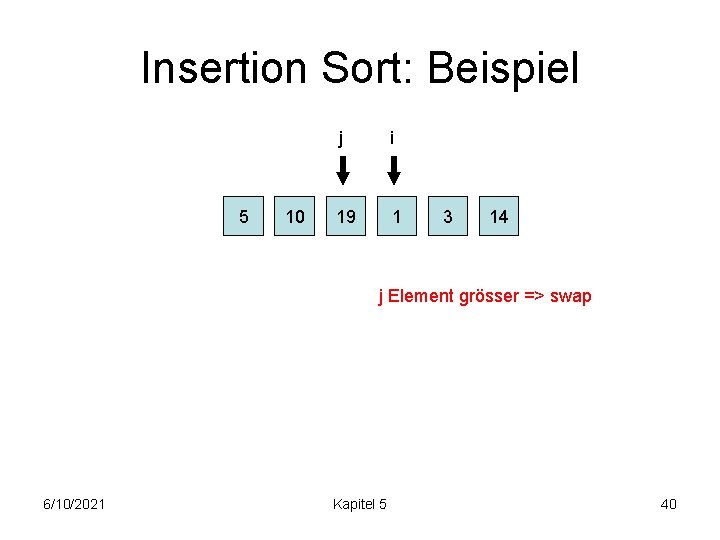
Insertion Sort: Beispiel j 5 i 10 19 1 3 14 j Element kleiner als j+1 Element => weiter 6/10/2021 Kapitel 5 39

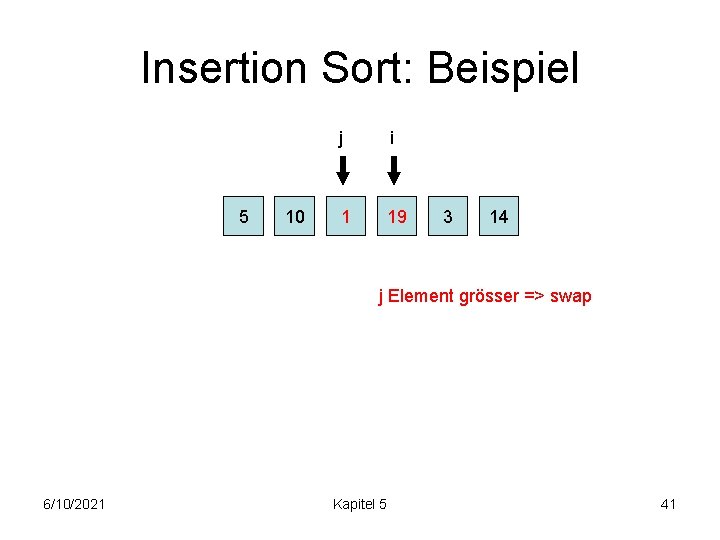
Insertion Sort: Beispiel 5 10 j i 19 1 3 14 j Element grösser => swap 6/10/2021 Kapitel 5 40

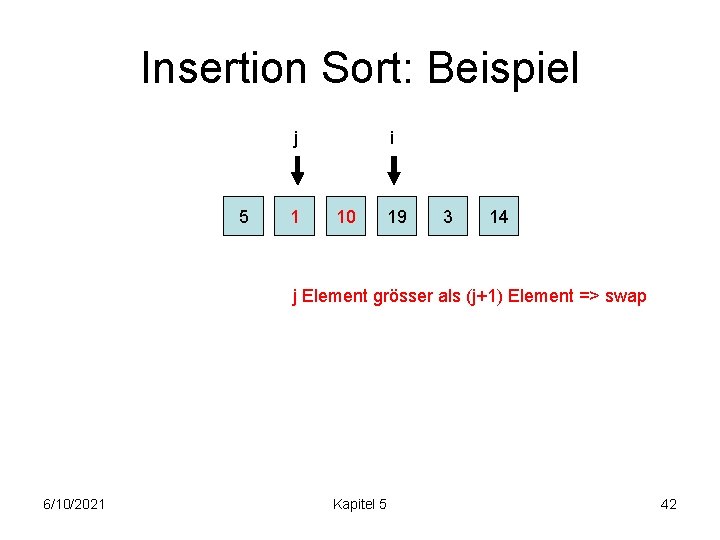
Insertion Sort: Beispiel 5 10 j i 1 19 3 14 j Element grösser => swap 6/10/2021 Kapitel 5 41

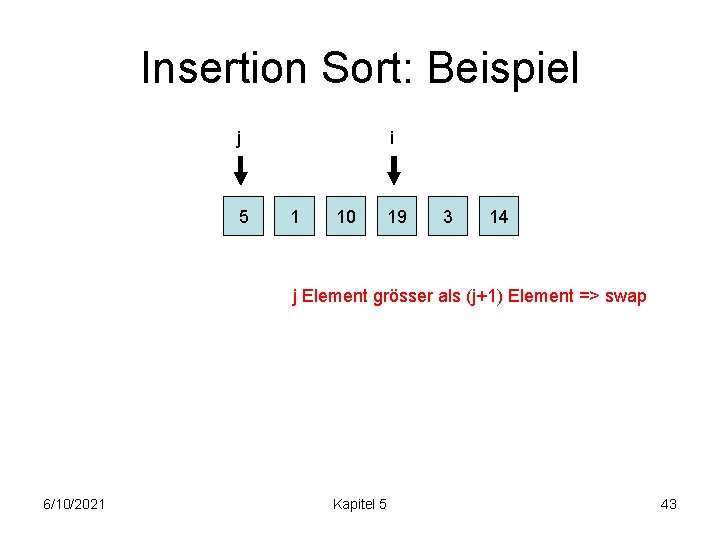
Insertion Sort: Beispiel j 5 1 i 10 19 3 14 j Element grösser als (j+1) Element => swap 6/10/2021 Kapitel 5 42

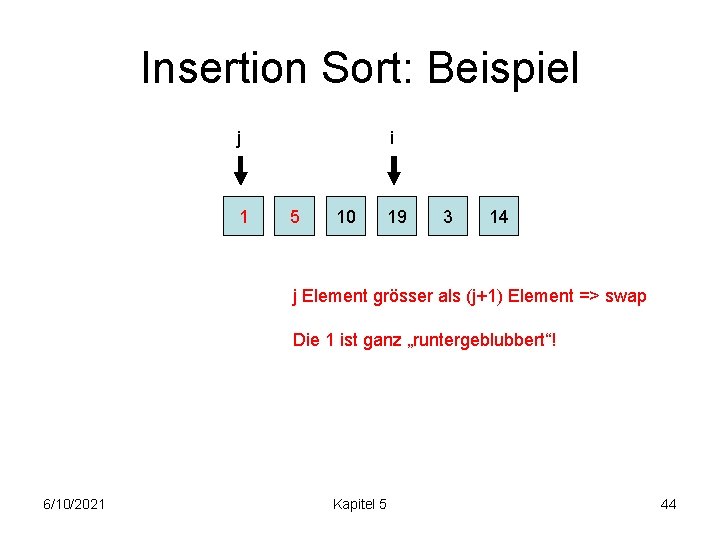
Insertion Sort: Beispiel j 5 i 1 10 19 3 14 j Element grösser als (j+1) Element => swap 6/10/2021 Kapitel 5 43

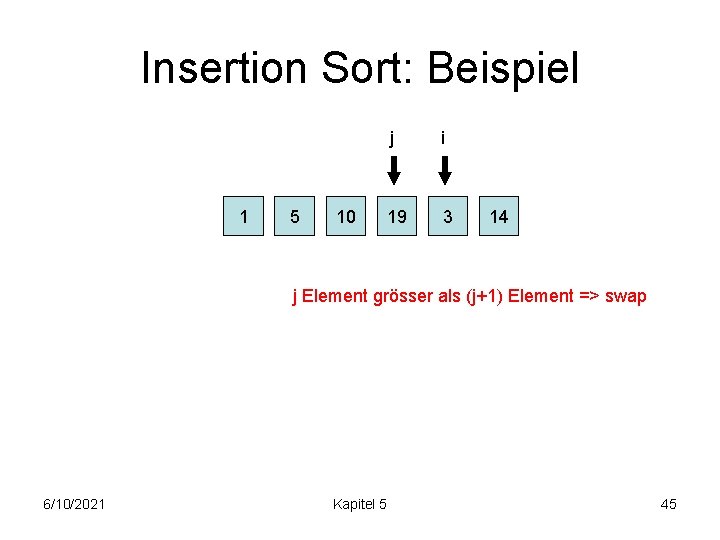
Insertion Sort: Beispiel j 1 i 5 10 19 3 14 j Element grösser als (j+1) Element => swap Die 1 ist ganz „runtergeblubbert“! 6/10/2021 Kapitel 5 44

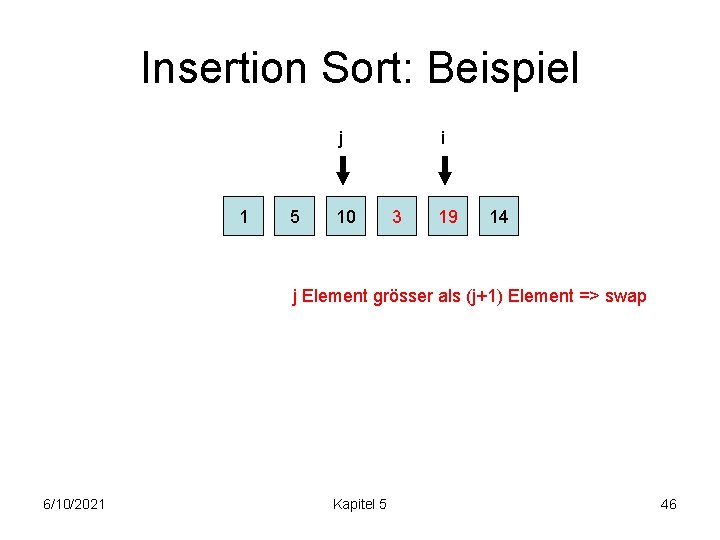
Insertion Sort: Beispiel 1 5 10 j i 19 3 14 j Element grösser als (j+1) Element => swap 6/10/2021 Kapitel 5 45

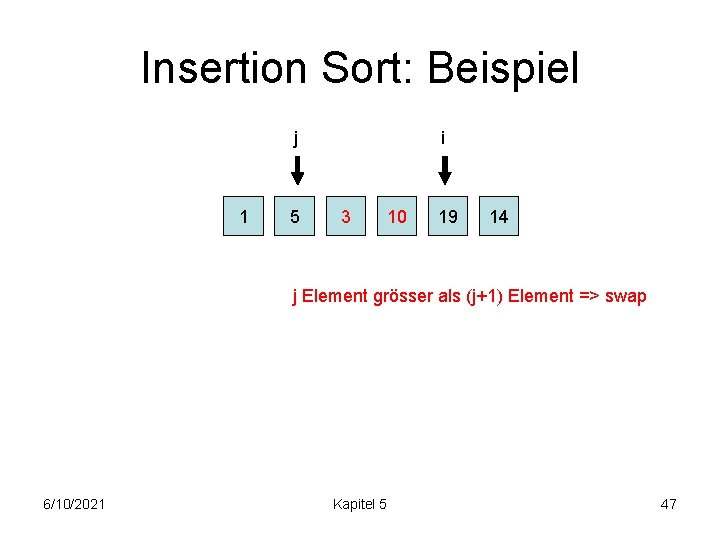
Insertion Sort: Beispiel j 1 5 10 i 3 19 14 j Element grösser als (j+1) Element => swap 6/10/2021 Kapitel 5 46

Insertion Sort: Beispiel j 1 5 i 3 10 19 14 j Element grösser als (j+1) Element => swap 6/10/2021 Kapitel 5 47

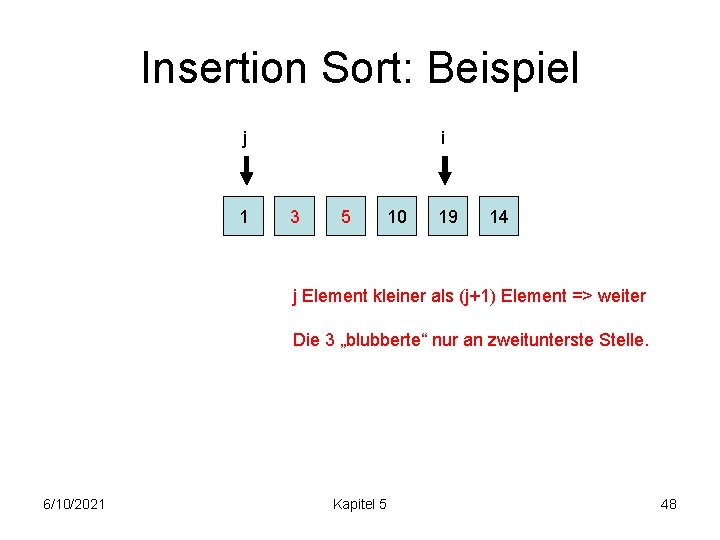
Insertion Sort: Beispiel j 1 i 3 5 10 19 14 j Element kleiner als (j+1) Element => weiter Die 3 „blubberte“ nur an zweitunterste Stelle. 6/10/2021 Kapitel 5 48

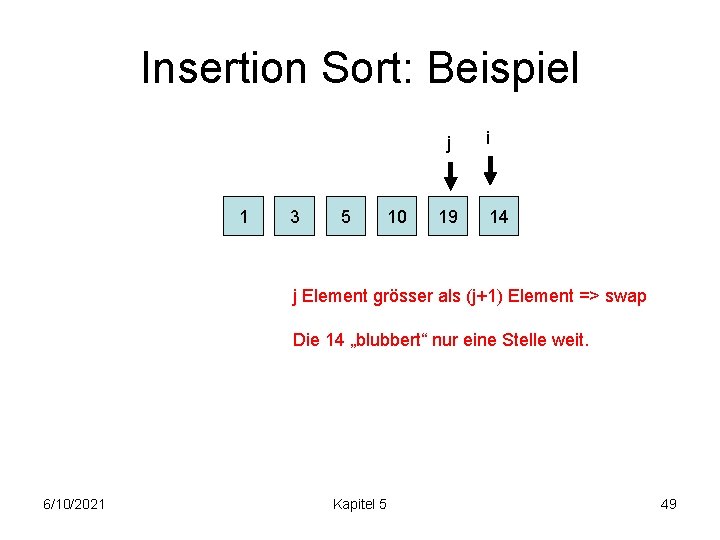
Insertion Sort: Beispiel j 1 3 5 10 19 i 14 j Element grösser als (j+1) Element => swap Die 14 „blubbert“ nur eine Stelle weit. 6/10/2021 Kapitel 5 49

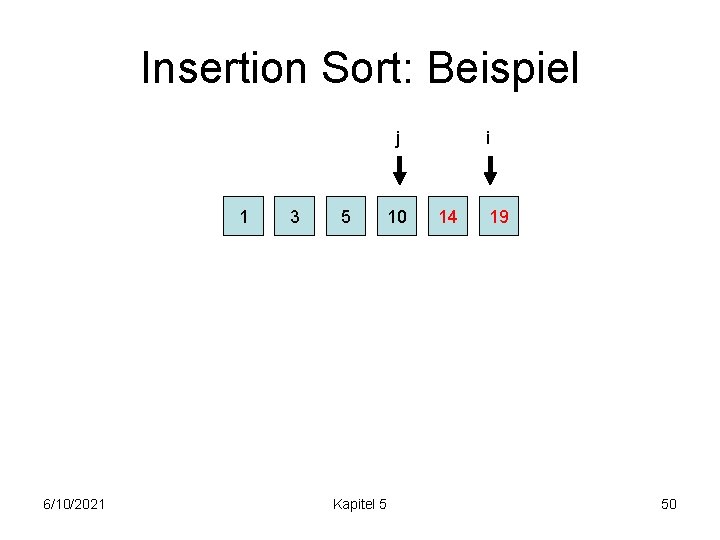
Insertion Sort: Beispiel j 1 6/10/2021 3 5 10 Kapitel 5 i 14 19 50

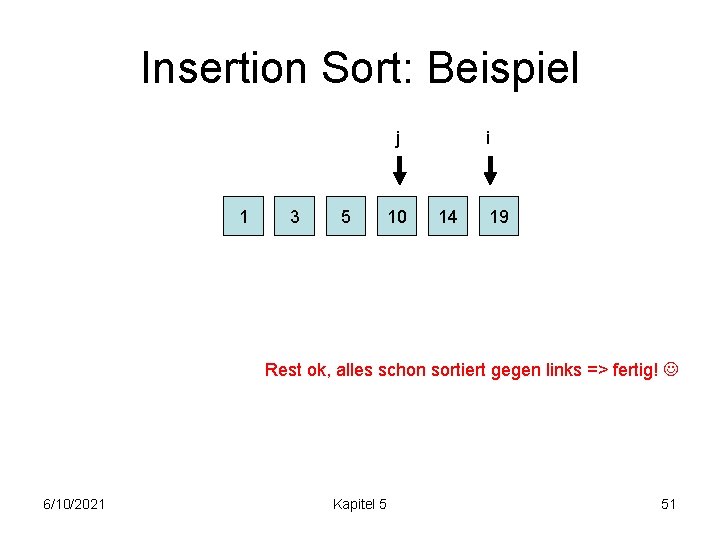
Insertion Sort: Beispiel j 1 3 5 10 i 14 19 Rest ok, alles schon sortiert gegen links => fertig! 6/10/2021 Kapitel 5 51

Einfache Sortierverfahren Selection Sort: • Mit besserer Minimumstrategie worst-case Laufzeit O(n log n) erreichbar (mehr dazu in Kapitel 6) Insertion Sort: • Mit besserer Einfügestrategie (lass Lücken) worst-case Laufzeit O(n log 2 n) erreichbar 6/10/2021 Kapitel 5 52

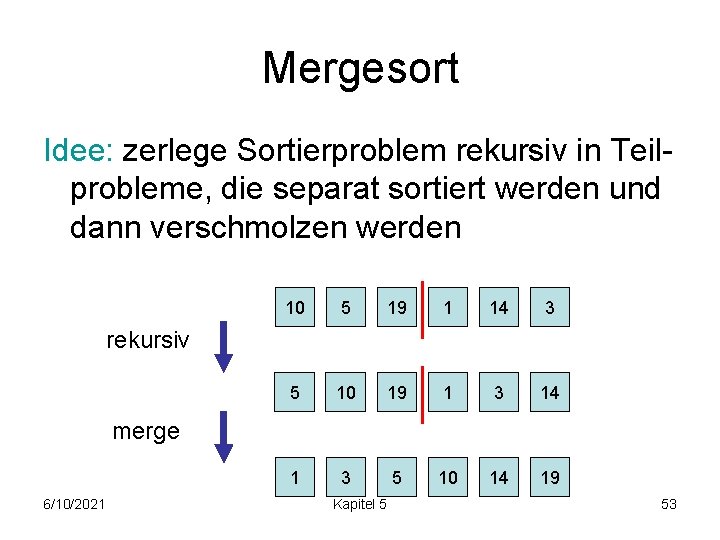
Mergesort Idee: zerlege Sortierproblem rekursiv in Teilprobleme, die separat sortiert werden und dann verschmolzen werden 10 5 19 1 14 3 5 10 19 1 3 14 1 3 5 10 14 19 rekursiv merge 6/10/2021 Kapitel 5 53

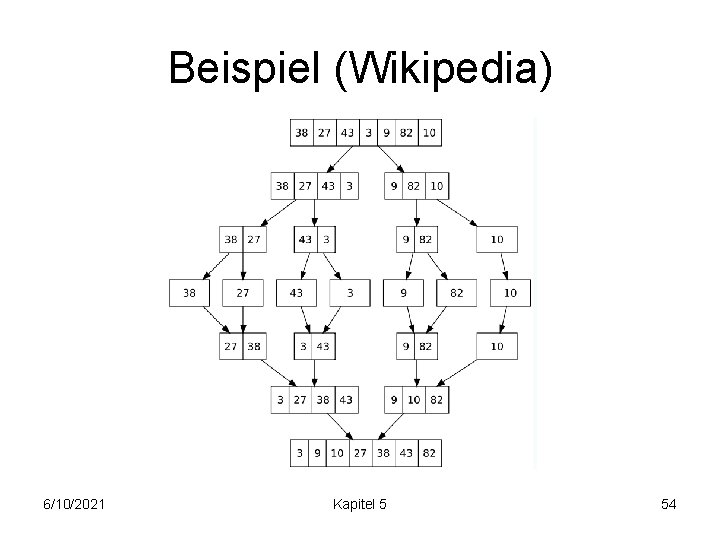
Beispiel (Wikipedia) 6/10/2021 Kapitel 5 54

Mergesort Procedure Mergesort(l, r: Integer) // a[l. . r]: zu sortierendes Feld if l=r then return // fertig m: = b(r+l)/2 c // Mitte Mergesort(l, m) Mergesort(m+1, r) j: =l; k: =m+1 for i: =1 to r-l+1 do // verwende Hilfsfeld b zum mergen if j>m then b[i]: =a[k]; k: =k+1 Erstes Feld schon leer! else if k>r then b[i]: =a[j]; j: =j+1 Zweites Feld schon leer! else if a[j]<a[k] then b[i]: =a[j]; j: =j+1 else b[i]: =a[k]; k: =k+1 for i: =1 to r-l+1 do a[l-1+i]: =b[i] 6/10/2021 Kapitel 5 55

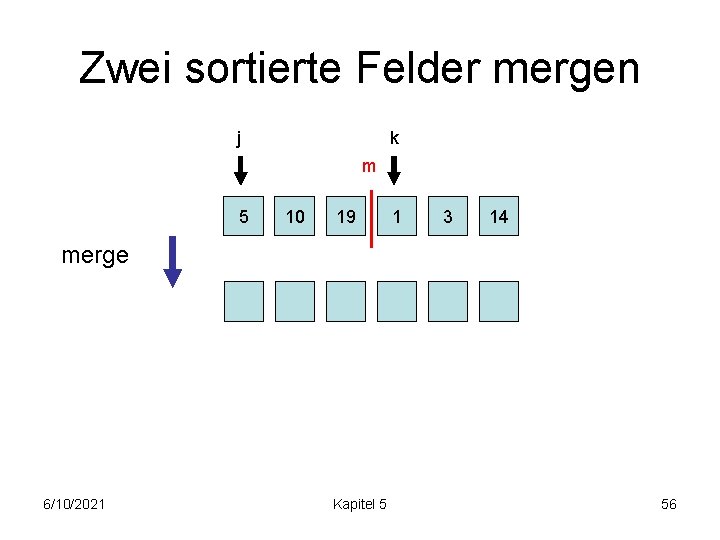
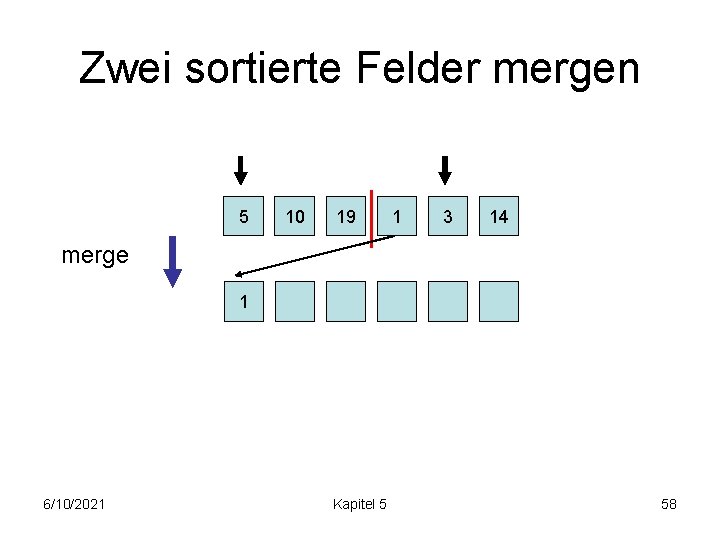
Zwei sortierte Felder mergen j k m 5 10 19 1 3 14 merge 6/10/2021 Kapitel 5 56

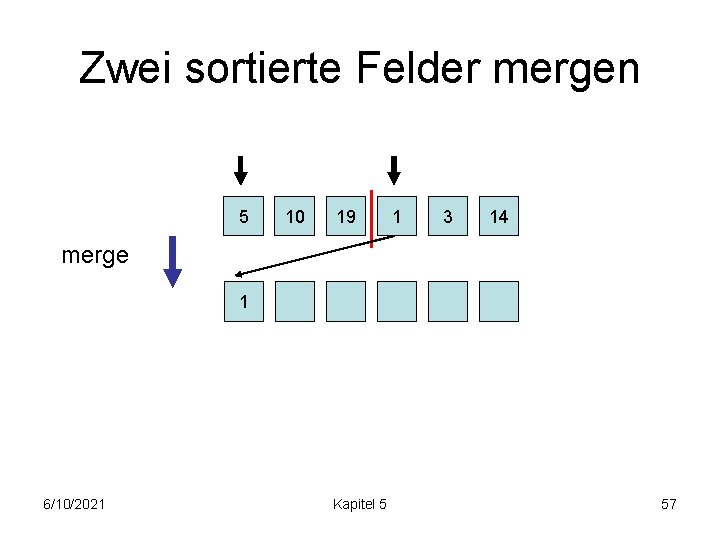
Zwei sortierte Felder mergen 5 10 19 1 3 14 merge 1 6/10/2021 Kapitel 5 57

Zwei sortierte Felder mergen 5 10 19 1 3 14 merge 1 6/10/2021 Kapitel 5 58

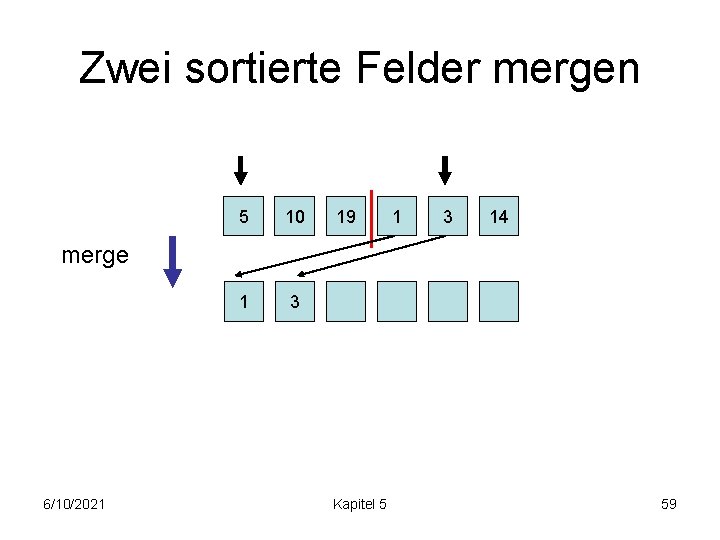
Zwei sortierte Felder mergen 5 10 1 3 19 1 3 14 merge 6/10/2021 Kapitel 5 59

Zwei sortierte Felder mergen 5 10 1 3 19 1 3 14 merge 6/10/2021 Kapitel 5 60

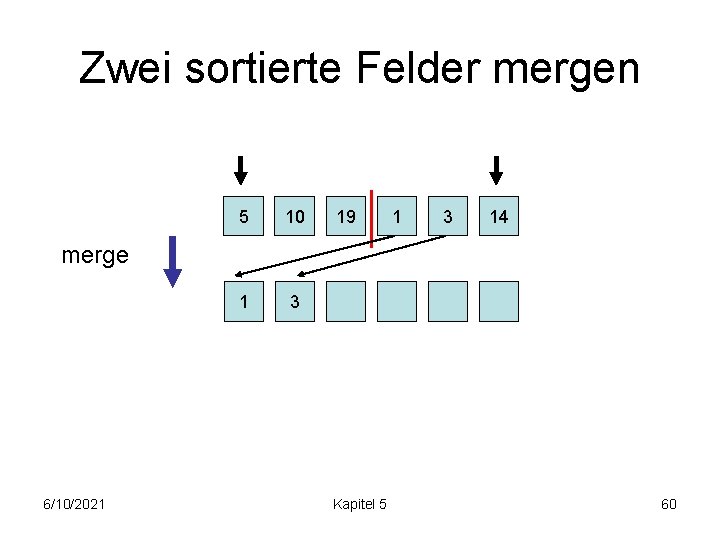
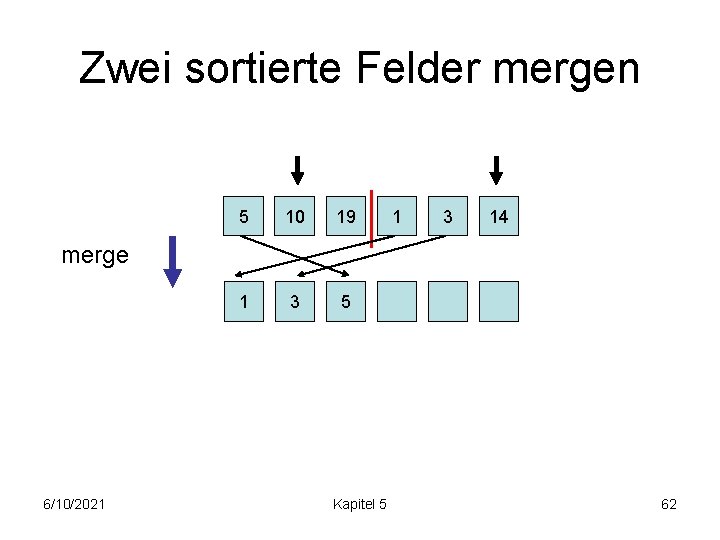
Zwei sortierte Felder mergen 5 10 19 1 3 5 1 3 14 merge 6/10/2021 Kapitel 5 61

Zwei sortierte Felder mergen 5 10 19 1 3 5 1 3 14 merge 6/10/2021 Kapitel 5 62

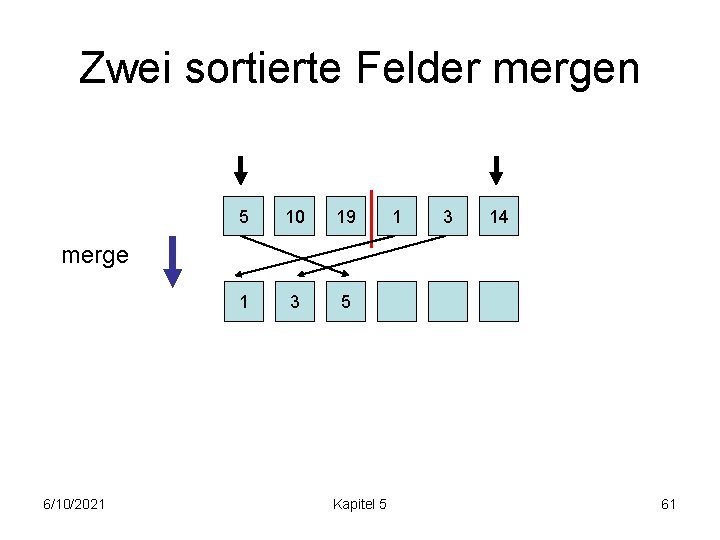
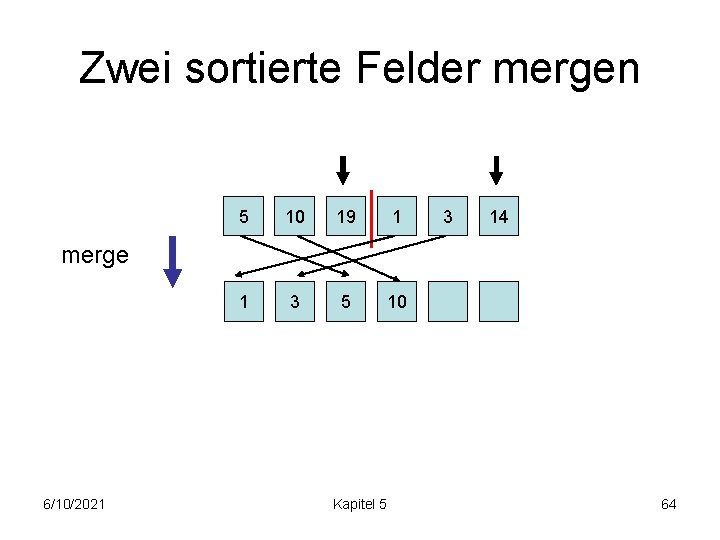
Zwei sortierte Felder mergen 5 10 19 1 1 3 5 10 3 14 merge 6/10/2021 Kapitel 5 63

Zwei sortierte Felder mergen 5 10 19 1 1 3 5 10 3 14 merge 6/10/2021 Kapitel 5 64

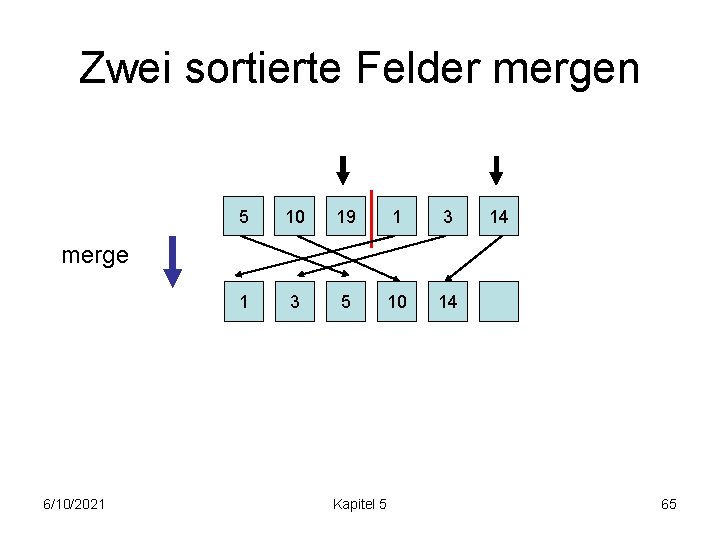
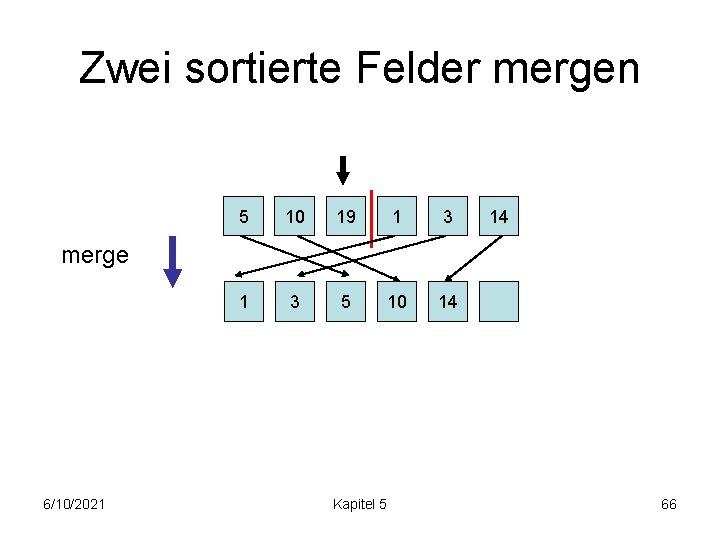
Zwei sortierte Felder mergen 5 10 19 1 3 5 10 14 14 merge 6/10/2021 Kapitel 5 65

Zwei sortierte Felder mergen 5 10 19 1 3 5 10 14 14 merge 6/10/2021 Kapitel 5 66

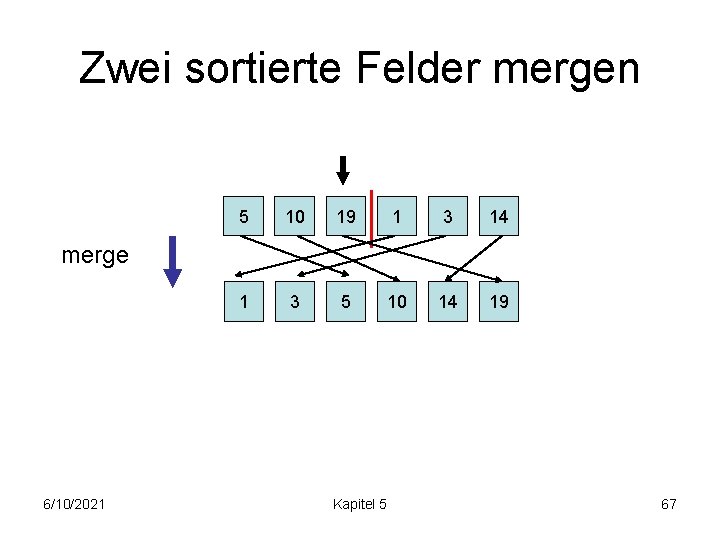
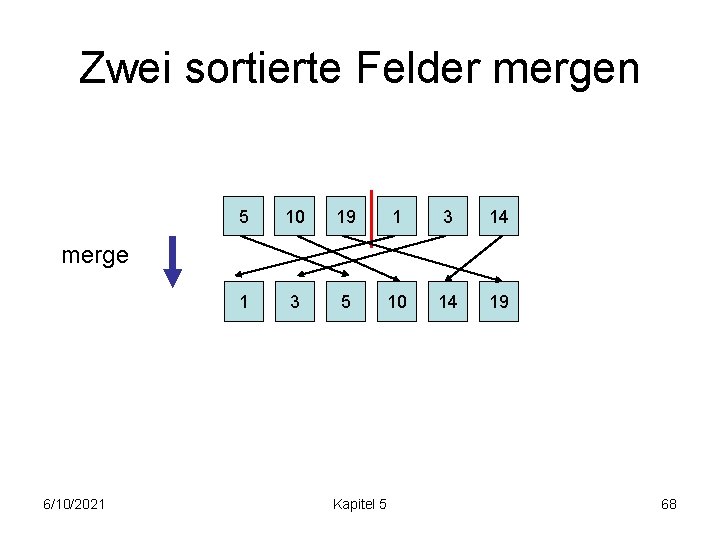
Zwei sortierte Felder mergen 5 10 19 1 3 14 1 3 5 10 14 19 merge 6/10/2021 Kapitel 5 67

Zwei sortierte Felder mergen 5 10 19 1 3 14 1 3 5 10 14 19 merge 6/10/2021 Kapitel 5 68

Mergesort Theorem 5. 2: Mergesort benötigt O(n log n) Zeit, um eine Folge der Länge n zu sortieren. Beweis: • T(n): Laufzeit bei Folgenlänge n • T(1) = (1) und T(n) = T(bn/2 c) + T(dn/2 e) + (n) • aus Übungsaufgabe: T(n)=O(n log n) 6/10/2021 Kapitel 5 69

Untere Schranke Ziel einer unteren Laufzeitschranke t(n): Zeige, dass kein Algorithmus (aus einer gewissen Klasse) eine bessere Laufzeit als O(t(n)) im worst case haben kann. Methodik: nutze strukturelle Eigenschaften des Problems Beispiel: vergleichsbasiertes Sortieren 6/10/2021 Kapitel 5 70

Untere Schranke Vergleichsbasiertes Sortieren: Wie oft muss jeder vergleichsbasierte Algo im worst case einen Vergleich e<e´ machen? Frage: Gegeben sei beliebige Menge S von n Elementen. Wieviele Möglichkeiten gibt es, S als Folge darzustellen? Antwort: n! = n¢(n-1)¢(n-2)… 2¢ 1 viele 6/10/2021 Kapitel 5 71

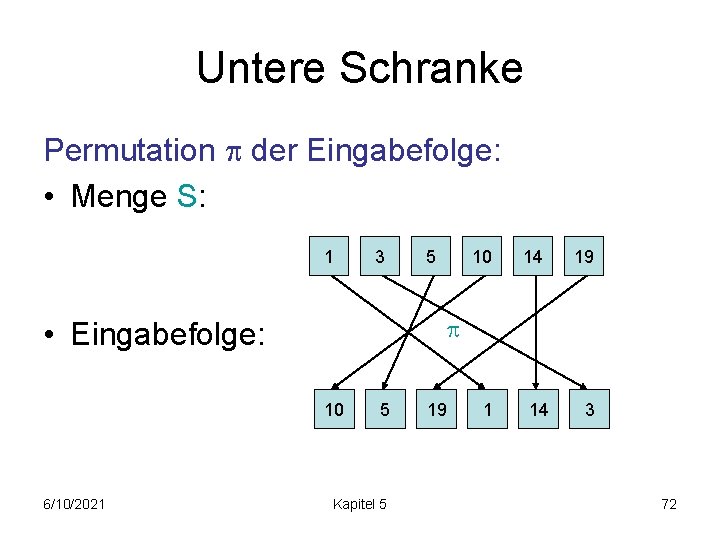
Untere Schranke Permutation der Eingabefolge: • Menge S: 1 3 5 14 19 • Eingabefolge: 10 6/10/2021 10 5 Kapitel 5 19 1 14 3 72

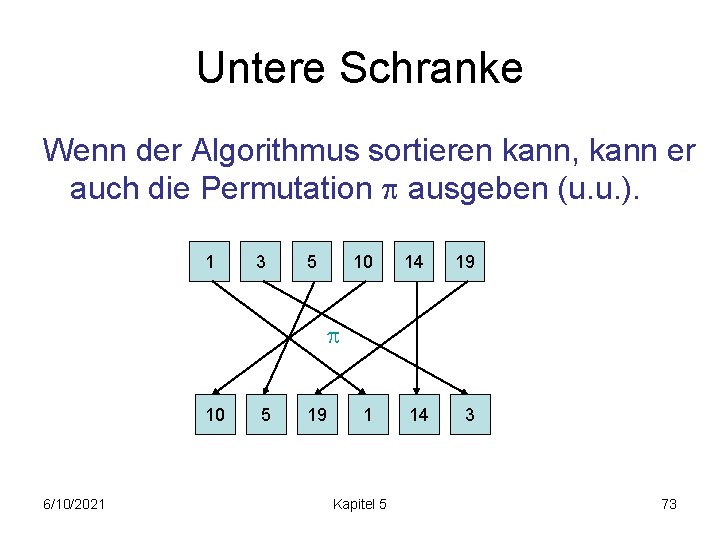
Untere Schranke Wenn der Algorithmus sortieren kann, kann er auch die Permutation ausgeben (u. u. ). 1 3 5 10 14 19 10 6/10/2021 5 19 1 Kapitel 5 14 3 73

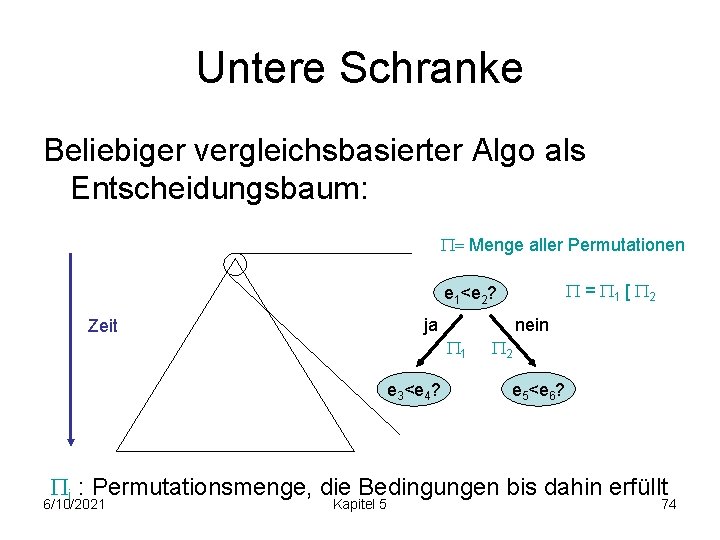
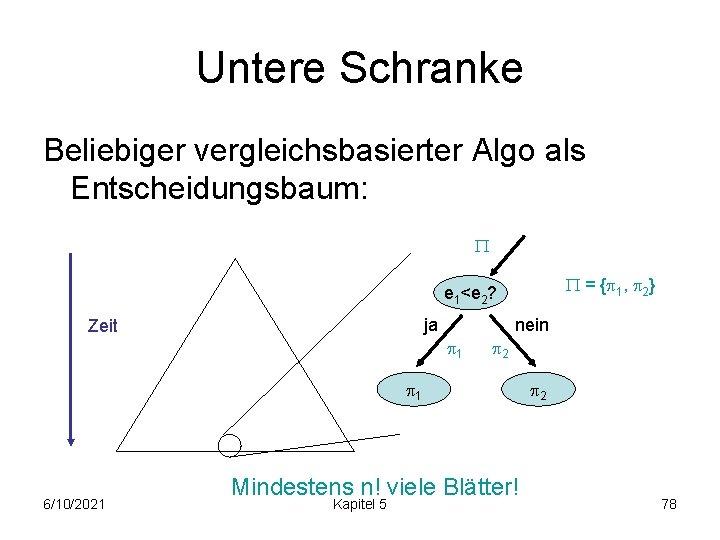
Untere Schranke Beliebiger vergleichsbasierter Algo als Entscheidungsbaum: = Menge aller Permutationen = 1 [ 2 e 1<e 2? ja Zeit nein 1 e 3<e 4? 2 e 5<e 6? i : Permutationsmenge, die Bedingungen bis dahin erfüllt 6/10/2021 Kapitel 5 74

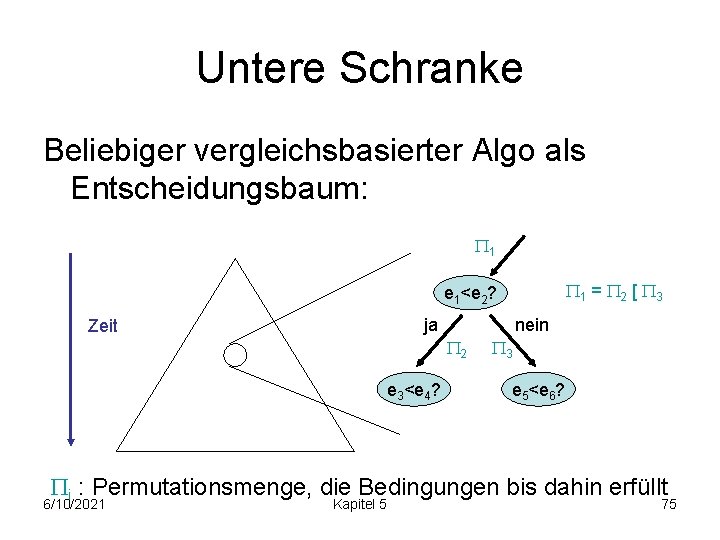
Untere Schranke Beliebiger vergleichsbasierter Algo als Entscheidungsbaum: 1 1 = 2 [ 3 e 1<e 2? ja Zeit nein 2 e 3<e 4? 3 e 5<e 6? i : Permutationsmenge, die Bedingungen bis dahin erfüllt 6/10/2021 Kapitel 5 75

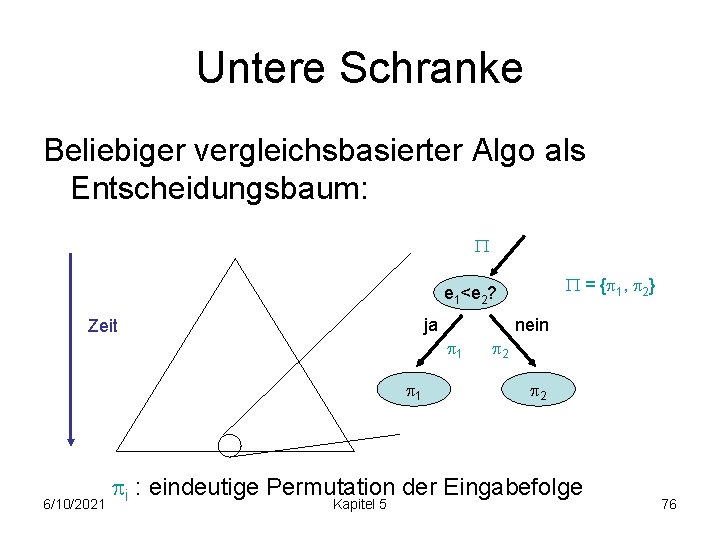
Untere Schranke Beliebiger vergleichsbasierter Algo als Entscheidungsbaum: = { 1, 2} e 1<e 2? ja Zeit 1 1 6/10/2021 nein 2 2 i : eindeutige Permutation der Eingabefolge Kapitel 5 76

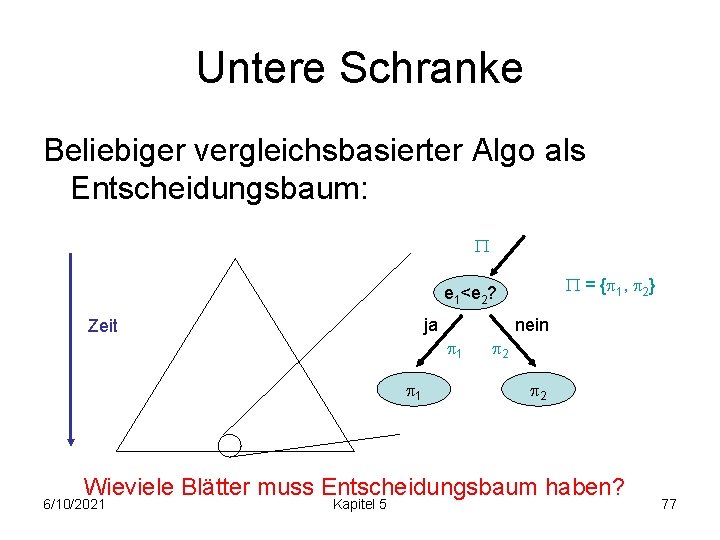
Untere Schranke Beliebiger vergleichsbasierter Algo als Entscheidungsbaum: = { 1, 2} e 1<e 2? ja Zeit nein 1 1 2 2 Wieviele Blätter muss Entscheidungsbaum haben? 6/10/2021 Kapitel 5 77

Untere Schranke Beliebiger vergleichsbasierter Algo als Entscheidungsbaum: = { 1, 2} e 1<e 2? ja Zeit nein 1 2 1 6/10/2021 Mindestens n! viele Blätter! Kapitel 5 2 78

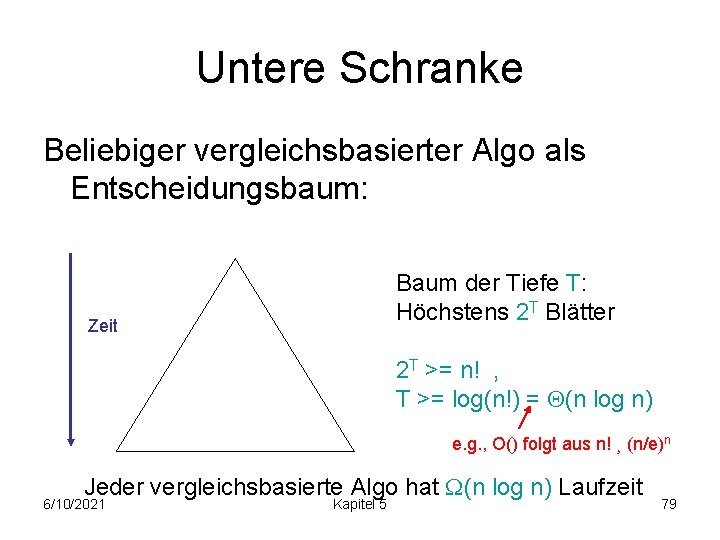
Untere Schranke Beliebiger vergleichsbasierter Algo als Entscheidungsbaum: Baum der Tiefe T: Höchstens 2 T Blätter Zeit 2 T >= n! , T >= log(n!) = (n log n) e. g. , O() folgt aus n! ¸ (n/e)n Jeder vergleichsbasierte Algo hat (n log n) Laufzeit 6/10/2021 Kapitel 5 79

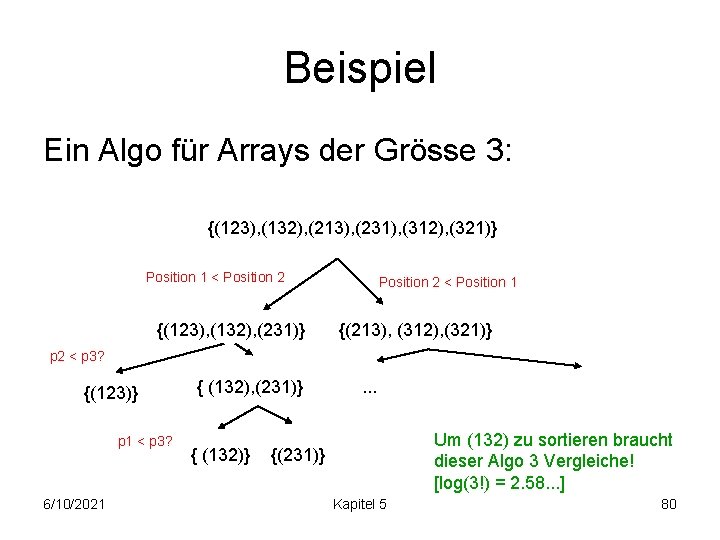
Beispiel Ein Algo für Arrays der Grösse 3: {(123), (132), (213), (231), (312), (321)} Position 1 < Position 2 {(123), (132), (231)} Position 2 < Position 1 {(213), (312), (321)} p 2 < p 3? {(123)} p 1 < p 3? 6/10/2021 { (132), (231)} { (132)} . . . Um (132) zu sortieren braucht dieser Algo 3 Vergleiche! [log(3!) = 2. 58. . . ] {(231)} Kapitel 5 80

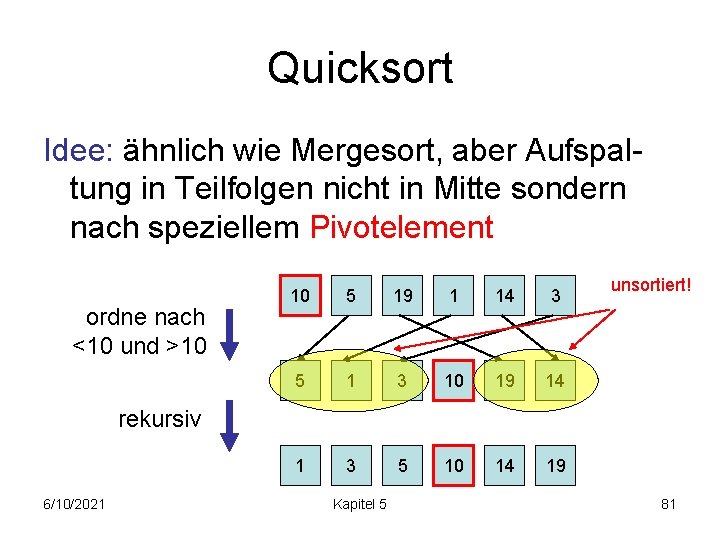
Quicksort Idee: ähnlich wie Mergesort, aber Aufspaltung in Teilfolgen nicht in Mitte sondern nach speziellem Pivotelement ordne nach <10 und >10 10 5 19 1 14 3 5 1 3 10 19 14 1 3 5 10 14 19 unsortiert! rekursiv 6/10/2021 Kapitel 5 81

Quicksort Procedure Quicksort(l, r: Integer) // a[l. . r]: zu sortierendes Feld if r>l then v: =a[r]; i: =l-1; j: =r repeat // ordne Elemente nach Pivot v repeat i: =i+1 until a[i]>=v repeat j: =j-1 until a[j]<=v if i<j then a[i] $ a[j] until j<=i a[i] $ a[r] Quicksort(l, i-1) // sortiere linke Teilfolge Quicksort(i+1, r) // sortiere rechte Teilfolge 6/10/2021 Kapitel 5 82

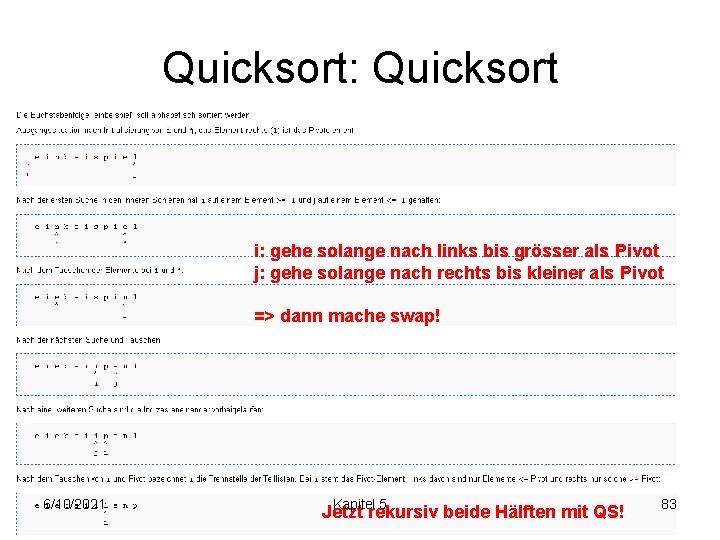
Quicksort: Quicksort i: gehe solange nach links bis grösser als Pivot j: gehe solange nach rechts bis kleiner als Pivot => dann mache swap! 6/10/2021 Kapitel 5 Jetzt rekursiv beide Hälften mit QS! 83

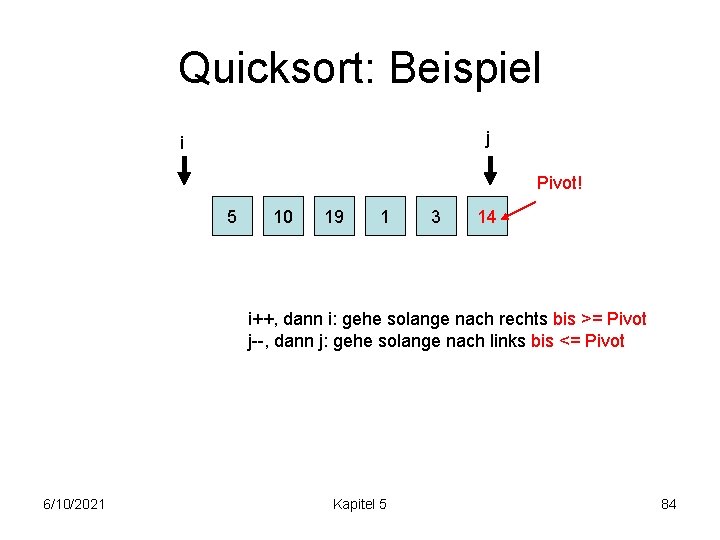
Quicksort: Beispiel j i Pivot! 5 10 19 1 3 14 i++, dann i: gehe solange nach rechts bis >= Pivot j--, dann j: gehe solange nach links bis <= Pivot 6/10/2021 Kapitel 5 84

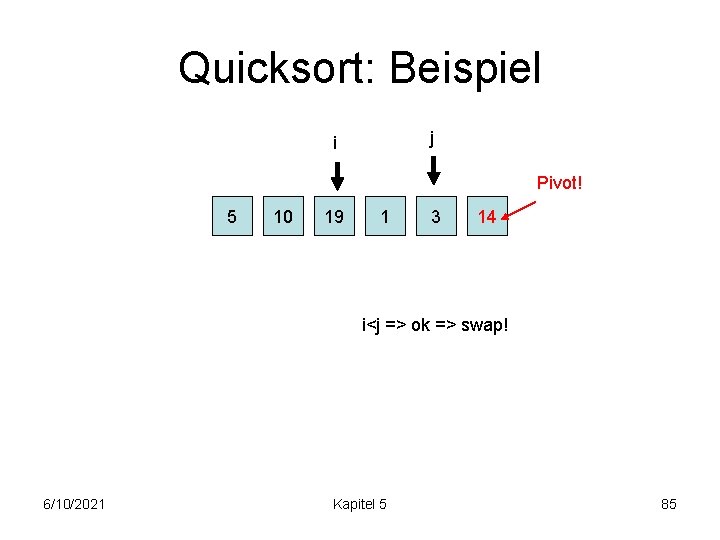
Quicksort: Beispiel j i Pivot! 5 10 19 1 3 14 i<j => ok => swap! 6/10/2021 Kapitel 5 85

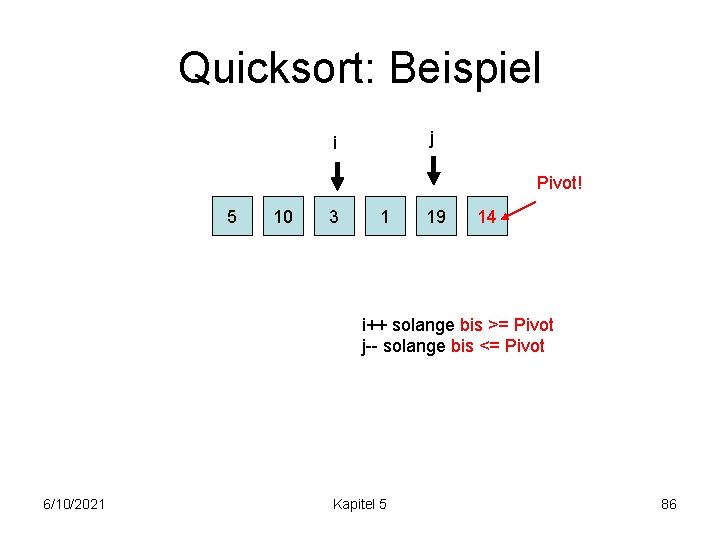
Quicksort: Beispiel j i Pivot! 5 10 3 1 19 14 i++ solange bis >= Pivot j-- solange bis <= Pivot 6/10/2021 Kapitel 5 86

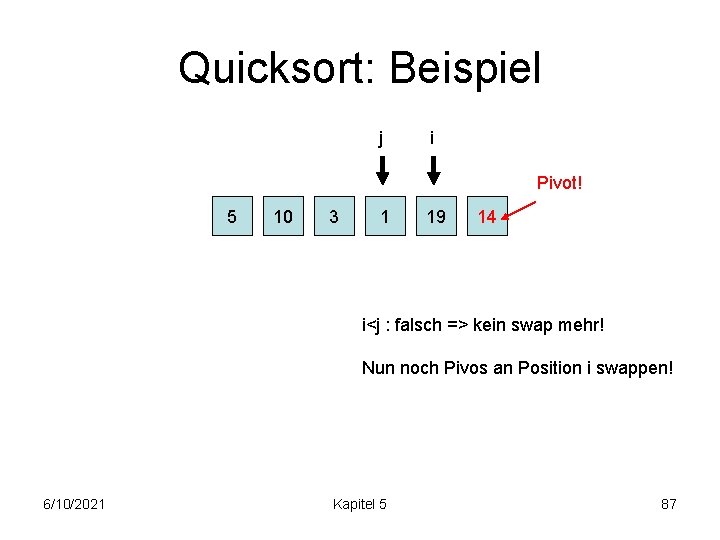
Quicksort: Beispiel j i Pivot! 5 10 3 1 19 14 i<j : falsch => kein swap mehr! Nun noch Pivos an Position i swappen! 6/10/2021 Kapitel 5 87

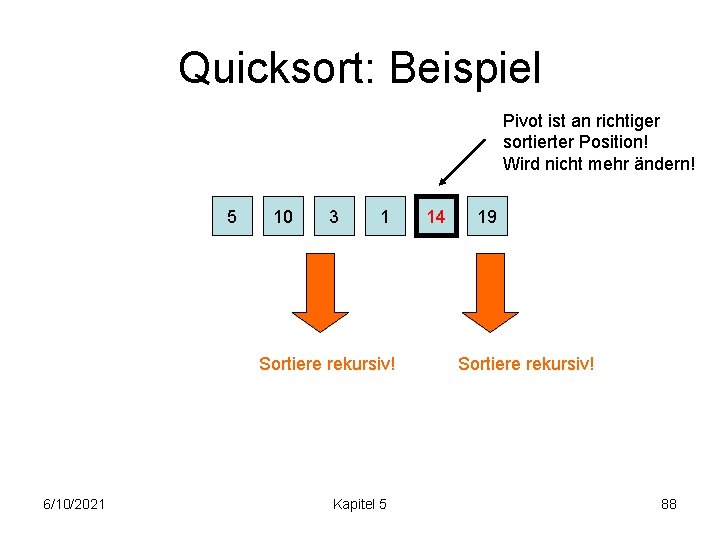
Quicksort: Beispiel Pivot ist an richtiger sortierter Position! Wird nicht mehr ändern! 5 10 3 1 Sortiere rekursiv! 6/10/2021 Kapitel 5 14 19 Sortiere rekursiv! 88

Quicksort Problem: im worst case kann Quicksort (n 2) Laufzeit haben (wenn schon sortiert) Lösungen: • wähle zufälliges Pivotelement (Laufzeit O(n log n) mit hoher W. keit) • berechne Median (Element in Mitte) ! dafür Selektionsalgorithmus (Kap 5. 5) 6/10/2021 Kapitel 5 89

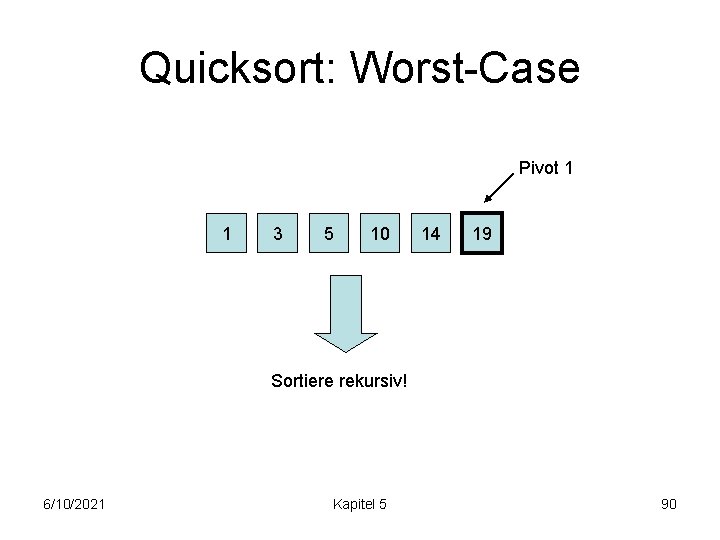
Quicksort: Worst-Case Pivot 1 1 3 5 10 14 19 Sortiere rekursiv! 6/10/2021 Kapitel 5 90

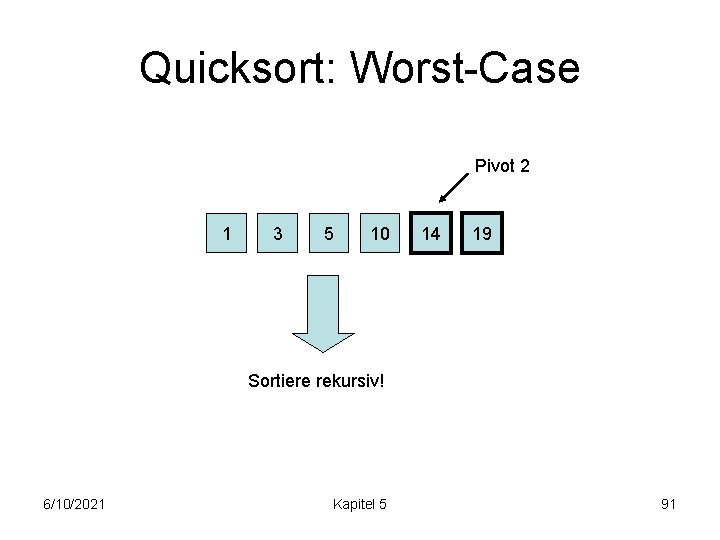
Quicksort: Worst-Case Pivot 2 1 3 5 10 14 19 Sortiere rekursiv! 6/10/2021 Kapitel 5 91

Quicksort: Worst-Case Pivot 3 1 3 5 10 14 19 Sortiere rekursiv! 6/10/2021 Kapitel 5 92

Quicksort: Worst-Case Pivot 3 1 3 5 10 14 19 Insgesamt n Rekursionen, jede Rekursion erfordert I (für i=1. . n) Vergleiche mit Pivotelement => O(n 2) 6/10/2021 Kapitel 5 93

Quicksort Laufzeit bei zufälligem Pivot-Element: • Zähle Anzahl Vergleiche (Rest macht nur konstanten Faktor aus) • C(n): erwartete Anzahl Vergleiche bei n Elementen Theorem 5. 6: C(n) <= 2 n ln n <= 1. 4 n log n 6/10/2021 Kapitel 5 94

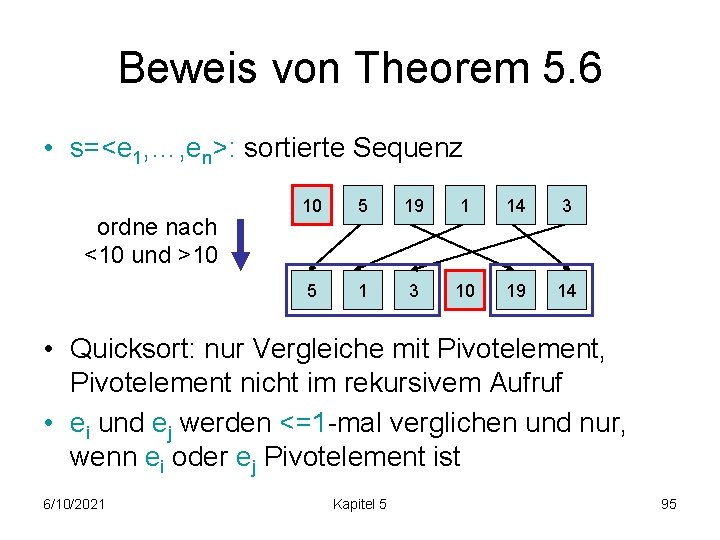
Beweis von Theorem 5. 6 • s=<e 1, …, en>: sortierte Sequenz ordne nach <10 und >10 10 5 19 1 14 3 5 1 3 10 19 14 • Quicksort: nur Vergleiche mit Pivotelement, Pivotelement nicht im rekursivem Aufruf • ei und ej werden <=1 -mal verglichen und nur, wenn ei oder ej Pivotelement ist 6/10/2021 Kapitel 5 95

Beweis von Theorem 5. 6 • Zufallsvariable Xi, j 2 {0, 1} • Xi, j = 1 , ei und ej werden verglichen C(n) = E[ i<j Xi, j] = i<j E[Xi, j] = i<j Pr[Xi, j = 1] Lemma 5. 7: Pr[Xi, j] = 2/(j-i+1) 6/10/2021 Kapitel 5 96

Beweis von Theorem 5. 6 Lemma 5. 7: Pr[Xi, j] = 2/(j-i+1) Beweis: • M={ei, …, ej} • Irgendwann wird Element aus M als Pivot ausgewählt (bis dahin bleibt M zusammen) • ei und ej werden nur verglichen, wenn ei oder ej als Pivot ausgewählt werden • Pr[ei oder ej in M ausgewählt]=2/|M| 6/10/2021 Kapitel 5 97

Beweis von Theorem 5. 6 C(n) = i<j Pr[Xi, j=1] = i<j 2/(j-i+1) = i=1 n k=2 n-i+1 2/k <= i=1 n k=2 n 2/k = 2 n k=2 n 1/k <= 2 n ln n Erwartungsgemäß ist Quicksort also sehr effizient (bestätigt Praxis). 6/10/2021 Kapitel 5 98

Harmonic Number Es gilt: Hn · ln n + 1 6/10/2021 Kapitel 5 99

Selektion Problem: finde k-kleinstes Element in einer Folge von n Elementen Lösung: sortiere Elemente, gib k-tes Element aus ! Zeit O(n log n) Geht das auch schneller? ? 6/10/2021 Kapitel 5 100

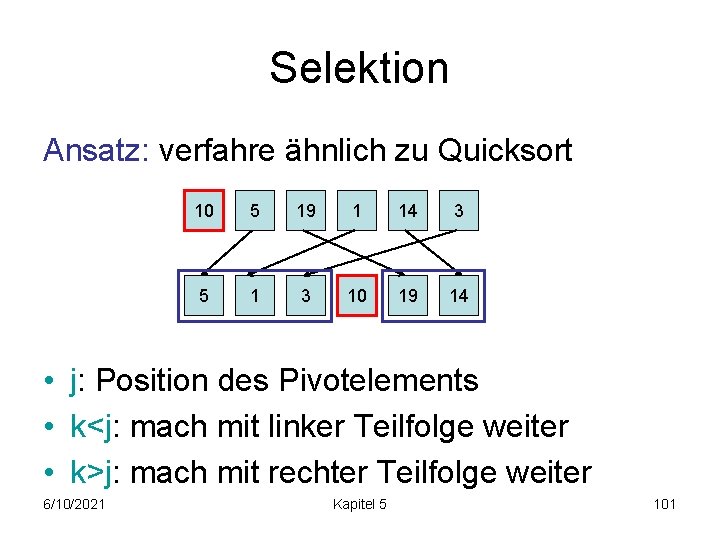
Selektion Ansatz: verfahre ähnlich zu Quicksort 10 5 19 1 14 3 5 1 3 10 19 14 • j: Position des Pivotelements • k<j: mach mit linker Teilfolge weiter • k>j: mach mit rechter Teilfolge weiter 6/10/2021 Kapitel 5 101

Selektion Function Quickselect(l, r, k: Integer): Element // a[l. . r]: Restfeld, k: k-kleinstes Element if r=l then return a[l] z: =zufällige Position in {l, . . , r}; a[z] $ a[r] v: =a[r]; i: =l-1; j: =r repeat // ordne Elemente nach Pivot v repeat i: =i+1 until a[i]>=v repeat j: =j-1 until a[j]<=v if i<j then a[i] $ a[j] until j<=i a[i] $ a[r] if k<i then e: =Quickselect(l, i-1, k) if k>i then e: =Quickselect(i+1, r, k) if k=i then e: =a[k] return e 6/10/2021 Kapitel 5 102

Quickselect • C(n): erwartete Anzahl Vergleiche Theorem 5. 8: C(n)=O(n) Beweis: • Pivot ist gut: keine der Teilfolgen länger als 2 n/3 • Sei p=Pr[Pivot ist gut] gut • p=1/3 6/10/2021 1/3 2/3 Kapitel 5 103

Quickselect • Pivot gut: Restaufwand <= C(2 n/3) • Pivot schlecht: Restaufwand <= C(n) <= n + p C(2 n/3) + (1 -p) C(n) , C(n) <= n/p + C(2 n/3) <= 3 n + C(2 n/3) <= 3(n+2 n/3+4 n/9+…) <= 3 n i>=0 (2/3)i <= 3 n / (1 -2/3) = 9 n 6/10/2021 Kapitel 5 104

Soweit gekommen am Dienstag. Start hier am Donnerstag! 6/10/2021 Kapitel 5 105

Ein paar Infos vorweg. . . • Morgen Freitag: 15: 00 -16: 30 Fragestunde von Prof. Scheideler im FMI HS 2 (Fragen zur Vorlesung bis jetzt) • Heute: - kurze Repetition von Quicksort - Noch schnellere Sortieralgorithmen! - Externes sortieren (was wenn nicht genug Speicher vorhanden für ganzes Feld? ) - Ev. noch was zur Analyse von While Schleifen 6/10/2021 Kapitel 5 106

Repetition (1) • Wie kann man etwas effizient sortieren? • Gesehen: „Minimum-Selektion “-Algo O(n 2), „Einfüge“Algo O(n 2), Algo durch „rekursives Mergen“ O(n log n), Quicksort Algo O(n 2) • Wieso ist Mergesort immer O(n log n) während Quicksort zum Teil O(n 2) ist? • Bei Quicksort können die beiden rekursiv zu bearbeitenden Teile unterschiedlich gross sein. . . 6/10/2021 Kapitel 5 107

Repetition (2) Weshalb ist es schlecht, wenn die Teile unterschiedlich gross sind? (Weshalb wird Quicksort dennoch verwendet in der Praxis? ) 6/10/2021 Kapitel 5 108

Repetition (3) Rekursion: Wie wird das z. B. ausgeführt? Procedure Quicksort(l, r: Integer) // a[l. . r]: zu sortierendes Feld if r>l then v: =a[r]; i: =l-1; j: =r repeat // ordne Elemente nach Pivot v repeat i: =i+1 until a[i]>=v repeat j: =j-1 until a[j]<=v if i<j then a[i] $ a[j] until j<=i a[i] $ a[r] Quicksort(l, i-1) // sortiere linke Teilfolge Quicksort(i+1, r) // sortiere rechte Teilfolge 6/10/2021 Kapitel 5 109

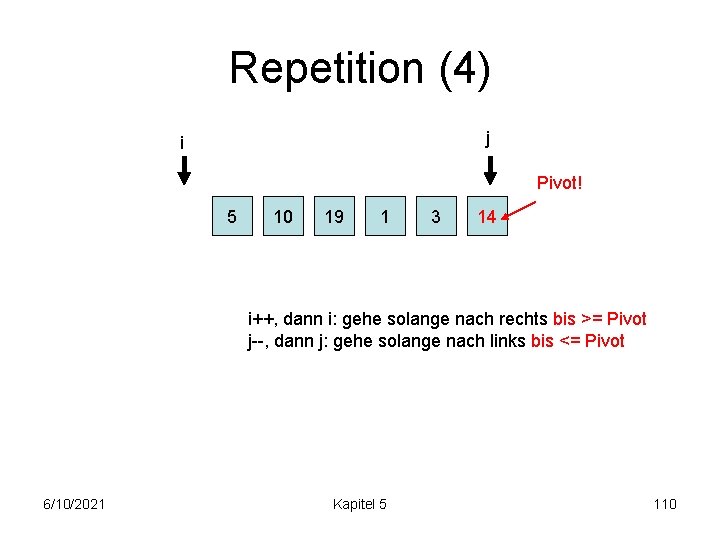
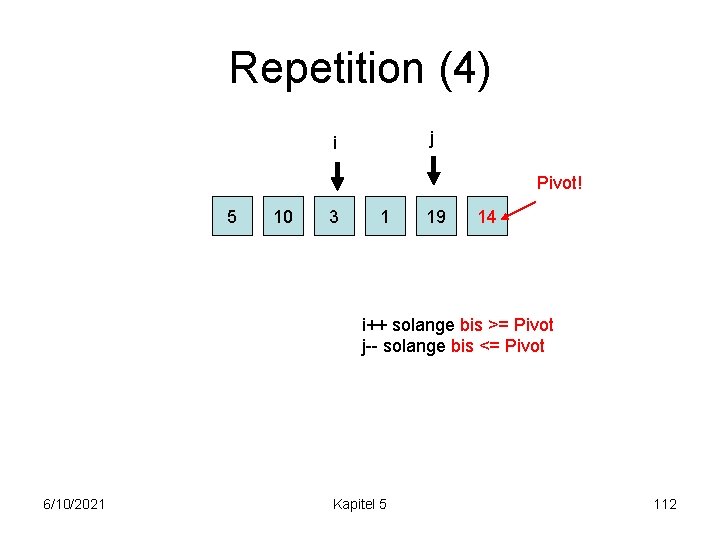
Repetition (4) j i Pivot! 5 10 19 1 3 14 i++, dann i: gehe solange nach rechts bis >= Pivot j--, dann j: gehe solange nach links bis <= Pivot 6/10/2021 Kapitel 5 110

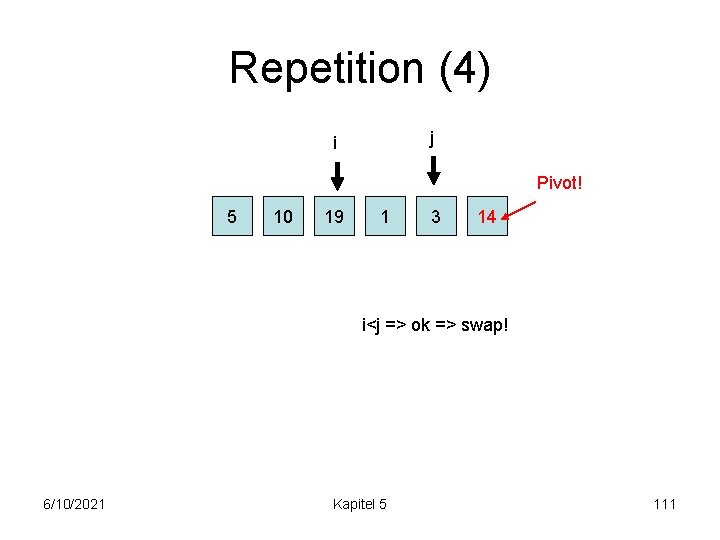
Repetition (4) j i Pivot! 5 10 19 1 3 14 i<j => ok => swap! 6/10/2021 Kapitel 5 111

Repetition (4) j i Pivot! 5 10 3 1 19 14 i++ solange bis >= Pivot j-- solange bis <= Pivot 6/10/2021 Kapitel 5 112

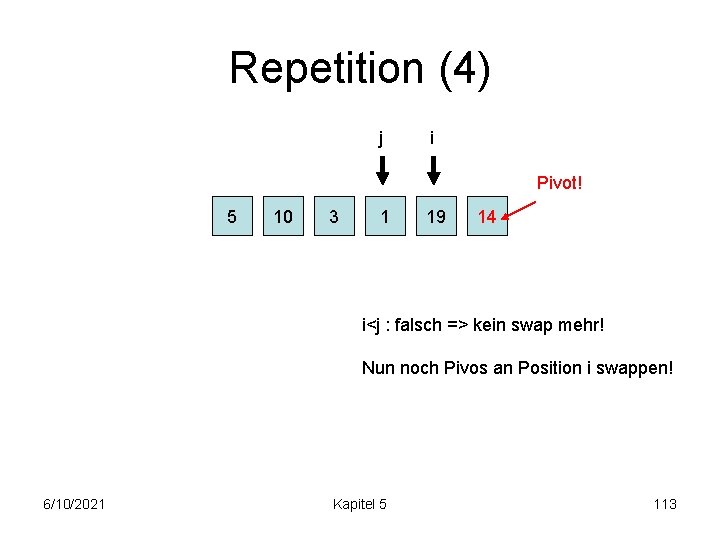
Repetition (4) j i Pivot! 5 10 3 1 19 14 i<j : falsch => kein swap mehr! Nun noch Pivos an Position i swappen! 6/10/2021 Kapitel 5 113

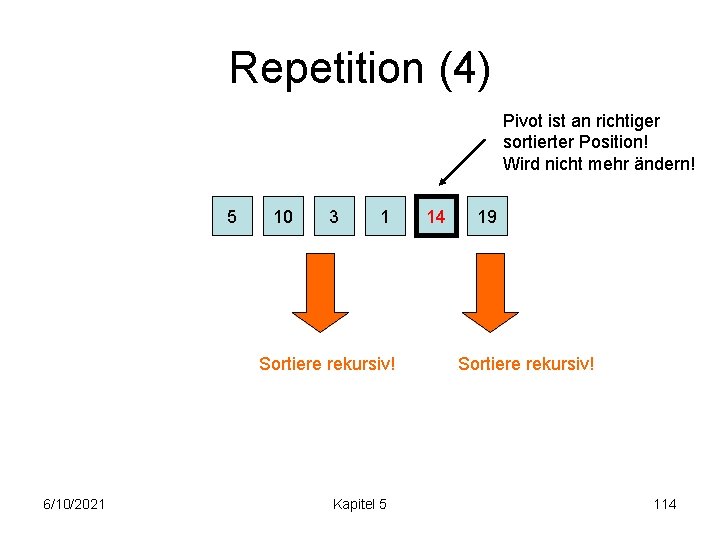
Repetition (4) Pivot ist an richtiger sortierter Position! Wird nicht mehr ändern! 5 10 3 1 Sortiere rekursiv! 6/10/2021 Kapitel 5 14 19 Sortiere rekursiv! 114

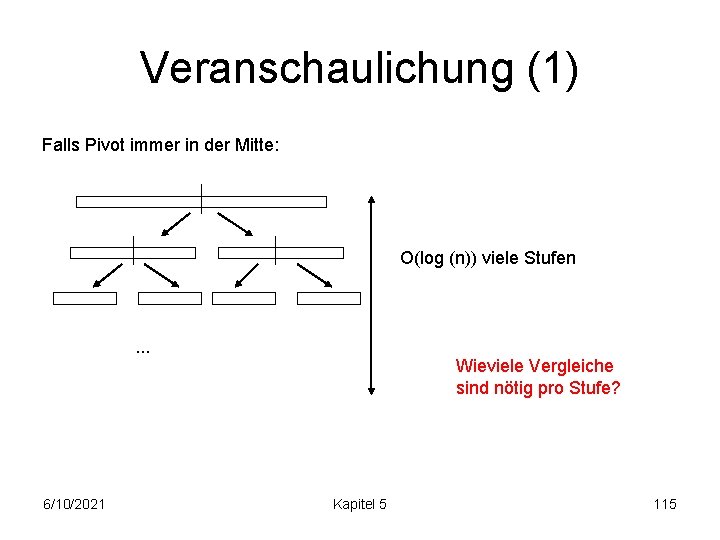
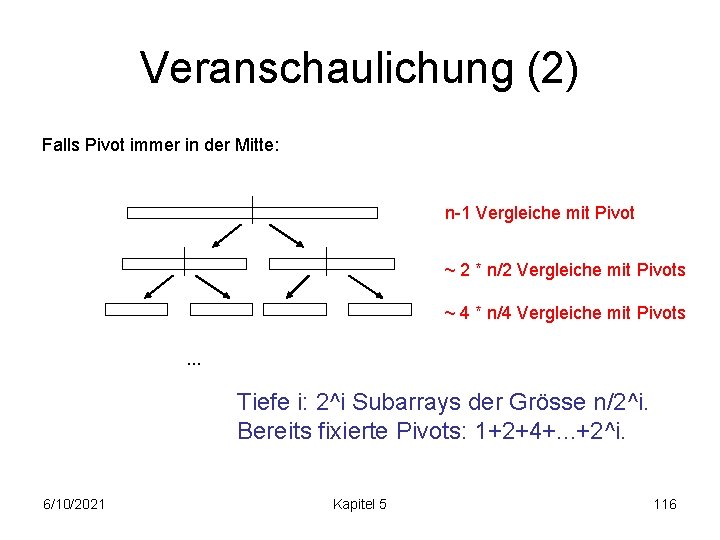
Veranschaulichung (1) Falls Pivot immer in der Mitte: O(log (n)) viele Stufen . . . 6/10/2021 Wieviele Vergleiche sind nötig pro Stufe? Kapitel 5 115

Veranschaulichung (2) Falls Pivot immer in der Mitte: n-1 Vergleiche mit Pivot ~ 2 * n/2 Vergleiche mit Pivots ~ 4 * n/4 Vergleiche mit Pivots. . . Tiefe i: 2^i Subarrays der Grösse n/2^i. Bereits fixierte Pivots: 1+2+4+. . . +2^i. 6/10/2021 Kapitel 5 116

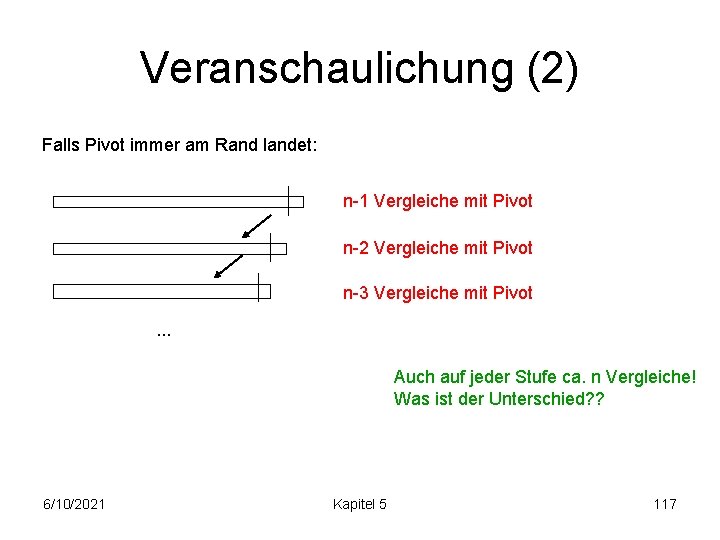
Veranschaulichung (2) Falls Pivot immer am Rand landet: n-1 Vergleiche mit Pivot n-2 Vergleiche mit Pivot n-3 Vergleiche mit Pivot. . . Auch auf jeder Stufe ca. n Vergleiche! Was ist der Unterschied? ? 6/10/2021 Kapitel 5 117

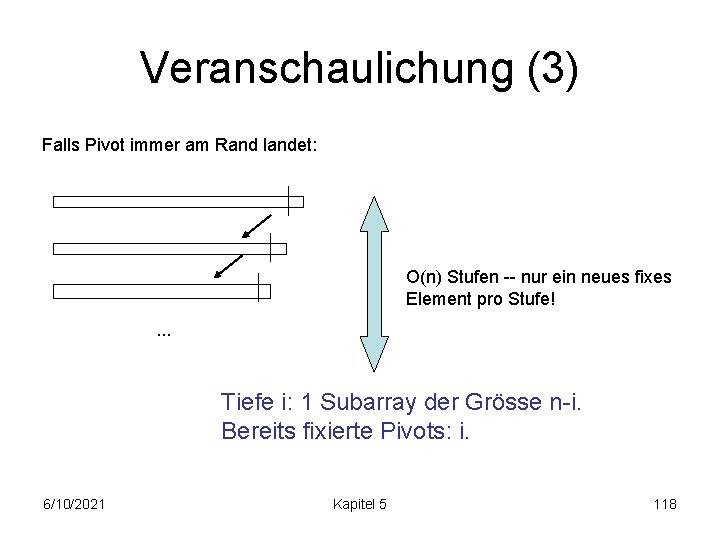
Veranschaulichung (3) Falls Pivot immer am Rand landet: O(n) Stufen -- nur ein neues fixes Element pro Stufe!. . . Tiefe i: 1 Subarray der Grösse n-i. Bereits fixierte Pivots: i. 6/10/2021 Kapitel 5 118

Repetition (5) • Wieviele Vergleiche braucht ein Algorithmus im Jahr 2050 mindestens um ein Feld der Grösse n zu sortieren? • Konzept der „unteren Schranke“ oder „lower bound“ • Lösung: mind. log(n!) 6/10/2021 Kapitel 5 119

Repetition (6) • Kann man nicht schneller sortieren? • Doch – falls Algorithmus nicht vergleichsbasiert ist oder das Problem / der Input eine spezielle Form hat! Z. B. : Algorithmus der nicht nur Keys als ganzes miteinander vergleicht, sondern die Repräsentation als einzelne Ziffern berücksichtigt! Oder: Felder die nur aus ganz wenigen sich wiederholenden Keys bestehen. 6/10/2021 Kapitel 5 120

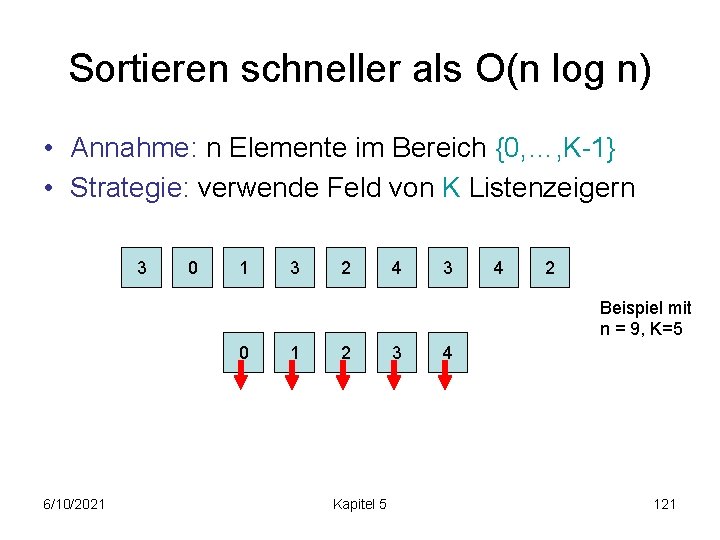
Sortieren schneller als O(n log n) • Annahme: n Elemente im Bereich {0, …, K-1} • Strategie: verwende Feld von K Listenzeigern 3 0 1 3 2 4 3 4 2 Beispiel mit n = 9, K=5 0 6/10/2021 1 2 Kapitel 5 3 4 121

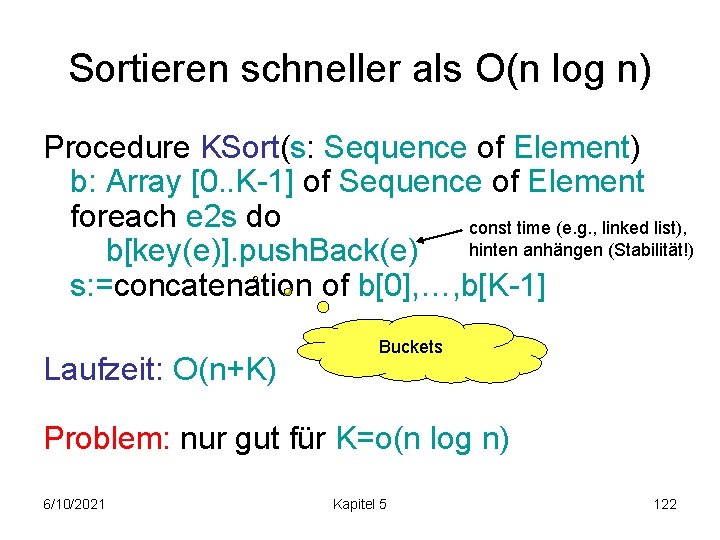
Sortieren schneller als O(n log n) Procedure KSort(s: Sequence of Element) b: Array [0. . K-1] of Sequence of Element foreach e 2 s do const time (e. g. , linked list), hinten anhängen (Stabilität!) b[key(e)]. push. Back(e) s: =concatenation of b[0], …, b[K-1] Laufzeit: O(n+K) Buckets Problem: nur gut für K=o(n log n) 6/10/2021 Kapitel 5 122

Erste Ziffer = Schlüsselraum {0, 1, 2, 3} K-Sort Example s = (<3, a>, <1, b>, <2, c>, <3, d>, <0, e>, <0, f>, <3, g>, <2, h>, <1, i>). . . wird zu: b = ([<0, e>, <0, f>], [<1, b>, <1, i>], [<2, c>, <2, h>], [<3, a>, <3, d>, <3, g>]) also (<0, e>, <0, f>, <1, b>, <1, i>, <2, c>, <2, h>, <3, a>, <3, d>, <3, g>) Beachte: K-Sort ist stabil, d. h. , Elemente mit gleichem Key bleiben in gleicher Reihenfolge wie in der Eingabe (wegen push. Back)! 6/10/2021 Kapitel 5 123

Radixsort Ideen: • Benutze Repräsentation der Schlüssel • K-adische Darstellung der Schlüssel • Sortiere Ziffer für Ziffer gemäß KSort • Behalte Ordnung der Teillisten bei 6/10/2021 Kapitel 5 124

Radixsort Procedure Radixsort(s: Sequence of Element) for i: =0 to d-1 do KSort(s, i) // sortiere gemäß keyi(x) // mit keyi(x) = (key(x) div Ki) mod K, // d. h. kleinste Ziffer zuerst! Laufzeit: O(d(n+K)) Falls maximale Zahlengröße O(log n), dann alle Zahlen <= nd für konstantes d. In diesem Fall Laufzeit für n Zahlen sortieren O(n). 6/10/2021 Kapitel 5 125

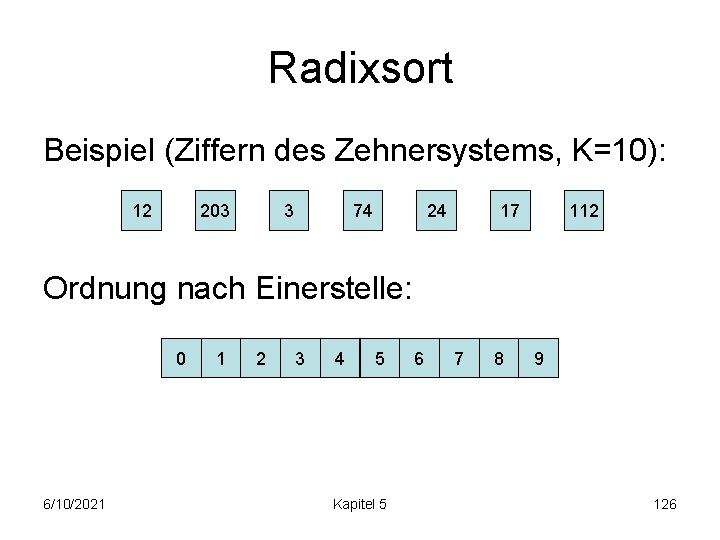
Radixsort Beispiel (Ziffern des Zehnersystems, K=10): 12 203 3 74 24 17 112 Ordnung nach Einerstelle: 0 6/10/2021 1 2 3 4 5 Kapitel 5 6 7 8 9 126

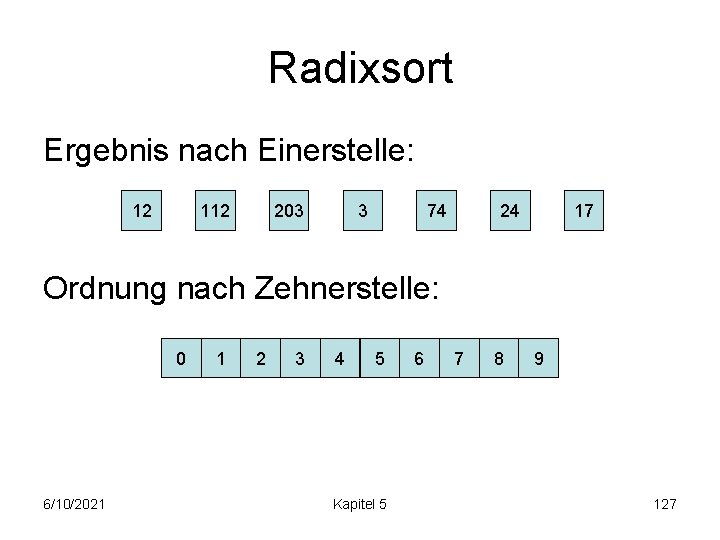
Radixsort Ergebnis nach Einerstelle: 12 112 203 3 74 24 17 Ordnung nach Zehnerstelle: 0 6/10/2021 1 2 3 4 5 Kapitel 5 6 7 8 9 127

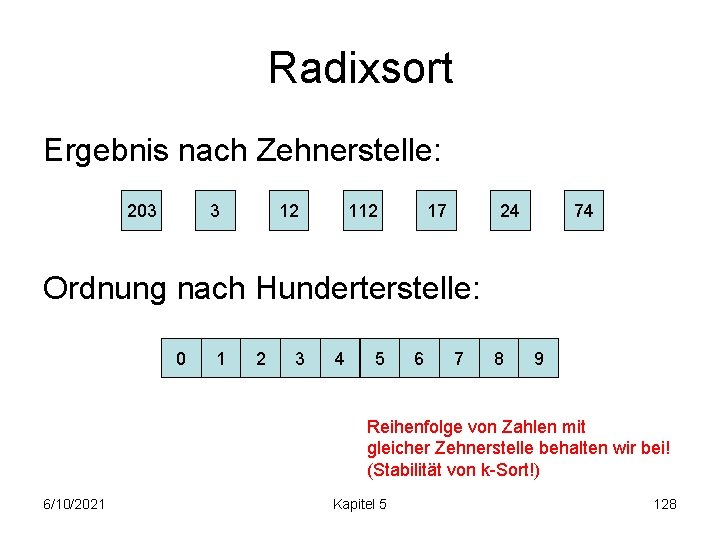
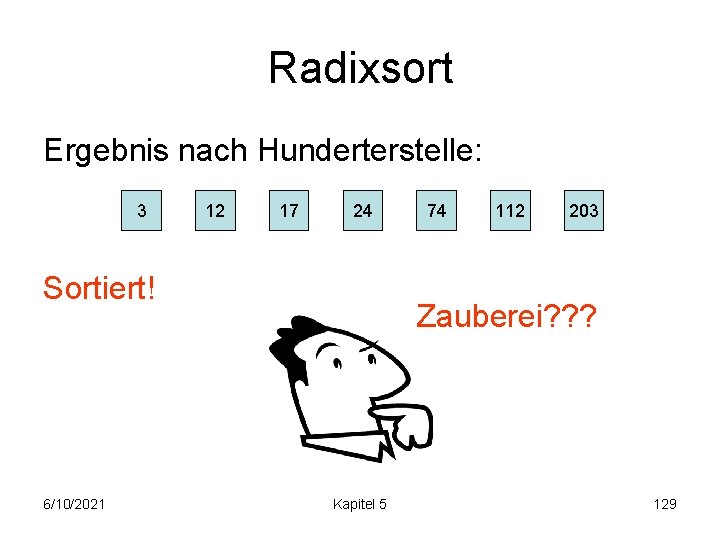
Radixsort Ergebnis nach Zehnerstelle: 203 3 12 17 24 74 Ordnung nach Hunderterstelle: 0 1 2 3 4 5 6 7 8 9 Reihenfolge von Zahlen mit gleicher Zehnerstelle behalten wir bei! (Stabilität von k-Sort!) 6/10/2021 Kapitel 5 128

Radixsort Ergebnis nach Hunderterstelle: 3 12 17 24 Sortiert! 6/10/2021 74 112 203 Zauberei? ? ? Kapitel 5 129

Radixsort 3135 < 3146 Korrektheit: • Für jedes Paar x, y mit key(x)<key(y) gilt: es existiert i mit keyi(x)<keyi(y) und keyj(x)=keyj(y) für alle j>i (j wächst gegen links: kleine Stellen zuerst) • Schleifendurchlauf für i: poss(x)<poss(y) (poss(z): Position von z in Folge s) • Schleifendurchlauf für j>i: Ordnung wird beibehalten wegen push. Back in KSort 6/10/2021 Kapitel 5 130

Radixsort: Beispiel Wikipedia Input Phase 1 Phase 2 Phase 3 6/10/2021 Kapitel 5 Output 131

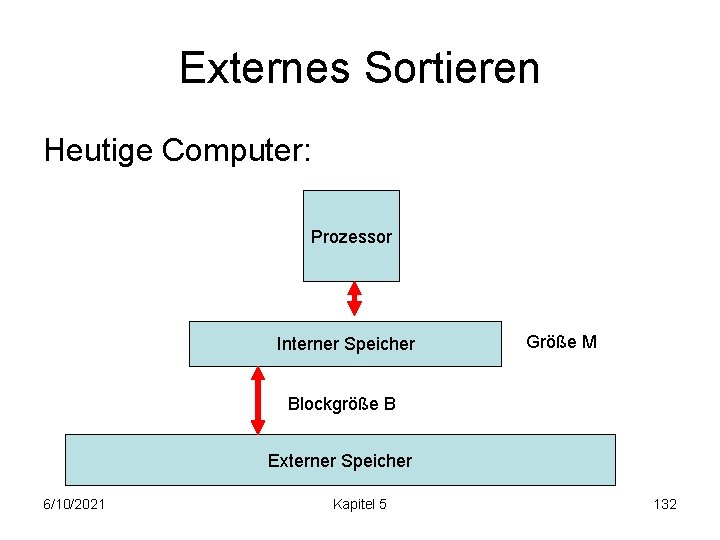
Externes Sortieren Heutige Computer: Prozessor Interner Speicher Größe M Blockgröße B Externer Speicher 6/10/2021 Kapitel 5 132

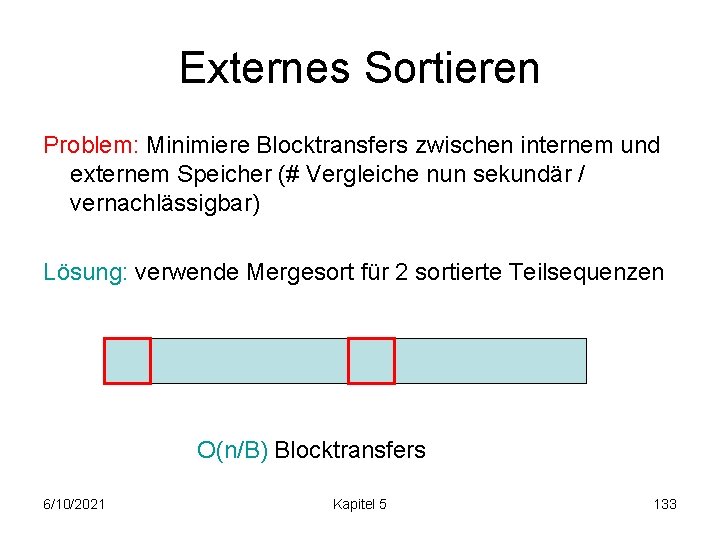
Externes Sortieren Problem: Minimiere Blocktransfers zwischen internem und externem Speicher (# Vergleiche nun sekundär / vernachlässigbar) Lösung: verwende Mergesort für 2 sortierte Teilsequenzen O(n/B) Blocktransfers 6/10/2021 Kapitel 5 133

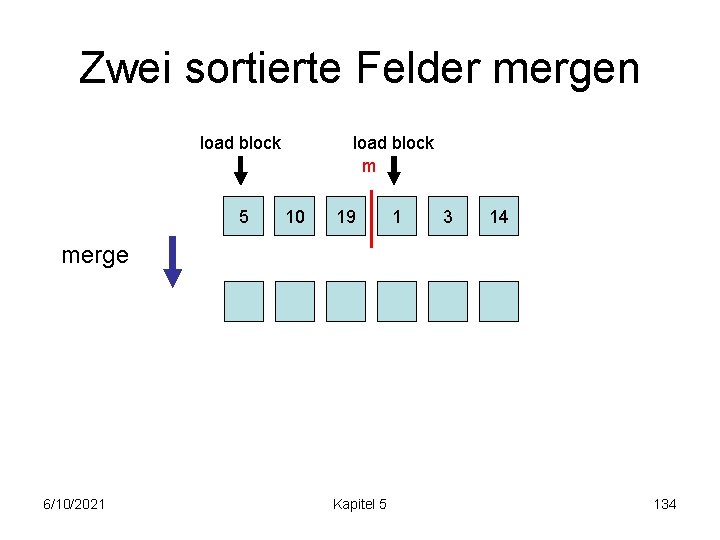
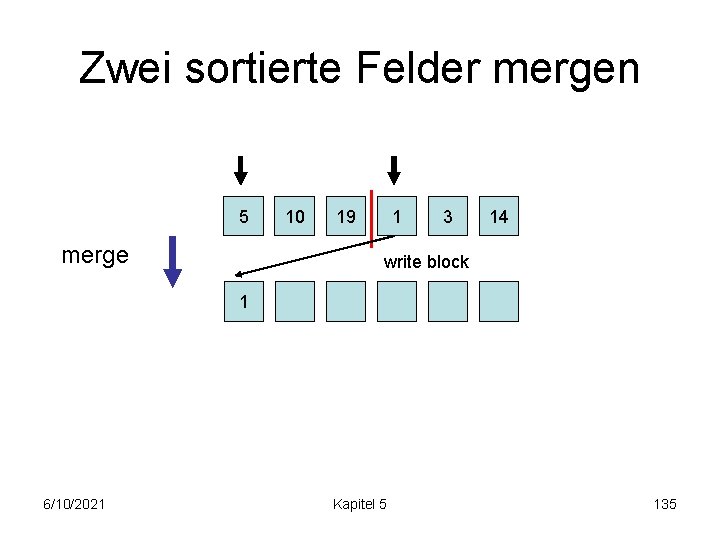
Zwei sortierte Felder mergen load block 5 load block m 10 19 1 3 14 merge 6/10/2021 Kapitel 5 134

Zwei sortierte Felder mergen 5 merge 10 19 1 3 14 write block 1 6/10/2021 Kapitel 5 135

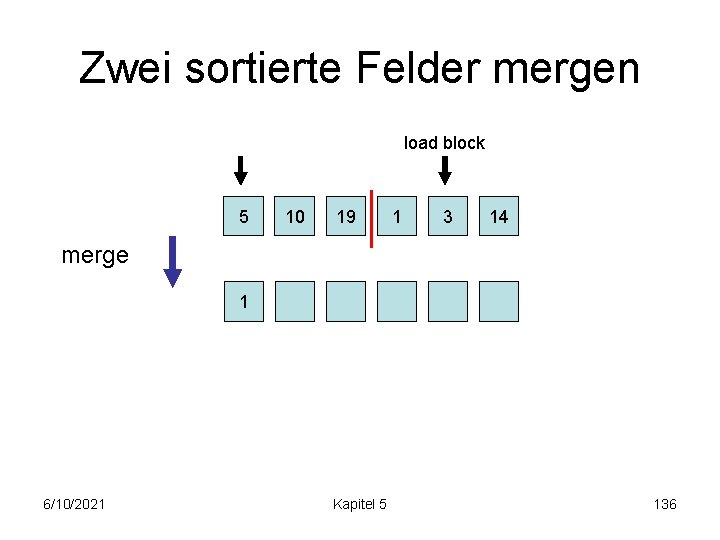
Zwei sortierte Felder mergen load block 5 10 19 1 3 14 merge 1 6/10/2021 Kapitel 5 136

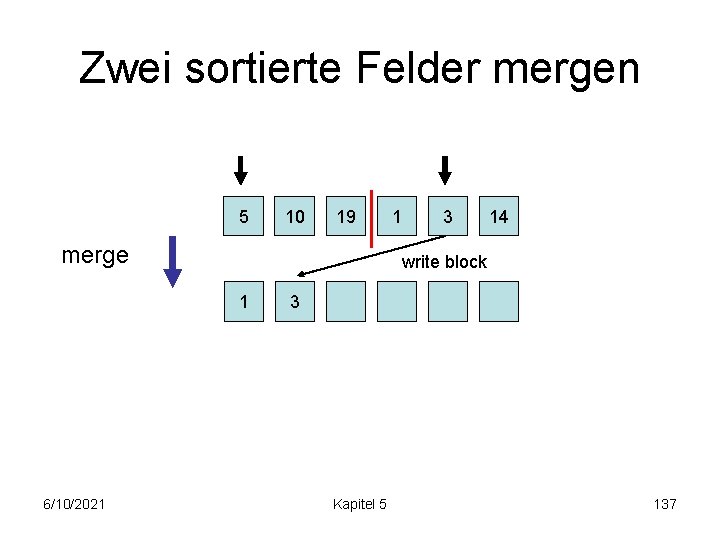
Zwei sortierte Felder mergen 5 10 19 merge 3 14 write block 1 6/10/2021 1 3 Kapitel 5 137

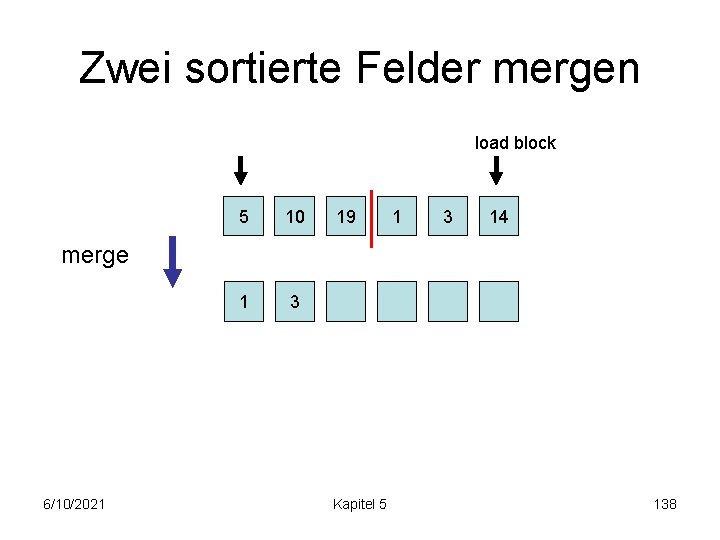
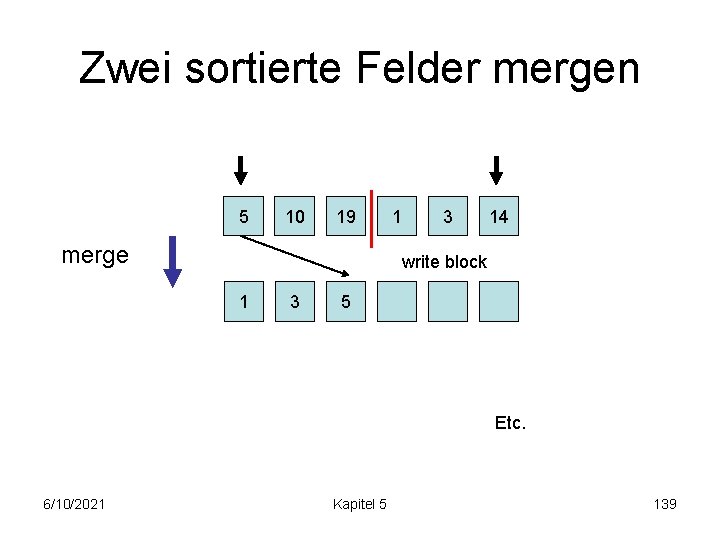
Zwei sortierte Felder mergen load block 5 10 1 3 19 1 3 14 merge 6/10/2021 Kapitel 5 138

Zwei sortierte Felder mergen 5 10 19 merge 1 3 14 write block 1 3 5 Etc. 6/10/2021 Kapitel 5 139

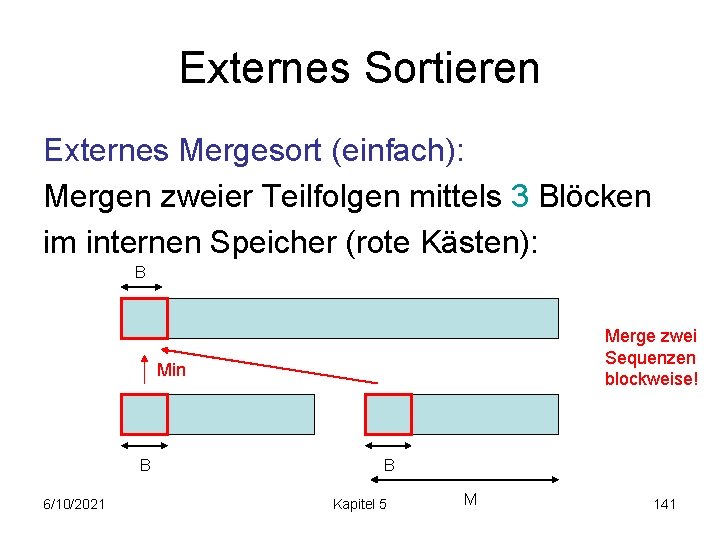
Externes Sortieren Externes Mergesort (einfach): • sortiere Folge in Abschnitten der Größe M (komplett intern möglich, e. g. , Quicksort) M M M • Merge von jeweils zwei Teilfolgen bis zur Gesamtfolge (<=1+log(n/M) Durchläufe) Anzahl Blocktransfers: O(2 n/B (1+log(n/M))) 6/10/2021 Kapitel 5 140

Externes Sortieren Externes Mergesort (einfach): Mergen zweier Teilfolgen mittels 3 Blöcken im internen Speicher (rote Kästen): B Merge zwei Sequenzen blockweise! Min B 6/10/2021 B Kapitel 5 M 141

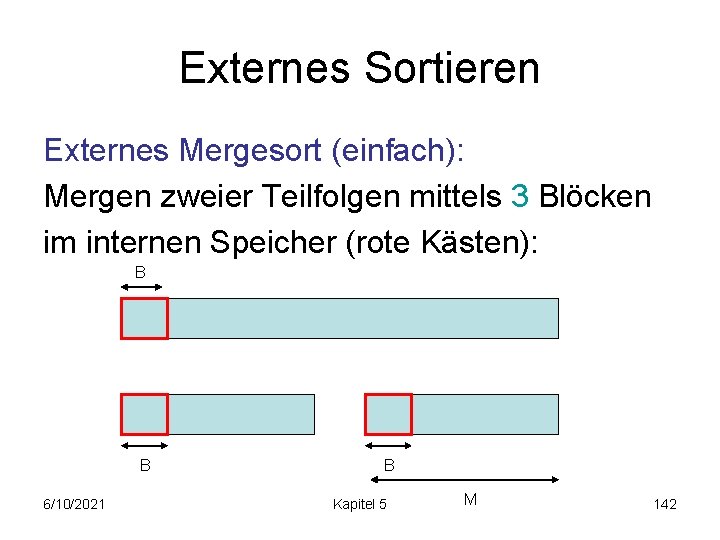
Externes Sortieren Externes Mergesort (einfach): Mergen zweier Teilfolgen mittels 3 Blöcken im internen Speicher (rote Kästen): B B 6/10/2021 B Kapitel 5 M 142

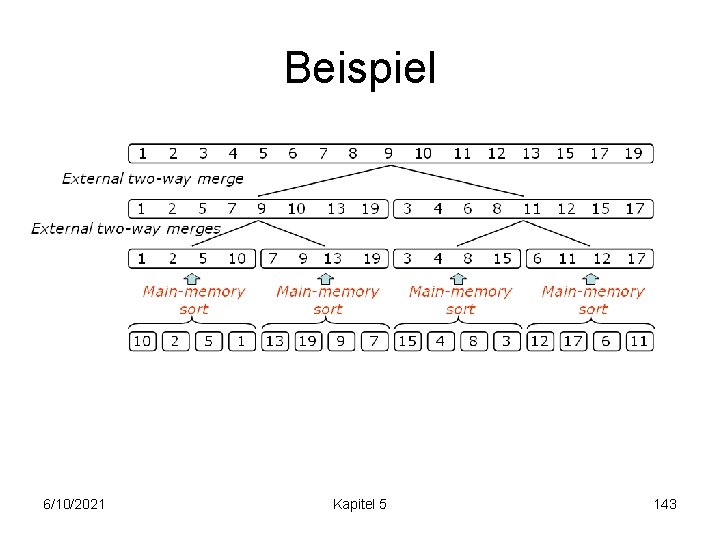
Beispiel 6/10/2021 Kapitel 5 143

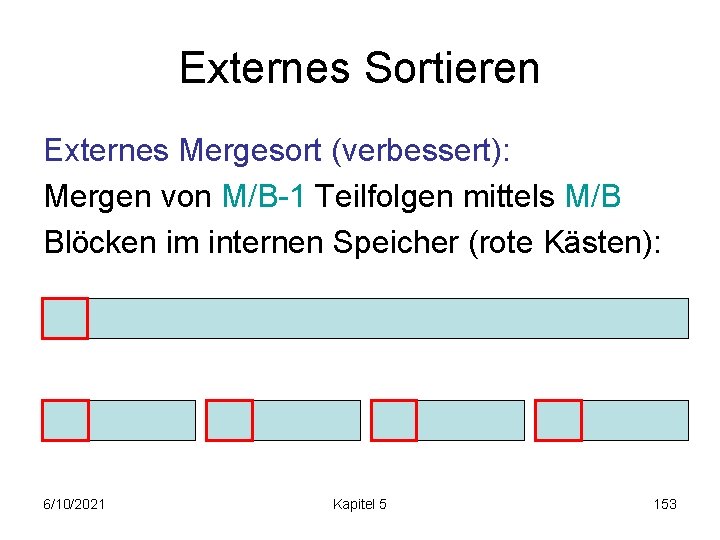
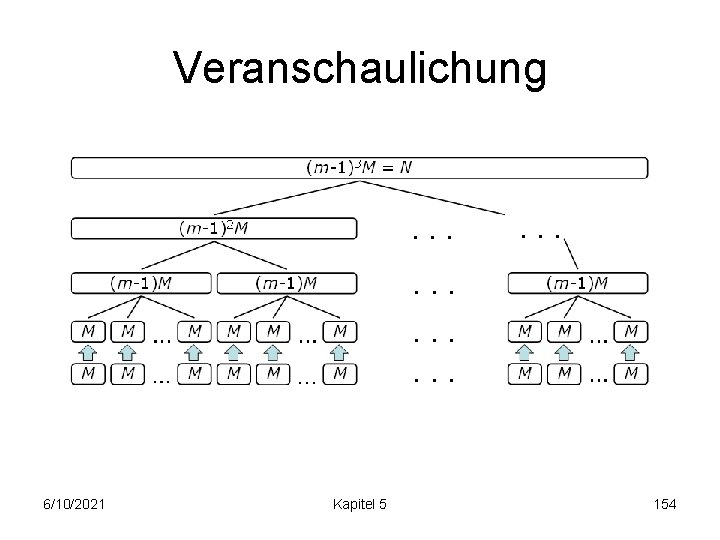
Externes Sortieren Externes Mergesort (verbessert): • sortiere Folge in Abschnitten der Größe M (komplett intern möglich) M M M • Merge von jeweils M/B-1 Teilfolgen bis zur Gesamtfolge (<=1+log. M/B(n/M) Durchläufe) Anzahl Blocktransf. : O(2 n/B (1+log. M/B(n/M))) 6/10/2021 Kapitel 5 144

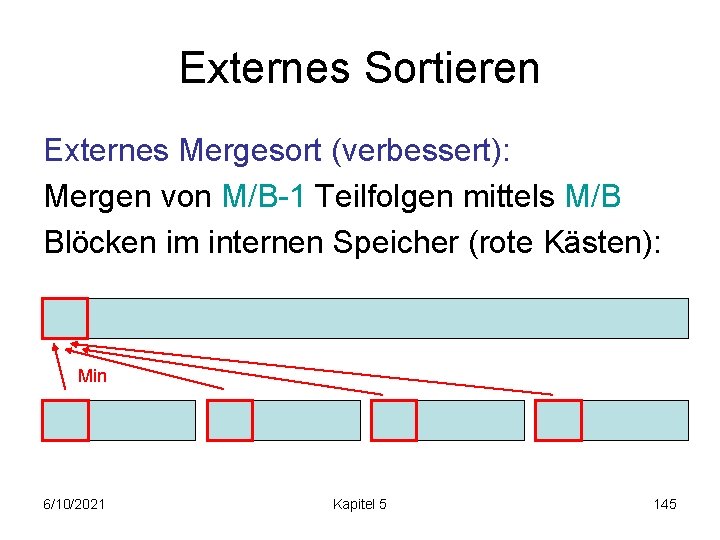
Externes Sortieren Externes Mergesort (verbessert): Mergen von M/B-1 Teilfolgen mittels M/B Blöcken im internen Speicher (rote Kästen): Min 6/10/2021 Kapitel 5 145

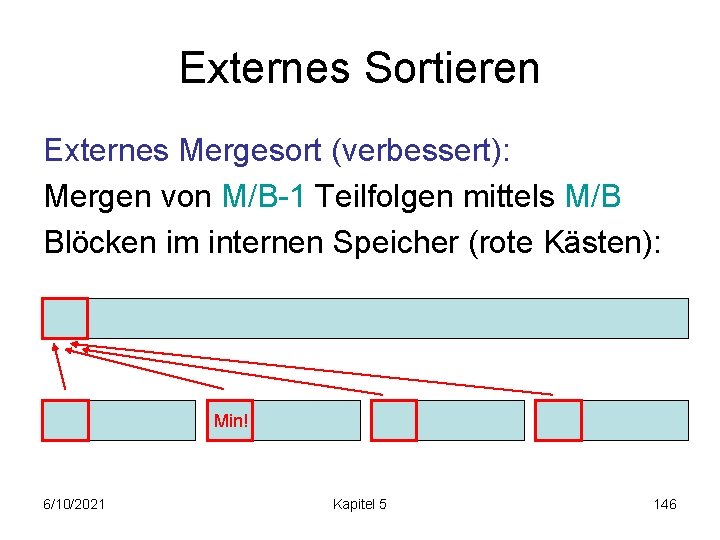
Externes Sortieren Externes Mergesort (verbessert): Mergen von M/B-1 Teilfolgen mittels M/B Blöcken im internen Speicher (rote Kästen): Min! 6/10/2021 Kapitel 5 146

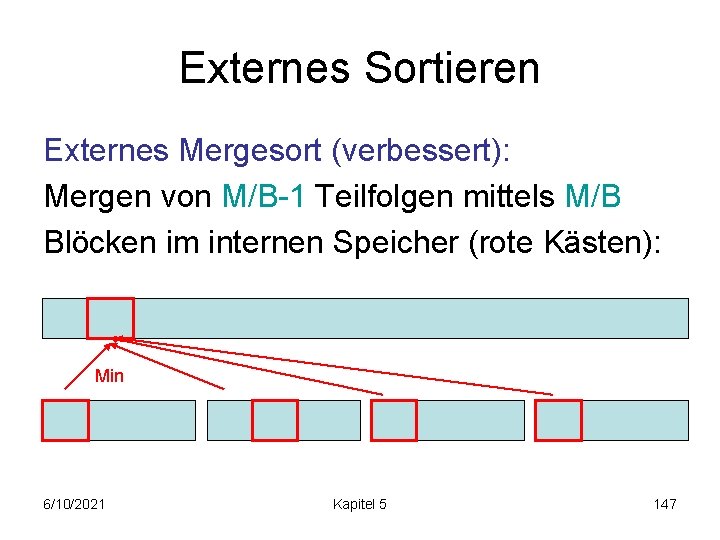
Externes Sortieren Externes Mergesort (verbessert): Mergen von M/B-1 Teilfolgen mittels M/B Blöcken im internen Speicher (rote Kästen): Min 6/10/2021 Kapitel 5 147

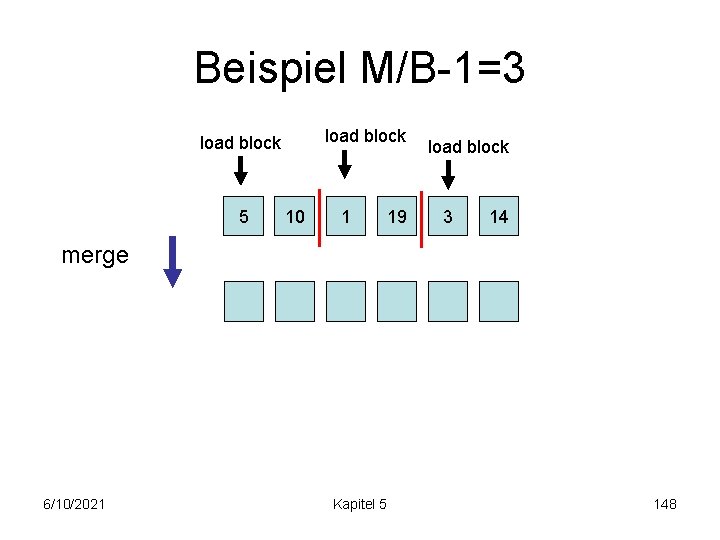
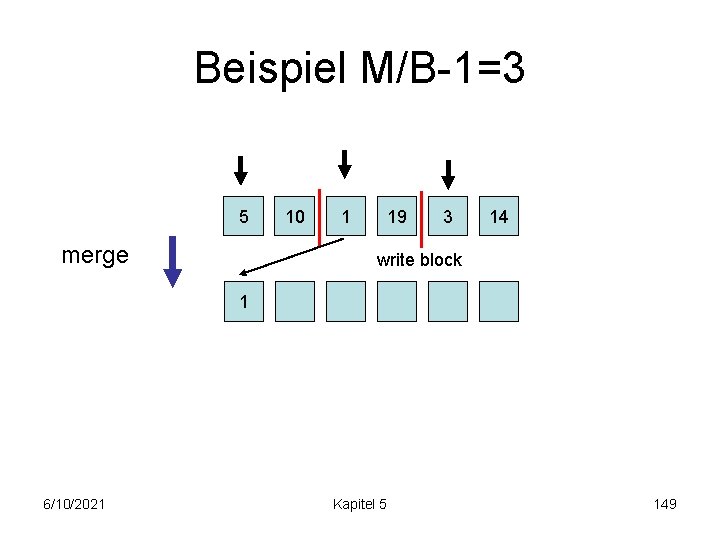
Beispiel M/B-1=3 load block 5 10 1 19 load block 3 14 merge 6/10/2021 Kapitel 5 148

Beispiel M/B-1=3 5 merge 10 1 19 3 14 write block 1 6/10/2021 Kapitel 5 149

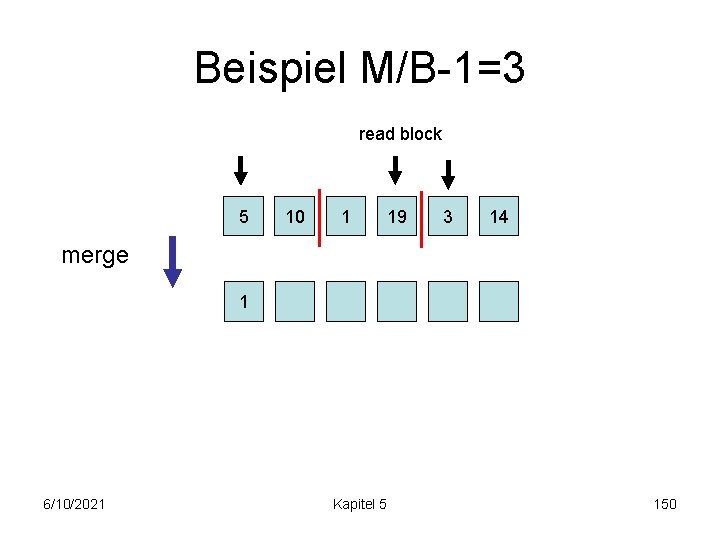
Beispiel M/B-1=3 read block 5 10 1 19 3 14 merge 1 6/10/2021 Kapitel 5 150

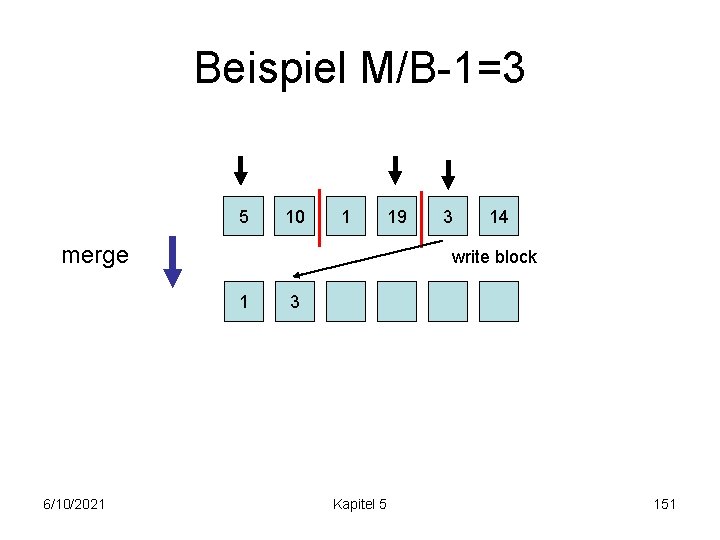
Beispiel M/B-1=3 5 10 1 19 merge 14 write block 1 6/10/2021 3 3 Kapitel 5 151

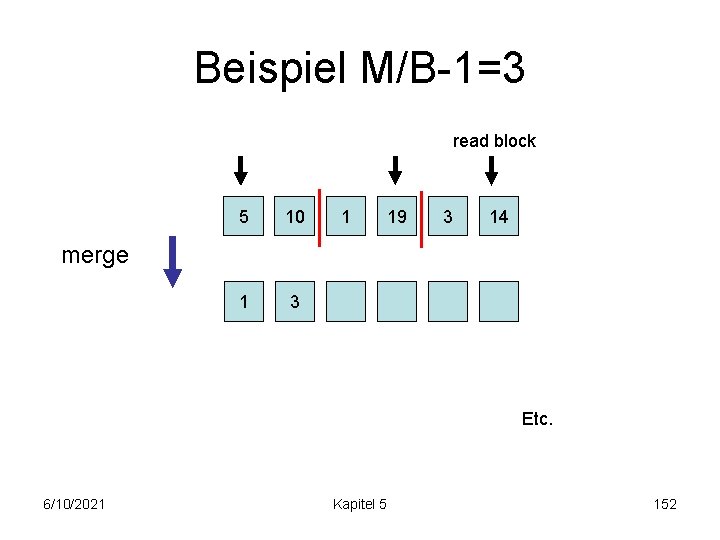
Beispiel M/B-1=3 read block 5 10 1 3 1 19 3 14 merge Etc. 6/10/2021 Kapitel 5 152

Externes Sortieren Externes Mergesort (verbessert): Mergen von M/B-1 Teilfolgen mittels M/B Blöcken im internen Speicher (rote Kästen): 6/10/2021 Kapitel 5 153

Veranschaulichung 6/10/2021 Kapitel 5 154

Nächstes Kapitel Priority Queues (Damit ist Selection Sort viel besser!) 6/10/2021 Kapitel 5 155

Nachtrag zu While Schleifen (1) • Wie kann man die Laufzeit von for-Schleifen analysieren? • Einfach: for-Schleifen haben Zähler - for (i=0, i<X, i++) {} wird X mal ausgeführt • while-Schleifen haben keinen Zähler - Idee: Führe künstlich einen „Zähler“ ein, resp. eine Grösse die in jeder (oder jeder zweiten etc. ) Iteration strikt zu oder abnimmt - Nennen wir Potenzialfunktion! - Hat nichts mit amortisierter Analyse mit Potenzialfunktionen zu tun! 6/10/2021 Kapitel 5 156

Nachtrag zu While Schleifen (2) • Beispiel: i : = N; while (i>1) i: =i/2; • Mögliche Potenzialfunktion: = i; • Es gilt – – – – 0 = N und j+1 = j / 2 Sobald j · 1 terminiert‘s Wieviel Iterationen hat die While-Schleife? Was wäre, wenn man in jedem Schritt i: =i-1 rechnen würde? Was wäre, wenn man in jedem Schritt i: =sqrt(i) rechnen würde? Was wäre, wenn man in jedem Schritt i: =log(i) rechnen würde? Was wäre, wenn in der Schleife noch mehr Code wäre? 6/10/2021 Kapitel 5 157