Grundlagen der Elektrochemie I Plan der Wiederholung 1

Grundlagen der Elektrochemie I Plan der Wiederholung 1. Elektrochemische Doppelschicht: Der Ort des Geschehens! 2. Elektrochemische Thermodynamik: Was ist erlaubt? 3. Elektrochemische Kinetik: Ist der Prozeß schnell oder gehemmt? 4. Transportprozesse: 5. Voltammetrie: Wie kommen die Ionen zur Grenzfläche? FU Berlin Anwendung des vorangegangenen und zugleich wichtige experimentelle und analytische Untersuchungsmethode Constanze Donner / Ludwig Pohlmann 2014 1

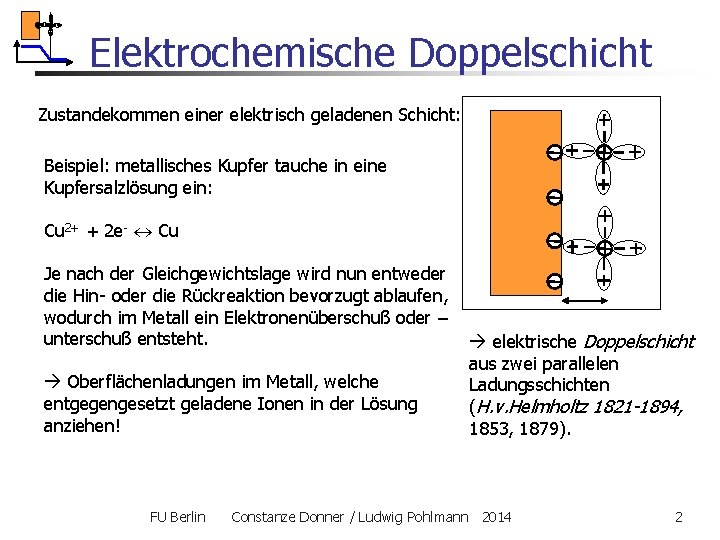
Elektrochemische Doppelschicht Zustandekommen einer elektrisch geladenen Schicht: Beispiel: metallisches Kupfer tauche in eine Kupfersalzlösung ein: Cu 2+ + 2 e- Cu Je nach der Gleichgewichtslage wird nun entweder die Hin- oder die Rückreaktion bevorzugt ablaufen, wodurch im Metall ein Elektronenüberschuß oder – unterschuß entsteht. Oberflächenladungen im Metall, welche entgegengesetzt geladene Ionen in der Lösung anziehen! FU Berlin elektrische Doppelschicht aus zwei parallelen Ladungsschichten (H. v. Helmholtz 1821 -1894, 1853, 1879). Constanze Donner / Ludwig Pohlmann 2014 2

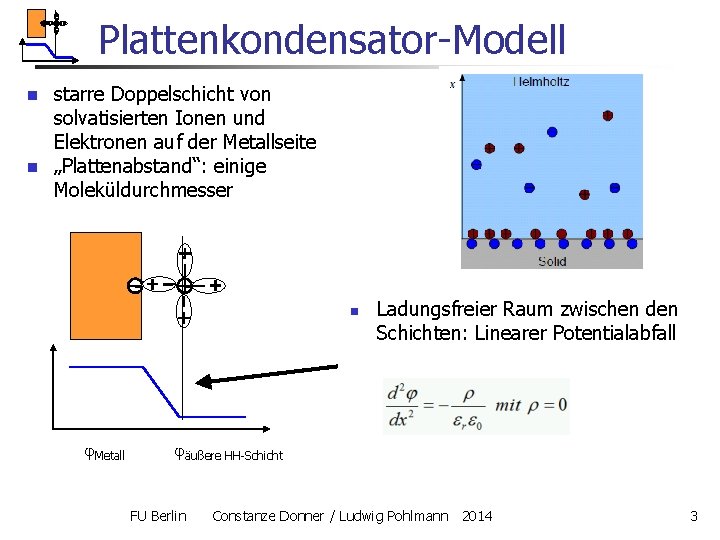
Plattenkondensator-Modell n n starre Doppelschicht von solvatisierten Ionen und Elektronen auf der Metallseite „Plattenabstand“: einige Moleküldurchmesser n Metall Ladungsfreier Raum zwischen den Schichten: Linearer Potentialabfall äußere HH-Schicht FU Berlin Constanze Donner / Ludwig Pohlmann 2014 3

Helmholtz FU Berlin Constanze Donner / Ludwig Pohlmann 2014 4

Konsequenzen I „Plattenkondensator“ mit kleinstmöglichem Plattenabstand! n n Extrem hohe Feldstärke: = 500 m. V, d = 0. 5 nm Feldstärke E = 109 V/m ! Zum Vergleich: Durchschlagsfeldstärke: Luft: 106, Quarz: 108 V/m Diese enormen Feldstärken sind notwendig (und hinreichend), um chemische Bindungen brechen bzw. neu formen zu können! Elektrochemische Reaktionen können nur in der Helmholtzschicht stattfinden! EC ist Surface Science! FU Berlin Constanze Donner / Ludwig Pohlmann 2014 5

Konsequenzen II „Plattenkondensator“ mit kleinstmöglichem Plattenabstand! n n n Riesige Kapazität: Kapazität pro Fläche beim Plattenkondensator: Wasser: r = 78, 5 C = 350 F/cm 2 in Wirklichkeit kleiner, ca. 10 -50 F/cm 2, da r in der starren Doppelschicht kleiner ist Anwendung für Kondensatoren! FU Berlin Constanze Donner / Ludwig Pohlmann 2014 6

Doppelschichtkondensatoren (Superkondensatoren) Kapazität: 10 -40 F/cm 2 n Prinzip: poröse Kohlenstoffelektroden mit einer sehr großen inneren Oberfläche! (Aktivkohle, Aerogele) n Kapazitäten bis zu 100 F / g ! n Seit 1971 (1957 Patent) FU Berlin n Energiedichte: 4 – 60 Wh / kg Constanze Donner / Ludwig Pohlmann 2014 7

Gouy-Chapman-Modell n n n Grundidee: zwei gegenläufig Prozesse Das elektrostatische Feld der Elektrode zieht entgegengesetzt geladene Ionen an Die Molekularbewegung zerstört immer wieder jede Ordnung FU Berlin Constanze Donner / Ludwig Pohlmann 2014 8

Gouy-Chapman II n n Analogie? n Vergleichbar mit der barometrischen Höhenformel? Allerdings: n n Das Gravitationspotential ist annähernd linear und unabhängig von der Luftdichte Das elektrische Potential hängt von der Ladungsdichte selbst ab: Wohl doch komplizierter!? und FU Berlin Constanze Donner / Ludwig Pohlmann 2014 9

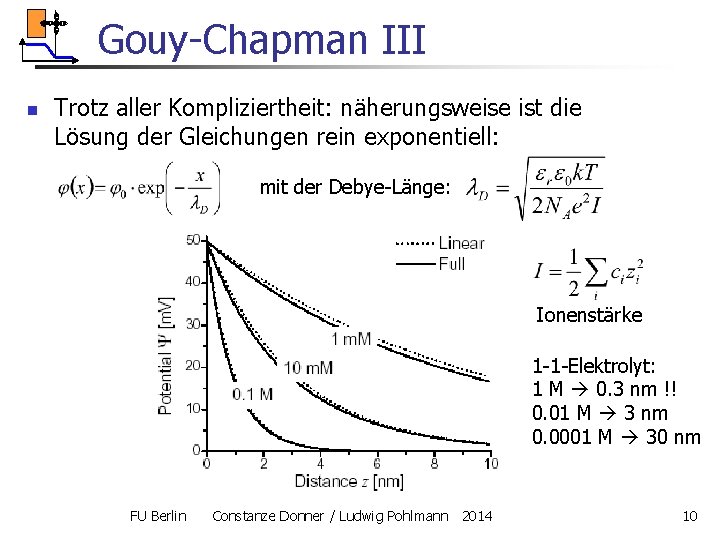
Gouy-Chapman III n Trotz aller Kompliziertheit: näherungsweise ist die Lösung der Gleichungen rein exponentiell: mit der Debye-Länge: Ionenstärke 1 -1 -Elektrolyt: 1 M 0. 3 nm !! 0. 01 M 3 nm 0. 0001 M 30 nm FU Berlin Constanze Donner / Ludwig Pohlmann 2014 10

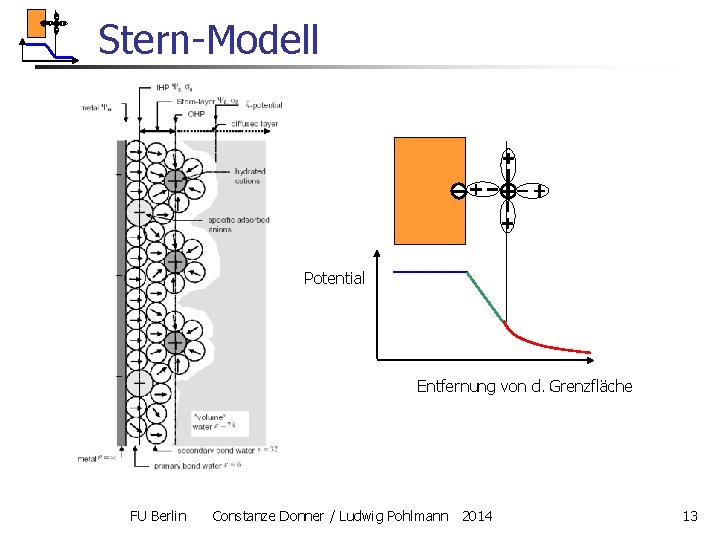
Synthese: Stern-Modell n n Das GC-Modell ist geeignet für die Nähe des Nullladungspotentials, das HH-Modell für größere Entfernungen davon HH-Schicht und die diffuse GC-Schicht sind geometrisch hintereinander angeordnet Logisch ist eine Synthese: Reihenschaltung beider Kondensatoren Modell von Stern 1888 -1969 (1924): FU Berlin Constanze Donner / Ludwig Pohlmann 2014 12

Stern-Modell Potential Entfernung von d. Grenzfläche FU Berlin Constanze Donner / Ludwig Pohlmann 2014 13

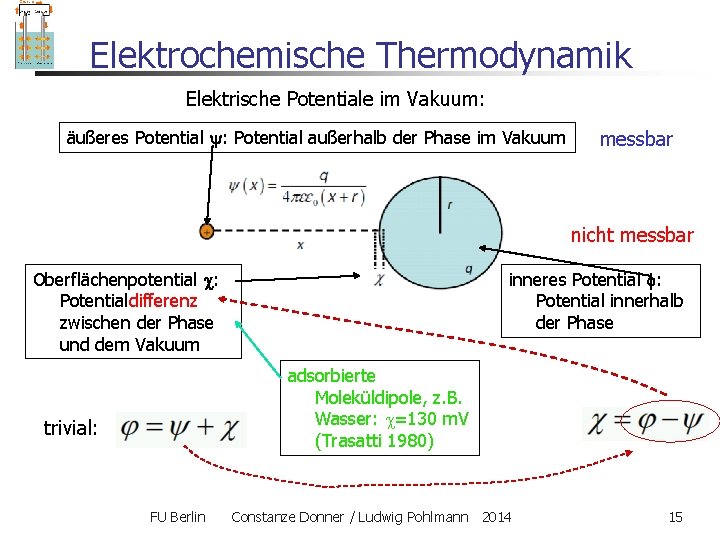
Elektrochemische Thermodynamik Elektrische Potentiale im Vakuum: äußeres Potential : Potential außerhalb der Phase im Vakuum messbar nicht messbar Oberflächenpotential : Potentialdifferenz zwischen der Phase und dem Vakuum inneres Potential : Potential innerhalb der Phase adsorbierte Moleküldipole, z. B. Wasser: =130 m. V (Trasatti 1980) trivial: FU Berlin Constanze Donner / Ludwig Pohlmann 2014 15

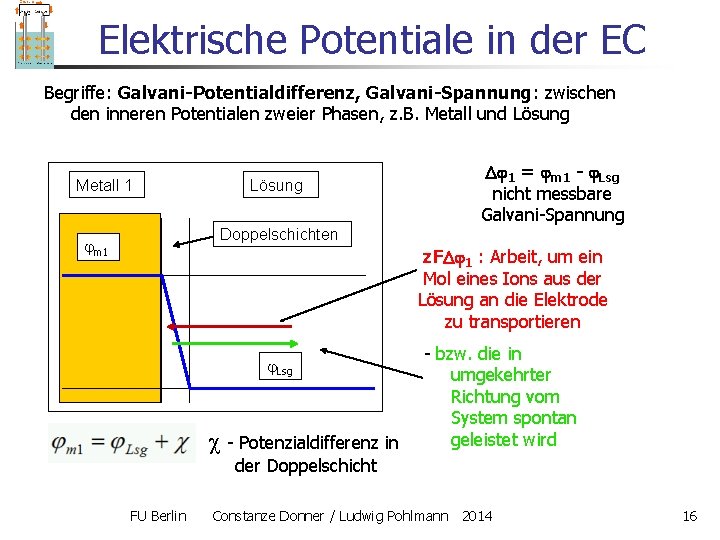
Elektrische Potentiale in der EC Begriffe: Galvani-Potentialdifferenz, Galvani-Spannung: zwischen den inneren Potentialen zweier Phasen, z. B. Metall und Lösung Metall 1 Lösung 1 = m 1 - Lsg nicht messbare Galvani-Spannung Doppelschichten m 1 z. F 1 : Arbeit, um ein Mol eines Ions aus der Lösung an die Elektrode zu transportieren Lsg - Potenzialdifferenz in - bzw. die in umgekehrter Richtung vom System spontan geleistet wird der Doppelschicht FU Berlin Constanze Donner / Ludwig Pohlmann 2014 16

Chemisches Potential Das chemische Potential ist das thermodynamische Maß für die „Neigung“ eines Stoffes (Ions, Elektrons), sich: - mit anderen Stoffen umzusetzen - gleichmäßig zu verteilen - in eine andere Phase umzuwandeln Jeder spontan ablaufende Prozess verläuft immer vom höheren chemische Potential zum niedrigeren – die Änderung der freien Enthalpie G (Gibbssche freie Energie) ist also immer negativ: Einheit: J/mol z. B. : H 2 , O 2 : 0 H 2 O: -237 C 6 H 6: 125 J. W. Gibbs (1839 -1909) spontan! FU Berlin Constanze Donner / Ludwig Pohlmann 2014 17

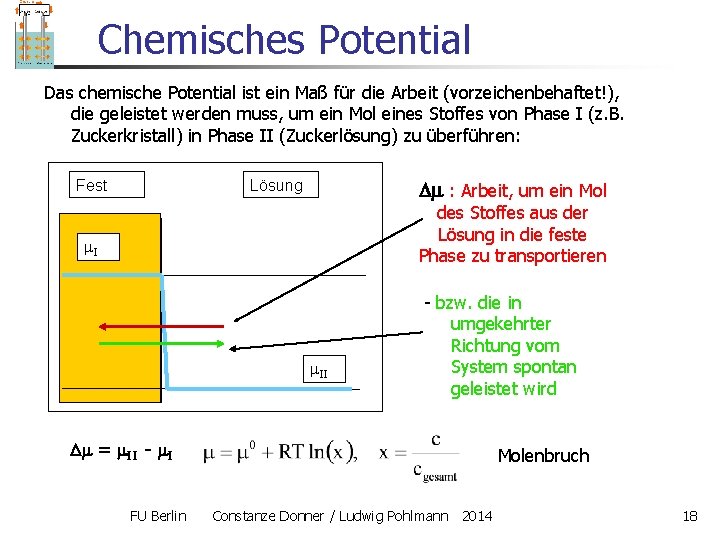
Chemisches Potential Das chemische Potential ist ein Maß für die Arbeit (vorzeichenbehaftet!), die geleistet werden muss, um ein Mol eines Stoffes von Phase I (z. B. Zuckerkristall) in Phase II (Zuckerlösung) zu überführen: Fest Lösung : Arbeit, um ein Mol des Stoffes aus der Lösung in die feste Phase zu transportieren I II - bzw. die in umgekehrter Richtung vom System spontan geleistet wird = II - I FU Berlin Molenbruch Constanze Donner / Ludwig Pohlmann 2014 18

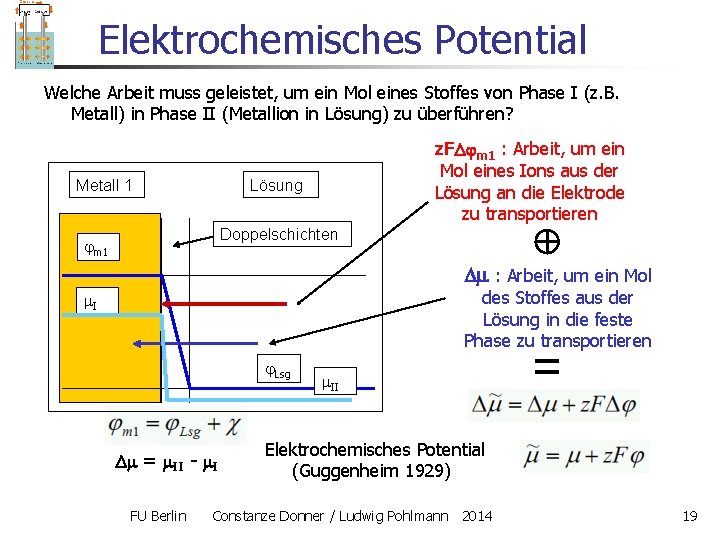
Elektrochemisches Potential Welche Arbeit muss geleistet, um ein Mol eines Stoffes von Phase I (z. B. Metall) in Phase II (Metallion in Lösung) zu überführen? Metall 1 z. F m 1 : Arbeit, um ein Mol eines Ions aus der Lösung an die Elektrode zu transportieren Lösung Doppelschichten m 1 : Arbeit, um ein Mol des Stoffes aus der Lösung in die feste Phase zu transportieren I Lsg = II - I FU Berlin II Elektrochemisches Potential (Guggenheim 1929) Constanze Donner / Ludwig Pohlmann 2014 19

Nernst-Gleichung Welches Potential stellt sich im Gleichgewicht an der Phasengrenze ein? Bedingung für das thermodynamische Gleichgewicht bei p, T = const. : Die freie Enthalpie G befindet sich im Minimum, d. h. G = 0 Beispiel: monomolekulare Reaktion Gleichheit der chemischen Potentiale von Ausgangsstoff und Reaktionsprodukt MWG FU Berlin Constanze Donner / Ludwig Pohlmann 2014 20

Nernst-Gleichung Welches Potential stellt sich im Gleichgewicht an der Phasengrenze ein? . Beispiel: Metallabscheidung: Gleichheit der elektrochemischen Potentiale von Ausgangsstoff und Reaktionsprodukt also: Umstellung nach der Galvanispannung: Standard-Galvanispannung und Nernst-Gleichung für das Gleichgewichts. Galvani-Potential einer Metallionenelektrode bzw. FU Berlin Constanze Donner / Ludwig Pohlmann 2014 21

Nernst-Gleichung Welches Potential stellt sich im Gleichgewicht an der Phasengrenze ein? . Beispiel: Redoxreaktion an inerter Elektrode : ergibt eine Nernst-Gleichung der Form: Achtung: Die so ermittelten Gleichgewichtspotentiale beziehen sich auf eine Halbzelle und sind deshalb nicht messbar! Messbar ist die Klemmspannung einer elektrochemischen Zelle, d. h. die Differenz der Gleichgewichtspotentiale der beiden Halbzellen! FU Berlin Constanze Donner / Ludwig Pohlmann 2014 22

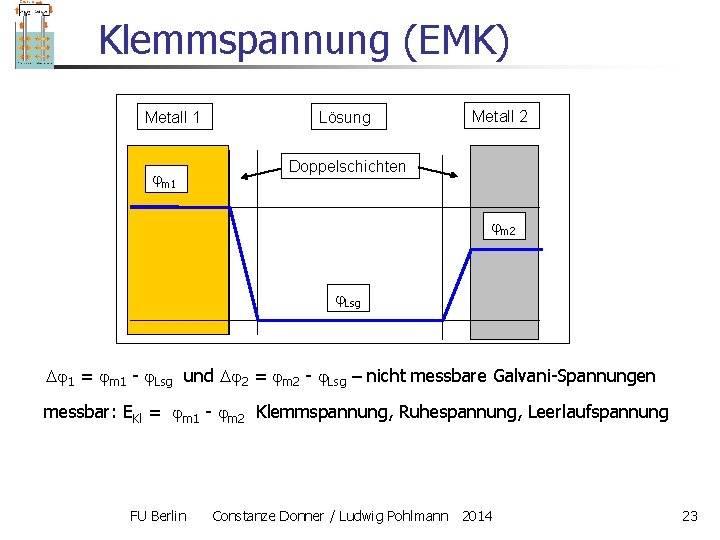
Klemmspannung (EMK) Metall 1 m 1 Lösung Metall 2 Doppelschichten m 2 Lsg 1 = m 1 - Lsg und 2 = m 2 - Lsg – nicht messbare Galvani-Spannungen messbar: EKl = m 1 - m 2 Klemmspannung, Ruhespannung, Leerlaufspannung FU Berlin Constanze Donner / Ludwig Pohlmann 2014 23

Geschichte galvanischer Zellen Volta 1800 eine Reihe von hintereinander geschalteten galvanischen Zellen. 1838 Daniell Element Batterie Voltasche Säule Vorläufer heutiger Batterien Grove Brennstoffzelle 1838 FU Berlin Constanze Donner / Ludwig Pohlmann 2014 24

Gleichgewicht ≠ Gleichgewicht Das elektrochemische Gleichgewicht ist nicht das chemische Gleichgewicht! Wenn G < 0, dann bewegt sich das System spontan zum Gleichgewicht Bewegungsrichtung: immer so, dass die Triebkraft der Bewegung verringert wird (1) Chemisches Gleichgewicht: • Auflösung von Zucker: solange, bis die Lösung gesättigt ist, also die Differenz der chemischen Potentiale Null wird • rein hypothetisch vergessen wir mal die Ladungen bei der Auflösung eines einzelnen Kupferblechs: läuft solange, bis die Lösung mit Cu. SO 4 gesättigt ist FU Berlin Constanze Donner / Ludwig Pohlmann 2014 25

Gleichgewicht ≠ Gleichgewicht (1) Elektrochemisches Gleichgewicht: • elektrochemische Auflösung von Kupfer: mit jedem Ion Cu 2+, welches in Lösung geht, lädt sich die Metalloberfläche um zwei Elektronen negativer auf: • Prozess läuft solange, bis der wachsende Potentialabfall in der Doppelschicht eine weitere Auflösung verhindert, d. h. die Differenz der elektrochemische Potentiale Null wird (EC-Gleichgewicht) • da ist aber noch lange nicht die Sättigungskonzentration (C-Gleichgewicht) erreicht! die freie Enthalpie des Systems im elektrochemischen GG liegt weit über dem Enthalpieminimum im Falle des chemischen GG! das chemische GG kann nur erreicht werde, wenn es gelingt, die Potentialdifferenz durch Kurzschließen der beiden Seiten der Grenzschicht zu beseitigen: das gelingt aber nur mit einer zweiten Elektrode: das aber ist ein galvanisches Element, die Energiedifferenz zwischen elektrochemischem und chemischen GG ist gleich der elektrischen Nutzenergie, die der Batterie entnommen werden kann!! FU Berlin Constanze Donner / Ludwig Pohlmann 2014 26