Lektion 5 Repetition kapitel 5 Modem Shannons regel




















- Slides: 30

Lektion 5 Repetition kapitel 5: Modem. Shannons regel.

Example 10 A constellation diagram consists of eight equally spaced points on a circle. If the bit rate is 4800 bps, what is the baud rate? Solution The constellation indicates 8 -PSK with the points 45 degrees apart. Since 23 = 8, 3 bits are transmitted with each signal unit. Therefore, the baud rate is 4800 / 3 = 1600 baud

Example 11 Compute the bit rate for a 1000 -baud 16 -QAM signal. Solution A 16 -QAM signal has 4 bits per signal unit since log 216 = 4. Thus, 1000· 4 = 4000 bps

Example 12 Compute the baud rate for a 72, 000 -bps 64 -QAM signal. Solution A 64 -QAM signal has 6 bits per signal unit since log 2 64 = 6. Thus, 72000 / 6 = 12, 000 baud

5. 2 Telephone Modems Modem Standards

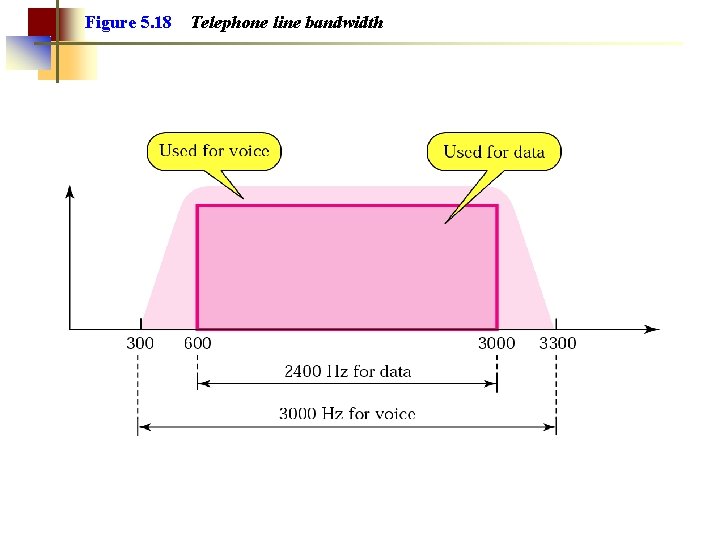
Note: A telephone line has a bandwidth of almost 2400 Hz for data transmission.

Figure 5. 18 Telephone line bandwidth

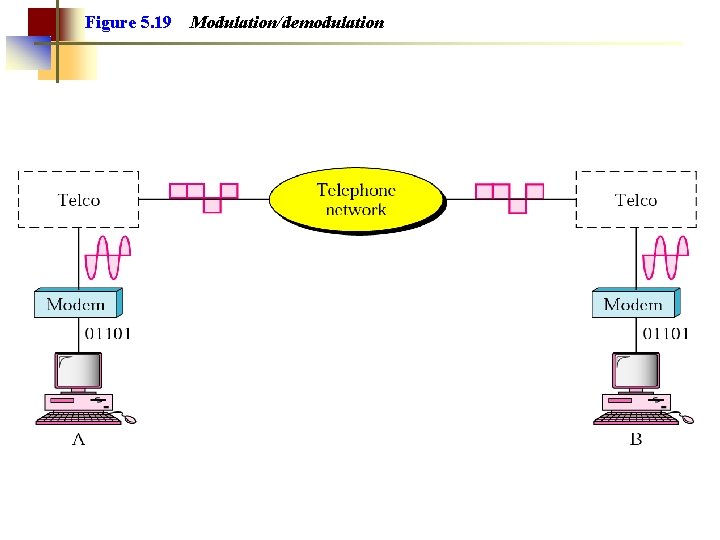
Note: Modem stands for modulator/demodulator.

Figure 5. 19 Modulation/demodulation

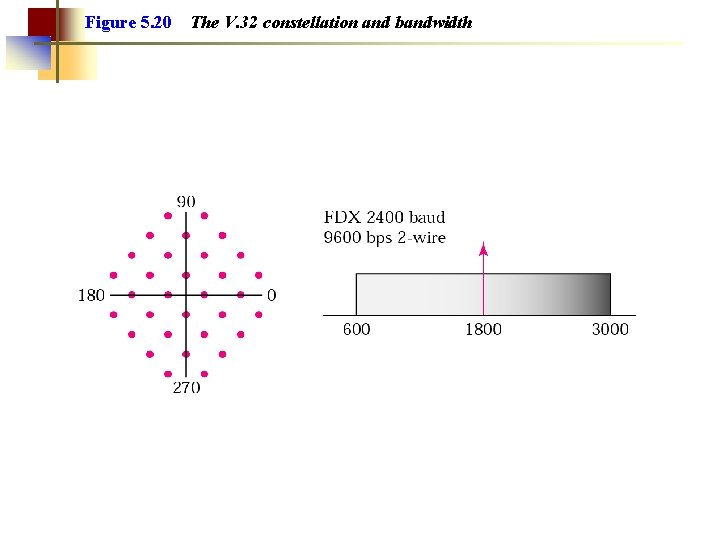
Figure 5. 20 The V. 32 constellation and bandwidth

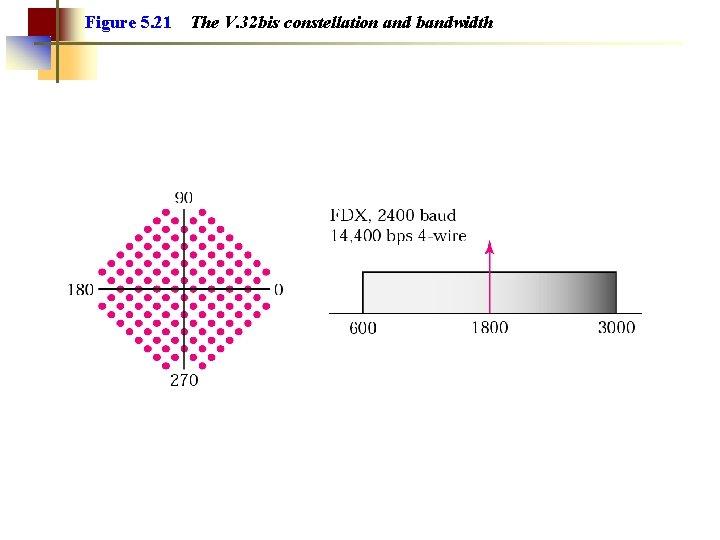
Figure 5. 21 The V. 32 bis constellation and bandwidth

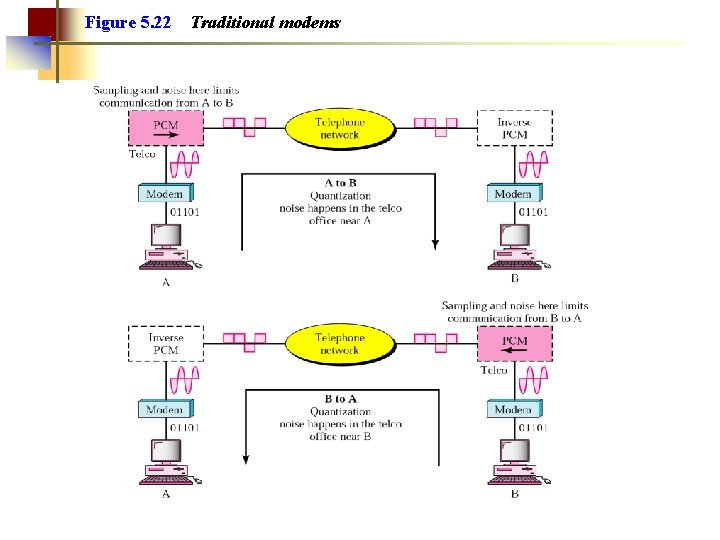
Figure 5. 22 Traditional modems

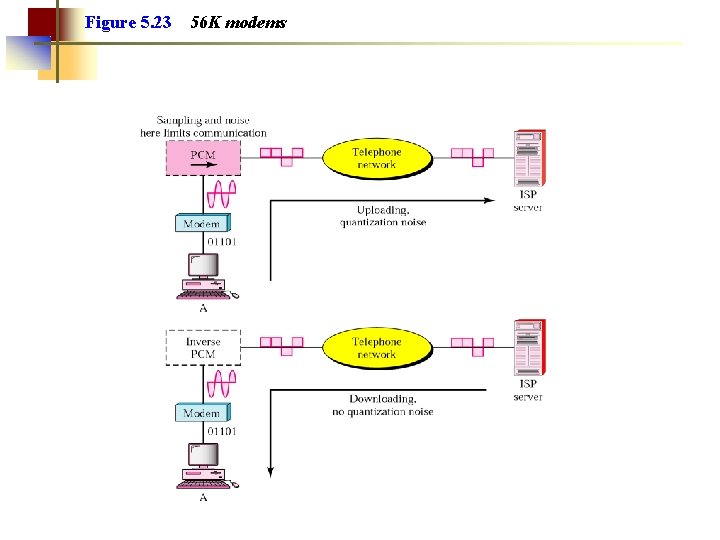
Figure 5. 23 56 K modems

Note: The total bandwidth required for AM can be determined from the bandwidth of the audio signal: BWt = 2 x BWm.

Example 7 Consider a noiseless channel with a bandwidth of 3000 Hz transmitting a signal with two signal levels. The maximum bit rate can be calculated as Bit Rate = 2 3000 log 2 2 = 6000 bps

Digital modulation • För att överföra N bit/symbol krävs M=2 N • Vid M symboler överförs N=log 2 M bit/symbol. • Baudrate fs= antal symboler per sekund. Enhet: baud eller symboler/sekund. • Symbollängd Ts= 1/fs. fs= 1/Ts • Bitrate R = datahastighet. Enhet: bps eller bit/s. • R= fslog 2 M

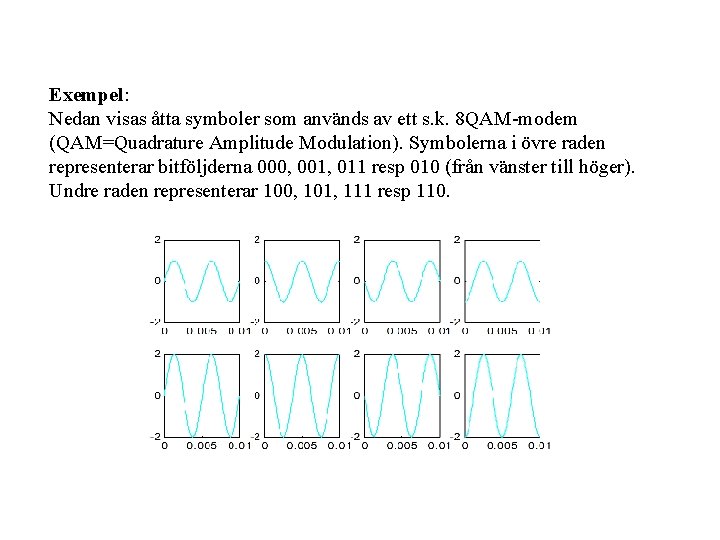
Exempel: Nedan visas åtta symboler som används av ett s. k. 8 QAM-modem (QAM=Quadrature Amplitude Modulation). Symbolerna i övre raden representerar bitföljderna 000, 001, 011 resp 010 (från vänster till höger). Undre raden representerar 100, 101, 111 resp 110.

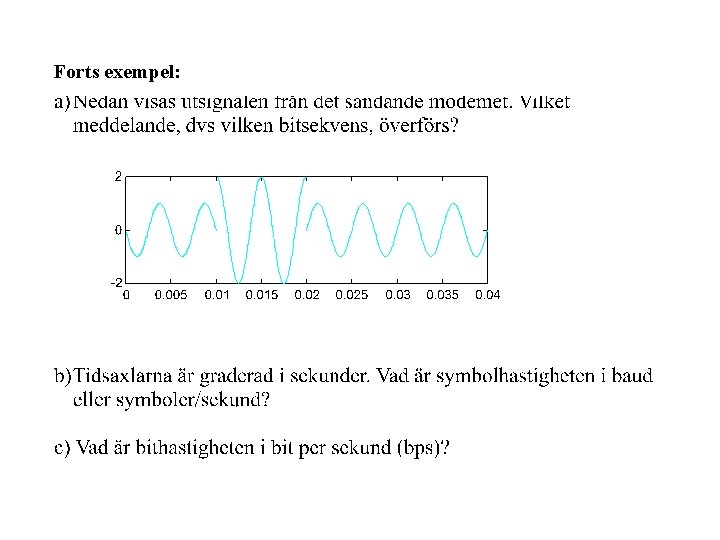
Forts exempel:

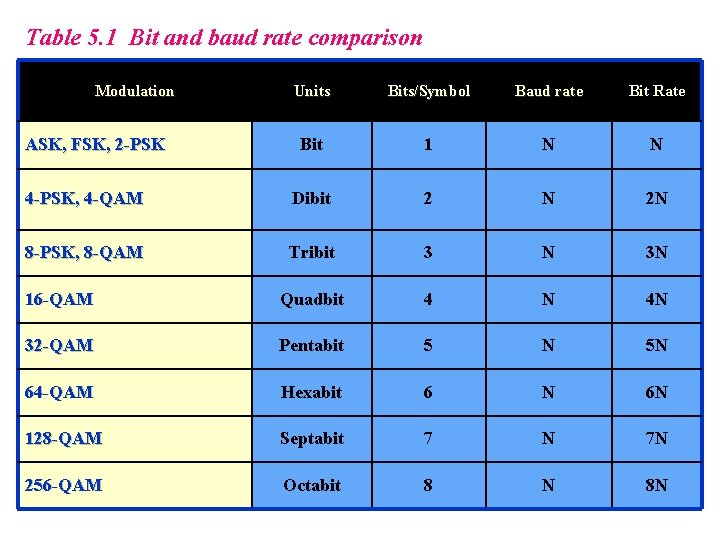
Table 5. 1 Bit and baud rate comparison Modulation Units Bits/Symbol Baud rate Bit Rate Bit 1 N N 4 -PSK, 4 -QAM Dibit 2 N 2 N 8 -PSK, 8 -QAM Tribit 3 N 3 N 16 -QAM Quadbit 4 N 4 N 32 -QAM Pentabit 5 N 5 N 64 -QAM Hexabit 6 N 6 N 128 -QAM Septabit 7 N 7 N 256 -QAM Octabit 8 N 8 N ASK, FSK, 2 -PSK

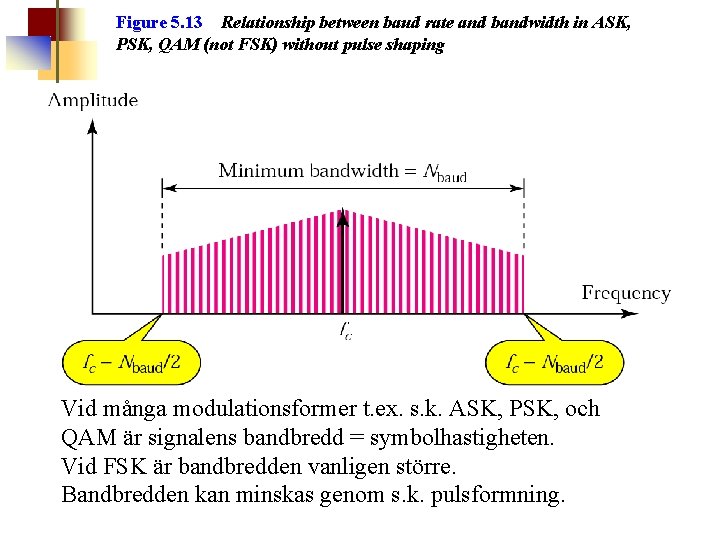
Figure 5. 13 Relationship between baud rate and bandwidth in ASK, PSK, QAM (not FSK) without pulse shaping Vid många modulationsformer t. ex. s. k. ASK, PSK, och QAM är signalens bandbredd = symbolhastigheten. Vid FSK är bandbredden vanligen större. Bandbredden kan minskas genom s. k. pulsformning.

Maximal kanalkapacitet enligt Nyquist

Example 8 Consider the same noiseless channel, transmitting a signal with four signal levels (for each level, we send two bits). The maximum bit rate can be calculated as: Bit Rate = 2 x 3000 x log 2 4 = 12, 000 bps

Shannons regel Kanalkapaciteten C är max antal bit per sekund vid bästa möjliga modulationsteknik och felrättande kodning: C = B log 2 (1+S/N), där B är ledningens bandbredd i Hertz (oftast ungefär lika med övre gränsfrekvensen), S är nyttosignalens medeleffekt i Watt och N (noice) är bruseffekten i Watt.

Example 9 Consider an extremely noisy channel in which the value of the signal-to-noise ratio is almost zero. In other words, the noise is so strong that the signal is faint. For this channel the capacity is calculated as C = B log 2 (1 + SNR) = B log 2 (1 + 0) = B log 2 (1) = B 0 = 0

Example 10 We can calculate theoretical highest bit rate of a regular telephone line. A telephone line normally has a bandwidth of 3000 Hz (300 Hz to 3300 Hz). The signal-to -noise ratio is usually 3162. For this channel the capacity is calculated as C = B log 2 (1 + SNR) = 3000 log 2 (1 + 3162) = 3000 log 2 (3163) C = 3000 11. 62 = 34, 860 bps

Example 11 We have a channel with a 1 MHz bandwidth. The SNR for this channel is 63; what is the appropriate bit rate and signal level? Solution First, we use the Shannon formula to find our upper limit. C = B log 2 (1 + SNR) = 106 log 2 (1 + 63) = 106 log 2 (64) = 6 Mbps Then we use the Nyquist formula to find the number of signal levels. 4 Mbps = 2 1 MHz log 2 L L = 4

Capacity Limits • Maximum bit rate (capacity) depends on: ○ The analog bandwidth available (in Hz) ○ The quality of the channel • The level of the noise is one of the characteristics of the channel. The ratio of the voltage of the signal sent and the noise present in the channel is important for the maximum data rate achieved. • Shannon’s theorem determines theoretical highest data rate of a noisy channel C = B log 2 (1 + S/N) S/N is the signal to noise ratio (often labeled as SNR)

Capacity Limits • Maximum bit rate (capacity) depends on: ○ The analog bandwidth available (in Hz) ○ The quality of the channel • The level of the noise is one of the characteristics of the channel. The ratio of the voltage of the signal sent and the noise present in the channel is important for the maximum data rate achieved. • Shannon’s theorem determines theoretical highest data rate of a noisy channel C = B log 2 (1 + S/N) S/N is the signal to noise ratio (often labeled as SNR)

Example: • Problem: Given S/N ratio of 30. 098756 d. B, bandwidth of 8 Khz, compute maximum data rate. • Answer: S/N = 30. 098756 d. B = 10 ^ 3. 0098756 = 1022. 9999205 1023 C = 8 Khz * log 2 (1 + 1023 ) C = 8 Khz * log 2 (1024 ) C = 8 * 1000 cycles/second * 10 bits/cycle C = 80 Kbps

How to calculate log 2 x • Calculators do not have a button for log 2 x calculation • To calculate log 2 x use the following formula: log 2 x = log 10 x/log 102 log 10 (x)/0. 3 Example: log 230 = log 30/log 2 1. 477/0. 3 4. 9
 Kapitel 5 lektion a answers
Kapitel 5 lektion a answers Dantes helvetestratt
Dantes helvetestratt Lektion 10
Lektion 10 Borklorid
Borklorid Lektion 2
Lektion 2 Heden dinosaurier
Heden dinosaurier Deutsch mit max 2 download
Deutsch mit max 2 download Lektion 3
Lektion 3 Malin nielsen
Malin nielsen åsa lillerskog
åsa lillerskog Lektion,se
Lektion,se Lektion 3 essen und trinken
Lektion 3 essen und trinken Schritte international 2 test zu lektion 10
Schritte international 2 test zu lektion 10 Lektion.se
Lektion.se Lektion des lebens
Lektion des lebens Lektion 6
Lektion 6 Lektion 6 test
Lektion 6 test Lektion se
Lektion se Lektion 14
Lektion 14 Lektion 24
Lektion 24 Im vorangegangenen kapitel
Im vorangegangenen kapitel Brief an die galater kapitel 6
Brief an die galater kapitel 6 The australian connection zusammenfassung kapitel 7
The australian connection zusammenfassung kapitel 7 Titelfigur der lindgren
Titelfigur der lindgren Korinthisieren
Korinthisieren Fabian oder der gang vor die hunde wien
Fabian oder der gang vor die hunde wien Mirjam pressler bitterschokolade zusammenfassung
Mirjam pressler bitterschokolade zusammenfassung Hiob kapitel 42
Hiob kapitel 42 Fliegender stern kapitel 5
Fliegender stern kapitel 5 Jb 12 kap
Jb 12 kap In diesem kapitel
In diesem kapitel