Datorntverk A lektion 5 Forts kapitel 5 Modem

Datornätverk A – lektion 5 Forts kapitel 5: Modem. Shannons regel. Kapitel 6: Transmission

5. 2 Telephone Modems Modem Standards

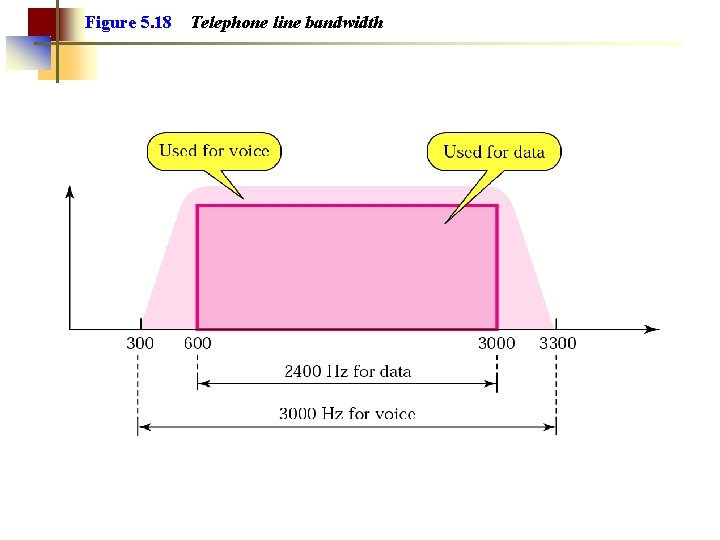
Note: A telephone line has a bandwidth of almost 2400 Hz for data transmission.

Figure 5. 18 Telephone line bandwidth

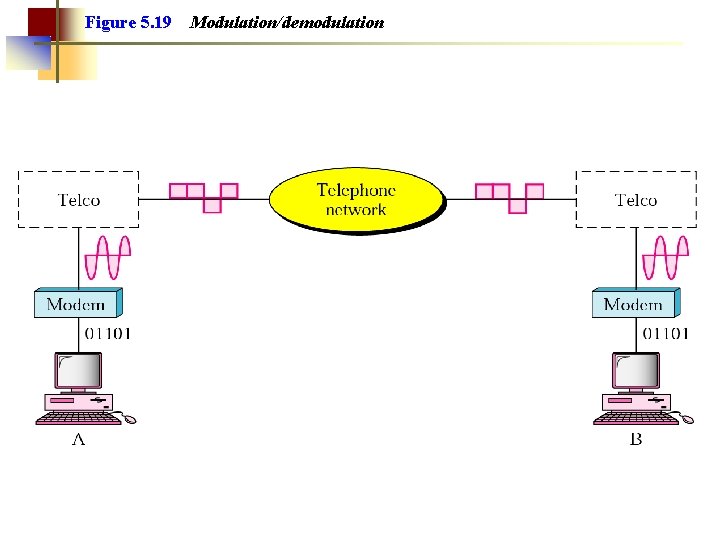
Note: Modem stands for modulator/demodulator.

Figure 5. 19 Modulation/demodulation

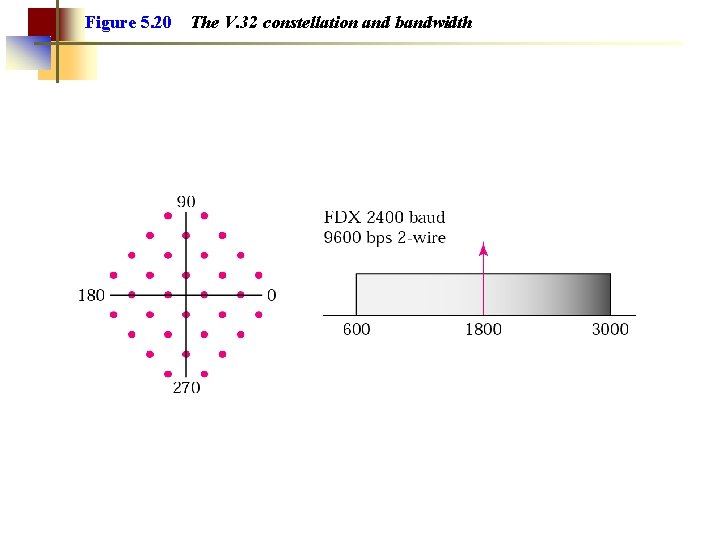
Figure 5. 20 The V. 32 constellation and bandwidth

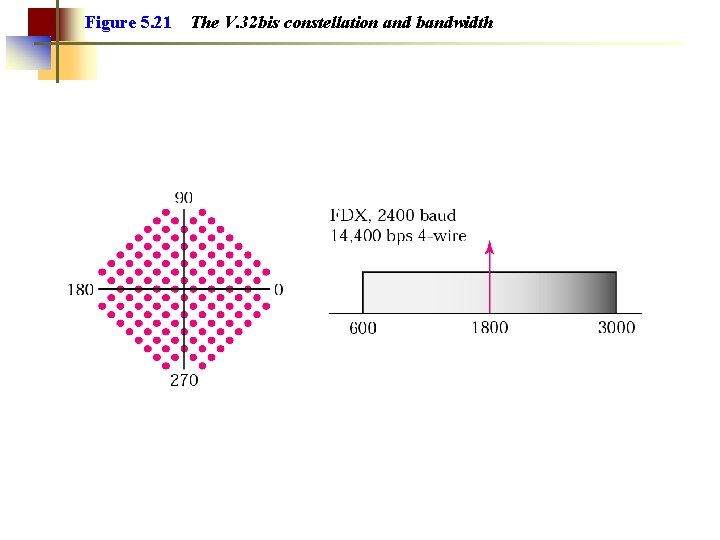
Figure 5. 21 The V. 32 bis constellation and bandwidth

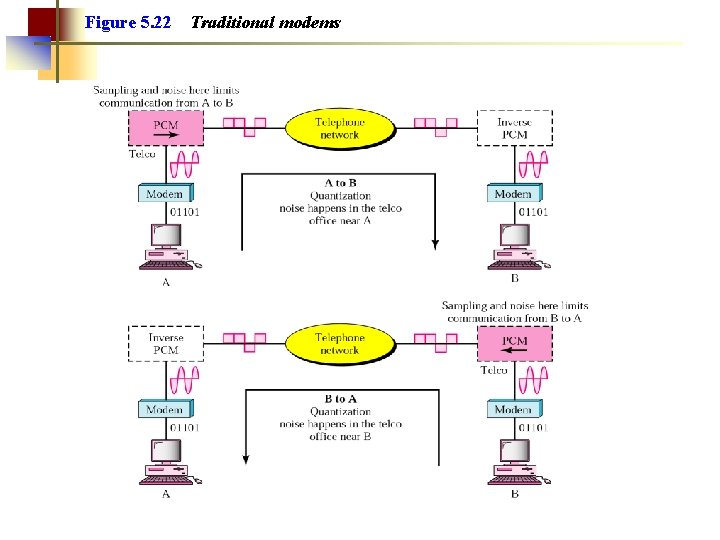
Figure 5. 22 Traditional modems

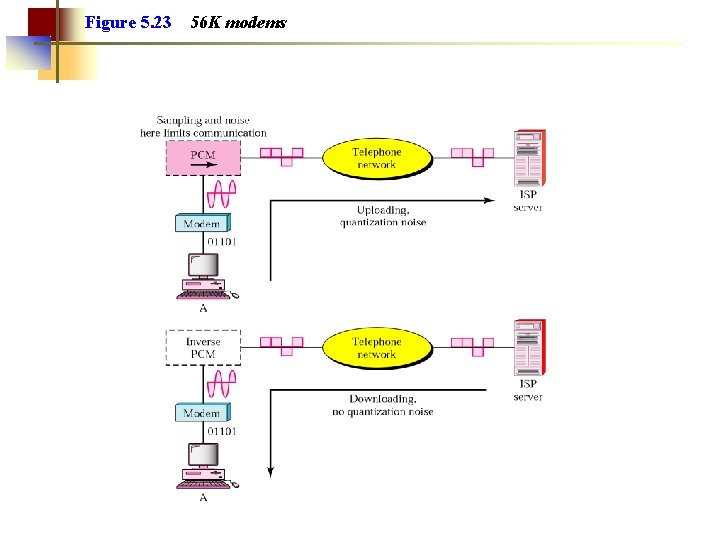
Figure 5. 23 56 K modems

Note: The total bandwidth required for AM can be determined from the bandwidth of the audio signal: BWt = 2 x BWm.

Example 7 Consider a noiseless channel with a bandwidth of 3000 Hz transmitting a signal with two signal levels. The maximum bit rate can be calculated as Bit Rate = 2 3000 log 2 2 = 6000 bps

Example 8 Consider the same noiseless channel, transmitting a signal with four signal levels (for each level, we send two bits). The maximum bit rate can be calculated as: Bit Rate = 2 x 3000 x log 2 4 = 12, 000 bps

Shannons regel Kanalkapaciteten C är max antal bit per sekund vid bästa möjliga modulationsteknik och felrättande kodning: C = B log 2 (1+S/N), där B är ledningens bandbredd i Hertz (oftast ungefär lika med övre gränsfrekvensen), S är nyttosignalens medeleffekt i Watt och N (noice) är bruseffekten i Watt.

Example 9 Consider an extremely noisy channel in which the value of the signal-to-noise ratio is almost zero. In other words, the noise is so strong that the signal is faint. For this channel the capacity is calculated as C = B log 2 (1 + SNR) = B log 2 (1 + 0) = B log 2 (1) = B 0 = 0

Example 10 We can calculate theoretical highest bit rate of a regular telephone line. A telephone line normally has a bandwidth of 3000 Hz (300 Hz to 3300 Hz). The signal-to -noise ratio is usually 3162. For this channel the capacity is calculated as C = B log 2 (1 + SNR) = 3000 log 2 (1 + 3162) = 3000 log 2 (3163) C = 3000 11. 62 = 34, 860 bps

Example 11 We have a channel with a 1 MHz bandwidth. The SNR for this channel is 63; what is the appropriate bit rate and signal level? Solution First, we use the Shannon formula to find our upper limit. C = B log 2 (1 + SNR) = 106 log 2 (1 + 63) = 106 log 2 (64) = 6 Mbps Then we use the Nyquist formula to find the number of signal levels. 4 Mbps = 2 1 MHz log 2 L L = 4

Capacity Limits • Maximum bit rate (capacity) depends on: ○ The analog bandwidth available (in Hz) ○ The quality of the channel • The level of the noise is one of the characteristics of the channel. The ratio of the voltage of the signal sent and the noise present in the channel is important for the maximum data rate achieved. • Shannon’s theorem determines theoretical highest data rate of a noisy channel C = B log 2 (1 + S/N) S/N is the signal to noise ratio (often labeled as SNR)

Capacity Limits • Maximum bit rate (capacity) depends on: ○ The analog bandwidth available (in Hz) ○ The quality of the channel • The level of the noise is one of the characteristics of the channel. The ratio of the voltage of the signal sent and the noise present in the channel is important for the maximum data rate achieved. • Shannon’s theorem determines theoretical highest data rate of a noisy channel C = B log 2 (1 + S/N) S/N is the signal to noise ratio (often labeled as SNR)

Example: • Problem: Given S/N ratio of 30. 098756 d. B, bandwidth of 8 Khz, compute maximum data rate. • Answer: S/N = 30. 098756 d. B = 10 ^ 3. 0098756 = 1022. 9999205 1023 C = 8 Khz * log 2 (1 + 1023 ) C = 8 Khz * log 2 (1024 ) C = 8 * 1000 cycles/second * 10 bits/cycle C = 80 Kbps

How to calculate log 2 x • Calculators do not have a button for log 2 x calculation • To calculate log 2 x use the following formula: log 2 x = log 10 x/log 102 log 10 (x)/0. 3 Example: log 230 = log 30/log 2 1. 477/0. 3 4. 9