Frelsning 8 9 Relationer prioritetsker grafer och grafalgoritmer

Föreläsning 8 -9 Relationer, prioritetsköer, grafer och grafalgoritmer © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Innehåll u Relationer ØSnabb genomgång, resten läses på egen hand. u Prioritetsköer ØModell, organisation, konstruktioner, implementationer u Grafalgoritmer u Kapitel 2 Datastrukturer och algoritmer 16, 14. 5 -8 och 17 i kursboken © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003 VT 2003

Relationer u En instans av datatypen Relationer består av alla de relationer (relationsobjekt) som kan bildas ur en domänbas för instansen. Ø”Kurstillfällen” är en relation över domänmängden (Kurskoder, År, Termin, Del av termin) med element som (TDBA 36, 03, VT, 1) och (TDBA 47, 03, VT, 2) Ø”Läsperioder” är en annan relation över samma mängd med element som (03, VT, 1), (98, HT, 3) etc. ØEn relationsdatatyp kan alltså ha Datastrukturer och algoritmer relationsobjekt med olika aritet. VT 2003 3 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Modell av Relation u Ofta beskriver man en relation med hjälp av en tabell över de element som ingår i relationen. u Relationen Kursansvar: Anders Broberg TDBA 36 Johan Eliasson TDBA 63 Lena Kallin Westin TDBA 47 4 Helena Lindgren TDBD 06 … … Datastrukturer och algoritmer © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003 VT 2003

Tillämpningar av Relation u Relationsdatabaser Lärare Kurskod År Termin Period TDBA 36 03 VT 1 TDBA 63 03 VT 1 TDBA 47 03 VT 2 HT 3 … … ØVilka undervisar på våren? Anders Broberglärare TDBA 36 TDBD 06 02 Johan Eliasson TDBA 63 … … Lena Kallin Westin TDBA 47 5 Helena Lindgren TDBD 06 … … Datastrukturer och algoritmer © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003 VT 2003

Prioritetskö u Modell: Patienterna på en akutmottagning, man kommer in i en viss tidsordning men behandlas utifrån en annan ordning. u Organisation: En mängd vars grundmängd är linjärt ordnad av en prioritetsordning. ØAvläsningar och borttagningar görs endast på de element som har högst prioritet. ØAndra mängdoperationer är inte Datastrukturer och algoritmer aktuella VT 2003 6 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Specifikation av prioritetskö u Gränsytan Pqueue(val, R): Empty () Pqueue(val, R) Insert (v: val, p: Pqueue(val, R)) Pqueue(val, R) Isempty (p: Pqueue(val, R)) Bool Inspect-first (p: Pqueue(val, R)) val Delete-first (p: Pqueue(val, R)) Pqueue(val, R) u. R är relationen för prioritetsordningen. u Ibland slås de två sista metoderna ihop. u Ytan ovan förutsätter statisk prioritet. Vill man ha dynamisk prioritet måste en update. Datastrukturer och algoritmer metod finnas. VT 2003 7 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Specifikation av prioritetskö u Man kan också tänka sig att prioritetskön tar element (val) som består av ett värde och en prioritet. ØFörra fallet antog man att värde = prioritet u Gränsytan kan varieras på flera sätt Øupdate har vi redan nämnt ØVi kan också vilja finna det högsta/minsta Datastrukturer och algoritmer prioritetsvärdet i kön VT 2003 8 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Stack och kö är specialfall av prioritetskön! en om 4! i ax 29 Se å s p u Om R är den totala relationen, dvs gäller för alla par av värden blir prioritetskön en stack. u Om R är den tomma relationen, dvs inte gäller för några par av värden, blir det en kö. u Dessutom: ØOm R är en strikt partiell ordning, som ”>”, kommer lika element behandlas som en kö. ØOm R är icke-strikt, som ”≥” behandlas lika Datastrukturer och algoritmer element som en stack. VT 2003 9 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Konstruktioner av Prioritetskö u Man utgår ofta från konstruktioner av Mängd eller Lexikon ØMen de har vi inte stött på än… u Lista, ej sorterad ØInsert O(1), Delete-first O(n) u Lista, sorterad ØInsert O(n), Delete-first O(1) Datastrukturer och algoritmer VT 2003 10 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Konstruktioner av Prioritetskö u Heap/Hög – ett partiellt sorterat binärt träd ØEtiketterna är sorterade efter en relation R så att a är förälder till b endast om a är före b i ordningen som ges av R. ØInsättningar och borttagningar görs så att trädet hålls komplett. ØInsert O(log n), Delete-first O(log n) Se och figu 14. r 14 11. s 2 10 96 ! 11 Datastrukturer och algoritmer © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003 VT 2003

Tillämpningar u Operativsystem som fördelar jobb mellan olika processer u Enkelt sätt att sortera något. ØStoppa in allt i en prioritetskö och plocka ut det igen. u Hjälpmedel vid traversering av graf ØJmfr att stack och kö används vid traversering av träd. Datastrukturer och algoritmer VT 2003 12 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Graf u Modell: 37 3 s 7. 1 0! 1 r igu f s 34 e 3 S. 17 h c o ØVägkarta med enkelriktade gator utritade. u Tillämpningar ØSignaturdiagrammen ØElektroniska kretsar ØNätverk (gator, flygrutter, kommunikation) ØNeurala nätverk Datastrukturer och algoritmer Ø… VT 2003 13 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Mängorienterad specifikation (vanlig inom matematiken) u En graf G = (V, E) består av ØV : en mängd av noder (vertices) ØE : en mängd av bågar (edges) som binder samman noderna i V. o En båge e = (u, v) är ett par av noder. b V = {a, b, c, d, e} a c d 14 e E = {(a, b), (a, c), a, d), (b, e), (c, d), (c, e), (d, e)} Datastrukturer och algoritmer © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003 VT 2003

Navigeringsorienterad specifikation u En graf är en mängd med noder där man till varje nod associerar en grannskapsmängd av noder som kallas grannar. ØAlla noder tillhör samma typ ØAlla ordnade par av en godtycklig nod och en av noderna i dess grannskapsmängd utgör en båge. u Denna specifikation passar ofta bättre i algoritmer eftersom de förutsätter effektiva Datastrukturer och algoritmer navigeringsoperationer. VT 2003 15 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Riktade/oriktade grafer a b c u Oriktade grafer d Ø Bågen är en mängd av två noder. Noderna är grannar till varandra. Ø Gradtalet = Antalet bågar till grannar (eller sig själv) u Riktade grafer a e b c Ø Bågen är ordnade par av noder. Ø Gradtalet indelas i d e o Ingradtalet = antalet bågar som går till noden o Utgradtalet = antalet bågar som startar i noden och går till en annan nod. Datastrukturer och algoritmer VT 2003 16 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Bokens informella specifikation: Empty – konstruerar en tom graf utan noder och bågar Insert-node(v, g) – sätter in noden v i grafen g Insert-edge(e, g) – sätter in en båge e i grafen g. Det förutsätts att noderna finns i grafen Isempty(g) – testar om grafen g är tom, dvs utan noder Has-no-edges(g) – testar om grafen g saknar bågar Choose-node(g) – väljer ut en nod ur grafen g Neighbours(v, g) – mängden av alla grannar till v i grafen g Delete-node(v, g) – tar bort noden v ur grafen g, förutsatt v inte ingår i någon båge och algoritmer Delete-edge(e, g) – tar bort bågen e ur grafen Datastrukturer g VT 2003 17 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

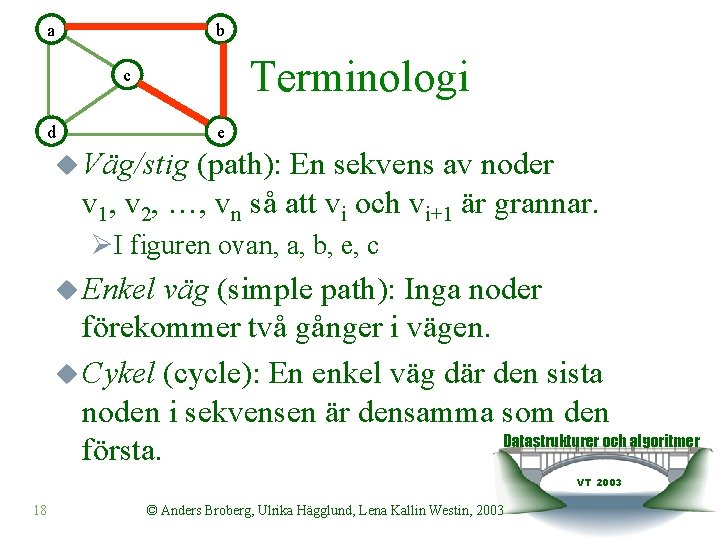
a b Terminologi c d e u Väg/stig (path): En sekvens av noder v 1, v 2, …, vn så att vi och vi+1 är grannar. ØI figuren ovan, a, b, e, c u Enkel väg (simple path): Inga noder förekommer två gånger i vägen. u Cykel (cycle): En enkel väg där den sista noden i sekvensen är densamma som den Datastrukturer och algoritmer första. VT 2003 18 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

a b a Terminologi c d e u Sammanhängande b c d e (connected) graf ØVarje nod har en väg till varje annan nod. u Delgraf (subgraf) en delmängd av noderna och kanterna som formar en graf. u Sammanhängande komponenter ØEn sammanhängande subgraf ØGrafen uppe till höger har två sammanhängande Datastrukturer och algoritmer komponenter. VT 2003 19 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

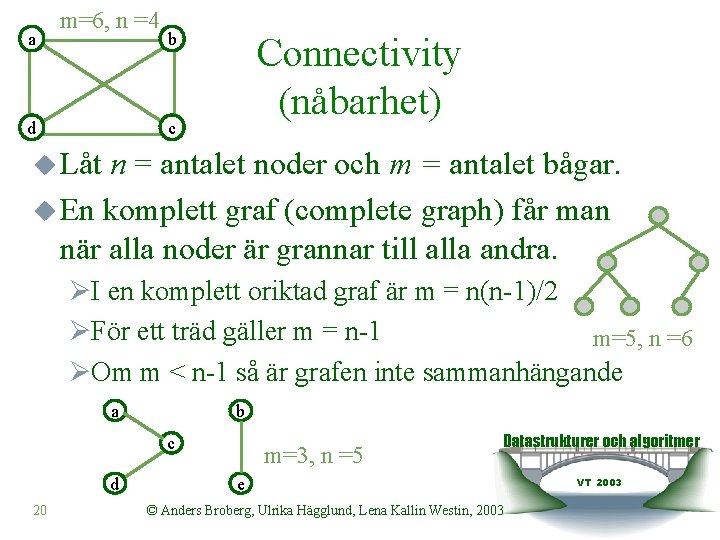
a m=6, n =4 d b Connectivity (nåbarhet) c u Låt n = antalet noder och m = antalet bågar. u En komplett graf (complete graph) får man när alla noder är grannar till alla andra. ØI en komplett oriktad graf är m = n(n-1)/2 ØFör ett träd gäller m = n-1 m=5, n =6 ØOm m < n-1 så är grafen inte sammanhängande a b c d 20 m=3, n =5 Datastrukturer och algoritmer e © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003 VT 2003

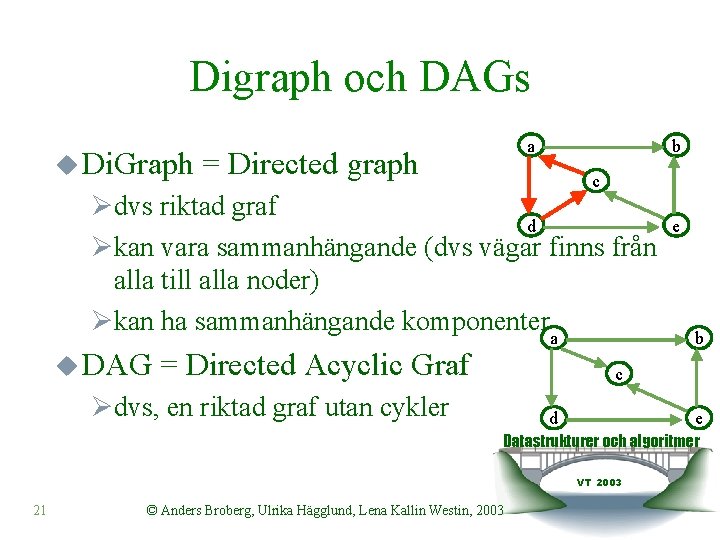
Digraph och DAGs u Di. Graph a = Directed graph b c Ødvs riktad graf d Økan vara sammanhängande (dvs vägar finns från alla till alla noder) Økan ha sammanhängande komponenter u DAG a = Directed Acyclic Graf e b c Ødvs, en riktad graf utan cykler d e Datastrukturer och algoritmer VT 2003 21 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Mer grafer… u Viktad graf ØEn graf där bågarna har vikter u Multigraf ØTillåtet med flera bågar mellan två noder. Dessa bågar har då olika egenskaper som måste lagras. u Ordnad graf har inbördes ordning mellan grannarna till en nod. Datastrukturer och algoritmer VT 2003 22 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

c Konstruktion av grafer u Förbindelsematris Ø Bågarna representeras av ettor i en matris. Ø Rad 1 visar vilka bågar man kan nå från a. Ø Kolumn 3 visar från vilka noder det kommer bågar till c. + Enkel att implementera och passar när man har siffror på noder och bågar. - Matrisen kan bli stor och gles och kräva specialtrick. a b d e 1 2 3 4 5 1 1 2 1 3 4 5 1 1 1 Datastrukturer och algoritmer VT 2003 23 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

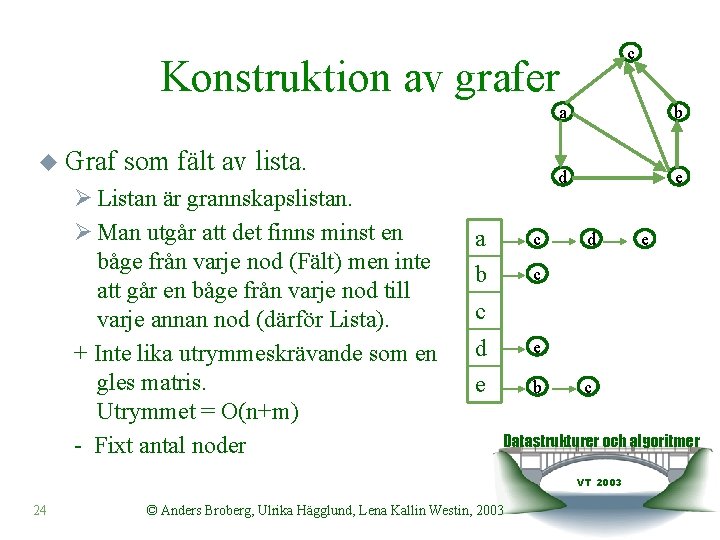
c Konstruktion av grafer u Graf som fält av lista. Ø Listan är grannskapslistan. Ø Man utgår att det finns minst en båge från varje nod (Fält) men inte att går en båge från varje nod till varje annan nod (därför Lista). + Inte lika utrymmeskrävande som en gles matris. Utrymmet = O(n+m) - Fixt antal noder a c b c a b d e d c d e e b c Datastrukturer och algoritmer VT 2003 24 e © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Grafalgoritmer u Traversering ØBredden-först och djupet-först u Konstruera ett (minsta) uppspännande träd u Finna vägarna från en nod till alla andra noder ØKortaste vägen mellan två noder u Finna maximala flödet ØFinna det maximala flödet mellan tvåDatastrukturer noder och algoritmer VT 2003 25 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Djupet-först-traversering u Man besöker utgångsnoden och sedan dess grannar djupet-först rekursivt. Ø Undersöka en labyrint genom att markera de vägar man gått med färg. u Om grafen innehåller cykler finns det risk för oändlig traversering Ø Löses genom att hålla reda på om noden är besökt eller ej. Om noden redan besökt görs ingen rekursivt anrop. Ø Endast de noder man kan nå från utgångsnoden kommer Datastrukturer och algoritmer att besökas. VT 2003 26 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Djupet-först-algoritm: Algoritm depth. First(Node n, Graph g) input: A node n in a graph g to be traversed visited(n, g) // Marks the node as visited neighbour. Set neighbours(n, g); for each neighbour in neighbour. Set do if not is. Visited(neighbour) depth. First(neighbour, g) Datastrukturer och algoritmer VT 2003 27 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

depth. First(A) A* B C E F G I J K Markera noden som besökt. Grannar = {E, F, B} E ej besökt, rekursivt anrop. Datastrukturer och algoritmer VT 2003 28 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

depth. First(A) depth. First(E) A B C E* F G I J K Markera noden som besökt. Grannar = {I, F, A} I ej besökt, rekursivt anrop. Datastrukturer och algoritmer VT 2003 29 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

depth. First(A) depth. First(E) depth. First(I) A B C E F G I* J K Markera noden som besökt. Grannar = {J, F, E} J ej besökt, rekursivt anrop. Datastrukturer och algoritmer VT 2003 30 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

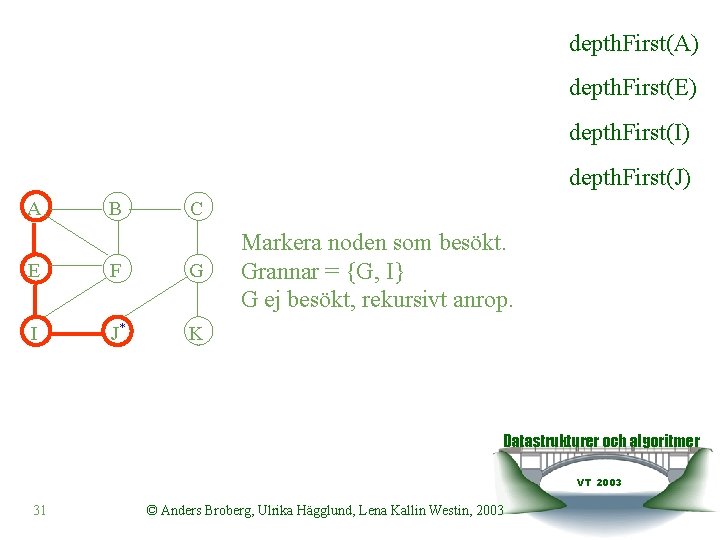
depth. First(A) depth. First(E) depth. First(I) depth. First(J) A B C E F G I J* K Markera noden som besökt. Grannar = {G, I} G ej besökt, rekursivt anrop. Datastrukturer och algoritmer VT 2003 31 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

depth. First(A) depth. First(E) depth. First(I) depth. First(J) A B C E F G* I J K Markera noden som besökt. Grannar = {C, K} C ej besökt, rekursivt anrop. depth. First(G) Datastrukturer och algoritmer VT 2003 32 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

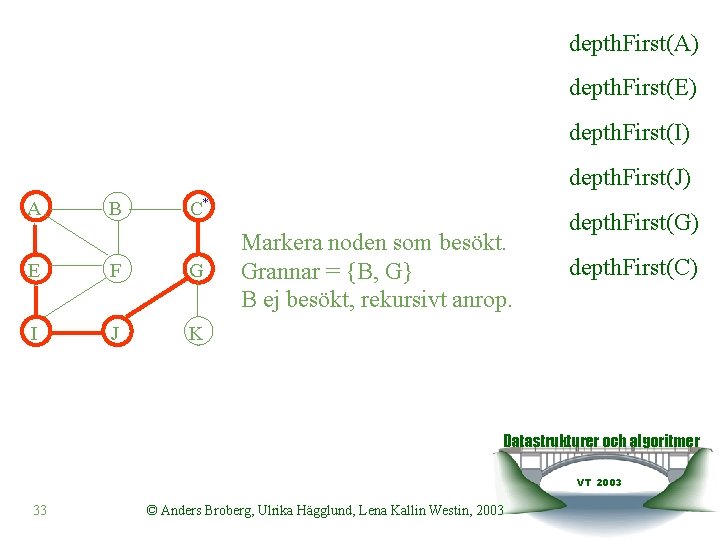
depth. First(A) depth. First(E) depth. First(I) depth. First(J) A B C* E F G I J K Markera noden som besökt. Grannar = {B, G} B ej besökt, rekursivt anrop. depth. First(G) depth. First(C) Datastrukturer och algoritmer VT 2003 33 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

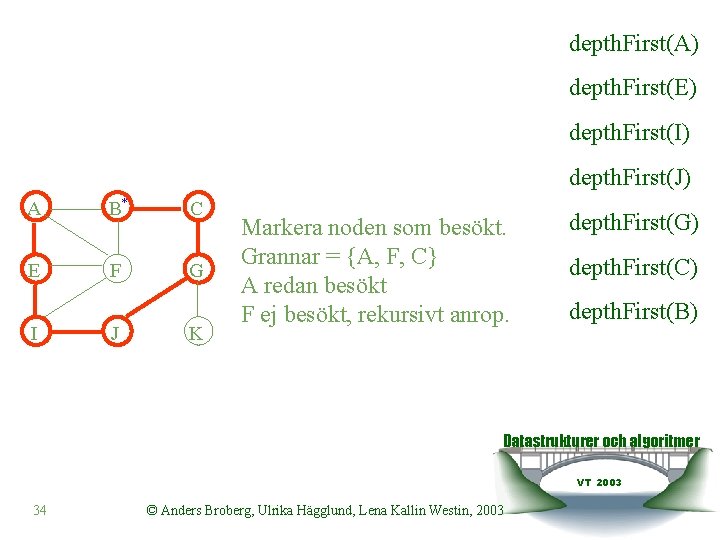
depth. First(A) depth. First(E) depth. First(I) depth. First(J) A B* C E F G I J K Markera noden som besökt. Grannar = {A, F, C} A redan besökt F ej besökt, rekursivt anrop. depth. First(G) depth. First(C) depth. First(B) Datastrukturer och algoritmer VT 2003 34 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

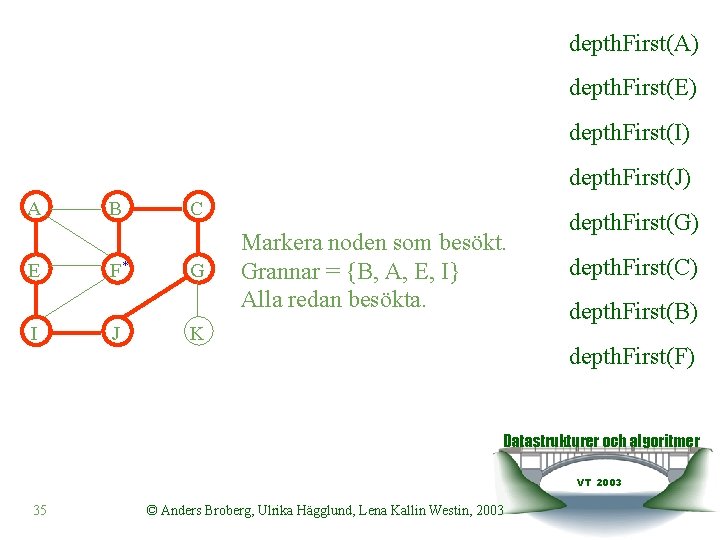
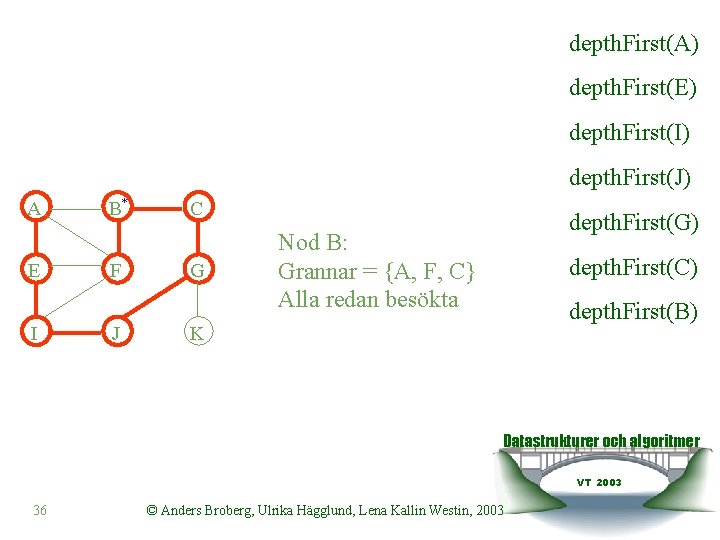
depth. First(A) depth. First(E) depth. First(I) depth. First(J) A E I B F* J C G Markera noden som besökt. Grannar = {B, A, E, I} Alla redan besökta. K depth. First(G) depth. First(C) depth. First(B) depth. First(F) Datastrukturer och algoritmer VT 2003 35 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

depth. First(A) depth. First(E) depth. First(I) depth. First(J) A E I B* F J C G depth. First(G) Nod B: Grannar = {A, F, C} Alla redan besökta depth. First(C) depth. First(B) K Datastrukturer och algoritmer VT 2003 36 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

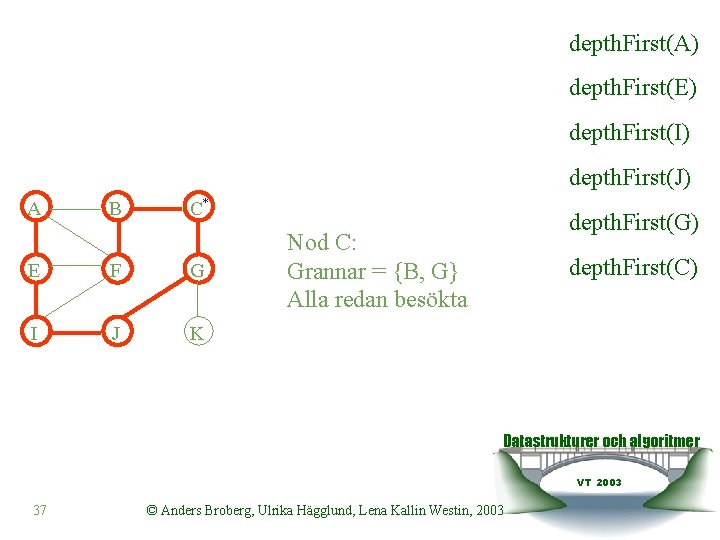
depth. First(A) depth. First(E) depth. First(I) depth. First(J) A B C* E F G I J K depth. First(G) Nod C: Grannar = {B, G} Alla redan besökta depth. First(C) Datastrukturer och algoritmer VT 2003 37 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

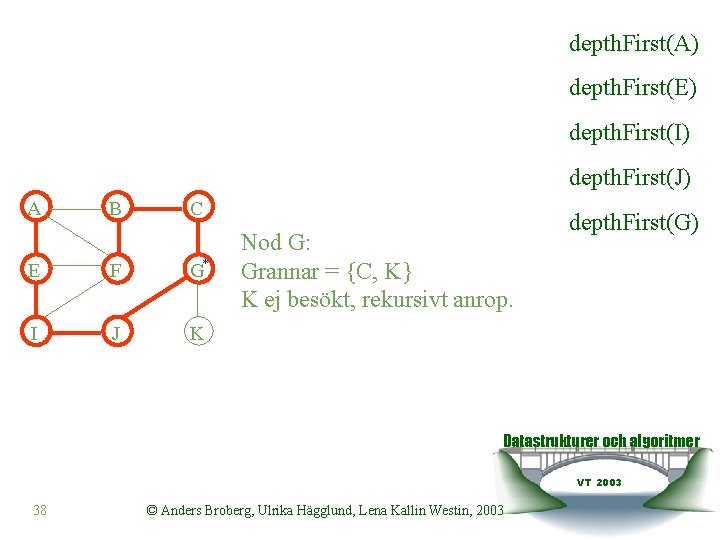
depth. First(A) depth. First(E) depth. First(I) depth. First(J) A B C E F G* I J K Nod G: Grannar = {C, K} K ej besökt, rekursivt anrop. depth. First(G) Datastrukturer och algoritmer VT 2003 38 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

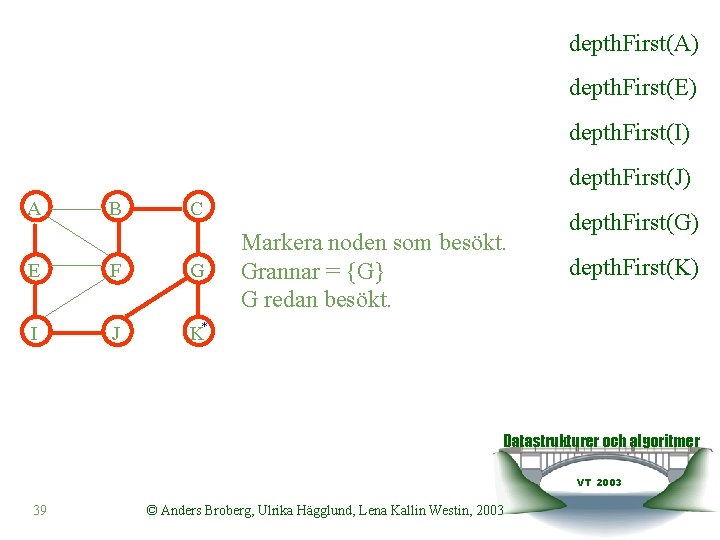
depth. First(A) depth. First(E) depth. First(I) depth. First(J) A B C E F G I J K* Markera noden som besökt. Grannar = {G} G redan besökt. depth. First(G) depth. First(K) Datastrukturer och algoritmer VT 2003 39 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

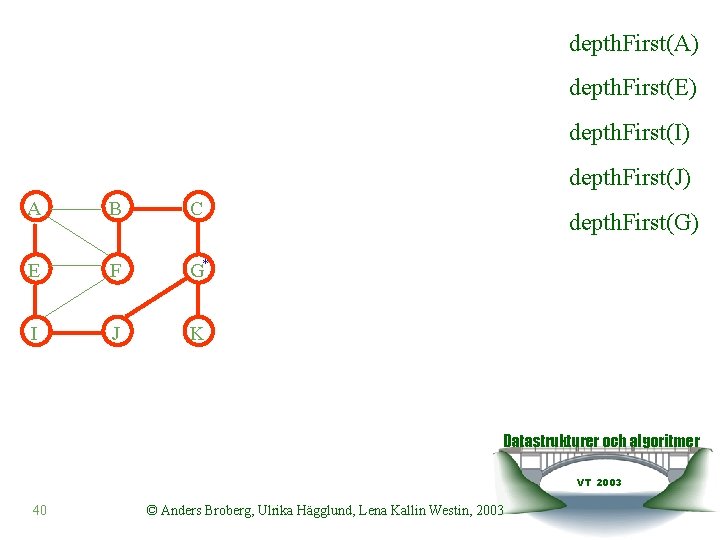
depth. First(A) depth. First(E) depth. First(I) depth. First(J) A B C E F G* I J K depth. First(G) Datastrukturer och algoritmer VT 2003 40 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

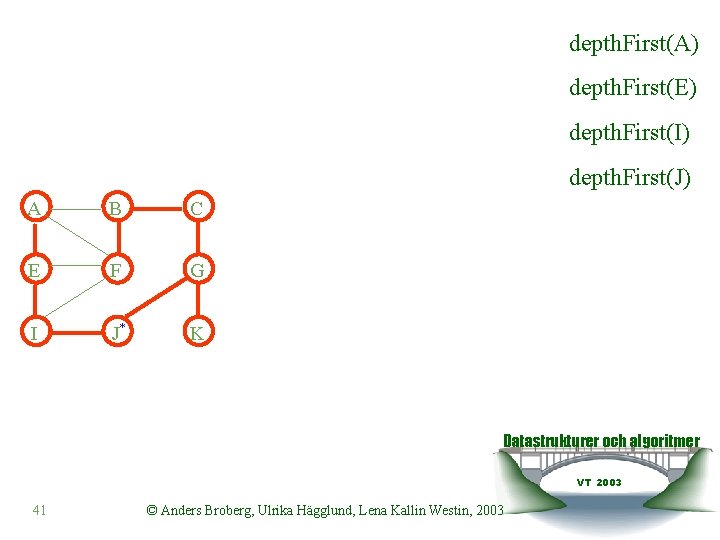
depth. First(A) depth. First(E) depth. First(I) depth. First(J) A B C E F G I J* K Datastrukturer och algoritmer VT 2003 41 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

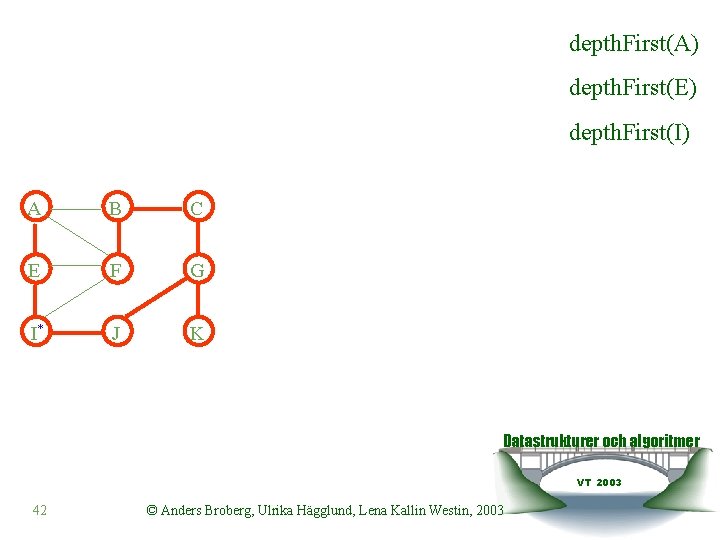
depth. First(A) depth. First(E) depth. First(I) A B C E F G I* J K Datastrukturer och algoritmer VT 2003 42 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

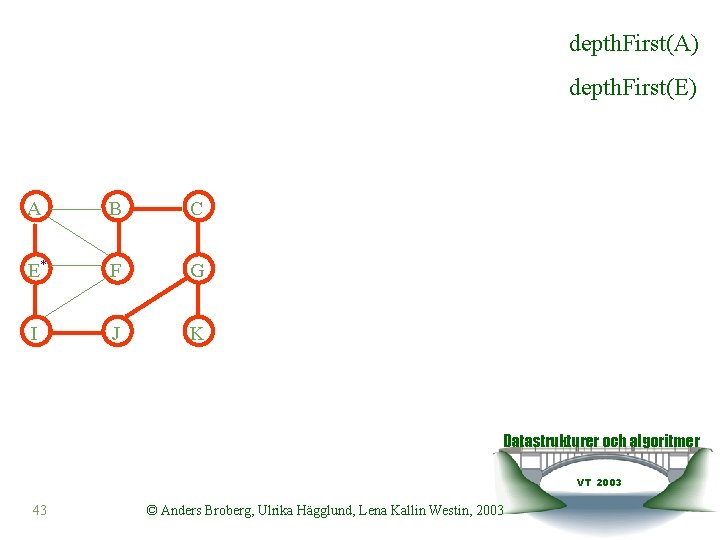
depth. First(A) depth. First(E) A B C E* F G I J K Datastrukturer och algoritmer VT 2003 43 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

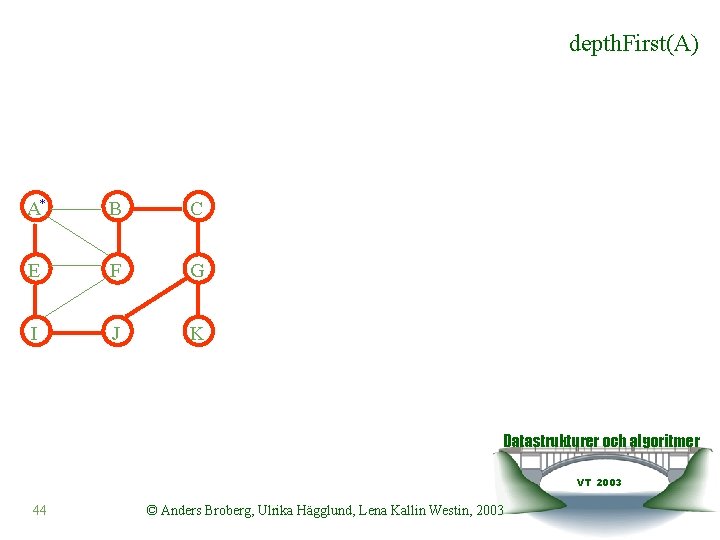
depth. First(A) A* B C E F G I J K Datastrukturer och algoritmer VT 2003 44 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

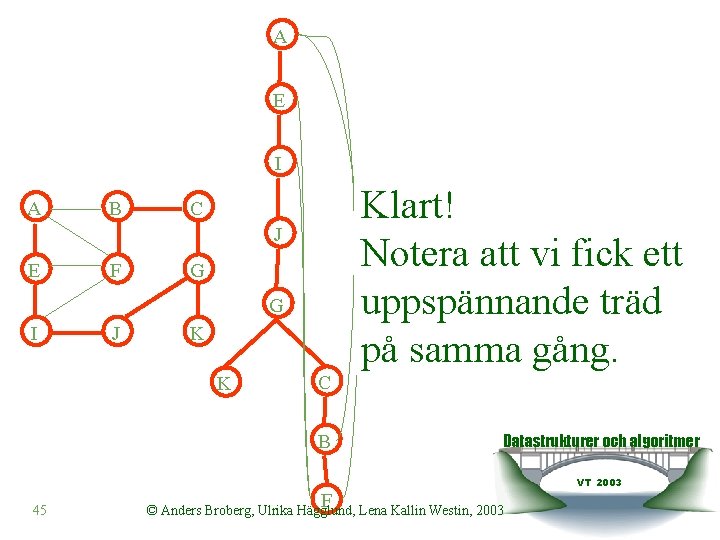
A E I A B Klart! Notera att vi fick ett uppspännande träd på samma gång. C J E F G G I J K K C B 45 F Datastrukturer och algoritmer © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003 VT 2003

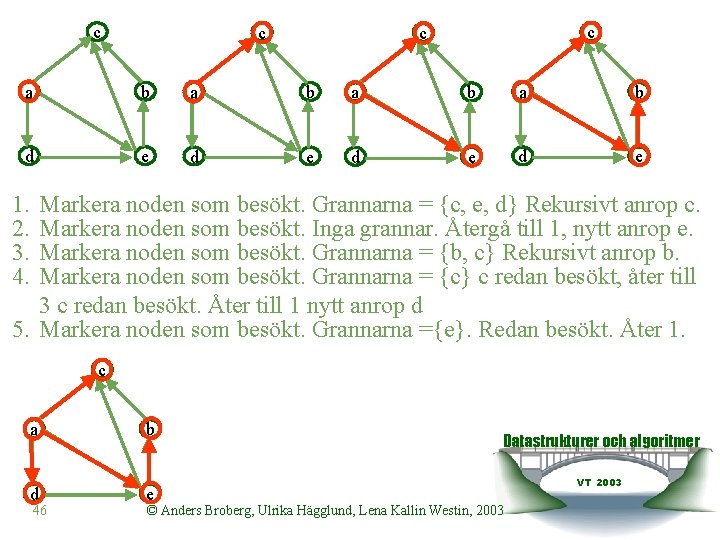
c c a b a b d e d e 1. 2. 3. 4. Markera noden som besökt. Grannarna = {c, e, d} Rekursivt anrop c. Markera noden som besökt. Inga grannar. Återgå till 1, nytt anrop e. Markera noden som besökt. Grannarna = {b, c} Rekursivt anrop b. Markera noden som besökt. Grannarna = {c} c redan besökt, åter till 3 c redan besökt. Åter till 1 nytt anrop d 5. Markera noden som besökt. Grannarna ={e}. Redan besökt. Åter 1. c a b d e 46 Datastrukturer och algoritmer © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003 VT 2003

Bredden-först-algoritm u Man undersöker först noden, sedan dess grannar, grannarnas grannar osv. u Finns risk för oändlig körning här med om man inte använder en markör för att noden besökts. u Endast noder till vilka det finns en väg från utgångsnoden kommer att besökas. u En kö hjälper oss hålla reda på Datastrukturer och algoritmer grannarna. VT 2003 47 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Bredden-först-algoritm: Algoritm breadth. First(Node n, Graph g) input: A node n in a graph g to be traversed Queue q empty(); visited(n, g) // Marks the node as visited q enqueue(n, q); while not isempty(q) do new. Node front(q) q dequeue(q); neighbour. Set neighbours(new. Node, g); for each neighbour in neighbour. Set do if not is. Visited(neighbour) visited(neighbour, g); q enqueue(neighbour, q); Datastrukturer och algoritmer VT 2003 48 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

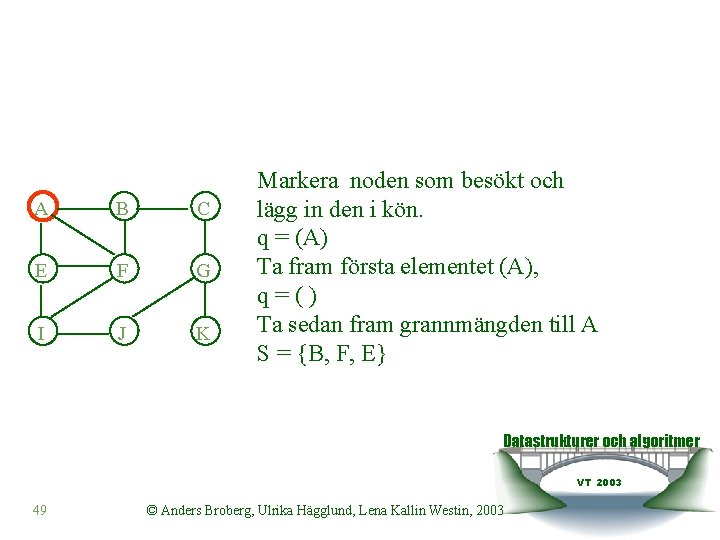
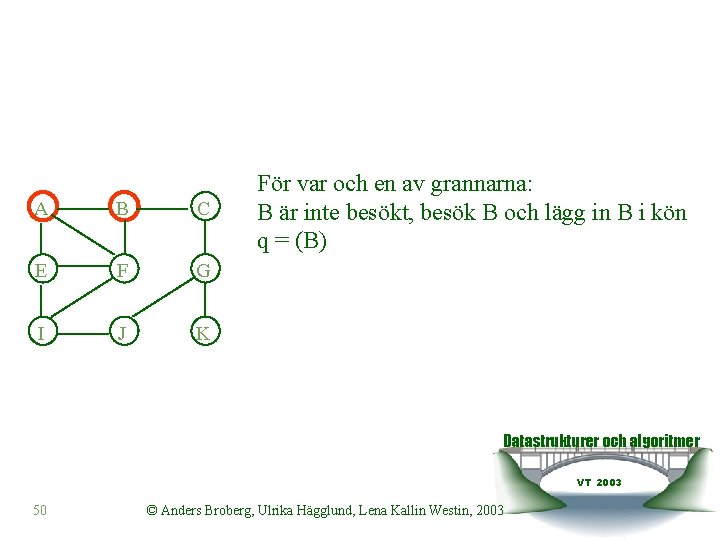
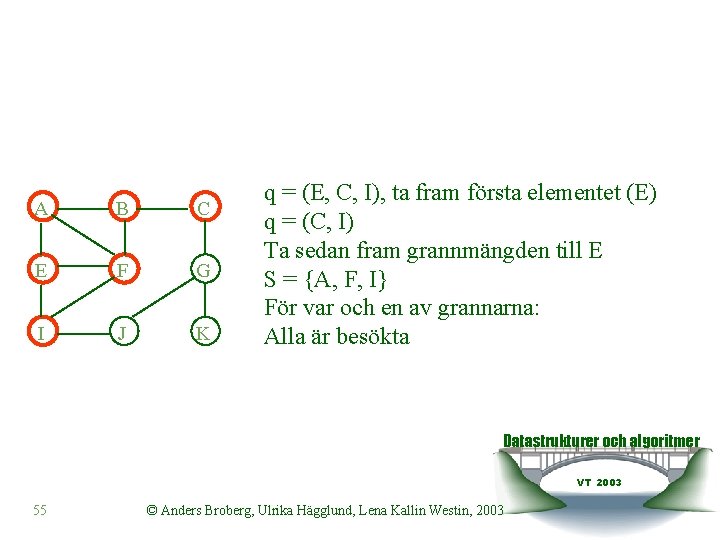
A B C E F G I J K Markera noden som besökt och lägg in den i kön. q = (A) Ta fram första elementet (A), q=() Ta sedan fram grannmängden till A S = {B, F, E} Datastrukturer och algoritmer VT 2003 49 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

A B C E F G I J K För var och en av grannarna: B är inte besökt, besök B och lägg in B i kön q = (B) Datastrukturer och algoritmer VT 2003 50 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

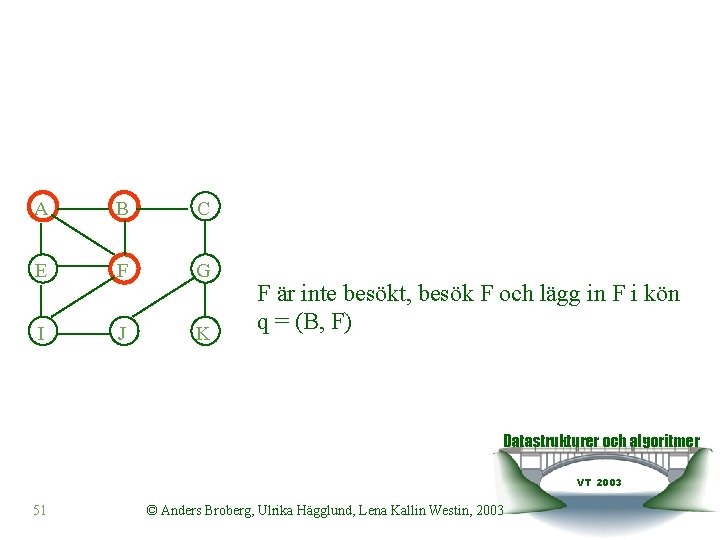
A B C E F G I J K F är inte besökt, besök F och lägg in F i kön q = (B, F) Datastrukturer och algoritmer VT 2003 51 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

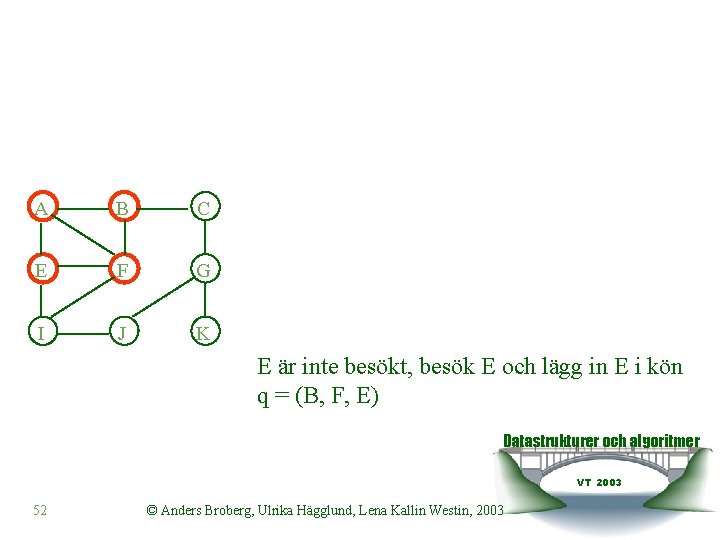
A B C E F G I J K E är inte besökt, besök E och lägg in E i kön q = (B, F, E) Datastrukturer och algoritmer VT 2003 52 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

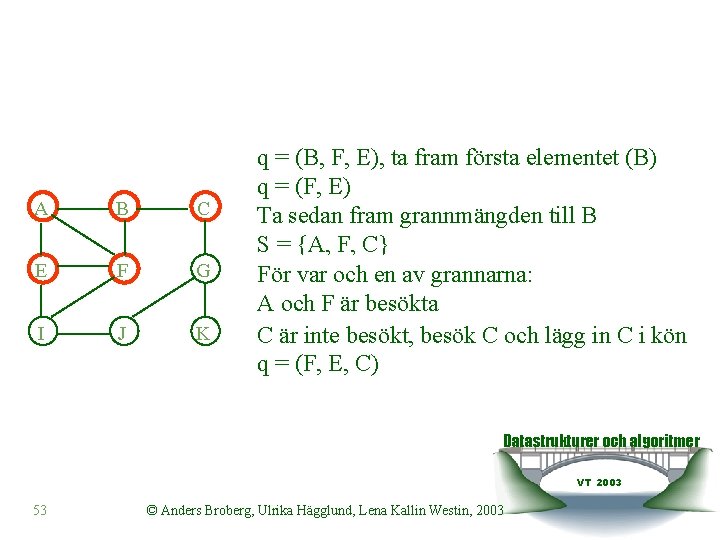
A B C E F G I J K q = (B, F, E), ta fram första elementet (B) q = (F, E) Ta sedan fram grannmängden till B S = {A, F, C} För var och en av grannarna: A och F är besökta C är inte besökt, besök C och lägg in C i kön q = (F, E, C) Datastrukturer och algoritmer VT 2003 53 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

A B C E F G I J K q = (F, E, C), ta fram första elementet (F) q = (E, C) Ta sedan fram grannmängden till F S = {B, A, E, I} B, A, och E är besökta I är inte besökt, besök I och lägg in I i kön q = (E, C, I) Datastrukturer och algoritmer VT 2003 54 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

A B C E F G I J K q = (E, C, I), ta fram första elementet (E) q = (C, I) Ta sedan fram grannmängden till E S = {A, F, I} För var och en av grannarna: Alla är besökta Datastrukturer och algoritmer VT 2003 55 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

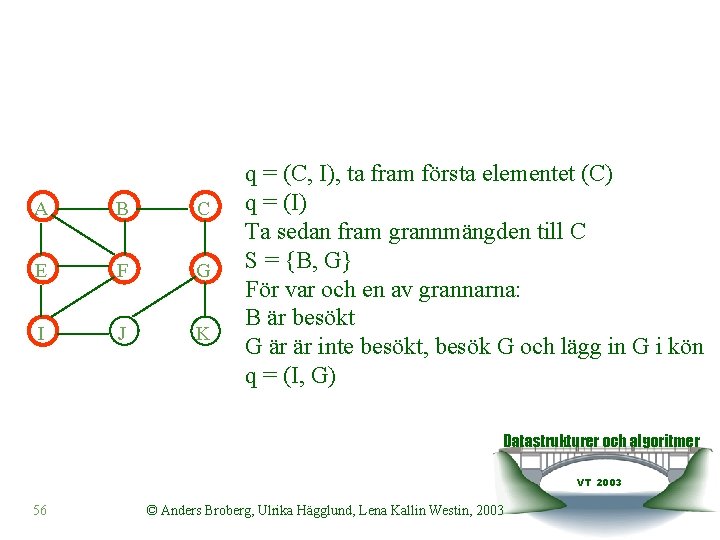
A B C E F G I J K q = (C, I), ta fram första elementet (C) q = (I) Ta sedan fram grannmängden till C S = {B, G} För var och en av grannarna: B är besökt G är är inte besökt, besök G och lägg in G i kön q = (I, G) Datastrukturer och algoritmer VT 2003 56 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

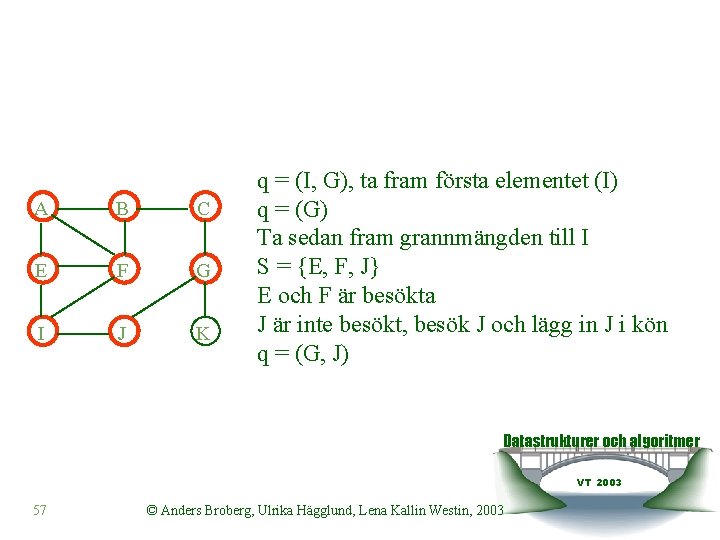
A B C E F G I J K q = (I, G), ta fram första elementet (I) q = (G) Ta sedan fram grannmängden till I S = {E, F, J} E och F är besökta J är inte besökt, besök J och lägg in J i kön q = (G, J) Datastrukturer och algoritmer VT 2003 57 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

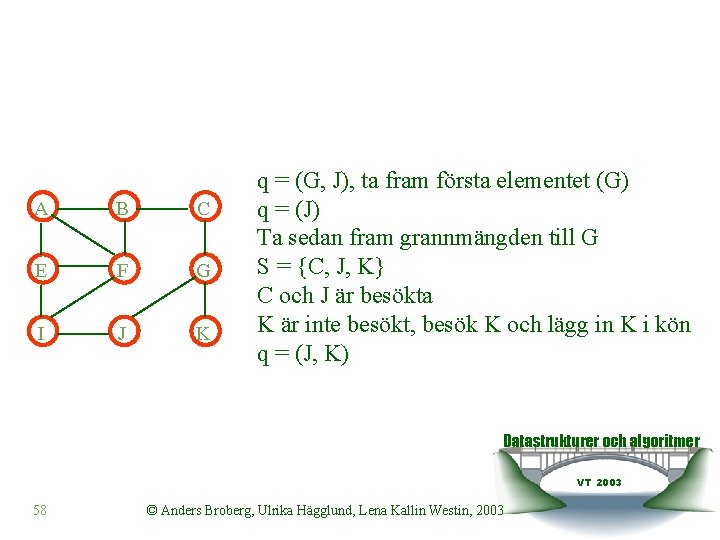
A B C E F G I J K q = (G, J), ta fram första elementet (G) q = (J) Ta sedan fram grannmängden till G S = {C, J, K} C och J är besökta K är inte besökt, besök K och lägg in K i kön q = (J, K) Datastrukturer och algoritmer VT 2003 58 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

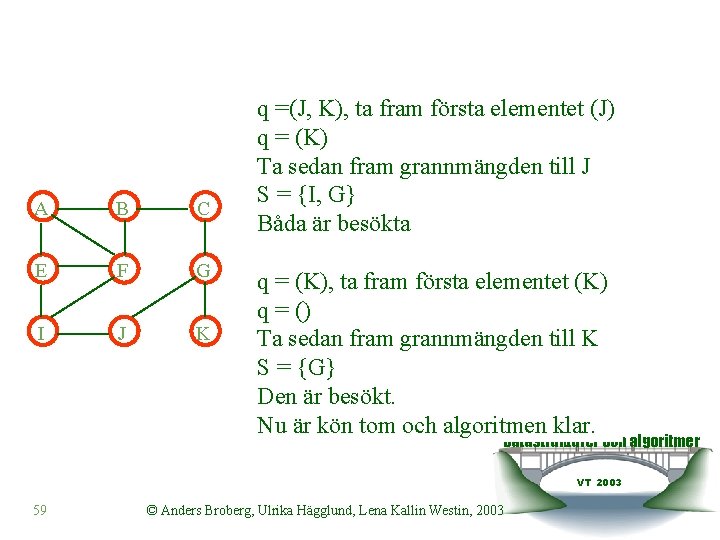
A B C E F G I J K q =(J, K), ta fram första elementet (J) q = (K) Ta sedan fram grannmängden till J S = {I, G} Båda är besökta q = (K), ta fram första elementet (K) q = () Ta sedan fram grannmängden till K S = {G} Den är besökt. Nu är kön tom och algoritmen klar. Datastrukturer och algoritmer VT 2003 59 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

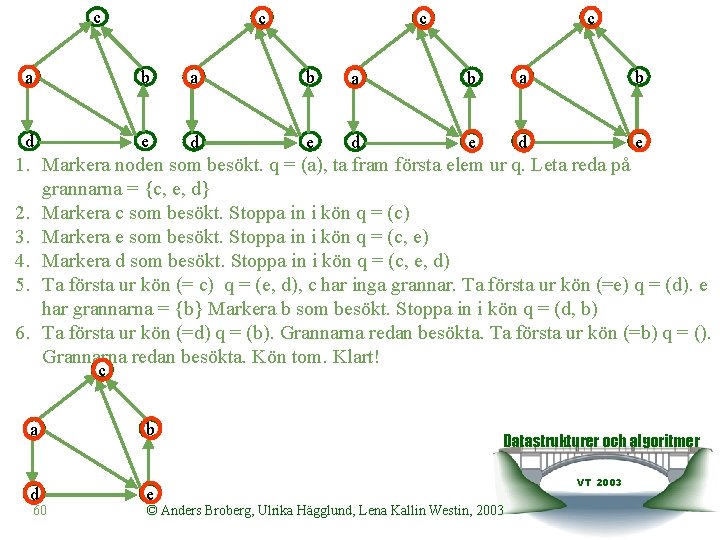
c c a b a b d e d e 1. Markera noden som besökt. q = (a), ta fram första elem ur q. Leta reda på grannarna = {c, e, d} 2. Markera c som besökt. Stoppa in i kön q = (c) 3. Markera e som besökt. Stoppa in i kön q = (c, e) 4. Markera d som besökt. Stoppa in i kön q = (c, e, d) 5. Ta första ur kön (= c) q = (e, d), c har inga grannar. Ta första ur kön (=e) q = (d). e har grannarna = {b} Markera b som besökt. Stoppa in i kön q = (d, b) 6. Ta första ur kön (=d) q = (b). Grannarna redan besökta. Ta första ur kön (=b) q = (). Grannarna redan besökta. Kön tom. Klart! c a b d e 60 Datastrukturer och algoritmer © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003 VT 2003

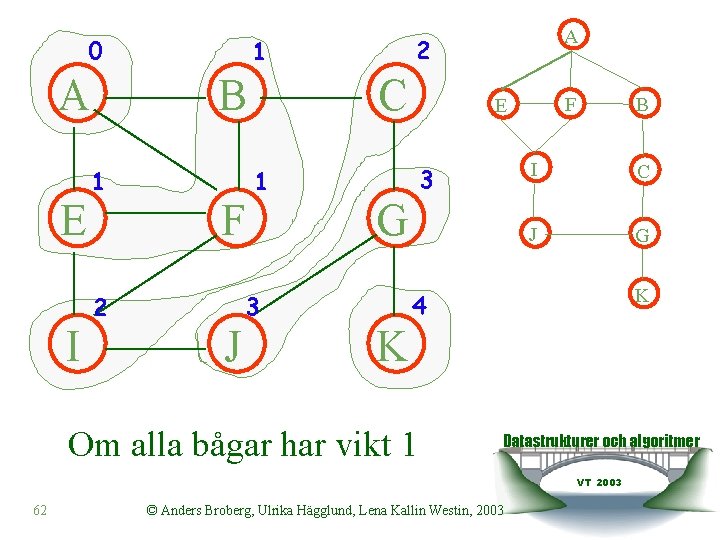
Kortaste-vägen-algoritm vid lika vikt u Om vi har en graf med lika vikter på alla bågar kan man använda en variant av bredden-först traversering för att beräkna kortaste vägen från en nod till de andra. Algoritm breadth. First(Node n, Graph g) input: A node n in a graph g to be traversed Queue q empty(); visited(n, g) // Marks the node as visited set. Dist(n, 0) q enqueue(n, q); while not isempty(q) do new. Node front(q) q dequeue(q); neighbour. Set neighbours(new. Node, g); for each neighbour in neighbour. Set do if not is. Visited(neighbour) visited(neighbour, g); set. Dist(neighbour, get. Dist(new. Node)+1) q enqueue(neighbour, q); Datastrukturer och algoritmer VT 2003 61 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

0 A E I 1 2 2 1 B F C 1 F E 3 G B I C J G K 4 3 J A K Om alla bågar har vikt 1 Datastrukturer och algoritmer VT 2003 62 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Tidskomplexitet u För både bredden-först och djupet-först gäller: ØVarje nod besöks exakt en gång O(n) ØFör varje nod följer man bågarna ut från noden för att hitta grannarna. Detta bör vara effektivt O(grad(v)), värsta fallet är O(n). o o o I bokens navigeringsorienterade spec. har vi O(grad(v)) Mängdorienterad spec. ger O(m) där m=antalet bågar i noden Eftersom grannmängden behöver evalueras en gång för varje nod blir komplexiteten O( grad(v)) =O(m) ØTotalt O(n) + O(m) Datastrukturer och algoritmer VT 2003 63 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Uppspännande träd u Både bredden-först och djupet-försttraverseringarna gav oss uppspännande träd. ØOm vi sparat undan informationen vill säga… ØMåste utöka grafspecifikationen med operationer som stöder detta. u Är det minimalt? ØDen totala längden i trädet ska vara minimalt. ØOm varje kant har samma vikt är trädet minimalt uppspännande för bredden-först Datastrukturer och algoritmer traversering. VT 2003 64 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

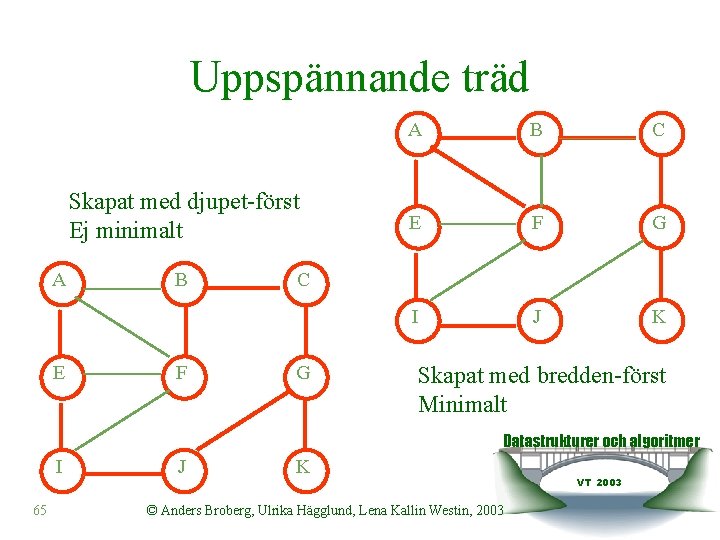
Uppspännande träd Skapat med djupet-först Ej minimalt A E B F A B C E F G I J K C G Skapat med bredden-först Minimalt Datastrukturer och algoritmer I 65 J K © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003 VT 2003

Uppspännande träd u Hur hanterar man grafer med vikter? R 4 8 6 B C ØMan söker ett uppspännande träd med A 3 D 4 3 minsta möjliga totala längd. 4 6 F o Det är alltså inte en kortaste-vägen G E algoritm 6 ØFör mängdorienterad specifikation finns Kruskals algoritm ØFör navigeringsorienterad specifikation Datastrukturer och algoritmer finns Prims algoritm 5 VT 2003 66 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Prims algoritm u Går ut på att bygga upp ett allt större träd som till slut spänner upp grafen eller en sammanhängande komponent av den. u Man väljer i varje steg en båge med minimal vikt. ØLika vikter måste behandlas konsekvent. Regeln styr hur det färdiga trädet ser ut. Datastrukturer och algoritmer VT 2003 67 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

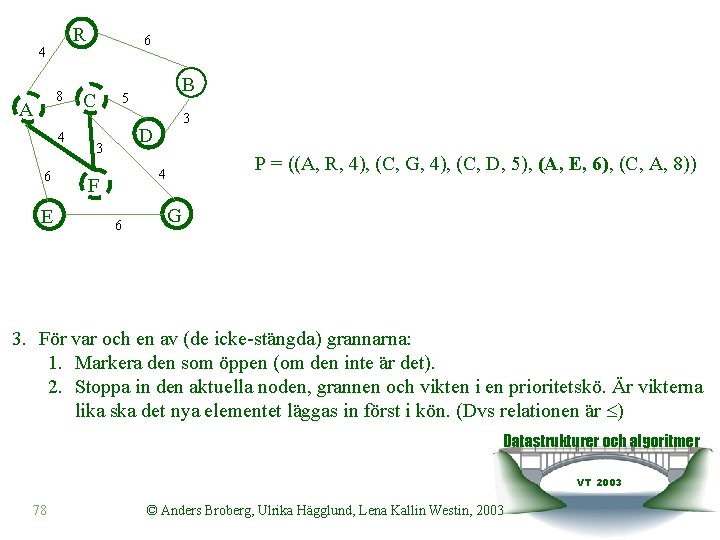
Prims algoritm: 1. Välj en nod vilken som helst och markera den som öppen. Låt den bli rot. 2. Markera den som stängd. 3. För var och en av (de icke-stängda) grannarna: 1. Markera den som öppen (om den inte är det). 2. Stoppa in den aktuella noden, grannen och vikten i en prioritetskö. Är vikterna lika ska det nya elementet läggas in först i kön. (Dvs relationen är ) 4. Ta fram ett element ur prioritetskön och bilda ett nytt delträd genom att lägga in den båge som finns i elementet i trädet. OBS! Lägg endast in bågen om slutnoden inte är stängd! Låt ändnoden bli den nya aktuella noden, stäng den och gå till 3. Datastrukturer och algoritmer VT 2003 68 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

R 4 8 A 4 6 E 6 C B 5 3 D 3 4 F 6 G 1. Välj en nod vilken som helst och markera den som öppen. Låt den bli rot. Datastrukturer och algoritmer VT 2003 69 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

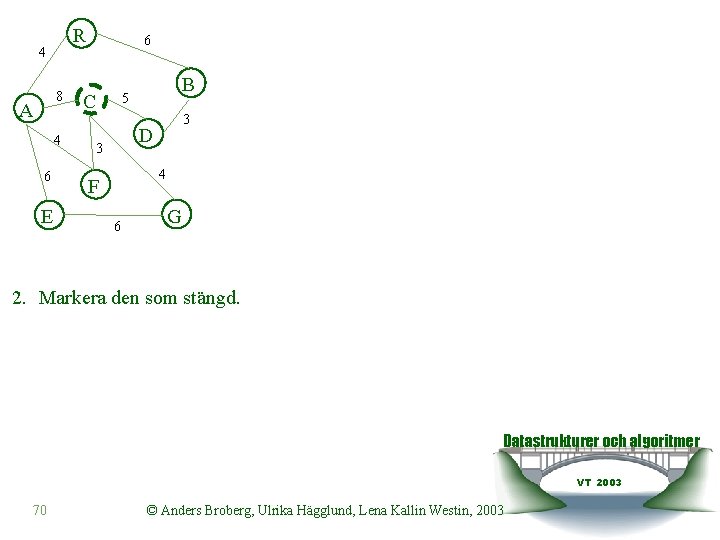
R 4 8 A 4 6 E 6 C B 5 3 D 3 4 F 6 G 2. Markera den som stängd. Datastrukturer och algoritmer VT 2003 70 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

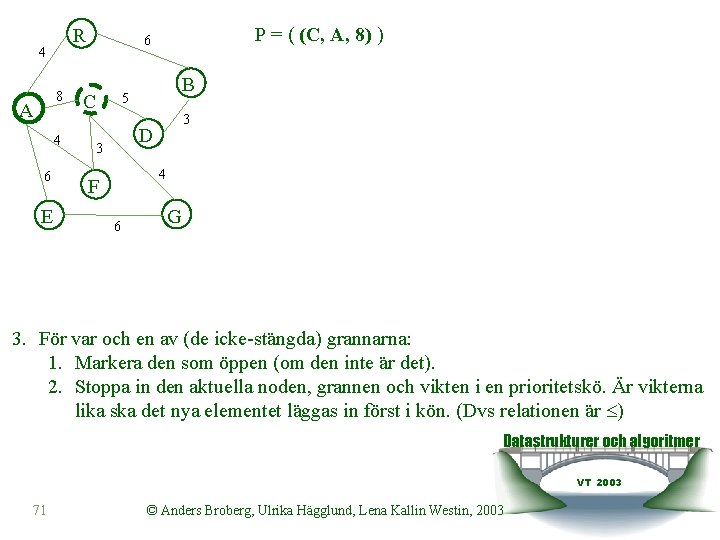
R 4 8 A 4 6 E P = ( (C, A, 8) ) 6 C B 5 3 D 3 4 F 6 G 3. För var och en av (de icke-stängda) grannarna: 1. Markera den som öppen (om den inte är det). 2. Stoppa in den aktuella noden, grannen och vikten i en prioritetskö. Är vikterna lika ska det nya elementet läggas in först i kön. (Dvs relationen är ) Datastrukturer och algoritmer VT 2003 71 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

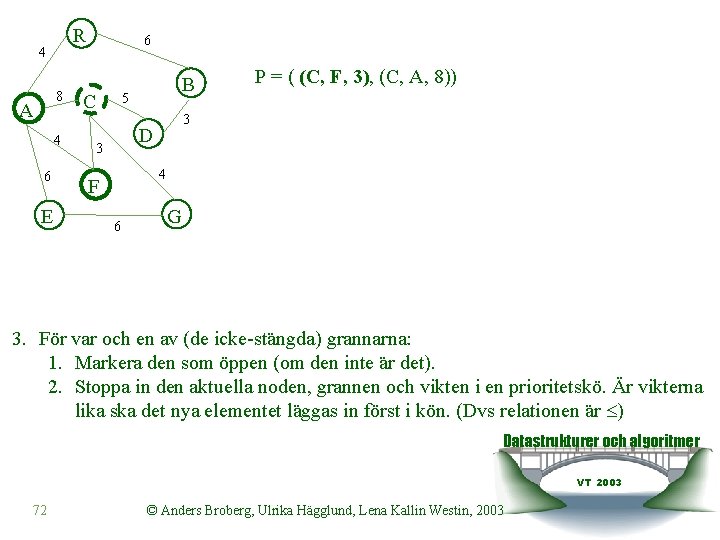
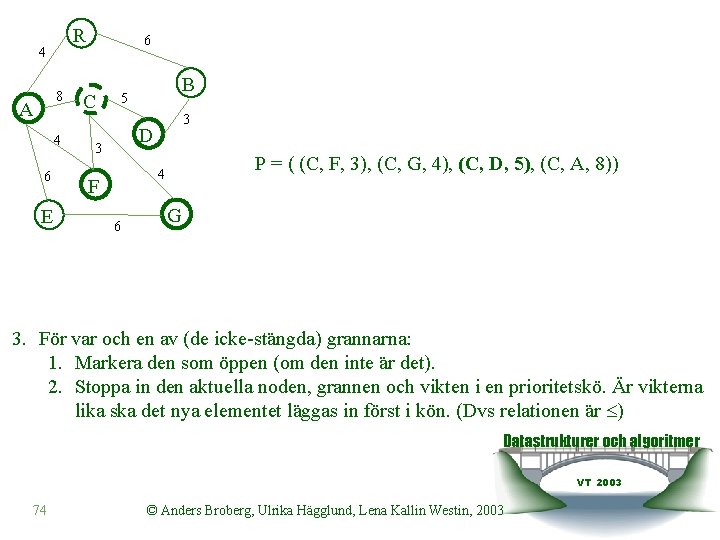
R 4 8 A 4 6 E 6 C B 5 3 D 3 P = ( (C, F, 3), (C, A, 8)) 4 F 6 G 3. För var och en av (de icke-stängda) grannarna: 1. Markera den som öppen (om den inte är det). 2. Stoppa in den aktuella noden, grannen och vikten i en prioritetskö. Är vikterna lika ska det nya elementet läggas in först i kön. (Dvs relationen är ) Datastrukturer och algoritmer VT 2003 72 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

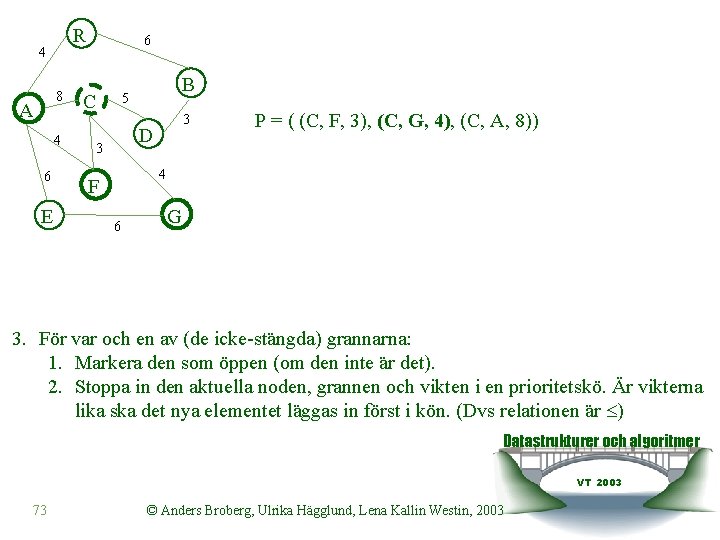
R 4 8 A 4 6 E 6 C B 5 3 D 3 P = ( (C, F, 3), (C, G, 4), (C, A, 8)) 4 F 6 G 3. För var och en av (de icke-stängda) grannarna: 1. Markera den som öppen (om den inte är det). 2. Stoppa in den aktuella noden, grannen och vikten i en prioritetskö. Är vikterna lika ska det nya elementet läggas in först i kön. (Dvs relationen är ) Datastrukturer och algoritmer VT 2003 73 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

R 4 8 A 4 6 E 6 C B 5 3 D 3 P = ( (C, F, 3), (C, G, 4), (C, D, 5), (C, A, 8)) 4 F 6 G 3. För var och en av (de icke-stängda) grannarna: 1. Markera den som öppen (om den inte är det). 2. Stoppa in den aktuella noden, grannen och vikten i en prioritetskö. Är vikterna lika ska det nya elementet läggas in först i kön. (Dvs relationen är ) Datastrukturer och algoritmer VT 2003 74 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

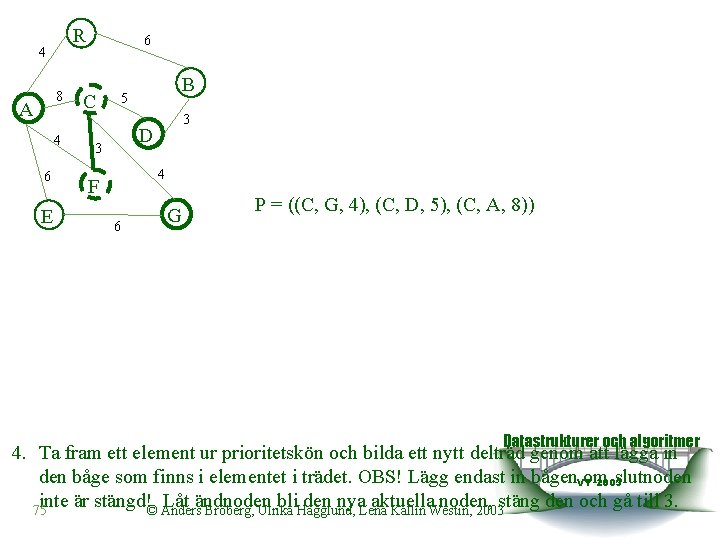
R 4 8 A 4 6 E 6 C B 5 3 D 3 4 F 6 G P = ((C, G, 4), (C, D, 5), (C, A, 8)) Datastrukturer och algoritmer 4. Ta fram ett element ur prioritetskön och bilda ett nytt delträd genom att lägga in den båge som finns i elementet i trädet. OBS! Lägg endast in bågen. VTom slutnoden 2003 inte är stängd!© Anders Låt ändnoden bli den nya aktuella noden, stäng den och gå till 3. 75 Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

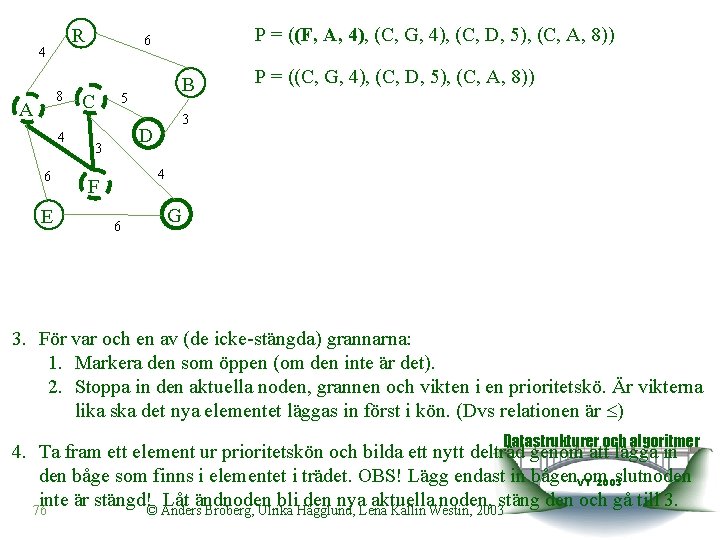
R 4 8 A 4 6 E P = ((F, A, 4), (C, G, 4), (C, D, 5), (C, A, 8)) 6 C B 5 3 D 3 P = ((C, G, 4), (C, D, 5), (C, A, 8)) 4 F 6 G 3. För var och en av (de icke-stängda) grannarna: 1. Markera den som öppen (om den inte är det). 2. Stoppa in den aktuella noden, grannen och vikten i en prioritetskö. Är vikterna lika ska det nya elementet läggas in först i kön. (Dvs relationen är ) Datastrukturer och algoritmer 4. Ta fram ett element ur prioritetskön och bilda ett nytt delträd genom att lägga in den båge som finns i elementet i trädet. OBS! Lägg endast in bågen. VTom slutnoden 2003 inte är stängd!© Anders Låt ändnoden bli den nya aktuella noden, stäng den och gå till 3. 76 Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

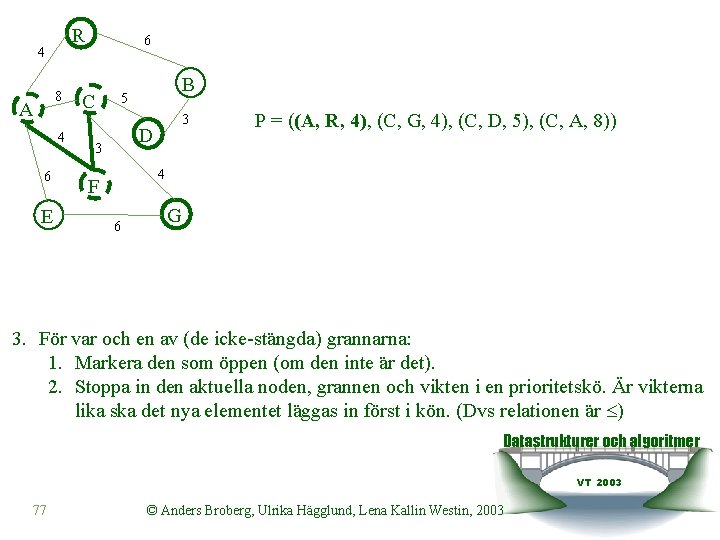
R 4 8 A 4 6 E 6 C B 5 3 D 3 P = ((A, R, 4), (C, G, 4), (C, D, 5), (C, A, 8)) 4 F 6 G 3. För var och en av (de icke-stängda) grannarna: 1. Markera den som öppen (om den inte är det). 2. Stoppa in den aktuella noden, grannen och vikten i en prioritetskö. Är vikterna lika ska det nya elementet läggas in först i kön. (Dvs relationen är ) Datastrukturer och algoritmer VT 2003 77 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

R 4 8 A 4 6 E 6 C B 5 3 D 3 P = ((A, R, 4), (C, G, 4), (C, D, 5), (A, E, 6), (C, A, 8)) 4 F 6 G 3. För var och en av (de icke-stängda) grannarna: 1. Markera den som öppen (om den inte är det). 2. Stoppa in den aktuella noden, grannen och vikten i en prioritetskö. Är vikterna lika ska det nya elementet läggas in först i kön. (Dvs relationen är ) Datastrukturer och algoritmer VT 2003 78 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

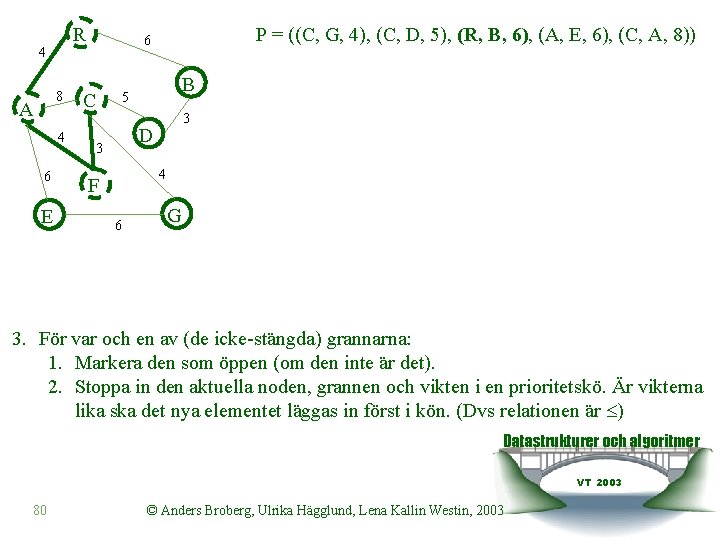
R 4 8 A 4 6 E 6 C B 5 3 D 3 4 F 6 G P = ((C, G, 4), (C, D, 5), (A, E, 6), (C, A, 8)) Datastrukturer och algoritmer 4. Ta fram ett element ur prioritetskön och bilda ett nytt delträd genom att lägga in den båge som finns i elementet i trädet. OBS! Lägg endast in bågen. VTom slutnoden 2003 inte är stängd!© Anders Låt ändnoden bli den nya aktuella noden, stäng den och gå till 3. 79 Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

R 4 8 A 4 6 E P = ((C, G, 4), (C, D, 5), (R, B, 6), (A, E, 6), (C, A, 8)) 6 C B 5 3 D 3 4 F 6 G 3. För var och en av (de icke-stängda) grannarna: 1. Markera den som öppen (om den inte är det). 2. Stoppa in den aktuella noden, grannen och vikten i en prioritetskö. Är vikterna lika ska det nya elementet läggas in först i kön. (Dvs relationen är ) Datastrukturer och algoritmer VT 2003 80 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

R 4 8 A 4 6 E 6 C B 5 3 D 3 P = ((C, D, 5), (R, B, 6), (A, E, 6), (C, A, 8)) P = ((C, D, 5), (G, E, 6), (R, B, 6), (A, E, 6), (C, A, 8)) 4 F 6 G 4. Ta fram ett element ur prioritetskön och bilda ett nytt delträd genom att lägga in den båge som finns i elementet i trädet. OBS! Lägg endast in bågen om slutnoden inte är stängd! Låt ändnoden bli den nya aktuella noden, stäng den och gå till 3. 3. För var och en av (de icke-stängda) grannarna: 1. Markera den som öppen (om den inte är det). 2. Stoppa in den aktuella noden, grannen och vikten i en prioritetskö. Är vikterna lika ska det nya elementet läggas in först i kön. (Dvs relationen är ) Datastrukturer och algoritmer VT 2003 81 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

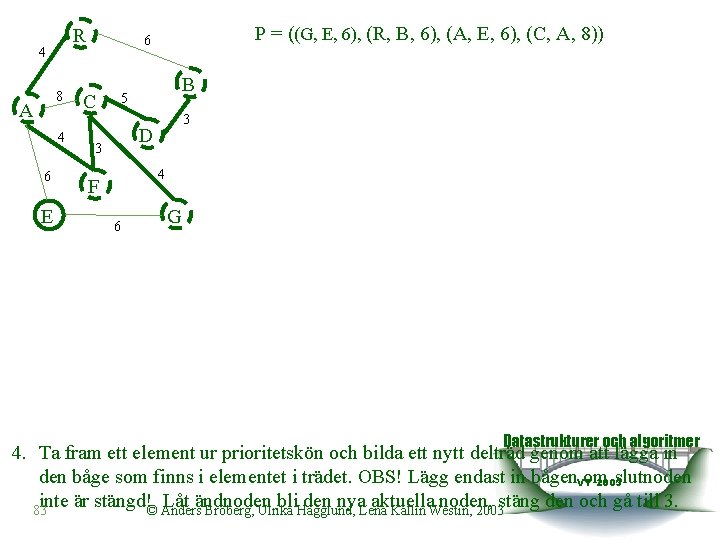
R 4 8 A 4 6 E 6 C B 5 3 D 3 P = ((G, E, 6), (R, B, 6), (A, E, 6), (C, A, 8)) 4 F 6 G P = ((D, B, 3), (G, E, 6), (R, B, 6), (A, E, 6), (C, A, 8)) 4. Ta fram ett element ur prioritetskön och bilda ett nytt delträd genom att lägga in den båge som finns i elementet i trädet. OBS! Lägg endast in bågen om slutnoden inte är stängd! Låt ändnoden bli den nya aktuella noden, stäng den och gå till 3. 3. För var och en av (de icke-stängda) grannarna: 1. Markera den som öppen (om den inte är det). 2. Stoppa in den aktuella noden, grannen och vikten i en prioritetskö. Är vikterna lika ska det nya elementet läggas in först i kön. (Dvs relationen är ) Datastrukturer och algoritmer VT 2003 82 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

R 4 8 A 4 6 E P = ((G, E, 6), (R, B, 6), (A, E, 6), (C, A, 8)) 6 C B 5 3 D 3 4 F 6 G Datastrukturer och algoritmer 4. Ta fram ett element ur prioritetskön och bilda ett nytt delträd genom att lägga in den båge som finns i elementet i trädet. OBS! Lägg endast in bågen. VTom slutnoden 2003 inte är stängd!© Anders Låt ändnoden bli den nya aktuella noden, stäng den och gå till 3. 83 Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

R 4 8 A 4 6 E 6 C B 5 3 D 3 6 P = ((A, E, 6), (C, A, 8)) P = ((C, A, 8)) 4 F P = ((R, B, 6), (A, E, 6), (C, A, 8)) G P = () Klart! 4. Ta fram ett element ur prioritetskön och bilda ett nytt delträd genom att lägga in den båge som finns i elementet i trädet. OBS! Lägg endast in bågen om slutnoden inte är stängd! Låt ändnoden bli den nya aktuella noden, stäng den och gå till 3. Datastrukturer och algoritmer VT 2003 84 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

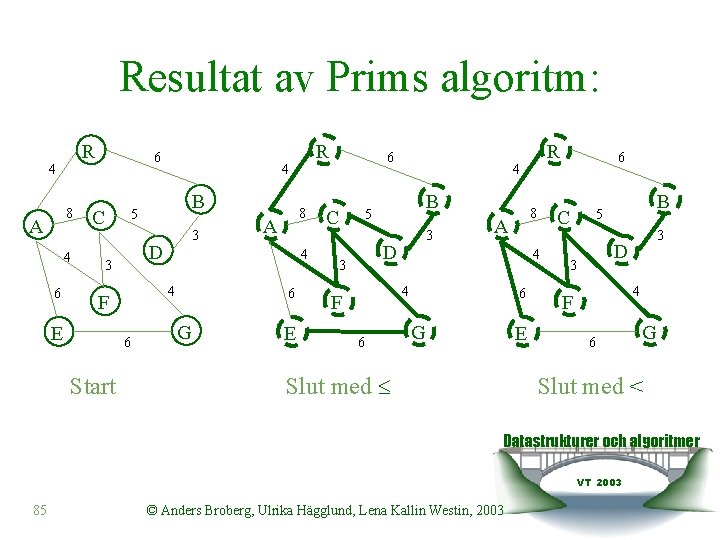
Resultat av Prims algoritm: R 4 8 A 4 6 6 C 3 8 A 4 4 6 Start B D F E 4 5 3 R 6 G E 6 C 4 B 5 3 D 3 6 8 A 6 G E Slut med 6 C 4 4 F R B 5 3 D 3 4 F 6 G Slut med < Datastrukturer och algoritmer VT 2003 85 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Prims algoritm - komplexitet u Man gör en traversering av grafen, dvs O(m) + O(n). u Sen tillkommer köoperationer ØFör varje båge sätter man in ett element i kön, inspekterar det och tar ut det. Detta blir O(m) ØOm man använder Heap (partiellt sorterat binärt träd) får vi O(log m). u Totalt: O(n) + O(m 2) eller O(n) + O(m log m) beroende på implementation av Datastrukturer och algoritmer prioritetskön. VT 2003 86 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Kruskals algoritm u Här väljer man också bågar allt eftersom men man bryr sig inte om att forma delträd under konstruktionen. u Man gör ingen traversering utan arbetar på ett annat sätt med bågarna. u Man färglägger bågarna för att hålla reda på vilken delgraf de tillhör. Datastrukturer och algoritmer VT 2003 87 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

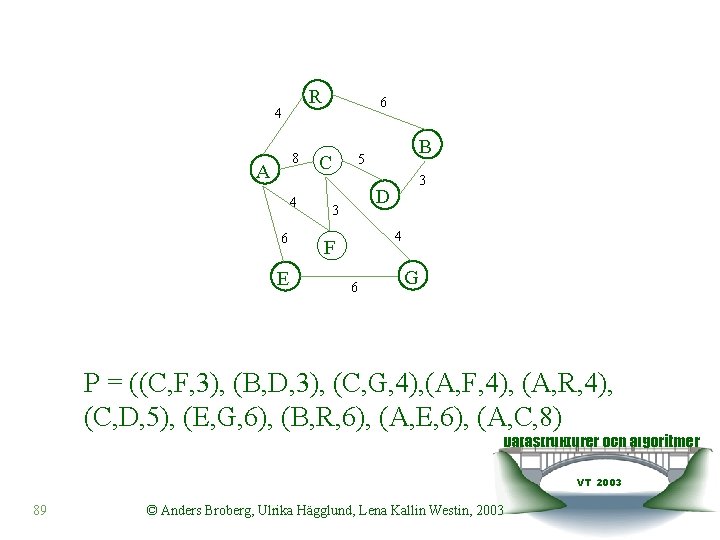
Kruskals algoritm 1. Skapa en prioritetskö av alla bågarna utifrån vikterna på dessa. 2. Den första bågen plockas fram och bildar den första delgrafen. Noderna färgläggs. 3. Upprepa tills kön är tom: 1. Ta fram en ny båge. 2. Om ingen av noderna är färgade 1. Färglägg med ny färg och bilda ny delgraf. 3. Om endast en nod är färgad 1. Ingen risk för cykel utöka grafen och färglägg. 4. Om båda noderna är färgade med olika färg 1. Välj en av färgerna och färga om den nya gemensamma grafen. Datastrukturer och algoritmer 5. Om båda noderna har samma färg VT 2003 1. Ignorera bågen, den skapar en cykel 88 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

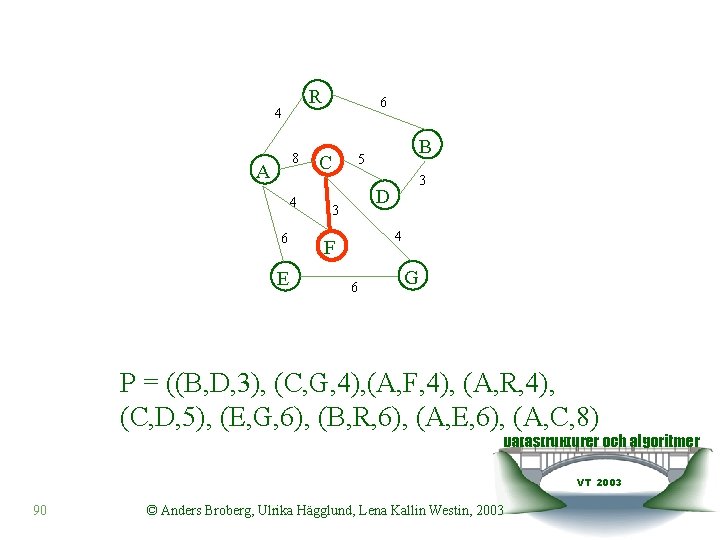
R 4 8 A 4 6 E 6 C B 5 3 D 3 4 F 6 G P = ((C, F, 3), (B, D, 3), (C, G, 4), (A, F, 4), (A, R, 4), (C, D, 5), (E, G, 6), (B, R, 6), (A, E, 6), (A, C, 8) Datastrukturer och algoritmer VT 2003 89 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

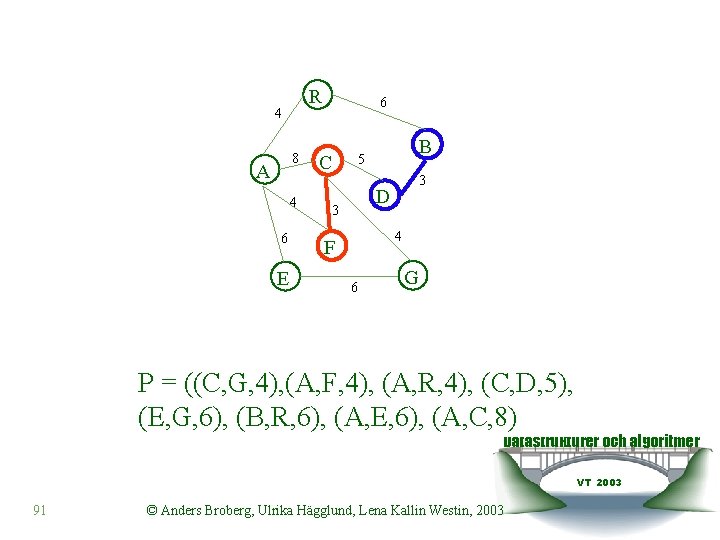
R 4 8 A 4 6 E 6 C B 5 3 D 3 4 F 6 G P = ((B, D, 3), (C, G, 4), (A, F, 4), (A, R, 4), (C, D, 5), (E, G, 6), (B, R, 6), (A, E, 6), (A, C, 8) Datastrukturer och algoritmer VT 2003 90 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

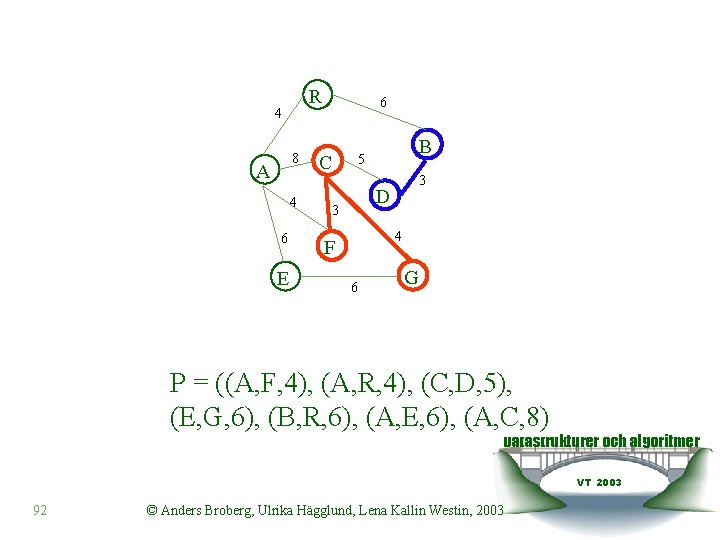
R 4 8 A 4 6 E 6 C B 5 3 D 3 4 F 6 G P = ((C, G, 4), (A, F, 4), (A, R, 4), (C, D, 5), (E, G, 6), (B, R, 6), (A, E, 6), (A, C, 8) Datastrukturer och algoritmer VT 2003 91 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

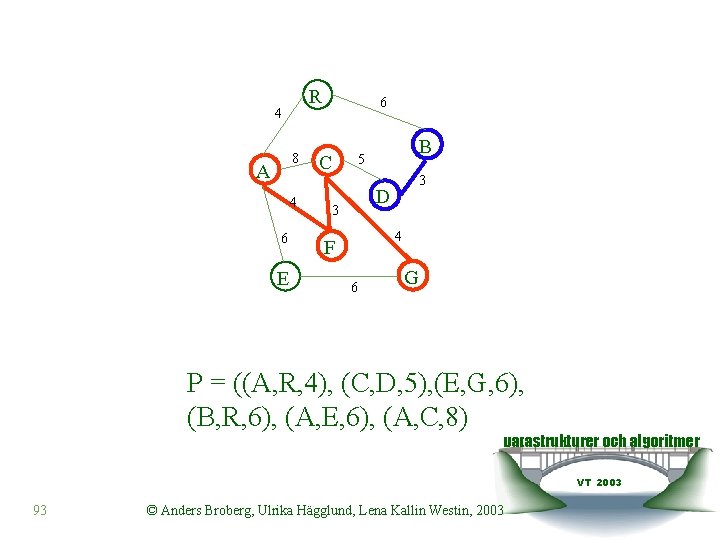
R 4 8 A 4 6 E 6 C B 5 3 D 3 4 F 6 G P = ((A, F, 4), (A, R, 4), (C, D, 5), (E, G, 6), (B, R, 6), (A, E, 6), (A, C, 8) Datastrukturer och algoritmer VT 2003 92 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

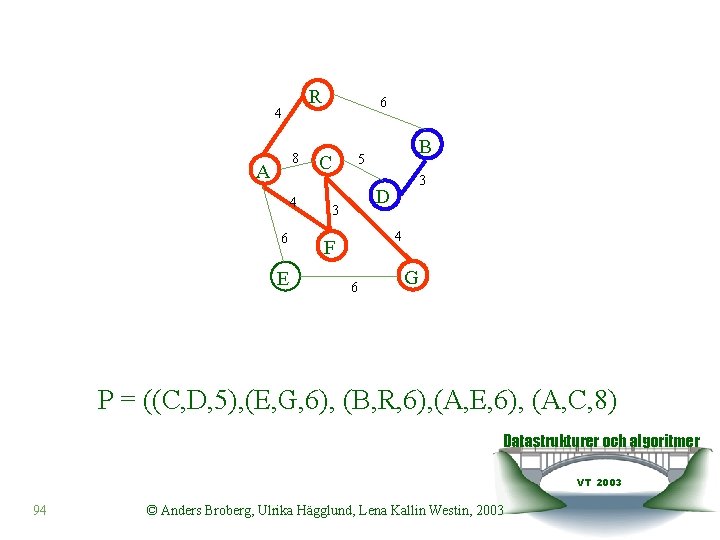
R 4 8 A 4 6 E 6 C B 5 3 D 3 4 F 6 G P = ((A, R, 4), (C, D, 5), (E, G, 6), (B, R, 6), (A, E, 6), (A, C, 8) Datastrukturer och algoritmer VT 2003 93 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

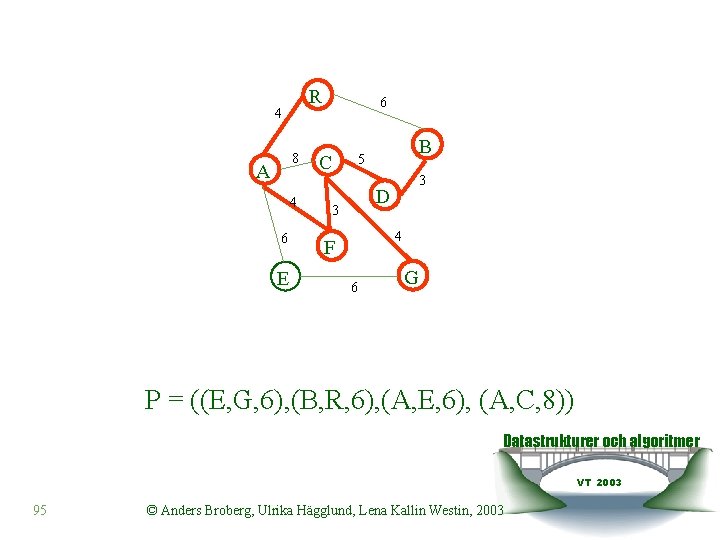
R 4 8 A 4 6 E 6 C B 5 3 D 3 4 F 6 G P = ((C, D, 5), (E, G, 6), (B, R, 6), (A, E, 6), (A, C, 8) Datastrukturer och algoritmer VT 2003 94 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

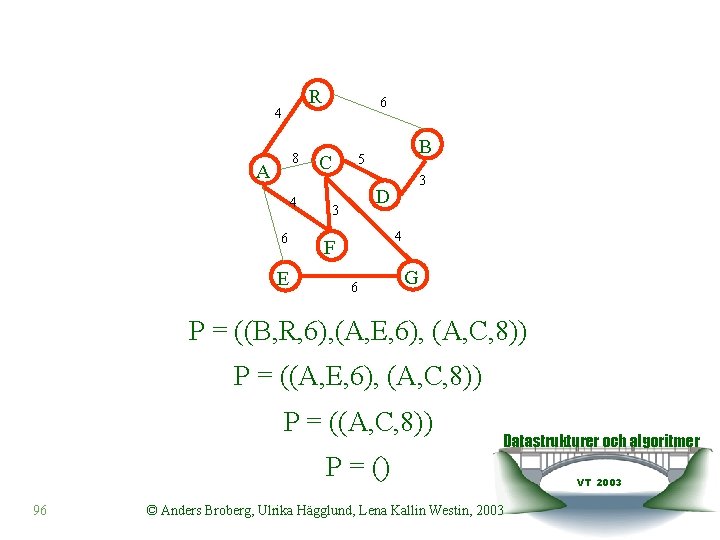
R 4 8 A 4 6 E 6 C B 5 3 D 3 4 F 6 G P = ((E, G, 6), (B, R, 6), (A, E, 6), (A, C, 8)) Datastrukturer och algoritmer VT 2003 95 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

R 4 8 A 4 6 E 6 C B 5 3 D 3 4 F 6 G P = ((B, R, 6), (A, E, 6), (A, C, 8)) P = ((A, C, 8)) Datastrukturer och algoritmer P = () 96 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003 VT 2003

Kruskals algoritm - komplexitet u Första steget i algoritmen bygger en prioritetskö utifrån en bågmängd. ØKomplexitet beror på implementationen av bågmängden och prioritetskön… u Varje båge traverseras en gång. u Resten kan delas in i fyra fall: ØTre fall med komplexitet O(1) där bågen kan läggas till utan problem. ØEtt fall där en delgraf måste färgas om. Komplexitet Datastrukturer och algoritmer O(n). VT 2003 97 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Finna vägen till en nod u Bredden-först traversering ger oss vägarna från en nod till alla andra. ØOm vi sparar undan vägen… u Är det den kortaste? ØJa, om alla vikter lika! ØAnnars då? Vi kommer titta på två algoritmer: o Floyds shortest path O(N 3) Datastrukturer och algoritmer o Dijkstras shortest path VT 2003 98 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

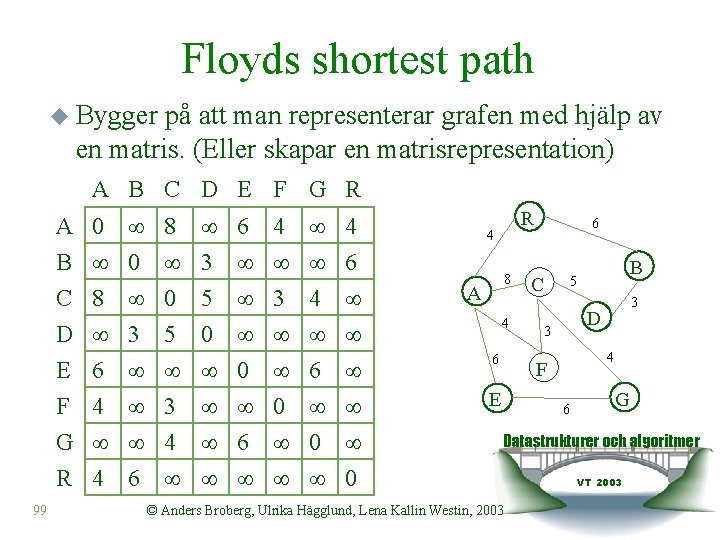
Floyds shortest path u Bygger på att man representerar grafen med hjälp av en matris. (Eller skapar en matrisrepresentation) A B C D E F G R A 0 8 B 0 3 C 8 0 5 D 3 5 0 E 6 F 4 3 G 4 R 4 6 99 4 6 3 4 6 4 0 6 0 R 4 8 A 4 6 6 C 3 D 3 4 F E B 5 6 G Datastrukturer och algoritmer © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003 VT 2003

Floyds shortest path Algoritm floyd(Graph g) input: A graph g to find shortest path in // Get matrix representation A(: , 0) get. Matrix(g) N get. No. Of. Nodes(g) for k=0 to N-1 for i=0 to N-1 for j=0 to N-1 A(i, j, k+1) = min(A(i, j, k), A(i, k, k)+ A(k, j, k)) A(: , N) innehåller kortaste avstånden men hur få tag på vägen? Spara på samma gång en föregångar. Datastrukturer och algoritmer matris. Det kommer också kosta O(N 3) så den ökar inte komplexiteten. VT 2003 100 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Uppdaterad Floyd Algoritm floyd(Graph g) input: A graph g to find shortest path in // Get matrix representation A(: , 0) get. Matrix(g) N get. No. Of. Nodes(g) for i = 0 to N-1 for j = 0 to N-1 if (i==j or A(i, j, 0)==inf) Path(i, j, 0) = -1 else Path(i, j, 0) = i for k=0 to N-1 for i=0 to N-1 for j=0 to N-1 A(i, j, k+1) = min(A(i, j, k), A(i, k, k)+A(k, j, k)) if (A(i, j, k) A(i, k, k)+A(k, j, k)) Path(i, j, k+1) = Path(i, j, k) else Path(i, j, k+1) = Path(k, j, k) Datastrukturer och algoritmer VT 2003 101 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

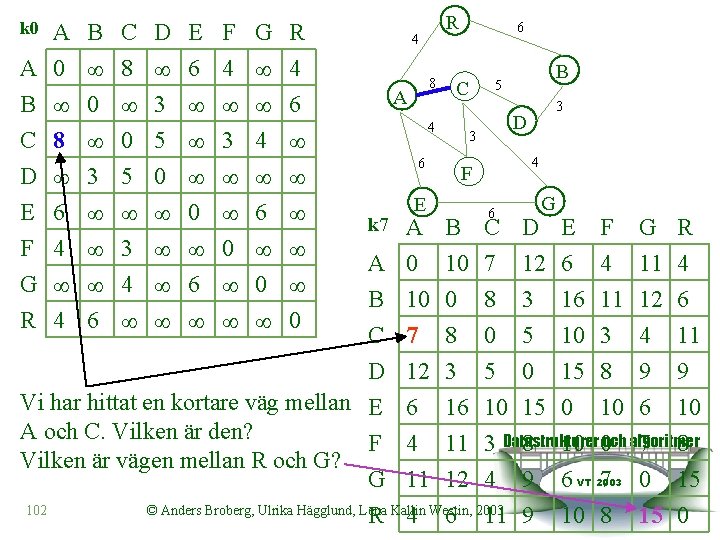
k 0 A B C A 0 8 B 0 C 8 0 D E F G R D E F G 6 4 3 5 3 4 3 5 0 6 4 3 4 4 6 0 R 4 4 0 6 C 4 k 7 E A A 0 B 10 C 7 12 6 4 11 R 4 B 5 3 D 3 6 D Vi har hittat en kortare väg mellan E A och C. Vilken är den? F Vilken är vägen mellan R och G? G 102 8 A 6 R 4 F 6 G B 10 0 8 C 7 8 0 3 16 11 12 5 0 15 8 9 9 10 15 0 10 6 10 3 Datastrukturer 8 10 0 och algoritmer 7 8 4 9 6 VT 2003 7 0 15 6 11 9 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003 D 12 3 5 E 6 16 10 F 4 11 3 10 8 G 11 12 4 R 4 6 11 15 0

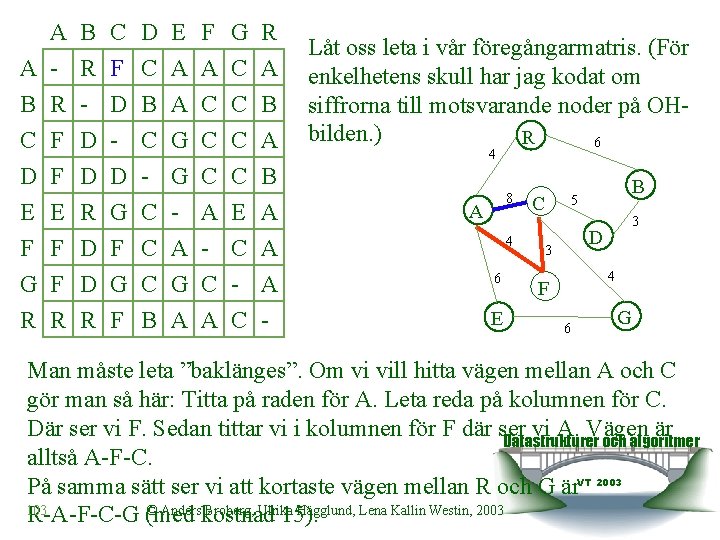
A B C D E F G R A - R F C A A C A B R - D B A C C B C F D - C G C C A D E F G R F E F F R D D R D G F C C C B G A C A C E C C B A A A - Låt oss leta i vår föregångarmatris. (För enkelhetens skull har jag kodat om siffrorna till motsvarande noder på OHbilden. ) R 6 4 8 A 4 6 E C B 5 3 D 3 4 F 6 G Man måste leta ”baklänges”. Om vi vill hitta vägen mellan A och C gör man så här: Titta på raden för A. Leta reda på kolumnen för C. Där ser vi F. Sedan tittar vi i kolumnen för F där ser vi A. Vägen är Datastrukturer och algoritmer alltså A-F-C. På samma sätt ser vi att kortaste vägen mellan R och G är. VT 2003 103 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003 R-A-F-C-G (med kostnad 15).

Dijkstras algoritm u Söker kortaste vägen från en nod n till alla andra noder. u Fungerar enbart på grafer med positiva vikter. u Låt varje nod ha följande attribut ØVisited – som blir sann när vi hittat en väg till den ØDistance – värdet på den kortaste vägen fram till noden ØParent – Referens till föregångaren på vägen Datastrukturer och algoritmer VT 2003 104 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Algoritm dijkstra(Node n, Graph g) input: A graph g to find shortest path starting from node n n. visited true; n. distance 0; n. parent null; Pqueue q empty(); q insert(n, q); while not isempty(q) v inspect-first(q); q delete-first(q); d v. distance; neighbour. Set neighbours(v, g); for each w in neighbour. Set do new. Dist d + get. Weight(v, w); if not is. Visited(w) w. visited true; w. distance new. Dist; w. parent v; q insert(w, q); else if new. Dist < w. distance new. Dist; Datastrukturer och algoritmer w. parent v; q update(w, q) VT 2003 Dijkstras algoritm 105 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

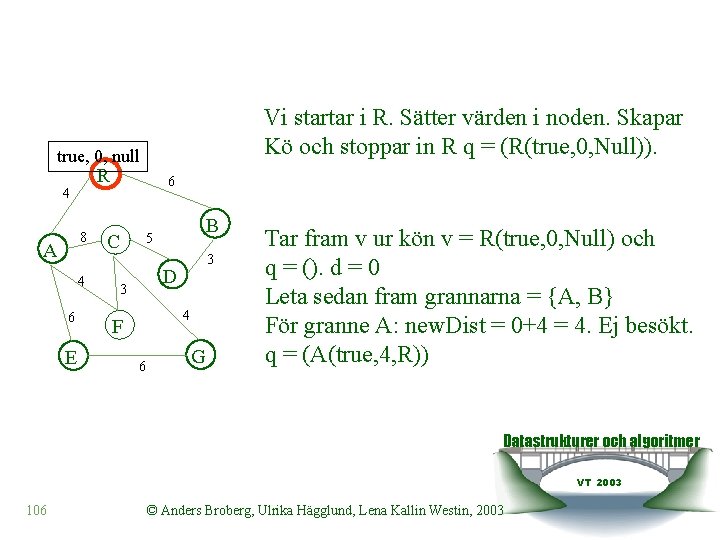
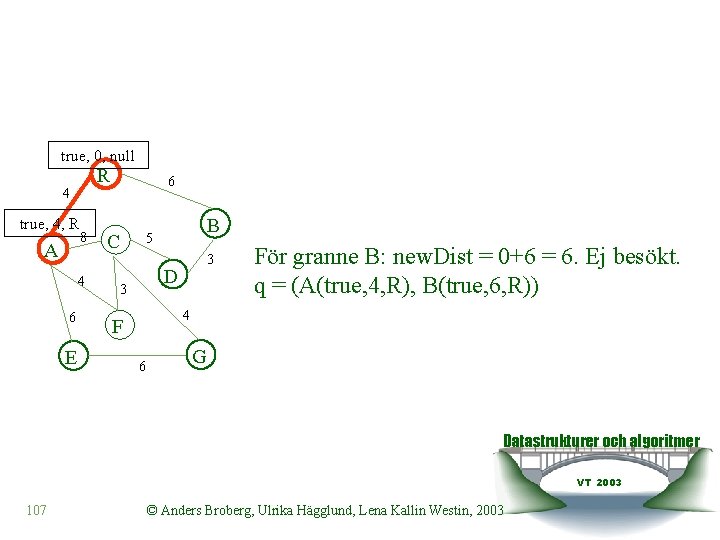
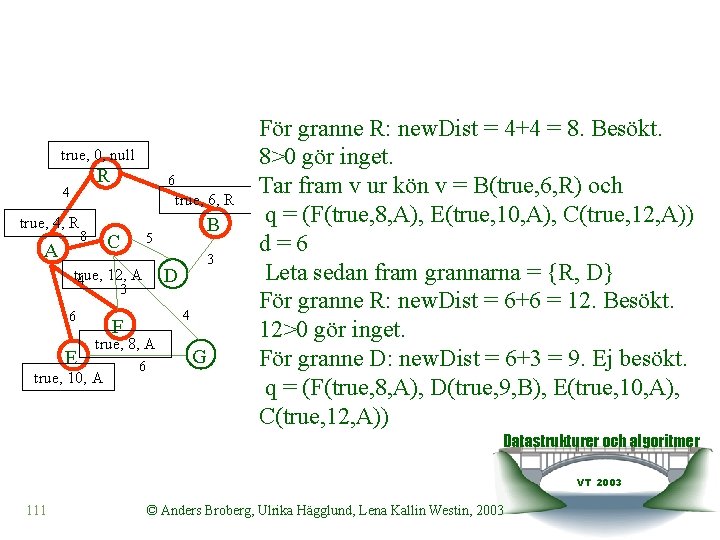
Vi startar i R. Sätter värden i noden. Skapar Kö och stoppar in R q = (R(true, 0, Null)). true, 0, null R 4 8 A 4 6 E 6 C B 5 3 D 3 4 F 6 G Tar fram v ur kön v = R(true, 0, Null) och q = (). d = 0 Leta sedan fram grannarna = {A, B} För granne A: new. Dist = 0+4 = 4. Ej besökt. q = (A(true, 4, R)) Datastrukturer och algoritmer VT 2003 106 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

true, 0, null R 4 true, 4, R A 8 4 6 E 6 C B 5 3 D 3 För granne B: new. Dist = 0+6 = 6. Ej besökt. q = (A(true, 4, R), B(true, 6, R)) 4 F 6 G Datastrukturer och algoritmer VT 2003 107 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

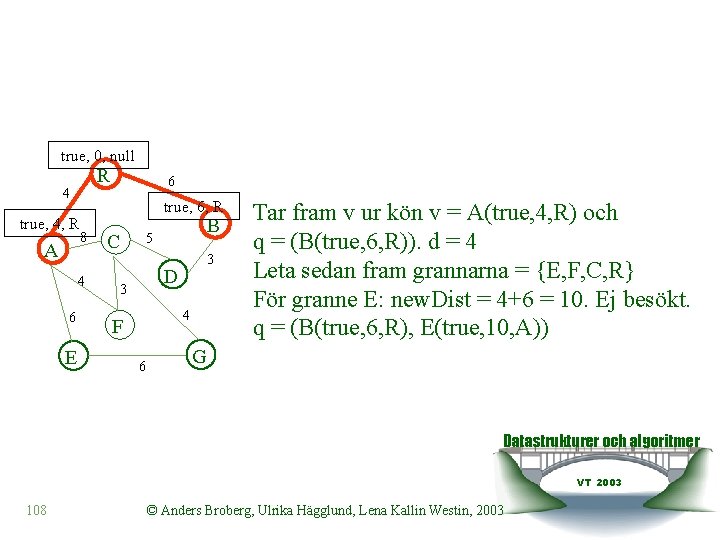
true, 0, null R 4 true, 4, R A true, 6, R 8 4 6 E 6 C B 5 3 D 3 4 F 6 Tar fram v ur kön v = A(true, 4, R) och q = (B(true, 6, R)). d = 4 Leta sedan fram grannarna = {E, F, C, R} För granne E: new. Dist = 4+6 = 10. Ej besökt. q = (B(true, 6, R), E(true, 10, A)) G Datastrukturer och algoritmer VT 2003 108 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

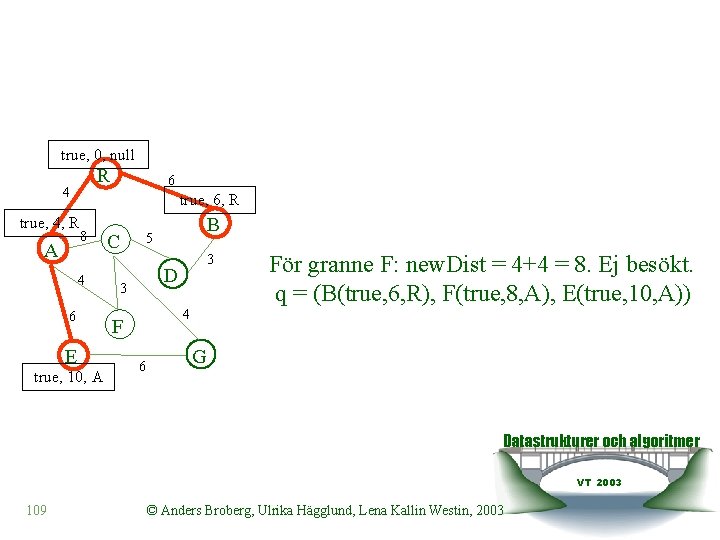
true, 0, null R 4 true, 6, R true, 4, R A 6 8 4 6 E true, 10, A C B 5 3 D 3 För granne F: new. Dist = 4+4 = 8. Ej besökt. q = (B(true, 6, R), F(true, 8, A), E(true, 10, A)) 4 F 6 G Datastrukturer och algoritmer VT 2003 109 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

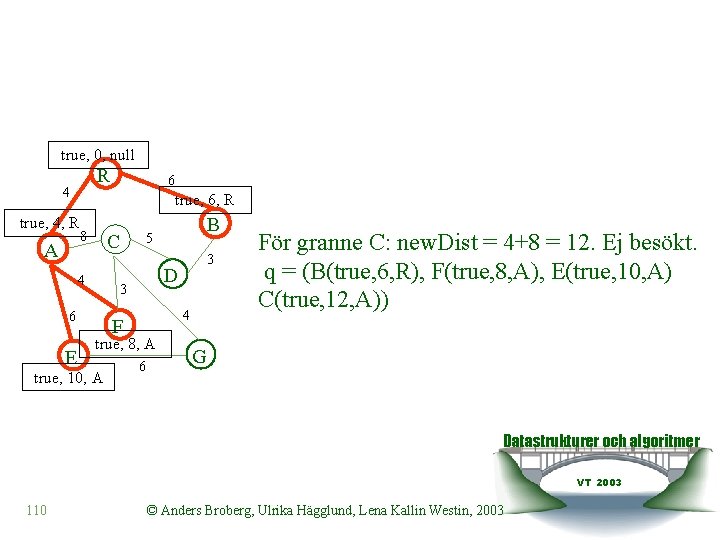
true, 0, null R 4 true, 6, R true, 4, R A 8 C 4 3 D 4 F true, 8, A true, 10, A B 5 3 6 E 6 6 För granne C: new. Dist = 4+8 = 12. Ej besökt. q = (B(true, 6, R), F(true, 8, A), E(true, 10, A) C(true, 12, A)) G Datastrukturer och algoritmer VT 2003 110 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

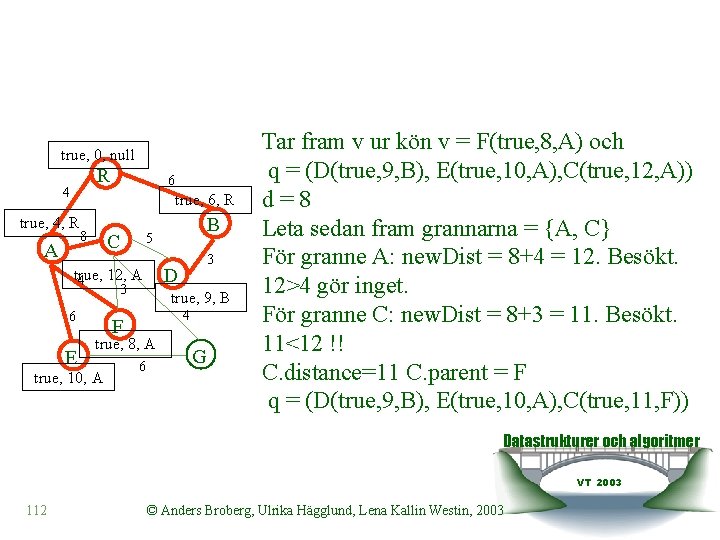
true, 0, null R 4 6 true, 6, R true, 4, R A 8 C 3 E 4 F true, 8, A true, 10, A 3 D true, 12, A 4 6 B 5 6 G För granne R: new. Dist = 4+4 = 8. Besökt. 8>0 gör inget. Tar fram v ur kön v = B(true, 6, R) och q = (F(true, 8, A), E(true, 10, A), C(true, 12, A)) d=6 Leta sedan fram grannarna = {R, D} För granne R: new. Dist = 6+6 = 12. Besökt. 12>0 gör inget. För granne D: new. Dist = 6+3 = 9. Ej besökt. q = (F(true, 8, A), D(true, 9, B), E(true, 10, A), C(true, 12, A)) Datastrukturer och algoritmer VT 2003 111 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

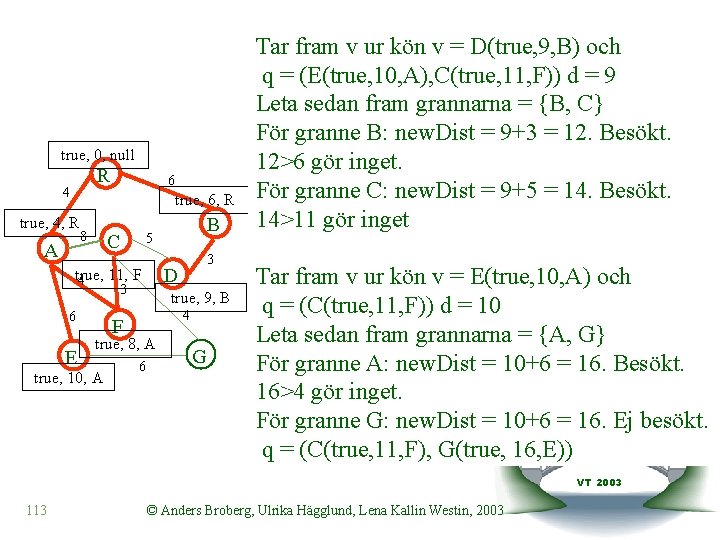
true, 0, null R 4 6 true, 6, R true, 4, R A 8 C 3 E true, 9, B 4 F true, 8, A true, 10, A 3 D true, 12, A 4 6 B 5 6 G Tar fram v ur kön v = F(true, 8, A) och q = (D(true, 9, B), E(true, 10, A), C(true, 12, A)) d=8 Leta sedan fram grannarna = {A, C} För granne A: new. Dist = 8+4 = 12. Besökt. 12>4 gör inget. För granne C: new. Dist = 8+3 = 11. Besökt. 11<12 !! C. distance=11 C. parent = F q = (D(true, 9, B), E(true, 10, A), C(true, 11, F)) Datastrukturer och algoritmer VT 2003 112 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

true, 0, null R 4 6 true, 6, R true, 4, R A 8 C 3 E true, 9, B 4 F true, 8, A true, 10, A 3 D true, 11, F 4 6 B 5 6 G Tar fram v ur kön v = D(true, 9, B) och q = (E(true, 10, A), C(true, 11, F)) d = 9 Leta sedan fram grannarna = {B, C} För granne B: new. Dist = 9+3 = 12. Besökt. 12>6 gör inget. För granne C: new. Dist = 9+5 = 14. Besökt. 14>11 gör inget Tar fram v ur kön v = E(true, 10, A) och q = (C(true, 11, F)) d = 10 Leta sedan fram grannarna = {A, G} För granne A: new. Dist = 10+6 = 16. Besökt. 16>4 gör inget. För granne G: new. Dist = 10+6 = 16. Ej besökt. q = (C(true, 11, F), G(true, Datastrukturer 16, E)) och algoritmer VT 2003 113 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

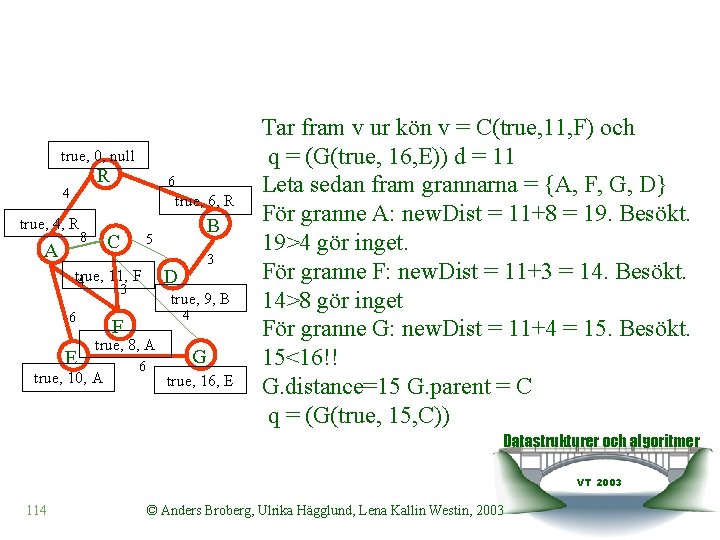
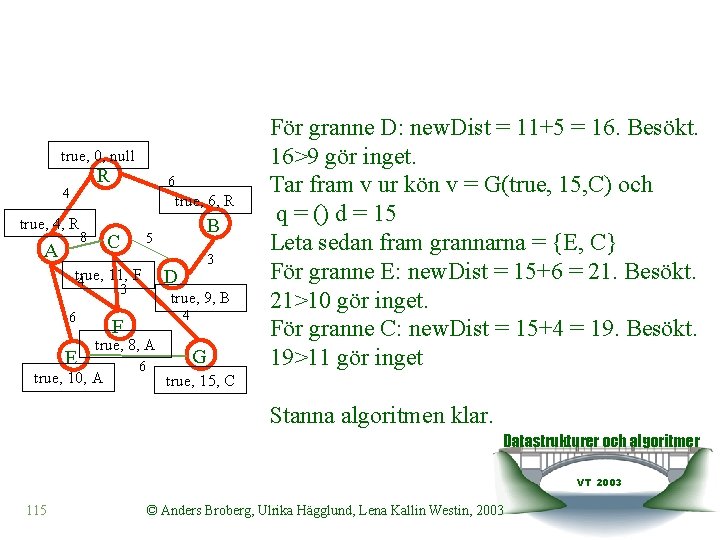
true, 0, null R 4 6 true, 6, R true, 4, R A 8 C 3 E true, 9, B 4 F true, 8, A true, 10, A 3 D true, 11, F 4 6 B 5 6 G true, 16, E Tar fram v ur kön v = C(true, 11, F) och q = (G(true, 16, E)) d = 11 Leta sedan fram grannarna = {A, F, G, D} För granne A: new. Dist = 11+8 = 19. Besökt. 19>4 gör inget. För granne F: new. Dist = 11+3 = 14. Besökt. 14>8 gör inget För granne G: new. Dist = 11+4 = 15. Besökt. 15<16!! G. distance=15 G. parent = C q = (G(true, 15, C)) Datastrukturer och algoritmer VT 2003 114 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

true, 0, null R 4 6 true, 6, R true, 4, R A 8 C 3 E true, 9, B 4 F true, 8, A true, 10, A 3 D true, 11, F 4 6 B 5 6 G För granne D: new. Dist = 11+5 = 16. Besökt. 16>9 gör inget. Tar fram v ur kön v = G(true, 15, C) och q = () d = 15 Leta sedan fram grannarna = {E, C} För granne E: new. Dist = 15+6 = 21. Besökt. 21>10 gör inget. För granne C: new. Dist = 15+4 = 19. Besökt. 19>11 gör inget true, 15, C Stanna algoritmen klar. Datastrukturer och algoritmer VT 2003 115 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Dijkstras algoritm - komplexitet u Vi sätter in varje nod i kön en gång. Ø Totalt n*O(insert) u Vi tar ut varje nod ur kön en gång. Ø Totalt n*O(delete-first) u Vi kan behöva uppdatera element i kön. Ø Maximalt m gånger, m*O(update) u Osorterad Om smart implementation… lista Ø n*O(1)+n*O(n) + m*O(1) = O(n 2) +O(m) u Heap Ø n*O(log n)+n*O(log n) + m*O(log n) = O((n+m)log n) Datastrukturer och algoritmer VT 2003 116 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Floyd vs. Dijkstra u Floyd O(n 3) hittar den kortaste vägen mellan alla noder. u Dijkstra O((n+m) log n) med heap, hittar kortaste vägen mellan en nod och alla andra. ØMåste köras N gånger för att få samma resultat som Floyd. Dvs O(n(n+m) log n). ØÄr bättre på stora glesa grafer. Datastrukturer och algoritmer VT 2003 117 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003

Flödet i en graf u Riktad graf med vikter cv, w, som anger flödeskapacitet över bågen (v, w). u Kapaciteten kan t. ex. vara mängden vätska som kan flöda genom ett rör, maximala mängden trafik på en väg eller kommunikationskapaciteten i ett datornät. u Grafen har två noder s (source) och t (sink) och uppgiften är att beräkna det maximala flödet mellan s och t. u Genom varje båge (u, v) kan vi maximalt ha ett flöde på cu, v enheter. u För varje node v gäller att det totala inkommande flödet måste vara lika med det utgående flödet. Datastrukturer och algoritmer VT 2003 118 © Anders Broberg, Ulrika Hägglund, Lena Kallin Westin, 2003