Grafalgoritmer I 1 Plan Grafer definition anvendelser terminologi

Grafalgoritmer I 1

Plan • Grafer - definition - anvendelser - terminologi - eksempler på grafproblemer • Grafgennemgang - dybde-først-gennemgang - bredde-først-gennemgang • Sammenhæng - 2 -sammenhæng - (foren-og-find) 2

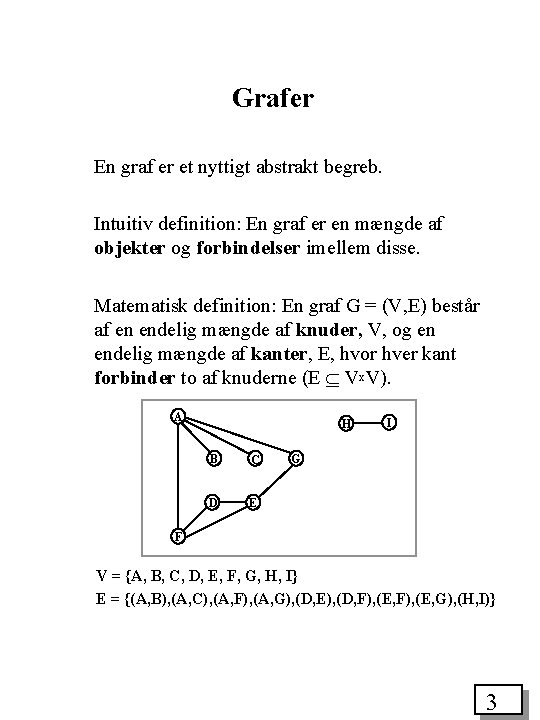
Grafer En graf er et nyttigt abstrakt begreb. Intuitiv definition: En graf er en mængde af objekter og forbindelser imellem disse. Matematisk definition: En graf G = (V, E) består af en endelig mængde af knuder, V, og en endelig mængde af kanter, E, hvor hver kant forbinder to af knuderne (E Vx. V). A H B C D E I G F V = {A, B, C, D, E, F, G, H, I} E = {(A, B), (A, C), (A, F), (A, G), (D, E), (D, F), (E, G), (H, I)} 3

Anvendelsesområder Alt, hvad der involverer relationer imellem objekter, kan modelleres ved hjælp af en graf Trafiknetværk: Knuder: byer, vejkryds Kanter: veje Elektriske kredsløb: Knuder: komponenter Kanter: ledninger Organiske molekyler: Knuder: atomer Kanter: bindinger Programsystemer: Knuder: rutiner Kanter: rutine A kan kalde rutine B Objektorienteret design (UML-diagrammering): Knuder: klasser/objekter Kanter: nedarvning, aggregering eller associering Projektplanlægning: Knuder: delopgaver Kanter: præcedenser (A skal udføres før B) 4

Terminologi En kants 2 knuder kaldes endeknuder for kanten. H I Hvis rækkefølgen af en kants endeknuder har betydning, kaldes kanten for orienteret. Dette angives på den grafiske repræsentation ved at kanten forsynes med en pil. Endeknuderne kaldes da for henholdsvis begyndelsesknuden og slutknuden. H I En orienteret graf er en graf, hvor alle kanter er orienterede. En ikke-orienteret graf er en graf, hvor ingen kanter er orienterede. 5

Terminologi (fortsat) En vej er en liste af knuder, hvor successive knuder er forbundet med en kant. En vej kaldes simpel, hvis ingen knude gentages. En cykel er en vej, der er simpel, bortset fra at den første og sidste knude er den samme. A B C D E G F Cykler: FDEF, AFEGA og AFDEGA. 6

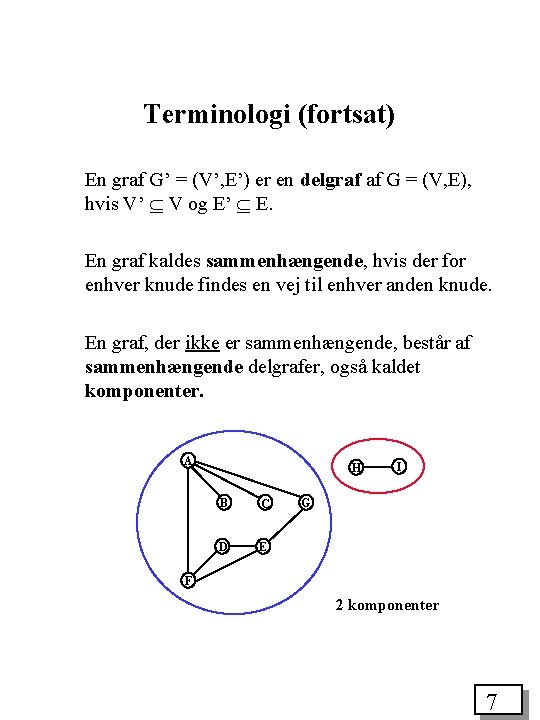
Terminologi (fortsat) En graf G’ = (V’, E’) er en delgraf af G = (V, E), hvis V’ V og E’ E. En graf kaldes sammenhængende, hvis der for enhver knude findes en vej til enhver anden knude. En graf, der ikke er sammenhængende, består af sammenhængende delgrafer, også kaldet komponenter. A H B C D E I G F 2 komponenter 7

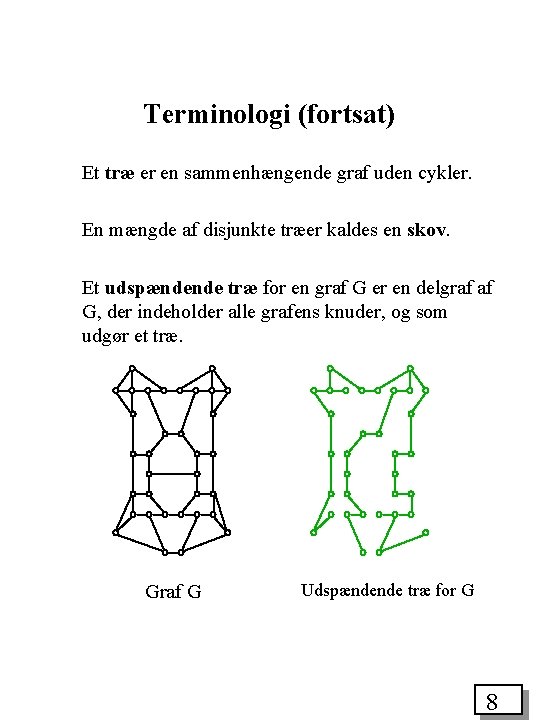
Terminologi (fortsat) Et træ er en sammenhængende graf uden cykler. En mængde af disjunkte træer kaldes en skov. Et udspændende træ for en graf G er en delgraf af G, der indeholder alle grafens knuder, og som udgør et træ. Graf G Udspændende træ for G 8

Terminologi (fortsat) En graf, hvor enhver knude er forbundet med enhver anden knude, kaldes for komplet. [ for en ikke-orienteret graf: E = V*(V-1)/2) ] En tynd graf er en graf med relativt få kanter. En tæt graf er en graf med relativt mange kanter. En vægtet graf er en graf, hvor kanterne er forsynet med talværdier, kaldet vægte. [ vægtene repræsenterer normalt omkostninger ] 9

Basale grafproblemer Veje: der en vej fra knude A til knude B? Er Cykler: Indeholder grafen en cykel? Sammenhæng (udspændende træ): Er der for hver knude en vej til enhver anden knude? 2 -sammenhæng: Vil grafen blive usammenhængende, hvis en af knuderne (og de tilstødende kanter) fjernes? Planaritet: Kan grafen tegnes, uden at to kanter krydser hinanden? 10

Basale grafproblemer (fortsat) Korteste vej: Hvilken vej er den korteste mellem knude A og knude B? Længste vej: Hvilken vej er den længste mellem knude A og knude B? Minimalt udspændende træ: Hvad er den billigste måde at forbinde alle knuder? Hamilton-cykel: Er der en cykel, som indeholder samtlige knuder? Den rejsende sælgers problem: Hvilken Hamilton-cykel er den billigste? Isomorfi: Symboliserer to grafrepræsentationer den samme graf? 11

Repræsentation af grafer Grafer er abstrakte matematiske objekter. Algoritmer må arbejde med konkrete repræsentationer. Mange mulige repræsentationer. Valget er bestemt af algoritmer og graftyper (tynde/tætte, vægtede/uvægtede, orienterede/ikke-orienterede). I det følgende gennemgås 3 repræsentationer: (1) kantmængde (2) nabomatrix (3) nabolister 12

(1) Kantmængde-repræsentation A H B C D E I G F end. Node[0][0] end. Node[1][0] end. Node[2][0] end. Node[3][0] end. Node[4][0] end. Node[5][0] end. Node[6][0] end. Node[7][0] end. Node[8][0] = = = = = A, A, A, E, F, H, F, A, G, end. Node[0][1] end. Node[1][1] end. Node[2][1] end. Node[3][1] end. Node[4][1] end. Node[5][1] end. Node[6][1] end. Node[7][1] end. Node[8][1] = = = = = G B C D D I E F E 13

Oprettelse af kantmængde class Graph { int V, E, end. Node[][]; void read() { V = IO. read. Int(); E = IO. read. Int(); end. Node = new int[E][2]; for (int i = 0; i < E; i++) { end. Node[i][0] = IO. read. Int(); end. Node[i][1] = IO. read. Int(); } } } Her identificeres knuderne ved heltal. Hvis knuderne er navngivet ved tegnstrenge kan metoderne index og name defineres int index(String node. Name) String name(int node. Index) 14

Kantmængde-repræsentation ved hjælp af kant-objekter class Edge { int v 1, v 2; Edge(int a, int b) { v 1 = a; v 2 = b; } } class Graph { int V, E; Vector edges; void read() { V = IO. read. Int(); E = IO. read. Int(); edges = new Vector(E); for (int i = 1; i <= E; i++) edges. add. Element( new Edge(IO. read. Int(), IO. read. Int()); } } 15

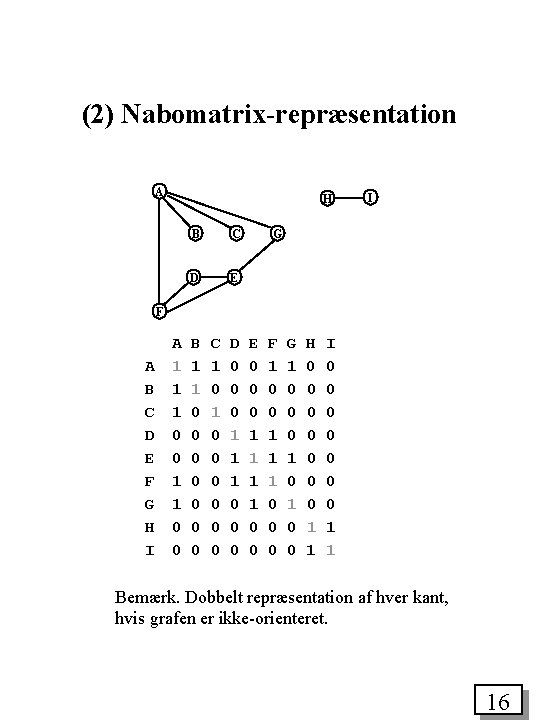
(2) Nabomatrix-repræsentation A H B C D E I G F A B C D E F G H I A 1 1 1 0 0 B 1 1 0 0 0 0 C 1 0 0 0 0 D 0 0 0 1 1 1 0 0 0 E 0 0 0 1 1 0 0 F 1 0 0 1 1 1 0 0 0 G 1 0 0 0 1 0 0 H 0 0 0 0 1 1 I 0 0 0 0 1 1 Bemærk. Dobbelt repræsentation af hver kant, hvis grafen er ikke-orienteret. 16

Oprettelse af nabomatrix class Graph { int V, E; boolean a[][]; void read() { V = IO. read. Int(); E = IO. read. Int(); a = new boolean[V+1]; for (int x = 1; x <= V; x++) a[x][x] = true; for (int i = 1; i <= E; i++) { int x = IO. read. Int(); int y = IO. read. Int(); a[x][y] = a[y][x] = true; } } } 17

Repræsentation ved hjælp af Javas class Bit. Set class Graph { int V, E; Bit. Set a[]; void read() { V = IO. read. Int(); E = IO. read. Int(); a = new Bit. Set[V+1]; for (int x = 1; x <= V; x++) { a[x] = new Bit. Set(V+1); a[x]. set(x); } for (int i = 1; i <= E; i++) { int x = IO. read. Int(); int y = IO. read. Int(); a[x]. set(y); a[y]. set(x); } } } a[x]. get(y): Er (x, y) kant i grafen? 18

(3) Naboliste-repræsentation A H B C D E I G F A: B: C: D: E: F: G: H: I: F C B G A A F E G F D A E D E A I H Bemærk. Dobbelt repræsentation af hver kant, hvis grafen er ikke-orienteret. 19

Oprettelse af nabolister class Node { int v; Node next; Node(int vv; Node nn) { v = vv; next = nn; } } class Graph { int V, E; Node adj[], z; void read() { V = IO. read. Int(); E = IO. read. Int(); adj = new Node[V+1]; z = new Node(0, null); z. next = z; for (int i = 1; i <= V; i++) adj[i] = z; for (int i = 1; i <= E; i++) { int x = IO. read. Int(); int y = IO. read. Int(); adj[x] = new Node(y, adj[x]); adj[y] = new Node(x, adj[y]); } } } 20

Sammenligning af repræsentationer Pladskrav: Kantmængde: Nabomatrix: Nabolister: O(E (+V)) O(V 2) O(V + E) Repræsentation påvirker algoritmers effektivitet. Værste tilfælde: Er der en kant fra knude A til knude B? Kantmængde: O(E) Nabomatrix: O(1) Nabolister: O(V) Er der en kant fra knude A? Kantmængde: O(E) Nabomatrix O(V) Nabolister: O(1) 21

Systematisk gennemgang af grafer Mål: at besøge enhver knude i grafen. Dybde-først-gennemgang: Rekursiv algoritme: * Mærk alle knuder “ubesøgt” (unseen). * Ved besøg af en knude k: Mærk knuden “besøgt” Besøg (rekursivt) alle ubesøgte knuder, der er forbundet med k. * Besøg knude 1. Besøg derefter en ubesøgt Fortsæt Løser nogle knude. simple grafproblemer: indtil alle knuder cykler er besøgt. (hvordan? ) sammenhæng, Basis for løsning af nogle vanskelige grafproblemer: 2 -sammenhæng, planaritet 22

Implementering af dybde-først-gennemgang void search() { int k; for (k = 1; k <= V; k++) val[k] = unseen; id = 0; // number of visited nodes for (k = 1; k <= V; k++) if (val[k] == unseen) visit(k); } void visit(int k) { // adjacency lists val[k] = ++id; for (Node t = adj[k]; t != z; t = t. next) if (val[t. v] == unseen) visit(t. v); } void visit(int k) { // adjacency matrix val[k] = ++id; for (int t = 1; t <= V; t++) if (a[k][t] && val[t] == unseen) visit(t); } 23

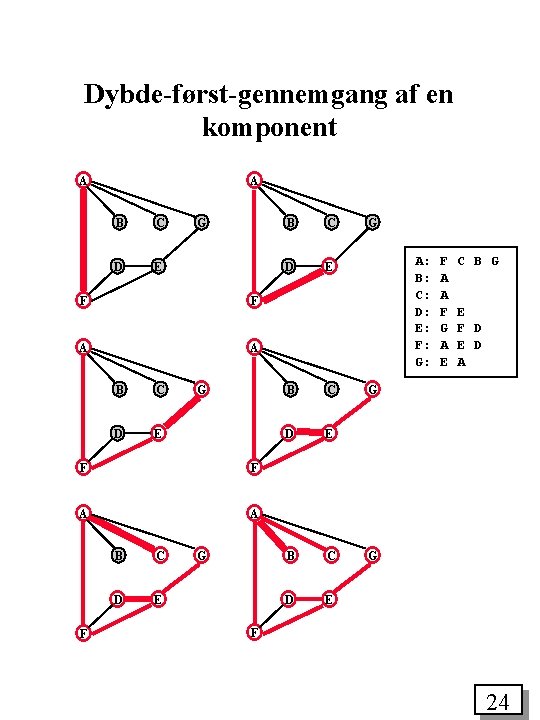
Dybde-først-gennemgang af en komponent A A B C D E G F F A A F B C D E G B C D E G A: B: C: D: E: F: G: F A A F G A E C B G E F D E D A G G F 24

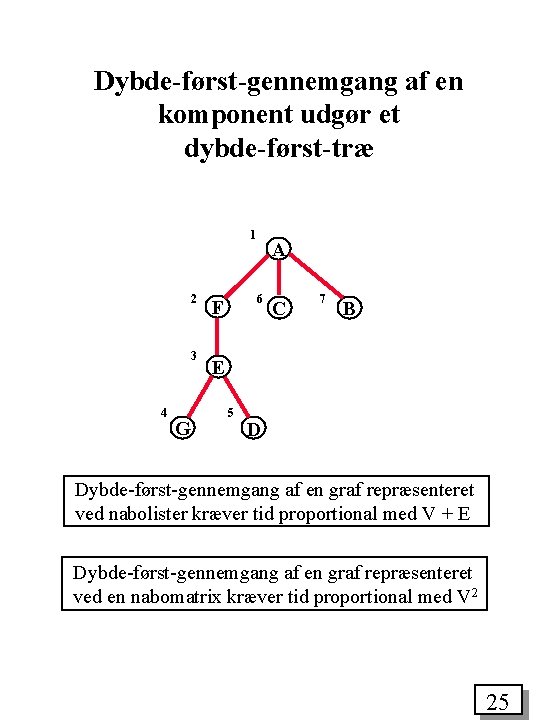
Dybde-først-gennemgang af en komponent udgør et dybde-først-træ 1 2 3 4 G A 6 F C 7 B E 5 D Dybde-først-gennemgang af en graf repræsenteret ved nabolister kræver tid proportional med V + E Dybde-først-gennemgang af en graf repræsenteret ved en nabomatrix kræver tid proportional med V 2 25

Ikke-rekursiv dybde-først-gennemgang Stack stack = new Stack(V); void visit(int k) { // adjacency lists stack. push(k); while (!stack. empty()) { k = stack. pop(); val[k] = ++id; for (Node t = adj[k]; t != z; t = t. next) if (val[t. v] == unseen) { stack. push(t. v); val[t. v] = -1; } } } Arrayet val benyttes til nummerering af knuderne i den rækkefølge, de besøges. Knuder med val-værdi -1 er på stakken (og dermed set), men er endnu ikke blevet besøgt. Knuder med val-værdi unseen (= 0) er endnu ikke set. 26

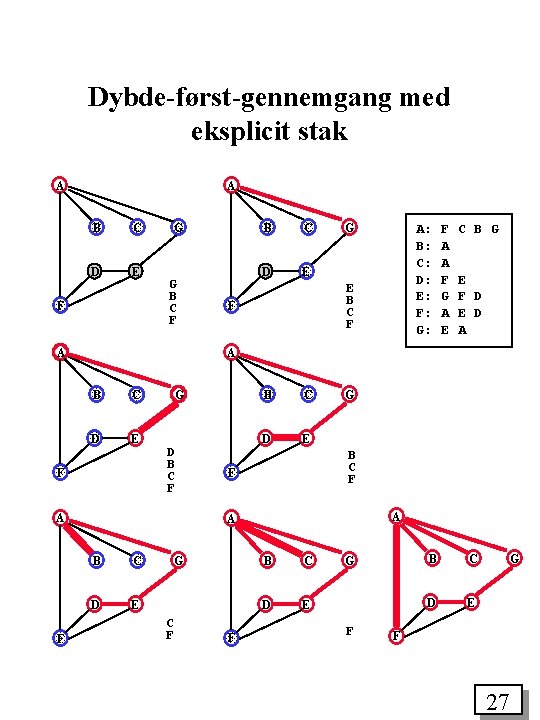
Dybde-først-gennemgang med eksplicit stak A A B C D E F G G B C F A C D E G A: B: C: D: E: F: G: E B C F F F A A F G A E C B G E F D E D A A B C D E F G D B C F A F B B C D E G B C F F A A B C D E G C F F B C D E G F 27

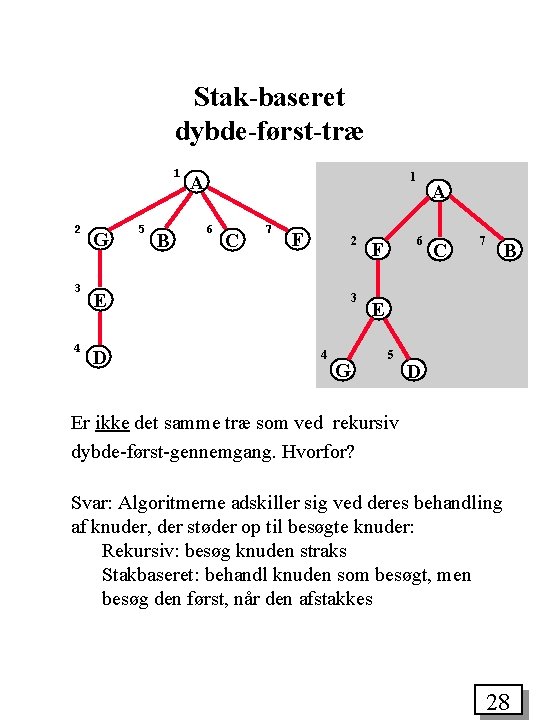
Stak-baseret dybde-først-træ 1 2 3 4 G 5 B 1 A 6 C 7 F 2 E D 3 4 G A 6 F C 7 B E 5 D Er ikke det samme træ som ved rekursiv dybde-først-gennemgang. Hvorfor? Svar: Algoritmerne adskiller sig ved deres behandling af knuder, der støder op til besøgte knuder: Rekursiv: besøg knuden straks Stakbaseret: behandl knuden som besøgt, men besøg den først, når den afstakkes 28

Alternativ ikke-rekursiv dybde-først-gennemgang void visit(int k) { // adjacency lists stack. push(k); val[k] = ++id; while (!stack. empty()) { k = stack. peek(); Node t; for (t = adj[k]; t != z && val[t. v] != unseen; t = t. next) ; if (t == z) stack. pop(); else { k = t. v; stack. push(k); val[k] = ++id; } } } Stakkens benyttes til at huske de knuder, der har ført til den aktuelle knude. Besøgsrækkefølgen er den samme som ved den rekursive udgave af visit. 29

Bredde-først-gennemgang Hvis stakken erstattes med en kø, fremkommer bredde-først-gennemgang. void visit(int k) { // adjacency lists queue. put(k); while (!queue. empty()) { k = queue. get(); val[k] = ++id; for (Node t = adj[k]; t != z; t = t. next) if (val[t. v] == unseen) { queue. put(t. v); val[t. v] = -1; } } } 30

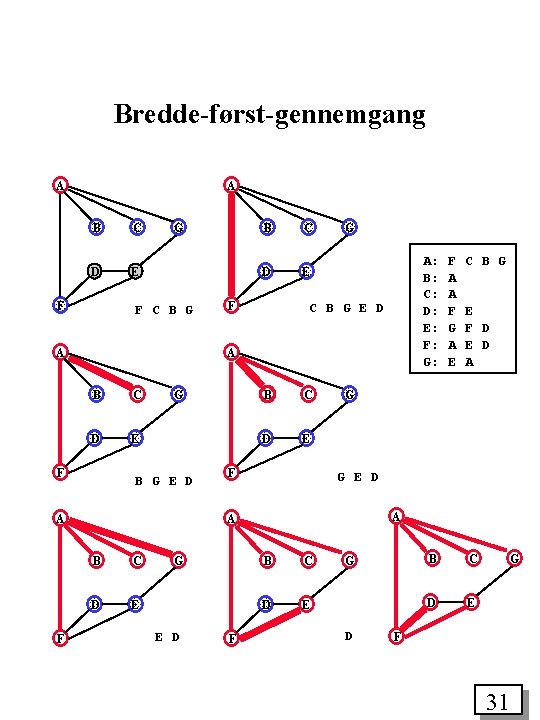
Bredde-først-gennemgang A A B C D E F G F C B G A C D E F G A: B: C: D: E: F: G: C B G E D A B C D E F G B G E D A F B B C D E F C D E G E D F C B G E F D E D A G G E D A A B F A A F G A E B C D E G D B C D E G F 31

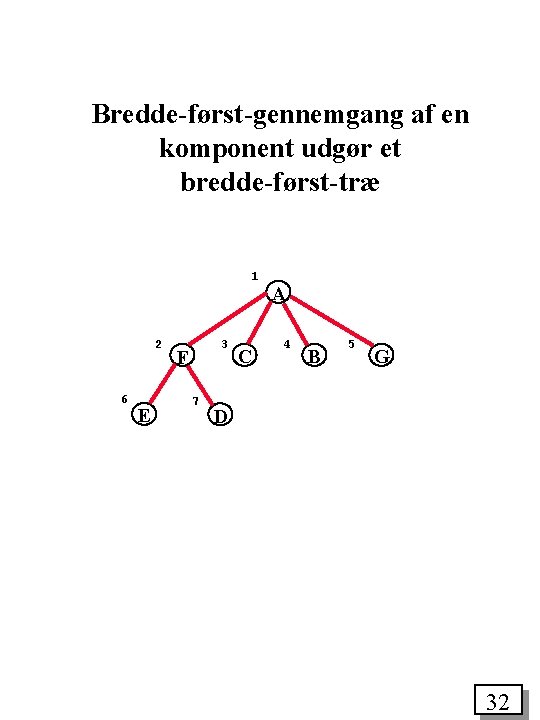
Bredde-først-gennemgang af en komponent udgør et bredde-først-træ 1 2 6 E 3 F 7 C A 4 B 5 G D 32

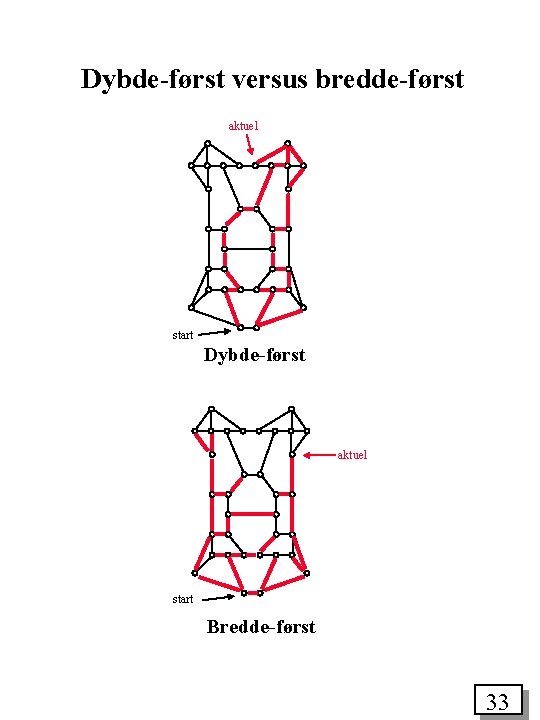
Dybde-først versus bredde-først aktuel start Dybde-først aktuel start Bredde-først 33

Sammenhæng Dybde-først-gennemgang kan benyttes til at finde grafens sammenhængende komponenter. Hver gang visit kaldes fra search, besøges samtlige knuder i en sammenhængende komponent. Dybde-først-gennemgang kan også benyttes til at afgøre om en graf er 2 -sammenhængende. En graf siges at være 2 sammenhængende, hvis der ikke findes nogen knude, hvor en sletning medfører en usammenhængende graf. Et knude i en sammenhængende graf kaldes et artikulationspunkt, hvis en sletning af knuden medfører, at grafen opdeles i 2 eller flere sammenhængende komponenter. En 2 -sammenhængende graf er en graf uden artikulationspunkter. 34

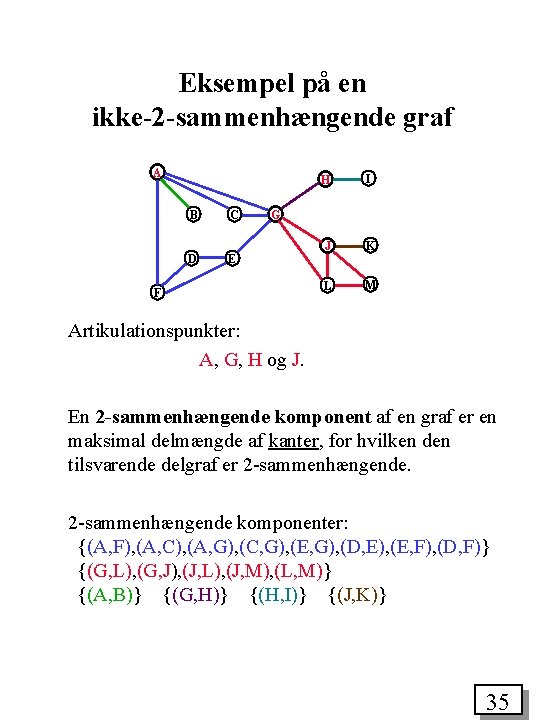
Eksempel på en ikke-2 -sammenhængende graf A B C D E H I J K L M G F Artikulationspunkter: A, G, H og J. En 2 -sammenhængende komponent af en graf er en maksimal delmængde af kanter, for hvilken den tilsvarende delgraf er 2 -sammenhængende komponenter: {(A, F), (A, C), (A, G), (C, G), (E, G), (D, E), (E, F), (D, F)} {(G, L), (G, J), (J, L), (J, M), (L, M)} {(A, B)} {(G, H)} {(H, I)} {(J, K)} 35

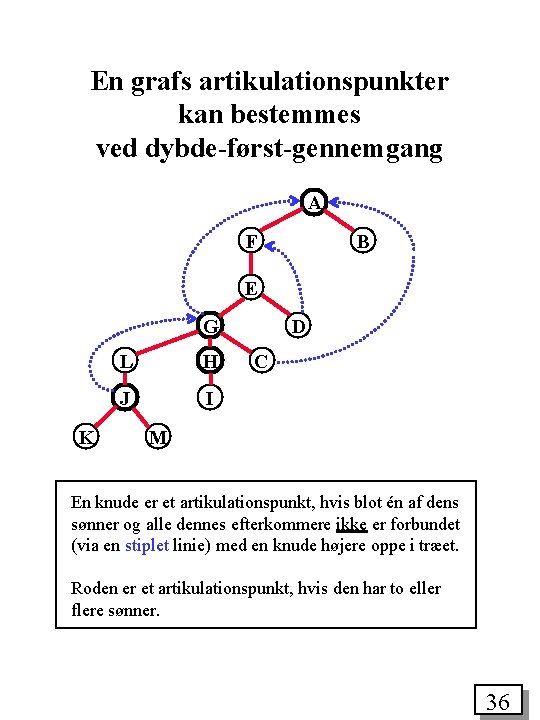
En grafs artikulationspunkter kan bestemmes ved dybde-først-gennemgang A F B E G K L H J I D C M En knude er et artikulationspunkt, hvis blot én af dens sønner og alle dennes efterkommere ikke er forbundet (via en stiplet linie) med en knude højere oppe i træet. Roden er et artikulationspunkt, hvis den har to eller flere sønner. 36

Ændring af metoden visit Metoden returnerer det mindste val-værdi for sete og besøgte knuder (knuden nærmest roden). Artikulationspunkterne udskrives undervejs. int visit(int k) { Node t; val[k] = ++id; int min = id; for (t = adj[k]; t != z; t = t. next) if (val[t. v] == unseen) { int m = visit(t. v); if (m < min) min = m; if (m >= val[k]) IO. println(name(k)); } else if (val[t. v] < min) min = val[t. v]; return min; } Test på rod udeladt 37

Bestemmelse af 2 -sammenhængende komponenter (opgave 30. 4 i lærebogen) Klassen Edge indføres: class Edge { int v 1, v 2; Edge(int a, int b) { v 1 = a; v 2 = b; } public boolean equals(Object o) { Edge e = (Edge) o; return (v 1 == e. v 1 && v 2 == e. v 2) || (v 1 == e. v 2 && v 2 == e. v 1); } public String to. String() { return "(" + name(v 1) + ", " + name(v 2) + ")"; } } Dernæst ændres metoden visit. En stak benyttes til at bestemme de 2 -sammenhængende komponenter. 38

int visit(int k) { val[k] = ++id; int min = id; for (Node t = adj[k]; t != z; t = t. next) { Edge e = new Edge(k, t. v); if (!stack. contains(e)) stack. push(e); if (val[t. v] == unseen) { int m = visit(t. v); if (m < min) min = m; if (m >= val[k]) { Edge x; do { x = (Edge) stack. pop(); IO. print(x + " "); } while (!x. equals(e)); IO. println(); } } else if (val[t. v] < min) min = val[t. v]; } return min; } 39

Repræsentation af 2 sammenhængende komponenter int visit(int k, Vector components) {. . . if (m >= val[k]) { Vector component = new Vector(); Edge x; do { x = (Edge) stack. pop(); component. add. Element(x); } while (!x. equals(e)); components. add. Element(component); }. . . } 40

Foren-og-find (ækvivalensklasser, komponenter) public class EQ { private int dad[]; EQ(int size) { dad = new int[1+size]; } public boolean find(int x, int y, boolean doit) { int i = x, j = y; while (dad[i] > 0) i = dad[i]; while (dad[j] > 0) j = dad[j]; if (doit && i != j) dad[j] = i; return (i != j); } } Princip: hver ækvivalensklasse repræsenteres som et træ. 41

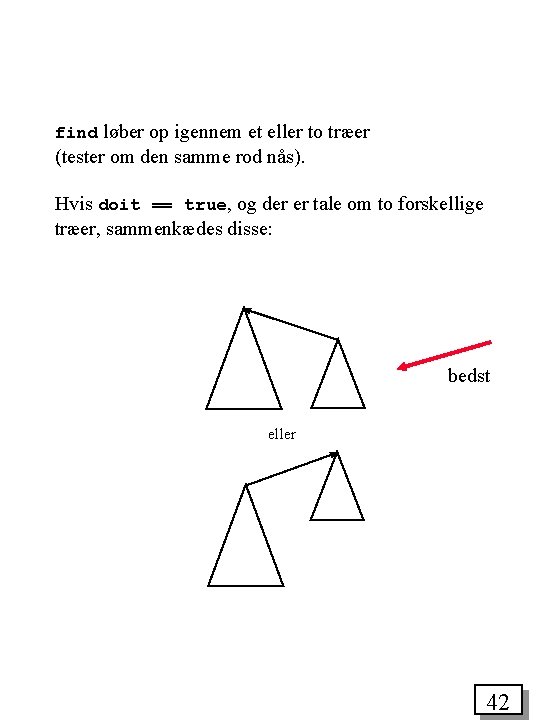
find løber op igennem et eller to træer (tester om den samme rod nås). Hvis doit == true, og der er tale om to forskellige træer, sammenkædes disse: bedst eller 42

Forbedret find public boolean find(int x, int y, boolean doit) { int t, i = x, j = y; while (dad[i] > 0) i = dad[i]; while (dad[j] > 0) j = dad[j]; // path compression while (dad[x] > 0) { t = x; x = dad[x]; dad[t] = i; } while (dad[y] > 0) { t = y; y = dad[y]; dad[t] = j; } if (doit && i != j) // weight balancing if (dad[j] < dad[i]) { dad[j] += dad[i] - 1; dad[i] = j; } else { dad[i] += dad[j] - 1; dad[j] = i; } return (i != j); } 43

Alternativ implementering int find(int p) { return dad[p] == p ? p : (dad[p] = find(dad[p])); } void union(int p, int q) { int i = find(p), j = find(q); if (i == j) return; if (size[i] < size[j]) { dad[i] = dad[p] = j; size[j] += size[i]; } else { dad[j] = dad[q] = i; size[i] += size[j]; } } 44

Ugeseddel 9 11. november - 17. november • Læs kapitel 31 og 32 i lærebogen (side 451 -481) • Løs følgende opgaver 1. Opgave 29. 1 og 29. 5. 2. Opgave 30. 1 og 30. 2. 45