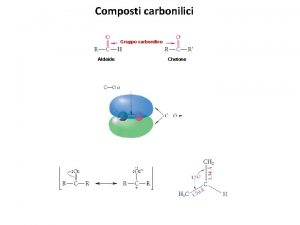
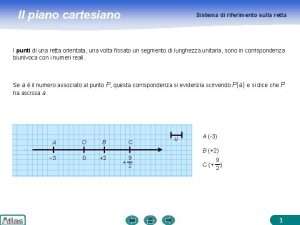
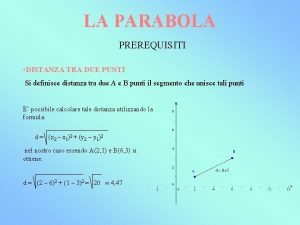
Teoria dei gruppi Simmetria di punto 1 Definizione

Teoria dei gruppi Simmetria di punto 1

Definizione di gruppo • In un insieme di elementi esiste una legge di moltiplicazione tale che se X e Y appartengono all’insieme allora Z=X. Y appartiene all’insieme • Esiste un elemento E tale che E. X=X. E per ogni X • Vale la proprietà associativa Z. (Y. X)=(Z. Y). X • Ogni elemento ha il suo inverso X-1=Y tale che Y. X=X. Y=E 2

Un esempio • Verificare che l’insieme dei numeri interi, positivi e negativi, incluso lo 0, costituiscono un gruppo rispetto all’addizione • 1, -1, i, -i • Numeri razionali 0 escluso 3

Ancora sui gruppi • Il numero di elementi dà l’ordine del gruppo. Gruppi finiti e gruppi infiniti • Il gruppo è commutativo (Abeliano) se per ogni coppia di elementi XY=YX. • Il gruppo è ciclico se tutti gli elementi sono ottenuti elevando una data operazione a potenza X, X 2, X 3…. • Un sottogruppo è un sottoinsieme di un gruppo che forma un gruppo di per sé 4

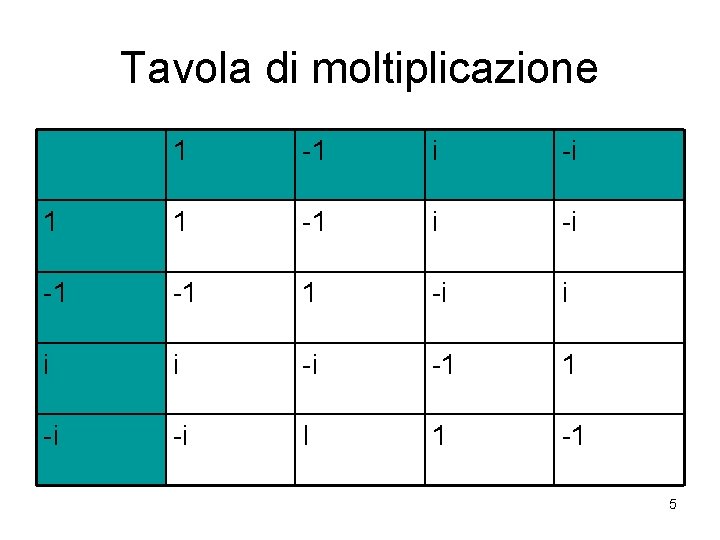
Tavola di moltiplicazione 1 -1 i -i 1 1 -1 i -i -1 -1 1 -i i -i -1 1 -i -i I 1 -1 5

Generatori di un gruppo • Un gruppo può venire generato da un insieme di elementi detti generatori • i o -i 6

Classi di un gruppo • A e B sono coniugati se esiste un C tale che A=CBC-1 • L’insieme di operazioni mutuamente coniugate costituisce una classe 7

Gruppi di simmetria • Operazioni di simmetria • Elementi di simmetria 8

An Example of the use of Symmetry Florence, The Baptistry 9

E di rottura della simmetria 10

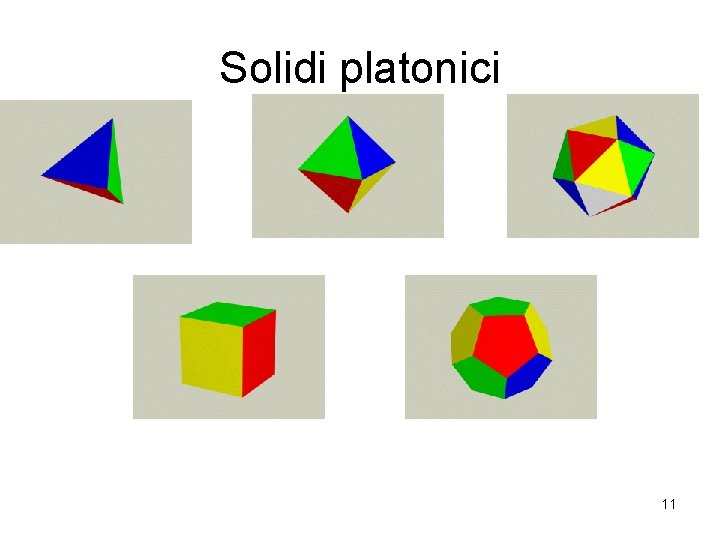
Solidi platonici 11

FULLERENE C 60 Questa nanostruttura, con dimensioni minime di 1 nm, è la capostipite molecolare dei composti a base di carbonio. . 12

Giant Molecular Antiferromagnets: Fe 30 Icosidodecaedro 13

The ferric wheel S. Lippard 14

15

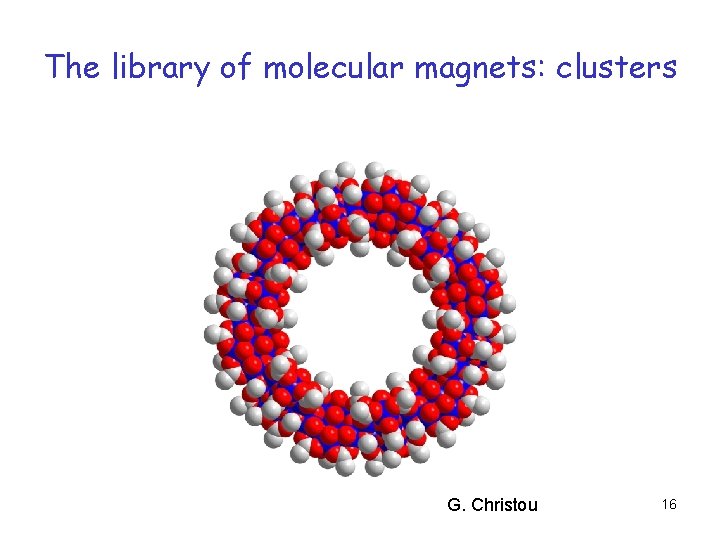
The library of molecular magnets: clusters G. Christou 16

Simmetrie dispari 17

18

19

20

21

Why symmetry? So our problem is to explain where symmetry comes from. Why is Nature so nearly symmetrical? No one has an idea why. The only thing we might suggest is something like this: There is a gate in Japan, a gate in Neiko, which is sometimes called by the Japanese the most beautiful gate in all Japan; it was built in a time when there was freat influence from the chinese art. The gate is very elaborate, with lots of gables and beautiful carving and lots of columns and dragon heads and princes carved ito the pillars, and so on. But when one looks closely he sees that in the elaborate and complex design along one of the pillars, one of the small design elements is carved upside down; otherwise thing is completely symmetrical. If one asks why this is, the story is that it was carved upside down so that the gods will not be jealous of the perfection of man. So they purposely put an error in there. So that the gods would not be jealous and get angry with human beings. We might like to turn the idea around and think that the true explanation of the near symmetry nature us this: that God made the lows only nearly symmetrical so that we should not be jealous of His perfection! The Feynmann Lectures on Physics 22

Simmetria • • • Simmetria di punto Simmetria traslazionale Elementi di simmetria Operazioni di simmetria Gruppi di simmetria 23

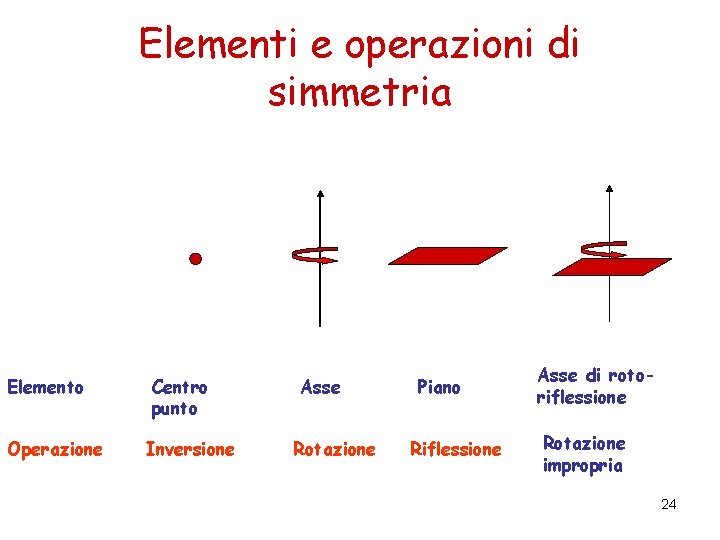
Elementi e operazioni di simmetria Elemento Operazione Centro punto Inversione Asse Rotazione Piano Riflessione Asse di rotoriflessione Rotazione impropria 24

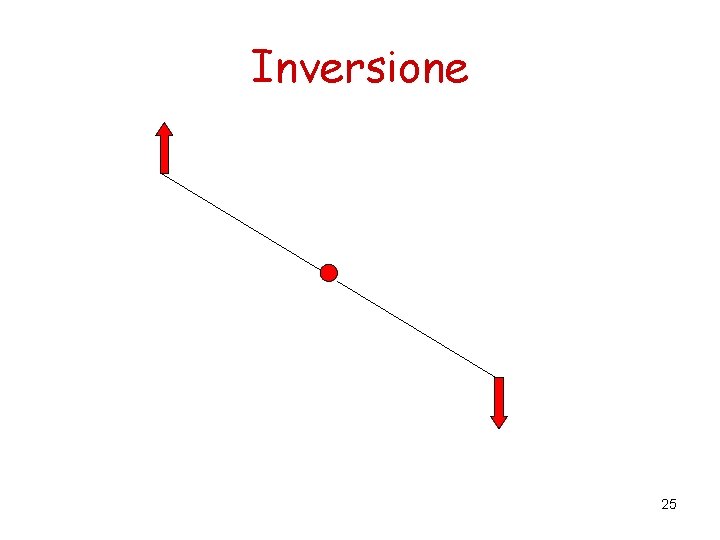
Inversione 25

26

Riflessione 27

28

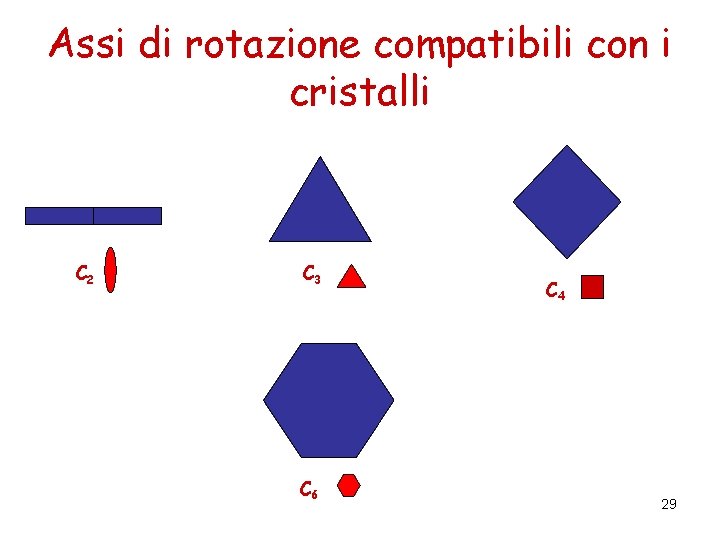
Assi di rotazione compatibili con i cristalli C 2 C 3 C 6 C 4 29

30

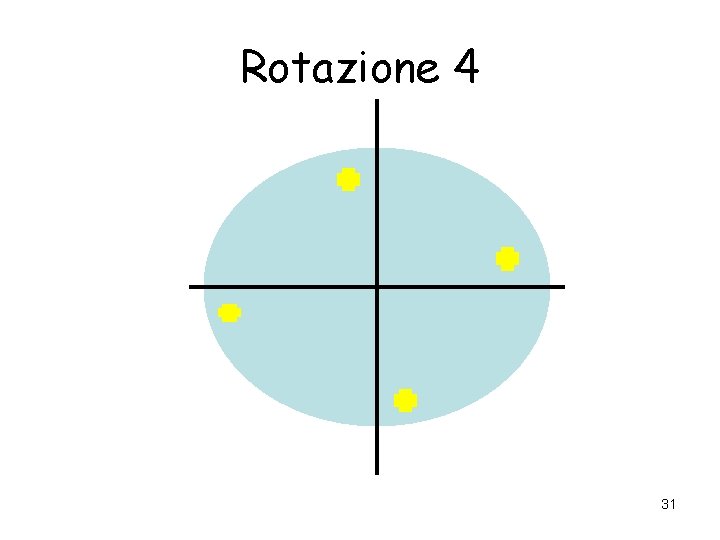
Rotazione 4 31

Se c’è un asse di ordine n quante rotazioni posso fare? 32

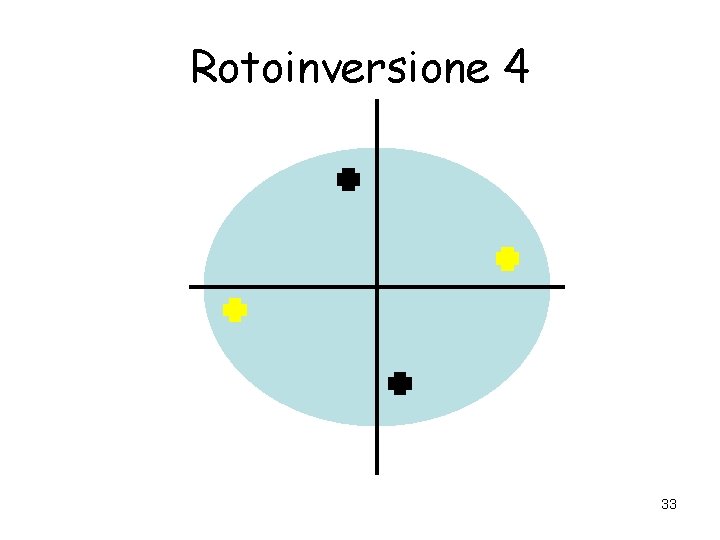
Rotoinversione 4 33

Gruppi di simmetria • Il prodotto di due operazioni corrisponde a effettuare le due operazioni una di seguito all’altra • Il prodotto di due operazioni è un’operazione del gruppo • Esiste un elemento neutro, E, tale che applicato a R lo lasci inalterato • Per ogni R del gruppo esiste R-1 tale che R. R-1=R-1. R= E 34

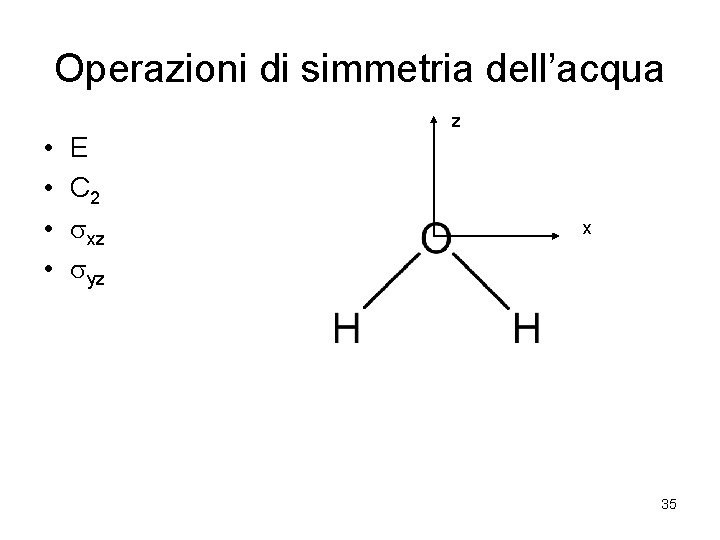
Operazioni di simmetria dell’acqua z • • E C 2 xz yz x 35

36

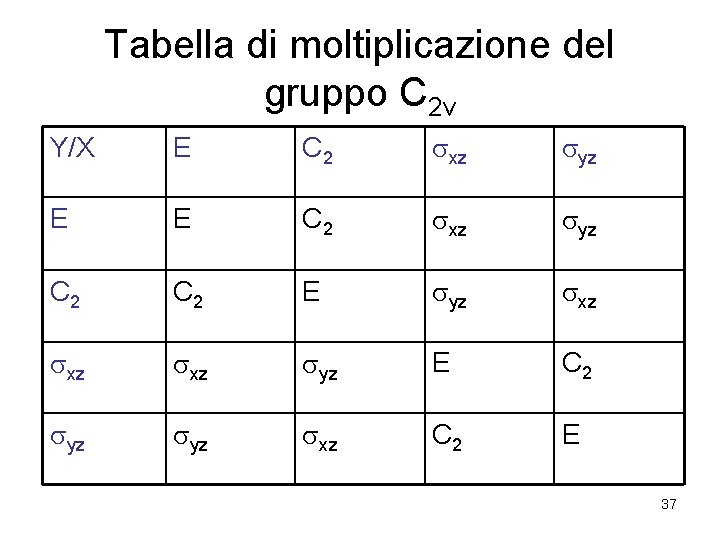
Tabella di moltiplicazione del gruppo C 2 v Y/X E C 2 xz yz E E C 2 xz yz C 2 E yz xz xz yz E C 2 yz xz C 2 E 37

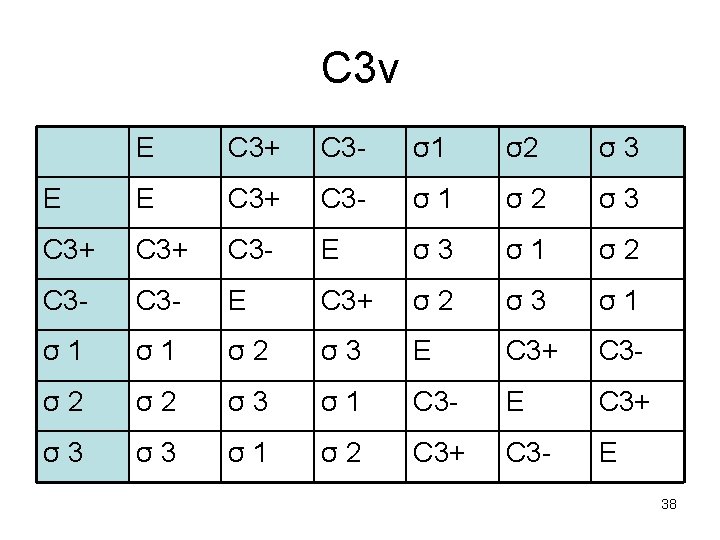
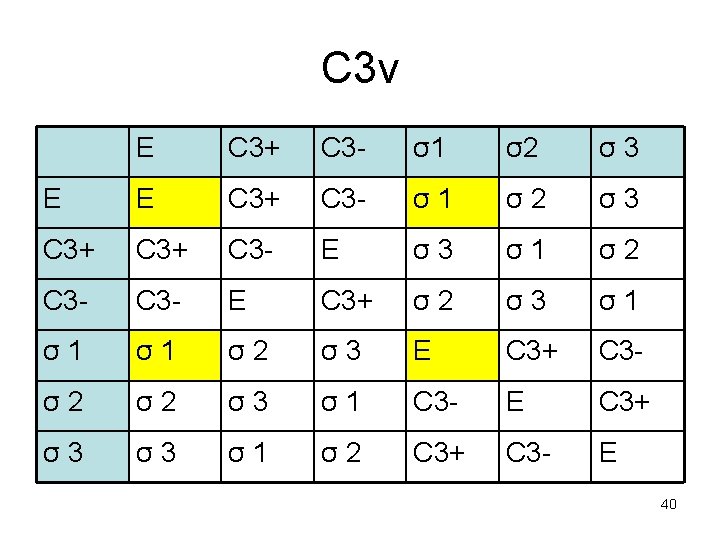
Sottogruppi di C 3 v • • (E, C 3+, C 3 -) (E, 1) (E, 2) (E, 3) 43

Classi di un gruppo • A e B sono coniugate se esiste una C tale che A=CBC-1 • L’insieme di operazioni mutuamente coniugate costituisce una classe • il gruppo C 2 v ha 4 classi • Il gruppo C 3 v ne ha 3: E, 2 C 3, 3σv 44

Tipi di gruppo di simmetria • Gruppi ciclici: asse di ordine n, Cn o Sn • Gruppi diedrici : asse di ordine n+ piano ortogonale Cnh • Gruppi diedrici: asse Cn + piano passante, Cnv • Gruppi diedrici: asse di ordine n + asse binario ortogonale, Dn • Gruppi diedrici: asse di ordine n + asse binario ortogonale + piano che biseca assi binari, Dnd • Gruppi diedrici: asse di ordine n + asse binario ortogonale+ piano ortogonale, Dnh 45

Gruppi cubici • Tre assi binari perp. facce cubo+ 4 assi ternari, T • Come T + inversione, Th • quattro assi ternari + tre S 4, Td • Quattro assi ternari+ 4 assi tetragonali, O • O+ inversione, Oh 46

Gruppi di punto • • • Gruppi di rotazione Cn Gruppi di rotoriflessione S 2 n Gruppi Cnh Gruppi Cnv Gruppi diedrici Dn Gruppi Dnh Gruppi Dnd Gruppi cubici T, Td, Th, O, Oh Gruppi icosaedrici I, Ih 47

48

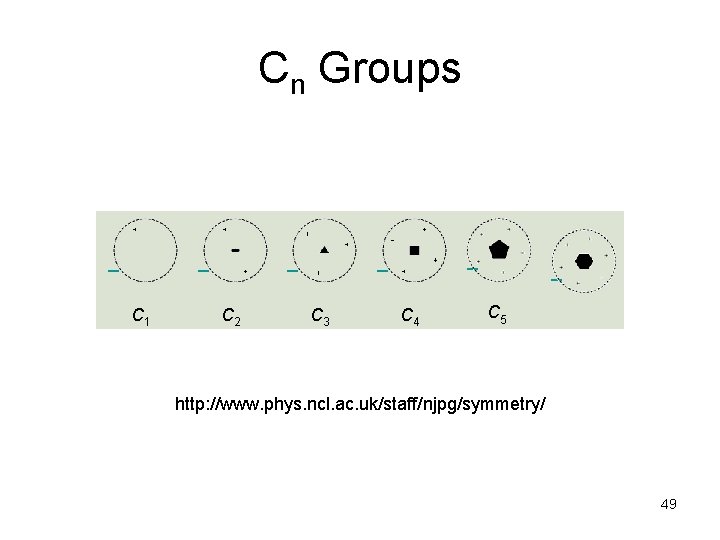
Cn Groups C 1 C 2 C 3 C 4 C 5 http: //www. phys. ncl. ac. uk/staff/njpg/symmetry/ 49

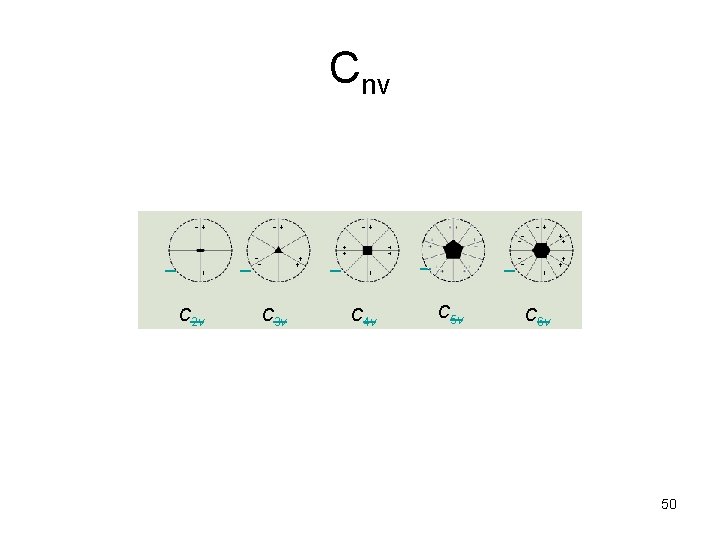
Cnv C 2 v C 3 v C 4 v C 5 v C 6 v 50

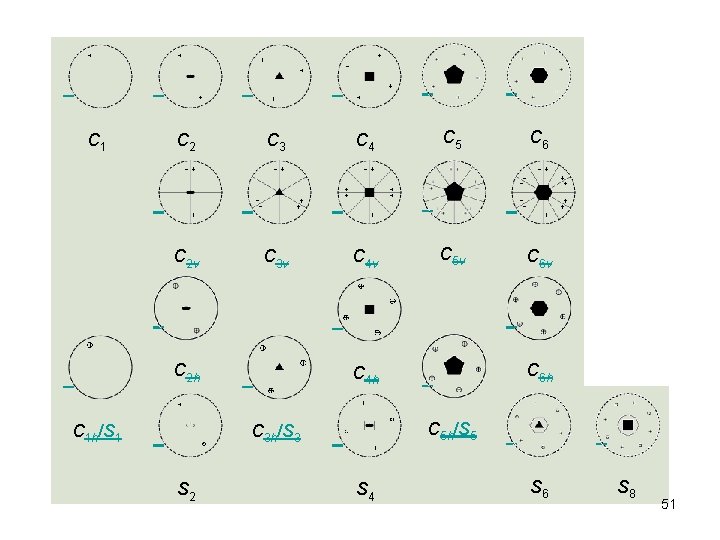
C 1 C 2 C 3 v C 1 h/S 1 C 5 C 6 C 2 v C 4 C 2 h S 2 C 4 v C 5 v C 3 h/S 3 C 4 h S 4 C 6 v C 5 h/S 5 C 6 h S 6 S 8 51

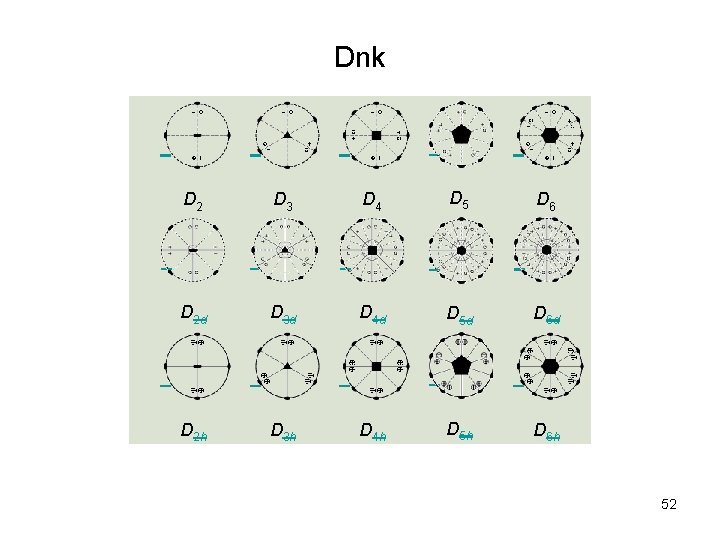
Dnk D 2 D 3 D 4 D 5 D 6 D 2 d D 3 d D 4 d D 5 d D 6 d D 2 h D 3 h D 4 h D 5 h D 6 h 52

C 1 C 2 v Cs C 3 C 4 C 6 C 3 v C 4 v C 6 v C 2 h Ci C 3 h C 4 h C 6 h S 4 S 6 53

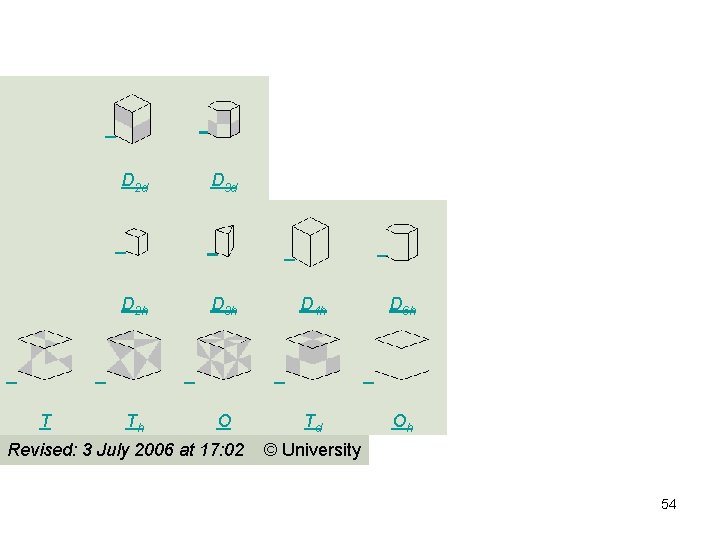
D 2 d D 3 d D 2 h D 3 h D 4 h D 6 h T Th O Revised: 3 July 2006 at 17: 02 Td Oh © University 54

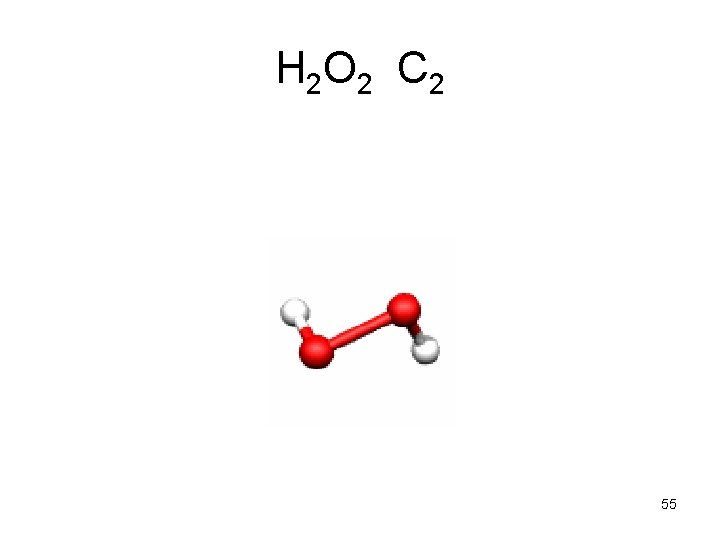
H 2 O 2 C 2 55

56

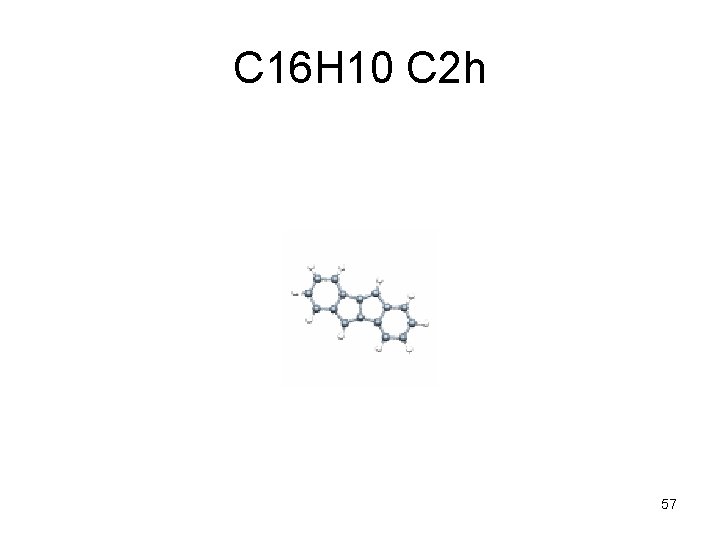
C 16 H 10 C 2 h 57

HCN Cinfv 58

59

60

Rappresentazioni di un gruppo • Dato un vettore a n componenti possiamo associare ad ogni operazione R del gruppo G una matrice D( R) che descrive le trasformazioni del vettore • L’insieme delle matrici costituisce un gruppo che ha la stessa tabella di moltiplicazione di G • Si è fatto una rappresentazione del gruppo G • La dimensione della rappresentazione è n 61

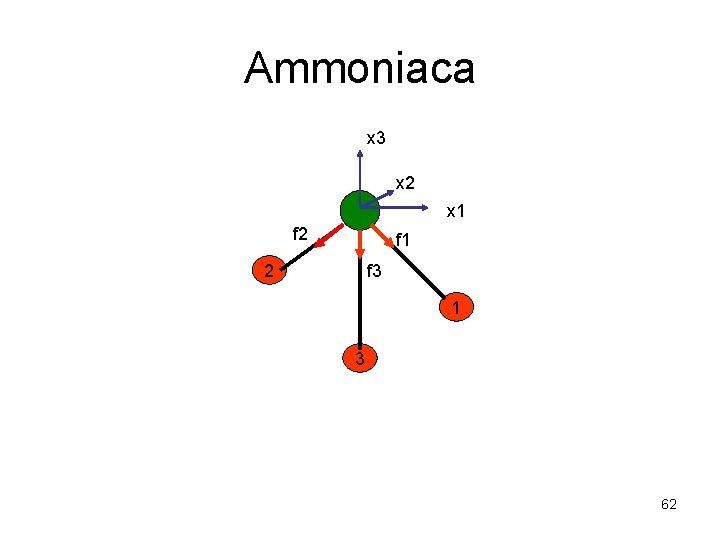
Ammoniaca x 3 x 2 x 1 f 2 f 1 f 3 2 1 3 62

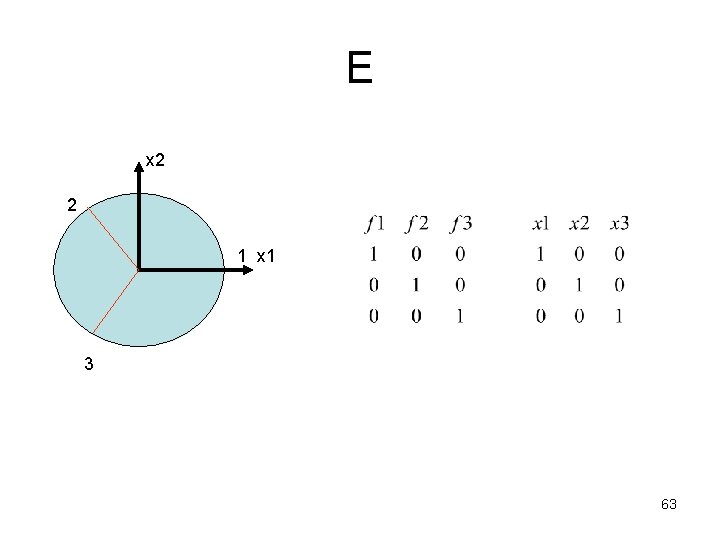
E x 2 2 1 x 1 3 63

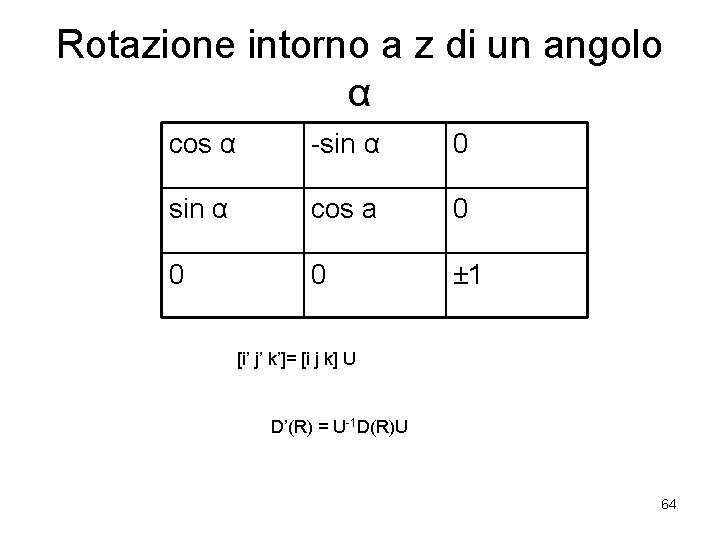
Rotazione intorno a z di un angolo α cos α -sin α 0 sin α cos a 0 0 0 ± 1 [i’ j’ k’]= [i j k] U D’(R) = U-1 D(R)U 64

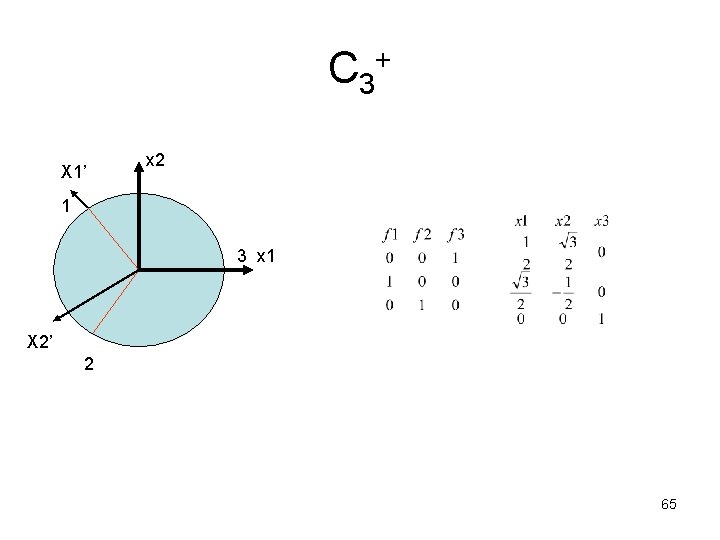
C 3+ X 1’ x 2 1 3 x 1 X 2’ 2 65

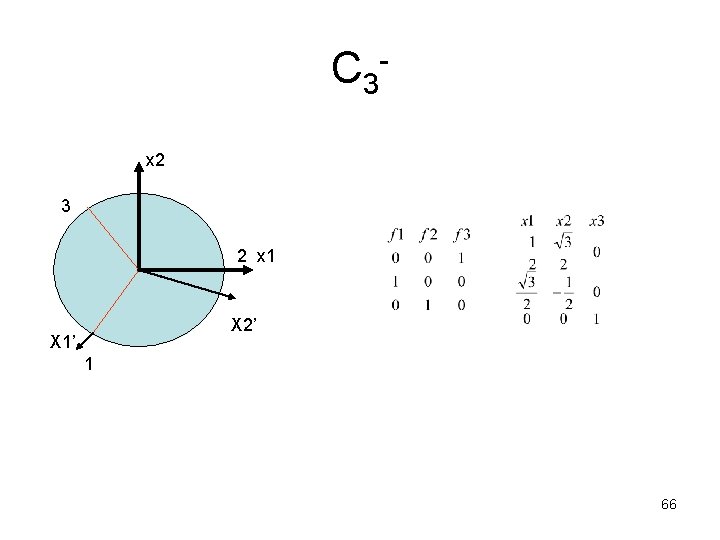
C 3 x 2 3 2 x 1 X 2’ X 1’ 1 66

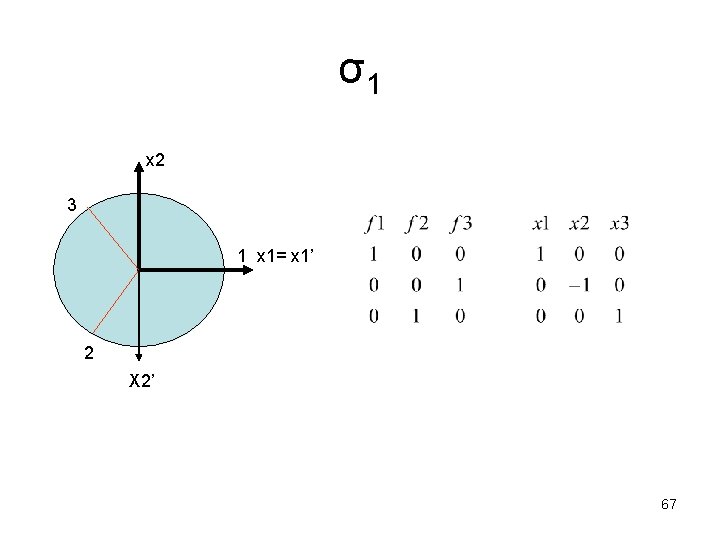
σ1 x 2 3 1 x 1= x 1’ 2 X 2’ 67

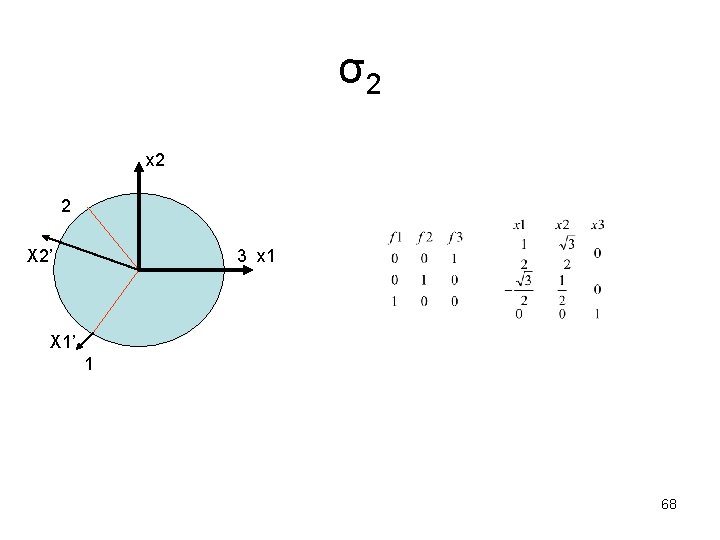
σ2 x 2 2 X 2’ 3 x 1 X 1’ 1 68

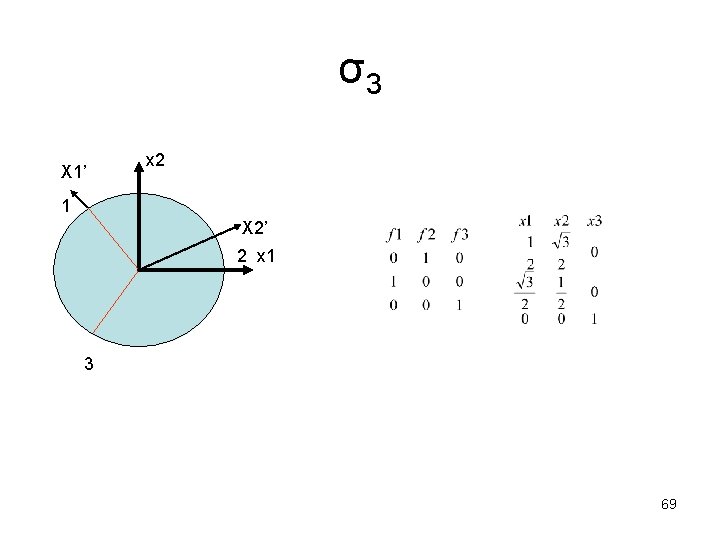
σ3 X 1’ x 2 1 X 2’ 2 x 1 3 69

Rappresentazioni riducibili ed irriducibili • La rotazione del sistema di coordinate (o il cambiamento della base) induce una trasformazione di similitudine delle matrici della rappresentazione • La nuova rappresentazione è equivalente a quella di partenza • Se le matrici sono diagonali a blocchi si scinde la rappresentazione di partenza in una somma di rappresentazioni di dimensioni più piccole • Il processo può continuare fino a che si raggiungono le dimensioni minime compatibili col gruppo G: rappresentazioni irriducibili 70

Somma diretta E C 3+ C 3 - σ1 σ2 σ3 71

Teorema di ortogonalità h è l’ordine del gruppo Gα è la dim. della RI D sono rappresentazoni irriducibili La somma è su tutte le operazioni del gruppo 72

Significato del teorema di ortogonalità • Si può leggere come il prodotto scalare tra due vettori in uno spazio di dimensioni h • Le componenti del vettore sono gli elementi di una data matrice • In un spazio h dimensionale si possono avere solo h vettori linearmente indipendenti 73

Ancora rappresentazioni irriducibili • Il numero di RI di un gruppo G è uguale al numero di classi • La somma dei quadrati delle RI è uguale alle dimensioni del gruppo: Σigi 2=h 74

I caratteri h è l’ordine del gruppo Si somma sugli elementi diagonali per ricavare la traccia o carattere 75

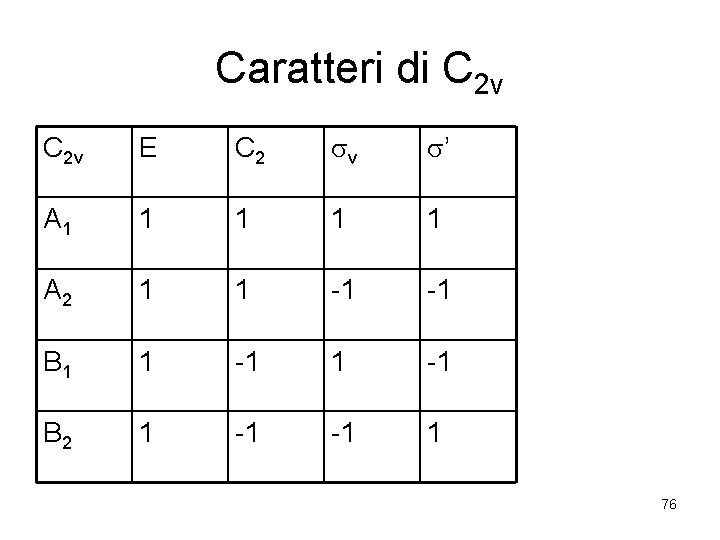
Caratteri di C 2 v E C 2 v ’ A 1 1 1 A 2 1 1 -1 -1 B 1 1 -1 B 2 1 -1 -1 1 76

Caratteri di C 3 v E 2 C 3 3 v Basi d A 1 1 z z 2 A 2 1 1 -1 Rz E 2 -1 0 x, y; Rx, Ry x 2 -y 2 , xy; xz, yz 77

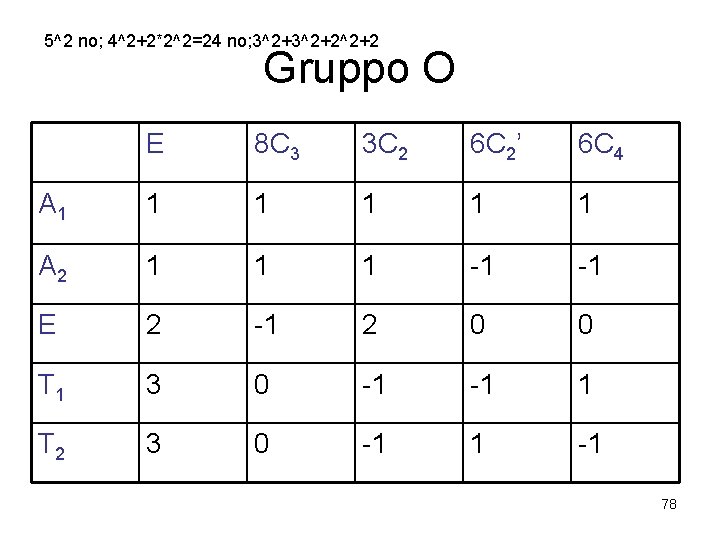
5^2 no; 4^2+2*2^2=24 no; 3^2+2^2+2 Gruppo O E 8 C 3 3 C 2 6 C 2’ 6 C 4 A 1 1 1 A 2 1 1 1 -1 -1 E 2 -1 2 0 0 T 1 3 0 -1 -1 1 T 2 3 0 -1 1 -1 78

Tabelle dei caratteri • Le rappresentazioni sono caratterizzate dal valore dei caratteri (delle tracce) delle matrici • Il numero di volte che una RI, Γi, è contenuta in una certa RR è data da: • nΓi=[ΣCχΓi (C) χRR( C) n( C)]/g dove C sono le classi del gruppo, n( C) il numero di elementi della classe 79

Vantaggi della simmetria • Classificando le funzioni per simmetria è possibile trovare delle regole di selezione, quindi evitare il calcolo di integrali che sono nulli per simmetria 80

Funzioni adattate per simmetria • Data una certa base, che induce una rappresentazione riducibile, si può effettuare una rotazione di coordinate che dia luogo ad una rappresentazione irriducibile 81

Funzioni adattate per simmetria fΓi = ΣR χΓi (R) R f fΓi è la funzione adattata per simmetria f è una componente della base riducibile La somma è su tutte le operazioni R del gruppo G 82

Esercizi • RI della base f di NH 3 • RI orbitali s e p di N e s di H in NH 3 • Combinaz. Lineari adattate alla simmetria in NH 3 • Orbitali d in O 83

Prodotto diretto di gruppi • G, H siano due gruppi • L=Gx. H prodotto diretto Lij= Gi Hj • L è un gruppo se G=H o se gli elementi di H e G commutano • Provare che C 3 v e Ci danno D 3 d 84

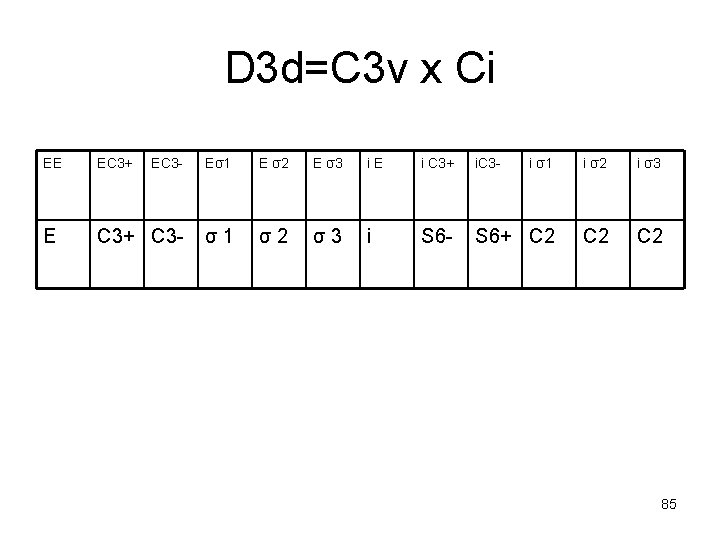
D 3 d=C 3 v x Ci EE EC 3+ EC 3 - Eσ1 E σ2 E σ3 i E E C 3+ C 3 - σ 1 σ 2 σ 3 i i C 3+ i. C 3 - i σ1 i σ2 i σ3 S 6 - S 6+ C 2 C 2 85

Prodotto diretto dei vettori l= fxg lij= fi gj D(L)= D(H)x D(G) 86

Carattere della rappresentazione del prodotto diretto all’interno dello stesso gruppo La totalsimmetrica si trova solo se α=β 87

Elementi di matrice e simmetria Se O è l’operatore Hamiltoniano è base per Γ 1. allora l’elemento di matrice è diverso da zero solo se Γi = Γk 88

Esercizi • Fare un diagramma degli orbitali molecolari di NH 3 • Sapendo che le transizioni elettroniche sono causate dal dipolo elettrico (si comporta come x, y, e z) spiegare perchè le transizioni nel visibile dei complessi dei metalli di transizione sono poco intense 89

Stati polielettronici 2 d 1 2 D d 2 3 F; 3 P; 1 G; 1 D; 1 S d 3 4 F; 4 P; 2 H; 2 G; 2 F; 2 D(2); 2 P d 4 5 D; 3 H; 3 G; 3 F(2); 3 D; 3 P(2); 1 I; 1 G(2); 1 F; 1 D(2); 1 S(2) d 5 6 S; 4 G; 4 F; 4 D; 4 P; 2 I; 2 H; 2 G(2); 2 F(2); 2 D(3), 2 P; 2 S Lo stato fondamentale è quello di massima molteplicità 90

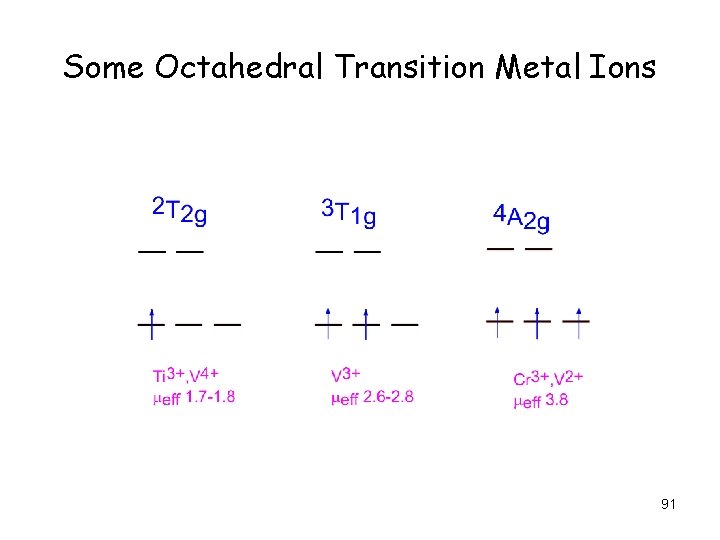
Some Octahedral Transition Metal Ions 91

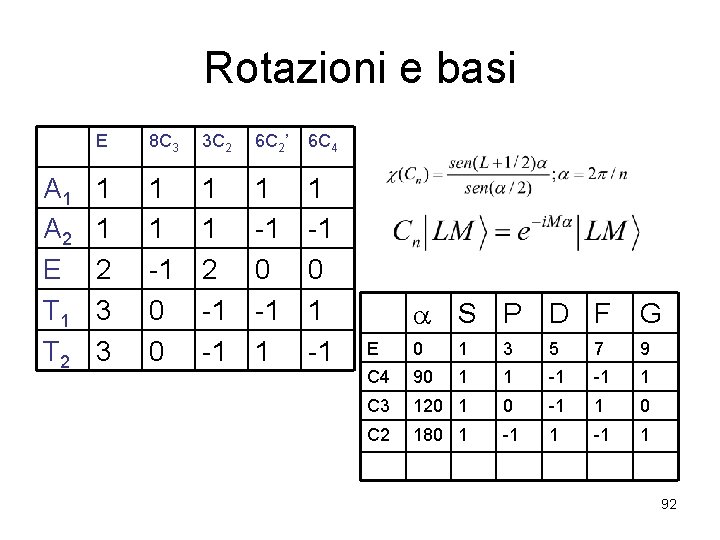
Rotazioni e basi A 1 A 2 E T 1 T 2 E 8 C 3 3 C 2 6 C 2’ 6 C 4 1 1 2 3 3 1 1 -1 0 0 1 1 2 -1 -1 0 -1 1 1 -1 0 1 -1 S P D F G E 0 1 3 5 7 9 C 4 90 1 1 -1 -1 1 C 3 120 1 0 -1 1 0 C 2 180 1 -1 1 92

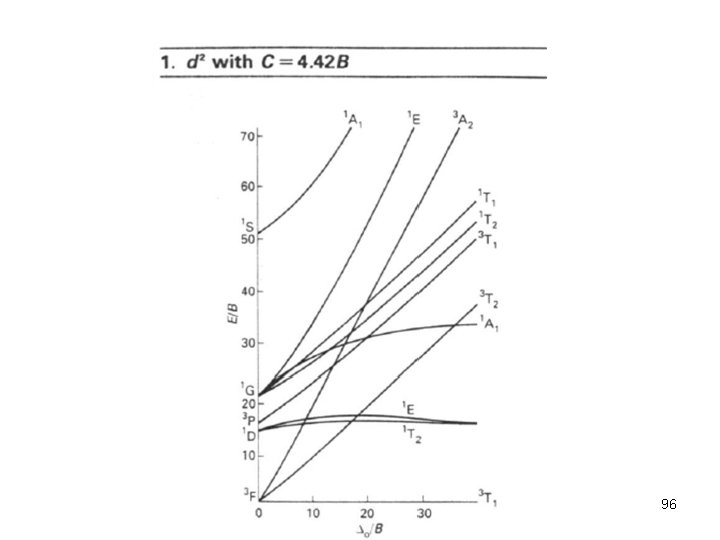
d 2 in O E 8 C 3 3 C 2 6 C 2’ 6 C 4 A 1 1 1 A 2 1 1 1 -1 -1 E -1 2 0 0 T 1 3 0 -1 -1 1 T 2 3 0 -1 1 -1 2 3 F→ 3 A 3 T , 3 T ; , 2 1 2 3 P→ 3 T 1 93

Campo forte 94

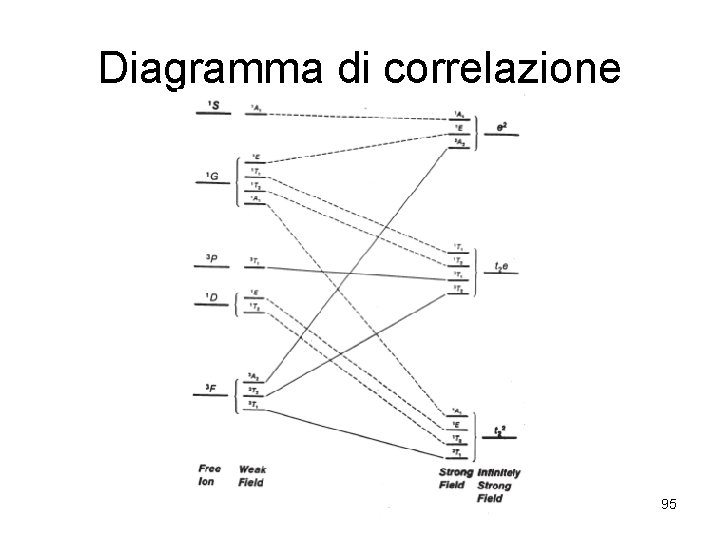
Diagramma di correlazione 95

96

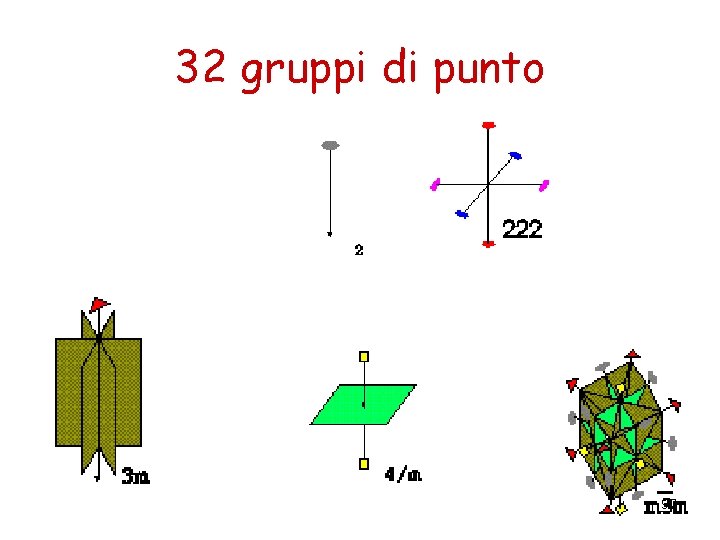
32 gruppi di punto 97

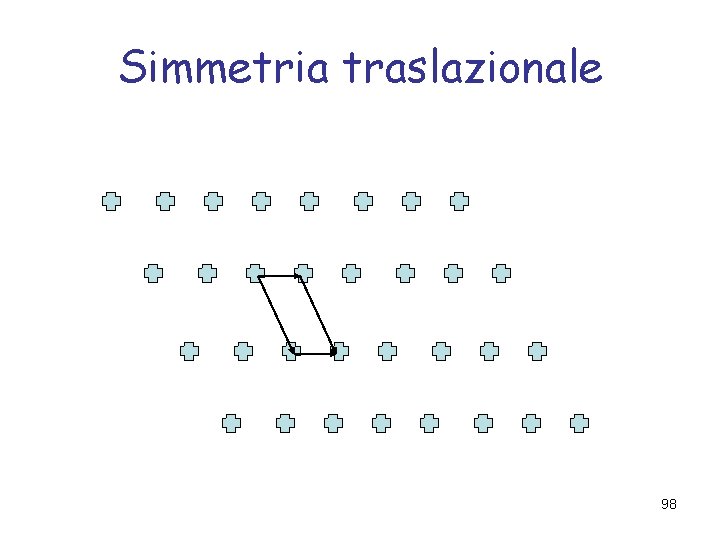
Simmetria traslazionale 98

99

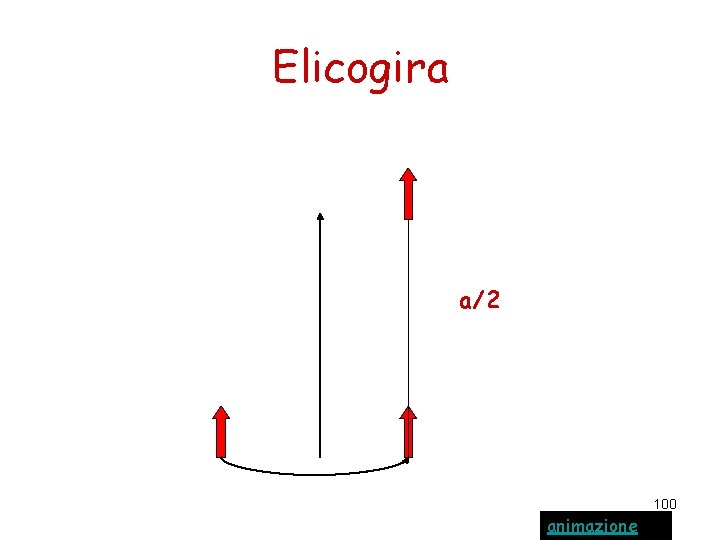
Elicogira a/2 100 animazione

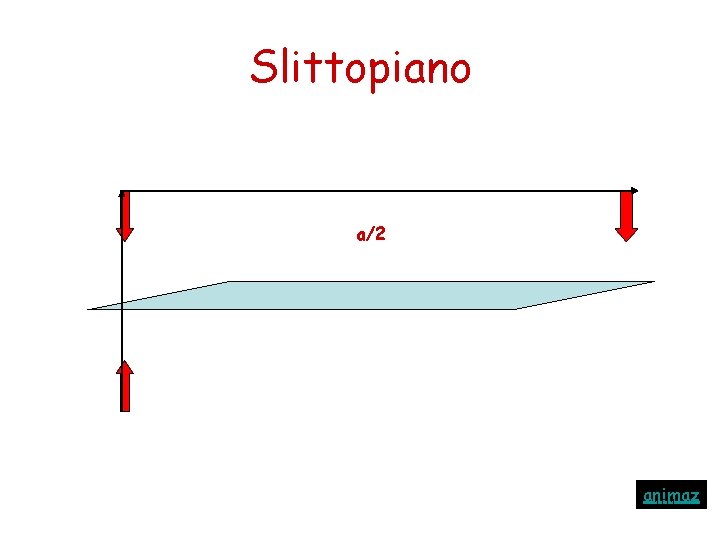
Slittopiano a/2 animaz 101

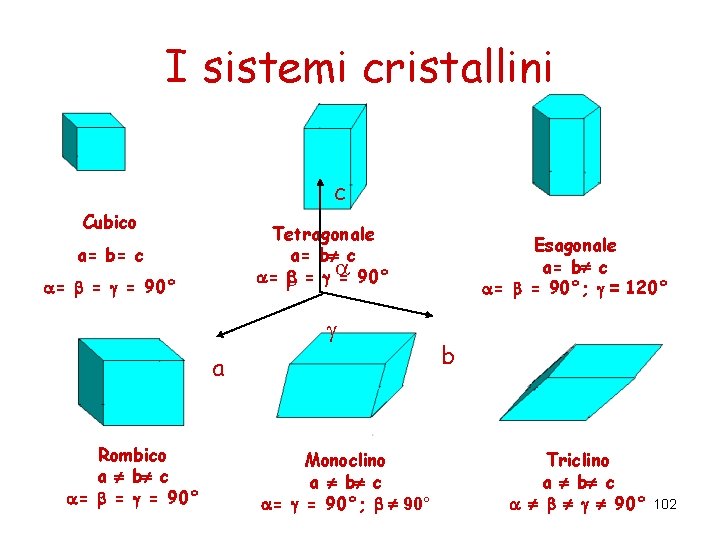
I sistemi cristallini c Cubico Tetragonale a= b c = = = 90° a= b= c = = = 90° a Rombico a b c = = = 90° Monoclino a b c = = 90°; 90° Esagonale a= b c = = 90°; = 120° b Triclino a b c 90° 102

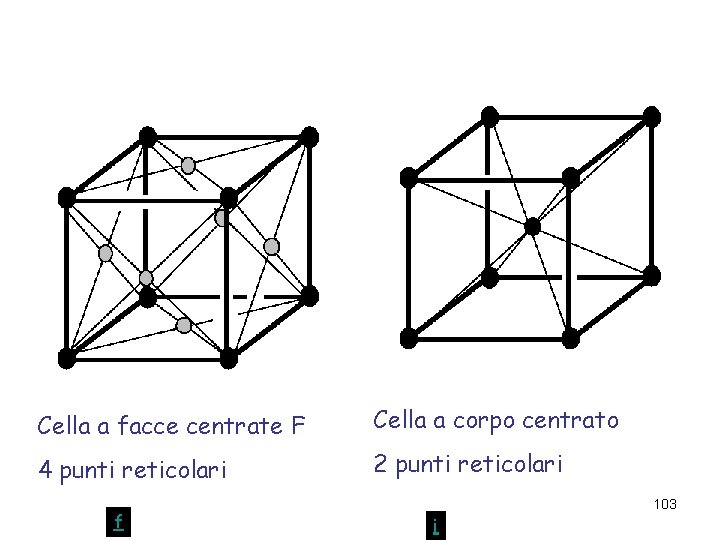
Cella a facce centrate F Cella a corpo centrato 4 punti reticolari 2 punti reticolari f 103 i

14 reticoli bravaisiani Triclino P Monoclino P, C Ortorombico P, C, I, F Tetragonale P, I Esagonale P Trigonale P Cubico P, I. F 104

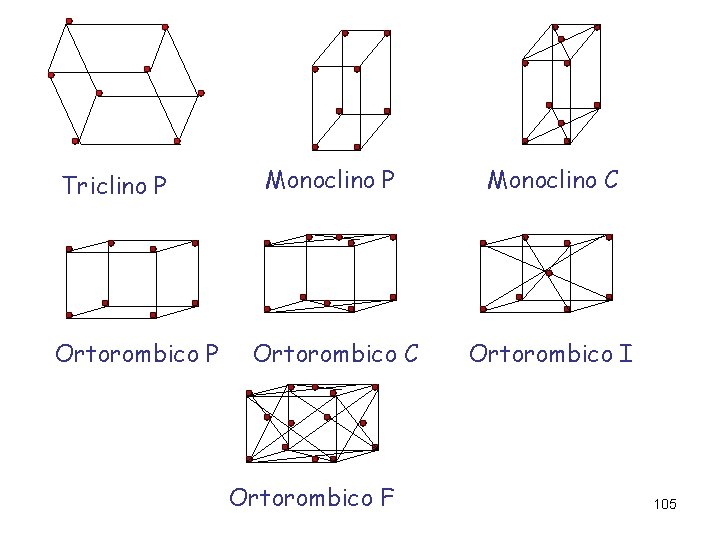
Triclino P Ortorombico P Monoclino C Ortorombico I Ortorombico F 105

230 gruppi spaziali 106

Un esempio 107

108

109

110

111

112