UNIDAD 6 CAPTULO IV PUNTOS ORDINARIOS Y PUNTOS

UNIDAD 6. CAPÍTULO IV. PUNTOS ORDINARIOS Y PUNTOS SINGULARES.

U-6. CAP. IV. PUNTOS ORDINARIOS Y PUNTOS SINGULARES. En la solución de ecuaciones diferenciales lineales con coeficientes variables, tales como: es necesario pensar en la solución cercana a un punto (alrededor de un punto) o la solución en la vecindad de un punto. Es decir, una ecuación coeficientes variables puede tener diferentes soluciones alrededor de diferentes puntos, o puede incluso no tener soluciones alrededor de algunos puntos.

U-6. CAP. IV. PUNTOS ORDINARIOS Y PUNTOS SINGULARES. Por tanto, es necesario especificar el intervalo o el punto alrededor del cual se requiere resolver una ecuación coeficientes variables. Como se verá, la solución de la ecuación alrededor de un punto no solo depende del punto mismo, sino también de la naturaleza o clase del punto con respecto a la ecuación diferencial. El método de resolución y la forma de la solución serán diferentes para diferentes clases de puntos. Por tanto, es necesario identificar qué clase de punto es, antes de resolver una ecuación dada alrededor de él.

U-6. CAP. IV. PUNTOS ORDINARIOS Y PUNTOS SINGULARES. Una ecuación de segundo orden coeficientes variables dada puede expresarse en la forma estándar dividiendo cada termino entre a(x). Toda explicación, definición o teorema será limitado, por su sencillez, a ecuaciones de segundo orden; sin embargo, puede extenderse a ecuaciones de orden superior. Un punto x 0 puede denominarse ordinario o singular, dependiendo del comportamiento de los coeficientes P(x) y Q(x) de la ecuación diferencial en ese punto.

U-6. CAP. IV. PUNTOS ORDINARIOS Y PUNTOS SINGULARES. Un punto x 0 se llama punto ordinario de una ecuación diferencial si ambas funciones P(x) y Q(x) son analíticas en ese punto. Un punto x 0 se llama punto singular de una ecuación diferencial si una de las funciones P(x) y Q(x), no es analítica en ese punto, o ninguna de las dos lo es. Un punto singular x 0 se llama punto singular regular de la ecuación diferencial si ambas funciones: son analíticas en ese punto. De no ser así, el punto x 0 se llama punto singular irregular de la ecuación diferencial.

U-6. CAP. IV. PUNTOS ORDINARIOS Y PUNTOS SINGULARES. En la práctica, la mayoría de las funciones a(x), b(x) y c(x) son polinomios, es decir, funciones analíticas. Entonces, las funciones P(x) y Q(x) son cuando mucho cocientes de polinomios, lo cual sigue siendo analítico excepto en los ceros de los denominadores. Los puntos ordinarios y singulares en este caso pueden definirse así: Cuando P(x) y Q(x) son cocientes de polinomios, los puntos en los que los denominadores se hacen cero son los puntos singulares y todos los demás puntos son puntos ordinarios de la ecuación diferencial.

U-6. CAP. IV. PUNTOS ORDINARIOS Y PUNTOS SINGULARES. Para el caso especial en que las funciones P(x) y Q(x) de una ecuación diferencial sean polinomios, cualquier punto x es ordinario. En un punto singular x 0, las funciones P(x) o Q(x) son infinitas. Una singularidad regular es relativamente débil y suave, por lo que se puede manejar confianza. Una singularidad irregular es más bien severa y difícil de manejar. La definición de punto singular regular implica que en el punto x 0 la singularidad en P(x) no es más severa que (x x 0) 1 y la singularidad en Q(x) no lo es más que (x x 0) 2.

U-6. CAP. IV. PUNTOS ORDINARIOS Y PUNTOS SINGULARES. Ejemplo: Determine los puntos ordinarios y singulares de la siguiente ecuación diferencial: Solución: La ecuación diferencial ya está en su forma estándar y se tiene: Ambos polinomios; por tanto, todos los puntos x son puntos ordinarios de la ecuación diferencial, ya que los polinomios son analíticos para toda x.

U-6. CAP. IV. PUNTOS ORDINARIOS Y PUNTOS SINGULARES. Ejemplo: Determine los puntos ordinarios y singulares de la siguiente ecuación diferencial: Solución: La ecuación diferencial puede expresarse en la forma estándar dividiendo cada término entre x: y así:

U-6. CAP. IV. PUNTOS ORDINARIOS Y PUNTOS SINGULARES. cocientes de polinomios ambos en donde el denominador de P(x) se hace cero en x = 0 y x = 1, mientras que el de Q(x) lo hace en x = 0. Por tanto, x = 0 y x = 1 son puntos singulares y todos los demás son puntos ordinarios de esta ecuación. Además, el punto x = 1 es singular regular y el punto x = 0 es singular irregular ya que:

U-6. CAP. IV. PUNTOS ORDINARIOS Y PUNTOS SINGULARES. La solución por series de una ecuación diferencial no esta completa sin establecer el intervalo en que converge. Para determinar el radio de convergencia de la serie se aplica una prueba de convergencia directamente a la serie. Una forma mas práctica consiste en determinar el radio de convergencia de las funciones P(x) y Q(x) y en seguida usar el siguiente teorema: Si x 0 es un punto ordinario de y´´ + P(x) y´ + Q(x) y = 0, la serie en la solución de esta ecuación tiene un radio de convergencia que es al menos tan grande como el más pequeño de los radios de convergencia de las funciones P(x) y Q(x).

U-6. CAP. IV. PUNTOS ORDINARIOS Y PUNTOS SINGULARES. Los radios de convergencia de P(x) y Q(x) se determina, en general, aplicando la prueba de convergencia. Pero cuando los numeradores y denominadores de P(x) y Q(x) son polinomios, los puntos singulares de ambas se pueden establecer en forma sencilla. Entonces, el radio mínimo de convergencia de la solución en series es igual a la distancia entre el punto especifico y el punto singular mas cercano de P(x) o Q(x). Al determinar esta distancia, es necesario considerar no solo los puntos singulares reales, sino también los complejos, lo que se ilustra con los siguientes ejemplos.

U-6. CAP. IV. PUNTOS ORDINARIOS Y PUNTOS SINGULARES. Ejemplo: Determine el radio de convergencia de la solución en series de la siguiente ecuación diferencial, alrededor de x = 5: Solución: La ecuación diferencial, expresada en su forma estándar es: entonces: Los denominadores (x 2 − 9) y x son cero en x = ± 3 y x = 0, por lo que éstos son puntos singulares. Todos los demás son puntos ordinarios.

U-6. CAP. IV. PUNTOS ORDINARIOS Y PUNTOS SINGULARES. La distancia entre el punto específico (x = 5) y el punto singular más cercano (x = 3) es 2. Por tanto, esta ecuación diferencial tiene una solución en series alrededor del punto x = 5, con un radio de convergencia de r = 2. Punto específico Puntos singulares − 3 0 3 x 0 = 5 Radio de convergencia La solución en series de la misma ecuación tiene distinto radio de convergencia alrededor de distintos puntos. Por ejemplo, r = 7 para x 0 = − 10; r = 1 para x 0 = 2 y r = 0 para x 0 = 3.

U-6. CAP. IV. PUNTOS ORDINARIOS Y PUNTOS SINGULARES. Ejemplo: Determine el radio de convergencia de la solución en series de la siguiente ecuación diferencial alrededor de x = 0: Solución: La ecuación diferencial en su forma estándar es: entonces: El denominador (x 2 − 4 x + 8) es cero en x = 2 ± 2 i , por lo que la ecuación tiene dos puntos singulares y éstos son complejos. Todos los demás son puntos ordinarios.

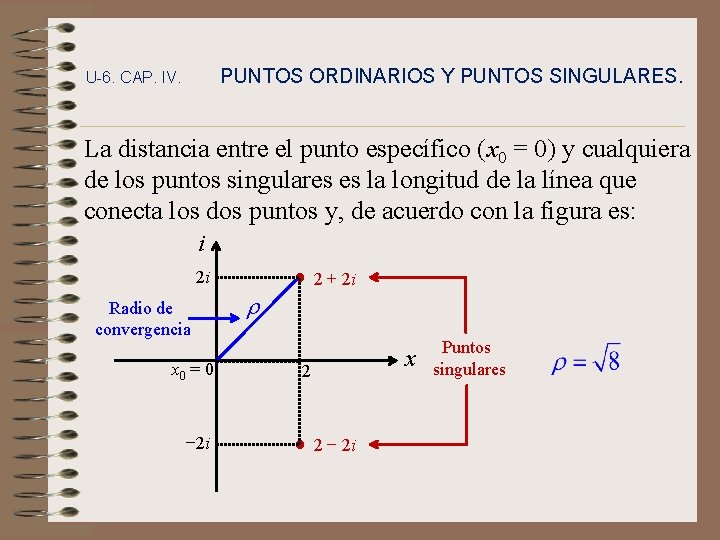
PUNTOS ORDINARIOS Y PUNTOS SINGULARES. U-6. CAP. IV. La distancia entre el punto específico (x 0 = 0) y cualquiera de los puntos singulares es la longitud de la línea que conecta los dos puntos y, de acuerdo con la figura es: i 2 i Radio de convergencia x 0 = 0 − 2 i 2 + 2 i r x 2 2 − 2 i Puntos singulares

U-6. CAP. IV. PUNTOS ORDINARIOS Y PUNTOS SINGULARES. Por tanto, esta ecuación tiene una solución en series alrededor del punto x 0 = 0 con un radio de convergencia: Observe nuevamente que la solución en series de la misma ecuación diferencial tiene radios de convergencia distintos alrededor de puntos diferentes. Por ejemplo, para x 0 = 2 el radio de convergencia r = 2.

U-6. CAP. IV. PUNTOS ORDINARIOS Y PUNTOS SINGULARES. Ejemplo: Determine el radio de convergencia de la solución en series de la ecuación diferencial: para las siguientes soluciones supuestas: a) b) Solución: La ecuación en su forma estándar es: entonces:

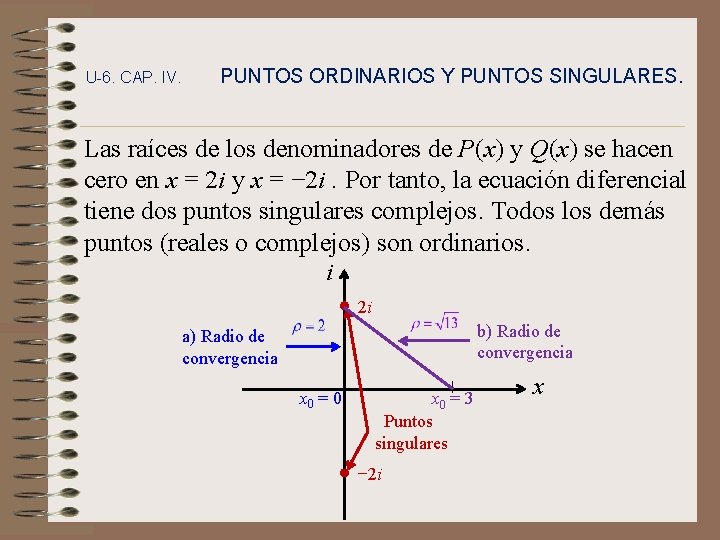
U-6. CAP. IV. PUNTOS ORDINARIOS Y PUNTOS SINGULARES. Las raíces de los denominadores de P(x) y Q(x) se hacen cero en x = 2 i y x = − 2 i. Por tanto, la ecuación diferencial tiene dos puntos singulares complejos. Todos los demás puntos (reales o complejos) son ordinarios. i 2 i b) Radio de convergencia a) Radio de convergencia x 0 = 0 x 0 = 3 Puntos singulares − 2 i x

U-6. CAP. IV. PUNTOS ORDINARIOS Y PUNTOS SINGULARES. a) La primera serie tiene al punto x 0 = 0 como centro y su radio de convergencia es la distancia entre este punto y cualquiera de los puntos singulares. Como se muestra en la figura anterior, r = 2, por tanto, la solución especificada converge para | x | < 2. b) La segunda serie tiene al punto x 0 = 3 como centro, y su radio de convergencia es: Por tanto, la solución en este caso converge para: