Introduccin Los polinomios y series de Taylor nos

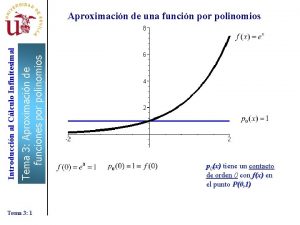
Introducción Los polinomios y series de Taylor nos permiten a menudo aproximar una función por polinomios, o hallar una serie de potencias que converja a la función. Los polinomios en general y las series de Taylor en particular son las funciones reales más fáciles de evaluar; por esta razón, cuando una función resulta difícil de evaluar con exactitud, de allí que se intenta buscar un polinomio que se le parezca y se usa dicho polinomio en su lugar. En este proceso es obvio que se pierde la exactitud de cálculo y se gana la operatividad, pues ni modo…aquí un ejemplo.

Aplicaciones a la aproximación

Aplicaciones a la aproximación ¿Qué significa la representación en serie de una función? Cualquier función periódica pueden representarse mediante una serie de funciones trigonométricas de frecuencias que son múltiplos enteros de la frecuencia fundamental de la señal dada. Esta serie es la denominada Serie de Fourier, que puede ser exponencial o trigonométrica. La serie converge el valor de la función, es decir, a medida que se suman más términos a la serie ésta es más “parecida” a la función que representa.

Series de Fourier Bueno, así como los polinomios y series de Taylor nos permiten a menudo aproximar una función por polinomios, o hallar una serie de potencias que converja a la función. El análisis de Fourier es muy similar, sólo que ahora nos plantearemos la aproximación de una función por combinaciones de funciones seno y coseno elegidas adecuadamente. Obviamente la primera pregunta que uno se hace es ¿por qué vamos a querer aproximar ahora una función por combinaciones de senos y cosenos ? . ¿Dónde se da esto de poder combinar senos con cosenos? .

En particular, lo que por ahora a un informático le interesa está relacionado con el análisis de circuitos, tratamiento de la señal, cuyo análisis se sustenta en el análisis de Fourier. Recientemente se ha desarrollado una herramienta, las ondículas (wavelets en inglés) que suponen un refinamiento del análisis de Fourier y que están teniendo una importancia decisiva en el tratamiento de la señal. Las wavelets se han usado para comprimir los archivos digitales de huellas dactilares del FBI, se usan en la mayoría de las películas de animación que se realizan en la actualidad, en los formatos de imagen jpg (a partir de 2000), en la detección de cánceres, en los estudios geológicos, entre otros.

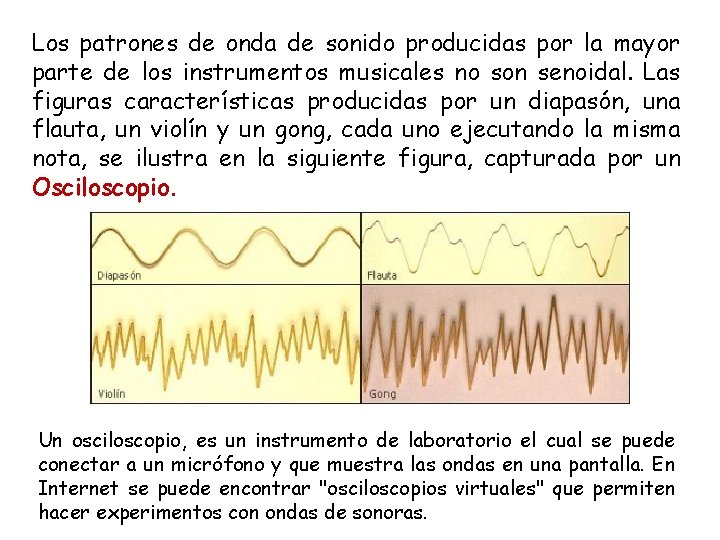
Los patrones de onda de sonido producidas por la mayor parte de los instrumentos musicales no son senoidal. Las figuras características producidas por un diapasón, una flauta, un violín y un gong, cada uno ejecutando la misma nota, se ilustra en la siguiente figura, capturada por un Osciloscopio. Un osciloscopio, es un instrumento de laboratorio el cual se puede conectar a un micrófono y que muestra las ondas en una pantalla. En Internet se puede encontrar "osciloscopios virtuales" que permiten hacer experimentos con ondas de sonoras.

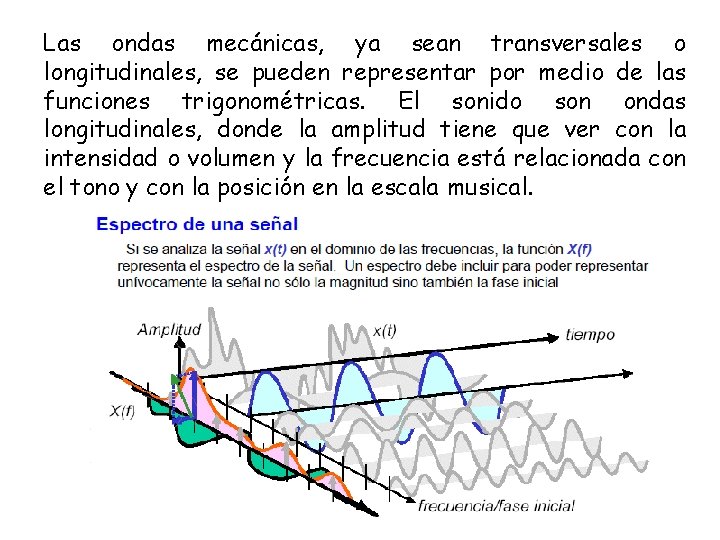
Las ondas mecánicas, ya sean transversales o longitudinales, se pueden representar por medio de las funciones trigonométricas. El sonido son ondas longitudinales, donde la amplitud tiene que ver con la intensidad o volumen y la frecuencia está relacionada con el tono y con la posición en la escala musical.

Las series de Fourier son series con términos coseno y surgen en la tarea práctica de representar funciones periódicas generales. Como aplicación constituyen una herramienta muy importante en la solución de problemas en los que intervienen ecuaciones diferenciales ordinarias y parciales. ¿Pero donde se pueden dar este tipo de funciones. ? ?

Los sucesos que se repiten con una cierta periodicidad son relativamente comunes en la naturaleza. Por ejemplo, las olas en el mar, las estaciones a lo largo del año, la transmisión del sonido, el péndulo de un reloj, las señales electromagnéticas emitidas por una antena, etc. Las series de Fourier y la transformada de Fourier han jugado y continúan jugando un papel fundamental en el estudio de estos problemas y el desarrollo de las Matemáticas.

En las ramas de la Electrónica e Ingeniería se trabajan diferentes formas de señales, ellas pueden ser: sinusoidal, cuadrada y triangular. Todas estas señales mencionadas son periódicas ósea que se repiten luego de un tiempo. La aplicación del osciloscopio nos permite entender un poco mejor como son estas señales que se pueden determinar calculando la Serie de Fourier para cada una de estas.

A la hora de estudiar fenómenos periódicos tenemos dos frentes abiertos. - Conocer las leyes de la física que gobiernan el sistema queremos modelar, ya se trate del movimiento de un fluido para estudiar las olas del mar y el otro que es - Cual es la relación entre la electricidad, el magnetismo, voltajes, resistencias y lo que sea necesario para estudiar una señal eléctrica.

Las serie de Fourier y, a diferencia de la serie de Taylor, puede describir funciones que no son completamente continuas o diferenciables.

Muchas ecuaciones de las ciencias se formulan con derivadas parciales y se resuelven, en ocasiones, descomponiendo la incógnita en series (sumas infinitas). Las series más interesantes son las potencias y por supuesto las de Fourier. de Lo sustantivo en este caso es el carácter periódico de tales sumas, las series de Fourier se aplican, por ejemplo, donde surgen procesos oscilantes, como ocurre en las series temporales de naturaleza económica, en electrónica (se aplican por ejemplo en teoría de señales ), en acústica o en óptica, y más….

https: //www. technologyreview. es/s/2712/tr 10 -unatransformada-de-fourier-mas-rapida

Las series de Fourier son series con términos coseno y surgen en la tarea práctica de representar funciones periódicas generales. Como aplicación constituyen una herramienta muy importante en la solución de problemas en los que intervienen ecuaciones diferenciales ordinarias y parciales. Por otra parte, la transformada de Laplace es una de las más importante en ingeniería. Desde el punto de vista de las aplicaciones, las siguientes en importancia serían quizás la transformada de Fourier, aún cuando su manejo resulta un tanto más difícil que la transformada de Laplace.

Los sucesos que se repiten con una cierta periodicidad son relativamente comunes en la naturaleza. Por ejemplo, las olas en el mar, las estaciones a lo largo del año, la transmisión del sonido, el péndulo de un reloj, las señales electromagnéticas emitidas por una antena, etc. Las series de Fourier y la transformada de Fourier han jugado y continúan jugando un papel fundamental en el estudio de estos problemas y el desarrollo de las Matemáticas.

En las ramas de la Electrónica e Ingeniería se trabajan diferentes formas de señales tales como: sinusoidal, cuadrada y triangular. Todas estas señales mencionadas son periódicas ósea que se repiten luego de un tiempo. La aplicación del osciloscopio nos permite entender un poco mejor como son estas señales que se pueden determinar calculando la Serie de Fourier para cada una de estas.

A la hora de estudiar fenómenos periódicos tenemos dos frentes abiertos. Por un lado es necesario conocer las leyes de la física que gobiernan el sistema queremos modelar, ya se trate del movimiento de un fluido para estudiar las olas del mar o cual es la relación entre la electricidad, el magnetismo, voltajes, resistencias y lo que sea necesario para estudiar una señal eléctrica.

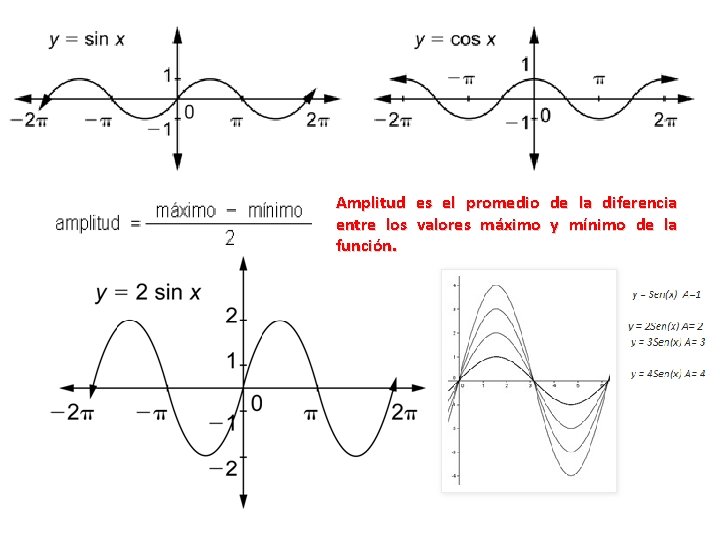
La función f(x) = sen (x) es periódica de periodo T=2π, ya que se cumple que: f(x) = f(x + K· 2π) para todo K ∈ Z. En efecto, sen(x) = sen(x + 2π) = sen(x + 4π) = sen(x + 6π) =. . . Además, sen(- x) = - sen(x) , por lo tanto es impar. F(x) = cos x = cos (x + 2π) = cos (x + 4π) = cos (x + 6π) =. . . es periódica, y es par. La función tangente tiene un periodo T = π, es decir: f(x) = tg x = tg (x + π) = tg (x + 2π) = tg (x + 3π) =. . .

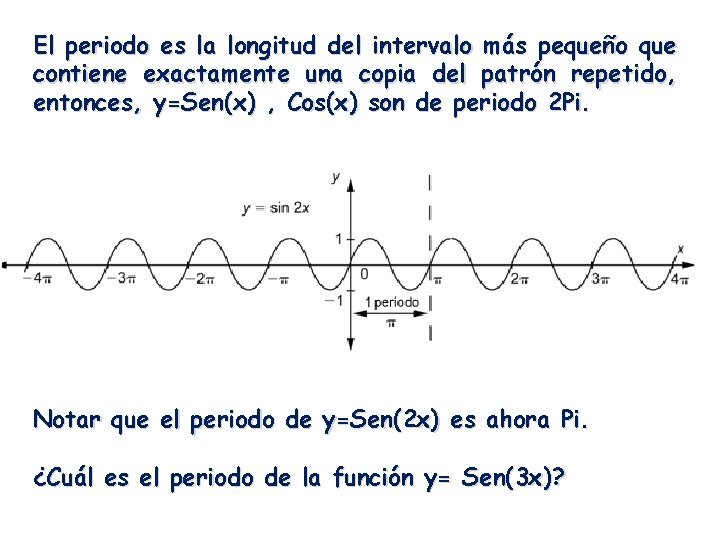
El periodo es la longitud del intervalo más pequeño que contiene exactamente una copia del patrón repetido, entonces, y=Sen(x) , Cos(x) son de periodo 2 Pi. Notar que el periodo de y=Sen(2 x) es ahora Pi. ¿Cuál es el periodo de la función y= Sen(3 x)?

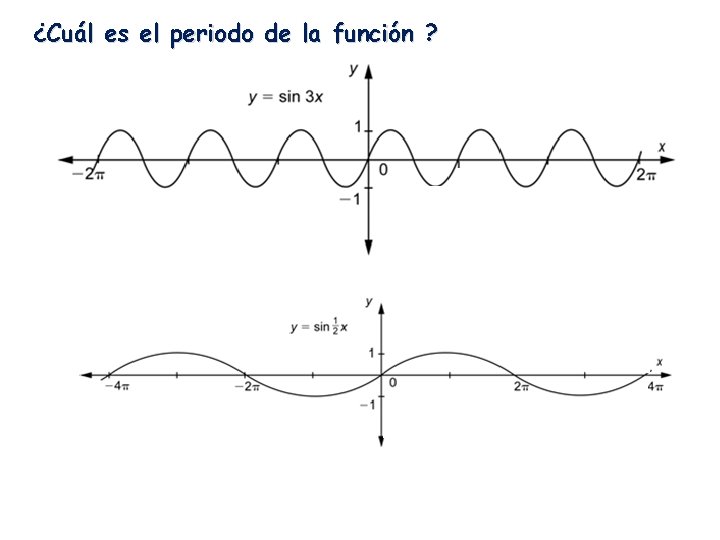
¿Cuál es el periodo de la función ?

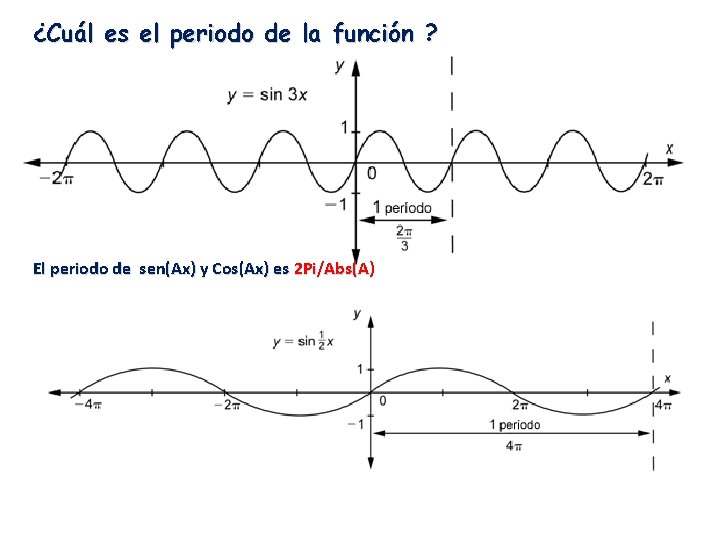
¿Cuál es el periodo de la función ? El periodo de sen(Ax) y Cos(Ax) es 2 Pi/Abs(A)

Amplitud es el promedio de la diferencia entre los valores máximo y mínimo de la función.

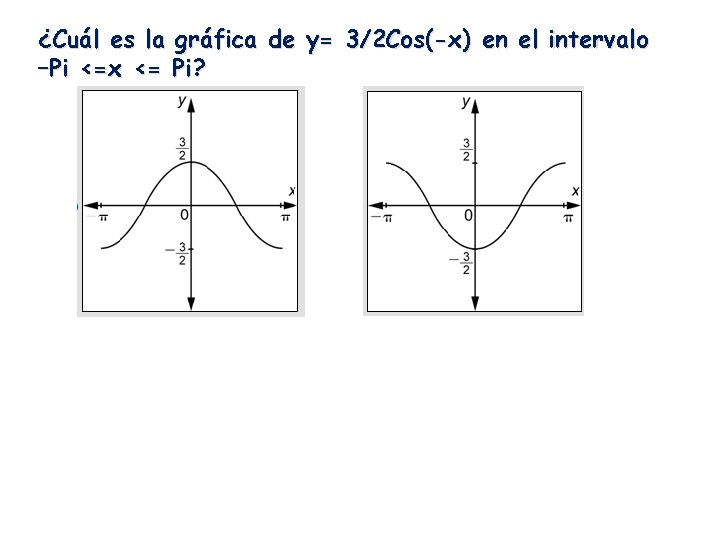
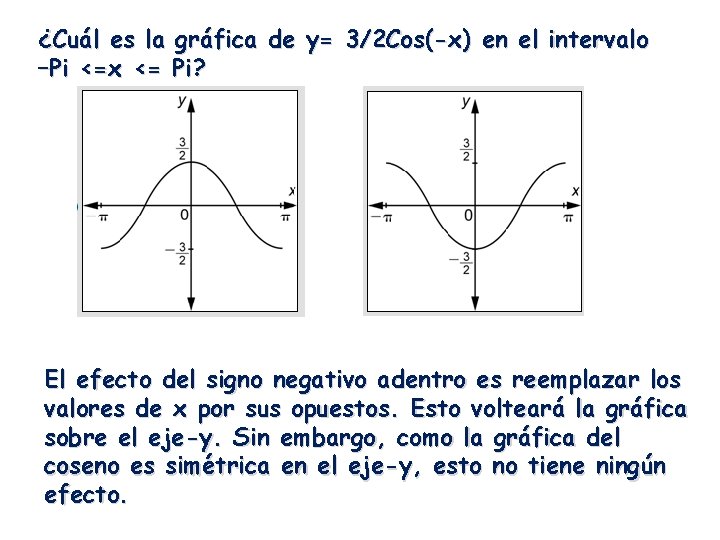
¿Cuál es la gráfica de y= 3/2 Cos(-x) en el intervalo –Pi <=x <= Pi?

¿Cuál es la gráfica de y= 3/2 Cos(-x) en el intervalo –Pi <=x <= Pi? El efecto del signo negativo adentro es reemplazar los valores de x por sus opuestos. Esto volteará la gráfica sobre el eje-y. Sin embargo, como la gráfica del coseno es simétrica en el eje-y, esto no tiene ningún efecto.

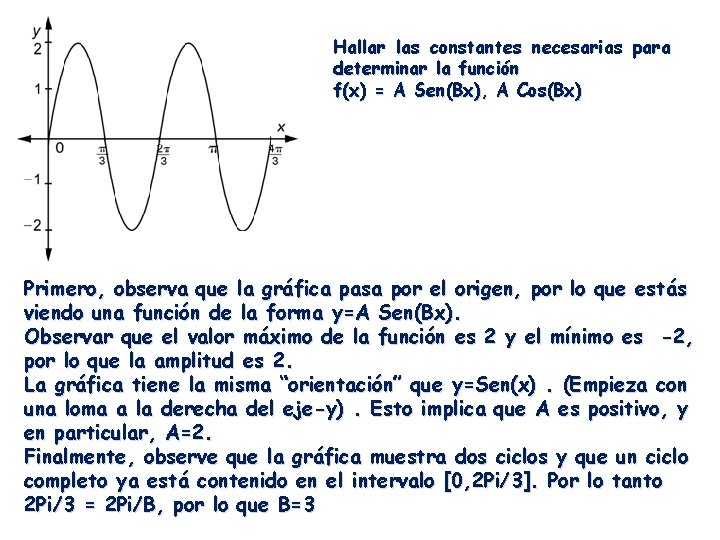
Hallar las constantes necesarias para determinar la función f(x) = A Sen(Bx), A Cos(Bx) Primero, observa que la gráfica pasa por el origen, por lo que estás viendo una función de la forma y=A Sen(Bx). Observar que el valor máximo de la función es 2 y el mínimo es -2, por lo que la amplitud es 2. La gráfica tiene la misma “orientación” que y=Sen(x). (Empieza con una loma a la derecha del eje-y). Esto implica que A es positivo, y en particular, A=2. Finalmente, observe que la gráfica muestra dos ciclos y que un ciclo completo ya está contenido en el intervalo [0, 2 Pi/3]. Por lo tanto 2 Pi/3 = 2 Pi/B, por lo que B=3

Y = A. sen(Bx + C) + D y = A. cos(Bx + C) + D A= AMPLITUD T= 2π/B = PERIODO d= -C/B = DESFASE (si es negativo se mueve a la derecha, si es positiva se mueve a la izquierda) D= DESPLAZAMIENTO El ángulo de fase determina el desplazamiento horizontal de la función respecto de la función y = Sen(x). Graficar y = Sen(x - π/2) A= AMPLITUD =1 T= 2π/B = PERIODO = 2 d= -C/B = DESFASE (si es negativo se mueve a la derecha, si es positiva se mueve a la izquierda). En este caso, es negativo el ángulo C, y se mueve a la derecha, d=Pi/2 D= DESPLAZAMIENTO Pi/2

y= cos(2 x−π/2). En este caso, A=1, B=2, C=-Pi/2, D=0 A= AMPLITUD=1 T= 2π/B = PERIODO = Pi d= -C/B = DESFASE (si es negativo se mueve a la derecha, si es positiva se mueve a la izquierda) = --Pi/2 / 2 = Pi/4 D= DESPLAZAMIENTO

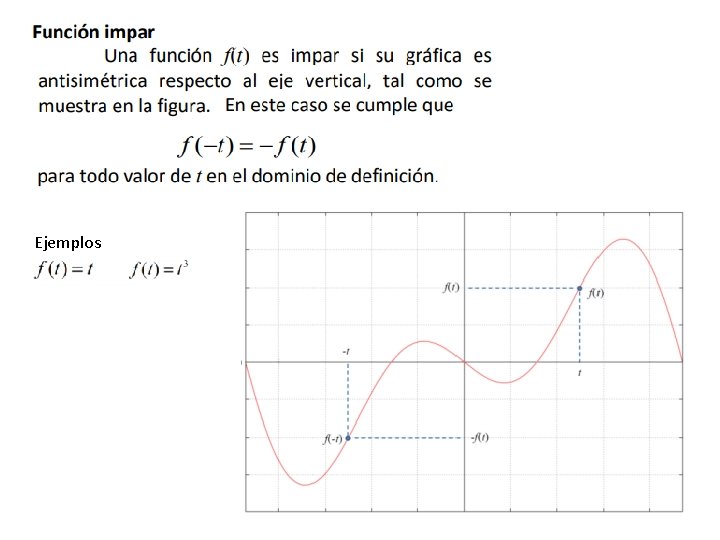
Ejemplos

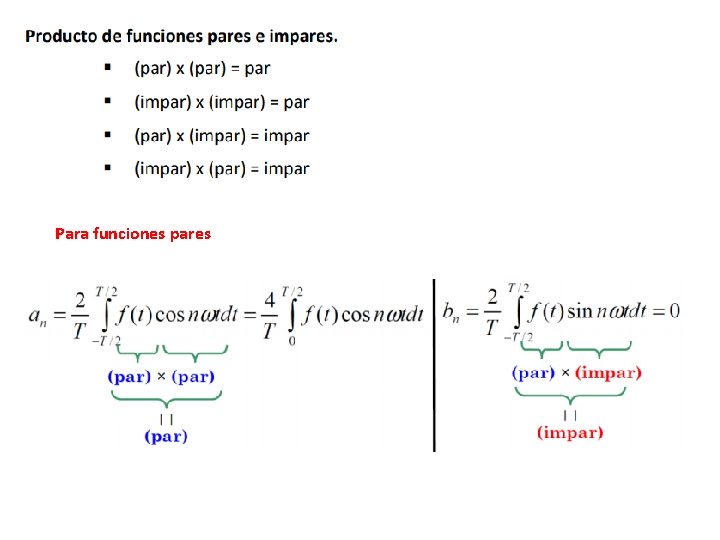
Para funciones pares

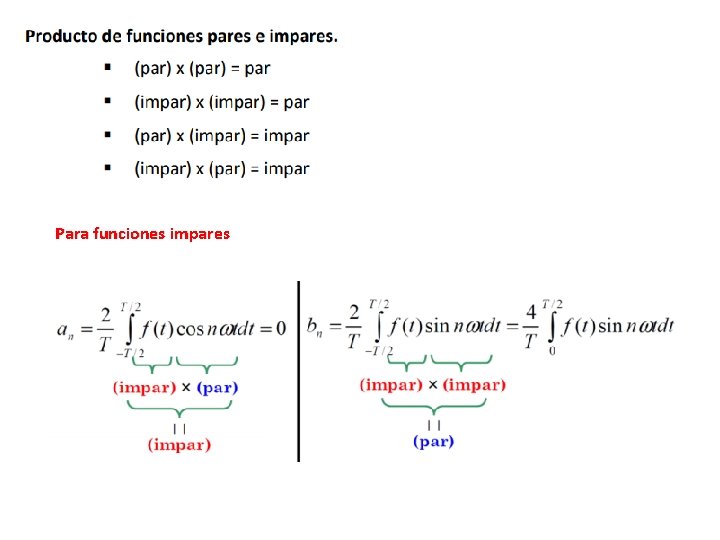
Para funciones impares

Hallar la serie de Fourier a la función

Las condiciones particulares que debe reunir una función f(t), a fin de que pueda representarse mediante una serie de Fourier, se conocen como condiciones de Dirichlet y son las siguientes: i. La función f(t) debe ser periódica; ii. La función debe ser continua, excepto (posiblemente) en un número finito de discontinuidades finitas; iii. La función debe tener solamente un número finito de máximos y mínimos dentro de un periodo. T; y iv. La integral de |f(t)| sobre un periodo T, debe ser convergente.

Vale la pena mencionar que cuando tenemos situaciones físicas (reales), las tres últimas condiciones de Dirichlet casi siempre se cumplen, no así la primera de ellas, ya que no todas las funciones son periódicas. Sin embargo, en muchas situaciones es posible representar una función no periódica como una serie de Fourier mediante la manipulación de la función para transformarla en una forma periódica, lo cual veremos más adelante.

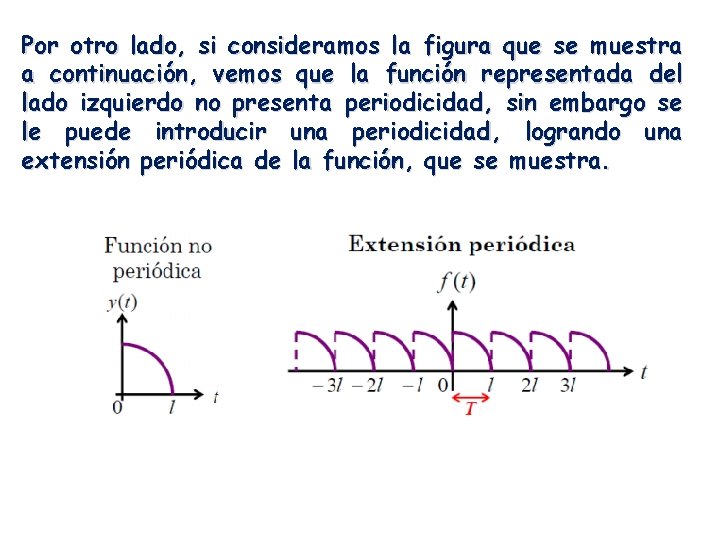
Por otro lado, si consideramos la figura que se muestra a continuación, vemos que la función representada del lado izquierdo no presenta periodicidad, sin embargo se le puede introducir una periodicidad, logrando una extensión periódica de la función, que se muestra.

A la cantidad que aparece en las expresiones anteriores se le conoce como frecuencia fundamental y está dada por donde T es el periodo de la función f(t)

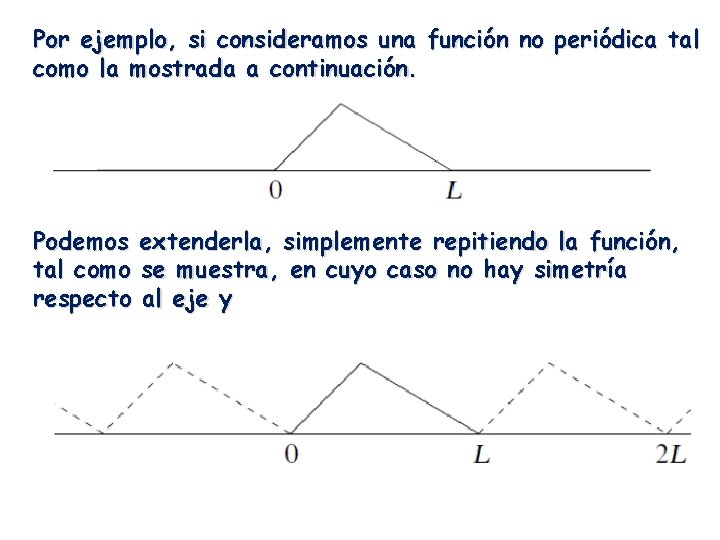
Por ejemplo, si consideramos una función no periódica tal como la mostrada a continuación. Podemos extenderla, simplemente repitiendo la función, tal como se muestra, en cuyo caso no hay simetría respecto al eje y

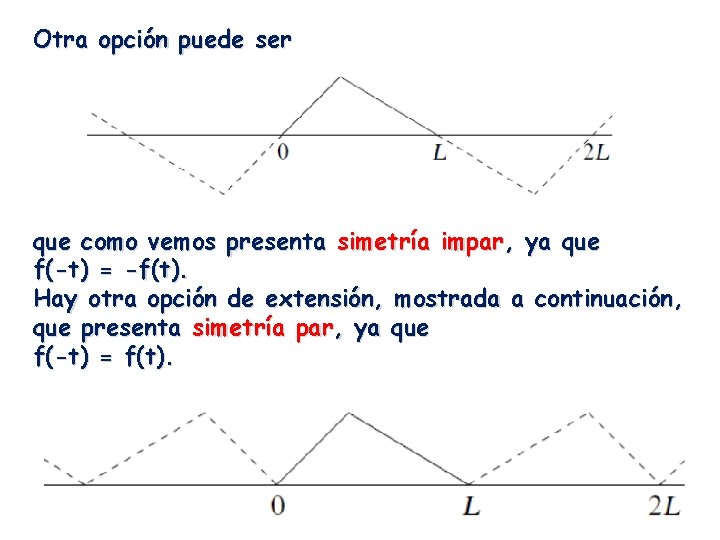
Otra opción puede ser que como vemos presenta simetría impar, ya que f(-t) = -f(t). Hay otra opción de extensión, mostrada a continuación, que presenta simetría par, ya que f(-t) = f(t).

Como pudimos ver, a menudo estamos en libertad de ampliar la función de varias maneras; sin embargo, normalmente es preferible usar alguna de las simetrías vistas anteriormente (par o impar) para la extensión periódica, en lugar de una extensión periódica normal; La ventaja es que el uso de una función con cierta simetría (par o impar) nos proporcionará coeficientes cero de cualquiera de los an o bn de la expansión, lo que puede proporcionar una expansión más sencilla de la serie de Fourier correspondiente.

Como puede verse, para la misma función f(t), las diferentes extensiones implican modificar el periodo, en el caso recién mostrado, un dominio inicialmente entre 0 y L, se mantiene sin cambios para una extensión normal, pero se duplicó para las extensiones par e impar.

En este punto no vamos a entrar, ya que nos interesa el aspecto matemático del problema. ¿Cómo podemos describir uno de estos sistemas? . El principio que vamos a aplicar es el de divide y vencerás. !!. ¿Cómo así. ? ? . . Se procede a dividir el problema en términos sencillos utilizando senos y cosenos y después combinar funciones de este tipo para obtener sistemas más complicados. Ejemplos varios

se obtiene lo siguiente.

Más aplicaciones de Series de Fourier