CICLO LECTIVO 2013 1 JORNADA AGENDA DE TRABAJO

CICLO LECTIVO 2013 1º JORNADA

AGENDA DE TRABAJO ANUAL JUNIO S 1 S 2 S 3 JULIO S 4 PRIMERA JORNADA S 1 S 2 A. D S 3 AGOSTO S 4 S 1 S 2 A. D S 3 SETIEMBRE S 4 S 1 SEGUNDA JORNADA S 2 S 3 S 4 A. D OCTUBRE S 1 S 2 S 3 S 4 TERCERA JORNADA NOVIEMBRE S 1 S 2 S 3 A. D S 4

OBJETIVO GENERAL Fortalecer la alfabetización numérica inicial para mejorar las trayectorias escolares de los alumnos del primer ciclo.

OBJETIVOS ESPECÍFICOS EL SISTEMA DE NUMERACIÓN • ANALIZAR EL SENTIDO DE ENSEÑAR MATEMÁTICA EN EL 1º CICLO BAJO LOS LINEAMIENTOS ACTUALES LAS OPERACIONES Y EL CÁLCULO EL ESPACIO Y LA GEOMETRÍA LA MEDIDA • GESTIONAR CLASES, CON DIVERSAS ESTRATEGIAS, QUE PERMITAN A TODOS LOS ALUMNOS APRENDER MÁS Y MEJOR A PARTIR DE SUS TRAYECTORIAS ESCOLARES REALES • PROMOVER INSTANCIAS DE REFLEXIÓN SOBRE LA PRÁCTICA DOCENTE PARA EL DESARROLLO DE PROPUESTAS DIDÁCTICAS SUPERADORAS

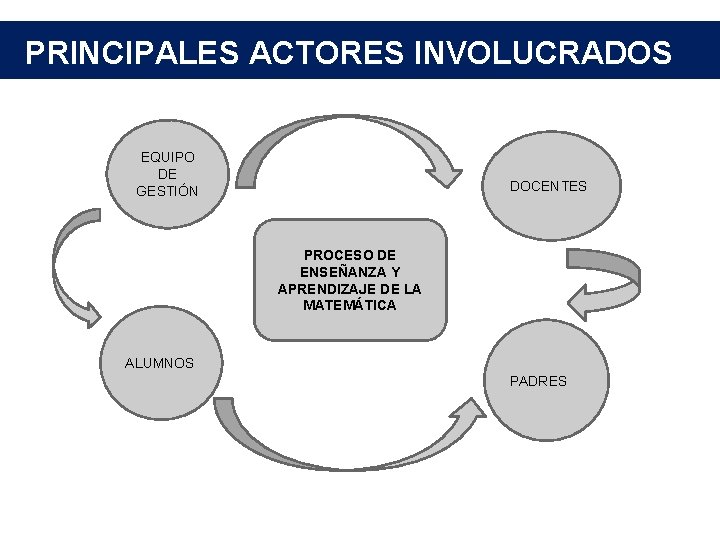
PRINCIPALES ACTORES INVOLUCRADOS EQUIPO DE GESTIÓN DOCENTES PROCESO DE ENSEÑANZA Y APRENDIZAJE DE LA MATEMÁTICA ALUMNOS PADRES

MARCO CURRICULAR DEL PROYECTO

PRIMER MOMENTO EL SISTEMA DE NUMERACIÓN EN EL PRIMER CICLO

¿Qué saben los chicos al comenzar Primer Grado?

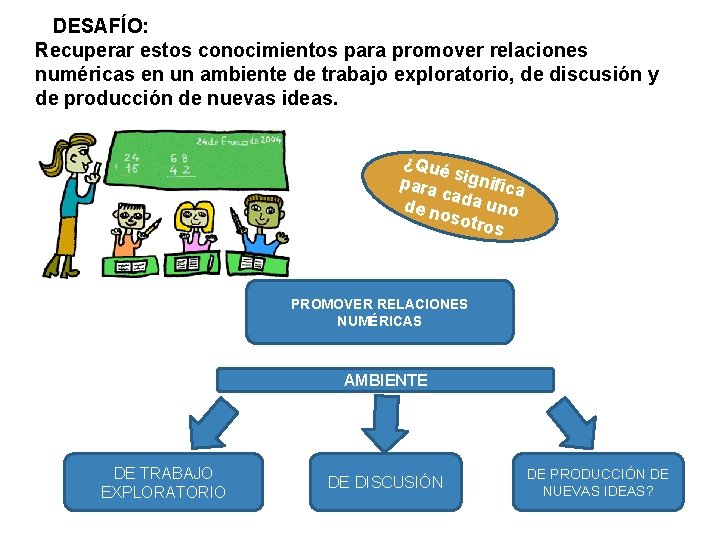
DESAFÍO: Recuperar estos conocimientos para promover relaciones numéricas en un ambiente de trabajo exploratorio, de discusión y de producción de nuevas ideas. ¿Qué para significa ca de n da uno osot ros PROMOVER RELACIONES NUMÉRICAS AMBIENTE DE TRABAJO EXPLORATORIO DE DISCUSIÓN DE PRODUCCIÓN DE NUEVAS IDEAS?

• Observamos un video que puede permitir: • Observar cómo lo hace otro docente • Describir qué estrategias utiliza ese docente • Comparar su forma de gestionar la clase y la que tengo yo en el aula……. . Entre todos responder las preguntas formuladas en la diapositiva anterior

¿CÓMO LO HACEMOS?

PISTAS NUMERADAS PROPÓSITO: Permiten plantear juegos donde los números funcionen tanto con su significado cardinal como ordinal. ¿CON QUIÉN? Pueden ser compartido entre pares y en familia. ¿ CÓMO? El docente podrá también fabricar nuevas pistas en las que aparezcan diferentes series numéricas (de 5 en 5, de 10 en 10, de 100 en 100) según los contenidos que desee enseñar. Cuando el docente lo considere adecuado puede fabricar tarjetas con prendas que los alumnos deberán extraer al caer en el casillero indicado.

EL CALENDARIO Este es el mes de un calendario, pero le faltan los números de algunos días, completalos ¿Cuántos días vas a ir a la escuela ese mes? ¿Cómo hiciste para calcularlo? ¿Por qué hay espacios sin números antes del 1 y después del 30? Anotá los números de los días sábados. ¿Cada cuántos días hay un sábado?

CARTAS: Para saber cuántos hay

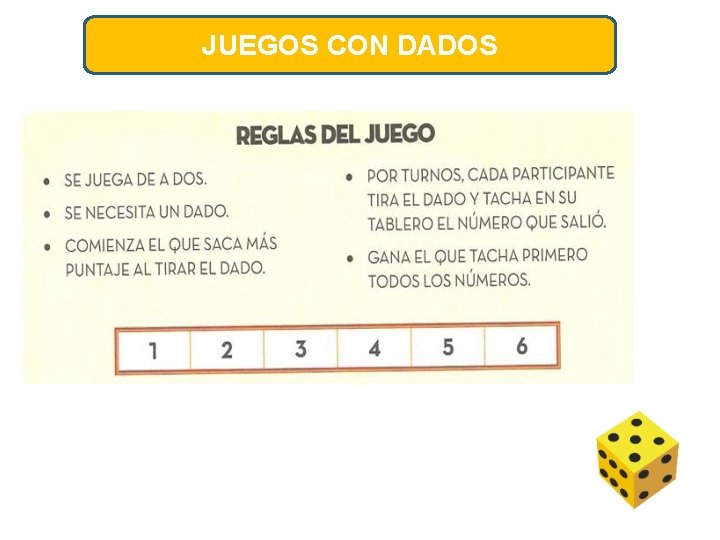
JUEGOS CON DADOS

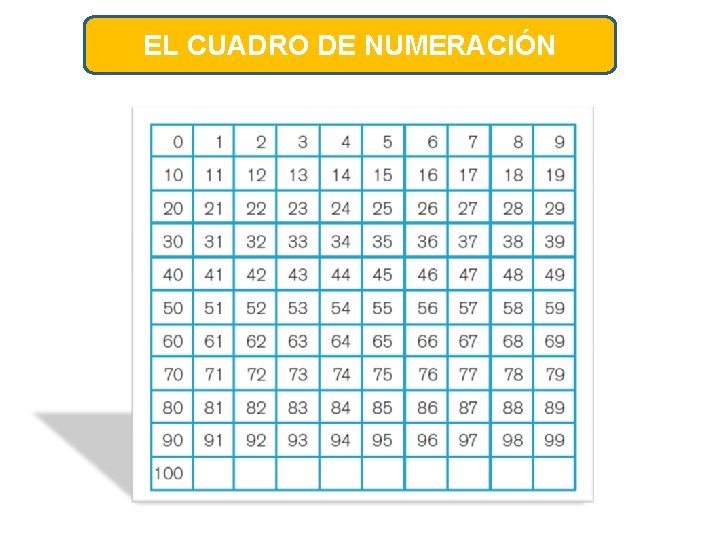
EL CUADRO DE NUMERACIÓN

¿Qué características comunes tienen los números de una misma fila? ¿En qué se diferencian los números de la primera con los de la tercera fila? ¿Si agrego 10 a un número del cuadro a qué casillero voy? ¿Qué características comunes tienen los números de una misma columna? ¿Cuántos números hay en cada familia? ¿Cuántos números terminados en 7 hay? ¿Y en 5? ¿ y en 9?

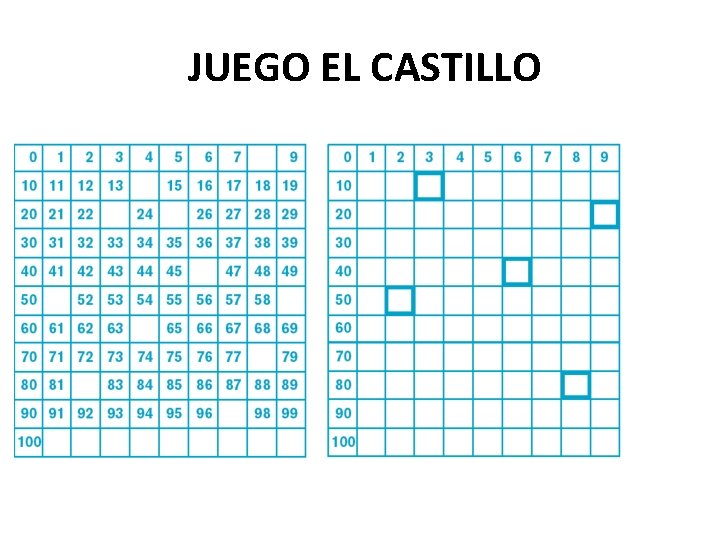
JUEGO EL CASTILLO

Esta figurita va antes, porque empieza con 1. Entre las otras dos, no puedo saber cuál va antes, porque comienzan con los mismos números Juan y Martín están ordenando figuritas. Martín tiene la figurita con el número 153 y. Juan tiene las figuritas con los números 253 y 235. Lee lo que dice Martín: ¿Estás de acuerdo con lo que dice él? Ésta es una parte del cuadro de control que usa Juan: 450 451 453 454 459 462 477 479 480 495 Éstas son las figuritas que le salieron en dos paquetes que le regalaron: ¿Qué números de figuritas puede acomodar en el cuadro? Ubicalas. ¿Le tocó alguna figurita que ya tenía? ¿Cuál?

Completá los cuadros 1. 100 1. 200 1. 110 1. 120 Si los dos cuadros empiezan en el mismo número, ¿por qué terminan diferentes?

JUEGOS CON TARJETAS ¿Con las tarjetas 2, 3 y 8, qué números se pueden formar? Martín recibió tarjetas con las cifras 5, 8 y 9. Indicá cuál es el mayor número y cuál el menor que puede formar. Nicolás sacó las tarjetas con las cifras 5, 6 y 3. Indicá cuál es el número menor que pudo formar.

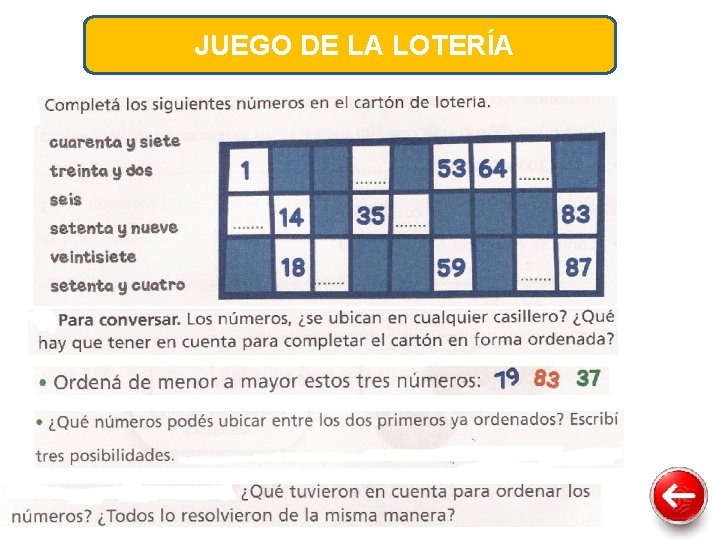
JUEGO DE LA LOTERÍA

“¿Aprender el concepto de decena ayuda realmente a conocer los números? ¿o es, más bien, el conocimiento de los números y de su escritura, lo que ayuda a comprender el concepto de decena? ” de . s d U n a s s a n r e o i t au é p u s a Q t ¿ es an? e u q lo es expr Lerner D. y Sadovsky P. (1994) “El sistema de numeración: un problema didáctico” en Parra C. y Saiz I. (comp. ) Didáctica de Matemáticas, aportes y reflexiones. Paidos, Bs. As.

EL SISTEMA DE NUMERACIÓN INVOLUCRA LA MULTIPLICACIÓN ES FRECUENTE QUE SE UTILICEN EXPRESIONES COMO 3 c, 4 d y 5 u para el 345 antes de haber iniciado la enseñanza de la multiplicación LAS OPCIONES DIDÁCTICAS EXPRESIONES ADITIVAS a partir de la numeración oral SU COMPRENSIÓN LLEVARÁ VARIOS AÑOS DE ESCOLARIDAD REPRESENTA -CIONES de cantidades cuando se agrupan sus elementos de a 10: grupos de 10 y elementos sueltos.

LOS JUEGOS PARA APRENDER MATEMÁTICA….

JUGAMOS AL TUTI FRUTI DE PRECIOS • Materiales: Billetes y monedas de todos los valores. Las cartas del 1 al 100 • Organización del grupo Se juega entre cuatro jugadores. • Reglas del juego: Se colocan en el centro de la mesa los billetes: 10 de $ 100, 10 de $ 50, 10 de $ 20, 15 de $ 10, 10 de $ 5, 10 de $ 2 y 20 de $ 1.

A un costado se deja el mazo de cartas del 1 al 100 mezcladas boca abajo. Los valores de las cartas indicarán los precios. Un jugador, en cada ronda, será el encargado de poner boca arriba una carta del mazo. Cada uno deberá “armar el precio con billetes de dos maneras diferentes”. El jugador que termine primero dirá “Basta” y los otros participantes interrumpirán su tarea sólo si ya han armado el número por lo menos de una forma. Se retornan al centro de la mesa los billetes de los números que no se terminaron de armar. Entre todos los integrantes del grupo controlarán los conjuntos de billetes de cada precio. Cada armado tiene un puntaje. El alumno que logró un armado original (es decir que no esté repetido entre los integrantes del grupo) se anotará dos puntos. En caso de que más de un alumno realizara la misma combinación de billetes, se anotarán un punto cada uno. Al terminar el turno se deberán retornar al pozo todos los billetes utilizados, pero previamente cada uno registrará en una hoja cómo lo hizo. Al cabo de 4 rondas se dará por finalizada la partida y ganará el que haya acumulado más puntos.

¡ A EMBOCAR! Organización de la clase: grupos de 4 a 6 jugadores. Desarrollo: cada jugador debe tirar las cinco pelotitas y anotar el puntaje obtenido al caer. Por cada acierto adentro de la lata, se obtienen 100 puntos; si caen sobre la mesa, 10 puntos, y si caen en el piso, 1 punto. Al cabo de cuatro vueltas de cinco tiros cada una, deberán averiguar quién es el ganador calculando el total de puntos obtenidos.

AHORA A COMPARTIR § ¿Qué promueve cada uno de estos juegos? § ¿Qué contenidos involucran? § ¿Ambos juegos tendrán el mismo o diferente propósito didáctico?

Ahora: - ¿se puede adaptar estos juegos para 1º grado? Y ¿para 3º? - ¿Cómo? - ¿El propósito será el mismo?

INICIO EN EL REGISTRO DEL VALOR POSICIONAL 1. Ordená de menor a a mayor estos tres números: 19 83 37 Ø¿Qué números podés ubicar entre los dos primeros ya ordenados? Escribí tres posibilidades. 2. Trabajá con un compañero para resolver las siguientes consignas. ØOrdenen de menor a mayor estos tres números: 145 176 154 Ø¿Están de acuerdo con lo que dice Sofía? ¿Por qué? Cualquiera de los números de la actividad 1 es más chico que éstos. ØElijan tres números que sean más grandes que los últimos que ordenaron. ØUno de ustedes escriba tres números de tres cifras, el compañero los debe ordenar al lado. 3. Para pensar y conversar: ¿Qué tuvieron en cuenta para ordenar los números? ¿Todos lo resolvieron de la misma manera?

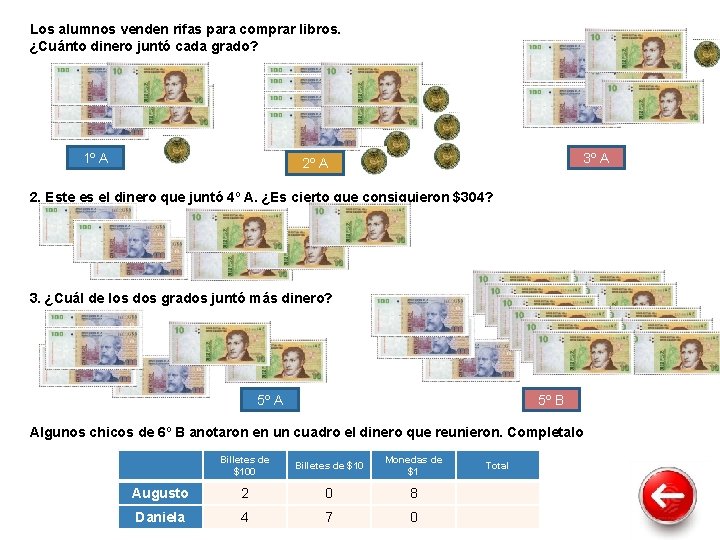
Los alumnos venden rifas para comprar libros. ¿Cuánto dinero juntó cada grado? 1º A 3º A 2. Este es el dinero que juntó 4º A. ¿Es cierto que consiguieron $304? 3. ¿Cuál de los dos grados juntó más dinero? 5º A 5º B Algunos chicos de 6º B anotaron en un cuadro el dinero que reunieron. Completalo Billetes de $100 Billetes de $10 Monedas de $1 Augusto 2 0 8 Daniela 4 7 0 Total

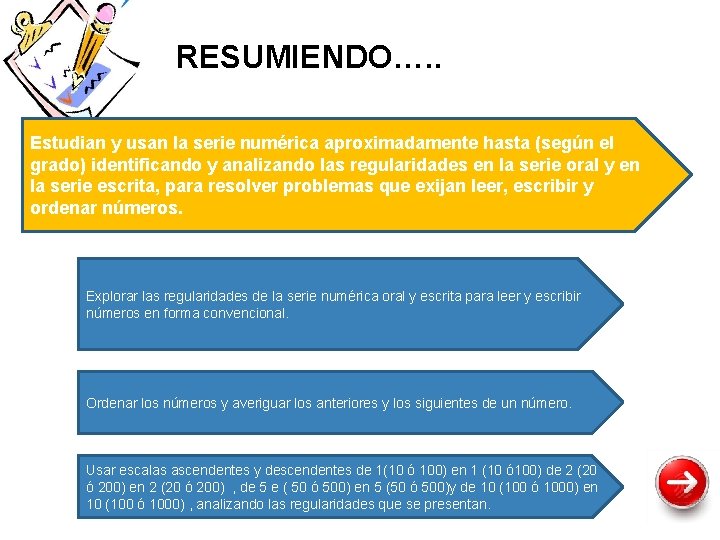
RESUMIENDO…. . Estudian y usan la serie numérica aproximadamente hasta (según el grado) identificando y analizando las regularidades en la serie oral y en la serie escrita, para resolver problemas que exijan leer, escribir y ordenar números. Explorar las regularidades de la serie numérica oral y escrita para leer y escribir números en forma convencional. Ordenar los números y averiguar los anteriores y los siguientes de un número. Usar escalas ascendentes y descendentes de 1(10 ó 100) en 1 (10 ó 100) de 2 (20 ó 200) en 2 (20 ó 200) , de 5 e ( 50 ó 500) en 5 (50 ó 500)y de 10 (100 ó 1000) en 10 (100 ó 1000) , analizando las regularidades que se presentan.

Explorar las regularidades de la serie numérica oral y escrita para leer y escribir números en forma convencional. Este es un cuadro con números hasta el 100. 1 2 3 0 5 7 12 20 24 24 75 62 19 38 93 58 68 73 80 90 18 48 50 71 9 28 37 40 8 74 84 93 -Hay cuatro números mal ubicados. Corregilos. -Escribí en el cuadro: a) Los números del 30 al 35 b) Los números 6, 16, 26, 36, 46, 56, 66, 76, 86, 96. c) El números que debe ubicarse en el casillero sombreado. - 78 87 Pintá los lugares donde irían todos los números que empiezan con “cuarenta y…” 88 98 99 BANCO COLOSAL $ 660 Páguese a ………………………. la cantidad de pesos ………………………………………………… $ ……… Páguese a ………………………. . . . La cantidad de pesos: cuatrocientos dos. --------

Ordenar los números y averiguar los anteriores y los siguientes de un número. El docente o un alumno piensa un número entre 0 y 1. 000 y el o los demás jugadores deben descubrir ese número usando la recta numérica para señalar los rangos de números que se van descartando y haciendo preguntas que se respondan por ”sí“ o por ”no“ como: “¿Es mayor que 600? , ¿Está entre 100 y 500? “ Un cartero tiene que entregar sobres en la siguiente numeración de una calle: 793, 797 y 769. ¿En qué orden hará la entrega? José, Matías y María están jugando al Sapo. José tiene 345 puntos. María tiene 1 punto menos que José y Matías tiene 1 punto más que José. Completá el cuadro de los puntajes. MARÍA JOSÉ 345 MATÍAS

Usar escalas ascendentes y descendentes de 1(10 ó 100) en 1 (10 ó 100) de 2 (20 ó 200) en 2 (20 ó 200) , de 5 e ( 50 ó 500) en 5 (50 ó 500)y de 10 (100 ó 1000) en 10 (100 ó 1000) , analizando las regularidades que se presentan. En la escuela se compran 50 litros de leche por semana. ¿Cuántos litros se comprarán en dos semanas? ¿Y en tres, cuatro y cinco semanas? Un coleccionista tiene 125 latitas. Si consigue 10 latitas por mes, ¿cuántas tendrá en los próximos meses? ¿Y si le regalaran 5 latitas por semana?

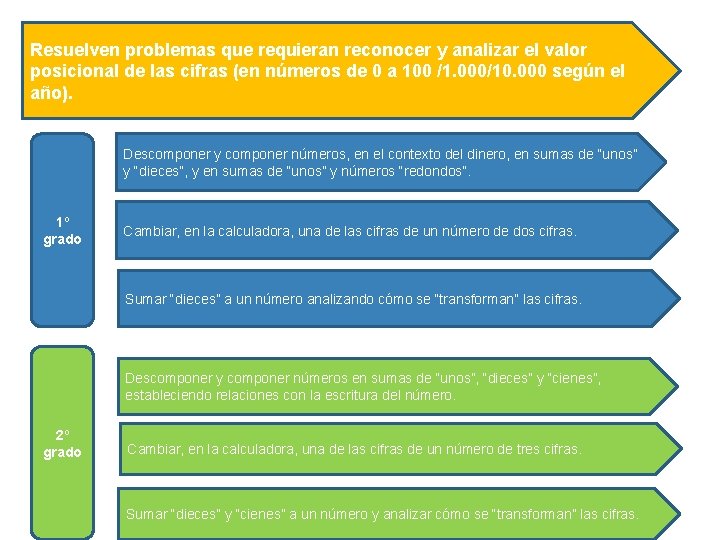
Resuelven problemas que requieran reconocer y analizar el valor posicional de las cifras (en números de 0 a 100 /1. 000/10. 000 según el año). Descomponer y componer números, en el contexto del dinero, en sumas de “unos” y “dieces”, y en sumas de “unos” y números “redondos”. 1º grado Cambiar, en la calculadora, una de las cifras de un número de dos cifras. Sumar “dieces” a un número analizando cómo se “transforman” las cifras. Descomponer y componer números en sumas de “unos”, “dieces” y “cienes”, estableciendo relaciones con la escritura del número. 2º grado Cambiar, en la calculadora, una de las cifras de un número de tres cifras. Sumar “dieces” y “cienes” a un número y analizar cómo se “transforman” las cifras.

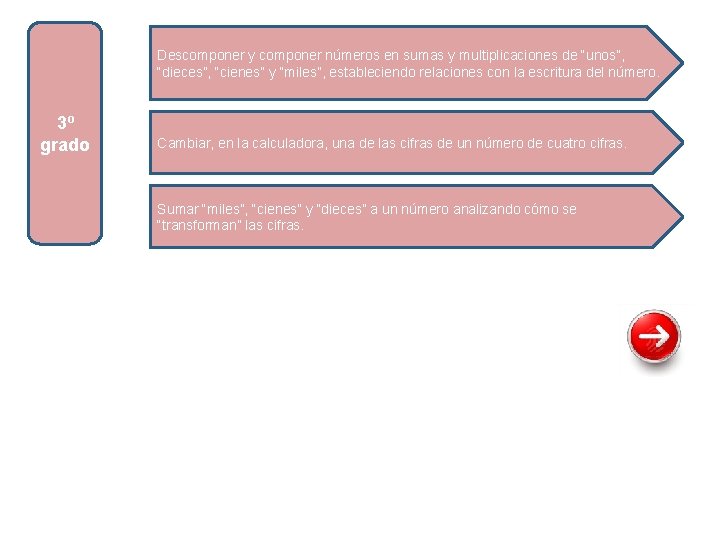
Descomponer y componer números en sumas y multiplicaciones de “unos”, “dieces”, “cienes” y “miles”, estableciendo relaciones con la escritura del número. 3º grado Cambiar, en la calculadora, una de las cifras de un número de cuatro cifras. Sumar “miles”, “cienes” y “dieces” a un número analizando cómo se “transforman” las cifras.

Descomponer y componer números, en el contexto del dinero, en sumas de “unos” y “dieces”, y en sumas de “unos” y números “redondos”. • Si tengo 3 monedas de $1 y 3 billetes de $10, ¿cuánto dinero tengo? • ¿Cuál es la menor cantidad de billetes de $10 y monedas de $1 qué necesito para formar $78? • ¿Con cuál de las siguientes sumas de billetes y monedas puedo formar $52? 10 + 1 + 1 + 1 10 + 10 + 10 + 1 + 1 + 1+1 + 1 + 1

Descomponer y componer números en sumas de “unos”, “dieces” y “cienes”, estableciendo relaciones con la escritura del número. • Si tengo 5 monedas de $1, 7 billetes de $10 y 5 billetes de $100, ¿cuánto dinero tengo? • ¿Cuántos billetes de $100, de $10 y monedas de $1 necesito para pagar $138? • ¿Con cuál de las siguientes sumas de billetes puedo formar $232? 100 + 1 + 1 + 1 100 + 10 + 10 + 1

Descomponer y componer números en sumas y multiplicaciones de “unos”, “dieces”, “cienes” y “miles”, estableciendo relaciones con la escritura del número. Unos amigos juegan a embocar pelotitas en frascos con distintos puntajes. Lucía embocó estas pelotitas. ¿Qué puntaje obtuvo? Ana y Lucía anotan los puntajes de esta jugada: ¿Por qué, si los cálculos que anotan al principio son distintos, llegan al mismo resultado? Martín anotó este cálculo para saber su puntaje: 5 x 1. 000 + 2 x 100 +4 x 10 + 3 x 1 Dibujá las pelotitas que embocó en cada frasco. ¿Qué puntaje obtuvo en esta jugada?

• • ¿Qué hay que sumarle o restarle a 34 para que el 4 se convierta en un 2? ¿Y para que el 3 cambie por 4? Anotar el 66 en el visor de la calculadora. Con una única resta hacer que aparezca el 56, luego el 46, el 36, el 26. Anoten 534. ¿Qué tienen que apretar para que cambie sólo el 5? ¿Y para que cambie sólo el 3? ¿Y para que cambie sólo el 4? Si en la calculadora tienen el número 234, ¿cuánto hay que restarle para convertirlo en 224? ¿Y en 134?

Cambiar, en la calculadora, una de las cifras de un número de cuatro cifras. En el visor de la calculadora se lee 1. 567, qué harías para que aparezca 1. 667? ¿ y 1. 577? Escribe en la calculadora 4. 582. ¿Cuánto hay que restarle para que aparezca en el visor 4. 482? ¿Y 4. 592?

Tengo 25 figuritas y cada semana me regalan 10. ¿Cuántas tendré después de una semana? ¿Y después de dos semanas? ¿Y después de tres, cuatro y cinco semanas? Un coleccionista tiene 146 estampillas y se propone juntar cada año 100 estampillas más. ¿Cuántas estampillas tendrá después de un año? ¿Y después de dos años? ¿Y de tres, cuatro y cinco años?

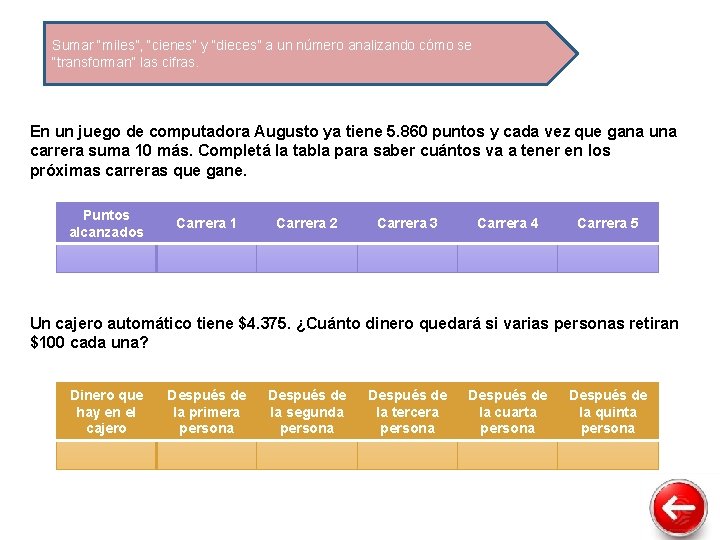
Sumar “miles”, “cienes” y “dieces” a un número analizando cómo se “transforman” las cifras. En un juego de computadora Augusto ya tiene 5. 860 puntos y cada vez que gana una carrera suma 10 más. Completá la tabla para saber cuántos va a tener en los próximas carreras que gane. Puntos alcanzados Carrera 1 Carrera 2 Carrera 3 Carrera 4 Carrera 5 Un cajero automático tiene $4. 375. ¿Cuánto dinero quedará si varias personas retiran $100 cada una? Dinero que hay en el cajero Después de la primera persona Después de la segunda persona Después de la tercera persona Después de la cuarta persona Después de la quinta persona

SEGUNDO MOMENTO ¿QUÉ SIGNIFICA ENSEÑAR A SUM Y A RESTAR?

PLANTEAR SITUACIONES PARA SUMAR CON DISTINTOS SIGNIFICADOS • Agregar. Tenía guardados 5 caramelos y cuando la abuela vino de visita me regaló otros 4. ¿Cuántos tengo ahora? • Juntar o reunir. María invitó a sus amigos y compró 5 caramelos y 4 chupetines ¿Cuántas golosinas compró? • Avanzar. En el juego de La Oca, Juan tiene su ficha en el casillero 5. Si saca 4 en el dado, ¿a qué casillero deberá mover su ficha?

PLANTEAR SITUACIONES PARA RESTAR CON DISTINTOS SIGNIFICADOS • Quitar. Cuando me reuní a jugar con mis amigos, tenía 15 figuritas y perdí 6. Cuántas me quedaron? • Retroceder. En el juego de la Oca mi ficha estaba en el casillero 15. Debo retroceder 6 casilleros. Indicá en que casillero colocaré mi ficha.

ESTRATEGIAS DE CÁLCULO INTRODUCCIÓN DEL SIGNO +

ESTRATEGIAS DE CÁLCULO

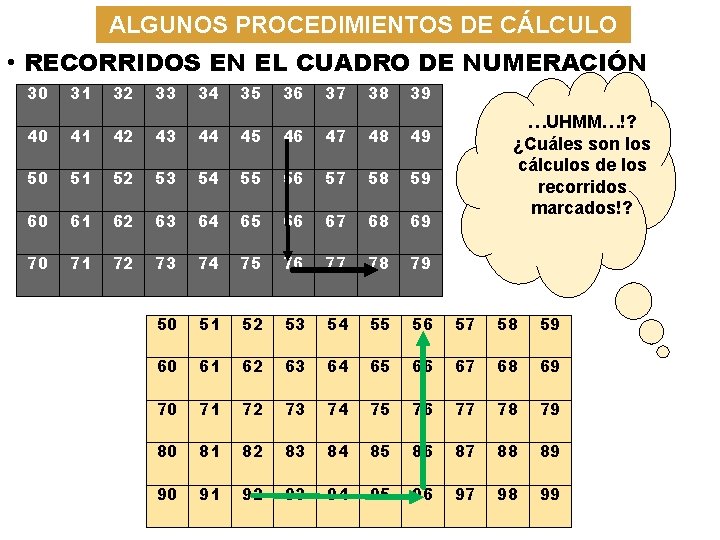
ALGUNOS PROCEDIMIENTOS DE CÁLCULO • RECORRIDOS EN EL CUADRO DE NUMERACIÓN 30 31 32 33 34 35 36 37 38 39 …UHMM…!? ¿Cuáles son los cálculos de los recorridos marcados!? 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99

DIFERENTES PROCEDIMIENTOS DE RESOLUCIÓN • «Tenía guardados 5 caramelos y cuando la abuela vino de visita me regaló otros 4. ¿Cuántos tengo ahora? ”.

“Cuando me reuní a jugar con mis amigos, tenía 15 figuritas y perdí 6. ¿Cuántas me quedaron? ”

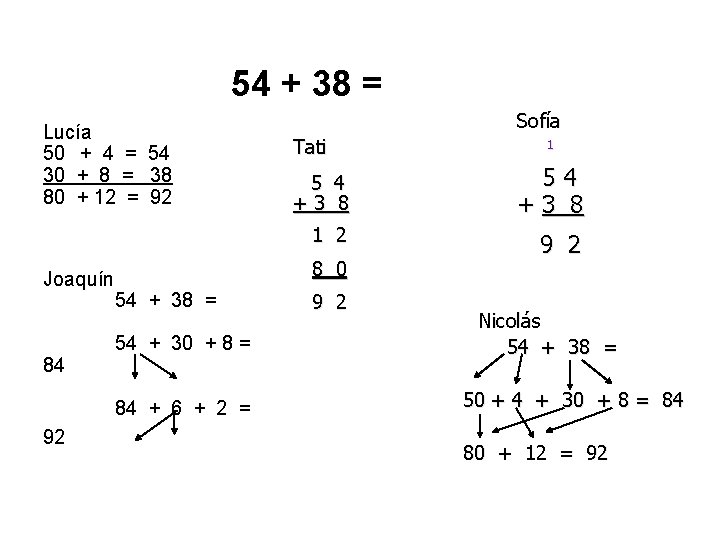
54 + 38 = Lucía 50 + 4 = 54 30 + 8 = 38 80 + 12 = 92 Joaquín 54 + 38 = 84 54 + 30 + 8 = 84 + 6 + 2 = 92 Tati Sofía 1 5 4 1 2 9 2 + 3 8 8 0 9 2 + 3 8 Nicolás 54 + 38 = 50 + 4 + 30 + 8 = 84 80 + 12 = 92

DEL MATERIAL A LA CUENTA Tengo $ 235 y debo pagar $ 53 ¿Cuánto me darán de vuelto?

235 - 53 = Sofía Joaquín 235 - 53 = 1 235 - 53 235 - 50 = 185 - 3 = 182 Nico 235 - 53 = 235 – 50 – 3 = 185 – 3 = 182 1 8 2 Tati 235 – 53 = 230 + 5 100 + 130 + 5 50 + 3 100 + 80 + 2

Descomposición aditiva (en sumas) números de cuatro cifras para resolver cálculos “horizontales” de suma y de resta • Para sumar 1. 200 + 1. 500, Guillermo hizo 1. 000 + 200 + 1. 000 + 500. Explicá cómo pensó. Para sumar 2. 800 + 3. 600, Paola hizo 1. 000 + 800 + 1. 000 +1000 + 1. 000 + 600 y Sergio hizo 2. 000 + 800 + 3. 000 + 600. Explicá cómo pensó cada uno. •

PRESENTACIÓN DEL SIGNO MÁS

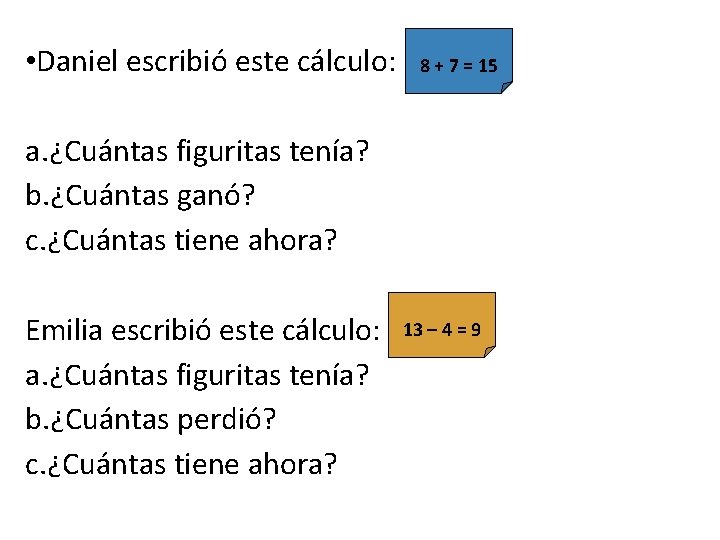
• Daniel escribió este cálculo: 8 + 7 = 15 a. ¿Cuántas figuritas tenía? b. ¿Cuántas ganó? c. ¿Cuántas tiene ahora? Emilia escribió este cálculo: a. ¿Cuántas figuritas tenía? b. ¿Cuántas perdió? c. ¿Cuántas tiene ahora? 13 – 4 = 9

Escribí los cálculos que representan cada jugada. C l a r a t e n í a C a m i l a

CÁLCULO MENTAL ü- Se hace con la cabeza üEs globalizador, toma el número como una totalidad que se puede descomponer aditiva o multiplicativamente, de forma tal que permite conservar el valor de los términos de la operación üBusca sustituir o alterar los datos iniciales para trabajar con otros más cómodos o más fáciles de calcular, usando las propiedades asociativa, conmutativa y distributiva üRequiere ciertas habilidades: conteo, recolocaciones, descomposiciones, redistribuciones, compensaciones; üSon particulares, ya que los procedimientos dependen de los distintos números involucrados üSirve para anticipar el resultado Chemello, G. “El cálculo en las escuela: las cuentas, ¿son un problema” en Los CBC y la enseñanza de la matemática. AZ ü

1 er grado: ° Sumas de sumandos iguales de una cifra (1 + 1 hasta 9 + 9). Sumas de decenas enteras iguales (10 + 10 hasta 90 + 90). Sumas que dan 10 (1 + 9; 9 + 1; 2 + 8; 8 + 2; etc. ). Sumas de números terminados en 0 que dan 100 (20 + 80). 2 do grado Sumas de sumandos distintos de una cifra (4 + 3, 8 + 6, etc. ). Sumas de decenas (40 + 30; 70 + 60; etc. ). Complementos a 100 (80 + … = 100; 40 + … = 100, etc. ). Sumas y restas de múltiplos de 5 (35 + 15; 50 – 15, etc. ). Dobles y mitades (el doble de 7, de 20; la mitad de 80, etc. ). Sumas de decenas enteras más unidades (10 + 8; 20 + 5, etc. ). Sumas + 10 (78 o 105 + 10; etc. ) y restas – 10 (28 o 35 – 10)

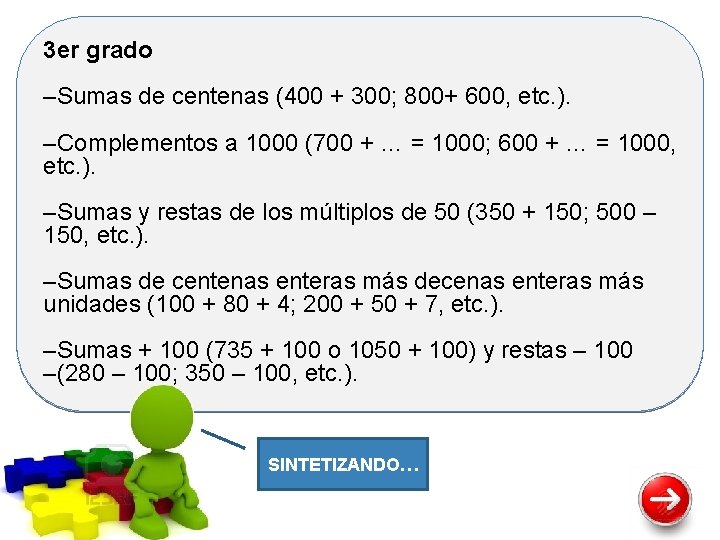
3 er grado –Sumas de centenas (400 + 300; 800+ 600, etc. ). –Complementos a 1000 (700 + … = 1000; 600 + … = 1000, etc. ). –Sumas y restas de los múltiplos de 50 (350 + 150; 500 – 150, etc. ). –Sumas de centenas enteras más decenas enteras más unidades (100 + 80 + 4; 200 + 50 + 7, etc. ). –Sumas + 100 (735 + 100 o 1050 + 100) y restas – 100 –(280 – 100; 350 – 100, etc. ). SINTETIZANDO…

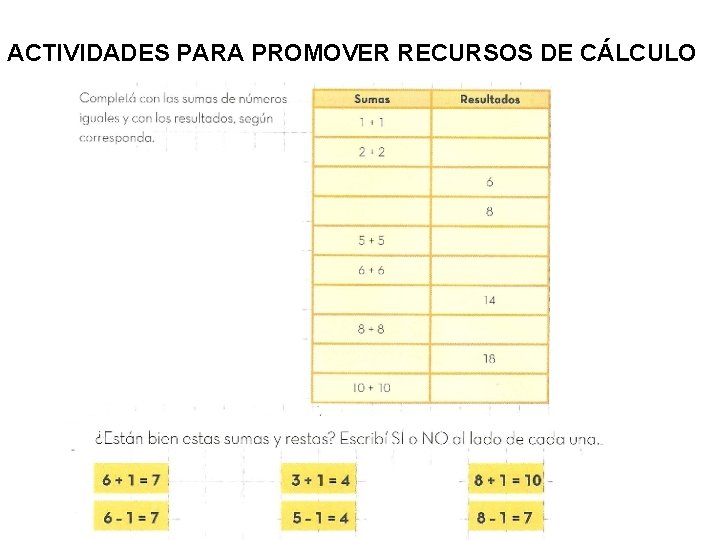
ACTIVIDADES PARA PROMOVER RECURSOS DE CÁLCULO

Para cada suma decidí si la podés hacer mentalmente o si te conviene hacer la cuenta: 100 + 85 = 237 + 49 = 184 + 128 = 517 + 3 = 150 + 150 = 210+220 = Escriban tres sumas que se puedan resolver mentalmente y cuyos resultados sean mayores que 400. Escriban tres sumas en las que convenga hacer la cuenta en columna y cuyos resultados sean menores que 700 El resultado de cada suma es uno de los números de la derecha. Antes de hacer la cuenta elegí el que te parece que corresponde. 2. 385 1. 184 + 1. 276 = 3. 360 2. 460 7. 156 2. 354 + 4. 162 = 6. 484 6. 516 ¿Habías elegido bien el resultado? Comenten en equipo cómo hacen para elegir un resultado y rechazar otro.

Ahora bien : ¿Qué cambia y qué permanece en cuanto a los aprendizajes que deben lograr nuestros alumnos en 1º, 2º y en 3º grado? ¿ Qué relación existe entre los problemas que tiene que resolver un alumno de 1º, uno de 2º y uno de 3º para lograr estos aprendizajes?

¿QUÉ TRABAJAR CON NUESTROS ALUMNOS HASTA EL PRÓXIMO ENCUENTRO?

• Resolver problemas de suma y resta que involucren los sentidos más sencillo de estas operaciones, por medio de diversos procedimientos. • Construir y utilizar estrategias de cálculo mental para resolver sumas y restas. • Explorar estrategias de cálculo aproximado de sumas y restas. • Sumar y restar en situaciones que presenten los datos en contextos variados.

BIBLIOGRAFÍA “Todos pueden aprender Matemática en 2º”. Educación para todos. Unicef. ü “Todos pueden aprender Matemática en 3º”. Educación para todos. Unicef. ü “Serie Cuadernos del Aula 1 -2 -3”. MECy. T. 2006. ü Broitman, Claudia, “Las operaciones en el Primer Ciclo: Aportes para el trabajo en el Aula”, Novedades Educativas. Bs. As. 2005. ü Itzcovich, Horacio, “La Matemática Escolar”, Ed. Aique. Bs. As. 2007. ü Parra, Cecilia; Saiz, Irma, “Enseñar aritmética a los más chicos: de la exploración al dominio” Ed. Homo Sapiens. Santa Fé. 2009. ü Chamorro, María del Carmen, “Didáctica de las Matemáticas para Primaria” Ed. Pearson. Madrid. 2006. ü Castro, Adriana y otros, “Enseñar Matemática en la Escuela Primaria”. Ed. Tinta Fresca. Bs. As. 2009. ü Broitman y otros, “Matemática en…”Ed. Santillana. Bs. As. 2012 ü Díaz, Adriana, “Aventura Matemática”. Ed. Aique. Bs. As. 2009 ü Bibliografía de distintas editoriales que se encuentran en las bibliotecas escolares.