Sec 4 1 THE TAYLOR SERIES Sec 4

  • Slides: 17
Download presentation
Sec: 4. 1 THE TAYLOR SERIES

Sec: 4. 1 THE TAYLOR SERIES

Sec: 4. 1 THE TAYLOR SERIES Taylor’s theorem states that any smooth function can

Sec: 4. 1 THE TAYLOR SERIES Taylor’s theorem states that any smooth function can be approximated as a polynomial. Taylor series ( center is a ) If the function f and its first n + 1 derivatives are continuous on an interval containing a and x, there exists a point ξ between a and x such that the reminder Maclaurin series ( center is 0 ) ξ between 0 and x

Sec: 4. 1 THE TAYLOR SERIES Taylor series ( center is a ) Example:

Sec: 4. 1 THE TAYLOR SERIES Taylor series ( center is a ) Example: f(x) = cos x, f'(x) = −sin x, f’’(x) = −cos x, f’’’(x) = sin x, f’’’’(x) = cos x, Let f (x) = cos x and a = 0. Determine (a) the second order approximation for f about a; and (b) Use (a) to approximate cos(0. 01) f(0) = 1, f'(0) = 0, f’’(0) = − 1, f’’’(0) = 0, f’’’’(0) = 1, syms x taylor(cos(x), x, 0, 'order', 3) 1 - x^2/2 ezplot('cos(x)', [-pi, pi]); hold on ezplot('1 -x. ^2/2', [-pi, pi]); hold off grid on

Sec: 4. 1 THE TAYLOR SERIES Example: Let f (x) = cos x and

Sec: 4. 1 THE TAYLOR SERIES Example: Let f (x) = cos x and a = 0. Determine (a) the second order approximation for f about a; and (b) Use (a) to approximate cos(0. 01) How accurate this approximation: approximation exact Hence the approximation 0. 99995 matches at least the first five digits of the exact

Sec: 4. 1 THE TAYLOR SERIES Example: Let f (x) = cos x and

Sec: 4. 1 THE TAYLOR SERIES Example: Let f (x) = cos x and a = 0. Determine (a) the second order approximation for f about a; and (b) Use (a) to approximate cos(0. 01) This example illustrates the two objectives of numerical analysis: (i) Find an approximation to the solution of a given problem. (ii) Determine a bound for the accuracy of the approximation

Sec: 4. 1 THE TAYLOR SERIES Why: we want to approximate a function by

Sec: 4. 1 THE TAYLOR SERIES Why: we want to approximate a function by a polynomial. Example: Let f (x) = cos x and a = 0. Determine (a) the third order approximation for f about a; and (b) Use (a) to approximate integrate both sides exact approximation

Sec: 4. 1 THE TAYLOR SERIES Taylor’s theorem states that any smooth function can

Sec: 4. 1 THE TAYLOR SERIES Taylor’s theorem states that any smooth function can be approximated as a polynomial. Taylor series ( center is a ) there exists a point ξ between a and x such that Another expression for the Reminder

Sec: 4. 1 THE TAYLOR SERIES Taylor series ( center is a ) It

Sec: 4. 1 THE TAYLOR SERIES Taylor series ( center is a ) It is often convenient to simplify the Taylor series by defining a step size h = xi+1 − xi and expressing above as Taylor series ( center is a )

Sec: 4. 1 THE TAYLOR SERIES Taylor series First-order approximation forward finite difference Move

Sec: 4. 1 THE TAYLOR SERIES Taylor series First-order approximation forward finite difference Move the first term to left side and divid by h Approximation to the derivative Truncation error

Sec: 4. 1 THE TAYLOR SERIES forward finite difference SIMILAR TO PROBLEM 4. 5/p

Sec: 4. 1 THE TAYLOR SERIES forward finite difference SIMILAR TO PROBLEM 4. 5/p 105: h = 0. 2 h = 0. 1 h = 0. 001

Sec: 4. 1 THE TAYLOR SERIES first finite divided difference SIMILAR TO PROBLEM 4.

Sec: 4. 1 THE TAYLOR SERIES first finite divided difference SIMILAR TO PROBLEM 4. 5/p 105: h = 0. 001

Sec: 4. 1 THE TAYLOR SERIES Taylor series ( center is a ) Taylor

Sec: 4. 1 THE TAYLOR SERIES Taylor series ( center is a ) Taylor series

Sec: 4. 1 THE TAYLOR SERIES Taylor series First-order approximation backward finite difference Move

Sec: 4. 1 THE TAYLOR SERIES Taylor series First-order approximation backward finite difference Move the first term to left side and divid by h Approximation to the derivative Truncation error

Sec: 4. 1 THE TAYLOR SERIES backward finite difference forward finite difference Centered finite

Sec: 4. 1 THE TAYLOR SERIES backward finite difference forward finite difference Centered finite difference

Sec: 4. 1 THE TAYLOR SERIES SIMILAR TO PROBLEM 4. 5/p 105: Error Table

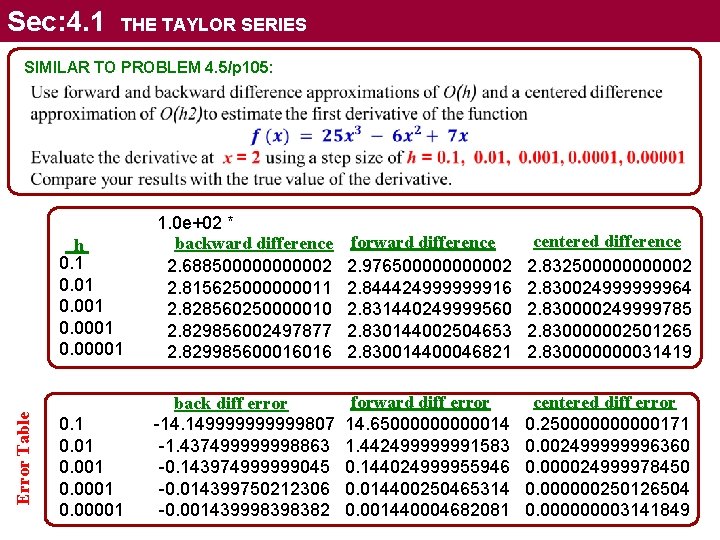
Sec: 4. 1 THE TAYLOR SERIES SIMILAR TO PROBLEM 4. 5/p 105: Error Table h 0. 1 0. 001 0. 00001 1. 0 e+02 * centered difference backward difference forward difference 2. 6885000002 2. 9765000002 2. 8325000002 2. 815625000000011 2. 844424999999916 2. 830024999999964 2. 828560250000010 2. 831440249999560 2. 830000249999785 2. 829856002497877 2. 830144002504653 2. 830000002501265 2. 829985600016016 2. 830014400046821 2. 83000031419 0. 1 0. 001 0. 00001 centered diff error forward diff error back diff error -14. 1499999807 14. 650000014 0. 2500000171 -1. 437499999998863 1. 442499999991583 0. 002499999996360 -0. 143974999999045 0. 144024999955946 0. 000024999978450 -0. 014399750212306 0. 014400250465314 0. 000000250126504 -0. 001439998398382 0. 001440004682081 0. 00003141849

Sec: 4. 1 THE TAYLOR SERIES function [bd, fd, cd] = num_diff(f, x, h)

Sec: 4. 1 THE TAYLOR SERIES function [bd, fd, cd] = num_diff(f, x, h) xi = x; xip 1 = xi+h; xim 1 = xi-h; bd = (f(xi) - f(xim 1))/h; fd = (f(xip 1) - f(xi) )/h; cd = (f(xip 1) - f(xim 1))/(2*h); end fun = @(x) 25*x^3 - 6*x^2+7*x; dfun = @(x) 75*x^2 - 12*x + 7; h=0. 2; x=2; [bd, fd, cd] = num_diff(fun, x, h) dfun(2) format short fun = @(x) 25*x^3 - 6*x^2+7*x; dfun = @(x) 75*x^2 - 12*x + 7; x=2; exact = dfun(2); h_vec=[0. 1 0. 001 0. 00001]; for i=1: 5 h = h_vec(i); [bd, fd, cd] = num_diff(fun, x, h); bd_vec(i) = bd; fd_vec(i) = fd; cd_vec(i) = cd; end format long res 1 = [ bd_vec' fd_vec' cd_vec'] res 2 = [h_vec' bd_vec' fd_vec' cd_vec'] err = [bd_vec' fd_vec' cd_vec']-exact; err_res = [h_vec' err]

Sec: 4. 1 THE TAYLOR SERIES Second Derivative Approximation forward finite difference backward finite

Sec: 4. 1 THE TAYLOR SERIES Second Derivative Approximation forward finite difference backward finite difference Centered finite difference

TAYLOR SERIES Maclaurin series center is 0 TaylorTAYLOR SERIES Maclaurin series center is 0 Taylor
Taylor Series Revisited 1 Taylor Series Revisited WhatTaylor Series Revisited 1 Taylor Series Revisited What
Sec 1 1 THE TAYLOR SERIES Sec 1Sec 1 1 THE TAYLOR SERIES Sec 1
BROOK TAYLOR 1685 1731 BROOK TAYLOR Brook TaylorBROOK TAYLOR 1685 1731 BROOK TAYLOR Brook Taylor
Frederick Taylor Paula Benevene Taylor Frederick Taylor FiladelfiaFrederick Taylor Paula Benevene Taylor Frederick Taylor Filadelfia
BROOK TAYLOR 1685 1731 BROOK TAYLOR Brook TaylorBROOK TAYLOR 1685 1731 BROOK TAYLOR Brook Taylor
Storage Series Ridgeline Series Veranda Series Frontier SeriesStorage Series Ridgeline Series Veranda Series Frontier Series
1000 Series 2000 Series 3000 Series 4000 Series1000 Series 2000 Series 3000 Series 4000 Series
Taylor and Maclaurin series is called the TaylorTaylor and Maclaurin series is called the Taylor
8 4 Taylor Series Brook Taylor was an8 4 Taylor Series Brook Taylor was an
Taylor Series Brook Taylor was an accomplished musicianTaylor Series Brook Taylor was an accomplished musician
Lecture 3 Taylor Series Expansion Inline function TaylorLecture 3 Taylor Series Expansion Inline function Taylor
9 7 Taylor Series Brook Taylor was an9 7 Taylor Series Brook Taylor was an
9 2 Taylor Series Brook Taylor was an9 2 Taylor Series Brook Taylor was an
Exam1 EXAMI Sec 1 1 THE TAYLOR SERIESExam1 EXAMI Sec 1 1 THE TAYLOR SERIES
Taylor Series The Coefficients of a Power SeriesTaylor Series The Coefficients of a Power Series