Maclaurin and Taylor Series Introduction A wide range

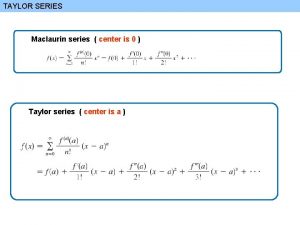
Maclaurin and Taylor Series

Introduction • A wide range of functions of x can be expressed as an infinite series (a bit like the Binomial Expansion) • These are sometimes called a ‘power series’ • These are used very often as they can allow us to find values of things such as Sinx or Cosx to whatever degree of accuracy we want • Remember that many values of Sin and Cos are irrational numbers, hence cannot always be calculated exactly • The series sum idea is possibly what your calculator does to calculate values such as Sin 20 etc…

Teachings for Exercise 6 a

Maclaurin and Taylor Series You need to be able to find and use higher derivatives of functions You will be familiar with the notation for differentiation You need to be able to find more and more differentials Fortunately, the notation is pretty much what you’d expect! 2 nd Differential 3 rd Differential 4 th Differential 1 st Differential nth Differential 6 A

Maclaurin and Taylor Series You need to be able to find and use higher derivatives of functions You also need to understand this next piece of notation: So this means find the value of the 4 th differential when x = 6 The nth differential Sub in x = a This means the same as the above 6 A

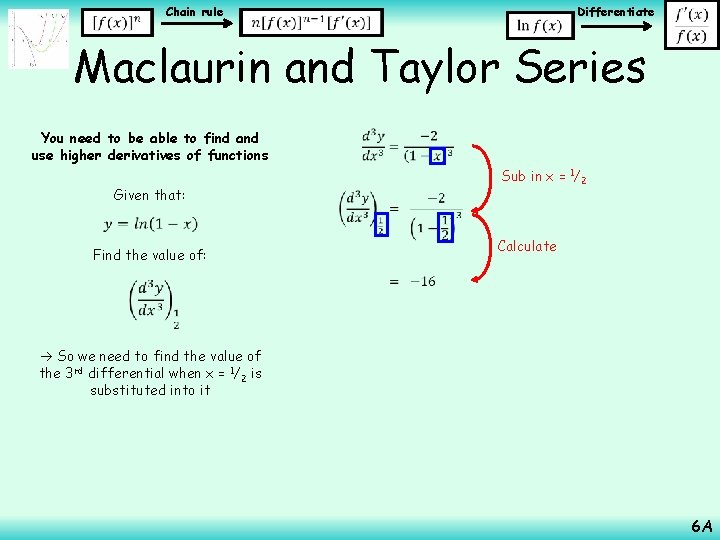
Chain rule Differentiate Maclaurin and Taylor Series You need to be able to find and use higher derivatives of functions Given that: Find the value of: So we need to find the value of the 3 rd differential when x = 1/2 is substituted into it Differentiate using the rule for ln (above) Differentiate using the chain rule (rewrite as a bracket to a power first) Differentiate using the chain rule again (rewrite as a bracket to a power first) If you prefer to leave the differentials in the ‘negative power’ form we use, that is ok. But be aware that Differentiate sometimes you can simplify these and you might miss if they aren’t written as above! this Simplify 6 A

Chain rule Differentiate Maclaurin and Taylor Series You need to be able to find and use higher derivatives of functions Given that: Sub in x = 1/2 Calculate Find the value of: So we need to find the value of the 3 rd differential when x = 1/2 is substituted into it 6 A

Differentiate Maclaurin and Taylor Series You need to be able to find and use higher derivatives of functions Given that: Differentiate using the rule for ‘e’ (above) Use the equation from the start to replace the exponential a) Show that: 6 A

Maclaurin and Taylor Series You need to be able to find and use higher derivatives of functions Given that: a) Show that: b) By differentiating the result twice more with respect to x, find f’’(x) and f’’’(x) In this chapter you will need to use the product rule A LOT! Differentiate using the product rule Differentiate (using the product rule for the second term) Simplify by grouping like terms Note that you could also get to f’’’(x) using the dy/ dx notation… Product Rule for 2 xf(x) Product Rule for 2 xf’(x) 6 A

Maclaurin and Taylor Series You need to be able to find and use higher derivatives of functions Given that: a) Show that: b) By differentiating the result twice more with respect to x, find f’’(x) and f’’’(x) c) Deduce the values of f(0), f’’(0) and f’’’(0) Start by finding f(0), and then using the result to work out f’(0) Sub in 0 Calculate, using f(0) and f’(0) Sub in 0 Calculate, using f(0), f’(0) and f’’(0) 6 A

Teachings for Exercise 6 b

Maclaurin and Taylor Series You can express many functions of x as an infinite series in ascending powers of x, by using Maclaurin’s expansion In C 4 differentiation, you have seen that functions such as: and Can be expressed as a series sum, when x is within certain limits. n = 1/2 x=x In C 4 we started by considering the general form of the binomial expansion Sub in n = 1/2 and x = x Simplify This series can be used to calculate an approximate value for the original expression, for particular values of x For the sequence to converge, x needs to be between -1 and 1. If not, the terms which are squared/cubed will increase exponentially and cause the sequence to diverge If we want a more accurate approximation, we can just calculate more terms in the series and include these as well! 6 B

Maclaurin and Taylor Series You can express many functions of x as an infinite series in ascending powers of x, by using Maclaurin’s expansion and Can be expressed as a series sum, when x is within certain limits. x = -2 x In C 4 we started by considering the general form of the binomial expansion In C 4 differentiation, you have seen that functions such as: n = -1 Sub in n = -1 and x = -2 x Simplify For this series to converge, we need to look at the term which is raised to a power Again, the value of this expression must be between -1 and 1 for it to converge. As the term itself is ‘-2 x’… 6 B

Maclaurin and Taylor Series You can express many functions of x as an infinite series in ascending powers of x, by using Maclaurin’s expansion More functions can be expressed this way, as series sums This is an extremely valuable tool as it allows us to calculate functions to any degree of accuracy It is also essentially the process a calculator goes through when calculating such values! 6 B

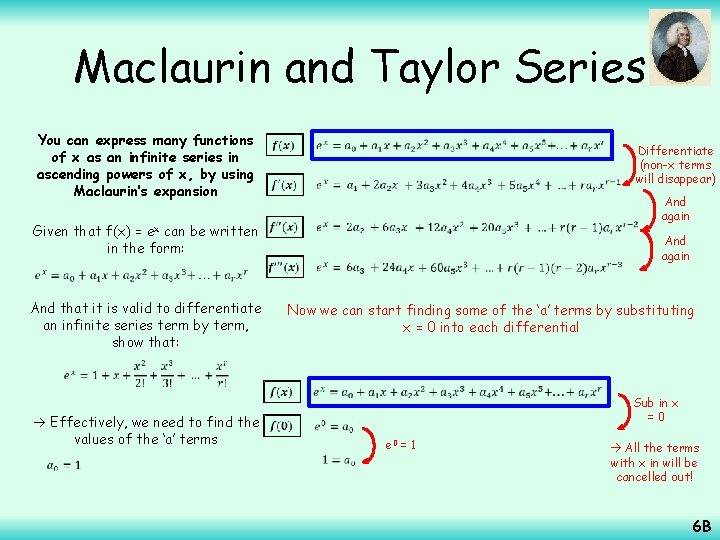
Maclaurin and Taylor Series You can express many functions of x as an infinite series in ascending powers of x, by using Maclaurin’s expansion Given that f(x) = ex can be written in the form: And that it is valid to differentiate an infinite series term by term, show that: Differentiate (non-x terms will disappear) And again Now we can start finding some of the ‘a’ terms by substituting x = 0 into each differential Effectively, we need to find the values of the ‘a’ terms Sub in x =0 e 0 = 1 All the terms with x in will be cancelled out! 6 B

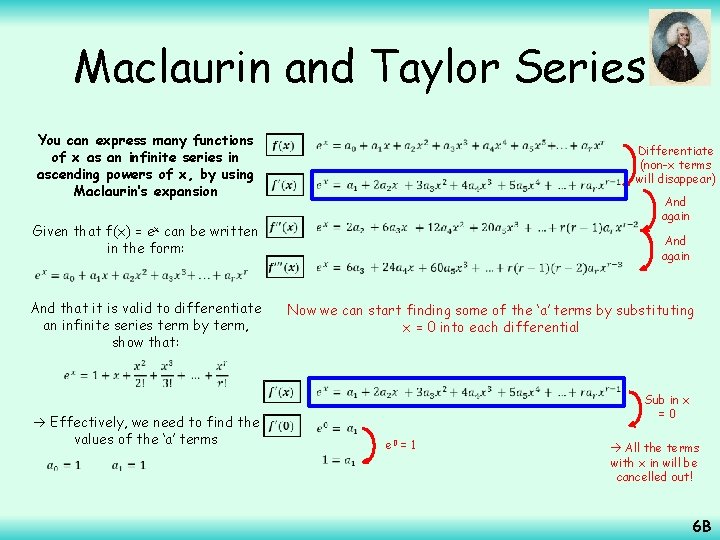
Maclaurin and Taylor Series You can express many functions of x as an infinite series in ascending powers of x, by using Maclaurin’s expansion Given that f(x) = ex can be written in the form: And that it is valid to differentiate an infinite series term by term, show that: Differentiate (non-x terms will disappear) And again Now we can start finding some of the ‘a’ terms by substituting x = 0 into each differential Effectively, we need to find the values of the ‘a’ terms e 0 = 1 Sub in x =0 All the terms with x in will be cancelled out! 6 B

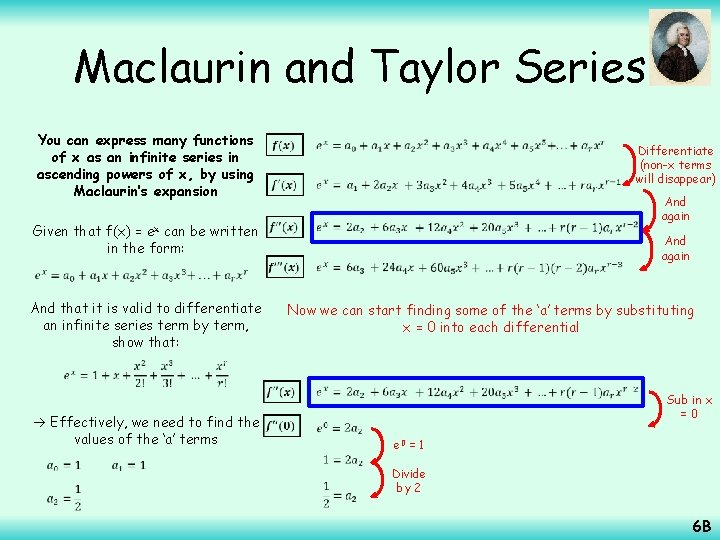
Maclaurin and Taylor Series You can express many functions of x as an infinite series in ascending powers of x, by using Maclaurin’s expansion Given that f(x) = ex can be written in the form: And that it is valid to differentiate an infinite series term by term, show that: Differentiate (non-x terms will disappear) And again Now we can start finding some of the ‘a’ terms by substituting x = 0 into each differential Effectively, we need to find the values of the ‘a’ terms Sub in x =0 e 0 = 1 Divide by 2 6 B

Maclaurin and Taylor Series You can express many functions of x as an infinite series in ascending powers of x, by using Maclaurin’s expansion Given that f(x) = ex can be written in the form: And that it is valid to differentiate an infinite series term by term, show that: Differentiate (non-x terms will disappear) And again Now we can start finding some of the ‘a’ terms by substituting x = 0 into each differential Effectively, we need to find the values of the ‘a’ terms Sub in x =0 e 0 = 1 Divide by 6 6 B

Maclaurin and Taylor Series You can express many functions of x as an infinite series in ascending powers of x, by using Maclaurin’s expansion We can now replace the ‘a’ terms with the values we calculated… Given that f(x) = ex can be written in the form: However, 1/2 = 1/2!, and 1/6 = 1/3! etc… And that it is valid to differentiate an infinite series term by term, show that: Note that for the first term, r is defined as being ‘ 0’ It is possible to go through similar processes to find series summations of other functions However in the early 18 th century a Scottish mathematician called Colin Maclaurin created a generalised solution that can be used in many expansions… 6 B

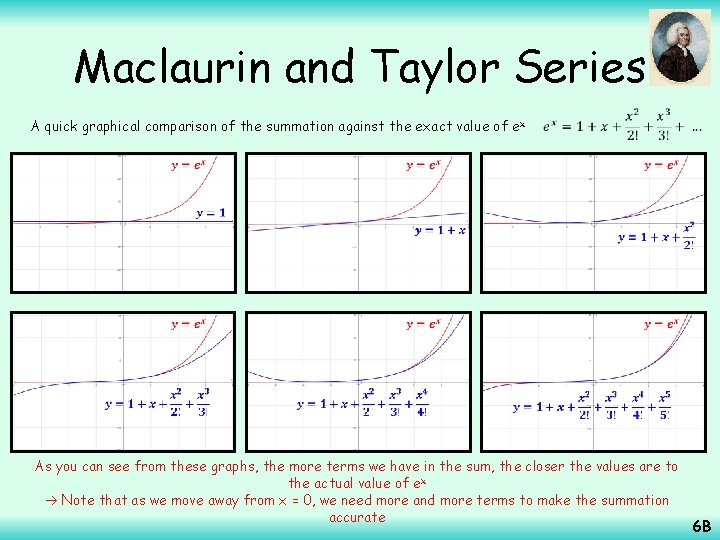
Maclaurin and Taylor Series A quick graphical comparison of the summation against the exact value of e x As you can see from these graphs, the more terms we have in the sum, the closer the values are to the actual value of ex Note that as we move away from x = 0, we need more and more terms to make the summation accurate 6 B

Maclaurin and Taylor Series You can express many functions of x as an infinite series in ascending powers of x, by using Maclaurin’s expansion For the continuous function: Provided that f(0), f’’(0), …, fr(0) all have finite values, then: You get given this result in the formula booklet! Some functions are only valid for certain values of x (similar to the binomial expansion) The ranges are given where appropriate in FP 2 6 B

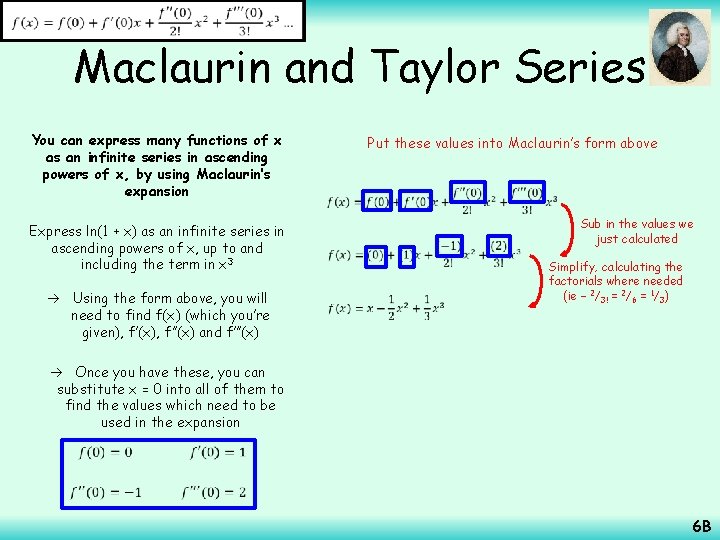
Differentiate Maclaurin and Taylor Series You can express many functions of x as an infinite series in ascending powers of x, by using Maclaurin’s expansion Express ln(1 + x) as an infinite series in ascending powers of x, up to and including the term in x 3 Using the form above, you will need to find f(x) (which you’re given), f’(x), f’’(x) and f’’’(x) Once you have these, you can substitute x = 0 into all of them to find the values which need to be used in the expansion Differentiate using the rule for the natural logarithm Differentiate by writing as a power and using the chain rule again Use the chain rule 6 B

Differentiate Maclaurin and Taylor Series You can express many functions of x as an infinite series in ascending powers of x, by using Maclaurin’s expansion Express ln(1 + x) as an infinite series in ascending powers of x, up to and including the term in x 3 Differentiate by writing as a power and using the chain rule again Substitute x = 0 into each of these to find the coefficients for the form above Once you have these, you can substitute x = 0 into all of them to find the values which need to be used in the expansion Differentiate by writing as a power and using the chain rule Using the form above, you will need to find f(x) (which you’re given), f’(x), f’’(x) and f’’’(x) Differentiate using the rule for the natural logarithm 6 B

Maclaurin and Taylor Series You can express many functions of x as an infinite series in ascending powers of x, by using Maclaurin’s expansion Express ln(1 + x) as an infinite series in ascending powers of x, up to and including the term in x 3 Using the form above, you will need to find f(x) (which you’re given), f’(x), f’’(x) and f’’’(x) Put these values into Maclaurin’s form above Sub in the values we just calculated Simplify, calculating the factorials where needed (ie – 2/3! = 2/6 = 1/3) Once you have these, you can substitute x = 0 into all of them to find the values which need to be used in the expansion 6 B

Maclaurin and Taylor Series You can express many functions of x as an infinite series in ascending powers of x, by using Maclaurin’s expansion Express ln(1 + x) as an infinite series in ascending powers of x, up to and including the term in x 3 Sub in x = 0. 05 Calculate This is accurate to 5 dp Sub in x = 0. 25 Calculate Using this series, find approximate values for: a) ln(1. 05) b) ln(1. 25) c) ln(1. 8) The Maclaurin’s expansion requires more terms to be accurate, as the value of x moves away from 0… This is accurate to 2 dp Sub in x = 0. 8 Calculate This is not even accurate to 1 dp! 6 B

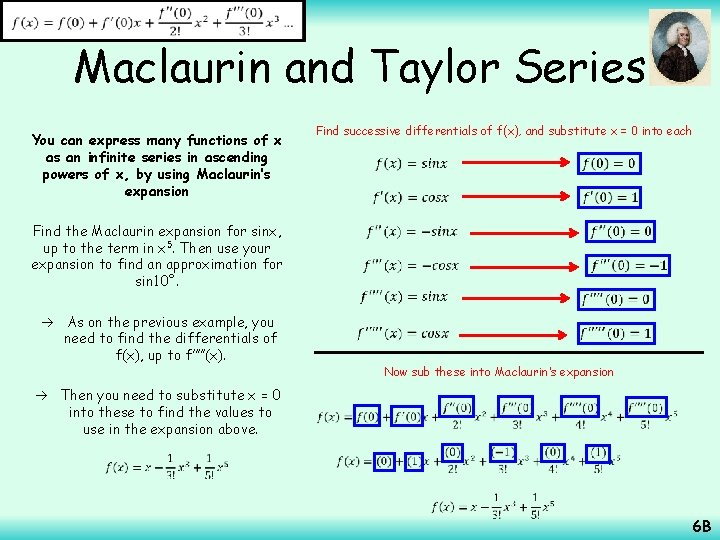
Maclaurin and Taylor Series Find successive differentials of f(x), and substitute x = 0 into each You can express many functions of x as an infinite series in ascending powers of x, by using Maclaurin’s expansion Find the Maclaurin expansion for sinx, up to the term in x 5. Then use your expansion to find an approximation for sin 10˚. As on the previous example, you need to find the differentials of f(x), up to f’’’’’(x). Then you need to substitute x = 0 into these to find the values to use in the expansion above. Now sub these into Maclaurin’s expansion 6 B

Maclaurin and Taylor Series The angle MUST be in radians for this process to work… You can express many functions of x as an infinite series in ascending powers of x, by using Maclaurin’s expansion Find the Maclaurin expansion for sinx, up to the term in x 5. Then use your expansion to find an approximation for sin 10˚. As on the previous example, you need to find the differentials of f(x), up to f’’’’’(x). 10˚ = π/18 radians (since 180˚ = π) Sub in x = π/18 Calculate Then you need to substitute x = 0 into these to find the values to use in the expansion above. 6 B

Teachings for Exercise 6 c

Maclaurin and Taylor Series You can find the series expansions of composite functions using known Maclaurin’s expansions You can use some known expansions to find more complicated ones Valid for -1 < x ≤ 1 These expansions are given to you in the formula booklet, so you just need to be able to recognise when to use them! Be aware that this formula is actually in the C 2 section of the booklet, rather than FP 2! Valid for all values of x Valid for -1 < x < 1 You can use any of these with the x terms replaced with 2 x, -5 x, x/2, x 2 etc… 6 C

Maclaurin and Taylor Series You can find the series expansions of composite functions using known Maclaurin’s expansions Write down the first 4 non-zero terms in the series expansion of cos(2 x 2) (in ascending powers of x) Start by writing out the expansion of cosx Replace ‘x’ terms with ‘ 2 x 2’ Work out the brackets and factorials Simplify where possible Then just replace all the ‘x’ terms with ‘ 2 x 2’ terms Make sure you use brackets!! 6 C

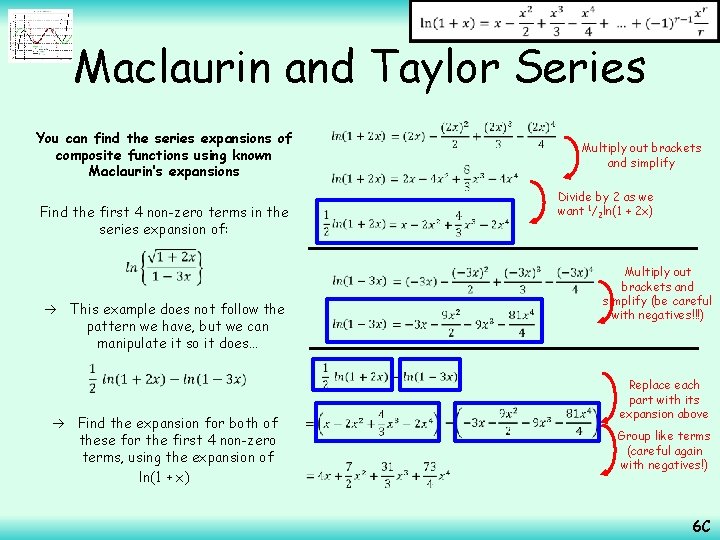
Maclaurin and Taylor Series You can find the series expansions of composite functions using known Maclaurin’s expansions Find the first 4 non-zero terms in the series expansion of: This example does not follow the pattern we have, but we can manipulate it so it does… Rewrite as a subtraction (log laws are from C 2) Write the first one using a power Use the power law This is equivalent to the original logarithm, but now both are in the form that we have an expansion for! 6 C

Maclaurin and Taylor Series You can find the series expansions of composite functions using known Maclaurin’s expansions Find the first 4 non-zero terms in the series expansion of: This example does not follow the pattern we have, but we can manipulate it so it does… Multiply out brackets and simplify Divide by 2 as we want 1/2 ln(1 + 2 x) Multiply out brackets and simplify (be careful with negatives!!!) Find the expansion for both of these for the first 4 non-zero terms, using the expansion of ln(1 + x) Replace each part with its expansion above Group like terms (careful again with negatives!) 6 C

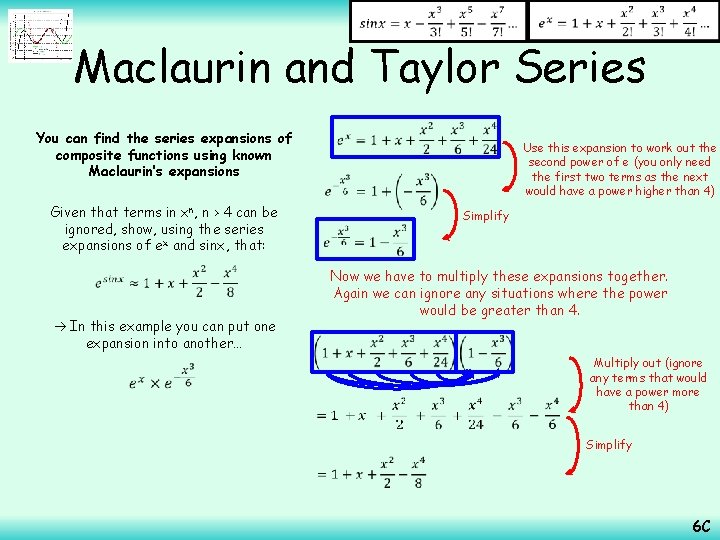
Maclaurin and Taylor Series You can find the series expansions of composite functions using known Maclaurin’s expansions Given that terms in xn, n > 4 can be ignored, show, using the series expansions of ex and sinx, that: In this example you can put one expansion into another… Replace sinx with the expansion as far as x 3 (as we are not using powers of greater than 4) This can be written as a multiplication (as when you multiply, you add the powers) Work out the factorial So we will multiply together these two expansions of e 6 C

Maclaurin and Taylor Series You can find the series expansions of composite functions using known Maclaurin’s expansions Given that terms in xn, n > 4 can be ignored, show, using the series expansions of ex and sinx, that: Simplify In this example you can put one expansion into another… Use this expansion to work out the second power of e (you only need the first two terms as the next would have a power higher than 4) Now we have to multiply these expansions together. Again we can ignore any situations where the power would be greater than 4. Multiply out (ignore any terms that would have a power more than 4) Simplify 6 C

Teachings for Exercise 6 d

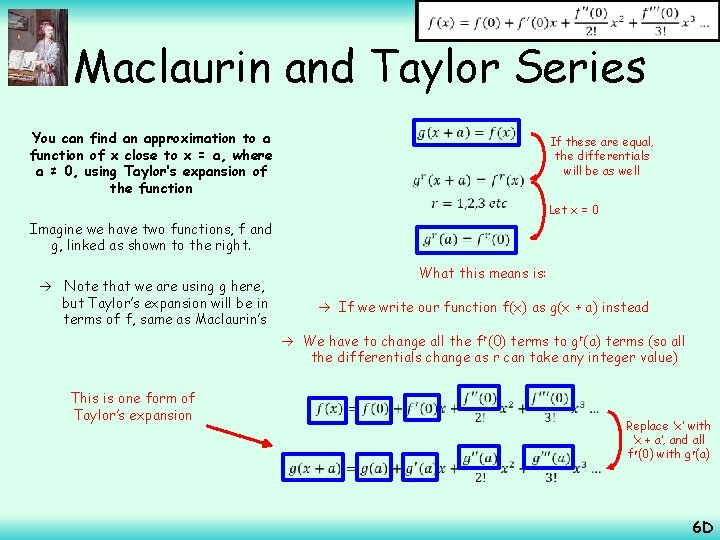
Maclaurin and Taylor Series You can find an approximation to a function of x close to x = a, where a ≠ 0, using Taylor’s expansion of the function The Maclaurin expansion is very effective and relatively straightforward to use, but as you’ve seen, it has some limitations Some functions, such as e√x and lnx cannot be expanded In addition to this, you have seen that the expansion focuses of values of x that are equal to or very close to 0 The idea of the Taylor Series came from the Scottish mathematician James Gregory, but was formally introduced later by the English mathematician Brook Taylor We can use Taylor’s expansion in a wider range of cases 6 D

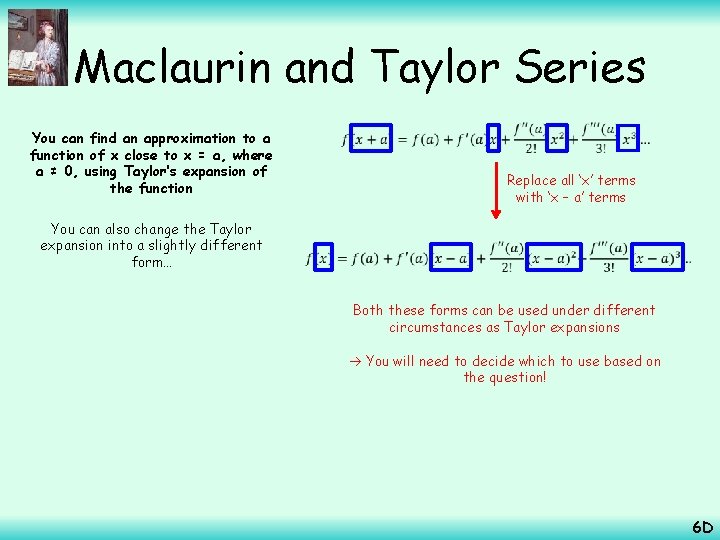
Maclaurin and Taylor Series You can find an approximation to a function of x close to x = a, where a ≠ 0, using Taylor’s expansion of the function If these are equal, the differentials will be as well Imagine we have two functions, f and g, linked as shown to the right. Let x = 0 What this means is: Note that we are using g here, but Taylor’s expansion will be in terms of f, same as Maclaurin’s If we write our function f(x) as g(x + a) instead We have to change all the fr(0) terms to gr(a) terms (so all the differentials change as r can take any integer value) This is one form of Taylor’s expansion Replace ‘x’ with ‘x + a’, and all fr(0) with gr(a) 6 D

Maclaurin and Taylor Series You can find an approximation to a function of x close to x = a, where a ≠ 0, using Taylor’s expansion of the function You can also change the Taylor expansion into a slightly different form… Replace all ‘x’ terms with ‘x – a’ terms Both these forms can be used under different circumstances as Taylor expansions You will need to decide which to use based on the question! 6 D

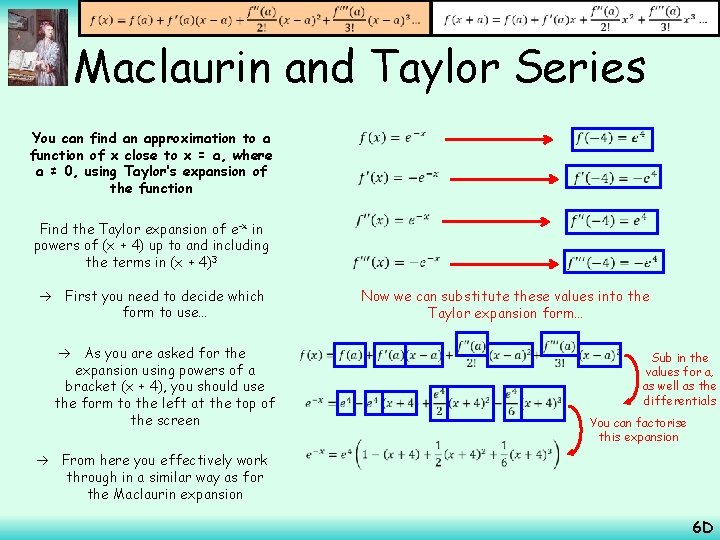
Maclaurin and Taylor Series You can find an approximation to a function of x close to x = a, where a ≠ 0, using Taylor’s expansion of the function Find the Taylor expansion of e-x in powers of (x + 4) up to and including the terms in (x + 4)3 You need to find successive differentials up to f’’’(x) The substitute ‘a’ into these (instead of 0 as you would have done with the Maclaurin expansion) The value ‘a’ will be -4 (compare the form of the expansion with the bracket!) First you need to decide which form to use… As you are asked for the expansion using powers of a bracket (x + 4), you should use the form to the left at the top of the screen From here you effectively work through in a similar way as for the Maclaurin expansion Now we can substitute these values into the Taylor expansion form… 6 D

Maclaurin and Taylor Series You can find an approximation to a function of x close to x = a, where a ≠ 0, using Taylor’s expansion of the function Find the Taylor expansion of e-x in powers of (x + 4) up to and including the terms in (x + 4)3 First you need to decide which form to use… As you are asked for the expansion using powers of a bracket (x + 4), you should use the form to the left at the top of the screen From here you effectively work through in a similar way as for the Maclaurin expansion Now we can substitute these values into the Taylor expansion form… Sub in the values for a, as well as the differentials You can factorise this expansion 6 D

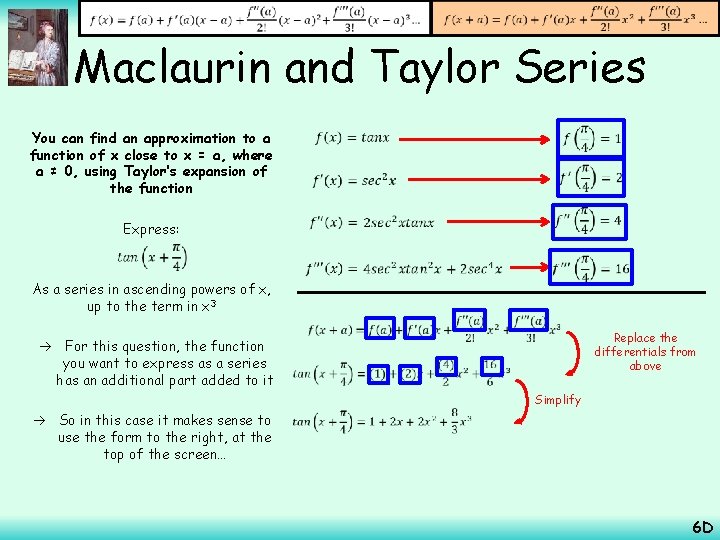
Maclaurin and Taylor Series You can find an approximation to a function of x close to x = a, where a ≠ 0, using Taylor’s expansion of the function For f(x) you can just use tanx The Taylor series takes into account the transformation to tan (x + π/4) Express: As a series in ascending powers of x, up to the term in x 3 For this question, the function you want to express as a series has an additional part added to it So in this case it makes sense to use the form to the right, at the top of the screen… Differentiate using the chain rule and product rule Product rule for 2 sec 2 xtanx Chain rule Simplify 6 D

Maclaurin and Taylor Series You can find an approximation to a function of x close to x = a, where a ≠ 0, using Taylor’s expansion of the function Express: As a series in ascending powers of x, up to the term in x 3 For this question, the function you want to express as a series has an additional part added to it So in this case it makes sense to use the form to the right, at the top of the screen… Replace the differentials from above Simplify 6 D

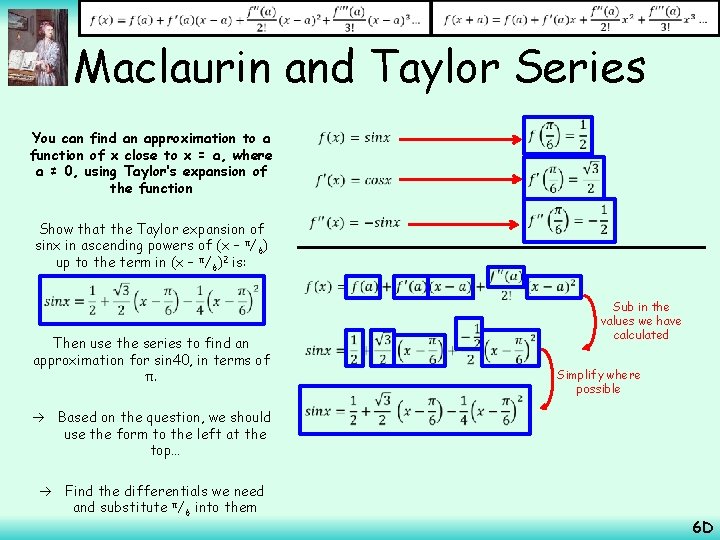
Maclaurin and Taylor Series You can find an approximation to a function of x close to x = a, where a ≠ 0, using Taylor’s expansion of the function Show that the Taylor expansion of sinx in ascending powers of (x – π/6) up to the term in (x – π/6)2 is: Then use the series to find an approximation for sin 40, in terms of π. Based on the question, we should use the form to the left at the top… Find the differentials we need and substitute π/6 into them Sub in the values we have calculated Simplify where possible 6 D

Maclaurin and Taylor Series The angle MUST be in radians for this process to work… You can find an approximation to a function of x close to x = a, where a ≠ 0, using Taylor’s expansion of the function Show that the Taylor expansion of sinx in ascending powers of (x – π/6) up to the term in (x – π/6)2 is: Then use the series to find an approximation for sin 40, in terms of π. Based on the question, we should use the form to the left at the top… Find the differentials we need and substitute π/6 into them 40º = 2π/9 radians (since 40º is 2/9 of 180º) Sub in x = Calculate the bracket parts 2π/ 9 Simplify 6 D

Teachings for Exercise 6 e

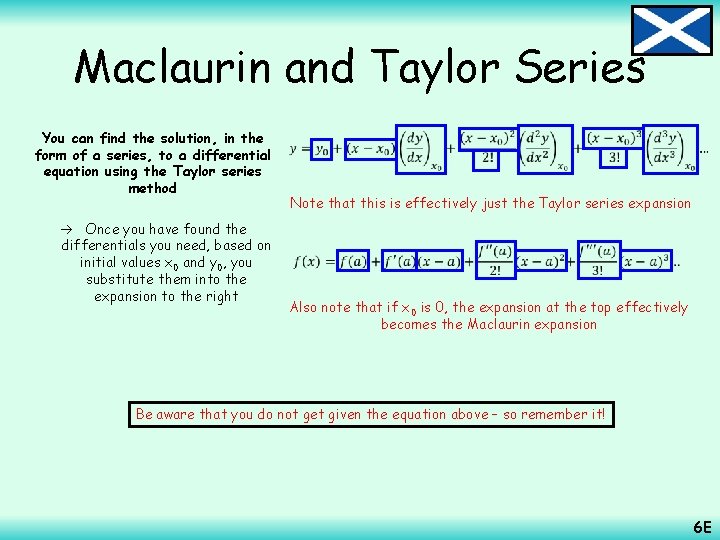
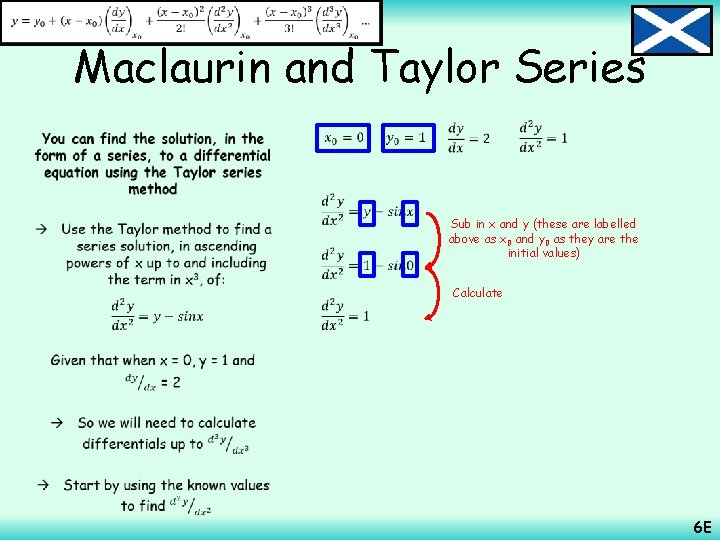
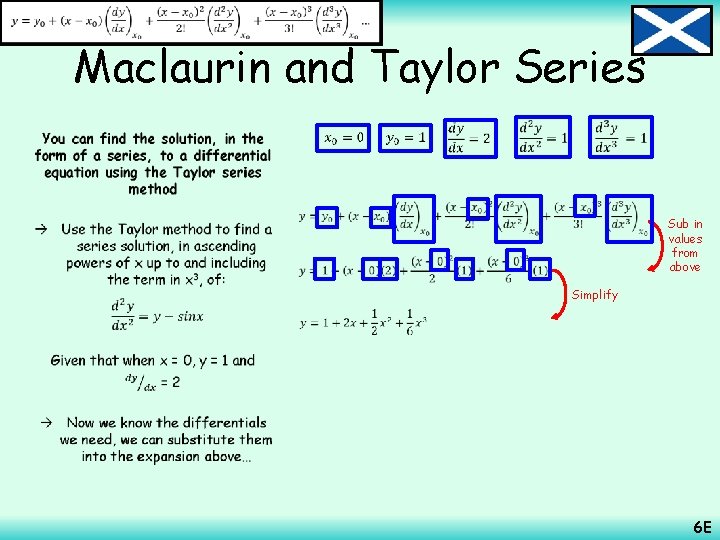
Maclaurin and Taylor Series Suppose you have a first order differential equation of the form: You can find the solution, in the form of a series, to a differential equation using the Taylor series method Some differential equations cannot be solved using the methods from chapters 4 and 5 However, for these it is often possible to find a series solution instead So the differential is a function of both x and y And we know two initial values 6 E

Maclaurin and Taylor Series You can find the solution, in the form of a series, to a differential equation using the Taylor series method Once you have found the differentials you need, based on initial values x 0 and y 0, you substitute them into the expansion to the right Note that this is effectively just the Taylor series expansion Also note that if x 0 is 0, the expansion at the top effectively becomes the Maclaurin expansion Be aware that you do not get given the equation above – so remember it! 6 E

Maclaurin and Taylor Series • Sub in x and y (these are labelled above as x 0 and y 0 as they are the initial values) Calculate 6 E

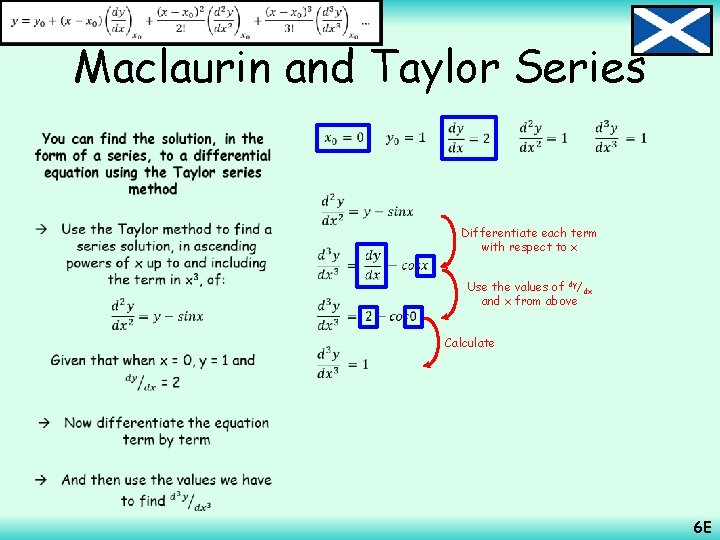
Maclaurin and Taylor Series • Differentiate each term with respect to x Use the values of dy/dx and x from above Calculate 6 E

Maclaurin and Taylor Series • Sub in values from above Simplify 6 E

Maclaurin and Taylor Series • Sub in values from above Simplify Calculate 6 E

Maclaurin and Taylor Series • Differentiate, using the product rule where needed Product for xy Sub in the values. Rule we have calculated up to this point Simplify Calculate 6 E

Maclaurin and Taylor Series • Differentiate each term (again using the product rule where appropriate) Product forwe xdyhave /dx Sub in the. Rule values so far (or group terms first – your choice!) Simplify Calculate 6 E

Maclaurin and Taylor Series You can find the solution, in the form of a series, to a differential equation using the Taylor series method Given that: Substitute in all the values we calculated… And that y = 1 and dy/dx = 2 when x = 1, express y as a series in ascending powers of (x – 1), up to and including the term in (x – 1)4 And you can now use the values you have calculated in the expansion above… Simplify 6 E

Maclaurin and Taylor Series • Sub in values Calculate 6 E

Maclaurin and Taylor Series • Differentiate each term Sub in values Calculate 6 E

Maclaurin and Taylor Series • dy Sub in values. Product rule for 2 y /dx Calculate 6 E

Maclaurin and Taylor Series • Now you can substitute these into the form above… Sub in values Simplify 6 E

Summary • You have learnt the forms of the Maclaurin and Taylor series • You have seen how they create an infinite sequence that can converge to a function • You have seen how to use these in differential equations