11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND




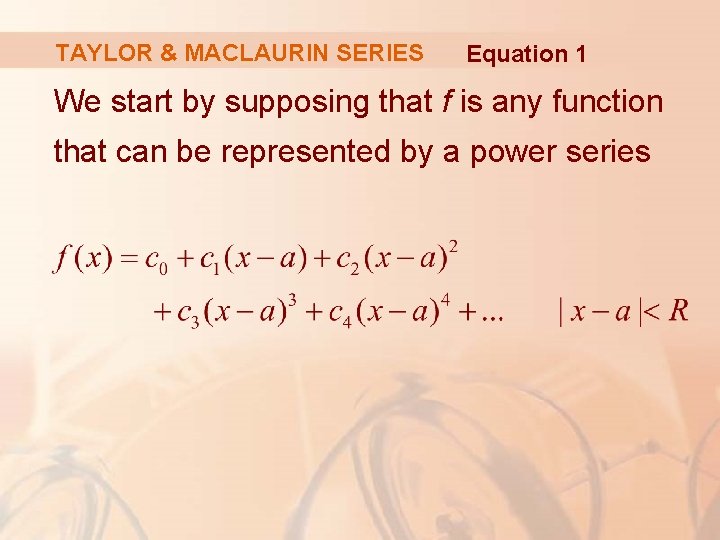


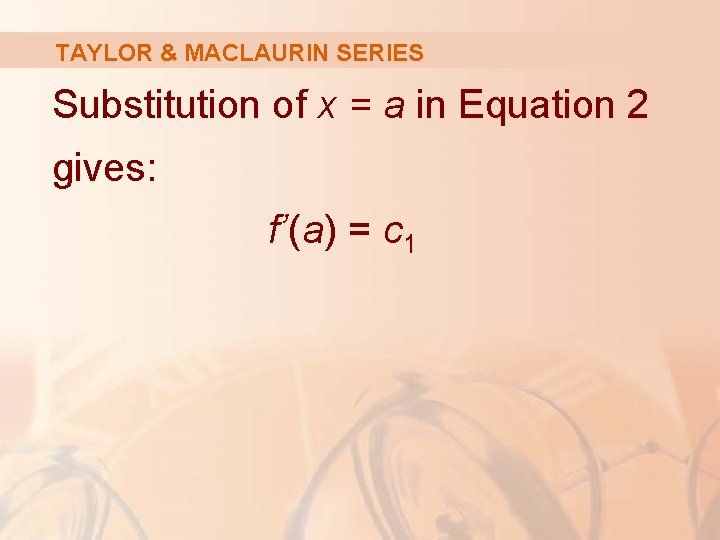
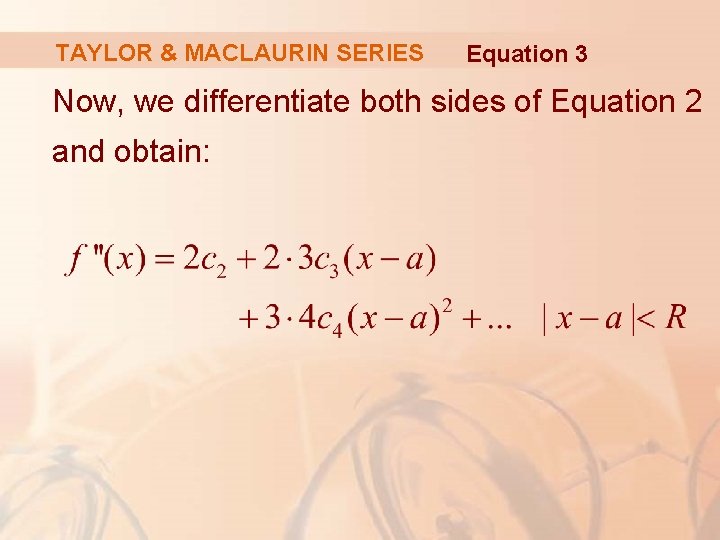
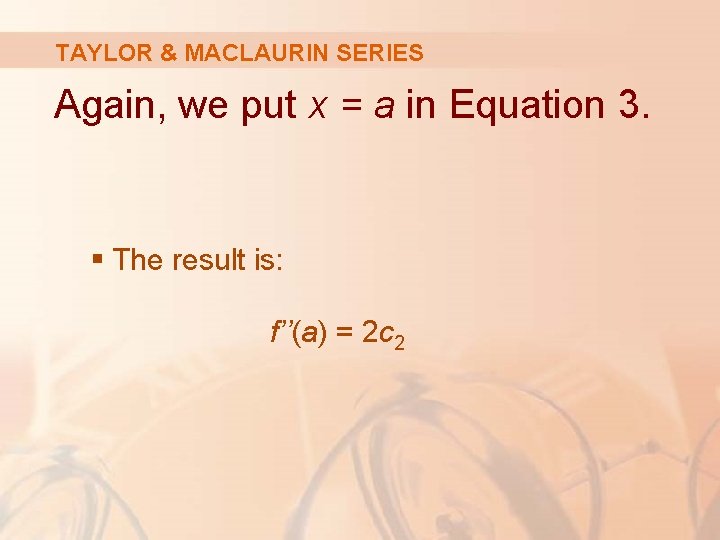

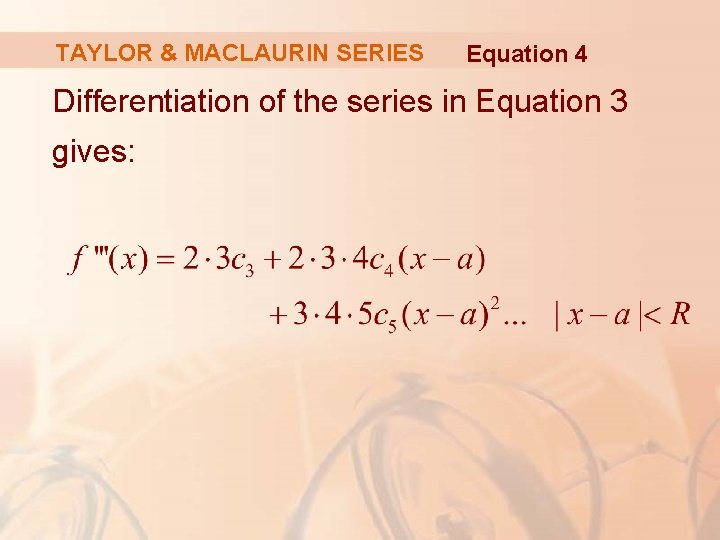
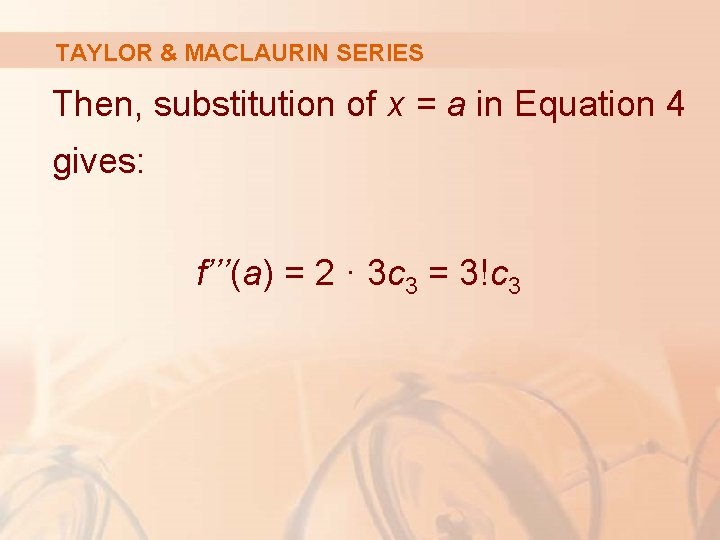





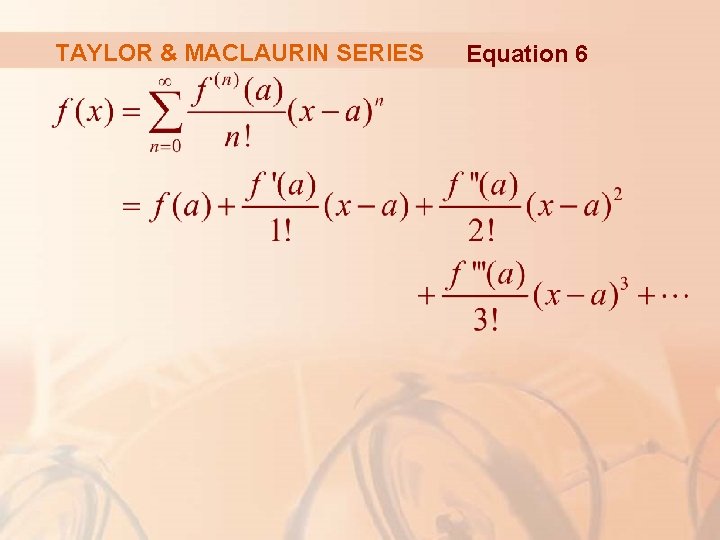







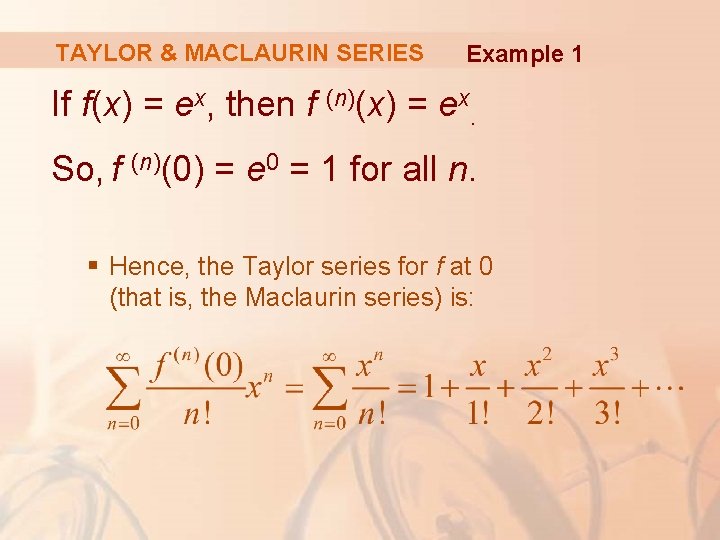

- Slides: 28

11 INFINITE SEQUENCES AND SERIES

INFINITE SEQUENCES AND SERIES In section 11. 9, we were able to find power series representations for a certain restricted class of functions.

INFINITE SEQUENCES AND SERIES Here, we investigate more general problems. § Which functions have power series representations? § How can we find such representations?

INFINITE SEQUENCES AND SERIES 11. 10 Taylor and Maclaurin Series In this section, we will learn: How to find the Taylor and Maclaurin Series of a function and to multiply and divide a power series.
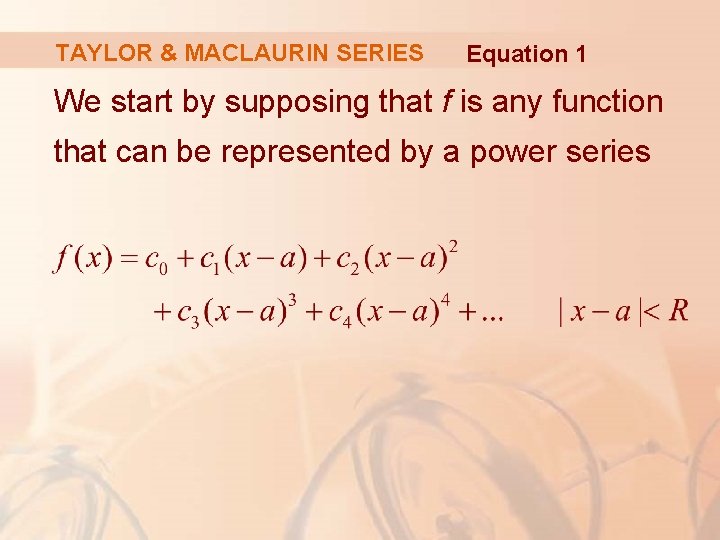
TAYLOR & MACLAURIN SERIES Equation 1 We start by supposing that f is any function that can be represented by a power series

TAYLOR & MACLAURIN SERIES Let’s try to determine what the coefficients cn must be in terms of f. § To begin, notice that, if we put x = a in Equation 1, then all terms after the first one are 0 and we get: f(a) = c 0

TAYLOR & MACLAURIN SERIES Equation 2 By Theorem 2 in Section 11. 9, we can differentiate the series in Equation 1 term by term:
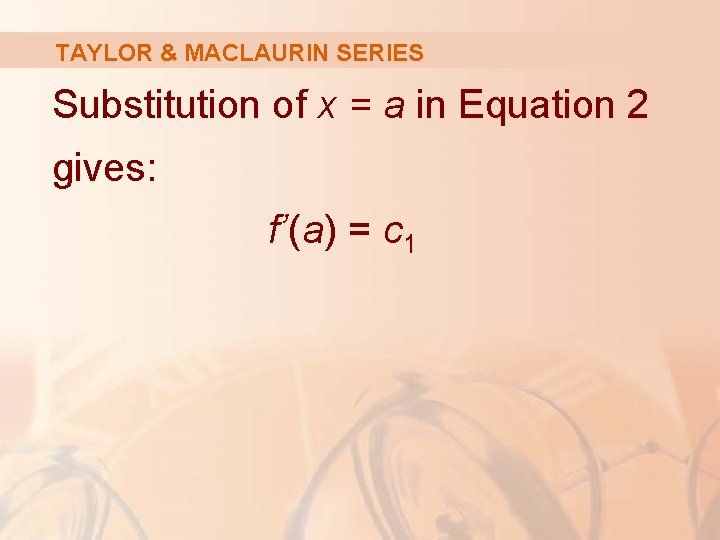
TAYLOR & MACLAURIN SERIES Substitution of x = a in Equation 2 gives: f’(a) = c 1
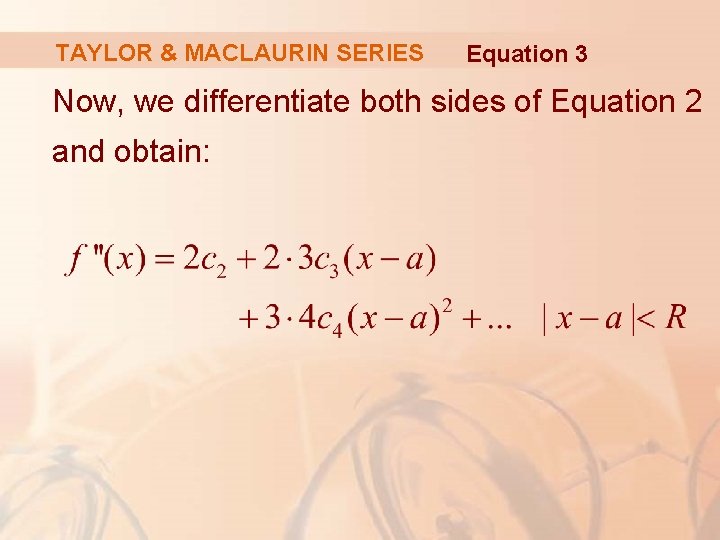
TAYLOR & MACLAURIN SERIES Equation 3 Now, we differentiate both sides of Equation 2 and obtain:
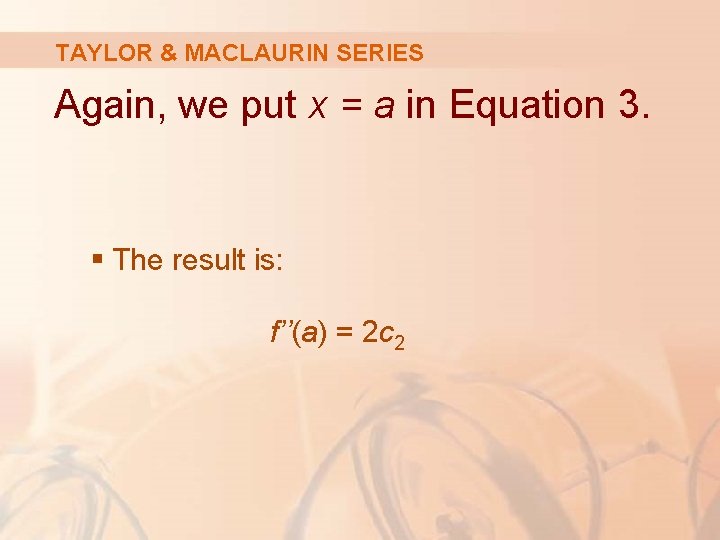
TAYLOR & MACLAURIN SERIES Again, we put x = a in Equation 3. § The result is: f’’(a) = 2 c 2

TAYLOR & MACLAURIN SERIES Let’s apply the procedure one more time.
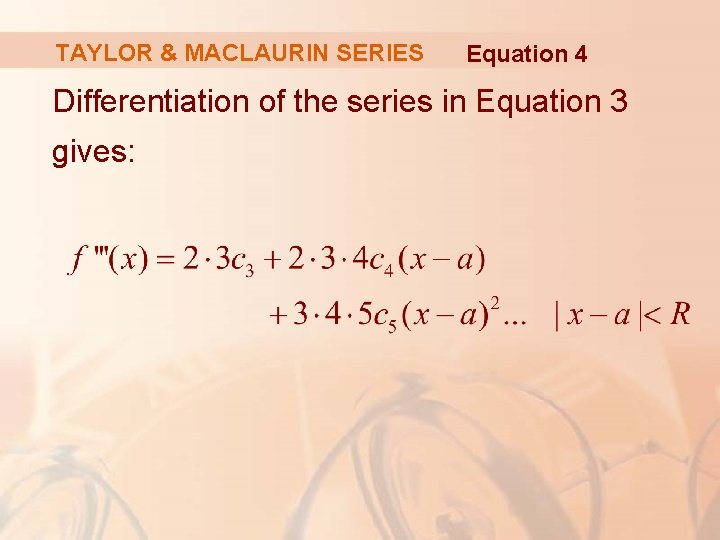
TAYLOR & MACLAURIN SERIES Equation 4 Differentiation of the series in Equation 3 gives:
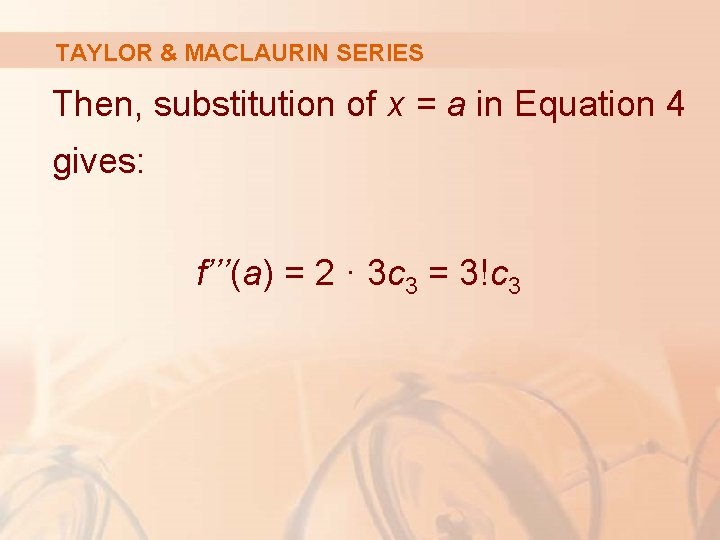
TAYLOR & MACLAURIN SERIES Then, substitution of x = a in Equation 4 gives: f’’’(a) = 2 · 3 c 3 = 3!c 3

TAYLOR & MACLAURIN SERIES By now, you can see the pattern. § If we continue to differentiate and substitute x = a, we obtain:

TAYLOR & MACLAURIN SERIES Solving the equation for the nth coefficient cn, we get:

TAYLOR & MACLAURIN SERIES The formula remains valid even for n = 0 if we adopt the conventions that 0! = 1 and f (0) = (f). § Thus, we have proved the following theorem.

TAYLOR & MACLAURIN SERIES Theorem 5 If f has a power series representation (expansion) at a, that is, if then its coefficients are given by:

TAYLOR & MACLAURIN SERIES Equation 6 Substituting this formula for cn back into the series, we see that if f has a power series expansion at a, then it must be of the following form.
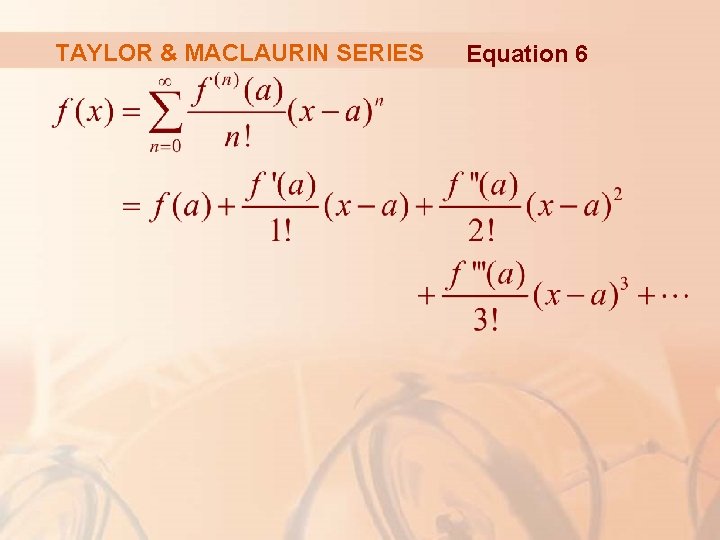
TAYLOR & MACLAURIN SERIES Equation 6

TAYLOR SERIES The series in Equation 6 is called the Taylor series of the function f at a (or about a or centered at a).

TAYLOR SERIES Equation 7 For the special case a = 0, the Taylor series becomes:

MACLAURIN SERIES Equation 7 This case arises frequently enough that it is given the special name Maclaurin series.

TAYLOR & MACLAURIN SERIES The Taylor series is named after the English mathematician Brook Taylor (1685– 1731). The Maclaurin series is named for the Scottish mathematician Colin Maclaurin (1698– 1746). § This is despite the fact that the Maclaurin series is really just a special case of the Taylor series.

MACLAURIN SERIES Maclaurin series are named after Colin Maclaurin because he popularized them in his calculus textbook Treatise of Fluxions published in 1742.

TAYLOR & MACLAURIN SERIES Note We have shown that if, f can be represented as a power series about a, then f is equal to the sum of its Taylor series. § However, there exist functions that are not equal to the sum of their Taylor series. § Give an Example?

TAYLOR & MACLAURIN SERIES Example 1 Find the Maclaurin series of the function f(x) = ex and its radius of convergence.
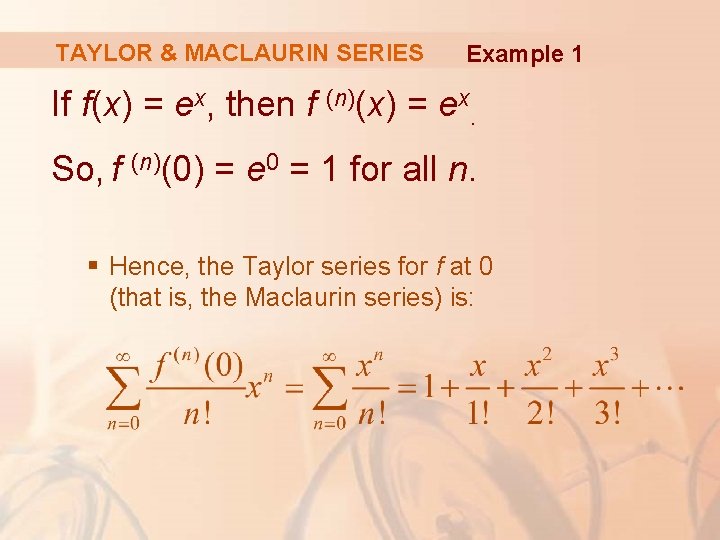
TAYLOR & MACLAURIN SERIES Example 1 If f(x) = ex, then f (n)(x) = ex. So, f (n)(0) = e 0 = 1 for all n. § Hence, the Taylor series for f at 0 (that is, the Maclaurin series) is:

TAYLOR & MACLAURIN SERIES To find the radius of convergence, we let an = xn/n! § Then, § So, by the Ratio Test, the series converges for all x and the radius of convergence is R = ∞.
 The alternating series estimation theorem
The alternating series estimation theorem Infinite diversity in infinite combinations
Infinite diversity in infinite combinations Arithmetic and geometric sequences and series
Arithmetic and geometric sequences and series Differentiate finite sequence and infinite sequence.
Differentiate finite sequence and infinite sequence. Unit 10 sequences and series homework 1 answers
Unit 10 sequences and series homework 1 answers Unit 10 sequences and series homework 1 answers
Unit 10 sequences and series homework 1 answers Chapter 12 sequences and series answers
Chapter 12 sequences and series answers 10-3 geometric sequences and series
10-3 geometric sequences and series Module 12 sequences and series
Module 12 sequences and series 10-3 skills practice geometric sequences and series
10-3 skills practice geometric sequences and series 10-2 arithmetic sequences and series answer key
10-2 arithmetic sequences and series answer key 10-1 sequences series and sigma notation
10-1 sequences series and sigma notation Sum of gp formula
Sum of gp formula Geometric sequence equation
Geometric sequence equation Sequences and series math 20-1
Sequences and series math 20-1 Chapter 1 sequences and series
Chapter 1 sequences and series Sequences and series math 20-1
Sequences and series math 20-1 This chapter focuses on
This chapter focuses on Sequences and series math 20-1
Sequences and series math 20-1 Sequences and series games
Sequences and series games Arithmetic
Arithmetic Sequences and series math 20-1
Sequences and series math 20-1 A series
A series Recursive formula for geometric sequence
Recursive formula for geometric sequence Dr frost rearranging formulae
Dr frost rearranging formulae Convergent progression
Convergent progression Sum of infinite terms
Sum of infinite terms Formula for infinite geometric series
Formula for infinite geometric series Geometric series
Geometric series



















































