Chapter 4 Truncation Error and the Taylor Series

Chapter 4 Truncation Error and the Taylor Series Lecture Notes Dr. Rakhmad Arief Siregar Universiti Malaysia Perlis Applied Numerical Method for Engineers 1

Background n n n Truncation error are those that results from using an approximation in place of an exact mathematical procedure. A truncation error was introduce into numerical solution because difference equation only approximates the true value of the derivative In order to gain insight into the properties of truncation error, the Taylor function is used 2

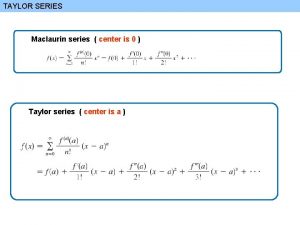
Taylor’s Theorem n n If the function f and its first n+1 derivatives are continuous on an interval containing a and x, then the value of the function at x is given by where remainder Rn is defined as 3

Taylor’s Theorem n n It is often convenient to simplify the Tailor series by defining a step size h = xi+1 - xi where remainder Rn is defined as is a value of x that lies somewhere between xi and xi+1 This value will be discussed later 4

Ex. 4. 1 Taylor Approximation of a Polynomial n n Use zero-through fourth-order Taylor series expansion to approximate the function From xi = 0 with h = 1. That is, predict the function’s value at xi+1 = 1 5

Ex. 4. 1 Taylor Approximation of a Polynomial n n n n Solution For x = 0 then f(0) = 1. 2 For x = 1 then f(1) = 0. 2 this is the true that we are trying to predict. Taylor series approximation with n = 0 Truncation error: Et = true value – approximation Et = 0. 2 -1. 2 = -1. 0 at x= 1 n = 1, the first derivative f’(0) = -0. 4(0)3 - 0. 45(0)2 - 1. 0(0) -0. 25 = -0. 25 Taylor series approximation with n = 1 6

Ex. 4. 1 Taylor Approximation of a Polynomial n n n Taylor series approximation with n = 1 Truncation error: Et = true value – approximation Et = 0. 2 -0. 95 = -0. 75 at x= 1 n = 2, the second derivative f’’(0) = -1. 2(0)2 - 0. 9(0) - 1. 0 = -1. 0 Taylor series approximation with n = 2 Truncation error: Et = true value – approximation Et = 0. 2 -0. 45 = -0. 25 at x= 1 7

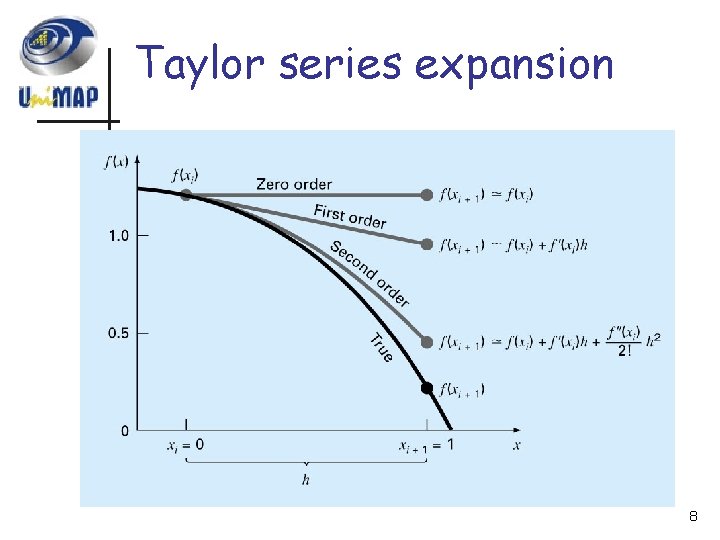
Taylor series expansion 8

Ex. 4. 2 n n Use Taylor series expansion with n = 0 to 6 to approximate f(x) = cos x, at xi+1 = /3 on the bases of the value of f(x) and its derivatives at xi = /4. Note this means that h = /3 - /4 = /12. 9

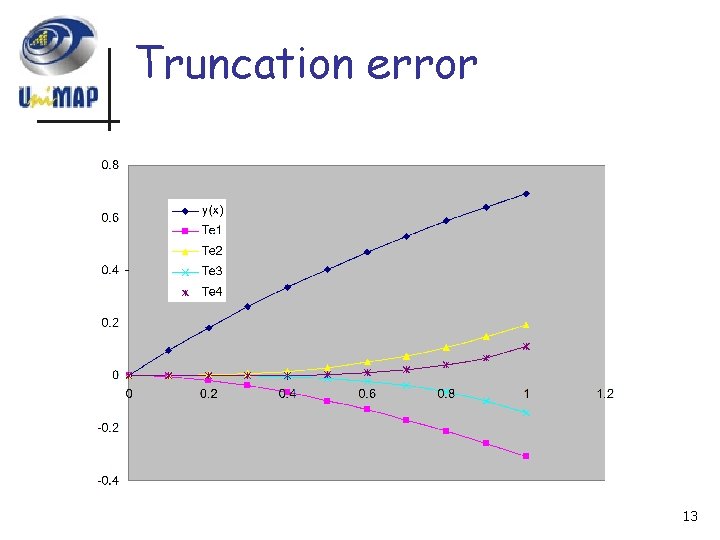
Ex. 4. 1 x n Find the truncation error in approximating the function n (a) n (b) n (c) n (d) n over the range 0 x 1 10

Ex. 4. 1 x (Solution) n We consider a representative value of x, x = 0. 5, and find the truncation error. The exact value of the function is given by n (a) n (b) 11

Ex. 4. 1 x (Solution) n We consider a representative value of x, x = 0. 5, and find the truncation error. The exact value of the function is given by n (c) n (d) 12

Truncation error 13

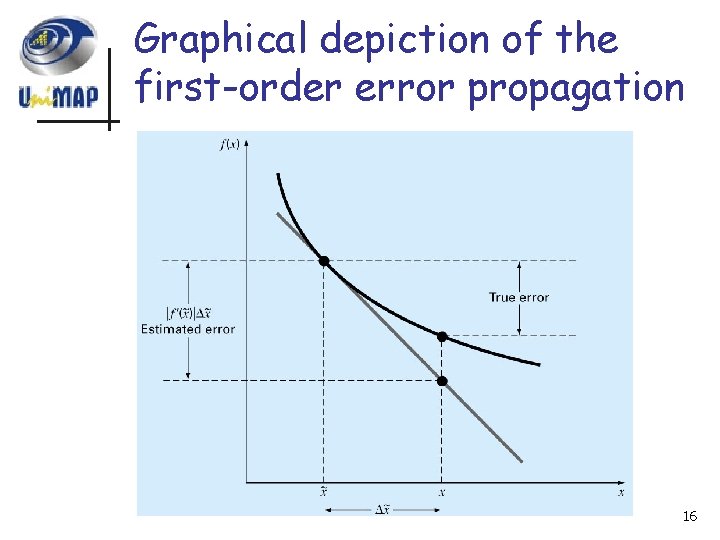
Error Propagation n The purpose of this section is to study how error in numbers can propagate through mathematical functions Assuming is an approximation of x, we would like to assess the effect of the discrepancy between x and on the value of the function. We estimate n We can use Taylor can be employed, why? n Dropping the second and high order terms and rearranging yields n n 14

Error Propagation n Dropping the second and high order terms and rearranging yields n Or can be rewrite as: n where: n an estimate of the error of the function n an estimate of the error of x 15

Graphical depiction of the first-order error propagation 16

Error Propagation in a function of a single variable n Given a value of = 2. 5 with an error of = 0. 01, estimate resulting error in the function f(x) = x 3 Solution n We predict for n = 2. 5 17

Function of more than one variable n For n independent variable having error following general relationship holds 18

Ex. 4. 6 x n Modified the question 19

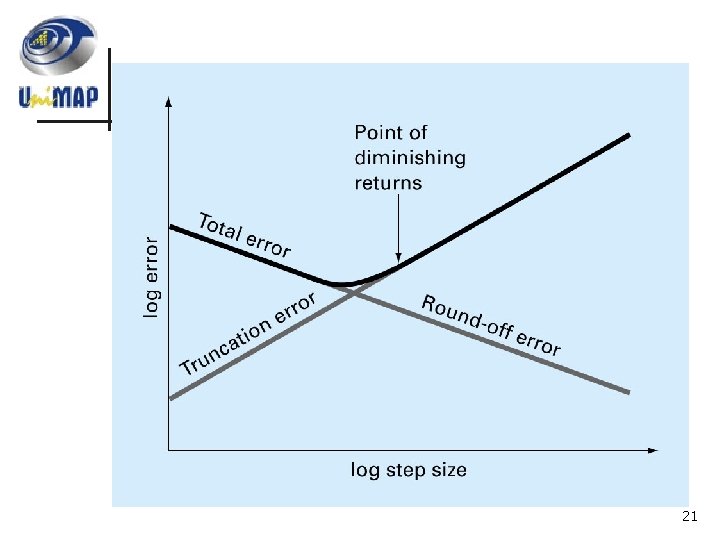
Total Numerical Error n n n Total Numerical error is the summation of the truncation and round-off errors To minimize round error is to increase the number of significant figure of the computer The truncation error can be reduce by decreasing the step size However the truncation errors are decrease as the round-off errors are increase In actual cases, such situation relatively uncommon because most computer carry enough significant figures that round-off error do not redominate 20

21

Blunders n n n Blunders or gross error could attributed to human imperfection Occurs in computer programs, also can occurs in any stage of mathematical modeling. Blunders are usually disregarded in discussion of numerical methods 22

Formulation Errors n n Formulation or model error relate to incomplete mathematical models. Ex. A negligible formulation error is the fact that Newton’s second law does not account for relativistic problem. 23

Data uncertainty n n Errors sometimes enter into an analysis because of uncertainty in the physical data Ex. In the case of falling parachutist n Our sensor of velocity can overestimate the velocity, etc 24

FYI - Greek Alphabetn n n Alpha Beta Gamma Delta Epsilon Zeta Eta Theta Iota Kappa Lambda Mu n n n Nu Xi Omicron Pi Rho Sigma Tau Upsilon Phi Rho Psi Omega 25