FRACCIONES Fracciones Comunes Una fraccin comn representa partes




























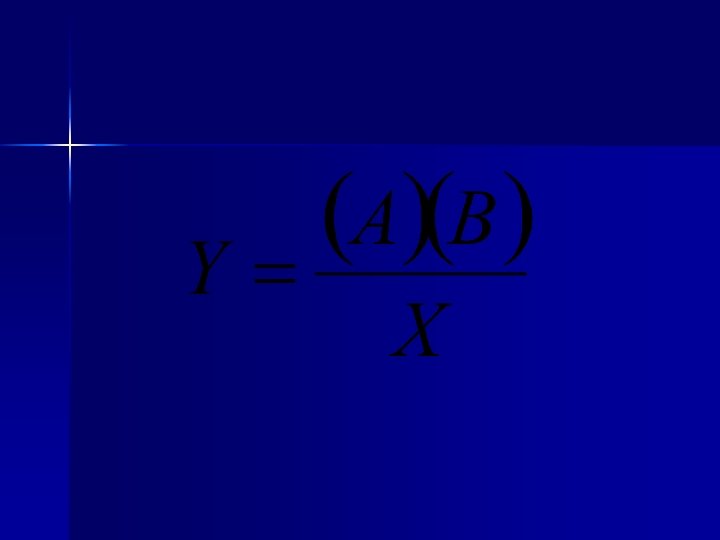






































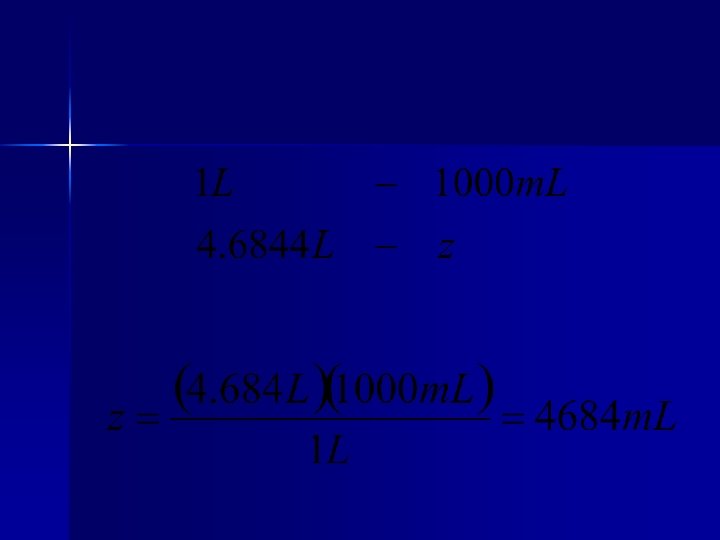




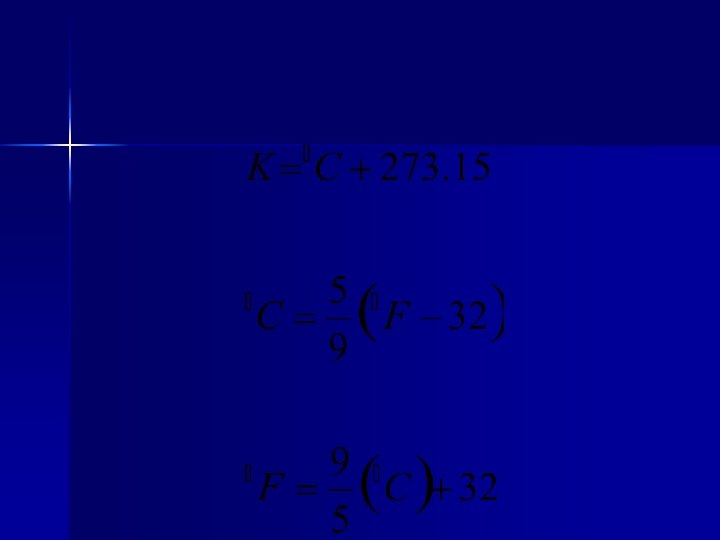


















































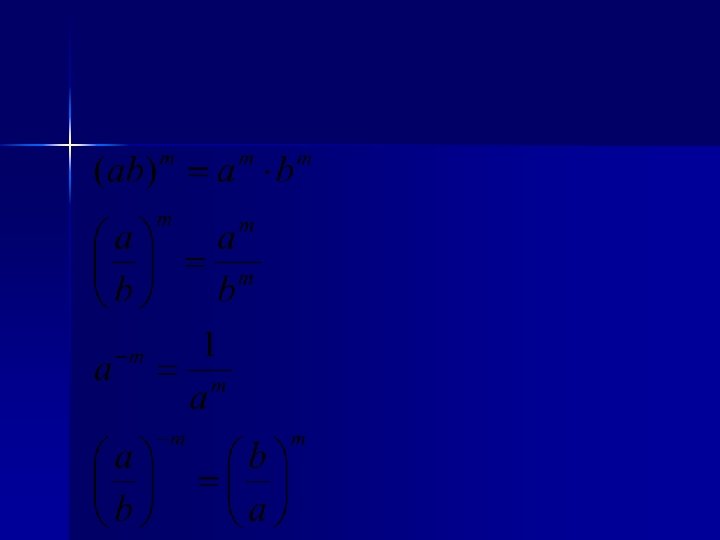





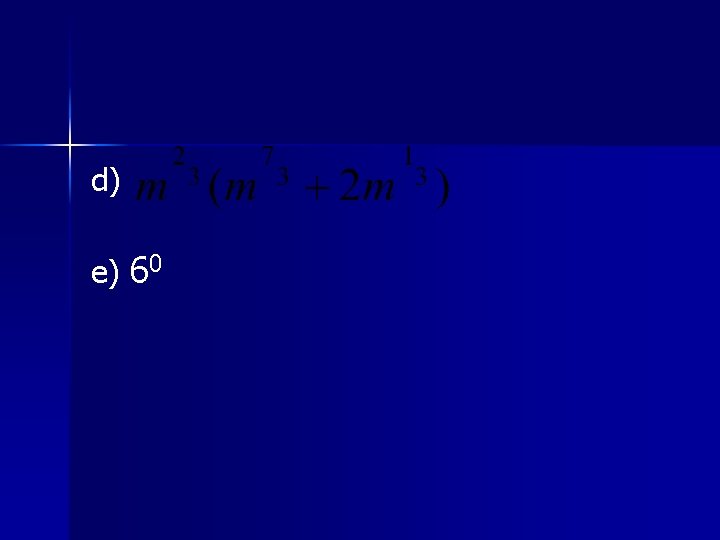







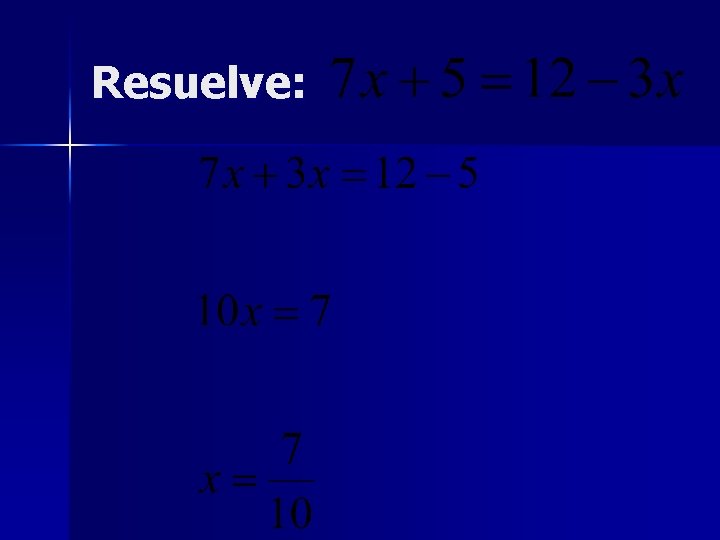




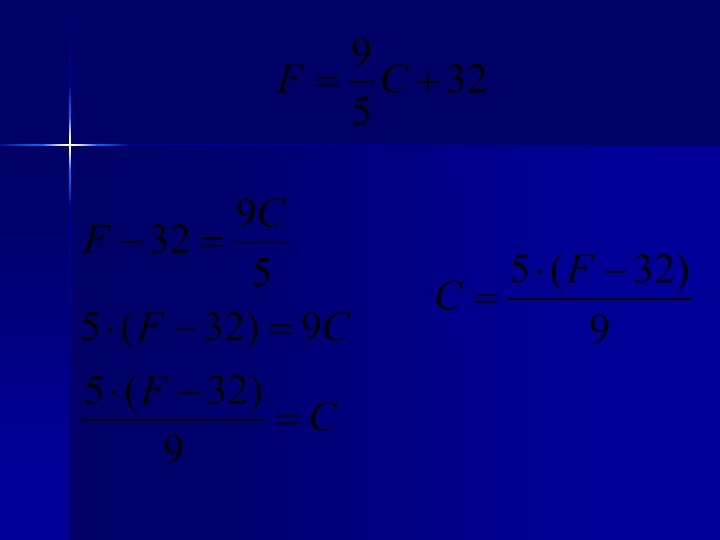



































- Slides: 185

FRACCIONES

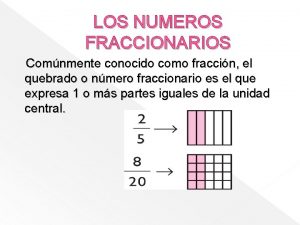
Fracciones Comunes Una fracción común representa partes iguales de un entero. Consiste de dos números y una barra fraccionaria, y se escribe de esta forma n

Regla 1 Cuando el denominador es 1, la fracción es igual al número del numerador.

Regla 2: Multiplicar

Ejemplo:

Regla 3: División

Ejemplo:

Regla 4: Suma

Ejemplo:

Ejercicio: Realice la operación que se le pide.

NOTACION CIENTIFICA

n Cualquier número positivo puede escribirse en notación científica, C x 10 m, donde 1≤c<10 y m es un entero.

n Esta notación proporciona una manera de trabajar con números muy grandes y números muy pequeños.

Ejemplo 1. La rapidez de la luz es de aproximadamente 300 000 m/s. 2. El punto de la en un libro tiene una masa de aproximadamente 0. 000 001 kg.

El problema se evita al usar un método que incorpora potencias del número 10: 100=1 101=10 102=10 x 10=100 103=10 x 10=1000 104=10 x 10 x 10=10000 105=10 x 10 x 10=100000

La rapidez de la luz es de aproximadamente 300 000 m/s. 3 x 108 m/s

Los números representativos menores que la unidad son los siguientes:

Otros ejemplos: El punto de la en un libro tiene una masa de aproximadamente 0. 000 001 kg. 1 x 10 -9

Por ejemplo, la distancia entre la Tierra y el Sol es de alrededor de 93, 000 millas. En notación científica 93, 000 millas = 9. 3 x 107 millas

La masa de una molécula de oxígeno es de alrededor de 0. 000 000 053 gramos n En notación científica: 5. 3 x 10 -23 g

Convierte a notación científica o viceversa a) 2. 375 x 108 e) 3. 98 x 10 -8 b) 0. 000000349 f) 0. 000489 c) 7. 36 x 10 -5 g) 8. 64 x 104 d) 9816762. 5 h) 0. 0357

REGLA DE TRES

La regla de tres es una forma de resolución de problemas de proporcionalidad entre tres o más valores conocidos y una incógnita.

Regla de tres Directa Inversa Mixta

REGLA DE TRES SIMPLE DIRECTA


n Si necesito 2 litros de leche para el desayuno de 8 niños, ¿Cuántos litros de leche se necesita para 15?

De los 800 alumnos de un colegio, han ido de viaje 600. ¿Qué porcentaje de alumnos ha ido de viaje?

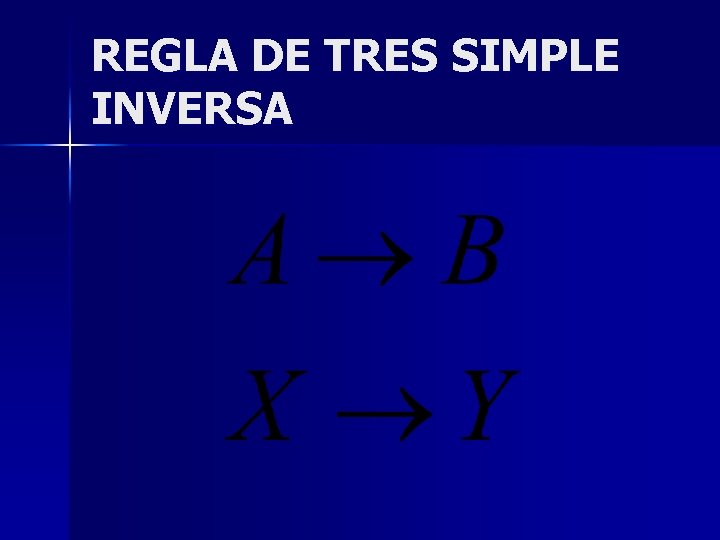
REGLA DE TRES SIMPLE INVERSA
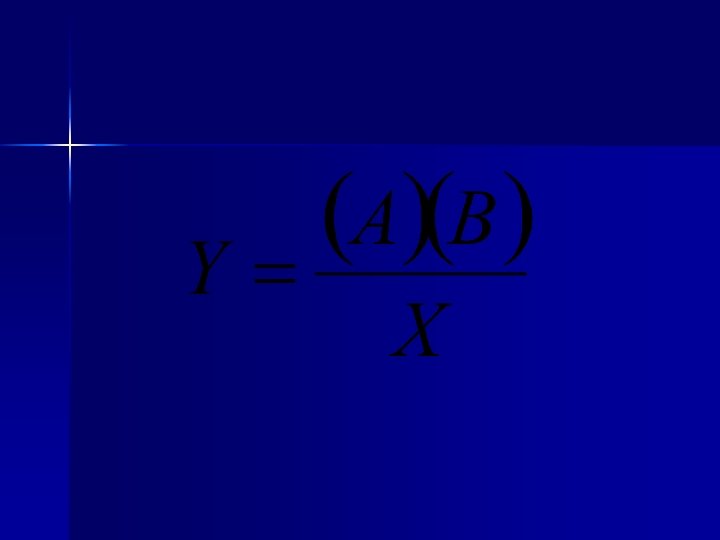

n si 8 trabajadores realizan todo su trabajo en 10 horas, ¿cuánto tardarán 3 trabajadores en realizar la misma cantidad de trabajo?

Dos ruedas están unidas por una correa transmisora. La primera tiene un radio de 25 cm y la segunda de 75 cm. Cuando la primera ha dado 300 vueltas, ¿cuántas vueltas habrá dado la segunda?

REGLA DE TRES SIMPLE MIXTA

Relación directa

Relación inversa

Relación mixta

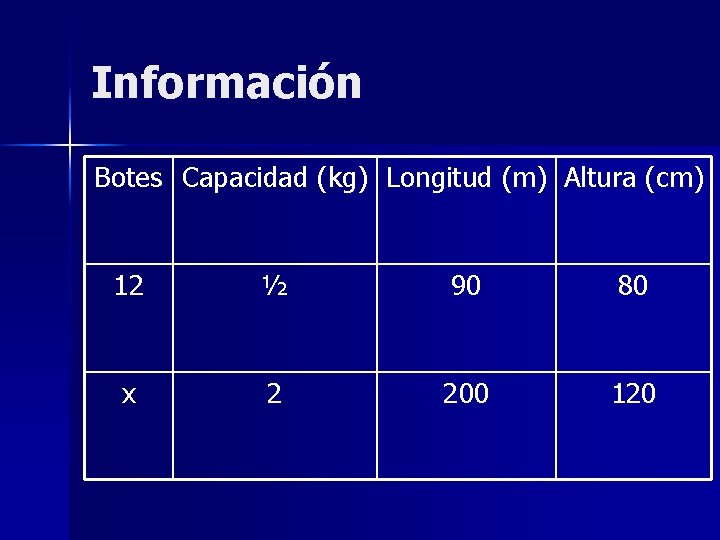
Ejemplo Con 12 botes conteniendo cada uno ½ kg de pintura se han pintado 90 m de reja de 80 cm de altura. Calcular cuántos botes de 2 kg de pintura serán necesarios para pintar una reja similar de 120 cm de altura y 200 metros de longitud.

Información Botes Capacidad (kg) Longitud (m) Altura (cm) 12 ½ 90 80 x 2 200 120

Información Botes Capacidad (kg) Longitud (m) Altura (cm) 12 ½ 90 80 x 2 200 120 Botes Capacidad (kg) 12 0. 5 x 2 Longitud (m) 90 Altura (m) 0. 8 Area (m 2) 72 200 1. 2 240

Botes 12 X Capacidad (kg) 0. 5 2 Relación Inversa Area (m 2) 72 240

Botes 12 X Capacidad (kg) 0. 5 2 Relación Directa Area (m 2) 72 240


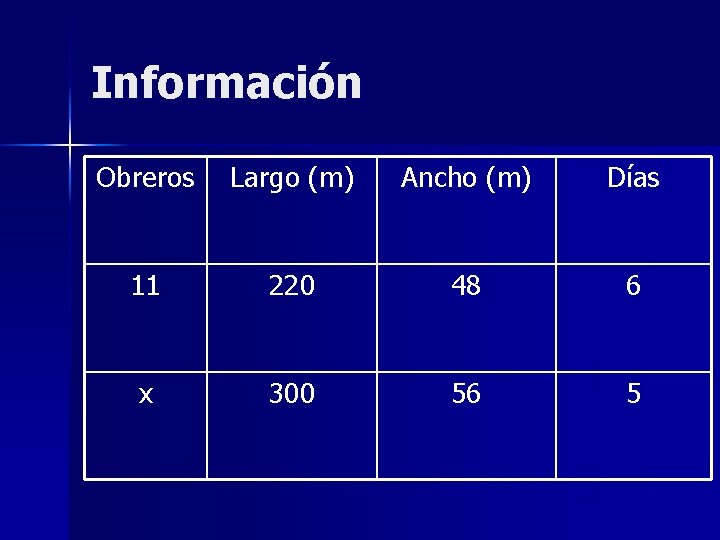
Ejemplo 11 obreros labran un campo rectangular de 220 m de largo y 48 de ancho en 6 días. ¿Cuántos obreros serán necesarios para labrar otro campo análogo de 300 m de largo por 56 m de ancho en cinco días?

Información Obreros Largo (m) Ancho (m) Días 11 220 48 6 x 300 56 5

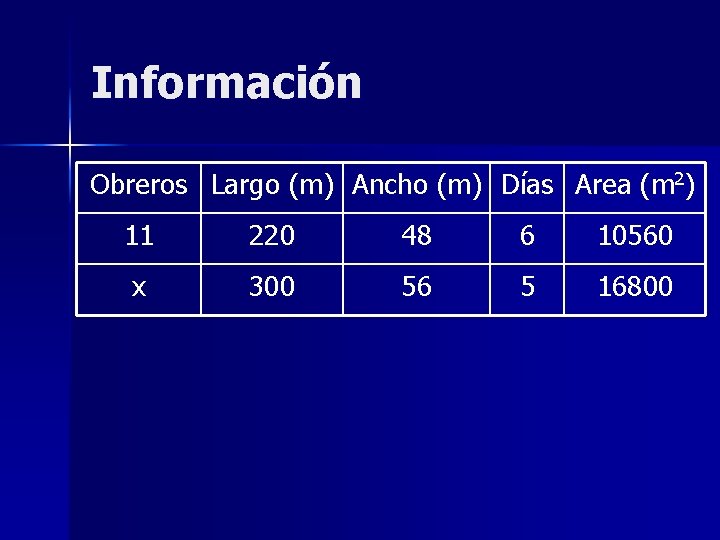
Información Obreros Largo (m) Ancho (m) Días Area (m 2) 11 220 48 6 10560 x 300 56 5 16800

Obreros 11 X Días 6 5 Relación Inversa Area (m 2) 10560 16800

Obreros 11 X Días 6 5 Relación Directa Area (m 2) 10560 16800


RESUELVE

Ejercicio 1 Un coche de Mérida a Valladolid tarda 3 horas a una velocidad de 80 kilómetros por hora. ¿Cuántas horas tardará a una velocidad de 120 km por hora?

Ejercicio 2 n Calcula la masa de 65 cm 3 de mercurio. Considera que éste presenta una densidad de 13. 6 g/cm 3

Ejercicio 3 Seis grifos, tardan 10 horas en llenar un depósito de 400 m³ de capacidad. ¿Cuántas horas tardarán cuatro grifos en llenar 2 depósitos de 500 m³ cada uno?

Ejercicio 4 n Un estudiante necesita 15. 0 g de etanol (alcohol etílico) para un experimento. Si la densidad del alcohol es de 0. 789 g/ml, ¿Cuántos mililitros de alcohol necesita?

Ejercicio 5 Leyendo 20 páginas cada día terminé un libro en 33 días. ¿Cuántos días tardaré leyendo 30 páginas diarias?

PROPORCIONES

Proporción es una igualdad entre dos razones. Donde… Razón es el cociente entre dos números o dos cantidades comparables entre sí, expresado como fracción.


Ejemplo Un abuelo reparte 4 0 pesos entre sus tres nietos de 8, 12 y 16 años de edad; proporcionalmente a sus edades. ¿Cuánto corresponde a cada uno?


Ejemplo Se asocian tres individuos aportando 5000, 7500 y 9000 pesos. Al cabo de un año han ganado 6450 pesos. ¿Qué cantidad corresponde a cada uno si hacen un reparto directamente proporcional a los capitales aportados?


Resuelve

Se reparte una cantidad de dinero, entre tres personas, directamente proporcional a 3, 5 y 7. Sabiendo que a la segunda le corresponde 735 pesos. Hallar lo que le corresponde a la primera y tercera.

UNIDADES DE MEDICION

MATERIA PROPIEDADES CUANTITATIVAS Mediciones científicas UNIDADES SI

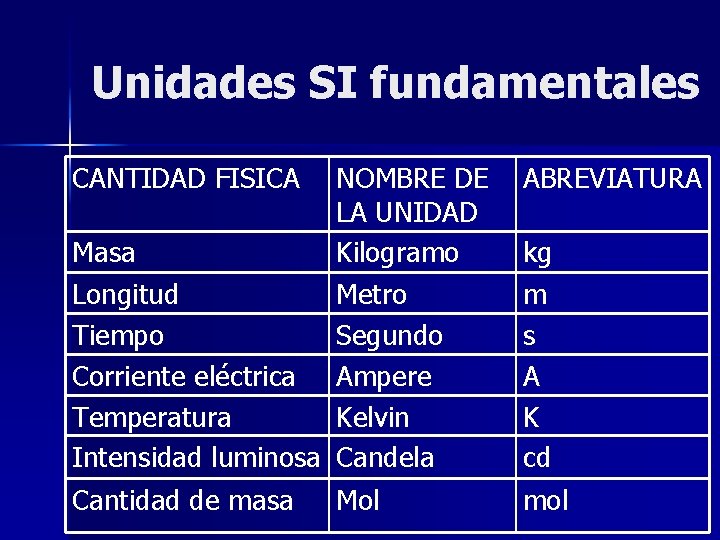
Unidades SI fundamentales CANTIDAD FISICA NOMBRE DE LA UNIDAD Masa Kilogramo Longitud Metro Tiempo Segundo Corriente eléctrica Ampere Temperatura Kelvin Intensidad luminosa Candela Cantidad de masa Mol ABREVIATURA kg m s A K cd mol

MASA 1 kg = 1000 g 1 g = 1000 mg 1 kg = 2. 2046 lb 1 lb = 0. 45359 kg

Cont… MASA 1 lb = 16 onzas 1 uma = 1. 6605402 x 10 -24 g

Ejemplo n Si una mujer tiene una masa de 115 lb, ¿qué masa tiene en gramos?

Ejercicio n La dosis recomendada para adultos de elixofilina, un fármaco empleado para el tratamiento de asma, es de 6 mg/kg de masa corporal. Calcule la dosis en miligramos para una persona de 150 lb.

VOLUMEN 1 L = 10 -3 m 3 = 1 dm 3 = 103 cm 3 = 1. 0567 qt = 1000 m. L

Cont… VOLUMEN 1 gal = 4 qt = 3. 7854 L 1 cm 3 = 1 m. L 1 pulg 3 = 16. 4 cm 3

Ejemplo n Convierta 4. 95 qt a m. L
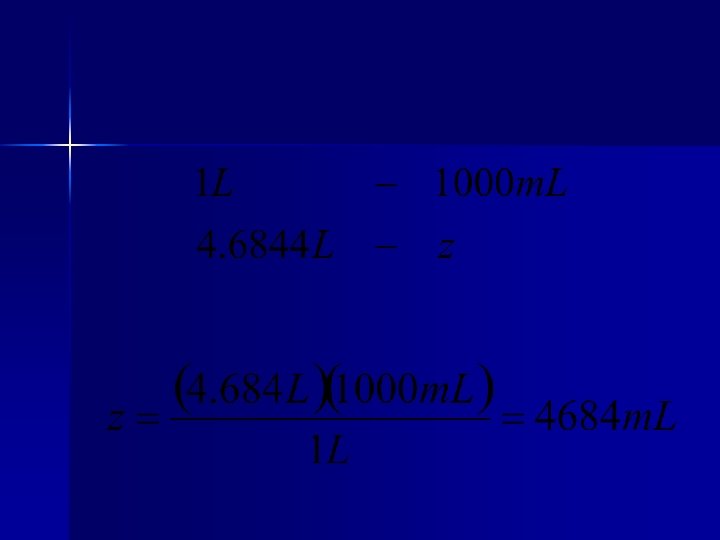

Ejemplo n Una persona ordinaria tiene alrededor de 200 mg de colesterol en 100 m. L de su sangre. Si el volumen total de sangre en una persona es de 5. 0 L, ¿Cuántos gramos de colesterol total contiene la sangre de ese individuo?

Ejemplo n Calcule la masa en gramos de 1. 00 galones de agua. La densidad del agua es de 1. 00 g/m. L.

PRESION 1 Pa = = 1 atm = = 1 N/m 2 1 kg/m-s 2 101. 325 Pa 760 torr = 14. 70 lb/pulg 2 1 bar = 105 Pa

TEMPERATURA 0 K = -273. 15ºC = -459. 67ºF
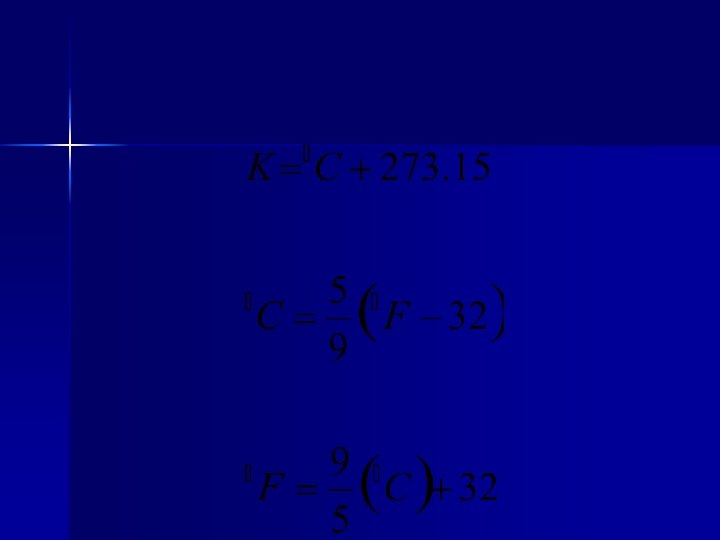

Ejemplo n Si un pronosticador del tiempo predice que durante el día la temperatura alcanzará 31ºC, calcule la temperatura predicha (a) en K; (b) en ºF.

(a) en K (b) en ºF

Ejercicio n El etilenglicol, principal ingrediente de los anticongelantes, se congela a 11. 5ºC. Calcule el punto de congelación en (a) K; (b) ºF.

DOSIFICACION

Por peso

n Un doctor ordena tomar 200 mg de Rocepin a un infante de 15. 4 lb cada 8 horas. La etiqueta del medicamento muestra que 75 -150 mg/kg por día es el rango de la dosis apropiada. ¿Se encuentra la orden del doctor dentro del rango apropiado?

Información. Infante: 15. 4 lb. Ordenado: 200 mg/8 h. Etiqueta: 75 -150 mg/kg x día

Información. Infante: 15. 4 lb (7 kg). Ordenado: 200 mg/8 h. Etiqueta: 75 -150 mg/kg x día

Ejemplo Se ordenó 1. 5 mg/kg de solumedrol a un niño con peso de 74. 8 lb. Solumedrol se encuentra disponible en 125 mg/2 m. L. ¿Cuántos m. L le debe proporcionar la enfermera?

Información. Niño: 74. 8 lb Orden: 1. 5 mg/kg. Etiqueta: 125 mg/2 ml

Información. Niño: 74. 8 lb (34 kg) Orden: 1. 5 mg/kg. Etiqueta: 125 mg/2 ml

Masa-Masa

Ejemplo Se ordenó 25 mg de Metroprolol está disponible en tabletas de 50 mg. ¿Cuántas tabletas debe la enfermera suministrar?



Ejemplo El cloruro de potasio se encuentra disponible en tabletas de 10 mg. Se ordenó, 40 mg de cloruro de potasio. ¿Cuántas tabletas debe administrar la enfermera?


Masa/líquido para líquidos

Dada una cantidad de masa por líquido, ¿Cuánto líquido se requiere?


Ejemplo n Se ordena suministrar 0. 1 g de Dilantin. Éste se encuentra disponible como 30 mg/5 m. L. ¿Cuánto se debe administrar?

DATOS Ordenado: 0. 1 g Disponible: 30 mg/5 ml

Ejemplo Si se ordena 40 mg de Lasix y éste se encuentra disponible en presentación de 80 mg/m. L, ¿Cuánto se debe suministra?

DATOS Ordenado: 40 mg Disponible: 80 mg/ml

PORCENTAJE

Ejemplo En un colegio, el 78% de 250 alumnos estudian francés como segundo idioma. ¿Cuántos alumnos estudian francés?

Ejemplo La población de una ciudad aumentó de 1. 078. 145 a 1. 192. 932 habitantes, según el censo realizado entre los años 2004 y 2005. ¿Cuál ha sido el porcentaje de aumento de la población entre las dos fechas?

1. 192. 932 - 1. 078. 145=114787

EXPRESION ALGEBRAICA

EXPRESION ALGEBRAICA n Se utiliza para representar una constante, una variable o una combinación de variables y constantes que implican un número finito de operaciones indicadas.

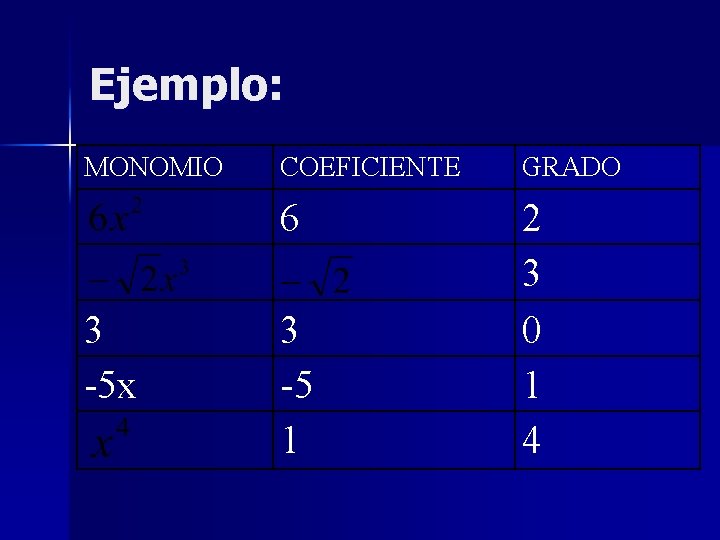
Monomio n Un monomio en una variable es el producto de una constante por una variable elevada a una potencia entera no negativa. De este modo, un monomio tiene forma.

Donde a es una constante, x una variable y k ≥ 0 un número entero. La constante a es el coeficiente del monomio. Si a≠ 0, entonces k es el grado del monomio.

Ejemplo: MONOMIO 3 -5 x COEFICIENTE GRADO 6 2 3 0 1 4 3 -5 1

Dos monomios axk y bxk del mismo grado y con la misma variable son términos semejantes.

Al sumar o restar estos monomios, los podemos combinar en un único monomio mediante la propiedad distributiva.

Ejemplo:

n La suma o la resta de dos monomios con grados distintos es un binomio. n La suma o la resta de tres monomios con grados distintos es un trinomio.

Ejemplo

POLINOMIO Un polinomio en una variable es una expresión algebraica de la forma anxn+ an-1 xn-1+ an-2 xn-2+…+ a 1 x+a 0 donde an, an-1, an-2, …, a 1, a 0 son constantes, llamadas coeficientes de un polinomio, n 0 es un entero y x una variable. Si an 0, se le llama coeficiente principal del polinomio y n es el grado del polinomio.

Los monomios que conforman a un polinomio son sus términos

Ejemplo Término Término

Ejemplo

EXPONENTES

Exponente, término utilizado en matemáticas para indicar el número de veces que una cantidad se ha de multiplicar por sí misma.

n Un exponente se escribe normalmente como un pequeño número o letra en la parte superior derecha de la expresión. Ejemplo: n x 2 n (x+y)3

Por lo tanto… n a denota el producto a. a. a…a (n factores)

Leyes de los exponentes:

Ejemplo

Ejemplo

Ejemplo

Ejemplo
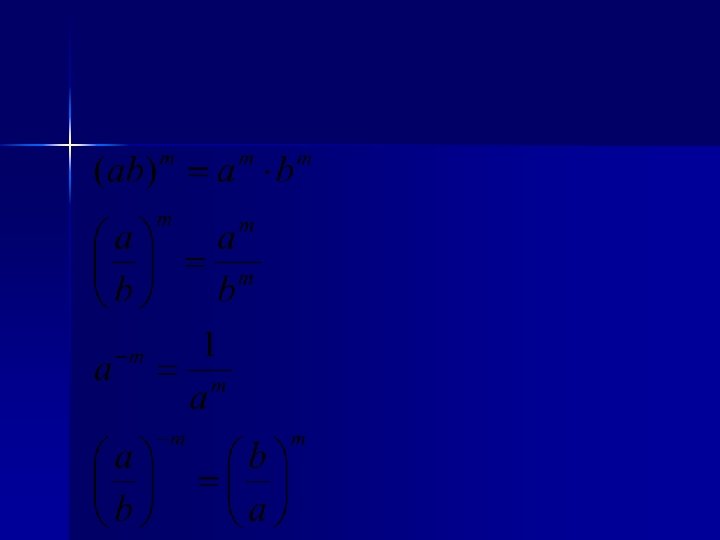

Ejemplo

Ejemplo

Ejemplo

Ejemplo

Ejercicio: Simplifica cada expresión. a) b) c)
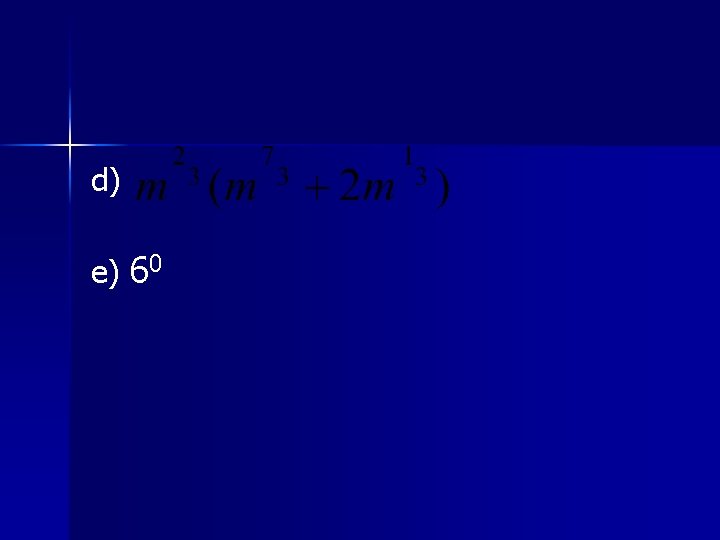
d) e) 60

ECUACIONES LINEALES

¿Qué es una ecuación? Una ecuación es una igualdad de dos expresiones algebraicas, cada una de ellas escrita a los lados del signo igual. ECUACION

La expresión que se escribe a la izquierda de la igualdad recibe el nombre de “primer miembro de la ecuación”, y la expresión de la derecha “segundo miembro”. PRIMER MIEMBRO SEGUNDO MIEMBRO

Los términos que llevan x se denominan “términos en x” y aquellos que no van multiplicando a la x se llaman términos independientes. Términos en x Términos independientes

Definición de una ecuación lineal n Una ecuación lineal en la variable x es una ecuación de la forma donde a y b son números reales y a≠ 0

Resolver una ecuación consiste en encontrar un valor para la incógnita que al sustituirlo en la ecuación haga que la igualdad se cumpla. Por lo tanto…

TEOREMA La ecuación lineal ax+b=0 (donde a≠ 0) tiene exactamente una solución,
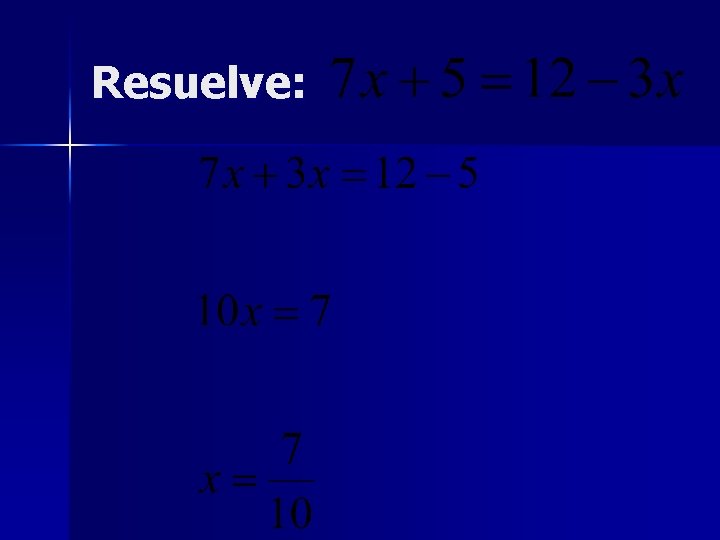
Resuelve:

Ejemplo: Resuelva la ecuación

Ejemplo: Resuelva la ecuación para x


n Si se lee la temperatura en dos termómetro, uno Fahrenheit y otro Celcius, entonces F grados es la temperatura Fahrenheit leída y C grados es la temperatura Celcius, la relación de estas temperaturas es: Resuelve esta ecuación para C.
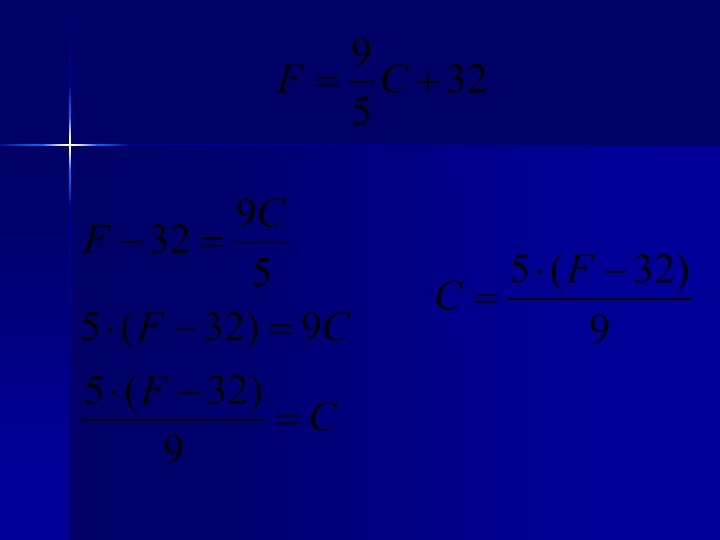

FACTORIZACION

Factorizar un polinomio que contenga la suma de monomios significa encontrar una expresión equivalente que es un producto.

Factorizar Suma de monomios Expresión equivalente que es un producto Dos factores de 10 x 2+15 x son 5 x y 2 x+3

FACTOR COMUN n Propiedad distributiva en dirección inversa. ab+ac=a(b+c)

Ejemplo Factoriza: a)18 x 3 + 27 x 2 En primer lugar, determina el máximo factor común. n 9 es el entero más grande que divide 18 y 27 18 x 3 + 27 x 2 es la expresión más grande que divide a x 3 y x 2

n El MFC de los términos del polinomio es 9 x 2. 18 x 3 + 27 x 2 =9 x 2(2 x)+9 x 2(3) =9 x 2(2 x+3)

b)x 2(x+3)+5(x+3) n En esta situación el máximo factor común es el binomio común (x+3). Este se factoriza como sigue: x 2(x+3)+5(x+3)=(x+3)(x 2+5) Se coloca fuera el binomio que es el factor común

FACTORIZAR POR AGRUPACION n Algunos polinomios sólo tienen un máximo factor común de 1; sin embargo, es posible factorizarlos con un agrupamiento adecuado de los términos. Este proceso se llama factorización por agrupación.

Ejemplo: n Factoriza: x 3+4 x 2+3 x+12 No hay ningún factor distinto de 1 que los términos tengan en común. No obstante, puede agruparse los términos de modo que tengan un factor común: x 3+4 x 2+3 x+12 El factor común es x 2 El factor común es 3

Ahora factorizamos el polinomio dado, como sigue: x 3+4 x 2+3 x+12 =(x 3+4 x 2)+(3 x+12) Agrupe términos con factores comunes =x 2(x+4)+3(x+4) Factorice el máximo factor común de los términos agrupados. Los otros dos términos ahora tienen al binomio x+4 como factor común. =(x+4)(x 2+3) Obtenga como factor MFC, x +4

FACTORIZACION DE TRINOMIOS Para factorizar un trinomio de la forma ax 2 + bx+ c son necesarios algunos intentos por ensayo y error n

Estrategia para factorizar 2 ax +bx+c Suponga, de momento, que no hay un máximo factor común. Encuentre dos primeros términos cuyo producto sea ax 2 ( x+ ) = ax 2+bx+c 1.

2. Encuentre dos últimos términos cuyo producto sea c: ( x+ ) = ax 2+bx+c

3. Repita los pasos 1 y 2, por ensayo y error, hasta que la suma del producto de los extremos (E) y la de los internos (I) sea bx: ( x+ )( x+ I E Suma de E + I ) = ax 2+bx+c

FACTORIZACION DE UNA DIFERENCIA DE CUADRADOS Si A y B son números reales, o expresiones algebraicas, entonces A 2 – B 2 = (A + B)(A – B) En palabras: la diferencia de los cuadrados de dos términos se factoriza como el producto de una suma y una resta de dichos términos.

Ejemplo n Factorice: Debemos expresar cada término como el cuadrado de algunos monomios y después usar la fórmula para factorizar A 2 – B 2 A 2 - B 2 = (A + B)(A - B)

FACTORIZACION DE TRINOMIOS CUADRADOS PERFECTOS Sean A y B números reales, variables o expresiones algebraicas. 1. 2.

Ejemplo n Factorice: A 2 + 2 A B + B 2 = (A + B)2

FACTORIZACION DE LA SUMA Y RESTA DE DOS CUBOS 1. Factorización de la suma de dos cubos A 3 + B 3 = (A + B)(A 2 – AB + B 2) Mismos signos Signos contrarios 2. Factorización de la diferencia de dos cubos A 3 - B 3 = (A - B)(A 2 + AB + B 2) Mismos signos Signos contrarios

Ejemplo n Factorice: A 3 + B 3 = (A + B)(A 2 – AB + B 2)

ESTRATEGIA PARA FACTORIZAR UN POLINOMIO 1. Si hubiera un factor común, factorice el MFC. 2. Determine el número de términos en el polinomio y trate de factorizar como se indica a continuación:

a) Si hay dos términos, ¿se puede factorizar el binomio en alguno de los siguientes productos notables? Diferencia de cuadrados: A 2 -B 2=(A+B)(A-B) Suma de dos cubos: A 3+B 3=(A+B)(A 2 -AB+B 2) Diferencia de dos cubos: A 3 -B 3=(A-B)(A 2+AB+B 2)

b) Si hay tres términos, ¿es un trinomio cuadrado perfecto? Si es así, factorícelo en un de los siguientes productos notables: A 2+2 AB+B 2=(A+B)2 A 2 -2 AB+B 2=(A-B)2 Si no es un trinomio cuadrado perfecto, trate de factorizarlo por ensayo y error

c) Si hay cuatro términos o más, intente factorizarlos por agrupación. 3. Verifique para ver si hay factores con más de un término en el polinomio factorizado que puedan factorizarse aún más. Si es así, factorice completamente.

EJERCICIOS Factoriza: n 4 y 2 -11 y+6 n 6 p 2 -7 pq-5 q 2 n 16 p 2 -40 pq+25 q 2 n 169 x 2+104 xy 2+16 y 4 n 4 m 2 -9 n 128 p 2 -98 q 2 n x 2+36

4 z 2+12 z+9 -w 2 n 256 k 4 -625 m 4 n k 3— 8 n 12 x 2 -26 x-10 n

FUNCIONES LOGARITMICAS

Definición de los logaritmos n Y=log x n Significa 10 y=x

Ejemplo n Para encontrar log 10, 000, pregúntese, ¿A qué exponente debe elevarse 10 para producir 10, 000?

Ejemplo n Para encontrar log 10, 000, pregúntese, ¿A qué exponente debe elevarse 10 para producir 10, 000? Como 104 = 10, 000, vemos que log 10, 000=4.

Asimismo…

PROPIEDADES BASICAS DE LOS LOGARITMOS Sea x y y números reales con x>0.

Ejemplo

PROPIEDADES BASICAS DE LOS LOGARITMOS Para 0<b≠ 1, x>0, y cualquier número real y.

Ejemplo
 Fraccin
Fraccin Mayor y menos en fracciones
Mayor y menos en fracciones Cuál es el numerador y cuál es el denominador
Cuál es el numerador y cuál es el denominador Proteinas plasmaticas
Proteinas plasmaticas Fraccion impropia de 9/17
Fraccion impropia de 9/17 Qué son las fracciones comunes
Qué son las fracciones comunes Los números fraccionarios
Los números fraccionarios Kahootit.comn
Kahootit.comn Naviance.comn
Naviance.comn Https tinyurl com cpbook49
Https tinyurl com cpbook49 Naviance.comn
Naviance.comn Ultralight sails
Ultralight sails Presin
Presin J.comn
J.comn El.comn
El.comn Lun.comn
Lun.comn Kahoot.comn
Kahoot.comn Cnbc.com
Cnbc.com As.comn
As.comn Marca.comn
Marca.comn Cual de los siguientes casos representa una traslacion
Cual de los siguientes casos representa una traslacion La coma marca una pausa intermedia
La coma marca una pausa intermedia Fracciones partes de un todo
Fracciones partes de un todo Sustantivos propios de cosas
Sustantivos propios de cosas Los elementos de las ondas
Los elementos de las ondas Himno del sena significado
Himno del sena significado Dioses imaginarios
Dioses imaginarios Serpiente que representa
Serpiente que representa Animales que representan a dios
Animales que representan a dios Que representa teotihuacan
Que representa teotihuacan A figura a seguir representa a vista frontal de homer
A figura a seguir representa a vista frontal de homer Farsa de ines pereira analise
Farsa de ines pereira analise Que representa
Que representa Leon representa a dios
Leon representa a dios Una empresa de arriendo de autos cobra 70000
Una empresa de arriendo de autos cobra 70000 Romance de la perdida de alhama analisis
Romance de la perdida de alhama analisis Cambio de energia
Cambio de energia Un dibujo que represente
Un dibujo que represente Toda igualdad de la forma ax + by = 0 representa
Toda igualdad de la forma ax + by = 0 representa ¿qué número decimal representa la expresión 1101?
¿qué número decimal representa la expresión 1101? Bodas de sangre temas principales y secundarios
Bodas de sangre temas principales y secundarios Objetivo de la revolución industrial
Objetivo de la revolución industrial Diagrama de hofler
Diagrama de hofler Que representa
Que representa La figura 2.74 representa el movimiento
La figura 2.74 representa el movimiento El rey moro que perdio alhama
El rey moro que perdio alhama Representá per
Representá per Determinar acidez
Determinar acidez 1
1 Que representa
Que representa Que representa
Que representa Que representa
Que representa Instituto federal
Instituto federal Probabilidad condicionada
Probabilidad condicionada En la figura se representa
En la figura se representa Que fracción representa cada figura del tangram
Que fracción representa cada figura del tangram Sambo caporal
Sambo caporal Miguel angel escultura david
Miguel angel escultura david Representa
Representa Lex orandi
Lex orandi O que essa imagem representa
O que essa imagem representa En la divina comedia que representa beatriz
En la divina comedia que representa beatriz Pontos de checagem do ciclo celular
Pontos de checagem do ciclo celular El golondrinero
El golondrinero Ciclo lítico
Ciclo lítico Vectores
Vectores Representa
Representa Weight meaning physics
Weight meaning physics Subconjunto
Subconjunto Quien representa el poder judicial
Quien representa el poder judicial Características de lazarillo de tormes
Características de lazarillo de tormes Constante de gravitacion universal
Constante de gravitacion universal Sistema
Sistema Qué es el poder judicial
Qué es el poder judicial Que representa
Que representa Dados os intervalos reais abaixo represente os por extenso
Dados os intervalos reais abaixo represente os por extenso O grafico representa
O grafico representa Partes en las que se divide un entero
Partes en las que se divide un entero Espelho
Espelho Representa
Representa Herramienta solver excel
Herramienta solver excel Nos jogos cooperativos cada indivíduo representa
Nos jogos cooperativos cada indivíduo representa Expulsión de los jesuitas reformas borbónicas
Expulsión de los jesuitas reformas borbónicas Ley de okun ejemplo
Ley de okun ejemplo Pirámide de la cadena trófica
Pirámide de la cadena trófica Desconcentrado y descentralizado
Desconcentrado y descentralizado Nbr 16877 download
Nbr 16877 download Que representa
Que representa Partes de la grapa dental
Partes de la grapa dental Partes de una unidad odontologica
Partes de una unidad odontologica Cartilla nacho pdf
Cartilla nacho pdf Partes de la computadora internas y externas
Partes de la computadora internas y externas Partes de una publicación
Partes de una publicación Nudos para rescate vertical
Nudos para rescate vertical Numeros mixtos
Numeros mixtos Partes de una raíz cuadrada
Partes de una raíz cuadrada Partes de una rubrica
Partes de una rubrica Partes de una piloteadora
Partes de una piloteadora Partes maquina de vapor
Partes maquina de vapor Cuadro sinóptico de las partes frontales del case.
Cuadro sinóptico de las partes frontales del case. Partes del discurso
Partes del discurso Partes de una brujula
Partes de una brujula Tarjeta madre y sus partes
Tarjeta madre y sus partes Texto expositivo de entrevista
Texto expositivo de entrevista Culata de motor diesel y sus partes
Culata de motor diesel y sus partes Ordenador y sus partes
Ordenador y sus partes Partes de la célula eucariota
Partes de la célula eucariota Elementos del circulo y circunferencia
Elementos del circulo y circunferencia Mira topografica partes
Mira topografica partes Partes de una expocicion
Partes de una expocicion Fipromax 20 sc para que sirve
Fipromax 20 sc para que sirve Plantas sin semilla para niños
Plantas sin semilla para niños Una historia
Una historia Un granjero tiene 2400 pies de cerca y desea
Un granjero tiene 2400 pies de cerca y desea Poder
Poder Estructura externa de la nota informativa
Estructura externa de la nota informativa Partes que consta una cuenta
Partes que consta una cuenta Partes de una escalera
Partes de una escalera Son todos los componentes intangibles de una computadora
Son todos los componentes intangibles de una computadora Romanico 2 eso
Romanico 2 eso Partes de una cuenca hidrográfica
Partes de una cuenca hidrográfica Funciones clase c1
Funciones clase c1 Caracteristicas de la noticia
Caracteristicas de la noticia La llama de amor
La llama de amor Partes de una bomba reciprocante
Partes de una bomba reciprocante Doctora balistica
Doctora balistica Partes de una mezquita
Partes de una mezquita Sonda nasogástrica calibres
Sonda nasogástrica calibres Introducción de una pieza musical
Introducción de una pieza musical Partes de una camara reflex analogica
Partes de una camara reflex analogica Partes de una monografia
Partes de una monografia Tipos de bosquejo
Tipos de bosquejo Parte ciclo de una moto
Parte ciclo de una moto Tipos de caldera
Tipos de caldera Polinomios y fracciones algebraicas 4 eso
Polinomios y fracciones algebraicas 4 eso Partes de las figuras 2d
Partes de las figuras 2d Las partes de una esfera
Las partes de una esfera Cuáles son las tres partes del rito de la confirmación
Cuáles son las tres partes del rito de la confirmación Slidetodoc.com
Slidetodoc.com Partes de una nefrona
Partes de una nefrona Lecture about flowers
Lecture about flowers Estructura del virus
Estructura del virus Dra karina ramos
Dra karina ramos Fecundación externa
Fecundación externa Cuáles son las características de la leyenda
Cuáles son las características de la leyenda Turbina a reaccion
Turbina a reaccion Trampas de grasa
Trampas de grasa Que es un epigrafe de una noticia
Que es un epigrafe de una noticia Un afiche sobre el agua
Un afiche sobre el agua Partes de una historieta
Partes de una historieta Dibujo de la boca
Dibujo de la boca Partes de la noticia para niños
Partes de la noticia para niños Cuales son las partes invariables de la oración
Cuales son las partes invariables de la oración Partes de una entrevista
Partes de una entrevista Partes de una estufa
Partes de una estufa Cuáles son las partes de la semilla
Cuáles son las partes de la semilla Tenemos muchos motivos valiosos por los cuales trabajar
Tenemos muchos motivos valiosos por los cuales trabajar Los mandatos formales
Los mandatos formales La zorra y la pantera moraleja
La zorra y la pantera moraleja Datos que lleva un sobre de carta
Datos que lleva un sobre de carta Oraciones compuestas simples
Oraciones compuestas simples Partes de la mariposa
Partes de la mariposa Que es el sustraendo
Que es el sustraendo Partes de una trinchera
Partes de una trinchera Estructura de la noticia
Estructura de la noticia Prueba de la división
Prueba de la división Celula eucariota y sus partes
Celula eucariota y sus partes Que es una carta
Que es una carta Nombre de los dedos de la mano en español
Nombre de los dedos de la mano en español Anillo abdominal
Anillo abdominal Partes de una unidad odontologica
Partes de una unidad odontologica Partes de una presa
Partes de una presa Psiclogo
Psiclogo Siete sustantivos propios
Siete sustantivos propios Divisores comunes
Divisores comunes Sustantivos imagen
Sustantivos imagen Geiser.seap.minhap.es
Geiser.seap.minhap.es Elementos comunes de las primeras civilizaciones
Elementos comunes de las primeras civilizaciones Un una el la los las
Un una el la los las Que significa creativas comunes
Que significa creativas comunes Estructuras comunes en las células animal y vegetal
Estructuras comunes en las células animal y vegetal Alergenos definicion
Alergenos definicion Recursos comunes a todos los microcontroladores
Recursos comunes a todos los microcontroladores Divsores de 30
Divsores de 30 Instrumento del pasacalle
Instrumento del pasacalle Dibujo de enfermedades comunes
Dibujo de enfermedades comunes