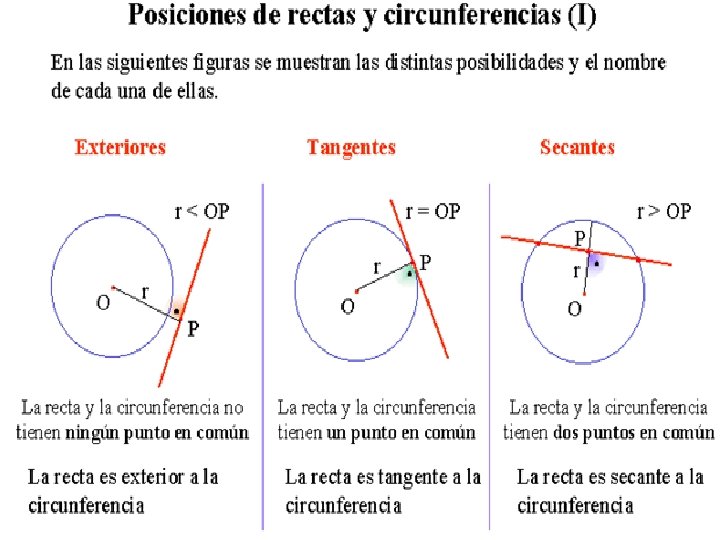
LA CIRCUNFERENCIA SUS ELEMENTOS Y NGULOS Otros elementos

LA CIRCUNFERENCIA SUS ELEMENTOS Y ÁNGULOS

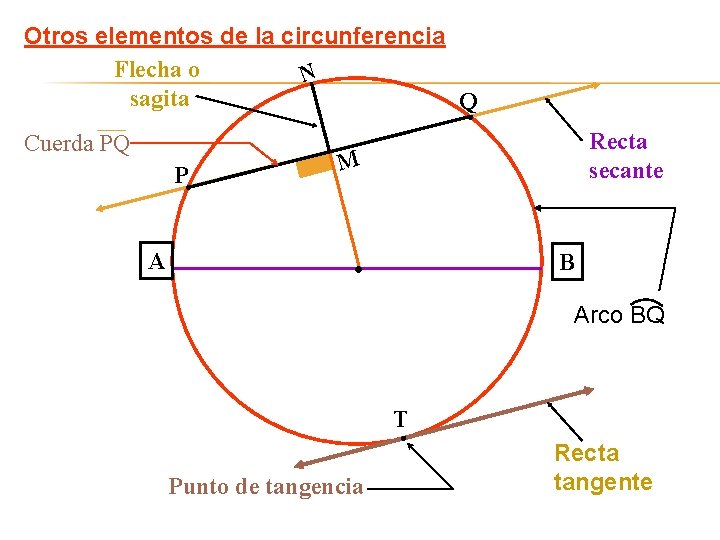
Otros elementos de la circunferencia Flecha o N sagita Q Cuerda PQ P Recta secante M A B Arco BQ T Punto de tangencia Recta tangente

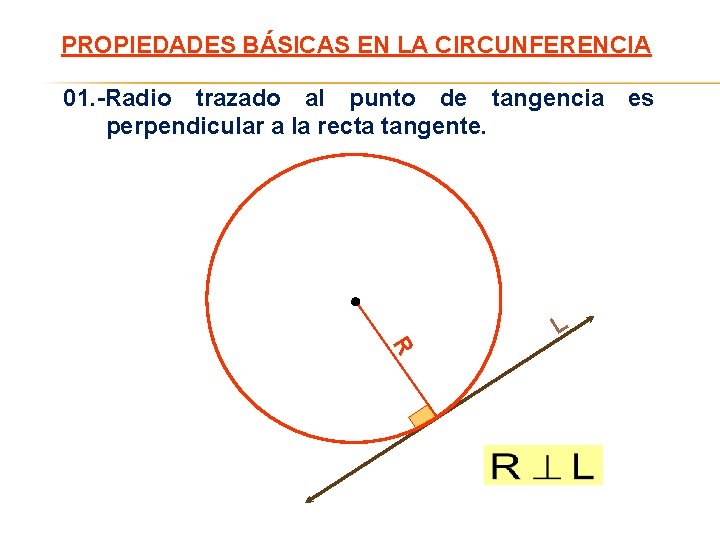
PROPIEDADES BÁSICAS EN LA CIRCUNFERENCIA 01. -Radio trazado al punto de tangencia perpendicular a la recta tangente. L es R

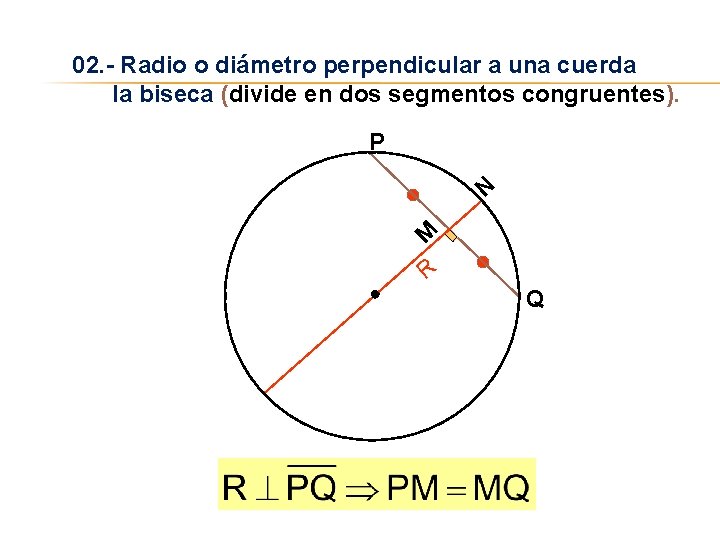
02. - Radio o diámetro perpendicular a una cuerda la biseca (divide en dos segmentos congruentes). P M N R Q

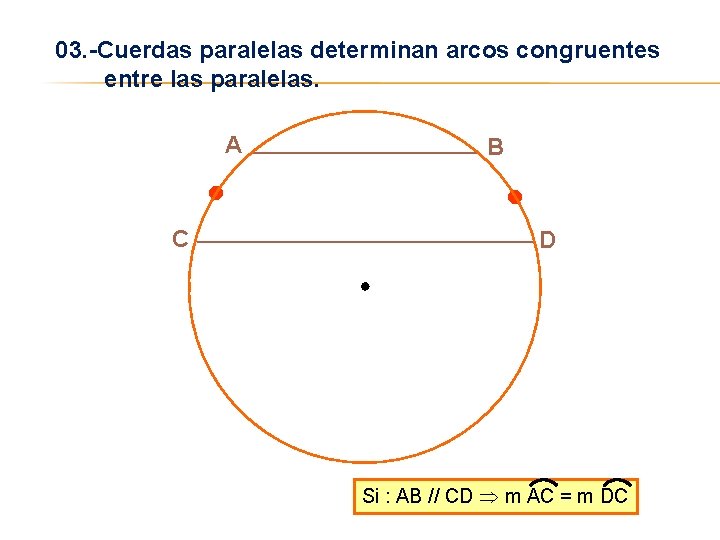
03. -Cuerdas paralelas determinan arcos congruentes entre las paralelas. A C B D Si : AB // CD m AC = m DC

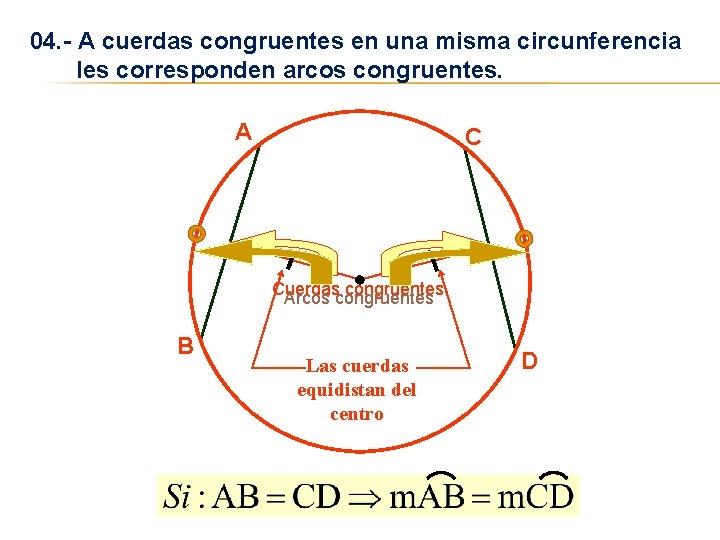
04. - A cuerdas congruentes en una misma circunferencia les corresponden arcos congruentes. A C Cuerdas congruentes Arcos congruentes B Las cuerdas equidistan del centro D

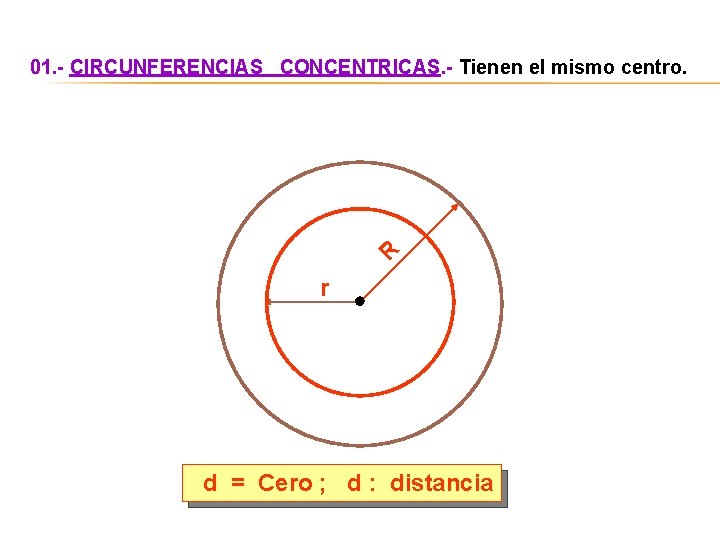
R 01. - CIRCUNFERENCIAS CONCENTRICAS. - Tienen el mismo centro. r d = Cero ; d : distancia

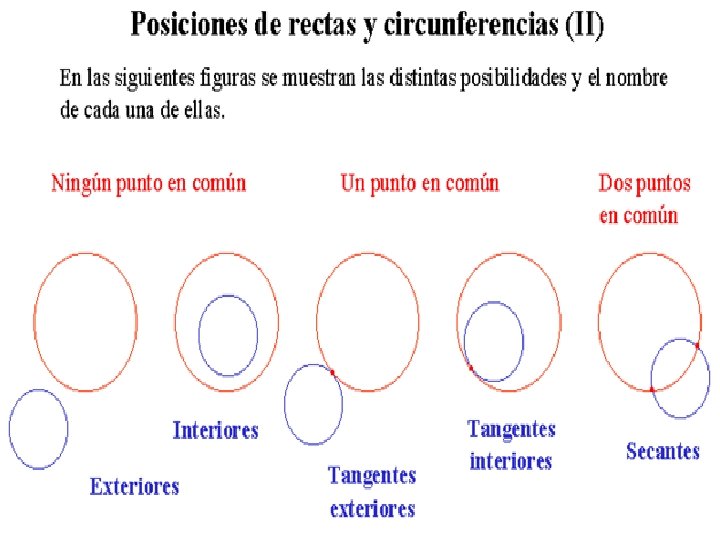
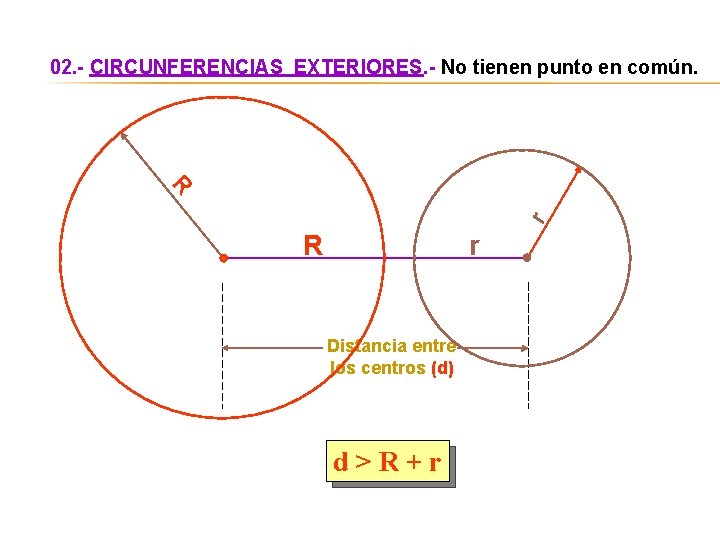
02. - CIRCUNFERENCIAS EXTERIORES. - No tienen punto en común. r R R r Distancia entre los centros (d) d>R+r

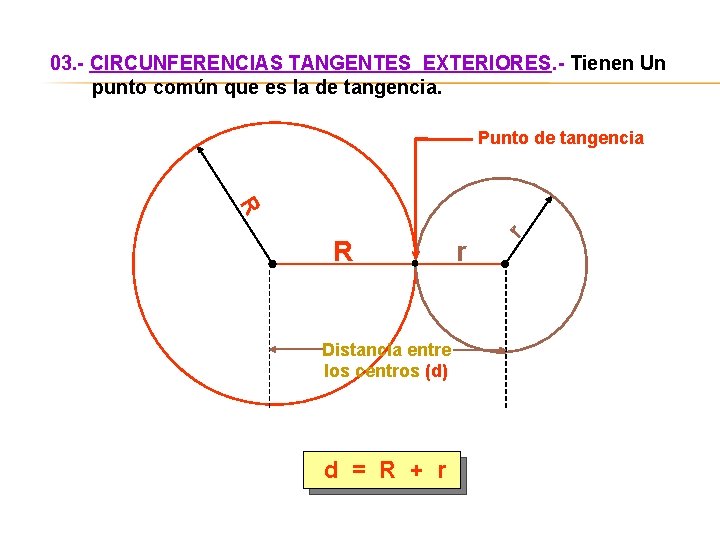
03. - CIRCUNFERENCIAS TANGENTES EXTERIORES. - Tienen Un punto común que es la de tangencia. Punto de tangencia Distancia entre los centros (d) d = R + r r r R R

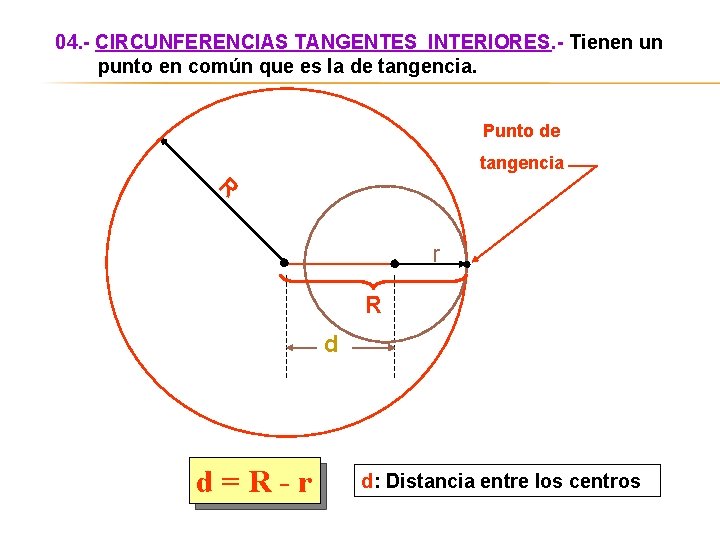
04. - CIRCUNFERENCIAS TANGENTES INTERIORES. - Tienen un punto en común que es la de tangencia. Punto de tangencia R r R d d=R-r d: Distancia entre los centros

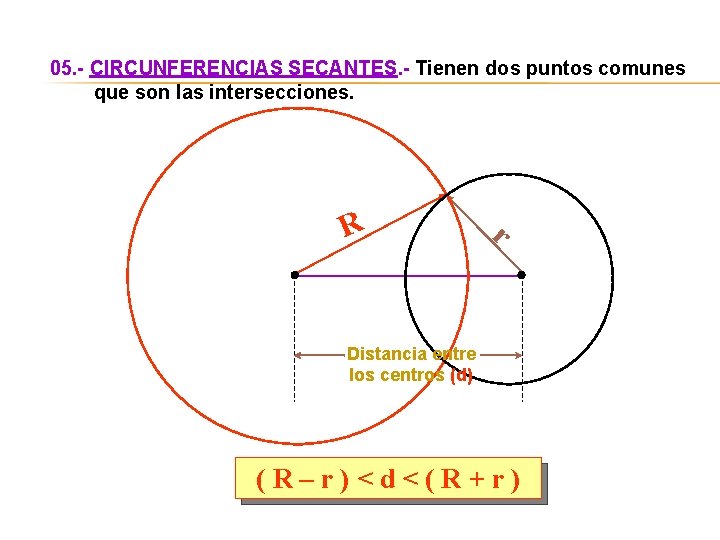
05. - CIRCUNFERENCIAS SECANTES. - Tienen dos puntos comunes que son las intersecciones. R r Distancia entre los centros (d) (R–r)<d<(R+r)

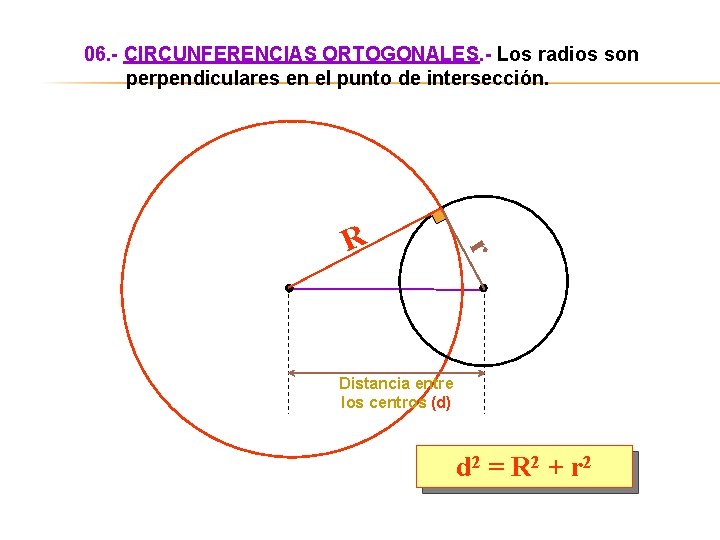
06. - CIRCUNFERENCIAS ORTOGONALES. - Los radios son perpendiculares en el punto de intersección. r R Distancia entre los centros (d) d 2 = R 2 + r 2

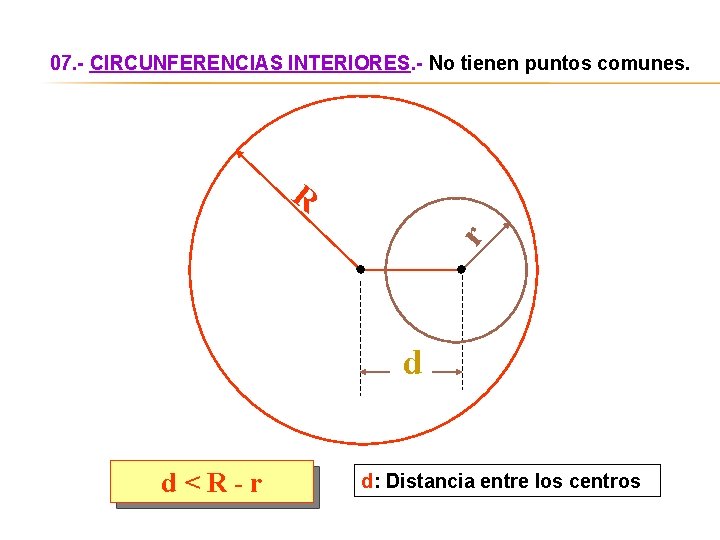
07. - CIRCUNFERENCIAS INTERIORES. - No tienen puntos comunes. r R d d<R-r d: Distancia entre los centros

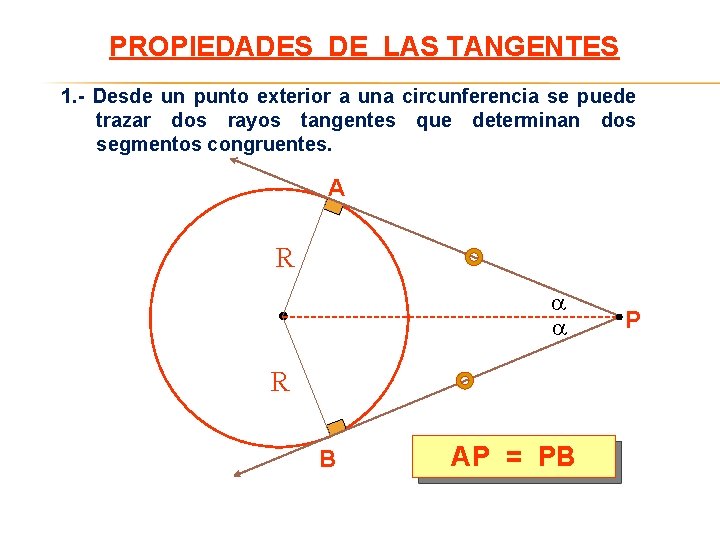
PROPIEDADES DE LAS TANGENTES 1. - Desde un punto exterior a una circunferencia se puede trazar dos rayos tangentes que determinan dos segmentos congruentes. A R R B AP = PB P

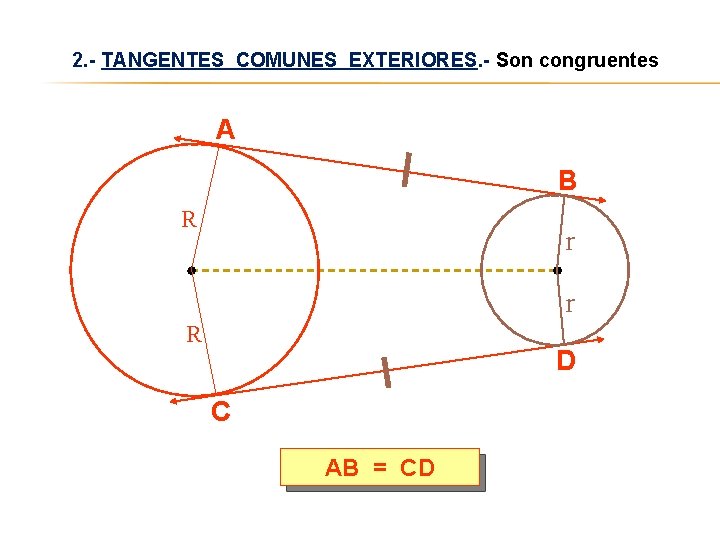
2. - TANGENTES COMUNES EXTERIORES. - Son congruentes A B R r r R D C AB = CD

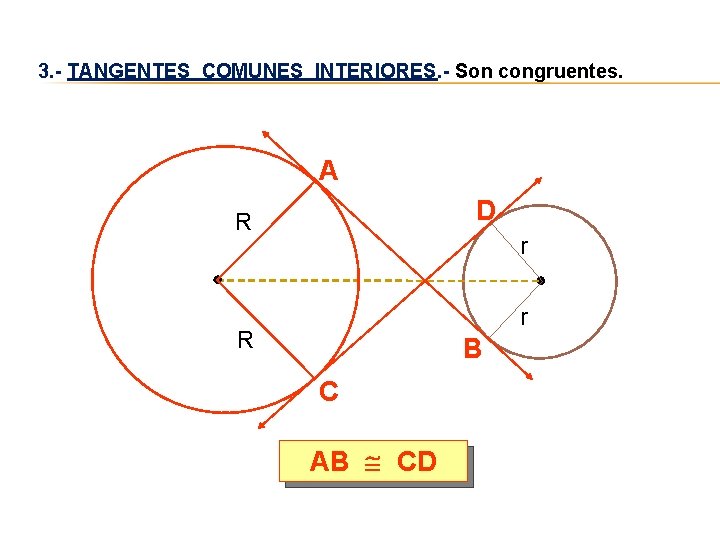
3. - TANGENTES COMUNES INTERIORES. - Son congruentes. A D R r r R B C AB CD

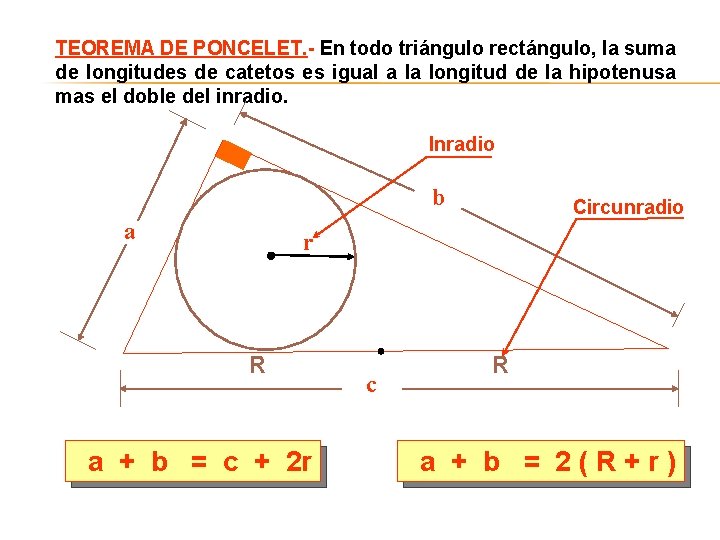
TEOREMA DE PONCELET. - En todo triángulo rectángulo, la suma de longitudes de catetos es igual a la longitud de la hipotenusa mas el doble del inradio. Inradio b a Circunradio r R a + b = c + 2 r c R a + b = 2(R+r)

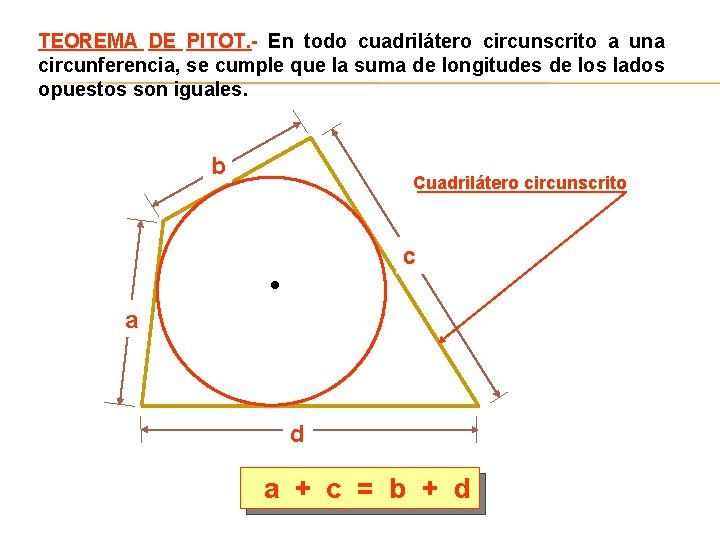
TEOREMA DE PITOT. - En todo cuadrilátero circunscrito a una circunferencia, se cumple que la suma de longitudes de los lados opuestos son iguales. b Cuadrilátero circunscrito c a d a + c = b + d

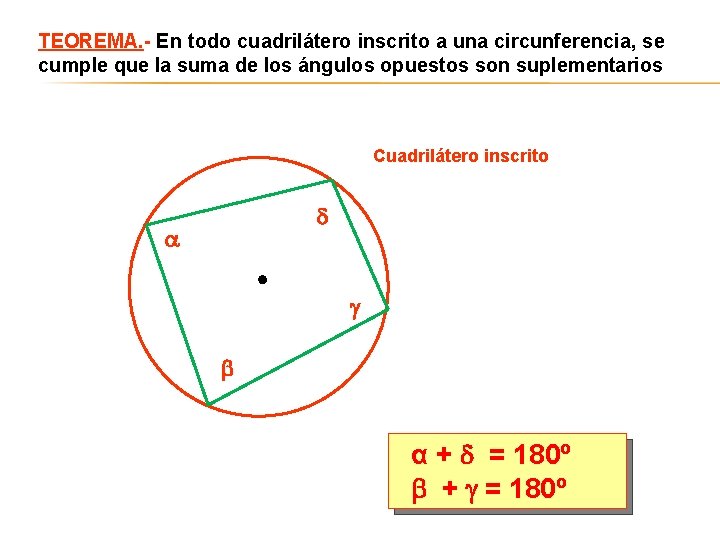
TEOREMA. - En todo cuadrilátero inscrito a una circunferencia, se cumple que la suma de los ángulos opuestos son suplementarios Cuadrilátero inscrito α + = 180º

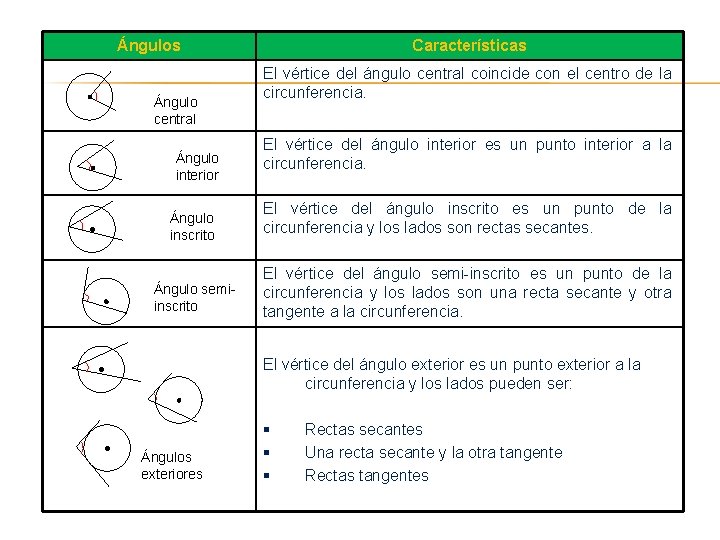
Ángulos Ángulo central Ángulo interior Características El vértice del ángulo central coincide con el centro de la circunferencia. El vértice del ángulo interior es un punto interior a la circunferencia. Ángulo inscrito El vértice del ángulo inscrito es un punto de la circunferencia y los lados son rectas secantes. Ángulo semiinscrito El vértice del ángulo semi-inscrito es un punto de la circunferencia y los lados son una recta secante y otra tangente a la circunferencia. El vértice del ángulo exterior es un punto exterior a la circunferencia y los lados pueden ser: Ángulos exteriores § § § Rectas secantes Una recta secante y la otra tangente Rectas tangentes

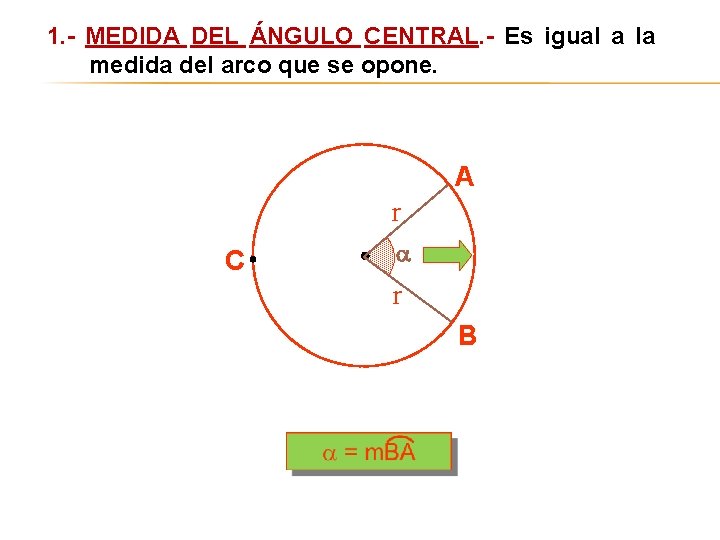
1. - MEDIDA DEL ÁNGULO CENTRAL. - Es igual a la medida del arco que se opone. A r C r B

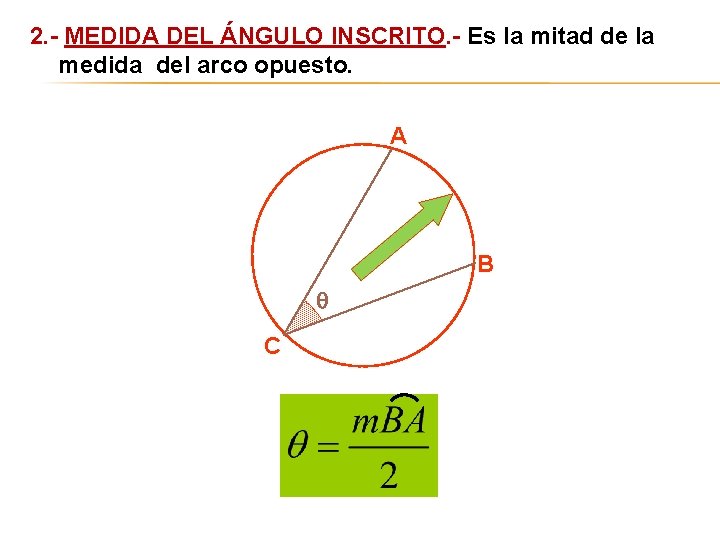
2. - MEDIDA DEL ÁNGULO INSCRITO. - Es la mitad de la medida del arco opuesto. A B C

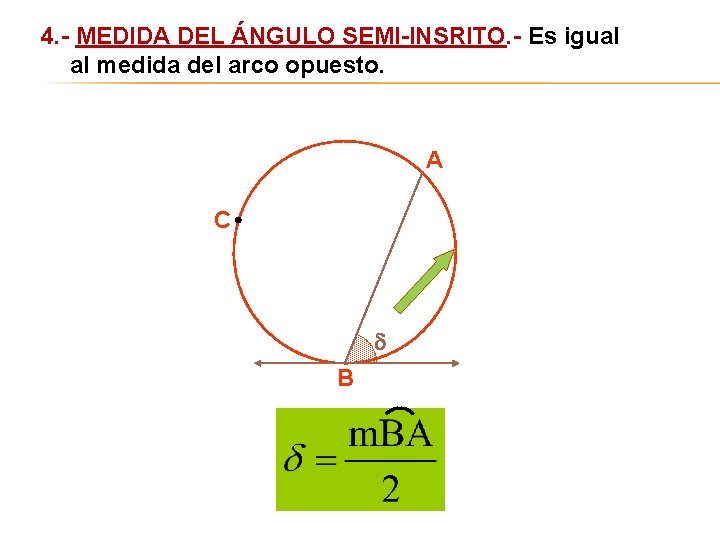
4. - MEDIDA DEL ÁNGULO SEMI-INSRITO. - Es igual al medida del arco opuesto. A C B

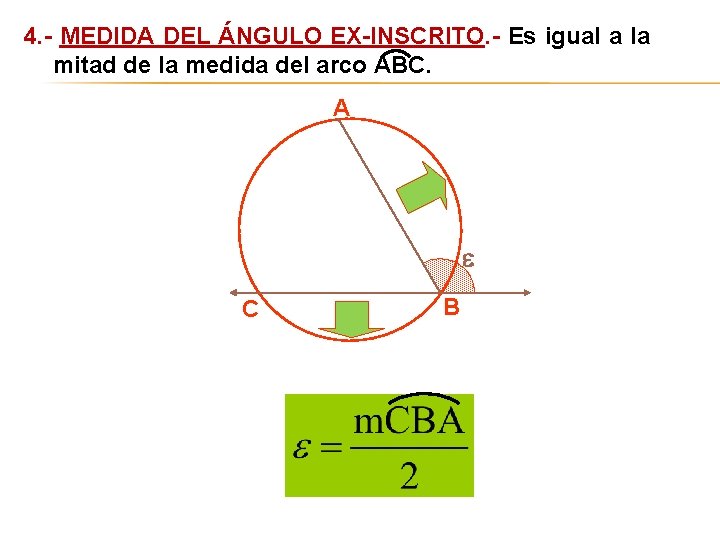
4. - MEDIDA DEL ÁNGULO EX-INSCRITO. - Es igual a la mitad de la medida del arco ABC. A C B

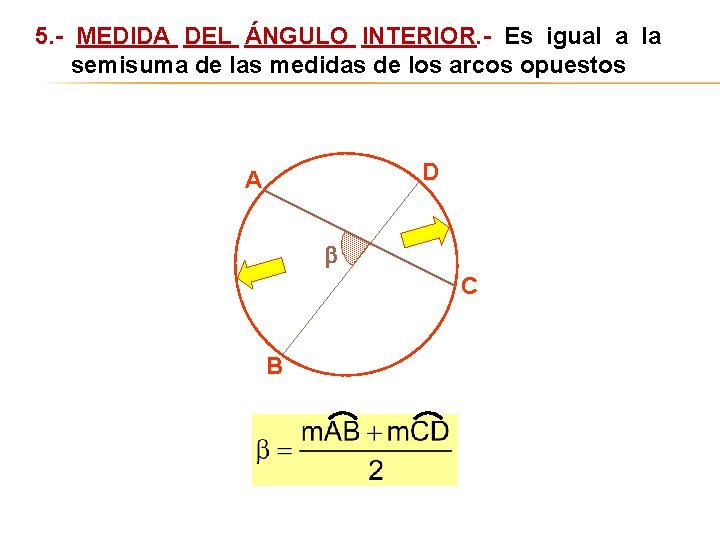
5. - MEDIDA DEL ÁNGULO INTERIOR. - Es igual a la semisuma de las medidas de los arcos opuestos D A C B

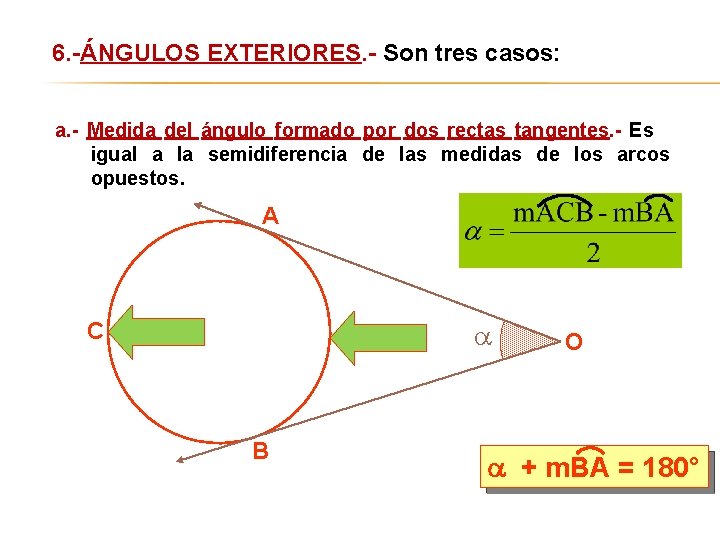
6. -ÁNGULOS EXTERIORES. - Son tres casos: a. - Medida del ángulo formado por dos rectas tangentes. - Es igual a la semidiferencia de las medidas de los arcos opuestos. A C B O + m. BA = 180°

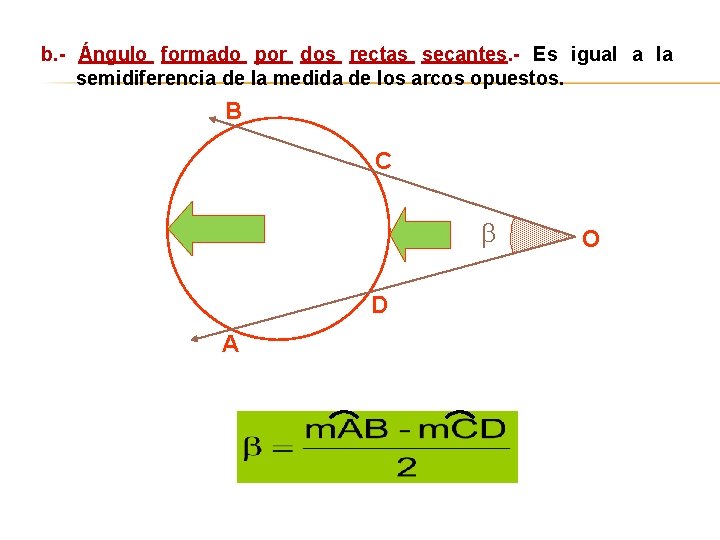
b. - Ángulo formado por dos rectas secantes. - Es igual a la semidiferencia de la medida de los arcos opuestos. B C D A O

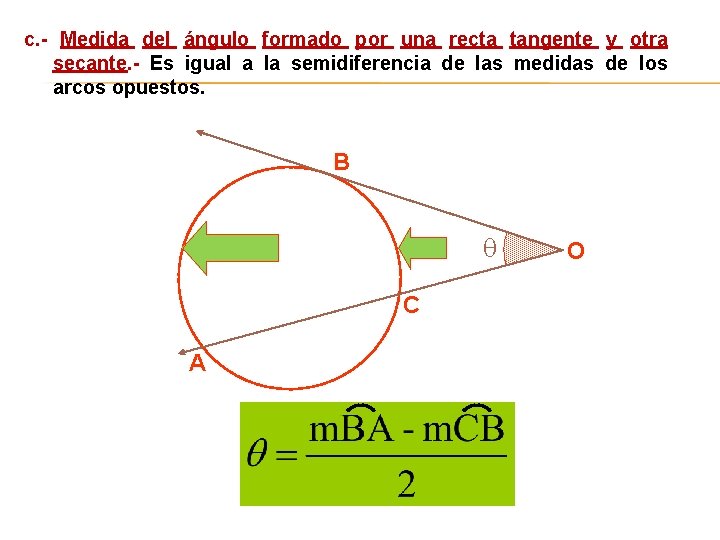
c. - Medida del ángulo formado por una recta tangente y otra secante. - Es igual a la semidiferencia de las medidas de los arcos opuestos. B C A O

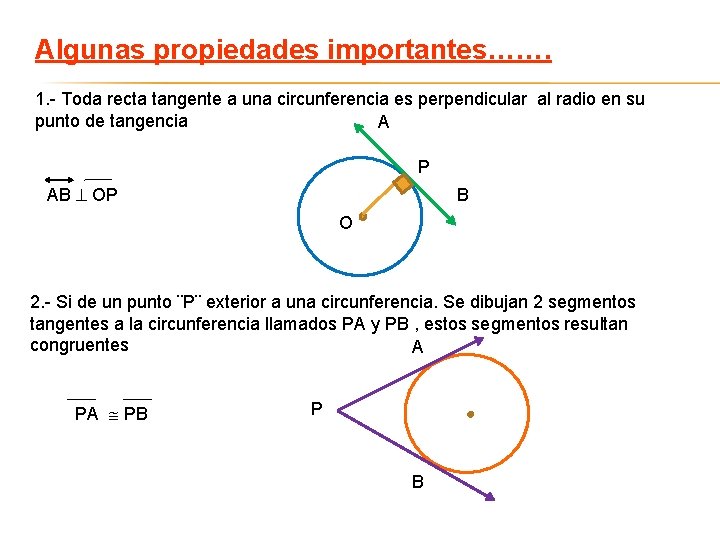
Algunas propiedades importantes……. 1. - Toda recta tangente a una circunferencia es perpendicular al radio en su punto de tangencia A P AB OP B O 2. - Si de un punto ¨P¨ exterior a una circunferencia. Se dibujan 2 segmentos tangentes a la circunferencia llamados PA y PB , estos segmentos resultan congruentes A PA PB P B

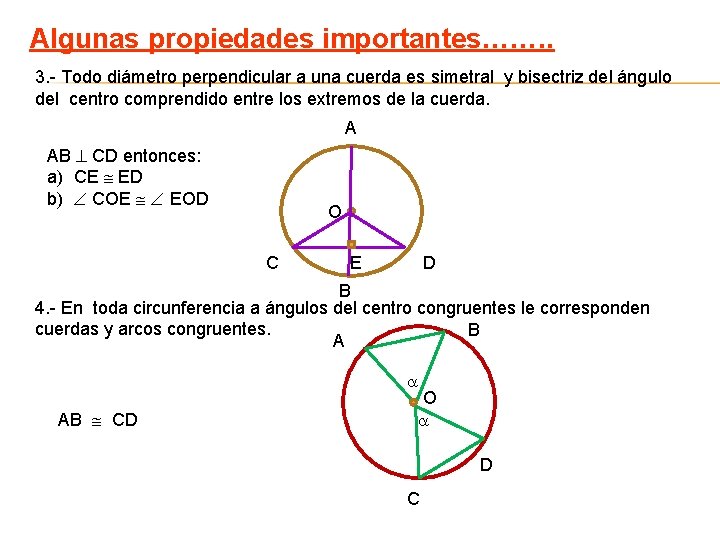
Algunas propiedades importantes……. . 3. - Todo diámetro perpendicular a una cuerda es simetral y bisectriz del ángulo del centro comprendido entre los extremos de la cuerda. A AB CD entonces: a) CE ED b) COE EOD O C E D B 4. - En toda circunferencia a ángulos del centro congruentes le corresponden cuerdas y arcos congruentes. B A AB CD O D C

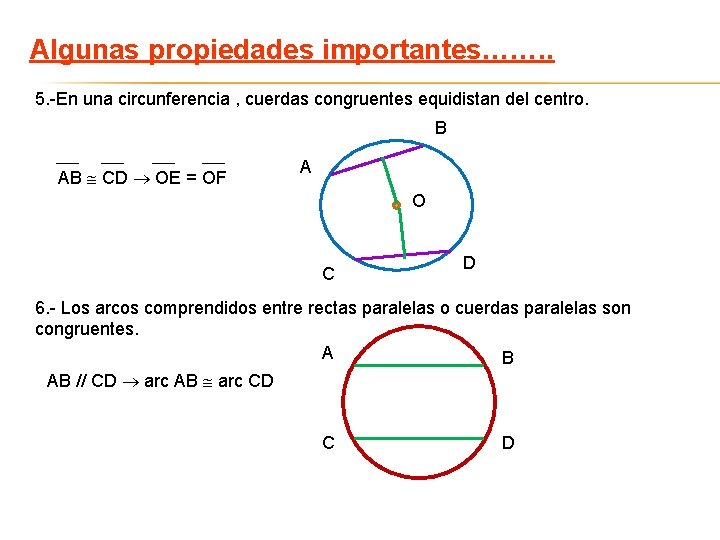
Algunas propiedades importantes……. . 5. -En una circunferencia , cuerdas congruentes equidistan del centro. B AB CD OE = OF A O C D 6. - Los arcos comprendidos entre rectas paralelas o cuerdas paralelas son congruentes. A B AB // CD arc AB arc CD C D

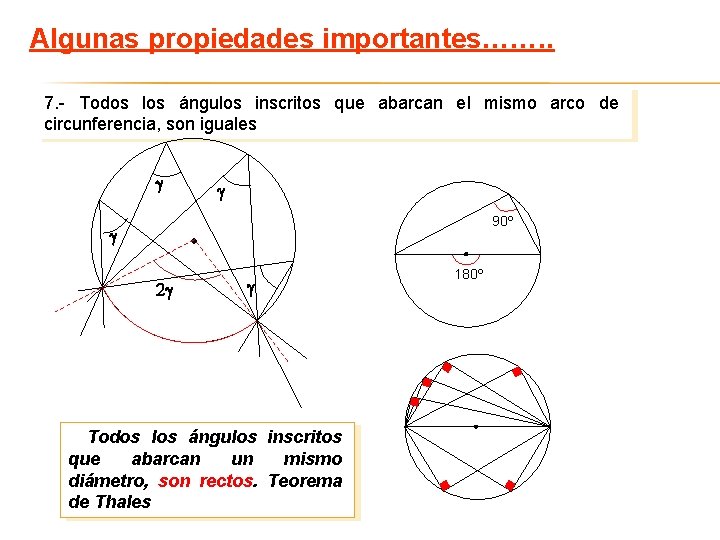
Algunas propiedades importantes……. . 7. - Todos los ángulos inscritos que abarcan el mismo arco de circunferencia, son iguales 90º 2 Todos los ángulos inscritos que abarcan un mismo diámetro, son rectos. Teorema de Thales 180º

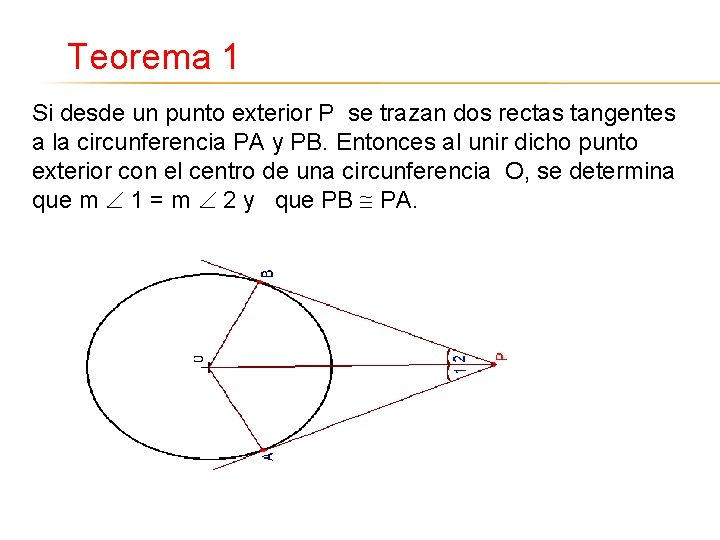
Teorema 1 Si desde un punto exterior P se trazan dos rectas tangentes a la circunferencia PA y PB. Entonces al unir dicho punto exterior con el centro de una circunferencia O, se determina que m 1 = m 2 y que PB PA.

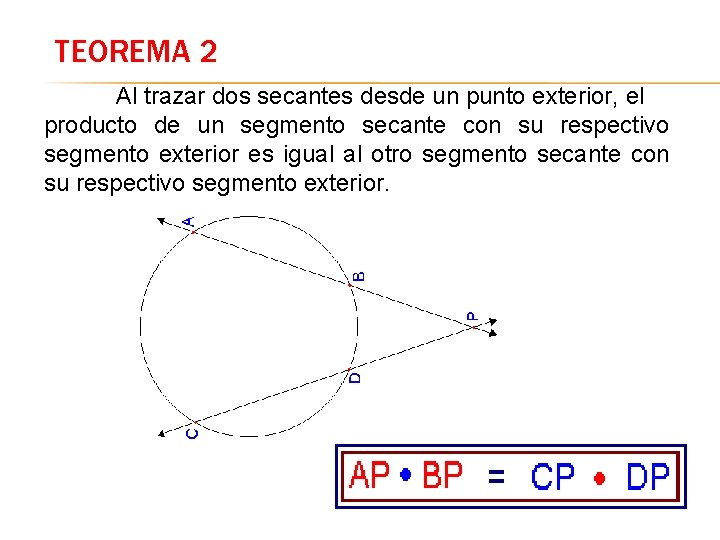
TEOREMA 2 Al trazar dos secantes desde un punto exterior, el producto de un segmento secante con su respectivo segmento exterior es igual al otro segmento secante con su respectivo segmento exterior.

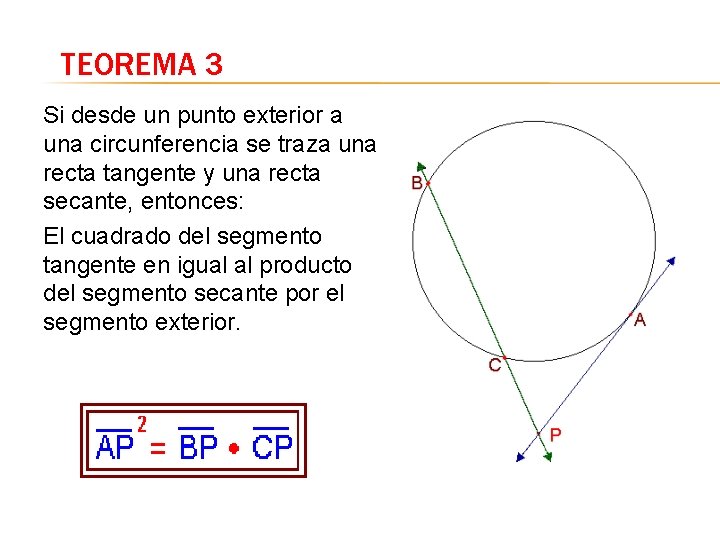
TEOREMA 3 Si desde un punto exterior a una circunferencia se traza una recta tangente y una recta secante, entonces: El cuadrado del segmento tangente en igual al producto del segmento secante por el segmento exterior.

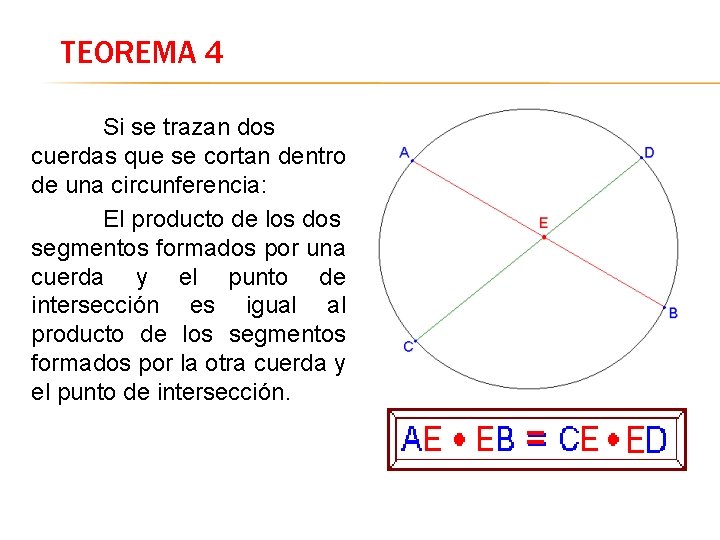
TEOREMA 4 Si se trazan dos cuerdas que se cortan dentro de una circunferencia: El producto de los dos segmentos formados por una cuerda y el punto de intersección es igual al producto de los segmentos formados por la otra cuerda y el punto de intersección.

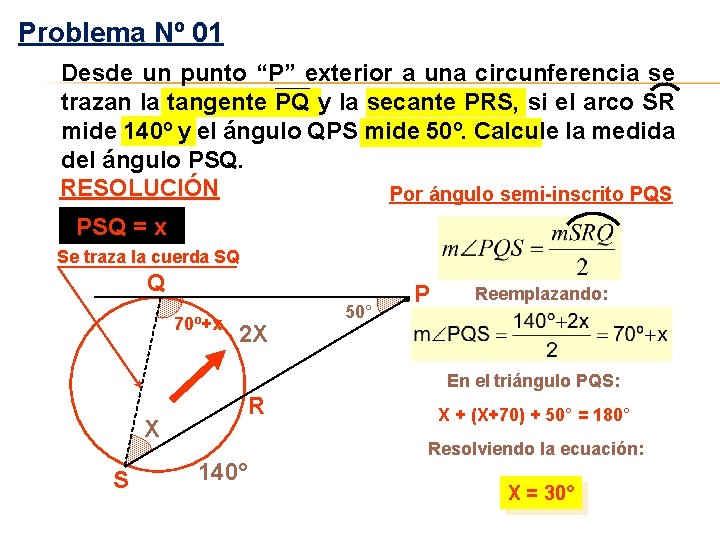
Problema Nº 01 Desde un punto “P” exterior a una circunferencia se trazan la tangente PQ y la secante PRS, si el arco SR mide 140º y el ángulo QPS mide 50º. Calcule la medida del ángulo PSQ. RESOLUCIÓN Por ángulo semi-inscrito PQS PSQ = x Se traza la cuerda SQ Q 70º+x 2 X 50° P Reemplazando: En el triángulo PQS: X S R 140° X + (X+70) + 50° = 180° Resolviendo la ecuación: X = 30°

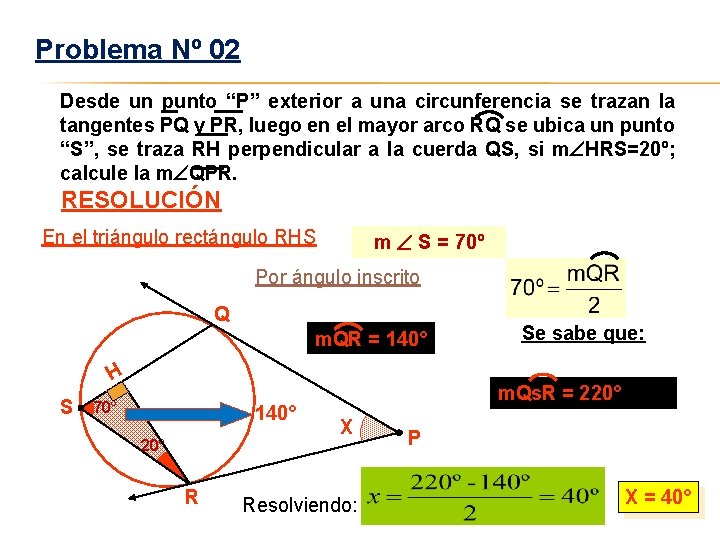
Problema Nº 02 Desde un punto “P” exterior a una circunferencia se trazan la tangentes PQ y PR, luego en el mayor arco RQ se ubica un punto “S”, se traza RH perpendicular a la cuerda QS, si m HRS=20º; calcule la m QPR. RESOLUCIÓN En el triángulo rectángulo RHS m S = 70º Por ángulo inscrito Q m. QR = 140° H S 70° 140° 20° R Se sabe que: m. Qs. R = 220° X Resolviendo: P X = 40°

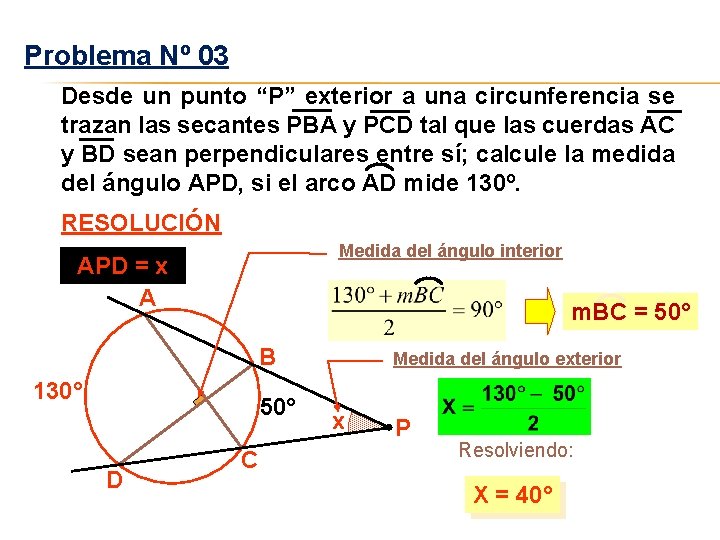
Problema Nº 03 Desde un punto “P” exterior a una circunferencia se trazan las secantes PBA y PCD tal que las cuerdas AC y BD sean perpendiculares entre sí; calcule la medida del ángulo APD, si el arco AD mide 130º. RESOLUCIÓN Medida del ángulo interior APD = x A m. BC = 50° B 130° 50° D C Medida del ángulo exterior x P Resolviendo: X = 40°

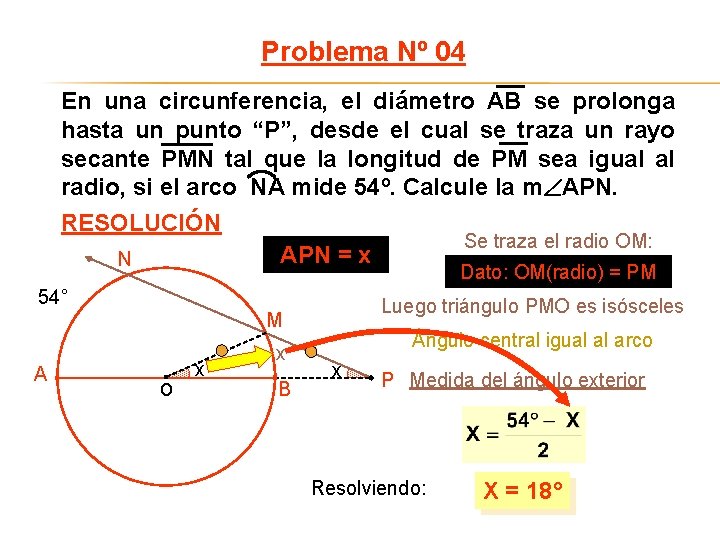
Problema Nº 04 En una circunferencia, el diámetro AB se prolonga hasta un punto “P”, desde el cual se traza un rayo secante PMN tal que la longitud de PM sea igual al radio, si el arco NA mide 54º. Calcule la m APN. RESOLUCIÓN Se traza el radio OM: APN = x N Dato: OM(radio) = PM 54° Luego triángulo PMO es isósceles M A o x x B Ángulo central igual al arco x P Medida del ángulo exterior Resolviendo: X = 18°

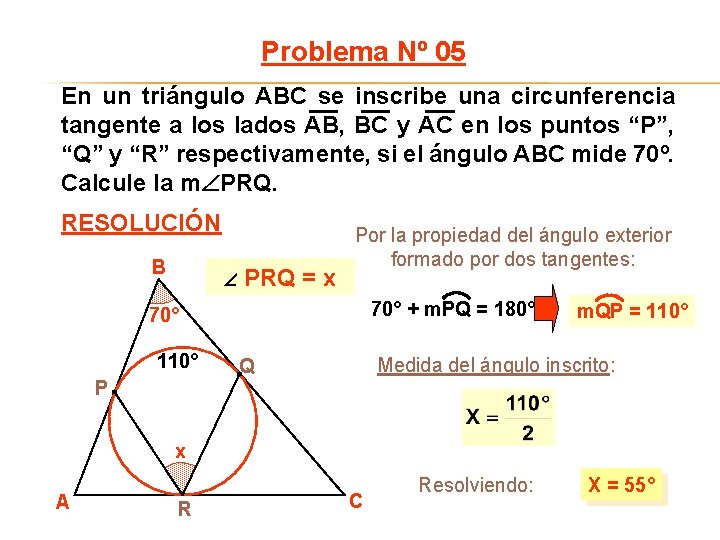
Problema Nº 05 En un triángulo ABC se inscribe una circunferencia tangente a los lados AB, BC y AC en los puntos “P”, “Q” y “R” respectivamente, si el ángulo ABC mide 70º. Calcule la m PRQ. RESOLUCIÓN B PRQ =x Por la propiedad del ángulo exterior formado por dos tangentes: 70° + m. PQ = 180° 70° 110° P m. QP = 110° Medida del ángulo inscrito: Q x A R C Resolviendo: X = 55°

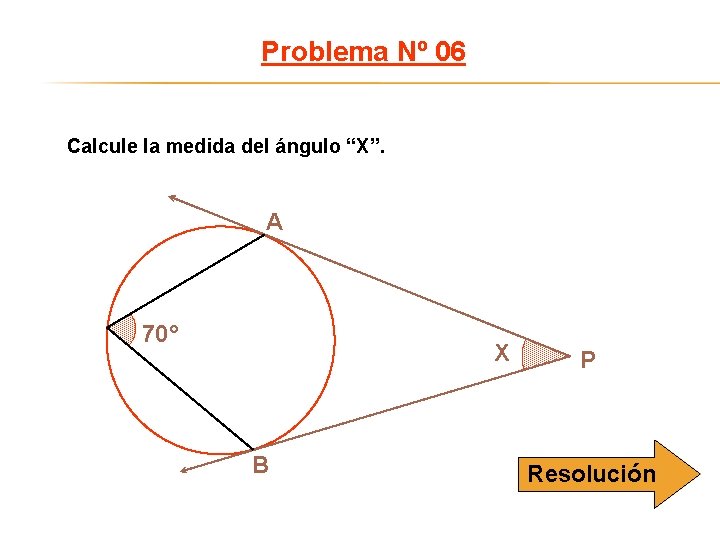
Problema Nº 06 Calcule la medida del ángulo “X”. A 70° X B P Resolución

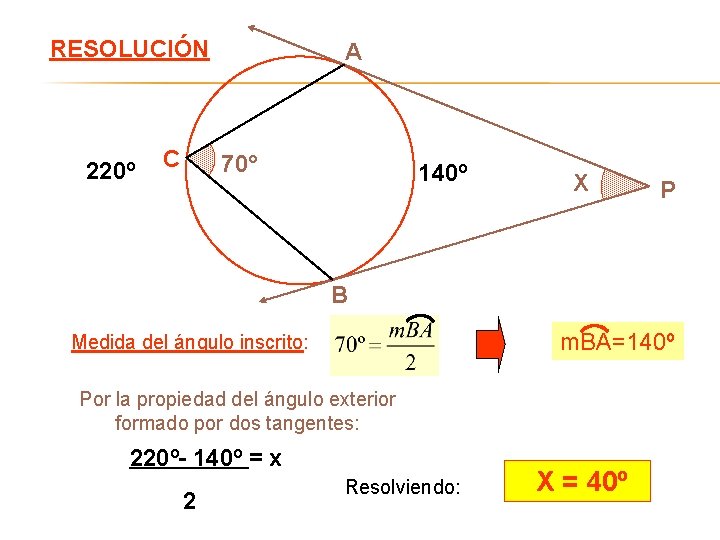
RESOLUCIÓN 220º C A 70° 140º X P B m. BA=140º Medida del ángulo inscrito: Por la propiedad del ángulo exterior formado por dos tangentes: 220º- 140º = x 2 Resolviendo: X = 40º

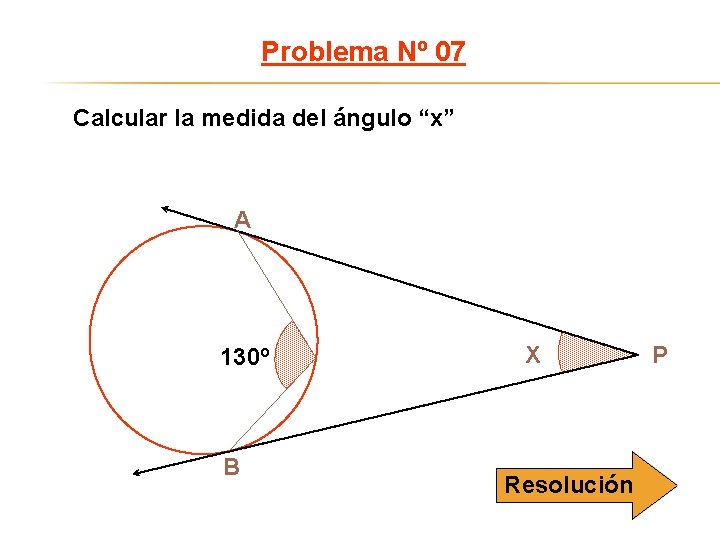
Problema Nº 07 Calcular la medida del ángulo “x” A 130º B X Resolución P

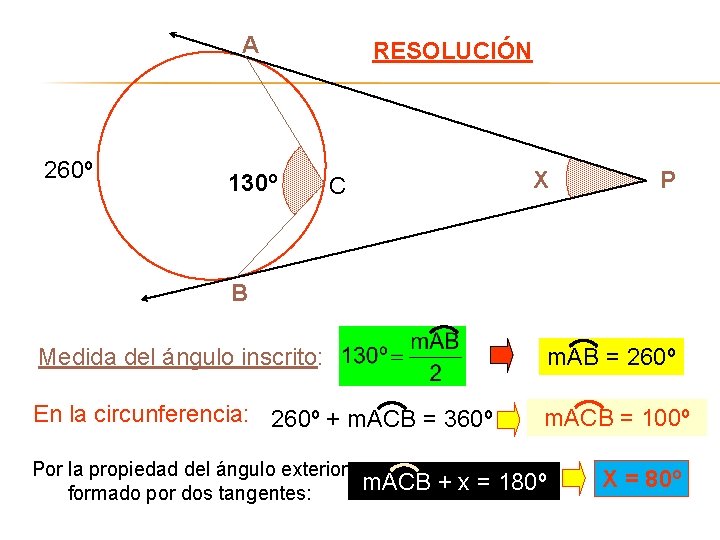
A 260º 130º RESOLUCIÓN X C P B Medida del ángulo inscrito: m. AB = 260º En la circunferencia: 260º + m. ACB = 360º m. ACB = 100º Por la propiedad del ángulo exterior formado por dos tangentes: m. ACB + x = 180º X = 80º

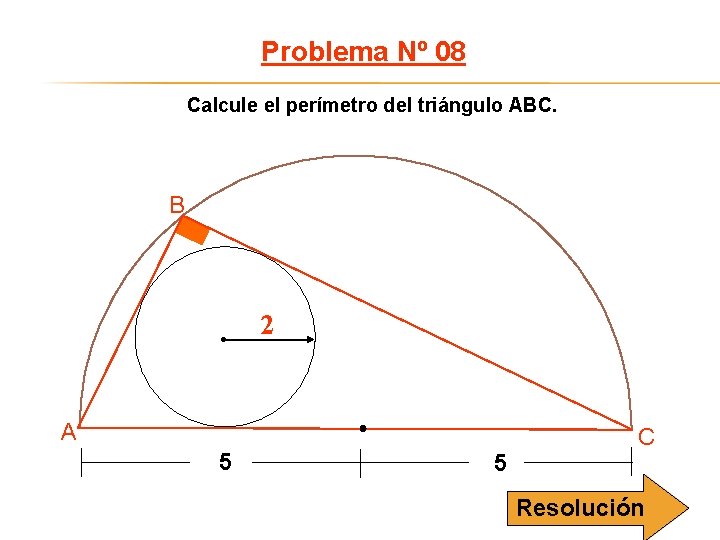
Problema Nº 08 Calcule el perímetro del triángulo ABC. B 2 A 5 5 C Resolución

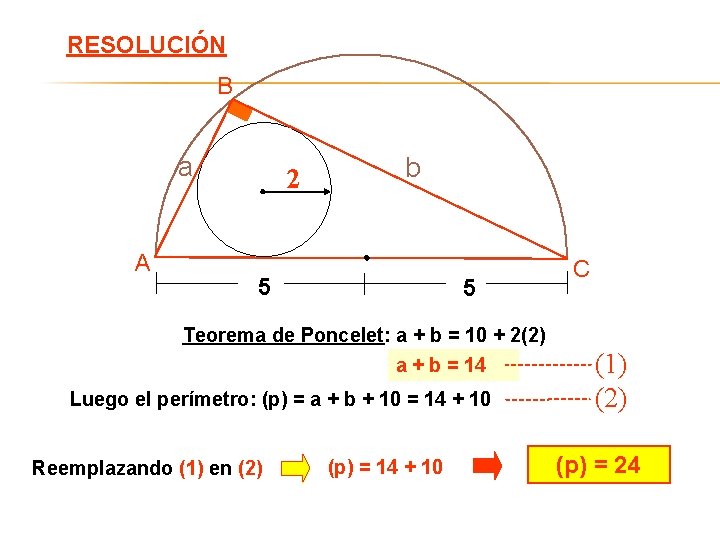
RESOLUCIÓN B a A 2 b 5 5 C Teorema de Poncelet: a + b = 10 + 2(2) a + b = 14 Luego el perímetro: (p) = a + b + 10 = 14 + 10 Reemplazando (1) en (2) (p) = 14 + 10 (1) (2) (p) = 24

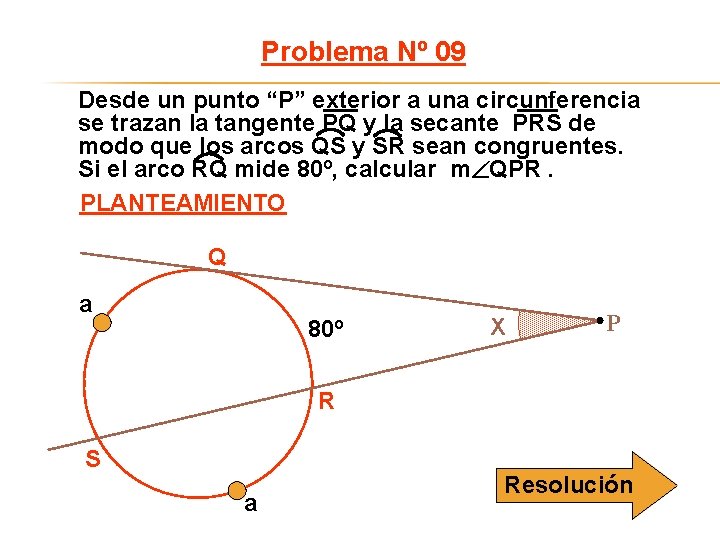
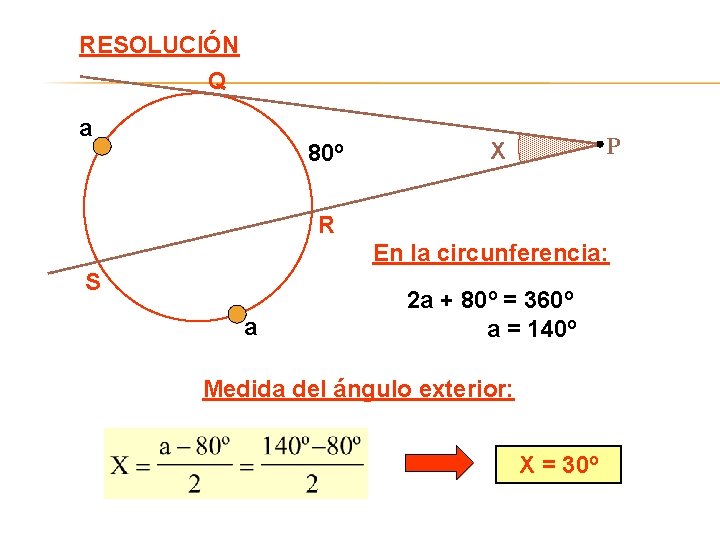
Problema Nº 09 Desde un punto “P” exterior a una circunferencia se trazan la tangente PQ y la secante PRS de modo que los arcos QS y SR sean congruentes. Si el arco RQ mide 80º, calcular m QPR. PLANTEAMIENTO Q a 80º X P R S a Resolución

RESOLUCIÓN Q a 80º P X R En la circunferencia: S a 2 a + 80º = 360º a = 140º Medida del ángulo exterior: X = 30º

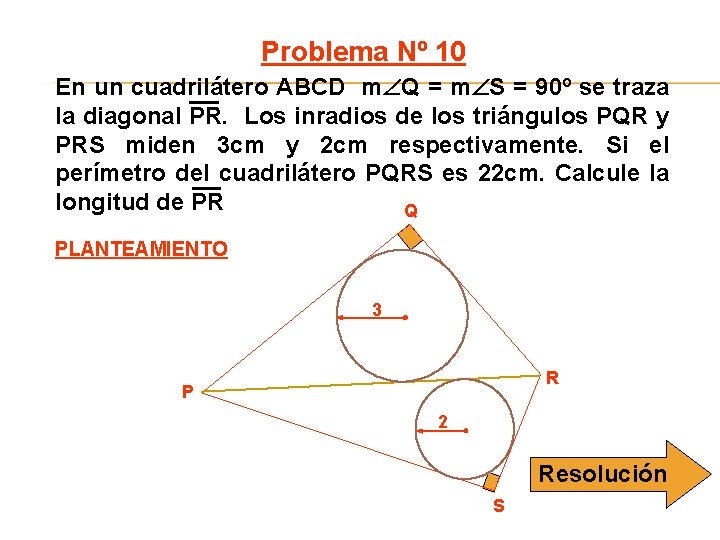
Problema Nº 10 En un cuadrilátero ABCD m Q = m S = 90º se traza la diagonal PR. Los inradios de los triángulos PQR y PRS miden 3 cm y 2 cm respectivamente. Si el perímetro del cuadrilátero PQRS es 22 cm. Calcule la longitud de PR Q PLANTEAMIENTO 3 R P 2 Resolución S

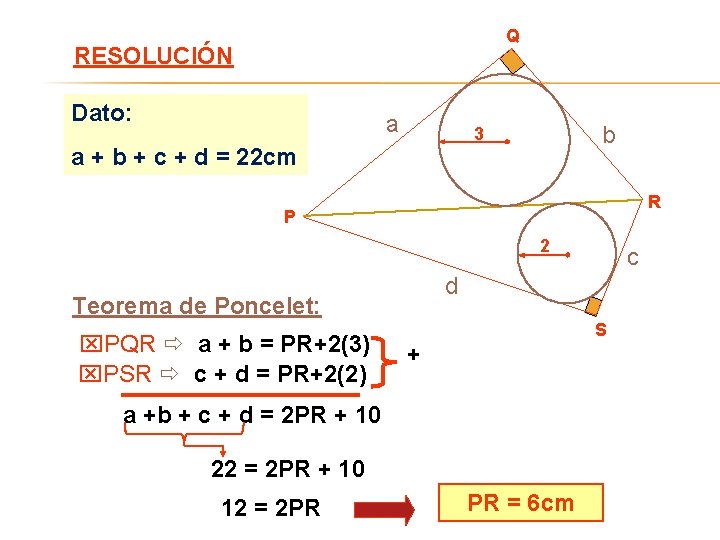
Q RESOLUCIÓN Dato: a b 3 a + b + c + d = 22 cm R P 2 d Teorema de Poncelet: PQR a + b = PR+2(3) PSR c + d = PR+2(2) S + a +b + c + d = 2 PR + 10 22 = 2 PR + 10 12 = 2 PR c PR = 6 cm

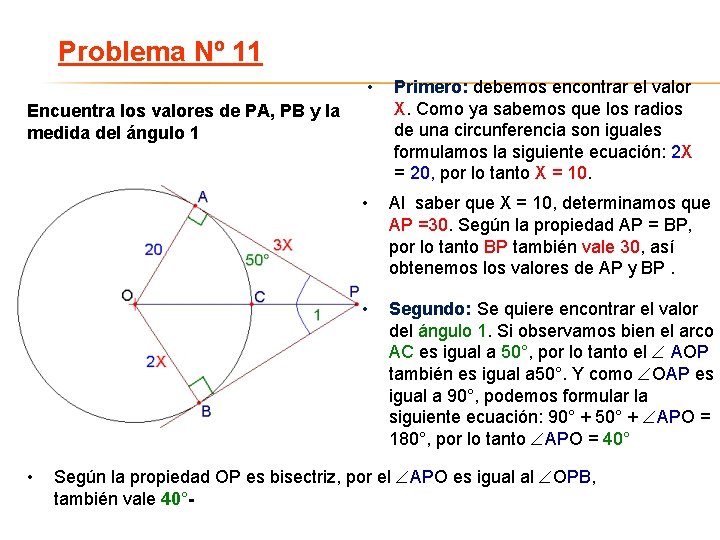
Problema Nº 11 • Encuentra los valores de PA, PB y la medida del ángulo 1 • Primero: debemos encontrar el valor X. Como ya sabemos que los radios de una circunferencia son iguales formulamos la siguiente ecuación: 2 X = 20, por lo tanto X = 10. • Al saber que X = 10, determinamos que AP =30. Según la propiedad AP = BP, por lo tanto BP también vale 30, así obtenemos los valores de AP y BP. • Segundo: Se quiere encontrar el valor del ángulo 1. Si observamos bien el arco AC es igual a 50°, por lo tanto el AOP también es igual a 50°. Y como OAP es igual a 90°, podemos formular la siguiente ecuación: 90° + 50° + APO = 180°, por lo tanto APO = 40° Según la propiedad OP es bisectriz, por el APO es igual al OPB, también vale 40°-

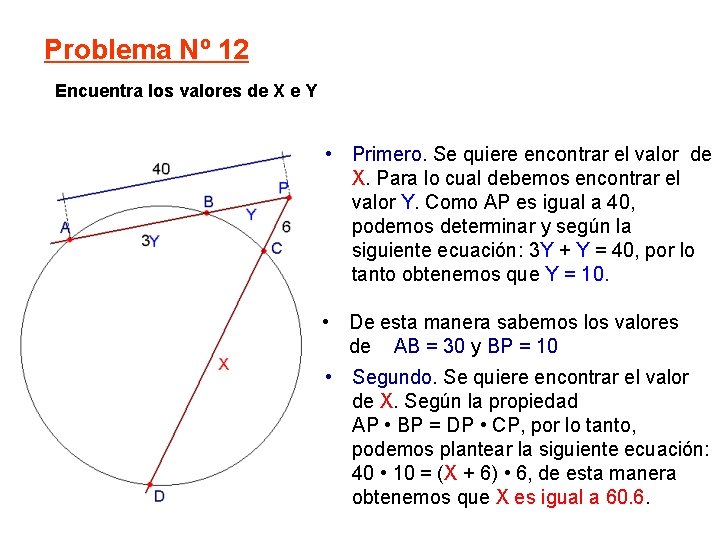
Problema Nº 12 Encuentra los valores de X e Y • Primero. Se quiere encontrar el valor de X. Para lo cual debemos encontrar el valor Y. Como AP es igual a 40, podemos determinar y según la siguiente ecuación: 3 Y + Y = 40, por lo tanto obtenemos que Y = 10. • De esta manera sabemos los valores de AB = 30 y BP = 10 • Segundo. Se quiere encontrar el valor de X. Según la propiedad AP • BP = DP • CP, por lo tanto, podemos plantear la siguiente ecuación: 40 • 10 = (X + 6) • 6, de esta manera obtenemos que X es igual a 60. 6.