Estadstica y Probabilidad Estadstica Descriptiva Estadstica descriptiva Mtodos

Estadística y Probabilidad

Estadística Descriptiva

Estadística descriptiva Métodos para recolectar, presentar y analizar un conjunto de datos con el fin de describir sus características. Análisis de datos Presentación de datos Tablas de frecuencia Gráficas Medidas de tendencia central Medidas de dispersión

Tablas de frecuencia • Porcentaje que representa cada clase con respecto del total de datos. • Se obtiene dividiendo la frecuencia de cada clase entre el total de datos. Frecuencia relativa acumulada • Número de datos que pertenecen a cada clase. Frecuencia relativa Frecuencia Tabla en la que los datos se organizan en categorías previamente establecidas llamadas clases. • Es el porcentaje acumulado que representa un grupo de clases de datos.

Tablas de frecuencia Categoría Frecuencia relativa acumulada [ 2, 4) [ 4, 6) [ 6, 8) [ 8, 10) [ 10, 12) [ 12, 14) Colegiaturas de 60 colegios (en miles de pesos ) 2. 4 3. 5 3. 6 3. 8 3. 9 3. 9 4. 1 4. 4 4. 5 4. 6 4. 7 4. 8 4. 9 4. 9 5. 0 5. 4 5. 8 5. 9 6. 0 6. 4 6. 6 7. 0 7. 2 7. 4 7. 9 8. 0 8. 3 8. 5 8. 6 8. 8 10. 4 10. 7 11. 0 11. 6 12. 0 Tabla de colegiaturas (fuente propia).

Tablas de frecuencia Colegiaturas de 60 colegios (en miles de pesos ) 2. 4 3. 5 3. 6 3. 8 3. 9 3. 9 4. 1 4. 4 4. 5 4. 6 4. 7 4. 8 4. 9 4. 9 5. 0 5. 4 5. 8 5. 9 6. 0 6. 4 6. 6 7. 0 7. 2 7. 4 7. 9 8. 0 8. 3 8. 5 8. 6 8. 8 10. 4 10. 7 11. 0 11. 6 12. 0 Categoría Frecuencia Tabla de colegiaturas (fuente propia). Frecuencia relativa acumulada [ 2, 4) 13 21. 67% [ 4, 6) 24 40% 61. 67% [ 6, 8) 9 15% 76. 67% [ 8, 10) 9 15% 91. 67% [ 10, 12) 4 6. 67% 98. 34% [ 12, 14) 1 1. 66% 100%

Histograma y polígono de frecuencia • Un histograma es una colección de barras verticales unidas que pueden representar la frecuencia, la frecuencia relativa o la frecuencia relativa acumulada de un conjunto de datos numéricos (Triola, 2013). • En el eje horizontal se colocan las clases en las que se organizaron los datos. • En el eje vertical se coloca la frecuencia (frecuencia relativa o frecuencia relativa acumulada). • La altura de las barras indica la frecuencia (frecuencia relativa o frecuencia relativa acumulada).

Histograma y polígono de frecuencia • Asociado a un histograma de frecuencia existe una gráfica adicional denominada polígono de frecuencia. • El polígono de frecuencia se forma uniendo los puntos medios de cada clase sobre cada una de las barras del histograma mediante un segmento de recta. • Si el histograma es de frecuencia relativa acumulada, el polígono se llama ojiva.

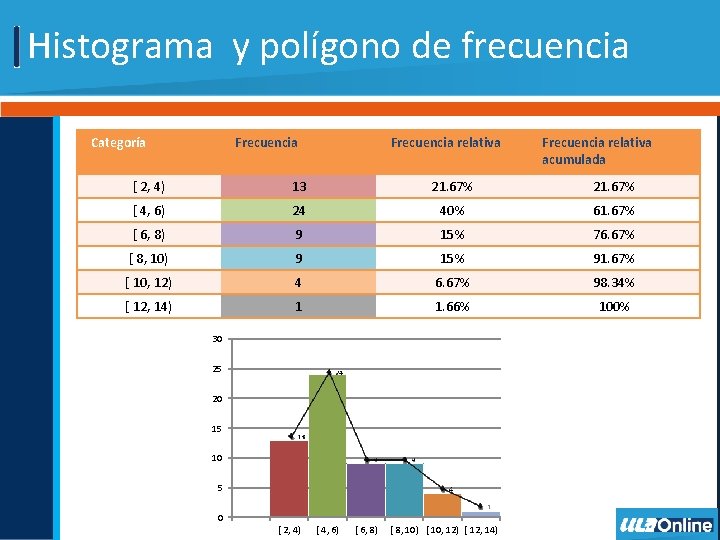
Histograma y polígono de frecuencia Categoría Frecuencia relativa acumulada [ 2, 4) 13 21. 67% [ 4, 6) 24 40% 61. 67% [ 6, 8) 9 15% 76. 67% [ 8, 10) 9 15% 91. 67% [ 10, 12) 4 6. 67% 98. 34% [ 12, 14) 1 1. 66% 100% 30 25 20 15 10 5 0 [ 2, 4) [ 4, 6) [ 6, 8) [ 8, 10) [ 10, 12) [ 12, 14)

Histograma y polígono de frecuencia relativa 100. 00% Categoría Frecuencia relativa acumulada 90. 00% 80. 00% [ 2, 4) 13 21. 67% 70. 00% [ 4, 6) 24 40% 61. 67% 60. 00% [ 6, 8) 9 15% 76. 67% [ 8, 10) 9 15% 91. 67% [ 10, 12) 4 6. 67% 98. 34% 20. 00% [ 12, 14) 1 1. 66% 100% 10. 00% 50. 00% 40. 00% 30. 00% [ 2, 4) [ 4, 6) [ 6, 8) [ 8, 10) [ 10, 12) [ 12, 14)

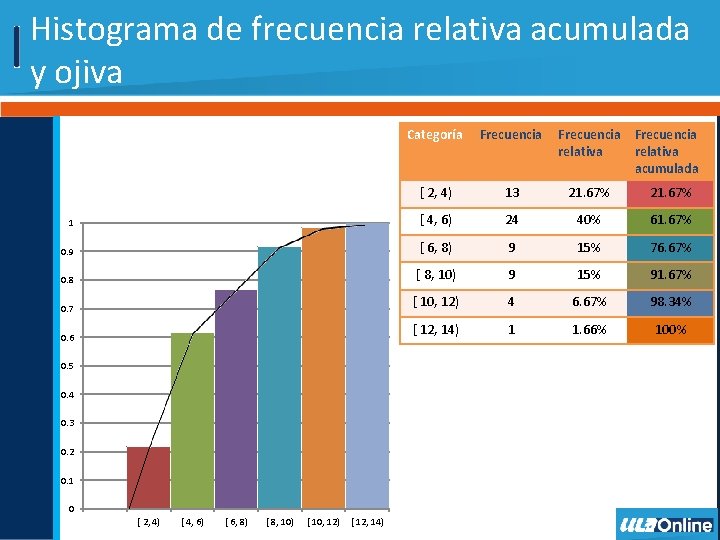
Histograma de frecuencia relativa acumulada y ojiva Categoría Frecuencia [ 2, 4) 13 21. 67% 1 [ 4, 6) 24 40% 61. 67% 0. 9 [ 6, 8) 9 15% 76. 67% 0. 8 [ 8, 10) 9 15% 91. 67% 0. 7 [ 10, 12) 4 6. 67% 98. 34% [ 12, 14) 1 1. 66% 100% 0. 6 0. 5 0. 4 0. 3 0. 2 0. 1 0 [ 2, 4) [ 4, 6) [ 6, 8) [ 8, 10) [ 10, 12) [ 12, 14) Frecuencia relativa acumulada

Observaciones El polígono de frecuencia es una representación de la forma de la distribución de los datos. Como el área bajo la distribución de un histograma de frecuencia relativa debe ser 100%, es necesario conectar el primer punto y el último con el eje horizontal, eso se hace con dos clases ficticias, una al inicio y otra la final con 0%. Tanto el eje vertical como el horizontal deben mostrar su verdadero cero y origen para no malinterpretar la información proporcionada por el gráfico.

Medidas de tendencia central Media o promedio Valor al que tienden a agruparse los datos Suma de todos los datos entre el total de datos Valor medio de los datos ordenados Mediana Se localiza su posición en el lugar (n + 1)/2 Moda Valor de la serie de datos con mayor frecuencia

Cuartiles y percentiles Cuartiles • Dividen al conjunto de datos en cuatro partes iguales. • Q 1 : = posición (n+1)/4 • Q 2 = mediana • Q 3 : = posición 3(n+1)/4 Percentiles • Dividen al conjunto de datos en 100 partes iguales.

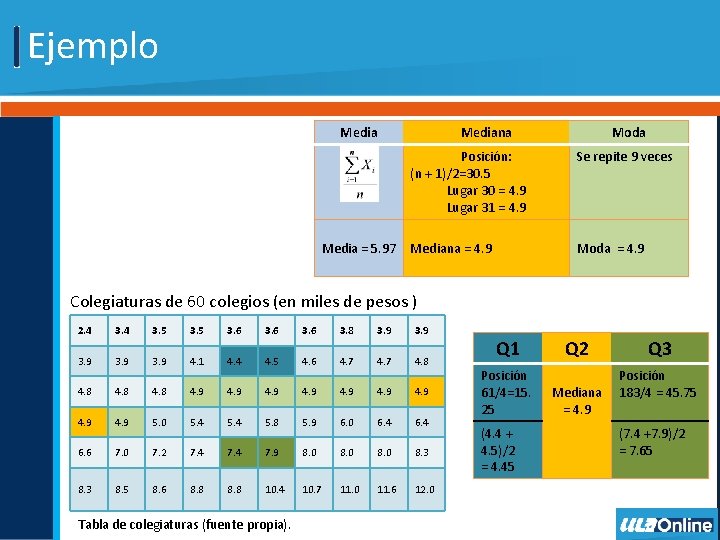
Ejemplo Media = 5. 97 Mediana Moda Posición: (n + 1)/2=30. 5 Lugar 30 = 4. 9 Lugar 31 = 4. 9 Se repite 9 veces Mediana = 4. 9 Moda = 4. 9 Colegiaturas de 60 colegios (en miles de pesos ) 2. 4 3. 5 3. 6 3. 8 3. 9 3. 9 4. 1 4. 4 4. 5 4. 6 4. 7 4. 8 4. 9 4. 9 5. 0 5. 4 5. 8 5. 9 6. 0 6. 4 6. 6 7. 0 7. 2 7. 4 7. 9 8. 0 8. 3 8. 5 8. 6 8. 8 10. 4 10. 7 11. 0 11. 6 12. 0 Tabla de colegiaturas (fuente propia). Q 1 Posición 61/4=15. 25 (4. 4 + 4. 5)/2 = 4. 45 Q 2 Mediana = 4. 9 Q 3 Posición 183/4 = 45. 75 (7. 4 +7. 9)/2 = 7. 65

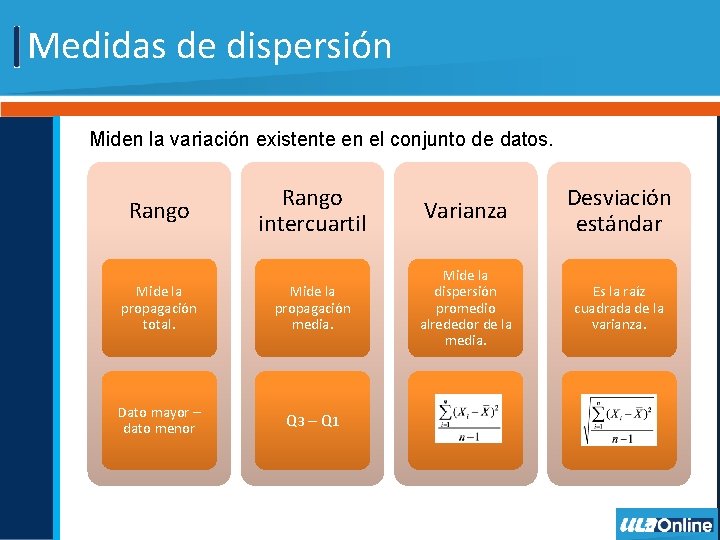
Medidas de dispersión Miden la variación existente en el conjunto de datos. Rango intercuartil Varianza Desviación estándar Mide la propagación total. Mide la propagación media. Mide la dispersión promedio alrededor de la media. Es la raíz cuadrada de la varianza. Dato mayor – dato menor Q 3 – Q 1 Rango

Ejemplo Rango Varianza Desviación estándar 5. 16 2. 27 12 – 2. 4 = 9. 6 Colegiaturas de 60 colegios (en miles de pesos ) 2. 4 3. 5 3. 6 3. 8 3. 9 3. 9 4. 1 4. 4 4. 5 4. 6 4. 7 4. 8 4. 9 4. 9 5. 0 5. 4 5. 8 5. 9 6. 0 6. 4 6. 6 7. 0 7. 2 7. 4 7. 9 8. 0 8. 3 8. 5 8. 6 8. 8 10. 4 10. 7 11. 0 11. 6 12. 0 Tabla de colegiaturas (fuente propia).

Interpretación medidas de dispersión En la mayoría de los conjuntos de datos: • Aproximadamente 68% de los datos se encuentran concentrados a una distancia de una desviación estándar alrededor de la media. • 95% de los datos están contenidos a una distancia aproximada de dos desviaciones estándar alrededor de la media.

Probabilidad y distribuciones de probabilidad

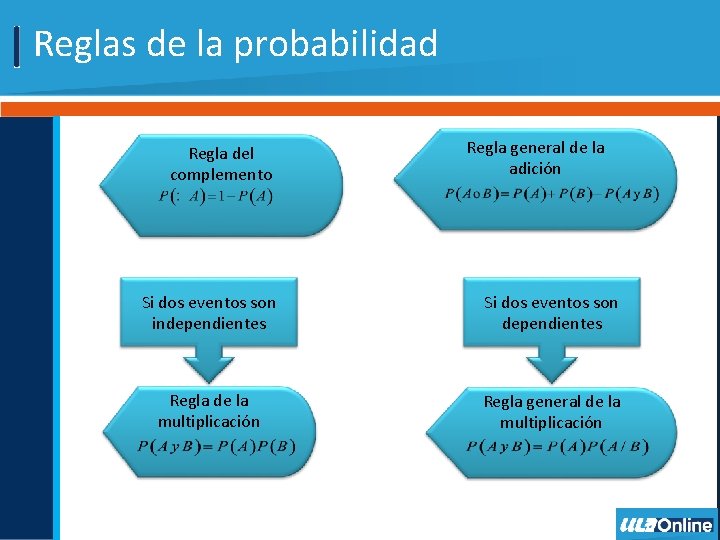
Reglas de la probabilidad Regla del complemento Regla general de la adición Si dos eventos son independientes Si dos eventos son dependientes Regla de la multiplicación Regla general de la multiplicación

Probabilidad condicional es la probabilidad de que un evento A ocurra dado que otro evento B haya acontecido (Lindt, Marchal & Wathen, 2008).

Tablas de contingencia y la probabilidad • Una encuesta de 150 personas fueron clasificadas según su género y la cantidad de libros que leyeron en el mes. Género # libros leídos Hombres Mujeres Total 0 20 40 60 1 40 30 70 2 10 10 20 Total 70 80 150 (Fuente propia)

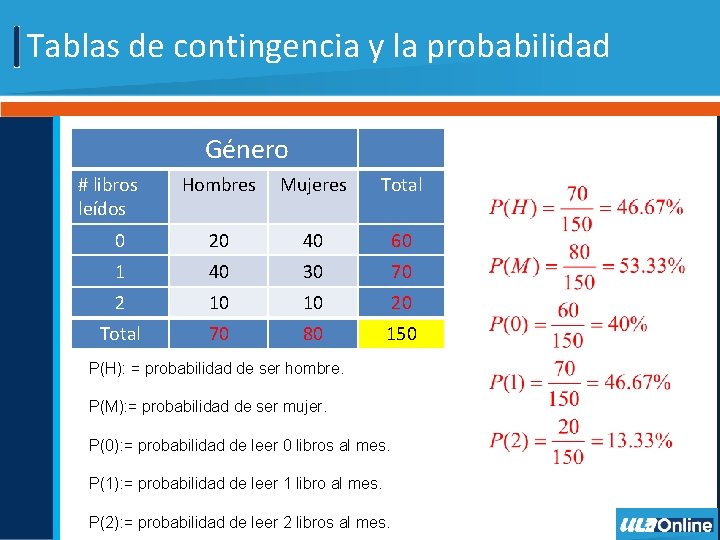
Tablas de contingencia y la probabilidad Género # libros leídos Hombres Mujeres Total 0 20 40 60 1 40 30 70 2 10 10 20 Total 70 80 150 P(H): = probabilidad de ser hombre. P(M): = probabilidad de ser mujer. P(0): = probabilidad de leer 0 libros al mes. P(1): = probabilidad de leer 1 libro al mes. P(2): = probabilidad de leer 2 libros al mes.

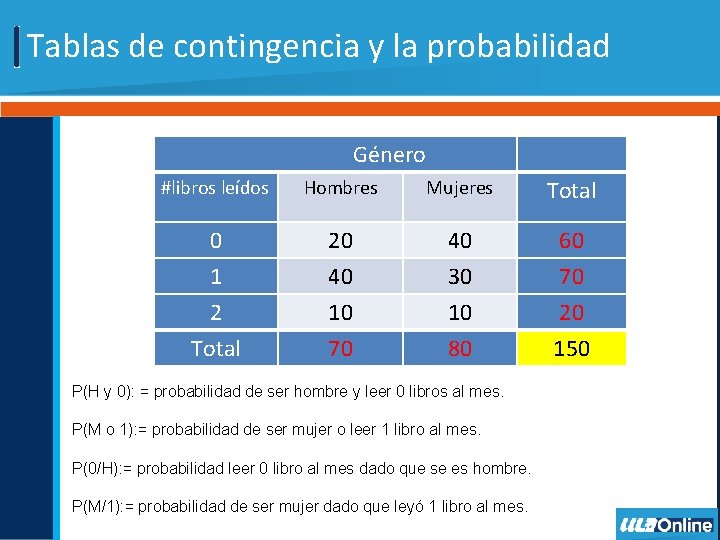
Tablas de contingencia y la probabilidad Género #libros leídos Hombres Mujeres Total 0 20 40 60 1 40 30 70 2 10 10 20 Total 70 80 150 P(H y 0): = probabilidad de ser hombre y leer 0 libros al mes. P(M o 1): = probabilidad de ser mujer o leer 1 libro al mes. P(0/H): = probabilidad leer 0 libro al mes dado que se es hombre. P(M/1): = probabilidad de ser mujer dado que leyó 1 libro al mes.

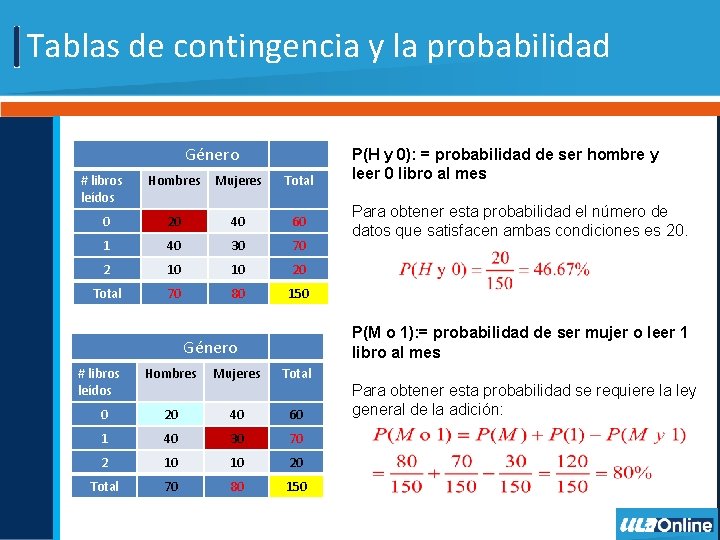
Tablas de contingencia y la probabilidad Género # libros leídos Hombres Mujeres Total 0 20 40 60 1 40 30 70 2 10 10 20 Total 70 80 150 Para obtener esta probabilidad el número de datos que satisfacen ambas condiciones es 20. P(M o 1): = probabilidad de ser mujer o leer 1 libro al mes Género # libros leídos P(H y 0): = probabilidad de ser hombre y leer 0 libro al mes Hombres Mujeres Total 0 20 40 60 1 40 30 70 2 10 10 20 Total 70 80 150 Para obtener esta probabilidad se requiere la ley general de la adición:

Tablas de contingencia y la probabilidad Género # libros leïdos Hombres Mujeres Total 0 20 40 60 1 40 30 70 2 10 10 20 Total 70 80 150 (Fuente propia) P(0 / H): = probabilidad de leer 0 libro al mes dado que se es hombre. Esta probabilidad se refiere a una probabilidad condicional. P(M / 1): = probabilidad de ser mujer dado que leyó 1 libro al mes. Esta probabilidad se refiere a una probabilidad condicional.

Distribución de probabilidad • Es un listado de todos los resultados de un experimento y la probabilidad asociada a cada resultado. • Se llama variable aleatoria a la cantidad que resulta de un experimento. • Una variable aleatoria puede ser discreta si adopta sólo valores enteros o continua si adopta valores que pueden ser decimales.

Distribución normal Es la distribución de variables continuas más utilizada. Tiene forma de campana con una sola cima en el centro de la distribución extendiéndose de forma asintótica en ambas direcciones. La media, moda y mediana son iguales y es simétrica respecto a la media. El área total bajo la curva representa la probabilidad total que es de 1. Su forma depende de dos parámetros: la media y la desviación estándar.

Distribución normal estándar • Es la distribución de probabilidad normal que tiene media 0 y desviación estándar 1. • Cualquier distribución de probabilidad normal puede convertirse en la distribución normal estándar mediante la fórmula: • El valor de Z es la distancia que hay entre la media y el valor de X en términos de desviaciones estándar

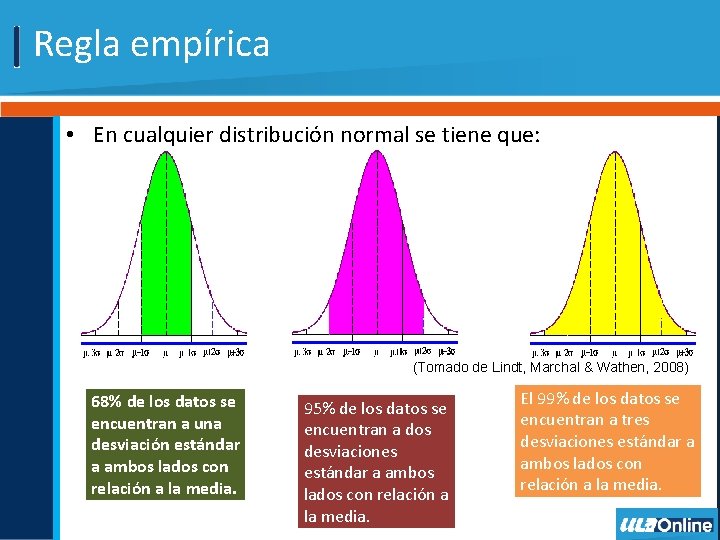
Regla empírica • En cualquier distribución normal se tiene que: (Tomado de Lindt, Marchal & Wathen, 2008) 68% de los datos se encuentran a una desviación estándar a ambos lados con relación a la media. 95% de los datos se encuentran a dos desviaciones estándar a ambos lados con relación a la media. El 99% de los datos se encuentran a tres desviaciones estándar a ambos lados con relación a la media.

Determinar probabilidades en la distribución normal estándar La probabilidad en una distribución normal está relacionada con la determinación del área bajo la curva de la distribución. Para ello se utiliza una tabla que nos permite localizar el área bajo la curva que se localiza entre la media y el valor elegido, que se identifica por X. (Tomado de Lindt, Marchal & Wathen, 2008)

Ejemplo Los empleados de Cartwright Manufacturing obtienen calificaciones mensuales de eficacia con base en factores como productividad, actitud y asistencia. Las calificaciones tienen una distribución normal con media de 400 puntos y desviación estándar de 50 puntos. (Tomado de Lindt, Marchal y Wathen, 2008)

Preguntas ¿Cuál es la probabilidad de que un empleado obtenga una puntuación entre 400 y 482? Obtener el valor de Z: Localizar el valor de Z en la tabla y por tanto el valor del área entre X y la media. (Tomado de Lindt, Marchal & Wathen, 2008)

Preguntas ¿Cuál es la probabilidad de que un empleado obtenga una puntuación entre 400 y 482? Obtener el valor de Z: Localizar el valor de Z en la tabla y por tanto el valor del área entre X y la media. La probabilidad de que un empleado obtenga una puntuación entre 400 y 482 es de 44. 95%. 0. 44950 (Tomado de Lindt, Marchal & Wathen, 2008) 400 482

Preguntas ¿Cuál es la probabilidad de que un empleado obtenga una puntuación mayor 480? Obtener el valor de Z: Localizar el valor de Z en la tabla y por tanto el valor del área entre X y la media. 400 480 (Tomado de Lindt, Marchal & Wathen, 2008)

Preguntas ¿Cuál es la probabilidad de que un empleado obtenga una puntuación mayor 480? . 44520 400 480 Obtener el valor de Z: Localizar el valor de Z en la tabla y por tanto el valor del área entre X y la media. En este caso, el área localizada en la tabla no es el área buscada; ésta se obtiene de restar a la mitad del área completa (0. 5) el valor localizado 0. 44520. 0. 5 – 0. 44520 = 0. 0548 (Tomado de Lindt, Marchal & Wathen, 2008)

Preguntas ¿Cuál es la probabilidad de que un empleado obtenga una puntuación mayor a 480? Obtener el valor de Z: La probabilidad de que un empleado obtenga una puntuación mayor a 480 es de 5. 68%. . 0568 (Tomado de Lindt, Marchal & Wathen, 2008) 400 480

Preguntas ¿Cuál es la probabilidad de que un empleado obtenga una puntuación entre 350 y 450? Obtener el valor de Z para cada valor de X: El valor negativo indica que el valor de X está a la izquierda de la media. El valor positivo indica que el valor de X está a la derecha de la media. 350 450 (Tomado de Lindt, Marchal & Wathen, 2008)

Preguntas ¿Cuál es la probabilidad de que un empleado obtenga una puntuación entre 350 y 450? Localizar los valores de Z en la tabla y por tanto el valor del área entre X y la media. Como se puede observar en la tabla no existen valores negativos porque la gráfica es simétrica, por tanto a ambos valores de Z les corresponde el mismo valor bajo la curva. (Tomado de Lindt, Marchal & Wathen, 2008)

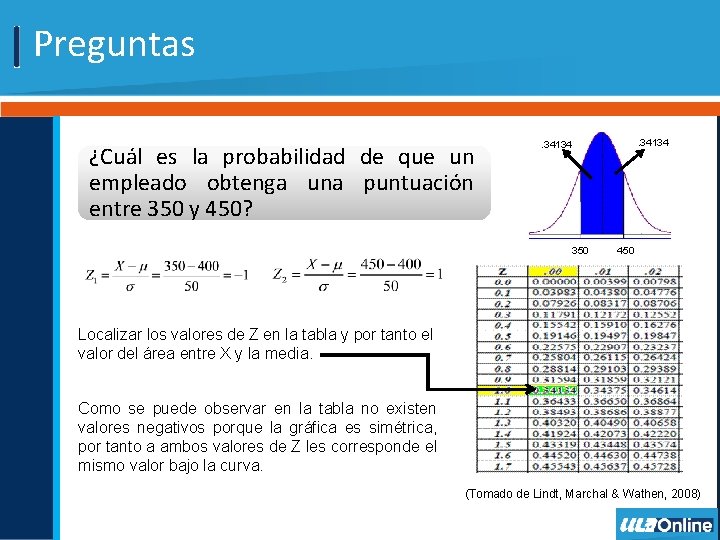
Preguntas ¿Cuál es la probabilidad de que un empleado obtenga una puntuación entre 350 y 450? . 34134 350 450 Localizar los valores de Z en la tabla y por tanto el valor del área entre X y la media. Como se puede observar en la tabla no existen valores negativos porque la gráfica es simétrica, por tanto a ambos valores de Z les corresponde el mismo valor bajo la curva. (Tomado de Lindt, Marchal & Wathen, 2008)

Preguntas ¿Cuál es la probabilidad de que un empleado obtenga una puntuación entre 350 y 450? . 34134 350 450 En este caso, el área buscada se obtiene como la suma de las dos áreas localizadas en la tabla. 0. 34134 + 0. 34134 = 0. 68268 La probabilidad de que un empleado obtenga una puntuación entre 350 y 450 es de 68. 27%. (Tomado de Lindt, Marchal & Wathen, 2008)

Fuentes de consulta • Lind, D. , Marchal, W. & Wathen, S. (2008). Estadística aplicada a los negocios y la economía. México: Mc. Graw Hill Interamericana. (Disponible en la Biblioteca Virtual ULA, colección Mc. Graw Hill). • Triola, M. (2013). Estadística. México: Pearson Educación. (Disponible en la Biblioteca Virtual ULA, colección Mc. Graw Hill).