Unidad 7 Fuerza y Masa 1 La fuerza


















































































- Slides: 97

Unidad 7 Fuerza y Masa 1 - La fuerza y sus efectos ¿Qué es una fuerza? Efectos de las fuerzas Masa 2 - Las Fuerzas de la Naturaleza 3 - Caída libre Problemas 4 - Las Leyes de Newton

Unidad 7 Fuerza y Masa 4 - Las Leyes de Newton Primera ley de Newton. Ley de la Inercia. Segunda ley de Newton. Ley de la dinámica. Tercera ley de Newton. Principio de Acción y reacción. Problemas

Unidad 7 Fuerza y Masa 4 - Las Leyes de Newton Equilibrio de fuerzas 5 - El peso Problemas 6 - La ley de hooke Problemas

Unidad 7 Fuerza y Masa 7 - Ley de Gravitación Universal Problemas 8 - Fuerzas de rozamiento o fricción 9 - Fuerzas magnéticas. Magnetismo 10 - Máquinas simples

¿Qué es una fuerza?

¿Qué es una fuerza?

¿Qué es una fuerza? Una fuerza es todo aquello capaz de causar un cambio en el movimiento de un cuerpo (pararlo o ponerlo en movimiento) o deformarlo. Pueden ser de dos tipos: Fuerzas de contacto Fuerzas sin contacto

¿Qué es una fuerza? Una fuerza es todo aquello capaz de causar un cambio en el movimiento de un cuerpo (pararlo o ponerlo en movimiento) o deformarlo. Pueden ser de dos tipos: Fuerzas de contacto Fuerzas sin contacto

¿Qué es una fuerza? Una fuerza es todo aquello capaz de causar un cambio en el movimiento de un cuerpo (pararlo o ponerlo en movimiento) o deformarlo. Pueden ser de dos tipos: Fuerzas de contacto Fuerzas sin contacto

¿Qué es una fuerza? Una fuerza es todo aquello capaz de causar un cambio en el movimiento de un cuerpo (pararlo o ponerlo en movimiento) o deformarlo. Pueden ser de dos tipos: Fuerzas de contacto Fuerzas sin contacto

¿Qué es una fuerza? Mayor intensidad de la fuerza mayor efecto Su unidad en el sistema internacional es el Newton (N) 1 N = 1 kg · m/s 2 Masa Es la cantidad de materia de lo que está hecho algo. Su unidad en el SI es el kilogramo (kg).

¿Qué es una fuerza? La medida de una fuerza se basa en: - La medida de las deformaciones que producen en los cuerpos - La medida de los cambios en el movimiento que producen en los cuerpos

Fuerzas de la Naturaleza (4) Fuerza gravitatoria Caída de los objetos, movimiento de los planetas alrededor del sol Fuerza electromagnética Rayos, corriente eléctrica, imanes Fuerza nuclear débil Responsable de un tipo de radioactividad Fuerza nuclear fuerte en el La que mantiene unidos a los protones y los neutrones núcleo atómico

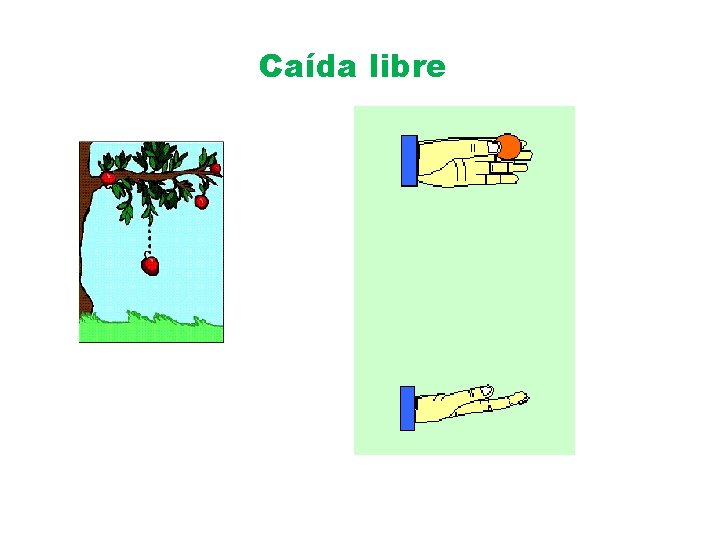
Caída libre

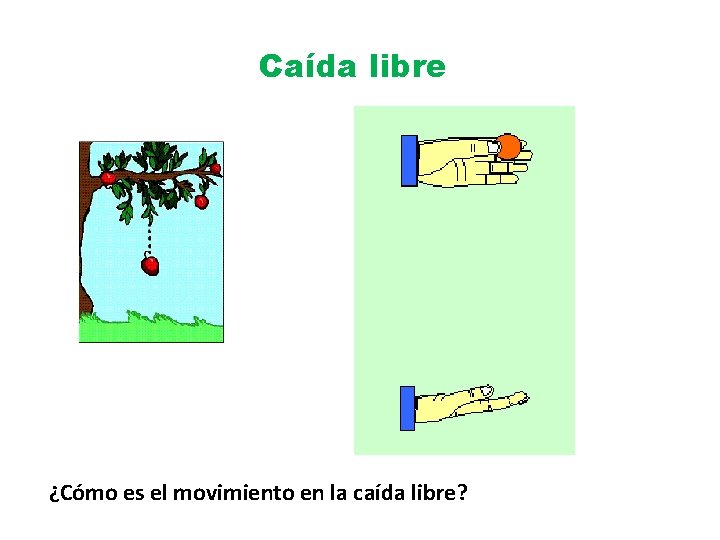
Caída libre ¿Cómo es el movimiento en la caída libre?

Caída libre MRUA

Caída libre MRUA S = S 0 + V 0 · t + ½ a · t 2

Caída libre MRUA S = S 0 + V 0 · t + ½ a · t 2 Aceleración= aceleración causada por la gravedad (g) g= 10 m/s 2 (9. 81 m/s 2) Velocidad inicial V 0= 0 m/s

Caída libre MRUA S = S 0 + V 0 · t + ½ a · t 2 Aceleración= aceleración causada por la gravedad (g) g= 10 m/s 2 (9. 81 m/s 2) Velocidad inicial V 0= 0 m/s S = S 0 + ½ g · t 2

Caída libre MRUA V = v 0 + a · t

Caída libre MRUA V = v 0 + a · t Velocidad inicial v 0 = 0 Aceleración= aceleración causada por la gravedad (g) V = g · t

Si la aceleración de la gravedad la tomamos como 10 m/s 2 , ¿qué velocidad tendrá un cuerpo al que se deja caer por un acantilado después de 2 segundos? ¿Y pasados 5 segundos? Una pelota cae desde un tejado y tarda en llegar al suelo 3 segundos. ¿Desde que altura cayó?

Si la aceleración de la gravedad la tomamos como 10 m/s 2 , ¿qué velocidad tendrá un cuerpo al que se deja caer por un acantilado después de 2 segundos? 20 m/s ¿Y pasados 5 segundos? Una pelota cae desde un tejado y tarda en llegar al suelo 3 segundos. ¿Desde que altura cayó?

Si la aceleración de la gravedad la tomamos como 10 m/s 2 , ¿qué velocidad tendrá un cuerpo al que se deja caer por un acantilado después de 2 segundos? 20 m/s ¿Y pasados 5 segundos? 50 m/s Una pelota cae desde un tejado y tarda en llegar al suelo 3 segundos. ¿Desde que altura cayó?

Si la aceleración de la gravedad la tomamos como 10 m/s 2 , ¿qué velocidad tendrá un cuerpo al que se deja caer por un acantilado después de 2 segundos? 20 m/s ¿Y pasados 5 segundos? 50 m/s Una pelota cae desde un tejado y tarda en llegar al suelo 3 segundos. ¿Desde que altura cayó? 45 m

Dejamos caer una piedra desde un edificio de 45 m respecto al suelo. a) ¿Cuánto tarda en llegar al suelo? b) ¿Con qué velocidad llega al suelo? Se suelta un cuerpo sin velocidad inicial. ¿Al cabo de cuanto tiempo su velocidad será de 45 km/h?

Dejamos caer una piedra desde un edificio de 45 m respecto al suelo. a) ¿Cuánto tarda en llegar al suelo? 3 s b) ¿Con qué velocidad llega al suelo? Se suelta un cuerpo sin velocidad inicial. ¿Al cabo de cuanto tiempo su velocidad será de 45 km/h?

Dejamos caer una piedra desde un edificio de 45 m respecto al suelo. a) ¿Cuánto tarda en llegar al suelo? 3 s b) ¿Con qué velocidad llega al suelo? 30 m/s Se suelta un cuerpo sin velocidad inicial. ¿Al cabo de cuanto tiempo su velocidad será de 45 km/h?

Dejamos caer una piedra desde un edificio de 45 m respecto al suelo. a) ¿Cuánto tarda en llegar al suelo? 3 s b) ¿Con qué velocidad llega al suelo? 30 m/s Se suelta un cuerpo sin velocidad inicial. ¿Al cabo de cuánto tiempo su velocidad será de 45 km/h? 1. 25 s

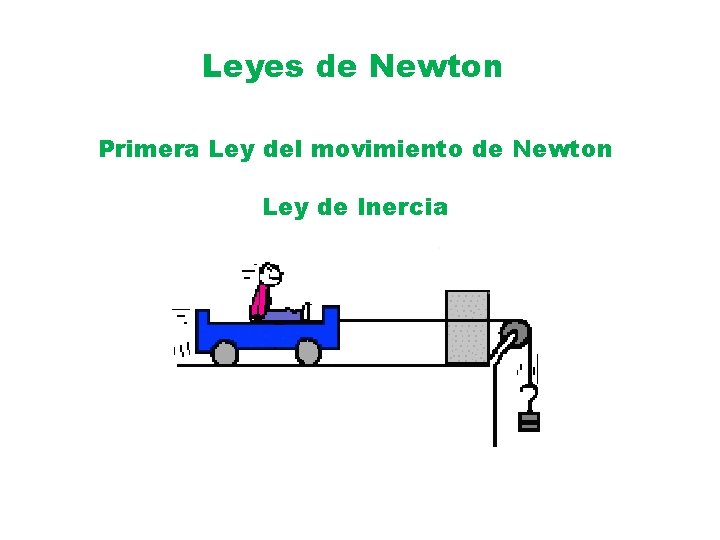
Leyes de Newton Primera Ley del movimiento de Newton Ley de Inercia

Leyes de Newton Primera Ley del movimiento de Newton Ley de Inercia

Leyes de Newton Primera Ley del movimiento de Newton Ley de Inercia Todo cuerpo permanecerá en estado de reposo o con un movimiento rectilíneo uniforme a no ser que una fuerza externa actúe sobre él.

Leyes de Newton Segunda Ley del movimiento de Newton Ley de la Dinámica

Leyes de Newton Segunda Ley del movimiento de Newton Ley de la Dinámica 1 N = 1 kg · m/s 2

Leyes de Newton Segunda Ley del movimiento de Newton Ley de la Dinámica Problemas 1 - ¿Qué fuerza hará que una masa de 4 kg alcance una aceleración de 5 m/s 2? 2 - Una fuerza de 50 N actúa sobre un balón de 2 kg. ¿Cuál será su aceleración?

Leyes de Newton Segunda Ley del movimiento de Newton Ley de la Dinámica Problemas 1 - ¿Qué fuerza hará que una masa de 4 kg alcance una aceleración de 5 m/s 2? F= 20 N 2 - Una fuerza de 50 N actúa sobre un balón de 2 kg. ¿Cuál será su aceleración?

Leyes de Newton Segunda Ley del movimiento de Newton Ley de la Dinámica Problemas 1 - ¿Qué fuerza hará que una masa de 4 kg alcance una aceleración de 5 m/s 2? F= 20 N 2 - Una fuerza de 50 N actúa sobre un balón de 2 kg. ¿Cuál será su aceleración? 25 m/s 2

Leyes de Newton Tercera Ley del movimiento de Newton Principio de acción y reacción

Leyes de Newton Tercera Ley del movimiento de Newton Principio de acción y reacción Cuando un cuerpo ejerce una fuerza sobre un segundo cuerpo, el segundo cuerpo ejerce una fuerza igual pero opuesta sobre el primer cuerpo

Action–reaction pairs

Leyes de Newton Problemas 1 - Razona: Se aplica la misma fuerza a dos objetos distintos. La aceleración del primero es 1. 8 m/s 2 y la del segundo 9. 8 m/s 2. ¿Cuál de los dos tiene mayor masa? 2 - Un coche de 1520 kg acelera a 1. 5 m/s 2. ¿Cuál es la fuerza actuando en el coche? 3 - Un tenista golpea una pelota con una fuerza de 65 N. Si la pelota tiene una masa de 0. 145 kg, ¿cuál será la aceleración de la pelota?

Leyes de Newton Problemas 1 - Razona: Se aplica la misma fuerza a dos objetos distintos. La aceleración del primero es 1. 8 m/s 2 y la del segundo 9. 8 m/s 2. ¿Cuál de los dos tiene mayor masa? 2 - Un coche de 1520 kg acelera a 1. 5 m/s 2. ¿Cuál es la fuerza actuando en el coche? 2280 N 3 - Un tenista golpea una pelota con una fuerza de 65 N. Si la pelota tiene una masa de 0. 145 kg, ¿cuál será la aceleración de la pelota?

Leyes de Newton Problemas 4 - Un camión de 28 toneladas cambia de velocidad en 100 s de 36 km/h a 54 km/h. Determina: la aceleración del camión, b) la fuerza ejercida sobre el mismo.

Leyes de Newton Problemas 4 - Un camión de 28 toneladas cambia de velocidad en 100 s de 36 km/h a 54 km/h. Determina: la aceleración del camión, b) la fuerza ejercida sobre el mismo. a) 0. 025 m/s 2 b) 700 N

Leyes de Newton Problemas 4 - Un camión de 28 toneladas cambia de velocidad en 100 s de 36 km/h a 54 km/h. Determina: la aceleración del camión, b) la fuerza ejercida sobre el mismo. a) 0. 05 m/s 2 b) 1400 N

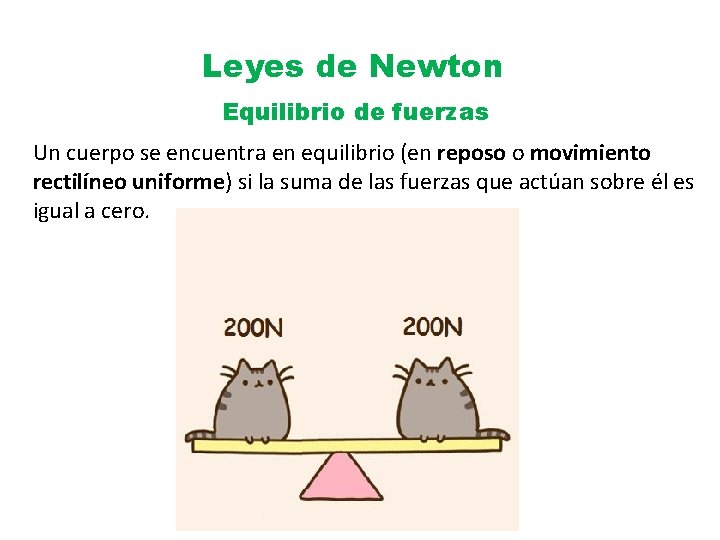
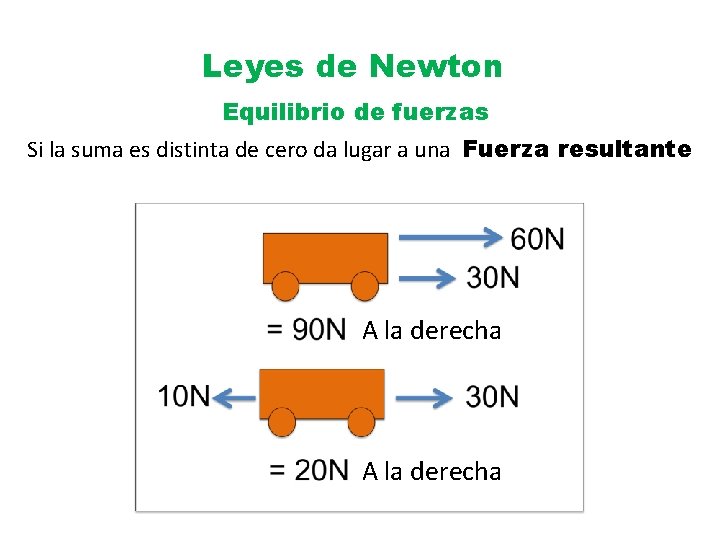
Leyes de Newton Equilibrio de fuerzas Un cuerpo se encuentra en equilibrio (en reposo o movimiento rectilíneo uniforme) si la suma de las fuerzas que actúan sobre él es igual a cero.

Leyes de Newton Equilibrio de fuerzas Si la suma es distinta de cero da lugar a una Fuerza resultante A la derecha

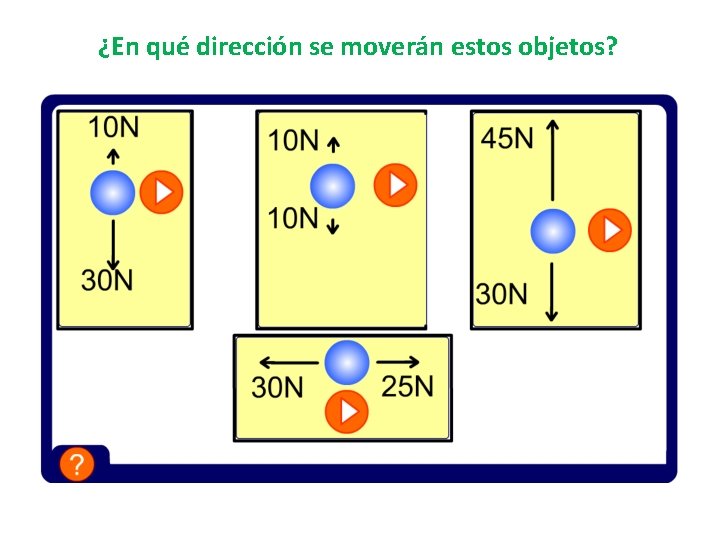
¿En qué dirección se moverán estos objetos?

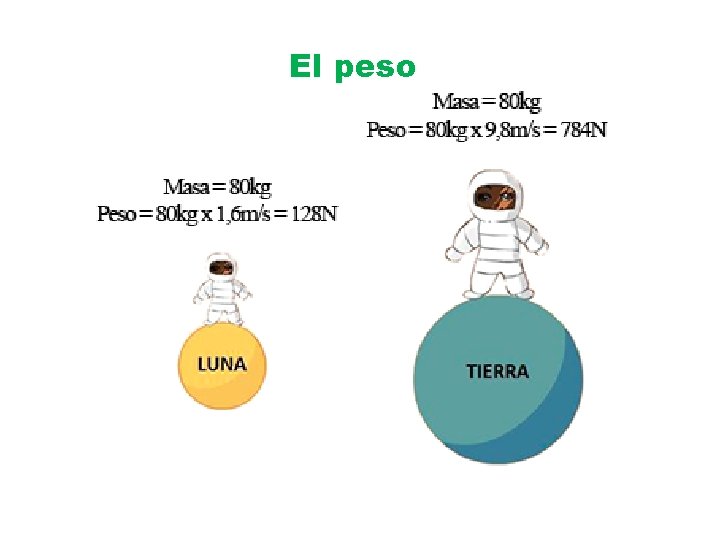
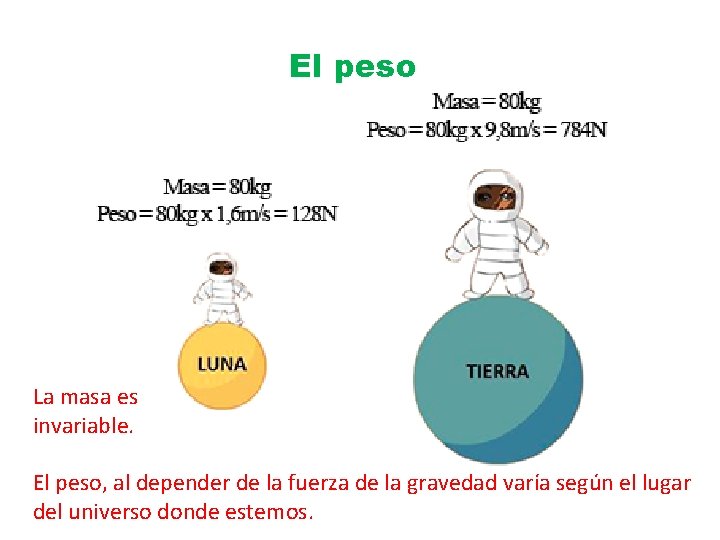
El peso es una fuerza. Es la fuerza que resulta de la acción de la gravedad sobre una masa. ¡¡No confundáis peso y masa!!

El peso Según la segunda ley de Newton: F (fuerza peso) m masa a

El peso Según la segunda ley de Newton: F (fuerza peso) m masa a aceleración de la gravedad g

El peso ¿Cuál es nuestro peso?

El peso

El peso La masa es invariable. El peso, al depender de la fuerza de la gravedad varía según el lugar del universo donde estemos.

7 - Un crucero de 5. 22 x 107 kg se mueve a su máxima velocidad llegando a puerto. Entonces el barco comienza una desaceleración de -0. 357 m/s 2 hasta que se para en el muelle. ¿Cuál es la fuerza neta que actúa sobre el barco mientras disminuye su velocidad? F= m· a m= 5. 22 x 107 kg a= -0. 357 m/s 2 F= 5. 22 x 107 · (-0. 357 m/s 2 ) = - 1. 86 x 107 N

8 - ¿Qué fuerza hay que aplicar a un cuerpo de 100 kg para que se mueva con una aceleración de 2 m/s 2? F= m· a m= 100 kg a= 2 m/s 2 F= 100 · 2 = 200 N

9 - ¿Cuál es la fuerza necesaria para que un móvil de 1500 kg, partiendo de reposo adquiera una velocidad de 2 m/s en 12 s? F= m· a m= 1500 kg a?

9 - ¿Cuál es la fuerza necesaria para que un móvil de 1500 kg, partiendo de reposo adquiera una velocidad de 2 m/s en 12 s? F= m· a m= 1500 kg a? a= (vf – vi)/t

9 - ¿Cuál es la fuerza necesaria para que un móvil de 1500 kg, partiendo de reposo adquiera una velocidad de 2 m/s en 12 s? F= m· a m= 1500 kg a? a= (vf – vi)/t vf= 2 m/s vi= 0 m/s t= 12 s a= (2 - 0) / 12 a= 0. 17 m/s 2 F= 1500 · 0. 17 = 255 N

10 - Sobre un cuerpo de 200 kg se ejerce una fuerza de 400 N. Calcula la aceleración que adquiere el cuerpo. Si parte del reposo con esa aceleración ¿Qué velocidad tendrá transcurridos 10 s? F= m· a; a= F /m m= 200 kg F= 400 N a= 400 / 200 a= 2 m/s 2

10 - Sobre un cuerpo de 200 kg se ejerce una fuerza de 400 N. Calcula la aceleración que adquiere el cuerpo. Si parte del reposo con esa aceleración ¿Qué velocidad tendrá transcurridos 10 s? F= m· a; a= F /m a= (vf – vi) / t m= 200 kg F= 400 N a= 2 m/s 2 vi= 0 m/s t= 10 s a= 400 / 200 a= 2 m/s 2 2 = (vf – 0) / 10 vf= 20 m/s

11 - ¿Qué fuerza impulsará a un barco cuyo motor le proporciona 100 N pero el viento sopla en contra con una fuerza de 20 N? ¿Qué aceleración puede adquirir si su masa es de 400 kg? F= 100 N -20 N m= 80 N

11 - ¿Qué fuerza impulsará a un barco cuyo motor le proporciona 100 N pero el viento sopla en contra con una fuerza de 20 N? ¿Qué aceleración puede adquirir si su masa es de 400 kg? F= 100 N -20 N m= 80 N a= F /m F= 80 N m= 400 kg a= 80 / 400 a= 0. 2 m/s 2

1 - Un cuerpo pesa 125 N en un lugar donde la aceleración de la gravedad es 10 m/s 2. Calcula: a) la masa del objeto, b) el peso del mismo objeto en un lugar donde la aceleración de la gravedad es 9. 65 m/s 2. Fp= m · g; m= Fp/ g Fp = 125 N g= 10 m/s 2 m= 125 / 10 m= 12. 5 kg

1 - Un cuerpo pesa 125 N en un lugar donde la aceleración de la gravedad es 10 m/s 2. Calcula: a) la masa del objeto, b) el peso del mismo objeto en un lugar donde la aceleración de la gravedad es 9. 65 m/s 2. Fp= m · g; m= Fp/ g Fp = 125 N g= 10 m/s 2 m= 125 / 10 m= 12. 5 kg g= 9. 65 m/s 2 Fp= 12. 5 · 9. 65 Fp= 120. 6 N

Ley de Hooke La deformación que experimenta un cuerpo es proporcional a la fuerza que se ejerce sobre él. K = Constante elástica del cuerpo. N/m X= Cuánto se ha estirado o encogido el objeto. m

Ley de Hooke

Ley de Hooke https: //phet. colorado. edu/sims/html/hookeslaw/latest/hookes-law_es. html https: //phet. colorado. edu/sims/mass-springlab/mass-spring-lab_es. html

1 - Si a un resorte se le cuelga una masa de 200 g y se deforma 15 cm, ¿cuál será el valor de su constante? K= 13. 3 N/m F= K · x m= 200 g · 1 kg/ 1000 g = 0. 2 Kg X= 15 cm · 1 m/ 100 cm = 0. 15 m g= 10 m/s 2 Fp = 0. 2 · 10 = 2 N K= 2/0. 15 = 13. 3 N/m

2 - Una carga de 50 N unida a un resorte que cuelga verticalmente estira el resorte 5 cm. El resorte se coloca ahora horizontalmente sobre una mesa y se estira 11 cm. a) ¿Qué fuerza se requiere para estirar el resorte esta cantidad? K= 1000 N/m; F= 110 N F= K · x Fp= 50 N X= 5 cm · 1 m/ 100 cm = 0. 05 m K=50/0. 05 = 1000 N/m X= 11 cm · 1 m/100 cm = 0. 11 m F= 1000 · 0. 11 = 110 N

3 - Se cuelga de un muelle una bola de masa de 15 kg, cuya constante elástica vale 2100 N/m, determinar el alargamiento del muelle en centímetros. X= 7, 1 cm F= K · x m= 15 kg K= 2100 N/m g= 10 m/s 2 Fp= 15 · 10 = 150 N X= 150 / 2100 = 0. 071 m 0. 071 m · 100 cm/ 1 m = 7. 1 cm

4 - Un resorte de acero de 30 cm de largo se estira hasta una longitud de 35. 6 cm cuando se suspende de su extremo inferior una masa de 2 kg. Encuentra la longitud del resorte cuando se agregan 500 g más a su extremo inferior. 37 cm F= K · x X= 35. 6 -30 = 5. 6 cm; 5. 6 cm· 1 m/ 100 cm= 0. 056 m m= 2 kg g= 10 m/s 2 Fp= m · g Fp= 2 · 10 = 20 N K =20/ 0. 056 =357. 14 N/m

4 - Un resorte de acero de 30 cm de largo se estira hasta una longitud de 35. 6 cm cuando se suspende de su extremo inferior una masa de 2 kg. Encuentra la longitud del resorte cuando se agregan 500 g más a su extremo inferior. 37 cm F= K · x K =20/ 0. 056 =357. 14 N/m m= 2 kg + 500 g; 2. 5 kg Fp = 2. 5 · 10 = 25 N X= 25/ 357. 14 = 0. 07 m 7 cm 30 + 7 = 37 cm

5 - Un grupo de alumnos estudió el comportamiento de un resorte concluyendo que cumple con la ley de Hooke y determinó que su constante de la elasticidad vale 12. 5 N/m. a) ¿Cuánto se estira este resorte al aplicarle una fuerza de 5. 0 N? b) ¿Qué fuerza debe aplicarse para estirarlo 4. 0 cm? 0, 4 m; 0, 5 N F= K · x K =12. 5 N/m a) X= 5/ 12. 5 = 0. 4 m b) F= 12. 5 · 0. 04 m F= 0. 5 N

6 - El extremo libre de un trampolín en una piscina queda a 55 cm por encima del agua. Si un hombre de 50 kg parado sobre el extremo del tablón lo hace bajar hasta 35 cm del agua, ¿cuánta ha de ser la carga para que baje hasta 5 cm del agua? F = 1500 N F= K · x m= 50 kg; Fp= 50 · 10 = 500 N X= 55 -35 = 20 cm; 20 cm· 1 m/100 cm = 0. 20 m K= 500/ 0. 20= 2500 N/m X= 55 -5 = 50 cm; 50 cm· 1 m/ 100 cm = 0. 50 m Fp = 2500 · 0. 50 = 1250 N

https: //phet. colorado. edu/sims/mass-springlab/mass-spring-lab_es. html Aplica la ley de Hooke y averigua la masa de las pesas de colores. Pista: La regla la puedes mover ; )

Ley de gravitación universal Dos cuerpos se atraen con una fuerza que es directamente proporcional a la masa de los mismos e inversamente proporcional al cuadrado de la distancia que los separa. F Fuerza gravitacional. G Constante gravitacional universal. M y m Masas de los dos cuerpos. d distancia entre los dos objetos.

Ley de gravitación universal El peso

Ley de gravitación universal El peso

Ley de gravitación universal El peso En la superficie de la tierra G, M y d se considera que permanecen constantes, así que se engloban en g, la aceleración de la gravedad.

Ley de gravitación universal G Constante de gravitación universal. M Masa de la tierra. d Distancia entre los dos objetos. Radio de la tierra.

1 - Una masa de 800 kg y otra de 500 kg se encuentran separadas por 3 m, ¿Cuál es la fuerza de atracción que experimenta la masa? G = 6, 7 × 10 -11 N m 2/ kg 2. F= 0. 536· 10 -11 N G = 6, 7 × 10 -11 N m 2/ kg 2 m 1= 800 kg; m 2= 500 kg d= 3 m F= 6, 7 × 10 -11 (800 · 500) / 9 = 0. 536· 10 -11 N

2 - La masa de Marte es de aproximadamente 6. 42· 1023 kg y su radio de 3400 km. Si sabemos que la constante de gravitación universal tiene un valor de 6. 67· 10 -11, calcula: a) La gravedad en este planeta, a= 3, 7 m/s 2 b) El peso de un astronauta cuya masa es 70 kg. 260 N G = 6, 7 × 10 -11 N m 2/ kg 2 M marte= 6. 42· 1023 kg ; m 2= 500 kg d= 3400 km a) g= 6, 7 × 10 -11 ·(6. 42· 1023 /(3400· 103 ) 2 ) = 3. 7 m/s 2 b) Fp= 70 · 3. 7 = 260 N

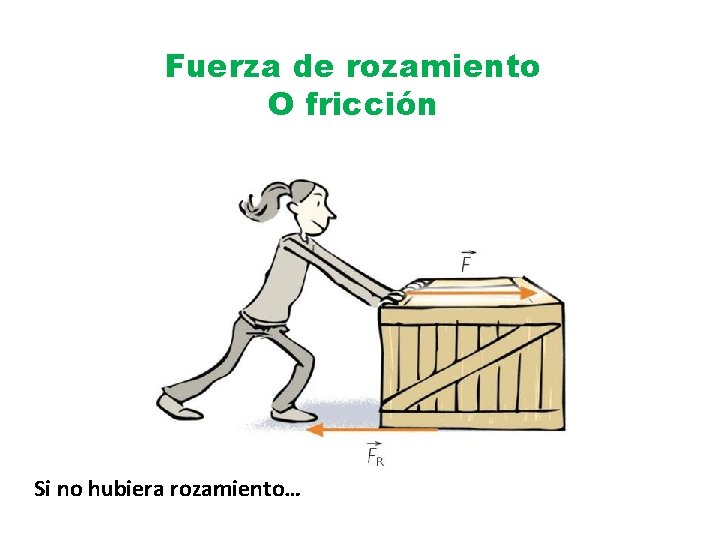
Fuerza de rozamiento O fricción Si no hubiera rozamiento…

Fuerza de rozamiento O fricción

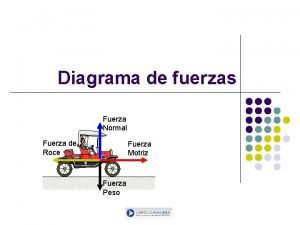
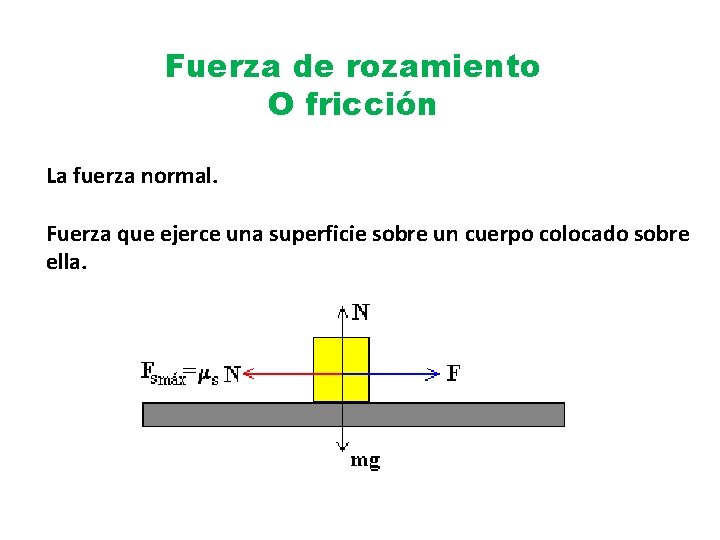
Fuerza de rozamiento O fricción La fuerza normal. Fuerza que ejerce una superficie sobre un cuerpo colocado sobre ella.

Fuerza de rozamiento O fricción https: //bit. ly/2 v. JTcef https: //bit. ly/2 uf. Gb. Na

Fuerzas magnéticas Son las fuerzas de atracción o repulsión generada por los imanes.

Fuerzas magnéticas El magnetismo es la propiedad por la cual unas sustancias (imanes) atraen otras.

Máquinas simples Dispositivos que permiten ahorrar trabajo al realizar ciertas tareas. Plano inclinado

Máquinas simples Dispositivos que permiten ahorrar trabajo al realizar ciertas tareas. Plano inclinado Cuña

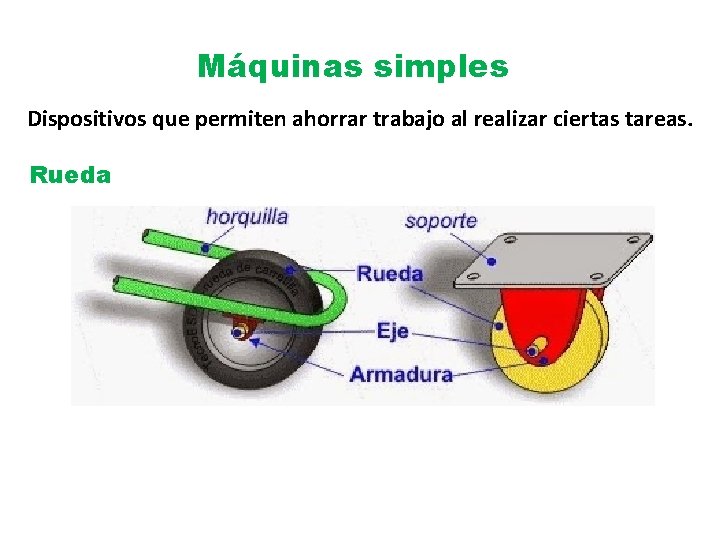
Máquinas simples Dispositivos que permiten ahorrar trabajo al realizar ciertas tareas. Rueda

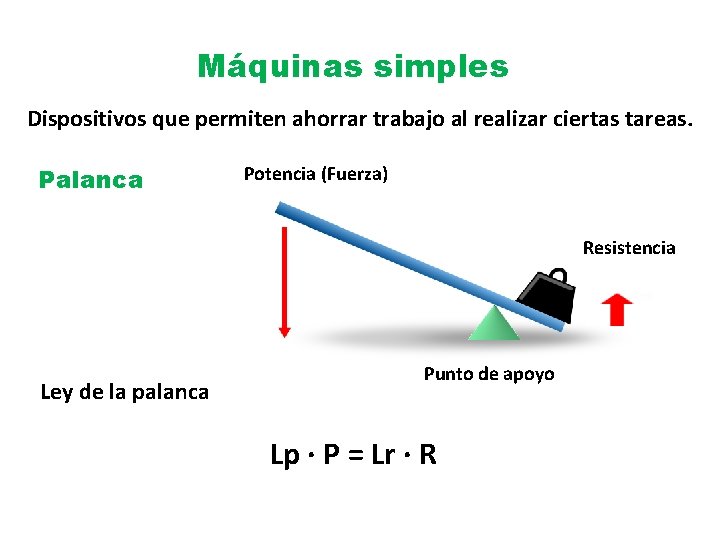
Máquinas simples Dispositivos que permiten ahorrar trabajo al realizar ciertas tareas. Palanca Potencia (Fuerza) Resistencia Ley de la palanca Punto de apoyo Lp · P = Lr · R

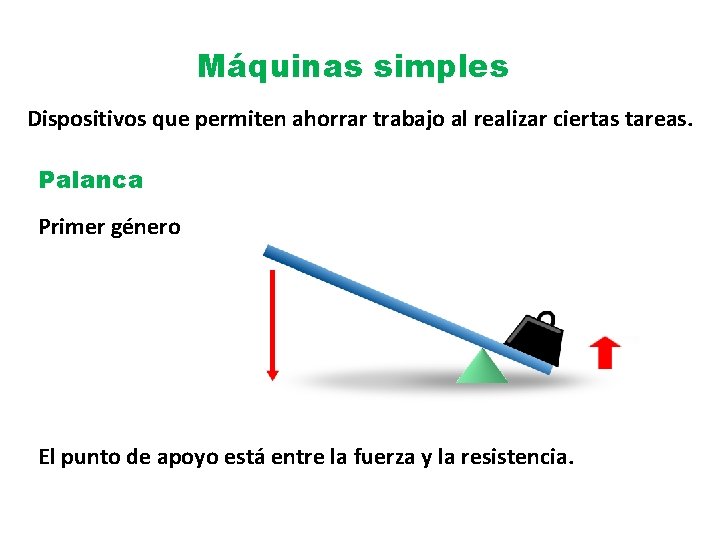
Máquinas simples Dispositivos que permiten ahorrar trabajo al realizar ciertas tareas. Palanca Primer género El punto de apoyo está entre la fuerza y la resistencia.

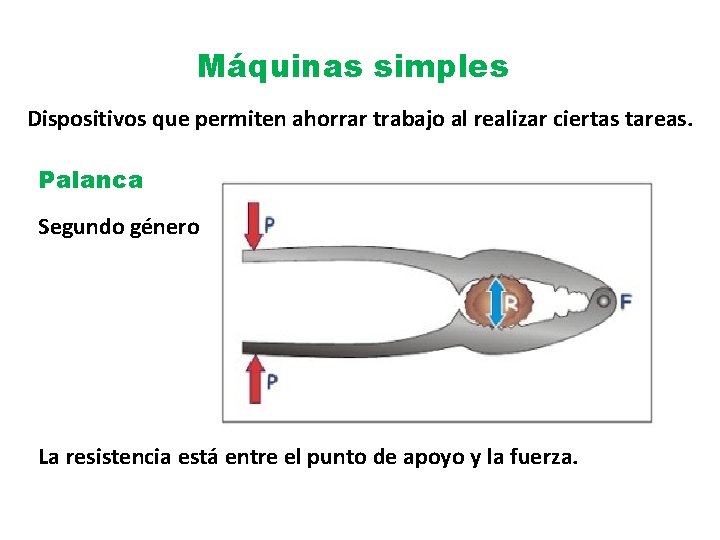
Máquinas simples Dispositivos que permiten ahorrar trabajo al realizar ciertas tareas. Palanca Segundo género La resistencia está entre el punto de apoyo y la fuerza.

Máquinas simples Dispositivos que permiten ahorrar trabajo al realizar ciertas tareas. Palanca Tercer género La fuerza está entre el punto de apoyo y la resistencia.

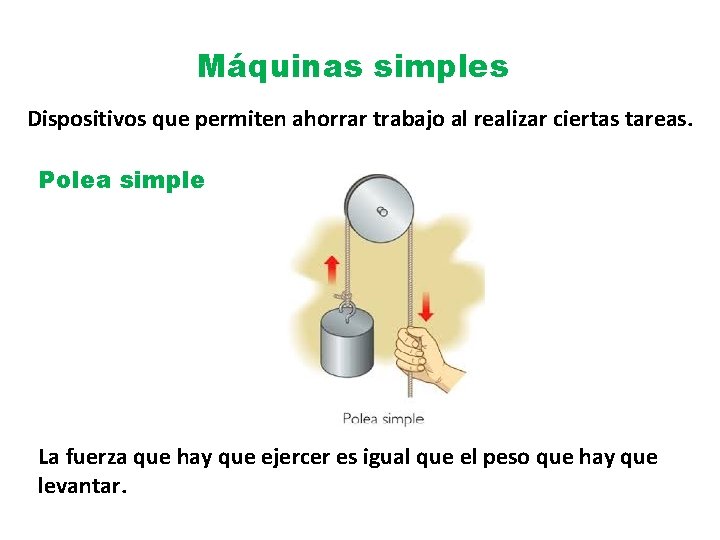
Máquinas simples Dispositivos que permiten ahorrar trabajo al realizar ciertas tareas. Polea simple La fuerza que hay que ejercer es igual que el peso que hay que levantar.
 Unidades de millar centenas decenas unidades
Unidades de millar centenas decenas unidades Propiedad en termodinamica
Propiedad en termodinamica Clasificación de unidades en física
Clasificación de unidades en física Cuales son los polos de un iman
Cuales son los polos de un iman Ejercicios de masa masa
Ejercicios de masa masa Perkembangan hardware
Perkembangan hardware Pendidikan masa kini dan masa depan
Pendidikan masa kini dan masa depan Relativna molekulska masa zadaci
Relativna molekulska masa zadaci Concentración molar
Concentración molar Masa molecular
Masa molecular Perkembangan mobil dari masa ke masa
Perkembangan mobil dari masa ke masa Perkembangan desain dari masa ke masa
Perkembangan desain dari masa ke masa Fuerza de contacto y a distancia
Fuerza de contacto y a distancia Unidad en lenguaje
Unidad en lenguaje Ley cualitativa de las cargas eléctricas
Ley cualitativa de las cargas eléctricas 4 dimensiones del ser humano
4 dimensiones del ser humano Unidades de medida bit
Unidades de medida bit Como calcular el trabajo de una fuerza variable
Como calcular el trabajo de una fuerza variable Unidad obtenida de una operación comercial
Unidad obtenida de una operación comercial L
L Uep del sur
Uep del sur Unidad educativa san juan bosco
Unidad educativa san juan bosco Unidad central de seguridad privada
Unidad central de seguridad privada Avancemos 3 unidad 2 leccion 2
Avancemos 3 unidad 2 leccion 2 Unidad 13 la etica en la empresa
Unidad 13 la etica en la empresa Unidad 2 marco legal
Unidad 2 marco legal Unidad 3
Unidad 3 Fórmula para calcular la molalidad
Fórmula para calcular la molalidad La capacidad se mide en
La capacidad se mide en Unidad 4 en romano
Unidad 4 en romano Comunicación y sociedad: unidad 1
Comunicación y sociedad: unidad 1 Bsico
Bsico Unidad educativa fiscomisional yachana inti
Unidad educativa fiscomisional yachana inti Calidad aplicada a la gestion empresarial unidad 1
Calidad aplicada a la gestion empresarial unidad 1 Elementos de la versificación
Elementos de la versificación Alcance tematico de un proyecto ejemplo
Alcance tematico de un proyecto ejemplo Avancemos 2 unidad 1 leccion 1
Avancemos 2 unidad 1 leccion 1 Unidad de analisis
Unidad de analisis Unidad fraccionaria ejemplos
Unidad fraccionaria ejemplos Partes de una unidad didactica
Partes de una unidad didactica Orden de banderas conquistadores
Orden de banderas conquistadores Unidad 1 el departamento de recursos humanos
Unidad 1 el departamento de recursos humanos Avancemos 1 unidad 2 leccion 1
Avancemos 1 unidad 2 leccion 1 Partes de una unidad odontologica
Partes de una unidad odontologica Quinta unidad modelo
Quinta unidad modelo Unidad funcional del musculo
Unidad funcional del musculo Deportivo valle del sol
Deportivo valle del sol Unidad academica ejemplos
Unidad academica ejemplos Fuerza variable
Fuerza variable Pasivo total sobre activo total
Pasivo total sobre activo total Unidad 8 spf
Unidad 8 spf Unidades de negocio
Unidades de negocio Parmalife
Parmalife Nanometro unidad de medida
Nanometro unidad de medida Utilidad marginal por unidad monetaria
Utilidad marginal por unidad monetaria Homogenea
Homogenea Propiedad de los logaritmos
Propiedad de los logaritmos Unidad 6 republica dominicana
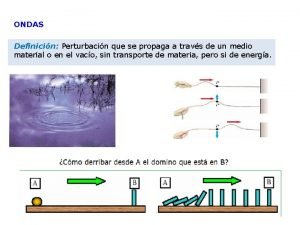
Unidad 6 republica dominicana Ondas transversales
Ondas transversales Formula longitud de onda y frecuencia
Formula longitud de onda y frecuencia Morla definicion
Morla definicion Proyecto de unidad nacional
Proyecto de unidad nacional Calor especifico
Calor especifico Unidad de análisis ejemplos
Unidad de análisis ejemplos Sensaciones de la vista
Sensaciones de la vista Musculos de la respiracion forzada
Musculos de la respiracion forzada Unidad fundamental de la vida
Unidad fundamental de la vida Neuronas golgi tipo 1
Neuronas golgi tipo 1 Segunda unidad de ingles
Segunda unidad de ingles Coulomb unidad
Coulomb unidad Unidad ci
Unidad ci Giovanni antonio farina educamos
Giovanni antonio farina educamos Cuenta 1705
Cuenta 1705 Unidad elemental
Unidad elemental Unidad 3 etapa 3 answers
Unidad 3 etapa 3 answers Unidad educativa fiscal provincia de loja
Unidad educativa fiscal provincia de loja Unidad 3 leccion 1
Unidad 3 leccion 1 Unidad 5 salud industrial
Unidad 5 salud industrial Avancemos 3 unidad 3 leccion 1
Avancemos 3 unidad 3 leccion 1 Unidad 12
Unidad 12 Bus de datos
Bus de datos Experimento de torricelli
Experimento de torricelli Gravedad especifica
Gravedad especifica Unidad de analisis
Unidad de analisis Unidad deportiva valle del sol
Unidad deportiva valle del sol Unidad docente medicina familiar y comunitaria madrid
Unidad docente medicina familiar y comunitaria madrid Unidad trabajo
Unidad trabajo Acromino
Acromino Transformador de unidad
Transformador de unidad Mgf2 electronegatividad
Mgf2 electronegatividad Unidad de analisis investigacion
Unidad de analisis investigacion Densidad especifica
Densidad especifica Portada de unidad 1
Portada de unidad 1 Resolucion de problemas unidad 4
Resolucion de problemas unidad 4 Unidad de estudio de la sintaxis
Unidad de estudio de la sintaxis Neurona conectora
Neurona conectora Unidad 5 leccion 2 vocabulario a
Unidad 5 leccion 2 vocabulario a Bandeja porta instrumentos dentales
Bandeja porta instrumentos dentales