TMEC053 Fundamentos de Aerodinmica Cap 03 Fundamentos de

TMEC-053 Fundamentos de Aerodinâmica Cap. 03: Fundamentos de escoamentos invíscidos e incompressíveis 1

Introdução • Os primeiros voos realizados, do início do Séc. XX ao início da Segunda Guerra Mundial, apresentavam velocidades relativamente baixas, de até cerca de 480 km/h. • Para tais velocidades, a densidade do ar permanece praticamente constante, com uma pequena variação, de modo que o escoamento resultante pode ser considerado incompressível. 2

Introdução • Seversky P-35 (Segunda Guerra Mundial) 3

Introdução • Cessna 425 Conquest (aeronave moderna) 4

Equação de Bernoulli • A Equação de Bernoulli foi desenvolvida durante o Séc. XVIII, envolvendo os trabalhos de Johann e Daniel Bernoulli e em especial Leonhard Euler. • Trata-se de uma das mais conhecidas equações na dinâmica de fluidos. 5

Equação de Bernoulli • Partindo-se da Eq. de Conservação de Quantidade de Movimento Linear na direção x, desconsiderando-se as forças de corpo e admitindo-se um fluido invíscido: 6

Equação de Bernoulli • No caso de regime permanente, , assim • Multiplicando-se a expressão por dx: 7

Equação de Bernoulli • Considerando-se o escoamento ao longo de uma linha de corrente tridimensional, tem-se que • Que, substituídas na relação anteriormente apresentada resulta em 8

Equação de Bernoulli • Ou seja, • Recordando-se do cálculo diferencial que, para uma função u = u(x, y, z) 9

Equação de Bernoulli • Obtém-se • Alternativamente, • De modo análogo, para as componentes y e z: 10

Equação de Bernoulli • Ao se somar as componentes nas três direções coordenadas, tem-se • Entretanto, 11

Equação de Bernoulli • O que conduz a • Ou seja, • Que é conhecida como Equação de Euler. 12

Equação de Bernoulli • A Equação de Euler é válida para escoamentos invíscidos sem forças de corpo e relaciona a variação de velocidade d. V ao longo de uma linha de corrente com a variação de pressão dp ao longo da mesma linha de corrente. 13

Equação de Bernoulli • Integrando-se a Equação de Euler entre dois pontos, 1 e 2, ao longo de uma linha de corrente e considerando-se um escoamento incompressível, tem-se 14

Equação de Bernoulli • Tem-se assim que • Essa equação é chamada de Equação de Bernoulli, que relaciona a pressão e a velocidade em um ponto 1 com a pressão e a velocidade em um ponto 2 do escoamento sobre uma linha de corrente. 15

Equação de Bernoulli • Tem-se, assim, que para uma linha de corrente em um escoamento incompressível, invíscido e sem forças de corpo: • Além disso, se o escoamento for irrotacional, essa expressão é válida para todas as linhas de corrente, ou seja, para todo o escoamento. 16

Equação de Bernoulli • Apesar de ter sido obtida a partir do princípio da Conservação da Quantidade de Movimento Linear, a Equação de Bernoulli também representa a Energia Mecânica de um escoamento incompressível. • Isto mostra que, no caso de um escoamento invíscido e incompressível, a equação da energia é redundante. 17

Equação de Bernoulli • Estratégia para resolver a maioria dos problemas relacionados a escoamentos invíscidos e incompressíveis: – Obter o campo de velocidades a partir das equações governantes. – Obter o campo de pressões resultante a partir da Equação de Bernoulli. 18

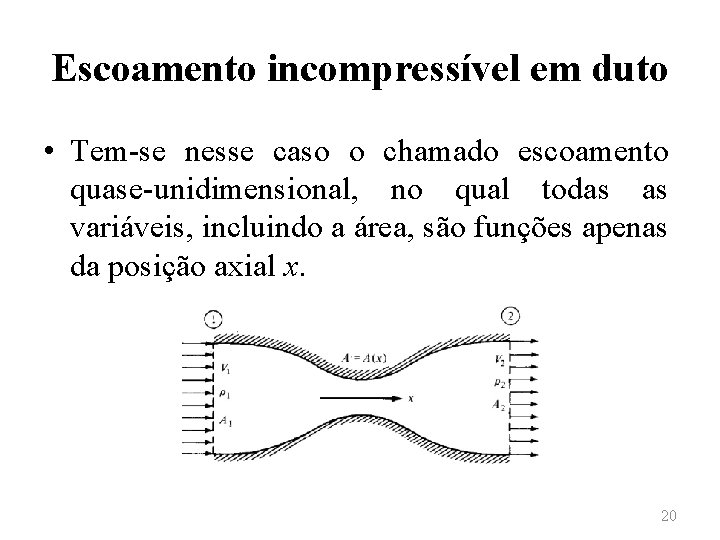
Escoamento incompressível em duto • Embora dutos normalmente apresentem formatos tridimensionais, para muitas aplicações pode-se assumir que a variação da área A = A(x) seja moderada, de modo que as propriedades do escoamento sejam uniformes em qualquer seção transversal ao escoamento. 19

Escoamento incompressível em duto • Tem-se nesse caso o chamado escoamento quase-unidimensional, no qual todas as variáveis, incluindo a área, são funções apenas da posição axial x. 20

Escoamento incompressível em duto • Considerando-se a equação da continuidade na forma integral: • Para regime permanente, tem-se: 21

Escoamento incompressível em duto • Ao aplicar essa expressão para um duto, dentro do qual se define um volume de controle como se segue, obtém-se: 22

Escoamento incompressível em duto • Ao longo das paredes, a velocidade deve ser tangente às mesmas, enquanto o vetor d. S é perpendicular às mesmas. Dessa forma, obtémse: 23

Escoamento incompressível em duto • Para as superfícies 1 e 2, tem-se as seguintes expressões: 24

Escoamento incompressível em duto • Desta forma, a equação da continuidade conduz à seguinte expressão: • Ou seja, • Para um escoamento incompressível, tem-se ainda que 25

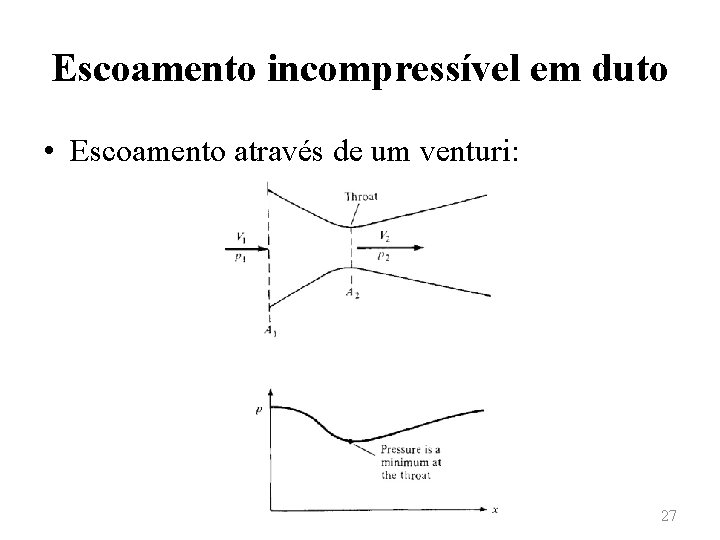
Escoamento incompressível em duto • Venturi: consiste em um tubo de área variável, composto por uma porção convergente seguida por uma porção divergente. À seção transversal que apresenta menor área é atribuída o nome de garganta. 26

Escoamento incompressível em duto • Escoamento através de um venturi: 27

Escoamento incompressível em duto • Uma aplicação do venturi em aerodinâmica é a medição de velocidade do ar. • Considerando-se que um venturi de razão entre áreas de entrada e de garganta seja A 1/A 2 e que a entrada do venturi esteja imersa no escoamento livre de ar, cuja velocidade V 1 é desconhecida. 28

Escoamento incompressível em duto • A diferença de pressão entre a entrada e a garganta do venturi, p 1 ‒ p 2, pode ser avaliada diretamente pelo uso de um manômetro. • Essa diferença de pressão pode, então, ser utilizada para a avaliação da velocidade do escoamento de ar. 29

Escoamento incompressível em duto • Da Equação de Bernoulli, tem-se • E da equação da continuidade 30

Escoamento incompressível em duto • Da combinação das expressões anteriores, obtém-se • Que resulta em 31

Escoamento incompressível em duto • A primeira utilização de um venturi para medição de velocidade ocorreu em janeiro de 1911, pelo capitão francês A. Eteve. • No entanto, atualmente o uso de venturis para medição de velocidade é restrito a algumas aeronaves experimentais. O instrumento mais empregado na atualidade é o tubo de Pitot. 32

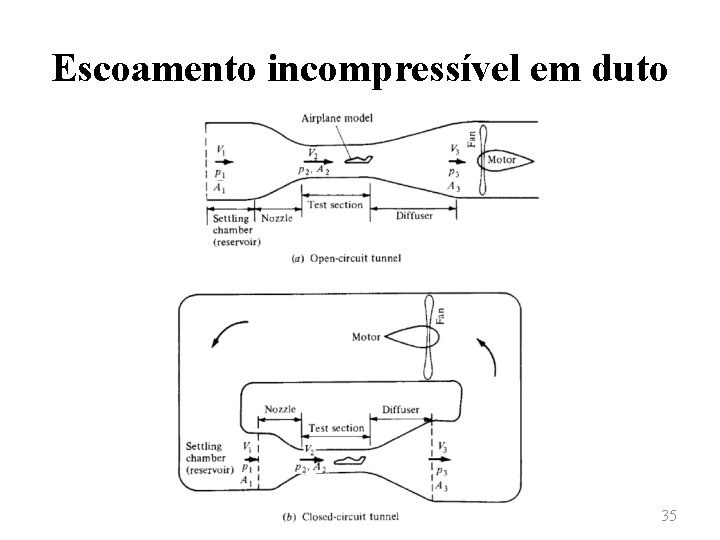
Escoamento incompressível em duto • Uma segunda aplicação do escoamento incompressível em dutos está relacionada a túneis de vento de baixa velocidade. • Tais túneis, na prática, podem ser considerados como venturis de grandes dimensões. • Nesse caso, o ar é admitido a uma pressão p 1 com uma baixa velocidade V 1. 33

Escoamento incompressível em duto • Na seção de testes, o ar é acelerado a uma velocidade V 2. tendo sua pressão reduzida para um valor p 2. • Após o escoamento do ar sobre o modelo aerodinâmico, o ar deve passar por um duto divergente, chamado difusor, no qual a área de seção é aumentada para um valor A 3 e, consequentemente, a velocidade aumenta para V 3 e a pressão diminui para p 3. 34

Escoamento incompressível em duto 35

Escoamento incompressível em duto • Utilizando-se a Equação de Bernoulli e da equação da continuidade, pode-se obter que • Nota-se, assim, que a velocidade do ar na seção de testes, V 2, depende da diferença de pressão p 1 ‒ p 2. 36

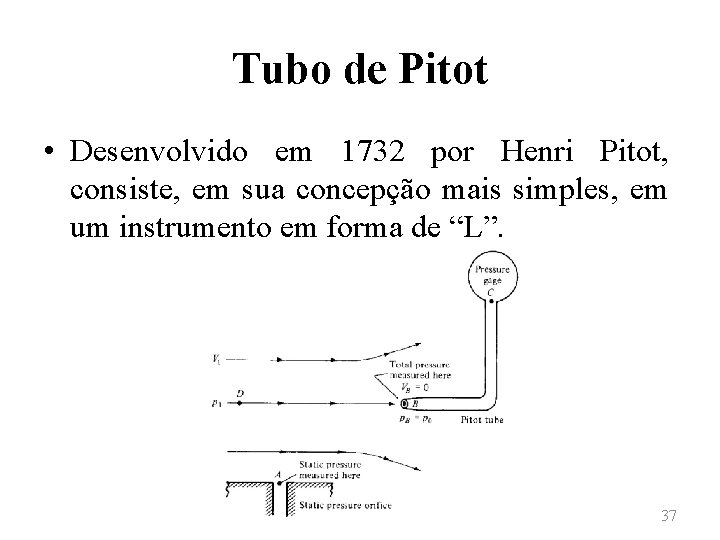
Tubo de Pitot • Desenvolvido em 1732 por Henri Pitot, consiste, em sua concepção mais simples, em um instrumento em forma de “L”. 37

Tubo de Pitot • A utilização do tubo de Pitot inclui os seguintes conceitos: – Pressão estática: medida da pressão devida somente ao movimento aleatório das moléculas que constituem um gás (ou um fluido qualquer) em escoamento. – Pressão de estagnação ou pressão total (p 0): medida da pressão quando o fluido é desacelerado isentropicamente até atingir velocidade nula. 38

Tubo de Pitot • No ponto B, tem-se que a velocidade é reduzida a zero, de modo que VB = 0, ou seja, a pressão no ponto B é chamada de pressão de estagnação ou pressão total. • Para que se possa medir a velocidade com o tubo de Pitot, deve-se, ainda, medir a pressão estática. Tal medida é feita através de uma tomada realizada na lateral do duto (ponto A). 39

Tubo de Pitot • Empregando-se a equação de Bernoulli, tem-se então: • De onde se obtém que: 40

Tubo de Pitot • Normalmente, o tubo de Pitot é concebido para medição tanto da pressão estática quanto da pressão de estagnação 41

Tubo de Pitot • Em geral, define-se pressão dinâmica como • E, desse modo, para incompressíveis, tem-se que escoamentos • Ou seja, a pressão estática somada à pressão dinâmica origina a pressão de estagnação. 42

Coeficiente de pressão • O coeficiente de pressão, CP, é definido como • sendo 43

Coeficiente de pressão • Para um escoamento incompressível, considerando-se a equação de Bernoulli • De modo que 44

Coeficiente de pressão • Pode-se, então, expressar o coeficiente de pressão, para escoamentos incompressíveis como • Nota-se, assim, que o maior coeficiente de pressão para um escoamento incompressível ocorre para o ponto de estagnação e apresenta valor unitário. 45

Escoamento incompressível irrotacional: Equação de Laplace • Para escoamentos incompressíveis, tem-se que • Além disso, considerando-se um escoamento irrotacional, pode-se definir uma velocidade potencial tal que: 46

Escoamento incompressível irrotacional: Equação de Laplace • Ao combinar as expressões anteriores, tem-se um escoamento incompressível e irrotacional, governado pela seguinte equação: • Tal equação se constitui na Equação de Laplace, cuja solução é obtida por meio de funções harmônicas. 47

Escoamento incompressível irrotacional: Equação de Laplace • Coordenadas cartesianas: • Coordenadas cilíndricas: 48

Escoamento incompressível irrotacional: Equação de Laplace • Coordenadas esféricas: 49

Escoamento incompressível irrotacional: Equação de Laplace • No caso de um escoamento bidimensional incompressível, a função de corrente ψ pode ser definida de modo que • Da equação da continuidade, tem-se que 50

Escoamento incompressível irrotacional: Equação de Laplace • Substituindo-se a função de corrente ψ na equação da continuidade, verifica-se que • Como a função de corrente é contínua e suave, as derivadas cruzadas serão iguais, de modo que a equação da continuidade sempre é satisfeita. 51

Escoamento incompressível irrotacional: Equação de Laplace • Se, além de incompressível, o escoamento for irrotacional, tem-se que a condição de irrotacionalidade deve ser satisfeita: • Empregando a função de corrente: 52

Escoamento incompressível irrotacional: Equação de Laplace • Obtém-se também a equação de Laplace: • Verifica-se, assim, que a função de corrente também satisfaz a equação de Laplace ao longo de (velocidade potencial). 53

Escoamento incompressível irrotacional: Equação de Laplace • Conclusões: – Qualquer escoamento incompressível irrotacional bidimensional possui uma velocidade potencial e uma função de corrente, ambas modeladas pela equação de Laplace. – Qualquer solução da equação de Laplace representa um potencial de velocidades ou uma função de corrente de um escoamento bidimensional, incompressível e irrotacional. 54

Escoamento incompressível irrotacional: Equação de Laplace • A equação de Laplace é uma equação diferencial parcial linear de segunda ordem. O fato de ser linear é interessante pois a soma de soluções particulares de uma equação diferencial parcial também é uma solução para a equação. Assim, se são n soluções da equação de Laplace, então sua soma também é solução: 55

Escoamento incompressível irrotacional: Equação de Laplace • Isto permite utilizar uma estratégia para a solução de escoamentos incompressíveis irrotacionais: estudar a solução de escoamentos elementares e combinar seus efeitos para a obtenção da solução de um escoamento que possua resultados práticos. 56

Escoamento incompressível irrotacional: Equação de Laplace • Como todos os escoamentos incompressíveis irrotacionais são modelados pela equação de Laplace, a única diferença entre todos se resume às condições de contorno. 57

Escoamento incompressível irrotacional: Equação de Laplace • Condições de contorno no infinito: • Condições de contorno na superfície sólida: – Para escoamentos invíscidos, o vetor velocidade deve tangenciar a superfície sólida. 58

Escoamento incompressível irrotacional: Equação de Laplace • Condições de contorno na superfície sólida: – Considerando o vetor unitário n normal à superfície sólida, tem-se que a seguinte condição deve ser satisfeita: – Ou seja, – sendo a velocidade potencial. 59

Escoamento incompressível irrotacional: Equação de Laplace • Condições de contorno na superfície sólida: – No caso de se trabalhar com a função de corrente ψ, tem-se a seguinte condição a ser satisfeita: – sendo s a distância medida ao longo da superfície do corpo. 60

Escoamento incompressível irrotacional: Equação de Laplace • Condições de contorno na superfície sólida: – Recordando-se que ψ é constante ao longo de uma linha de corrente e considerando-se que o formato do corpo possa ser modelado por uma função – tem-se que: 61

Escoamento incompressível irrotacional: Equação de Laplace • Condições de contorno na superfície sólida: – Se as condições de contorno forem dadas em termo das componentes da velocidade u e v, tem-se, a partir da condição obtida a partir da equação da linha de corrente, que: 62

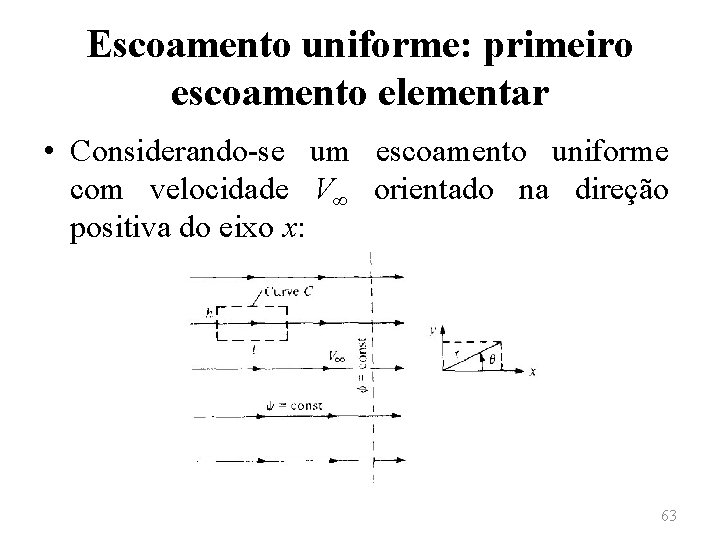
Escoamento uniforme: primeiro escoamento elementar • Considerando-se um escoamento uniforme com velocidade V∞ orientado na direção positiva do eixo x: 63

Escoamento uniforme: primeiro escoamento elementar • Neste caso, é facilmente observável que um escoamento uniforme atende ao critério de incompressibilidade e irrotacionalidade: • Assim, em termos da velocidade potencial para um escoamento uniforme tem-se: 64

Escoamento uniforme: primeiro escoamento elementar • Tem-se, dessa forma, que • Integrando-se a primeira equação em relação a x, tem-se 65

Escoamento uniforme: primeiro escoamento elementar • Integrando-se a segunda equação em relação a y, tem-se que: • Comparando-se ambas as equações, observa-se que g(x) deve ser V∞x e f (y) deve ser uma constante. Assim: 66

Escoamento uniforme: primeiro escoamento elementar • Uma vez que para problemas práticos a importância recai sobre a velocidade e não sobre a velocidade potencial, sem perda de rigor, pode-se dizer que • No caso da função de corrente, tem-se 67

Escoamento uniforme: primeiro escoamento elementar • Integrando-se as equações anteriores, a primeira com relação a x e a segunda em relação a y e comparando-se os resultados conclui-se que • Das relações obtidas para a função de corrente e para a velocidade potencial, observa-se que: – As linhas de corrente são linhas horizontais – As linhas equipotenciais são linhas verticais 68

Escoamento uniforme: primeiro escoamento elementar • Em termos de coordenadas polares, onde • Tem-se: • Com relação à circulação, Γ, definida como 69

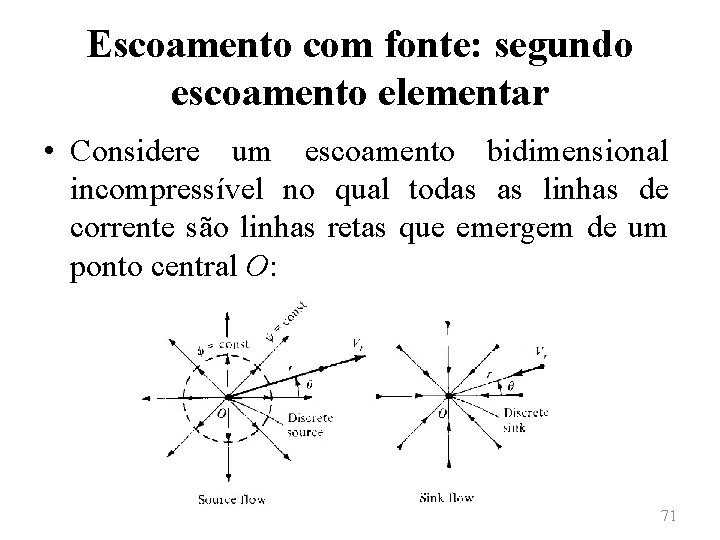
Escoamento uniforme: primeiro escoamento elementar • Se considerada uma curva fechada C em um escoamento uniforme, como por exemplo, um retângulo de base l e altura h, tem-se: • Esse resultado é válido para qualquer curva fechada nesse escoamento. 70

Escoamento com fonte: segundo escoamento elementar • Considere um escoamento bidimensional incompressível no qual todas as linhas de corrente são linhas retas que emergem de um ponto central O: 71

Escoamento com fonte: segundo escoamento elementar • Em um escoamento com fonte, as linhas de corrente são direcionadas a partir de um ponto de origem. • Em um escoamento com sorvedouro, as linhas de corrente são direcionadas para um ponto. • Para um escoamento com fonte, a seguinte condição é válida para todo o campo, exceto para a origem: 72

Escoamento com fonte: segundo escoamento elementar • Tendo-se, por definição, que a velocidade é inversamente proporcional à distância radial r, de modo que • sendo c uma constante relacionada ao volume de escoamento a partir da fonte. 73

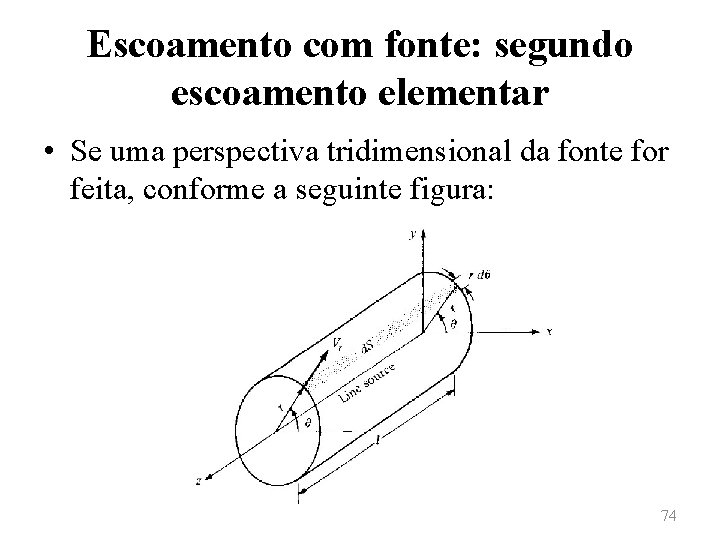
Escoamento com fonte: segundo escoamento elementar • Se uma perspectiva tridimensional da fonte for feita, conforme a seguinte figura: 74

Escoamento com fonte: segundo escoamento elementar • Nesse caso, a massa elementar de escoamento através da superfície do elemento d. S é dado por • Nesse caso, o escoamento total de massa através da superfície do cilindro é dada por 75

Escoamento com fonte: segundo escoamento elementar • Denotando-se, então, a taxa de volumétrica de escoamento, tem-se • E, definindo-se a taxa volumétrica de escoamento por unidade de comprimento como 76

Escoamento com fonte: segundo escoamento elementar • Tem-se desse modo • A constante c vale • A intensidade da linha da fonte é definida por Λ e possui por unidade m 2/s. 77

Escoamento com fonte: segundo escoamento elementar • A velocidade potencial pode ser obtida a partir das seguintes expressões • Integrando a primeira relação em relação a r e a segunda em relação a θ tem-se 78

Escoamento com fonte: segundo escoamento elementar • Comparando-se ambas as equações, e, também não se perdendo generalidade, chega-se a • Para a obtenção da função de corrente, considera-se 79

Escoamento com fonte: segundo escoamento elementar • Integrando a primeira expressão com relação a θ e a segunda relação em relação a r, obtém-se • Comparando-se as expressões anteriores, conclui-se, sem perda de generalidade, que 80

Escoamento com fonte: segundo escoamento elementar • Da expressão anterior, verifica-se que para as linhas de corrente, θ = const, o que em coordenadas polares resulta em linhas retas a partir de uma origem. • No caso das linhas equipotenciais, deve-se ter que r = const, o que é representado por circunferências com centro na origem. 81

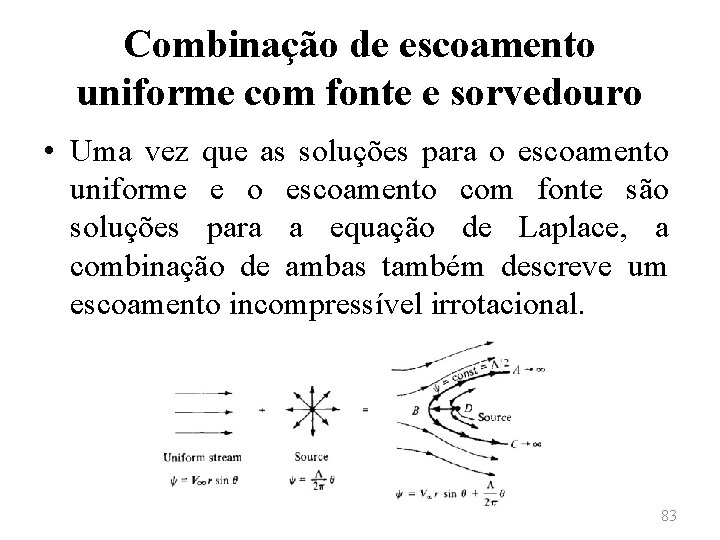
Combinação de escoamento uniforme com fonte e sorvedouro • Considerando-se um sistema de coordenadas polares com uma fonte de intensidade Λ localizado na origem. Associando-se a esse escoamento um fluxo uniforme com velocidade V∞ movendo-se da esquerda para a direita, tem-se que a função de corrente do escoamento resultante é dado por 82

Combinação de escoamento uniforme com fonte e sorvedouro • Uma vez que as soluções para o escoamento uniforme e o escoamento com fonte são soluções para a equação de Laplace, a combinação de ambas também descreve um escoamento incompressível irrotacional. 83

Combinação de escoamento uniforme com fonte e sorvedouro • As linhas de corrente do escoamento serão, nesse caso, • O campo de velocidades é obtido ao se diferenciar a expressão anterior, resultando em 84

Combinação de escoamento uniforme com fonte e sorvedouro • e • Os pontos de estagnação do escoamento podem ser obtidos ao se igualar as expressões anteriores a zero: 85

Combinação de escoamento uniforme com fonte e sorvedouro • Resolvendo-se as equações anteriores para r e θ, encontra-se o ponto de estagnação B, localizado em • Substituindo essas coordenadas na função de corrente, obtém-se 86

Combinação de escoamento uniforme com fonte e sorvedouro • Observa-se, assim, que a linha de corrente correspondente ao ponto de estagnação é dado por ψ= Λ/2, correspondente à curva ABC. 87

Combinação de escoamento uniforme com fonte e sorvedouro • Como o escoamento é invíscido, em que a velocidade sobre uma superfície sólida é tangente ao corpo, qualquer linha de corrente do escoamento combinado pode ser trocado por uma superfície sólida de mesmo formato. • Todo o fluido para fora da região ABC é correspondente ao escoamento livre e todo fluido dentro da região ABC se deve à fonte. 88

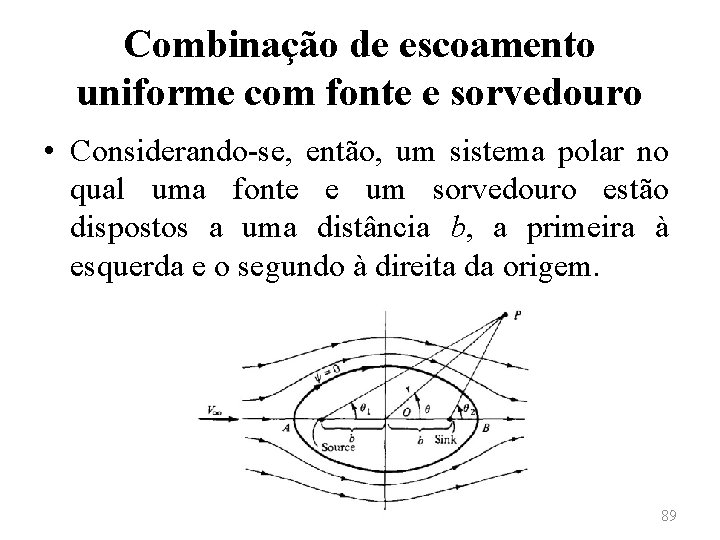
Combinação de escoamento uniforme com fonte e sorvedouro • Considerando-se, então, um sistema polar no qual uma fonte e um sorvedouro estão dispostos a uma distância b, a primeira à esquerda e o segundo à direita da origem. 89

Combinação de escoamento uniforme com fonte e sorvedouro • Considera-se, também, que a fonte e o sorvedouro tenham intensidades de Λ e ‒Λ, respectivamente, e que um escoamento uniforme de velocidade V∞ move-se da esquerda para a direita. • Nesse caso, tem-se que as linhas de corrente sem um ponto P qualquer podem ser dadas por 90

Combinação de escoamento uniforme com fonte e sorvedouro • O campo de velocidades é obtido pela diferenciação da expressão anterior. • Existem dois pontos de estagnação para o escoamento anterior, localizados em • A equação das linhas de corrente será então 91

Combinação de escoamento uniforme com fonte e sorvedouro • Nota-se que θ = θ 1 = θ 2 = π no ponto A e que θ = θ 1 = θ 2 = 0 no ponto B. Desse modo, obtém-se que a constante para a linha de corrente de estagnação é nula e assim • Tal expressão representa uma elipse, chamada de oval de Rankine. 92

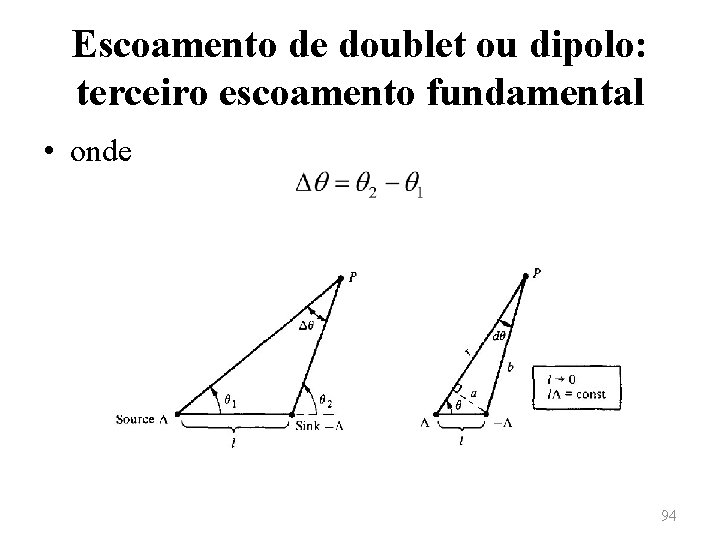
Escoamento de doublet ou dipolo: terceiro escoamento fundamental • Este caso consiste em um caso especial, degenerado, de par fonte-sorvedouro, que conduz a uma singularidade chamada de doublet ou dipolo. • Considerando-se uma fonte de intensidade Λ e um sorvedouro de intensidade ‒Λ, separados por uma distância l. Para um ponto qualquer P no escoamento, tem-se para função de corrente 93

Escoamento de doublet ou dipolo: terceiro escoamento fundamental • onde 94

Escoamento de doublet ou dipolo: terceiro escoamento fundamental • Considerando-se, então, que a distância l se aproxime de zero enquanto o módulo da intensidade Λ aumente, de modo que o produto l Λ permaneça constante. No limite em que l tenda a zero, tem-se um caso especial chamado de doublet ou dipolo. A intensidade κ do doublet ou dipolo é dada por 95

Escoamento de doublet ou dipolo: terceiro escoamento fundamental • Já a função de corrente pode ser avaliada por • Nota-se que no limite, • Considerando-se que r e b sejam as distâncias de um ponto P para uma fonte e um sorvedouro, respectivamente. 96

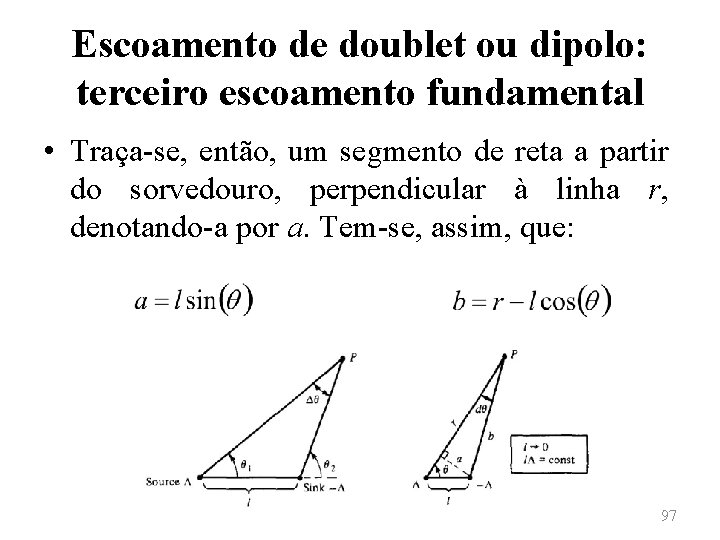
Escoamento de doublet ou dipolo: terceiro escoamento fundamental • Traça-se, então, um segmento de reta a partir do sorvedouro, perpendicular à linha r, denotando-a por a. Tem-se, assim, que: 97

Escoamento de doublet ou dipolo: terceiro escoamento fundamental • Dessa forma, • E, com isso, 98

Escoamento de doublet ou dipolo: terceiro escoamento fundamental • De modo análogo, mas considerando-se a velocidade potencial, pode-se obter • As linhas de corrente de um doublet ou dipolo, podem, então ser avaliadas como 99

Escoamento de doublet ou dipolo: terceiro escoamento fundamental • Ou seja, • Da geometria analítica, tem-se que uma expressão do tipo • É a representação de um círculo de diâmetro d no eixo vertical com centro localizado em d/2 acima da origem. 100

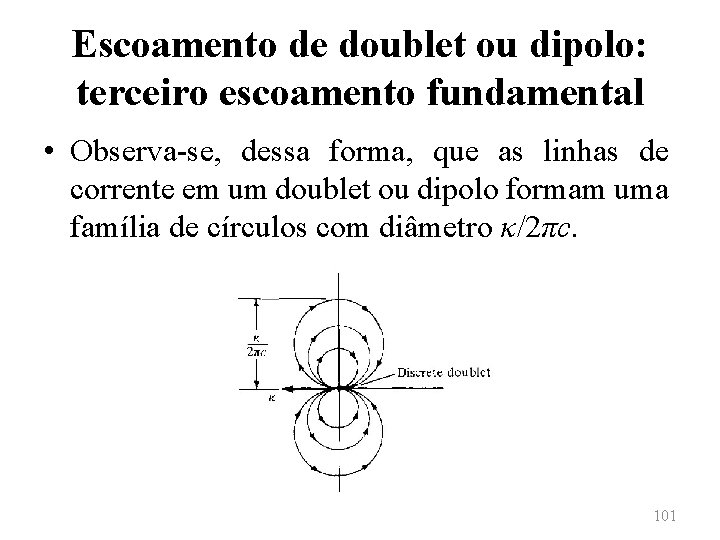
Escoamento de doublet ou dipolo: terceiro escoamento fundamental • Observa-se, dessa forma, que as linhas de corrente em um doublet ou dipolo formam uma família de círculos com diâmetro κ/2πc. 101

Escoamento de doublet ou dipolo: terceiro escoamento fundamental • Observa-se, dessa forma, que um doublet ou dipolo é uma singularidade que induz um padrão de escoamento circular em duplo lóbulo. 102

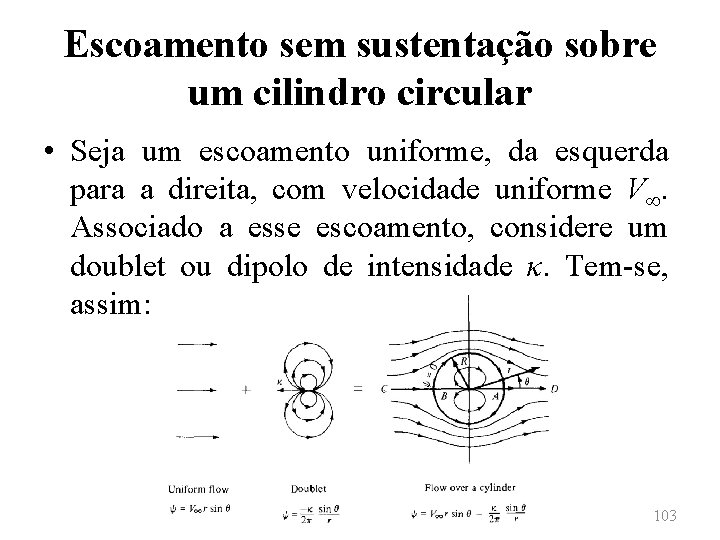
Escoamento sem sustentação sobre um cilindro circular • Seja um escoamento uniforme, da esquerda para a direita, com velocidade uniforme V∞. Associado a esse escoamento, considere um doublet ou dipolo de intensidade κ. Tem-se, assim: 103

Escoamento sem sustentação sobre um cilindro circular • As linhas de corrente, nesse caso, serão dadas por • Tomando-se 104

Escoamento sem sustentação sobre um cilindro circular • Tem-se então que as linhas de corrente podem ser avaliadas como • Essa expressão modela, ao mesmo tempo, tanto as linhas de corrente do escoamento uniforme combinado com um dipolo (doublet) quanto um escoamento sobre um cilindro de raio R. 105

Escoamento sem sustentação sobre um cilindro circular • O campo de velocidades, para o escoamento apresentado, pode ser obtido como – Velocidade radial: 106

Escoamento sem sustentação sobre um cilindro circular – Velocidade angular: • Para o(s) ponto(s) de estagnação, deve-se atender aos seguintes critérios: 107

Escoamento sem sustentação sobre um cilindro circular • Tem-se, assim, que os pontos de estagnação estão localizados em • Esses pontos são denotados como A e B, respectivamente. 108

Escoamento sem sustentação sobre um cilindro circular • Ao se substituir as coordenadas dos pontos A e B na expressão que fornece a linha de corrente, obtém-se ψ = 0. Assim, uma mesma linha de corrente passa através de ambos os pontos. • Além disso, a expressão • é automaticamente satisfeita para r = R para todo ângulo θ. 109

Escoamento sem sustentação sobre um cilindro circular • Recordando-se que R é constante, uma vez que • E que, no plano polar, r = const. = R é a equação de um círculo de raio R centrado na origem, tem-se que a linha de corrente ψ = 0 separa o escoamento em duas porções. 110

Escoamento sem sustentação sobre um cilindro circular • Existe um escoamento interno ao círculo devido ao doublet ou dipolo e um escoamento externo ao círculo, devido ao escoamento uniforme. • Assim, ao se substituir o escoamento interno ao círculo por uma superfície sólida, o escoamento externo não se modificará. 111

Escoamento sem sustentação sobre um cilindro circular • Desta forma, tem-se que o escoamento invíscido, irrotacional e incompressível sobre um cilindro circular de raio R pode ser obtido ao se combinar um escoamento uniforme de velocidade V∞ a um doublet ou dipolo de intensidade κ, sendo R avaliado como 112

Escoamento sem sustentação sobre um cilindro circular • Nota-se que as linhas de corrente nas superfícies superior e inferior do cilindro são simétricas. Dessa forma, a distribuição de pressão sobre o mesmo também o é e, por isso, a força de sustentação sobre o cilindro é nula. • De modo similar, as distribuições de pressão na parte frontal e traseira do cilindro também são simétricas, o que resulta em uma força de arrasto nula. 113

Escoamento sem sustentação sobre um cilindro circular • Para um cilindro em um escoamento real, no entanto, o arrasto resultante observado nunca é nulo. Tem-se, assim, um paradoxo entre o resultado teórico de arrasto nulo e o conhecimento de que o arrasto é finito, que foi observado pela primeira vez em 1744 por Jean Le Rond d’Alembert e que ficou conhecido como “Paradoxo de d’Alembert”. 114

Escoamento sem sustentação sobre um cilindro circular • A solução do aparente paradoxo está relacionada aos efeitos viscosos que provocam tensões de cisalhamento sobre a superfície do corpo e que causam o aparecimento de uma esteira viscosa ou turbulenta pela separação do escoamento (descolamento da camada-limite). • Essa esteira viscosa destroi a simetria do escoamento em relação ao eixo vertical, o que gera um arrasto resultante. 115

Escoamento sem sustentação sobre um cilindro circular • Como os efeitos viscosos não foram considerados nas análises realizadas (escoamento invíscido), não se observam assimetrias no escoamento, de modo que o arrasto resultante é nulo. • Matematicamente, o arrasto nulo é obtido partindo-se da distribuição de velocidades sobre a superfície do cilindro (r = R): 116

Escoamento sem sustentação sobre um cilindro circular • Para um escoamento incompressível, o coeficiente de pressão pode ser expresso como • Combinando-se a velocidade, tem-se então 117

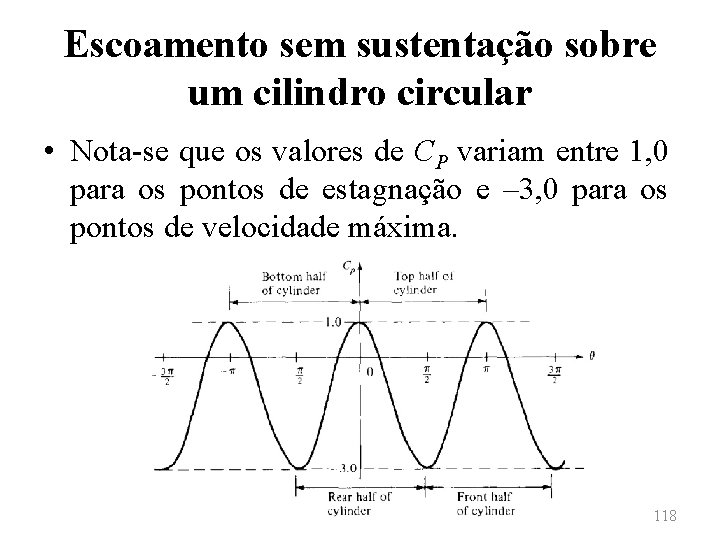
Escoamento sem sustentação sobre um cilindro circular • Nota-se que os valores de CP variam entre 1, 0 para os pontos de estagnação e ‒ 3, 0 para os pontos de velocidade máxima. 118

Escoamento sem sustentação sobre um cilindro circular • Ao se observar o comportamento do coeficiente de pressão ao longo dos ângulos do cilindro, pode-se afirmar que: – As regiões correspondentes às metades superior e inferior do cilindro possuem distribuições de pressão idênticas, de modo que a sustentação deve ser nula. – As regiões frontal e traseira do cilindro também possuem distribuições de pressões idênticas e, por isso, o arrasto é teoricamente nulo. 119

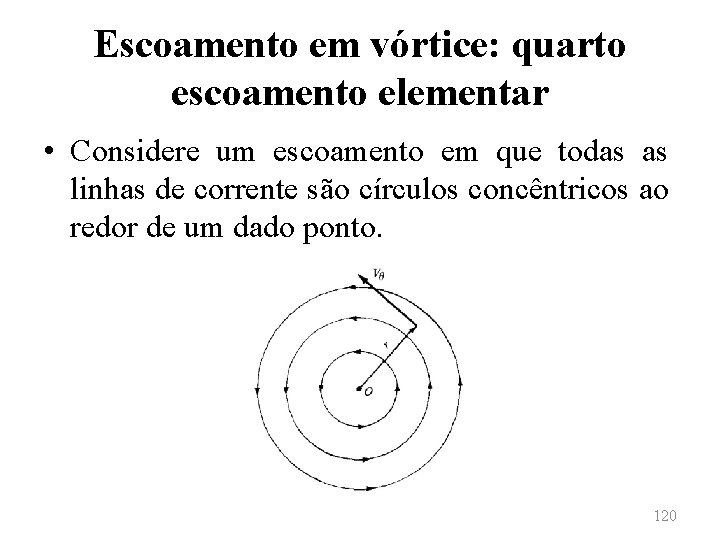
Escoamento em vórtice: quarto escoamento elementar • Considere um escoamento em que todas as linhas de corrente são círculos concêntricos ao redor de um dado ponto. 120

Escoamento em vórtice: quarto escoamento elementar • Para esse escoamento, considera-se que a velocidade ao longo de uma linha de corrente seja constante. • A velocidade, contudo, deve variar de uma linha de corrente para outra, de forma inversamente proporcional à distância em relação ao centro comum. • Tem-se, então, um escoamento chamado de escoamento em vórtice. 121

Escoamento em vórtice: quarto escoamento elementar • Para esse escoamento, observa-se que • Esse campo de escoamento satisfaz tanto o critério de incompressibilidade quanto o de irrotacionalidade (exceto na origem): 122

Escoamento em vórtice: quarto escoamento elementar • Para a avaliação da constante C, considera-se a circulação ao longo de uma linha de corrente de raio r: • De onde se obtém 123

Escoamento em vórtice: quarto escoamento elementar • Ao se comparar as expressões para a velocidade angular, conclui-se que • Desse resultado, conclui-se que a circulação para todas as linhas de corrente apresentam o mesmo valor 124

Escoamento em vórtice: quarto escoamento elementar • A grandeza Γ é conhecida como intensidade do escoamento em vórtice. • Para se saber o que ocorre em r = 0, recorre-se à relação entre a circulação e a vorticidade: • Que pode ser reescrito como 125

Escoamento em vórtice: quarto escoamento elementar • Uma vez que tanto o rotacional quanto o vetor área são perpendiculares ao plano do escoamento, tem-se • Considerando-se, então, uma pequeno círculo infinitesimal ao redor da origem, tem-se 126

Escoamento em vórtice: quarto escoamento elementar • Assim, no limite em que r → 0, tem-se • ou seja, • Contudo, quando r → 0, d. S → 0 e assim 127

Escoamento em vórtice: quarto escoamento elementar • Como conclusão, tem-se que o escoamento em vórtice é irrotacional em todos os pontos, exceto em r = 0, onde a vorticidade é infinita. • A velocidade potencial para o escoamento em vórtice é obtida como: 128

Escoamento em vórtice: quarto escoamento elementar • Dessa forma, obtém-se a seguinte expressão • No caso da linha de corrente, consideram-se as seguintes expressões 129

Escoamento em vórtice: quarto escoamento elementar • Dessa forma, obtém-se para a função de corrente a seguinte expressão 130

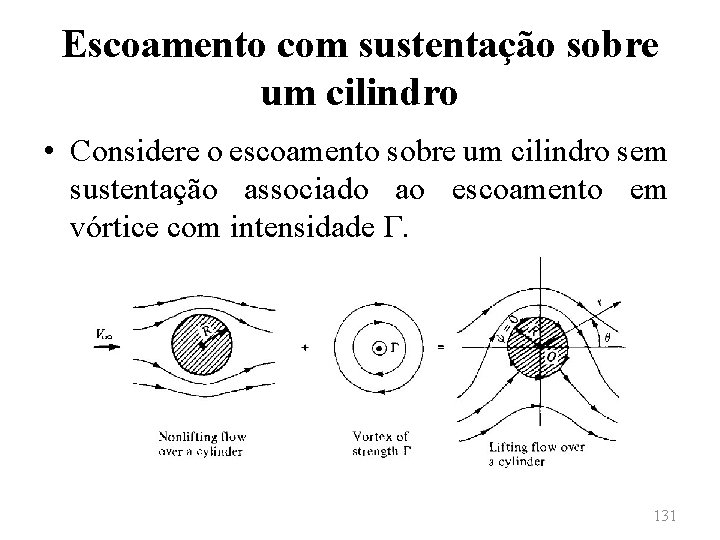
Escoamento com sustentação sobre um cilindro • Considere o escoamento sobre um cilindro sem sustentação associado ao escoamento em vórtice com intensidade Γ. 131

Escoamento com sustentação sobre um cilindro • A função de corrente para um escoamento sobre um cilindro sem sustentação é • No caso de um vórtice de intensidade Γ, a função de corrente é 132

Escoamento com sustentação sobre um cilindro • Nesse caso, pode-se fazer a constante valer • Obtém-se 133

Escoamento com sustentação sobre um cilindro • A função corrente para o escoamento combinado será, então • Observa-se que, se r = R, tem-se a função de corrente nula para todos os ângulos. 134

Escoamento com sustentação sobre um cilindro • Tem-se assim que a equação é válida para o escoamento invíscido e incompressível sobre um cilindro de raio R. • O campo de velocidades pode ser obtido da diferenciação da expressão da função de corrente: – Velocidade radial: 135

Escoamento com sustentação sobre um cilindro – Velocidade angular • A localização dos pontos de estagnação é feita igualando-se as componentes da velocidade a zero: – Velocidade radial: 136

Escoamento com sustentação sobre um cilindro – Velocidade angular: • Para r = R e resolvendo-se a equação anterior para θ obtém-se 137

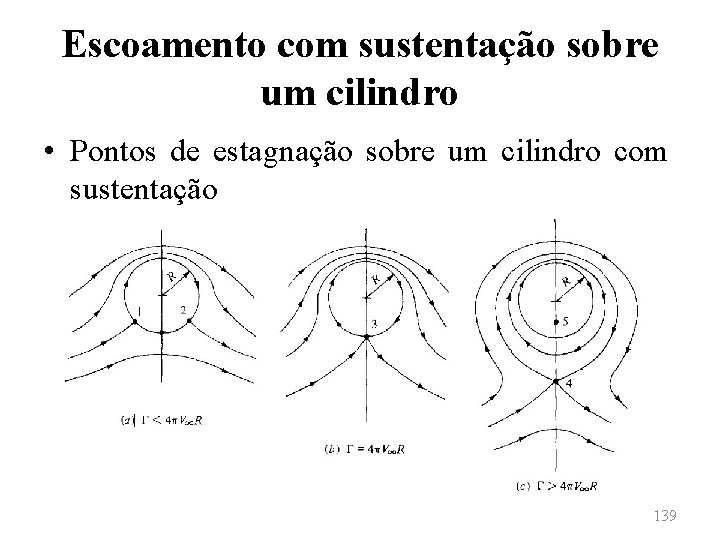
Escoamento com sustentação sobre um cilindro • Como Γ é um número positivo, o ângulo θ deve pertencer aos terceiro e quarto quadrantes. Assim, podem haver dois pontos de estagnação na superfície inferior do cilindro, porém, apenas se a seguinte relação for satisfeita 138

Escoamento com sustentação sobre um cilindro • Pontos de estagnação sobre um cilindro com sustentação 139

Escoamento com sustentação sobre um cilindro • Caso a seguinte expressão for satisfeita • Será verificado apenas um ponto de estagnação sobre a superfície do cilindro. Nesse caso, o ponto de estagnação estará localizado no ponto 140

Escoamento com sustentação sobre um cilindro • No caso da seguinte expressão ser verificada • Também existirão dois pontos de estagnação no escoamento. Para se determinar tais pontos, deve-se considerar θ = π/2, de onde se obtém 141

Escoamento com sustentação sobre um cilindro • Nota-se, assim, que há um ponto de estagnação fora e outro dentro do cilindro, ambos sobre o eixo vertical. • Pela observação de simetria (ou falta dela) para os escoamentos com circulação, verifica-se que a força normal (e consequentemente a sustentação) não é nula. • Com relação ao arrasto, no entanto, o paradoxo de d’Alembert permanece. 142

Escoamento com sustentação sobre um cilindro • Velocidade na superfície do cilindro (r = R): • Nesse caso, o coeficiente de pressão é: 143

Escoamento com sustentação sobre um cilindro • Coeficiente de arrasto – Para coordenadas polares: 144

Escoamento com sustentação sobre um cilindro – Notando-se que c = 2 R, tem-se – Integrais trigonométricas: 145

Escoamento com sustentação sobre um cilindro – Associando-se todas as expressões, obtém-se que • Coeficiente de sustentação: – Para coordenadas polares: 146

Escoamento com sustentação sobre um cilindro – Tem-se então que – Integrais trigonométricas: 147

Escoamento com sustentação sobre um cilindro – Dessa forma, tem-se – E a sustentação será dada por 148

Escoamento com sustentação sobre um cilindro • Pela expressão anterior, tem-se que a sustentação, por unidade de comprimento, é diretamente proporcional à circulação. Esse resultado é conhecido com Teorema de Kutta. Joukowski. • Os resultados de escoamentos invíscidos podem não fornecer resultados acurados quanto ao arrasto; com relação à sustentação, no entanto, são bastante realísticos. 149

Escoamento com sustentação sobre um cilindro • Cilindro sem sustentação: 150

Escoamento com sustentação sobre um cilindro • Cilindro com rotação (velocidade periférica): 151

Escoamento com sustentação sobre um cilindro • Cilindro com rotação (velocidade periférica): 152

Teorema de Kutta-Joukowski e geração de sustentação • Seja uma curva fechada A em um escoamento de tal modo que encapsule um aerofólio. 153

Teorema de Kutta-Joukowski e geração de sustentação • Se o aerofólio produz sustentação, o campo de velocidades ao redor do aerofólio deve ser tal que a integral de linha da velocidade ao redor de A deve ser finita, ou seja, a circulação deve ser finita. • Assim, a sustentação comprimento será por unidade de 154

Teorema de Kutta-Joukowski e geração de sustentação • O escoamento sobre um cilindro circular com sustentação pode ser obtido ao se combinar um escoamento uniforme, um escoamento de doublet (ou dipolo) e um escoamento em vórtice. • Todos os três escoamentos são irrotacionais para todos os pontos, exceto pelo escoamento em vórtice, para o qual a vorticidade é infinita na origem. 155

Teorema de Kutta-Joukowski e geração de sustentação • Se for avaliada a circulação em uma curva fechada qualquer que não contenha a origem, tem-se que Γ= 0. • Apenas se considerada uma curva fechada que inclua a origem que se terá a Γ igual à intensidade do vórtice. 156

Teorema de Kutta-Joukowski e geração de sustentação • O teorema de Kutta-Joukowski prediz que o valor da circulação Γ deve ser avaliada ao redor de uma curva fechada que inclua o corpo; tal curva, no entanto, pode apresentar qualquer forma arbitrária, desde que encapsule o corpo em seu interior. 157

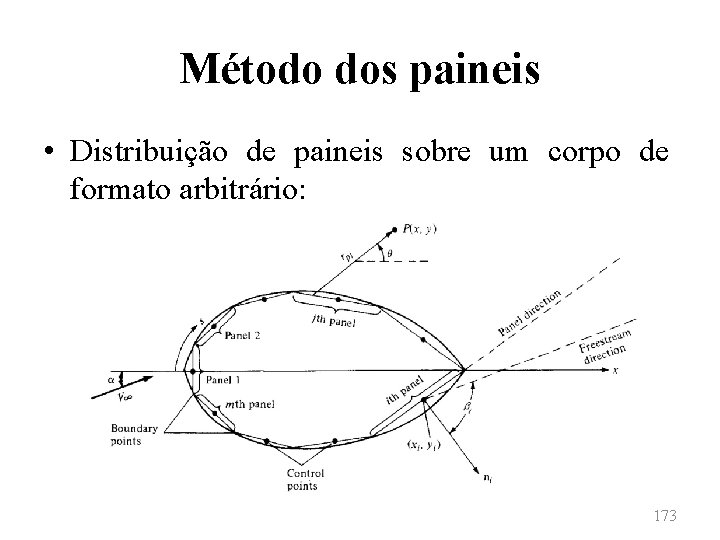
Método dos paineis • Apesar de útil, a combinação de escoamentos elementares para a determinação de geometrias não é prática para a grande maioria dos corpos imersos em um escoamento. • Deseja-se, na realidade, que dada uma geometria, possa-se resolver uma distribuição de singularidades que, combinadas a um escoamento uniforme, produza os efeitos desse corpo no escoamento. 158

Método dos paineis • Um método voltado para isso é o chamado método dos paineis, desenvolvido no final da década de 1960. • Tal técnica é apropriada para a solução numérica de escoamentos sem sustentação sobre aerofólios arbitrários. • Para tanto, deve-se estender os conceitos de fonte e sumidouro pontuais para linhas de fonte e de sumidouro. 159

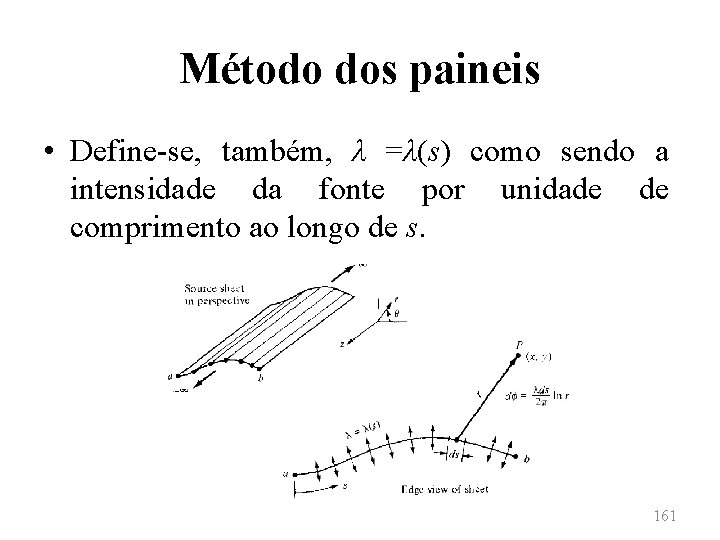
Método dos paineis • Considerando-se um número infinito de linhas de fonte posicionadas lado a lado, sendo a intensidade de cada linha infinitesimalmente pequena. Tem-se, assim, a formação de uma superfície de fontes, para a qual a intensidade de cada linha é infinitesimalmente pequena. • Seja s a distância medida ao longo da superfície de fontes. 160

Método dos paineis • Define-se, também, λ =λ(s) como sendo a intensidade da fonte por unidade de comprimento ao longo de s. 161

Método dos paineis • Nesse caso, a intensidade de uma porção infinitesimal ds da superfície é dada por λ ds. Assim, uma pequena seção da superfície pode ser tratada como uma fonte distinta de intensidade λ ds. • Considerando-se, então, um ponto P localizado no escoamento a uma distância r de ds. 162

Método dos paineis • Nesse caso, a fonte infinitesimal λ ds induz um pequeno potencial no ponto P dado por • A velocidade potencial completa no ponto P pode ser obtida pela integração de toda a superfície de fonte: 163

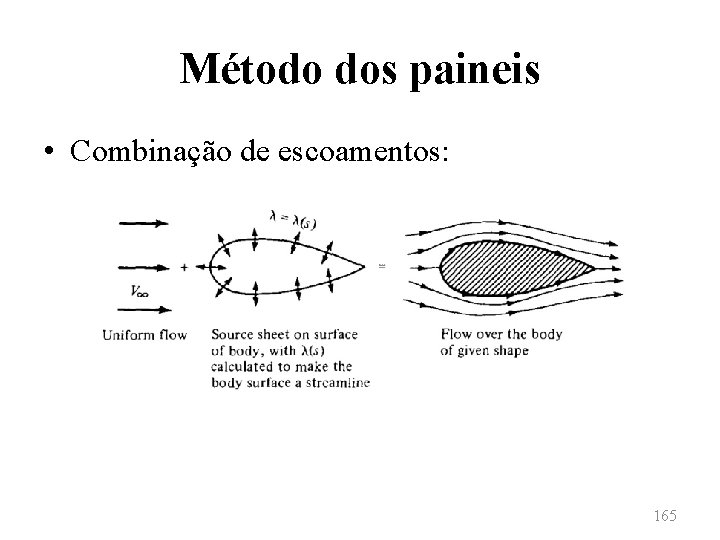
Método dos paineis • Considerando-se, então, um corpo de um formato arbitrário em um escoamento uniforme de velocidade uniforme V∞. Deseja-se, então, cobrir a superfície do corpo com uma superfície de fontes λ(s) de modo que, ao se combinar o escoamento uniforme com a superfície de fontes se obtenha a geometria do corpo através de uma das linhas de corrente do escoamento. 164

Método dos paineis • Combinação de escoamentos: 165

Método dos paineis • A superfície de fontes será, então, aproximada por uma série de paineis planos. Além disso, considera-se que a intensidade λ por unidade de comprimento é constante para um dado painel, mas pode variar de um painel para outro. Se o total de paineis for n, então a intensidade de cada painel será dada por 166

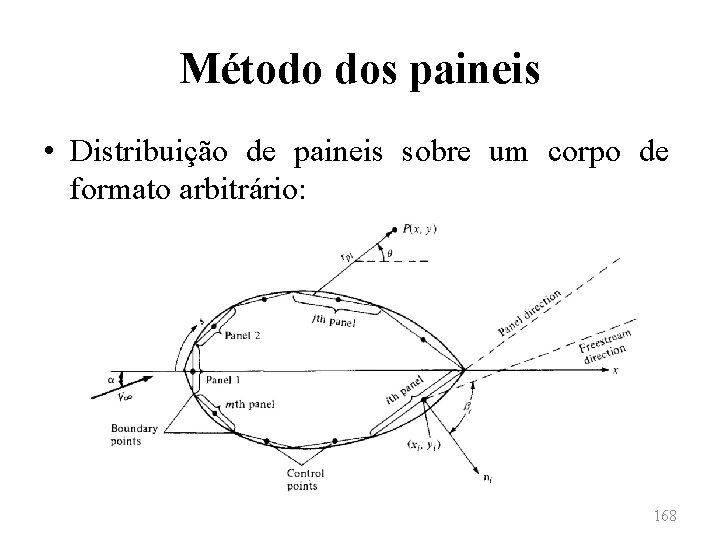
Método dos paineis • As intensidades de cada painel são desconhecidas. Deve-se, assim, encontrar λj, para todos os n paineis, de modo que a superfície do corpo possa ser descrita por uma linha de corrente do escoamento. • Isto é feito definindo-se o ponto médio de cada painel como sendo um ponto de controle e determinando cada λj de modo que a componente normal da velocidade seja nula. 167

Método dos paineis • Distribuição de paineis sobre um corpo de formato arbitrário: 168

Método dos paineis • Considerando-se um ponto P localizado no escoamento em (x, y) e sendo rpj a distância de qualquer ponto do painel j ao ponto P. A velocidade potencial induzida em P devido ao painel j é dada por 169

Método dos paineis • Na expressão anterior, λj é constante sobre todo o painel j e a integral é avaliada sobre um único painel. Assim, para se avaliar o potencial de todos os paineis sobre o ponto P, tem-se a seguinte expressão • sendo 170

Método dos paineis • Como o ponto P é um ponto arbitrário, pode-se posicioná-lo sobre o ponto de controle do iésimo painel. Nesse caso, obtém-se: 171

Método dos paineis • As condições de contorno devem ser aplicadas nos pontos de controle. Assim, a componente normal à velocidade do escoamento é nula nesses pontos. • É importante, por isso, avaliar a componente da velocidade perpendicular ao painel. 172

Método dos paineis • Distribuição de paineis sobre um corpo de formato arbitrário: 173

Método dos paineis • Seja ni o vetor normal unitário ao painel i direcionado para fora do mesmo. • A inclinação desse painel pode ser avaliada como sendo • Além disso, admite-se um ângulo de incidência α do escoamento livre. 174

Método dos paineis • Nesse caso, tem-se • Sendo βi o ângulo entre o vetor velocidade e a normal ao painel. • A componente normal da velocidade induzida em (xi, yi) pelo painel é 175

Método dos paineis • Combinando-se todas as componentes da velocidade normal induzidas por todos os paineis em um ponto de controle i tem-se: • Somando-se, então, as componentes induzidas e a componente do escoamento livre, tem-se: 176

Método dos paineis • A expressão anterior pode, então, ser escrita como • Tal expressão é o ponto central do método dos paineis. Os valores das integrais dependem apenas da geometria dos paineis, sem influência do escoamento. 177

Método dos paineis • Denotando-se Ii, j como sendo o valor da integral quando o ponto de controle avaliado está sobre o painel i e a integral é realizada sobre o painel j, pode-se reescrever a expressão anterior como: • Que se constitui em uma equação algébrica linear de n incógnitas. 178

Método dos paineis • Similarmente, ao se aplicar essa equação para todos os n paineis, será possível avaliar todas as incógnitas (λ 1, λ 2, . . . , λn) ao se resolver um sistema de equações lineares. • No caso de aerofólios, é interessante utilizar uma maior quantidade de paineis na região da borda de ataque, de modo a representar acuradamente a curvatura dessa região. 179

Método dos paineis • A componente tangencial da velocidade, para o painel i, pode ser avaliada como • Ao se considerar todos os paineis, a velocidade tangencial induzida é avaliada por 180

Método dos paineis • Ao se combinar as componentes induzida e proveniente do escoamento livre, tem-se a seguinte expressão: 181

Método dos paineis • Por sua vez, o coeficiente de pressão no ponto de controle i pode ser avaliado como • A acurácia dos resultados obtidos pelo método dos paineis pode ser avaliada do seguinte modo: 182

Método dos paineis – Considerando-se Sj o comprimento do painel j e que λj é a intensidade desse painel por unidade de comprimento, então a intensidade do painel j pode ser avaliada como sendo λj Sj. Para um corpo de geometria fechada, a resultante de todas as fontes e sorvedouros somados deve ser nula, de modo que a seguinte relação deve ser satisfeita: 183

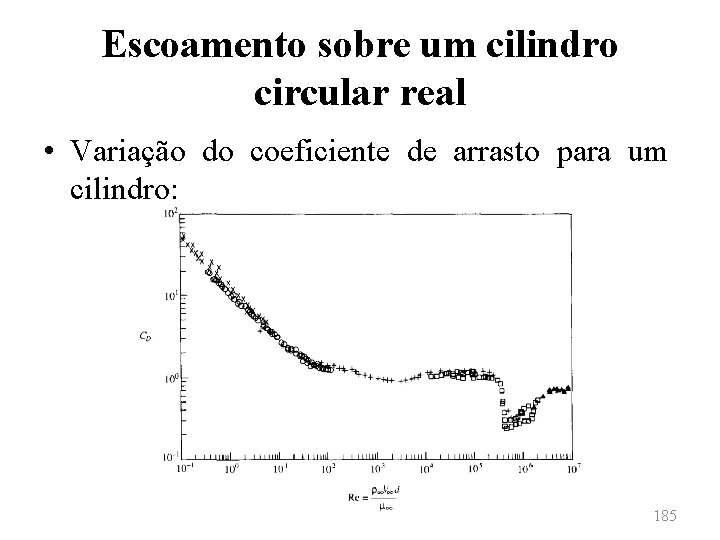
Escoamento sobre um cilindro circular real • Ao se estudar o escoamento incompressível e invíscido sobre um cilindro, observou-se que, analiticamente, o arrasto de pressão teórico avaliado é nulo, resultado este conhecido como Paradoxo de d’Alembert. • No caso de um cilindro em condições reais, o arrasto avaliado nunca é zero, sendo uma função do número de Reynolds para um escoamento incompressível. 184

Escoamento sobre um cilindro circular real • Variação do coeficiente de arrasto para um cilindro: 185

Escoamento sobre um cilindro circular real • Aspectos qualitativos: – Para valores de Reynolds muito baixos, ou seja, para a faixa de 0 ≤ Re ≤ 4, as linhas de corrente são praticamente simétricas e o escoamento permanece aderido ao cilindro. Tal regime de escoamento viscoso é chamado de escoamento de Stokes. 186

Escoamento sobre um cilindro circular real – Para valores de Reynolds baixos, entre 4 e 40, ocorre a separação do escoamento na porção traseira do cilindro, formando-se dois vórtices distintos e estáveis. 187

Escoamento sobre um cilindro circular real – Para valores de Reynolds superiores a 40, o escoamento após o cilindro torna-se instável, formando-se uma esteira de vórtices alternados. Tal configuração é conhecida como “Esteira de von Karman”. 188

Escoamento sobre um cilindro circular real – Se o número de Reynolds aumentar ainda mais, a esteira de von Karman se desfaz e tem-se a formação de uma esteira viscosa, que se separa a cerca de 80° a partir do ponto de estagnação do escoamento sobre o cilindro. 189

Escoamento sobre um cilindro circular real – Se o número de Reynolds estiver entre 3 x 105 e 3 x 106, a esteira viscosa se separa do cilindro mas, na sequência, tende a se conectar novamente à superfície do corpo em um ângulo de cerca de 120°. Isto se deve à transição entre o escoamento laminar e o turbulento na esteira viscosa. O efeito de reconexão da camada limite reduz o arrasto de pressão sobre o cilindro. 190

Escoamento sobre um cilindro circular real – Caso o número de Reynolds seja superior a 3 x 106, o escoamento passa a ser totalmente turbulento e a separação da esteira viscosa ocorre a cerca de 120º após o ponto de estagnação. 191