Modelowanie i podstawy identyfikacji 20152016 Identyfikacja metoda najmniejszych

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Modelowanie i podstawy identyfikacji - studia stacjonarne Kazimierz Duzinkiewicz, dr hab. Inż. Katedra Inżynierii Systemów Sterowania Wykład 9+10 - 2015/2016 Identyfikacja – metoda najmniejszych kwadratów – wybrane algorytmy wersji wsadowej Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 1

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Identyfikacja - metoda najmniejszych kwadratów Typowa forma zadania estymacji parametrów Dany jest system dynamiczny, dla którego proponowany jest model matematyczny oparty na doświadczeniu proponującego i który: ▪ zgodny jest ze wszystkimi znanymi prawami rządzącymi zachowaniem się systemu, ▪ pozwala wykorzystać dostępne w systemie pomiary dla porównania zachowania się modelu i systemu ▪ jego struktura spełnia wymagania pozwalające uzyskać pożądaną dokładność ale zawiera szereg niezbyt dobrze znanych parametrów Należy określić „najlepsze” estymaty wszystkich nieznanych dobrze parametrów tak, aby model matematyczny zapewniał „optymalną estymatę” zachowania systemu Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 2

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Każda metoda rozwiązująca zadanie o podanej strukturze – realizacja procesu estymacji Zadania estymacji: bardzo łatwe . . . nierozwiązywalne Podstawa wielu procesów estymacji – metoda najmniejszych kwadratów Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 3

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów W procesie estymacji z każdą włączoną zmienną/wielkością związane są trzy wartości: w ten proces - wartość prawdziwa (rzeczywista) zmiennej - wartość mierzona zmiennej - wartość estymowana zmiennej Co można powiedzieć o tych wartościach? - wartość praktycznie nieznana - wartość uzyskiwana z czujnika lub z innego pomiaru, nigdy nierówna wartości prawdziwej, obarczona błędem pomiaru - wartość zmiennej uzyskiwana jako wynik procesu estymacji W zadaniu estymacji zmienne x – parametry modelu Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 4

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Dwa błędy: 1. Błąd pomiaru (measurement error) wartość mierzona wartość prawdziwa 2. Błąd resztkowy (residual error) wartość mierzona błąd pomiaru błąd resztkowy – residuum) wartość estymowana Co można powiedzieć o tych błędach: - wartość praktycznie nigdy nieznana; mechanizm generujący ten błąd zwykle jest aproksymowany przez pewien znany proces (np. szum gaussowski o zerowej wartości średniej i znanej wariancji σ2; - wartość znana w momencie wyznaczenia wartości estymowanej Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 5

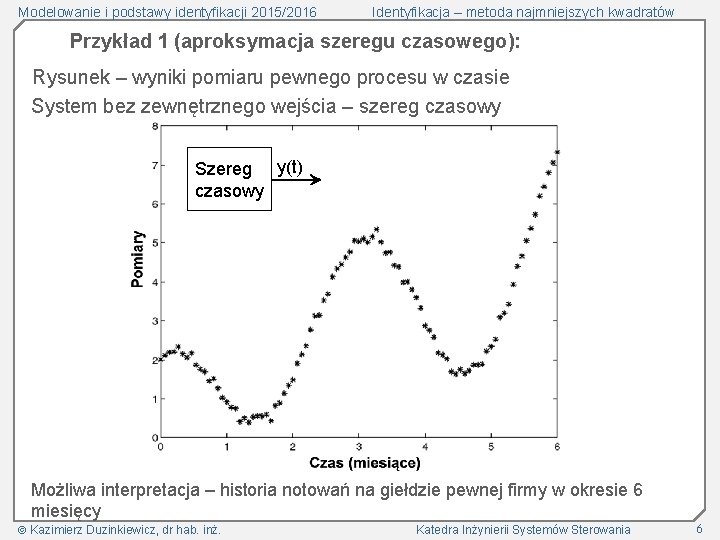
Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Przykład 1 (aproksymacja szeregu czasowego): Rysunek – wyniki pomiaru pewnego procesu w czasie System bez zewnętrznego wejścia – szereg czasowy Szereg y(t) czasowy Możliwa interpretacja – historia notowań na giełdzie pewnej firmy w okresie 6 miesięcy Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 6

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Zadanie – zbudować model y(t) do predykcji perspektyw firmy Dane: (np. notowań zamknięcia giełdy), oznaczone Pomiary dane dla przedziału 6 miesięcy Wymagania: Wartość bezwzględna błędów resztkowych (residuów) |μ| nie większa niż 0. 0075: Odchylenie standardowe błędów resztkowych (residuów) σ nie większa od 0. 125 Średnia z próby: Wariancja z próby: Kazimierz Duzinkiewicz, dr hab. inż. m – liczba próbek, liczba pomiarów Katedra Inżynierii Systemów Sterowania 7

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Proponowane modele: - czas [miesiące – m] - stałe współczynniki – parametry Modelu 1 - stałe współczynniki – parametry Modelu 2 Ocena: Jak dobrze każdy z proponowanych modeli z „optymalnymi” wartościami współczynników ci oraz di dokonuje predykcji pomiarów? W statystyce: proces „wpasowywania” krzywej takiej jak np. Model 1 lub Model 2 w posiadane pomiary - regresja Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 8

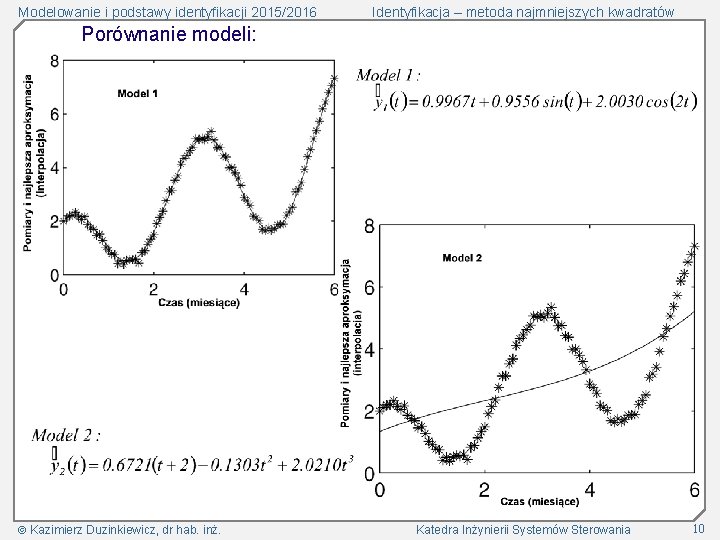
Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Załóżmy, że znamy metodę najmniejszych kwadratów i zastosowaliśmy algorytm tej metody do wyznaczenia „optymalnych” wartości współczynników ci Modelu 1 oraz di Modelu 2 „Optymalne” wartości współczynników ci Modelu 1 „Optymalne” wartości współczynników di Modelu 2 Modele z „optymalnymi” współczynników Kazimierz Duzinkiewicz, dr hab. inż. wartościami Katedra Inżynierii Systemów Sterowania 9

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Porównanie modeli: Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 10

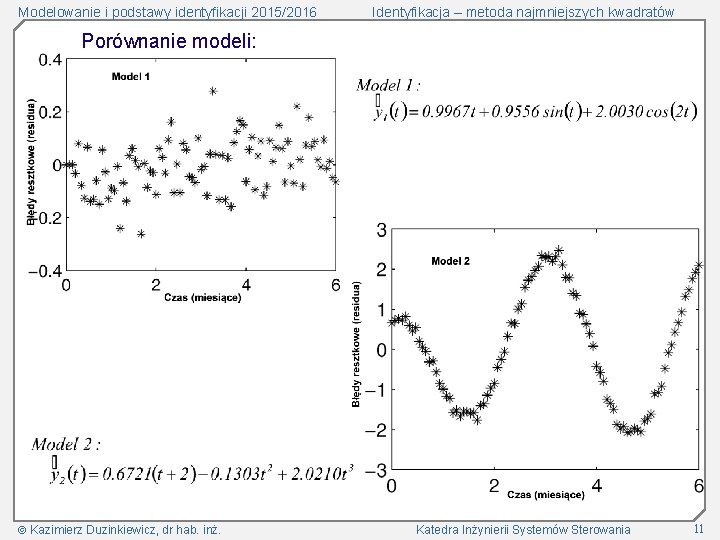
Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Porównanie modeli: Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 11

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Porównanie modeli: Średnia z próby błędów resztkowych (residuów): Odchylenie standardowe z próby błędów resztkowych (residuów): Konkluzja: Nie mając podstaw przypuszczać istnienia systematycznych błędów w pomiarach stwierdzamy, że Model 1 może być używany do dokładnej oceny zachowania y(t) Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 12

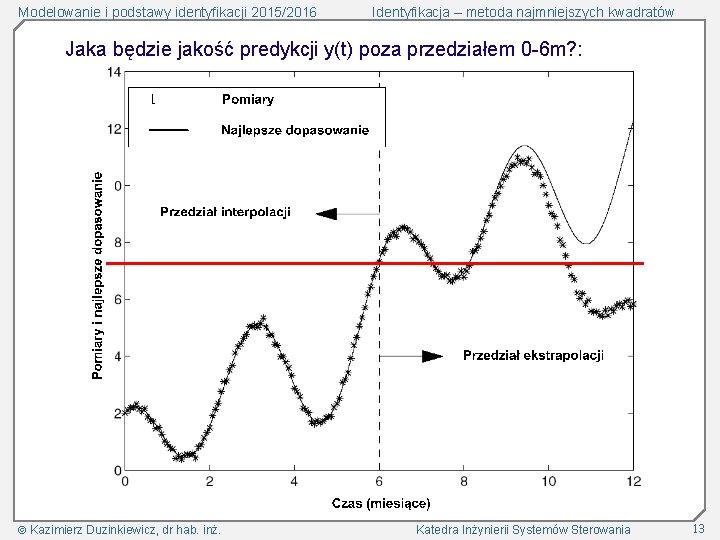
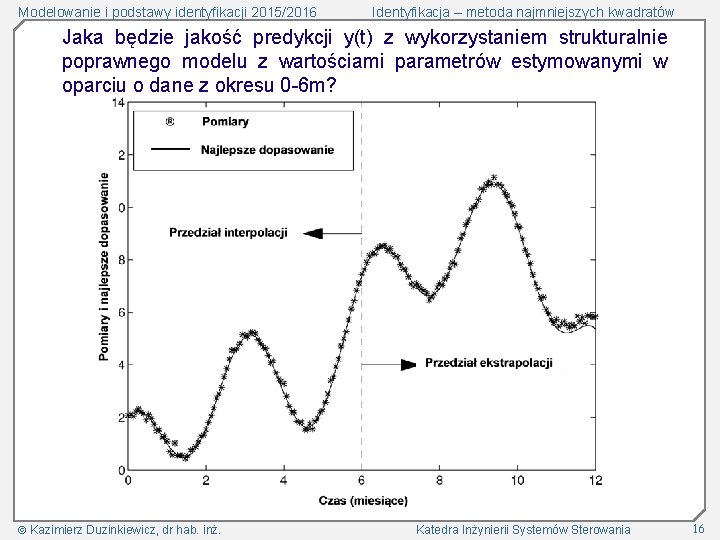
Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Jaka będzie jakość predykcji y(t) poza przedziałem 0 -6 m? : Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 13

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Kuchnia naszego zadania: Pomiary generowane zgodnie z równaniem Symulacja błędu pomiaru: generator szumu gaussowskiego o zerowej wartości średniej i odchyleniu standardowym σ = 0. 1 Propozycja strukturalnie poprawnego modelu: „Optymalne” wartości współczynników xi Modelu 3 Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 14

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Model strukturalnie poprawny – różnice wartości prawdziwych i wartości estymowanych parametrów Prawdziwe wartości współczynników xi Modelu 3 Estymowane „optymalnie” wartości współczynników xi Modelu 3 (dane z okresu 0 -6 m) Jedyna przyczyna – błędy pomiarów Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 15

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Jaka będzie jakość predykcji y(t) z wykorzystaniem strukturalnie poprawnego modelu z wartościami parametrów estymowanymi w oparciu o dane z okresu 0 -6 m? Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 16

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Wnioski z Przykładu 1 ogromne znaczenie w praktyce estymacji poprawnego strukturalnie modelu matematycznego systemu zaproponowanie strukturalnie poprawnego modelu jest zadaniem trudnym dla nie – specjalisty z dziedziny aplikacji pominięte elementy modelu oraz błędy estymacji parametrów modelu mogą prowadzić do błędnych wyników uzyskiwanych z modelu, szczególnie poza obszarami objętymi pomiarami Teoria estymacji może być rozwijana bez zwracania uwagi na konkretne systemy dynamiczne, ale udane zastosowania teorii estymacji prawie zawsze oparte są na łącznym zrozumieniu teorii estymacji i zasad rządzących zachowaniem się rozważanego systemu Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 17

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Metoda najmniejszych kwadratów - jednokrotna estymacja liniowa – (linear batch estimation) Dane: (1) Pomiary Proponowany model: Liniowy względem parametrów (2) - określony zbiór niezależnych funkcji bazowych (3) Parametry nieznane Założenie: Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 18

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Poszukiwanie: Estymaty nieznanych parametrów Kryterium jakości doboru wartości estymowanych parametrów – jak dobrze proponowany model dokonuje predykcji pomiarów Argument kryterium – błędy resztkowe (residua) Liczba błędów resztkowych – liczba pomiarów Pamiętać należy też: błąd pomiędzy wartością prawdziwą a wartością estymowaną – powody: - błąd pomiaru - niepoprawny wybór wartości parametrów xi, i=1, . . . , n - niepoprawna struktura modelu – błąd modelowania Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 19

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Zależności: - model pomiaru (4) (5) gdzie - błędy pomiaru: zakładamy na razie, że ich mechanizm nie jest znany i może mieć charakter przypadkowy lub deterministyczny Przyjmujemy (6) gdzie - błędy resztkowe Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 20

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Zależności w zwartej postaci (4 a) - wektor prawdziwych wartości parametrów - wektor estymowanych wartości parametrów - wektor wartości mierzonych y - wektor wartości estymowanych y - wektor błędów pomiarów Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 21

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Zależności w zwartej postaci –c. d. : (6 a) - wektor wartości mierzonych y - wektor estymowanych wartości parametrów - wektor błędów resztkowych (residuów) Macierz obserwacji Równania (4 a) oraz (6 a) – równania obserwacji Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 22

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Przykład 2: rozpuszczalność azotanu sodu w zależności od temperatury Funkcje bazowe: Pomiar Temperatura Rozpuszczalnoś j uj ć yj 1 0 66, 7 2 4 71, 0 3 10 76, 3 4 15 80, 6 5 21 85, 7 6 29 92, 9 7 36 99, 4 8 51 113, 6 9 68 125, 1 Proponowany model Kazimierz Duzinkiewicz, dr hab. inż. Wektor wartości mierzonych y: Wektor wartości estymowanych y: Wektor wartości prawdziwych parametrów: Wektor wartości estymowanych parametrów: Katedra Inżynierii Systemów Sterowania 23

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Równania obserwacji: Wektor błędów pomiaru: Wektor błędów resztkowych: Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 24

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Metoda najmniejszych kwadratów – przypadek liniowy Metoda najmniejszych kwadratów Gauss’a proponuje jako optymalny wybór dla wartości nieznanych parametrów, wartość który minimalizuje sumę kwadratów błędów resztkowych (residuów) z (6 a) Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 25

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Przykład 2: c. d. Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 26

Modelowanie i podstawy identyfikacji 2015/2016 Kazimierz Duzinkiewicz, dr hab. inż. Identyfikacja – metoda najmniejszych kwadratów Katedra Inżynierii Systemów Sterowania 27

Modelowanie i podstawy identyfikacji 2015/2016 Kazimierz Duzinkiewicz, dr hab. inż. Identyfikacja – metoda najmniejszych kwadratów Katedra Inżynierii Systemów Sterowania 28

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Co możemy powiedzieć o : 1. Możemy napisać - J jest funkcjonałem Metoda najmniejszych kwadratów zadanie minimalizacji funkcjonału bez ograniczeń; zadanie minimalizacji bez ograniczeń Dla danego w oparciu o równania obserwacji funkcjonału J(x) poszukujemy wartości x* dającej minimalną wartość tego funkcjonału Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 29

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów 2. Metoda najmniejszych kwadratów Funkcja celu ma postać formy kwadratowej Forma kwadratowa gdzie: A - macierz symetryczna Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 30

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Przypomnienie z rachunku różniczkowego ? Warunki konieczne i wystarczające, jakie musi spełnić punkt x, aby można było go uznać za dający minimalną wartość funkcjonału wyprowadzane są w oparciu o jego rozwinięcie Taylor’a w otoczeniu punktu x Przypomnienie z rachunku różniczkowego oraz podanie wybranych faktów z teorii optymalizacji - Dodatek A Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 31

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Warunki konieczne i wystarczające minimum metody najmniejszych kwadratów Warunek konieczny pierwszego rzędu: (1) Warunek konieczny drugiego rzędu: dla dowolnych dodatnio półokreślona Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania (2) 32

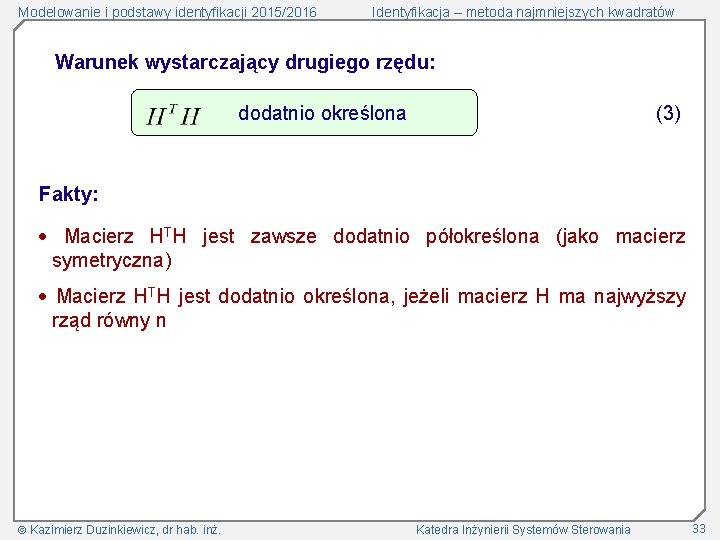
Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Warunek wystarczający drugiego rzędu: dodatnio określona (3) Fakty: Macierz HTH jest zawsze dodatnio półokreślona (jako macierz symetryczna) Macierz HTH jest dodatnio określona, jeżeli macierz H ma najwyższy rząd równy n Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 33

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Obliczanie wartości estymowanych nieznanych parametrów – układ równań normalnych wynikający z warunku koniecznego pierwszego rzędu Układ równań normalnych (4) Jeżeli macierz HTH jest nieosobliwa - posiada macierz odwrotną - otrzymujemy jawne rozwiązanie optymalnej estymaty (5) Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 34

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Fakty: Jawne rozwiązanie optymalnej estymaty wymaga nieosobliwości macierzy HTH macierz HTH jest nieosobliwa jeżeli rząd macierzy H wynosi n, czyli liczba liniowo niezależnych równań obserwacji jest większa lub co najmniej równa liczbie poszukiwanych estymat xi Stąd warunek: zbiór funkcji bazowych powinien być liniowo niezależny Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 35

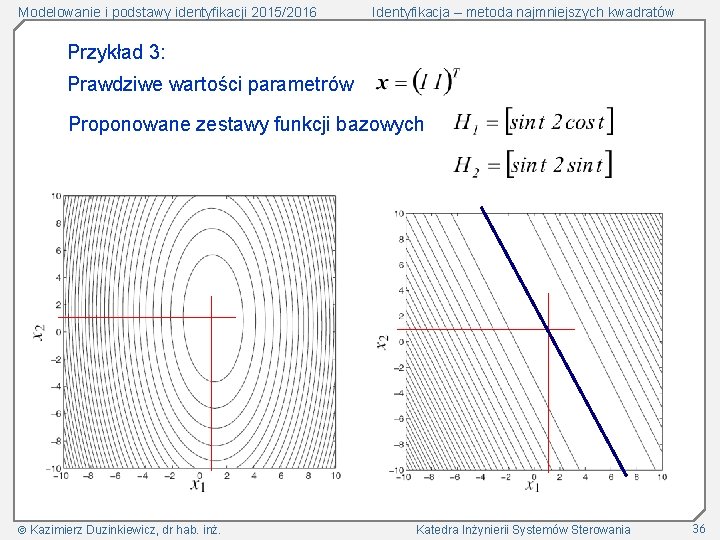
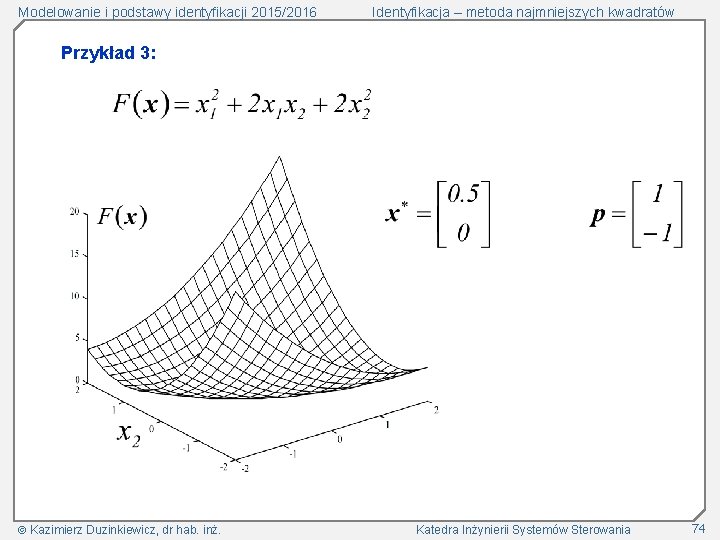
Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Przykład 3: Prawdziwe wartości parametrów Proponowane zestawy funkcji bazowych Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 36

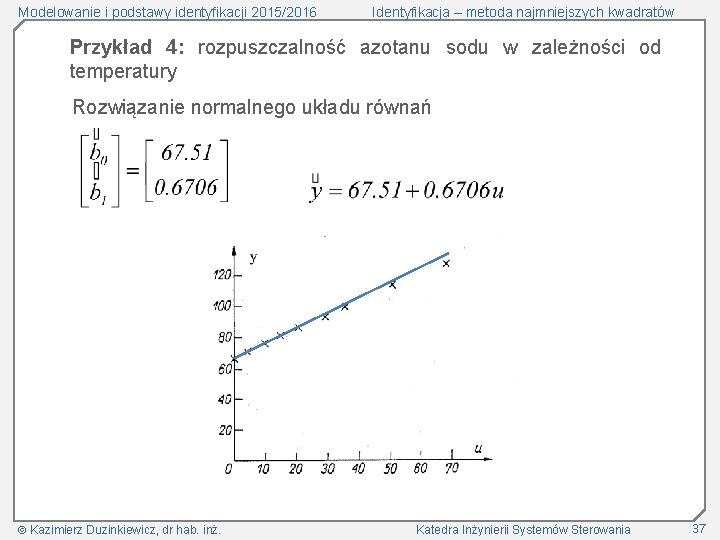
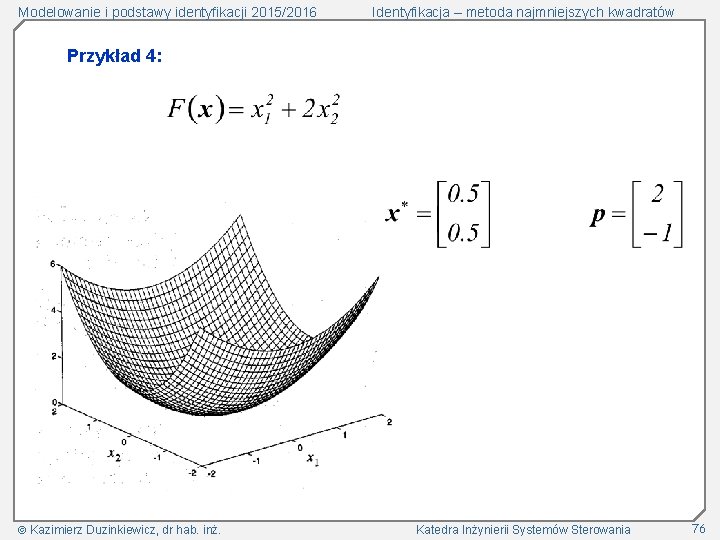
Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Przykład 4: rozpuszczalność azotanu sodu w zależności od temperatury Rozwiązanie normalnego układu równań Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 37

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Przykład 5: (estymacja parametrów prostego układu dynamicznego) System Dyskretna reprezentacja systemu z przedziałem dyskretyzacji Δt gdzie: Zadanie: określić wartości stałych AD oraz BD wykorzystując zbiór pomiarów dyskretnych oraz Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 38

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Jak została zaproponowana reprezentacja dyskretna systemu – - powtórzenie dla tego przykładu z SD Poszukujemy odpowiedzi systemu na dowolne wymuszenie w przedziale czasu [t 0, t) – patrz wykłady z Podstaw automatyki u(t) Obiekt x(t) Dla dowolnego wejścia u(t) określonego w przedziale [t 0, t] odpowiedź systemu Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 39

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Przyjmując przedział dyskretyzacji Ts możemy policzyć Przemnażamy pierwszą zależność przez i odejmujemy od drugiej Ostatnia zależność po uporządkowaniu Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 40

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Zmieniamy zmienną całkowania Otrzymujemy Przyjmując stałość wejścia w przedziale próbkowania AD Kazimierz Duzinkiewicz, dr hab. inż. BD Katedra Inżynierii Systemów Sterowania 41

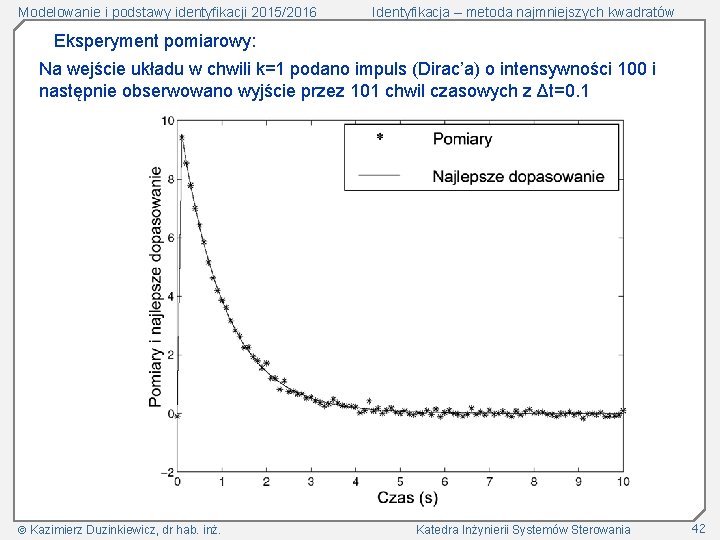
Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Eksperyment pomiarowy: Na wejście układu w chwili k=1 podano impuls (Dirac’a) o intensywności 100 i następnie obserwowano wyjście przez 101 chwil czasowych z Δt=0. 1 Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 42

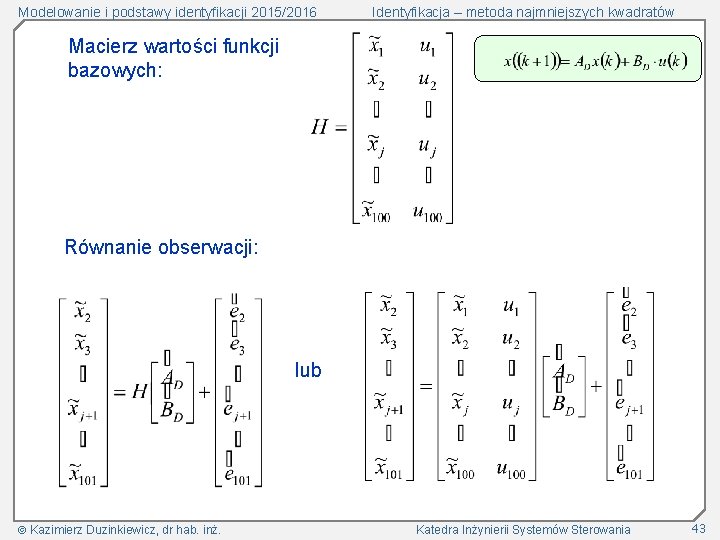
Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Macierz wartości funkcji bazowych: Równanie obserwacji: lub Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 43

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Korzystając z (5): Otrzymamy: Kuchnia naszego zadania: Pomiary generowane były z wykorzystaniem następujących wartości prawdziwych Symulacja błędu pomiaru: generator szumu gaussowskiego o zerowej wartości średniej i odchyleniu standardowym σ = 0. 08 Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 44

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Metoda ważonych najmniejszych kwadratów Poprzednie podejście: jednakowe znaczenie wszystkich pomiarów Ważniejsze te pomiary, które wykonywane są z mniejszym błędem – dołączenie wag pomiarów do metody najmniejszych kwadratów Znaleźć wartości nieznanych parametrów minimalizujące gdzie - symetryczna macierz wag Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 45

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Warunek konieczny pierwszego rzędu: (6) Warunek dostateczny drugiego rzędu: dodatnio określona (7) W dodatnio określona Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 46

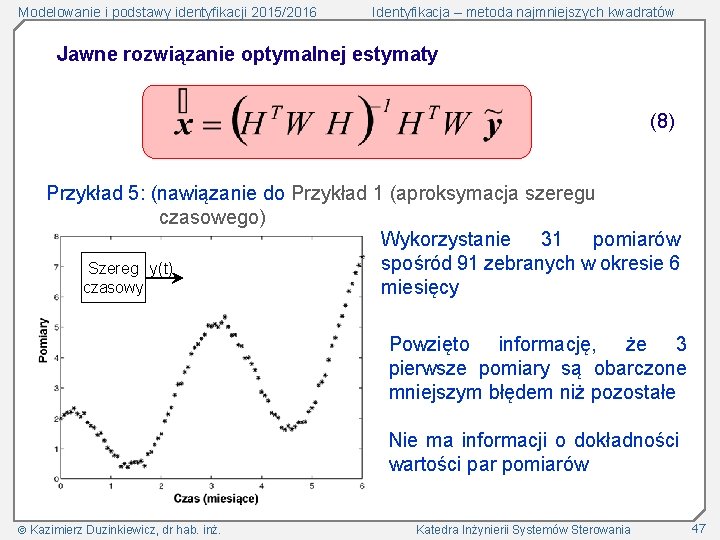
Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Jawne rozwiązanie optymalnej estymaty (8) Przykład 5: (nawiązanie do Przykład 1 (aproksymacja szeregu czasowego) Wykorzystanie 31 pomiarów spośród 91 zebranych w okresie 6 Szereg y(t) czasowy miesięcy Powzięto informację, że 3 pierwsze pomiary są obarczone mniejszym błędem niż pozostałe Nie ma informacji o dokładności wartości par pomiarów Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 47

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Proponowana macierz wag: Wykorzystujemy Model 1: - czas [miesiące – m] - stałe współczynniki – parametry Modelu 1 Pierwsza estymacja: 31 pomiarów Wyniki gorsze niż przy wykorzystaniu dostępnych 91 pomiarów Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 48

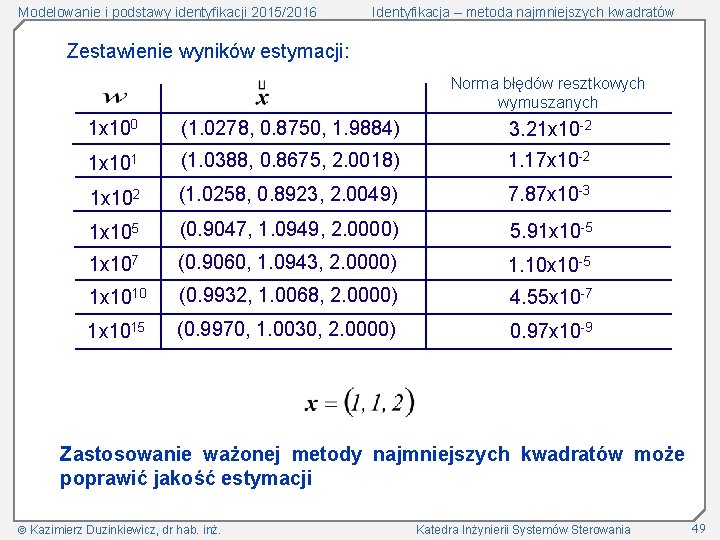
Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Zestawienie wyników estymacji: Norma błędów resztkowych wymuszanych 1 x 100 (1. 0278, 0. 8750, 1. 9884) 3. 21 x 10 -2 1 x 101 (1. 0388, 0. 8675, 2. 0018) 1. 17 x 10 -2 1 x 102 (1. 0258, 0. 8923, 2. 0049) 7. 87 x 10 -3 1 x 105 (0. 9047, 1. 0949, 2. 0000) 5. 91 x 10 -5 1 x 107 (0. 9060, 1. 0943, 2. 0000) 1. 10 x 10 -5 1 x 1010 (0. 9932, 1. 0068, 2. 0000) 4. 55 x 10 -7 1 x 1015 (0. 9970, 1. 0030, 2. 0000) 0. 97 x 10 -9 Zastosowanie ważonej metody najmniejszych kwadratów może poprawić jakość estymacji Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 49

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Poprzednie podejścia: jednakowe znaczenie wszystkich pomiarów – wszystkie pomiary wykonywane z jednakową dokładnością (jednakowo wiarygodne) różne znaczenie poszczególnych pomiarów – część pomiarów charakteryzuje się większą dokładnością (większą wiarygodnością) inne mniejszą dokładnością (mniejszą wiarygodnością Rozważymy jeszcze jedną możliwość: część pomiarów jest dokładna (wykonywana z błędem pomijalnie małym w stosunku do innych pomiarów) Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 50

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Wszystkie obserwacje-pomiary o liczebności m podzielimy na dwie kategorie: m 1 pomiarów-obserwacji wykonanych z ograniczoną dokładnością m 2 pomiarów-obserwacji dokładnych m 1 + m 2 = m - wektor wartości y mierzonych z ograniczoną dokładnością m 1 Pomiary-obserwacje w obrębie tej kategorii mogą być zróżnicowane – wprowadzenie macierzy W 1 - wektor wartości y mierzonych dokładnie m 2 Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 51

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Dla wszystkich przeprowadzonych pomiarów określane są macierze wartości funkcji bazowych, odpowiednio H 1, dla pomiarów niedokładnych i H 2, dla pomiarów dokładnych Macierze wartości funkcji bazowych m 1 n m 2 n Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 52

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Dla pierwszej kategorii pomiarów: m 1 Dla drugiej kategorii pomiarów: m 2 Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 53

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Równanie obserwacji będzie miało postać: (1) lub (2) (3) Przyjmiemy z naturalnych powodów: Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 54

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Poszukujemy wektora wartości estymowanych nieznanych parametrów - wektor estymowanych wartości parametrów Zadanie poszukiwania tego wektora możemy sformułować: , który minimalizuje Znaleźć wektor sumę kwadratów błędów resztkowych (residuów) pomiarów niedokładnych (4) spełniając ograniczenia równościowe pomiarów dokładnych (5) Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 55

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Rozwiązanie postawionego zadania nieoznaczonych mnożników Lagrange’a estymacji metodą Przedstawienie metody: wprowadzamy wektor dodatkowych zmiennych nazywanych nieoznaczonymi mnożnikami Lagrange’a λ; wymiar wektora jest równy liczbie ograniczeń równościowych ograniczenia równościowe przemnożone przez wektor mnożników Lagrange’a włączone zostają jako składnik do rozszerzonej funkcji celu wartości optymalne oryginalnych zmiennych oraz mnożników Lagrange’a wyznaczane są drogą rozwiązania układu równań będących zapisem warunku koniecznego pierwszego rzędu minimum rozszerzonej funkcji celu Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 56

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Wektor nieoznaczonych mnożników Lagrange’a dla zagadnienia (4) – (5): (6) Rozszerzona funkcja celu zagadnienia (4) – (5): (7) Warunki konieczne minimum rozszerzonej funkcji celu zagadnienia (4) – (5): (8) (9) Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 57

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Rozwiązujemy (8) względem (10) Wynik (10) podstawiamy do (9) (11) Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 58

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Wynik (11) podstawiamy do (10) Macierz zależna od wartości funkcji bazowych (wejść) i wag pomiarów – macierz stała Kazimierz Duzinkiewicz, dr hab. inż. Optymalne wartości estymowane nieznanych parametrów wyznaczone w oparciu o pomiary niedokładne (patrz (8) z poprzedniego wykładu) Katedra Inżynierii Systemów Sterowania 59

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Możemy podać wynik rozwiązania zadania (4)-(5): (12) gdzie: (13) (14) K – macierz wzmocnień Optymalne wartości estymowane nieznanych parametrów wyznaczone w oparciu o pomiary niedokładne Kazimierz Duzinkiewicz, dr hab. inż. Wartości y mierzone dokładnie Predykcja wartości y z wykorzystaniem wartości estymowanych nieznanych parametrów wyznaczonych w oparciu o niedokładne pomiary Katedra Inżynierii Systemów Sterowania 60

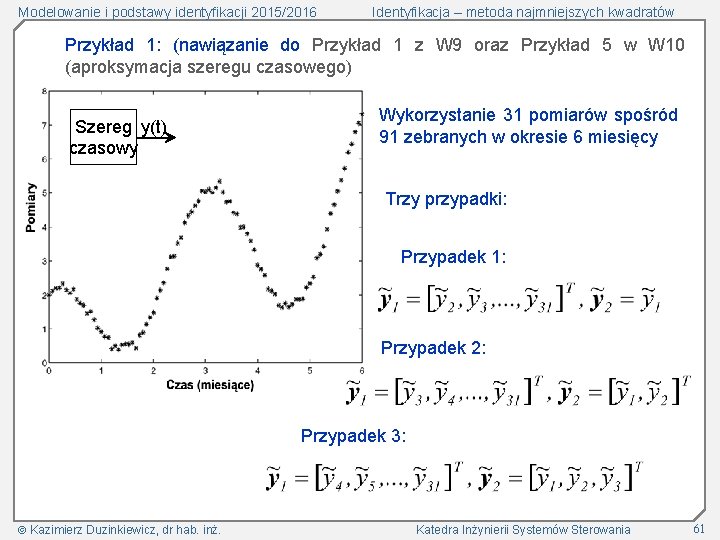
Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Przykład 1: (nawiązanie do Przykład 1 z W 9 oraz Przykład 5 w W 10 (aproksymacja szeregu czasowego) Szereg y(t) czasowy Wykorzystanie 31 pomiarów spośród 91 zebranych w okresie 6 miesięcy Trzy przypadki: Przypadek 1: Przypadek 2: Przypadek 3: Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 61

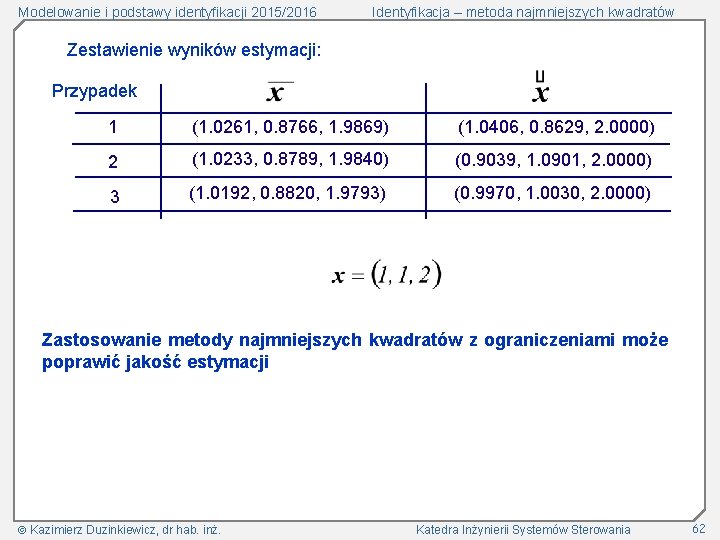
Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Zestawienie wyników estymacji: Przypadek 1 (1. 0261, 0. 8766, 1. 9869) (1. 0406, 0. 8629, 2. 0000) 2 (1. 0233, 0. 8789, 1. 9840) (0. 9039, 1. 0901, 2. 0000) 3 (1. 0192, 0. 8820, 1. 9793) (0. 9970, 1. 0030, 2. 0000) Zastosowanie metody najmniejszych kwadratów z ograniczeniami może poprawić jakość estymacji Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 62

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Dziękuję – koniec materiału prezentowanego podczas wykładu Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 63

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Dodatek A Przypomnienie z rachunku różniczkowego oraz podanie wybranych faktów z teorii optymalizacji Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 64

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Mamy funkcjonał: Rozwinięcie funkcjonału F w szereg Taylor’a w otoczeniu punktu x* ma postać: Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 65

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów W najprostszym przypadku: Rozwinięcie funkcjonału F w szereg Taylor’a w otoczeniu punktu x* ma postać: Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 66

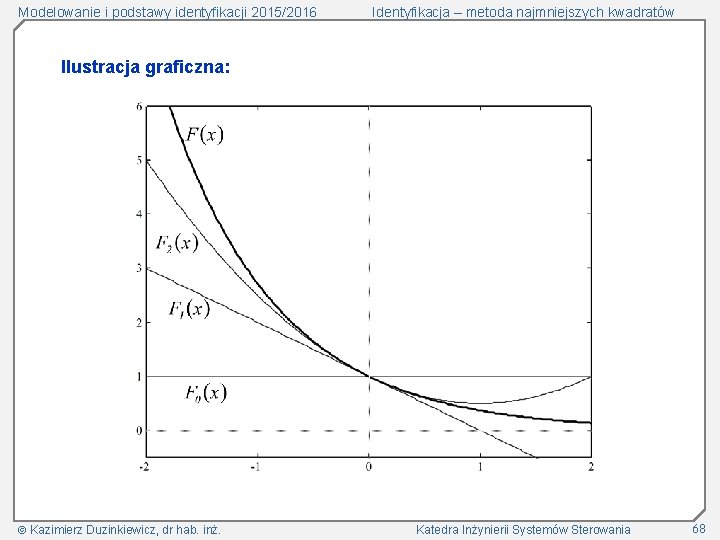
Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Przykład 1 - skalarny: Rozwinięcie w szereg Taylor’a w otoczeniu Aproksymacja Kazimierz Duzinkiewicz, dr hab. inż. : skończoną liczbą wyrazów szeregu Taylor’a: Katedra Inżynierii Systemów Sterowania 67

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Ilustracja graficzna: Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 68

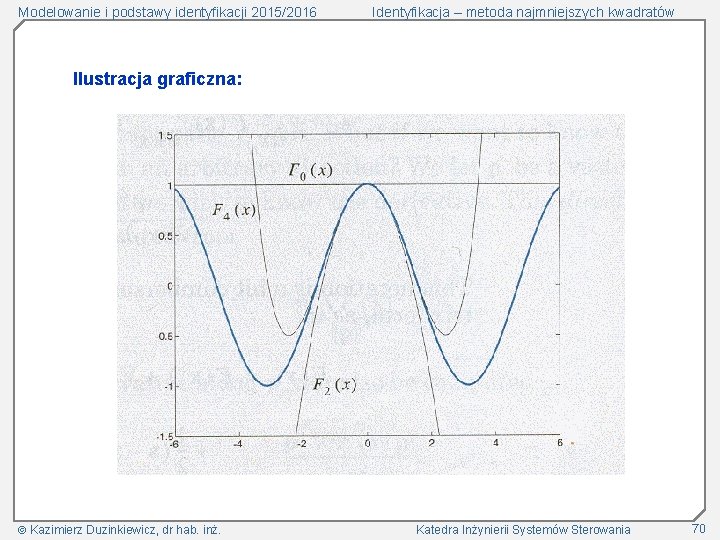
Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Przykład 2 – skalarny: Rozwinięcie w szereg Taylor’a w otoczeniu Aproksymacja Kazimierz Duzinkiewicz, dr hab. inż. skończoną liczbą wyrazów szeregu Taylor’a: Katedra Inżynierii Systemów Sterowania 69

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Ilustracja graficzna: Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 70

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Jeżeli przyjąć oznaczenia: jakobian - gradient funkcjonału Warto pamiętać, że: Kierunek gradientu w punkcie x pokrywa się z kierunkiem normalnej do powierzchni stałej wartości funkcjonału przechodzącej przez punkt x. Zwrot gradientu w punkcie x odpowiada zwrotowi najszybszego wzrostu wartości funkcjonału w otoczeniu punktu x. hessian funkcjonału Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 71

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Postać macierzowa szeregu Taylor’a: Pierwsza pochodna (nachylenie) funkcjonału wzdłuż osi : - i-ty element gradientu wzdłuż osi Druga pochodna (krzywizna) funkcjonału : - (i, i)-ty element hessianu Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 72

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Pierwsza pochodna (nachylenie) funkcjonału Druga pochodna (krzywizna) funkcjonału Kazimierz Duzinkiewicz, dr hab. inż. : wzdłuż wektora Katedra Inżynierii Systemów Sterowania : 73

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Przykład 3: Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 74

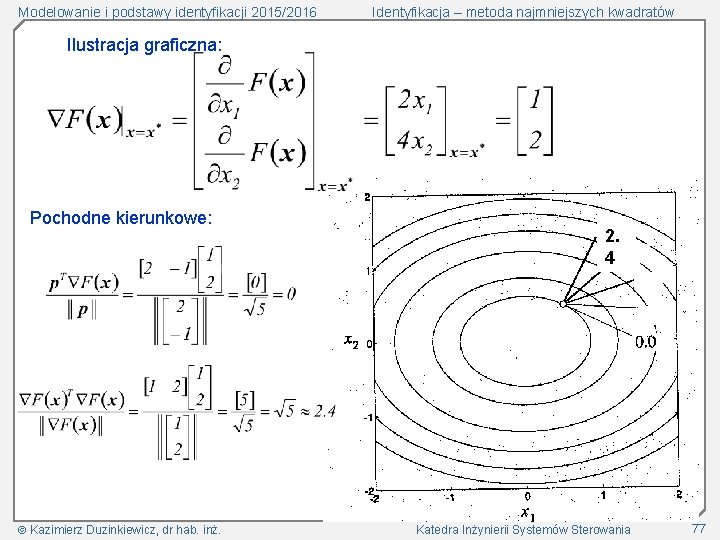
Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Ilustracja graficzna: Pochodne kierunkowe: 1. 4 1. 3 1. 0 0. 5 0. 0 Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 75

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Przykład 4: Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 76

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Ilustracja graficzna: Pochodne kierunkowe: Kazimierz Duzinkiewicz, dr hab. inż. 2. 4 Katedra Inżynierii Systemów Sterowania 77

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Optymalność Minimum globalne: Punkt , jest unikatowym minimum globalnym funkcjonału dla wszystkich jeżeli zachodzi Minimum silne (lokalne): Punkt jest minimum silnym (lokalnym) funkcjonału , taki, że zachodzi jeżeli istnieje skalar dla wszystkich , takich, że Minimum słabe (lokalne): , jeżeli jest minimum słabym (lokalnym) funkcjonału Punkt , taki, że zachodzi nie jest minimum silnym , a istnieje skalar dla wszystkich Kazimierz Duzinkiewicz, dr hab. inż. takich, że Katedra Inżynierii Systemów Sterowania 78

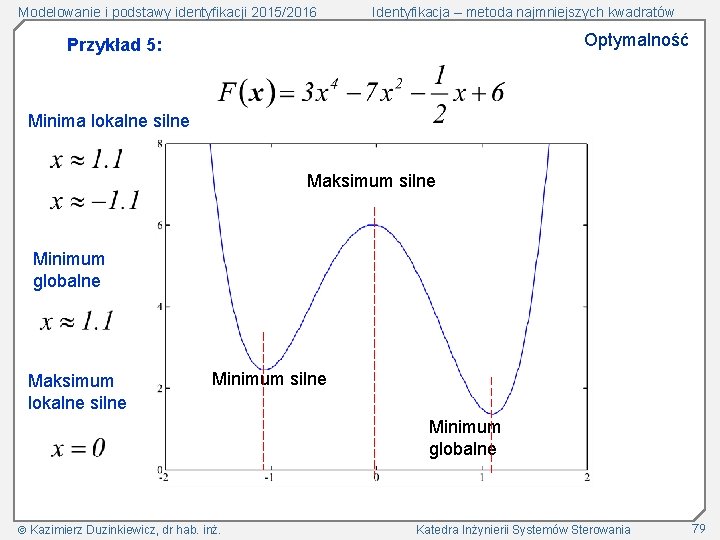
Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Optymalność Przykład 5: Minima lokalne silne Maksimum silne Minimum globalne Maksimum lokalne silne Minimum globalne Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 79

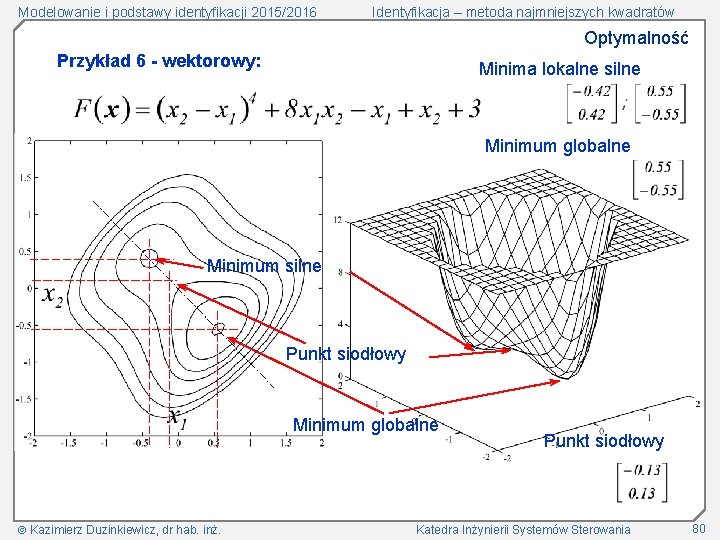
Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Optymalność Przykład 6 - wektorowy: Minima lokalne silne Minimum globalne Minimum silne Punkt siodłowy Minimum globalne Kazimierz Duzinkiewicz, dr hab. inż. Punkt siodłowy Katedra Inżynierii Systemów Sterowania 80

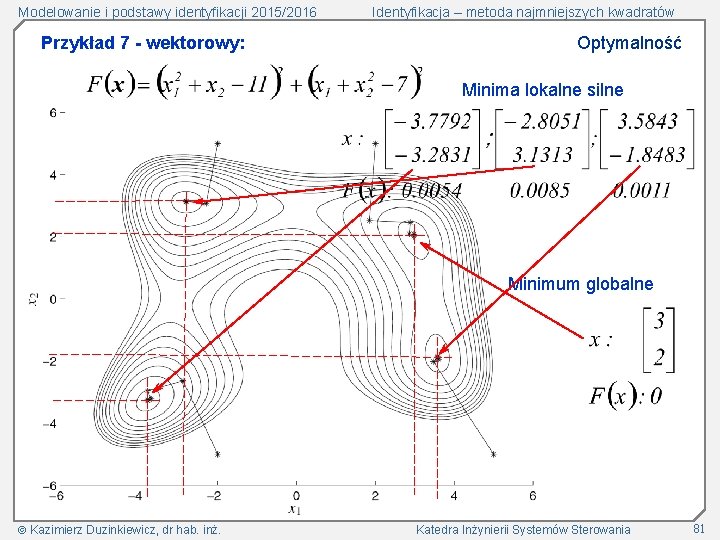
Modelowanie i podstawy identyfikacji 2015/2016 Przykład 7 - wektorowy: Identyfikacja – metoda najmniejszych kwadratów Optymalność Minima lokalne silne Minimum globalne Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 81

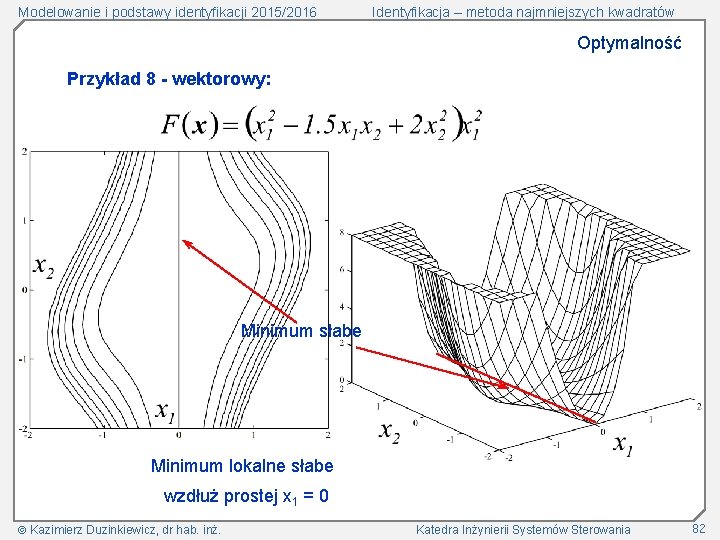
Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Optymalność Przykład 8 - wektorowy: Minimum słabe Minimum lokalne słabe wzdłuż prostej x 1 = 0 Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 82

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Optymalność Warunki konieczne minimum Rozwinięcie Kazimierz Duzinkiewicz, dr hab. inż. w szereg Taylor’a w otoczeniu , takiego, że Katedra Inżynierii Systemów Sterowania 83

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Optymalność Warunki konieczne minimum Warunek pierwszego rzędu: Jeżeli x* jest punktem lokalnego minimum i F jest różniczkowalne w sposób ciągły w otwartym otoczeniu x*, wówczas Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 84

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Optymalność Warunek drugiego rzędu: Jeżeli x* jest punktem lokalnego minimum i 2 F jest ciągłe w pewnym otwartym otoczeniu x*, wówczas dla dowolnych Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 85

Modelowanie i podstawy identyfikacji 2015/2016 Przykład 9: Identyfikacja – metoda najmniejszych kwadratów Optymalność Warunek punkt stacjonarnego Punkt stacjonarny - jedyny Sprawdzenie warunków rzędu drugiego Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 86

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Optymalność Punkt x*=0 spełnia warunki konieczne pierwszego i drugiego rzędu dla minimum Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 87

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Optymalność Warunki określoności macierzy hessianu można badać przez sprawdzenie wartości własnych tej macierzy Macierz hessianu jest dodatnio określona, jeżeli wszystkie jej wartości własne są dodatnie Macierz hessianu jest dodatnio półokreślona, jeżeli wszystkie jej wartości własne są nieujemne Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 88

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Optymalność Przykład 10: Warunek punkt stacjonarnego Punkt stacjonarny - jedyny Sprawdzenie warunków rzędu drugiego Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 89

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Optymalność Pozyskanie informacji o określoności macierzy hessianu Nie można stwierdzić czy macierz hessianu jest dodatnio określona lub dodatnio półokreślona Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 90

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Optymalność Wartości własne hessianu Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 91

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Optymalność Minimum silne w Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 92

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Optymalność Warunki wystarczające minimum Warunek drugiego rzędu: Jeżeli dla pewnego x*, 2 F jest ciągłe w pewnym otwartym jego otoczeniu i F(x*) = 0 i 2 F(x*) jest dodatnio określona, wówczas x* jest silnym minimum lokalnym Warunek globalnego minimum Jeżeli F jest funkcją wypukłą (a nawet tylko pseudowypukłą), wówczas każde minimum lokalne jest minimum globalnym. Jeżeli dodatkowo F jest różniczkowalna, wówczas każdy punkt stacjonarny jest globalnym minimum Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 93

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Forma kwadratowa gdzie: A - macierz symetryczna; (jeżeli macierz A nie jest symetryczna, to może być zastąpiona przez macierz symetryczną dającą te same wartości F(x) - to samo przekształcenie F(x)) Pożyteczne właściwości gradientu: gdzie jest stałym wektorem dla symetrycznych Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 94

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Forma kwadratowa Gradient formy kwadratowej Hessian formy kwadratowej Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 95

Modelowanie i podstawy identyfikacji 2015/2016 Słuszne są twierdzenia: Identyfikacja – metoda najmniejszych kwadratów Forma kwadratowa Jeżeli wartości własne hessianu są wszystkie dodatnie – forma posiada pojedyncze silne minimum Jeżeli wartości własne hessianu są wszystkie ujemne – forma posiada pojedyncze silne maksimum Jeżeli pewne wartości własne hessianu są dodatnie, a inne ujemne – forma posiada pojedynczy punkt siodłowy Jeżeli wszystkie wartości własne hessianu są nieujemne, ale niektóre są równe zeru – forma albo posiada słabe minimum albo nie ma punktu stacjonarnego Jeżeli wszystkie wartości własne hessianu są niedodatnie, ale niektóre są równe zeru – forma albo posiada słabe maksimum albo nie ma punktu stacjonarnego Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 96

Modelowanie i podstawy identyfikacji 2015/2016 Identyfikacja – metoda najmniejszych kwadratów Koniec zestawu slajdów Kazimierz Duzinkiewicz, dr hab. inż. Katedra Inżynierii Systemów Sterowania 97