QCD from the vacuum to high temperature an

QCD – from the vacuum to high temperature an analytical approach

Analytical description of phase transition Needs model that can account simultaneously for the correct degrees of freedom below and above the transition temperature. n Partial aspects can be described by more limited models, e. g. chiral properties at small momenta. n

Higgs picture of QCD “spontaneous breaking of color “ in the QCD – vacuum octet condensate for Nf = 3 ( u, d, s ) C. Wetterich, Phys. Rev. D 64, 036003(2001), hep-ph/0008150

Many pictures … … of the QCD vacuum have been proposed monopoles, instantons, vortices, spaghetti vacuum … in principle, no contradiction – there may be more than one valid picture most proposals say essentially nothing about the low mass excitations in real QCD, i. e mesons and baryons different for Higgs picture !

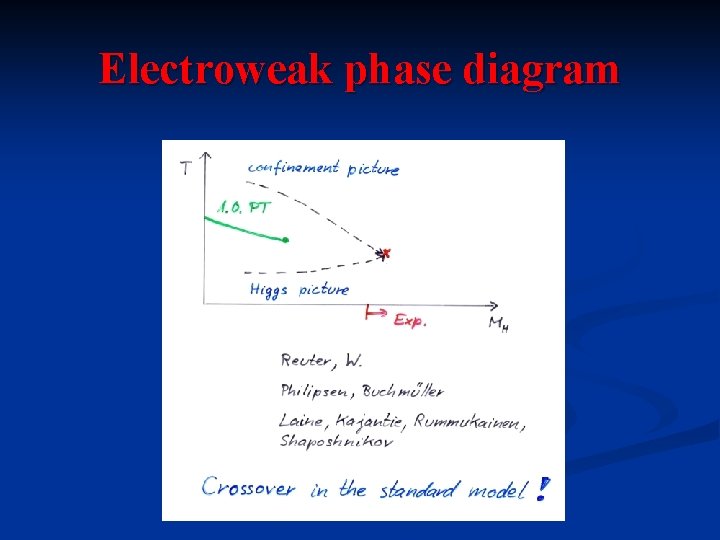
Electroweak phase diagram

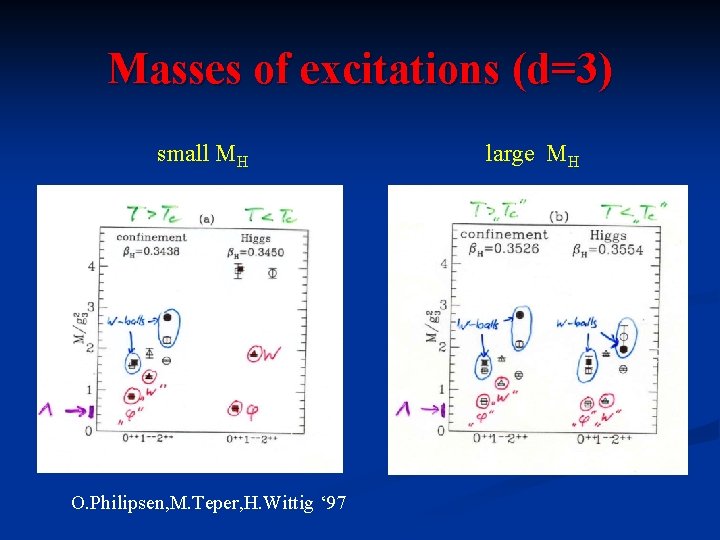
Masses of excitations (d=3) small MH O. Philipsen, M. Teper, H. Wittig ‘ 97 large MH

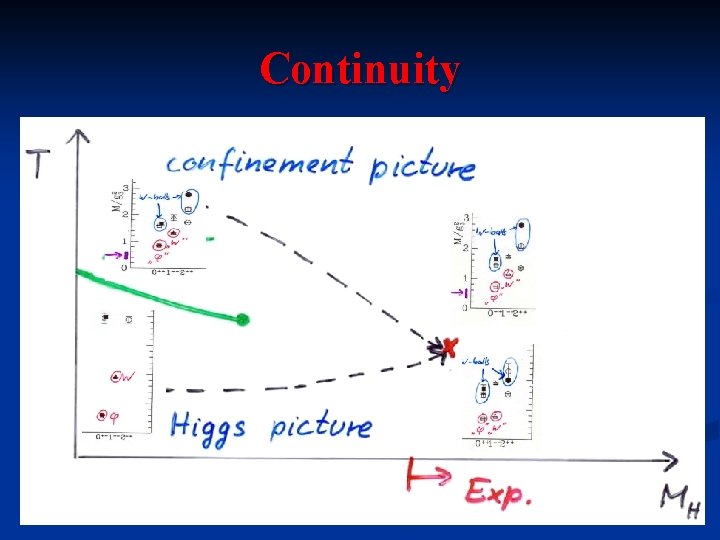
Continuity

Higgs phase and confinement can be equivalent – then simply two different descriptions (pictures) of the same physical situation Is this realized for QCD ? Necessary condition : spectrum of excitations with the same quantum numbers in both pictures - known for QCD : mesons + baryons -

Spontaneous breaking of color Condensate of colored scalar field n Equivalence of Higgs and confinement description in real (Nf=3) QCD vacuum n Gauge symmetries not spontaneously broken in formal sense ( only for fixed gauge ) Similar situation as in electroweak theory n No “fundamental” scalars n Symmetry breaking by quark-antiquarkcondensate n

Analogy between weak and strong interactions

Quark –antiquark condensate

Octet condensate < octet > ≠ 0 : n “Spontaneous breaking of color” n Higgs mechanism n Massive Gluons – all masses equal n Eight octets have vev n Infrared regulator for QCD

Electric charge < octet > ≠ 0 : n Spontaneous breaking of electromagnetic U(1) symmetry (some components of octet carry electric charge – similar to Higgs mechanism for hypercharge in electroweak theory) n Combined U(1) symmetry survives (cf. Q=I 3 + ½ Y in e. w. standard model)

Electric charge of “quarks”

Flavor symmetry for equal quark masses : octet preserves global SU(3)-symmetry “diagonal in color and flavor” “color-flavor-locking” (cf. Alford, Rajagopal, Wilczek ; Schaefer, Wilczek) All particles fall into representations of the “eightfold way” quarks : 8 + 1 , gluons : 8

Related earlier ideas: K. Bardakci, M. Halpern; I. Bars ’ 72 R. Mohapatra, J. Pati, A. Salam ’ 76 A. De Rujula, R. Giles, R. Jaffe ‘ 78 T. Banks, E. Rabinovici ’ 79 E. Fradkin, S. Shenker ’ 79 G. t’Hooft ’ 80 S. Dimopoulos, S. Raby, L. Susskind ’ 80 T. Matsumoto ’ 80 B. Iijima, R. Jaffe ’ 81 M. Yasue ’ 90 M. Alford, K. Rajagopal, F. Wilczek ’ 99 T. Schaefer, F. Wilczek ‘ 99

Color-flavor-locking Chiral symmetry breaking : SU(3)L x SU(3)R Color symmetry breaking : SU(3)c x SU(3)V Quarks : Gluons : _ 3 x 3 8 x 1 color~ flavor SU(3)V SU(3)diagonal 8 + 1 8 Similar to high density QCD : Alford, Rajagopal, Wilczek ; Schaefer, Wilczek

Octet condensate Color symmetry breaking : SU(3)c x SU(3)V <χ> : 8 color~ x 8 flavor SU(3)diagonal 1+…

Quarks and gluons carry the observed quantum numbers of isospin and strangeness of the baryon and vector meson octets ! They are integer charged!

Duality

Quantum numbers match ! Of course , there are many more excitations (resonances ). Strong interactions bound states

Higgs description seems possible is it simple ?

Effective low energy model for QCD Composite scalars ( quark-antiquark- bound states ) n Gauge invariance n Approximation: renormalizable interactions for QCD with scalars n Comparison with observation? n

Low energy effective action γ=φ+χ

Simplicity This simple effective action will yield the masses and couplings of the baryons, pseudoscalars and vector mesons, ( including electromagnetic couplings by covariant derivatives ) ! ( five parameters , to be later determined by QCD )

New scalar interactions Gauge covariant kinetic term n Effective potential n Yukawa coupling to quarks n

Calculability n Remember : no fundamental scalars n Effective couplings should be calculable from QCD – i. e. gauge coupling or confinement scale

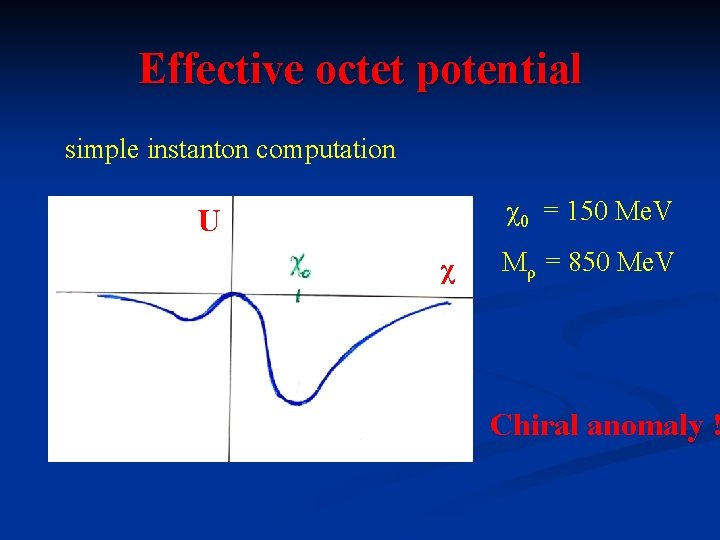
Effective octet potential simple instanton computation χ0 = 150 Me. V U χ Mρ = 850 Me. V Chiral anomaly !

Masses of physical particles determine three phenomenological parameters

Phenomenological parameters n 5 undetermined parameters n predictions

Chiral perturbation theory + all predictions of chiral perturbation theory + determination of parameters

First conclusions Spontaneous color symmetry breaking plausible in QCD - computation of effective vector mass needed n Simple effective action can account for mass spectrum of light baryons and mesons as well as their couplings n Gluon - Meson duality n Quark - Baryon duality n

Nonlinear formulation Use of nonlinear fields makes physical content of the effective action more transparent. n Similar to nonlinear fields for pions n Selection of nonlinear fields follows symmetry content of theory n

Gauge invariance n n Higgs picture is a guide for ideas and a way to compute gauge invariant quantities at the end Intuition can be misleading for certain questions Effective action, U( φ, χ ) : gauge invariant Nonlinear fields : gauge singlets Only assumptions : A) minimum of U preserves global SU(3) B) minimum not for χ=0 ( for appropriate gauge and normalization of χ )

Nonlinear fields : π, K, η, η’

Nonlinear fields : diquark cloud The product W • v transforms as an antidiquark n B=-2/3 n v : color triplet n

How quarks get dressed as baryons

Gauge bosons/vector mesons

All fields except v are gauge singlets

Effective action in terms of physical fields

Effective action in terms of physical fields linear fields nonlinear fields Insert expressions for ψ, A, χ, φ

Nonlinear local symmetry Has been investigated since long ago in the context of chiral theories, describes ρ - bosons Here : n Not postulated n Consequence of local color symmetry + “SSB” n Gauge bosons = gluons = ρ - bosons Predictions correct !

Reparameterization symmetry Decomposition into nonlinear fields is not unique. E. g. N can be multiplied by unitary transformation from left, and W from right. local U(3) reparameterization symmetry infinitesimal transformation

Baryons

Pion nucleon coupling Two more successful predictions F, D are not fixed by chiral symmetry !

Pseudoscalar mesons Kinetic term for pseudoscalar mesons as in chiral perturbation theory meson decay constant

Vector mesons

Electromagnetic interactions include by covariant derivative

ρ - couplings

ρ - couplings experiment : prediction : Vector dominance is realized by Higgs picture of QCD

Connection to gauge invariant formulation for linear fields n Vector channel : use singlet fields (in addition to A, φ, χ ; fermions omitted here ) n Solve field equations for colored bosons n Γ[φ, ρ] contains directly the information for gauge invariant correlation functions

A - ρ mixing Insert solution A[ρ] Mixing produces mass shift

Conclusion (2) Phenomenology works well for simple effective action

Chiral phase transition at high temperature High temperature phase transition in QCD : Melting of octet condensate Lattice simulations : Deconfinement temperature = critical temperature for restoration of chiral symmetry Why ?

Simple explanation :

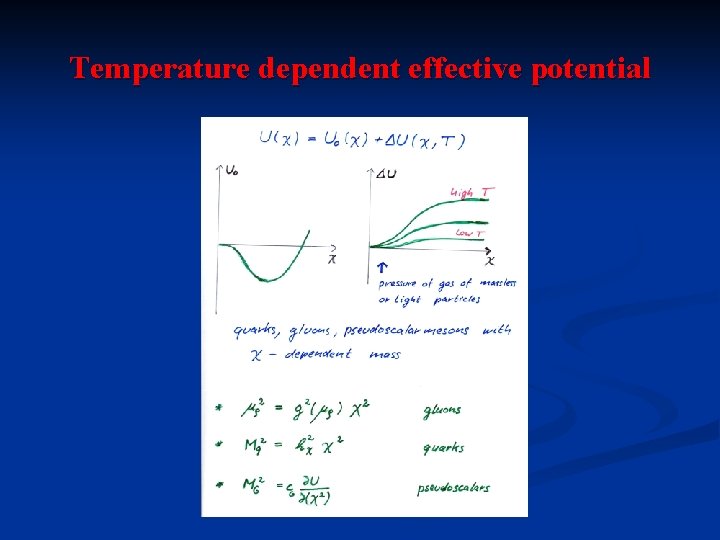
Temperature dependent effective potential

Temperature corrections to effective octet potential

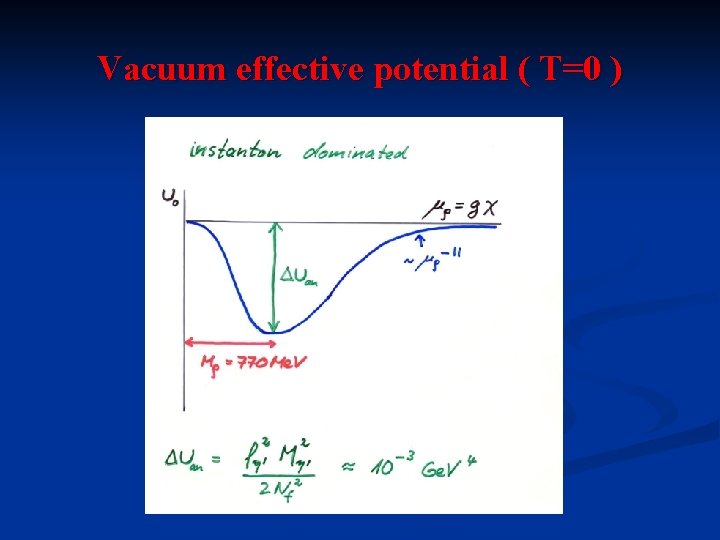
Vacuum effective potential ( T=0 )

Interesting relation between Tc and η’ properties

A simple mean field calculation

Conclusions ( 3 ) Coherent picture for phase diagram of QCD is emerging n Gluon meson duality allows for analytical calculations n Quark-baryon duality : Direct contact to quantities of nuclear physics n

Questions ?

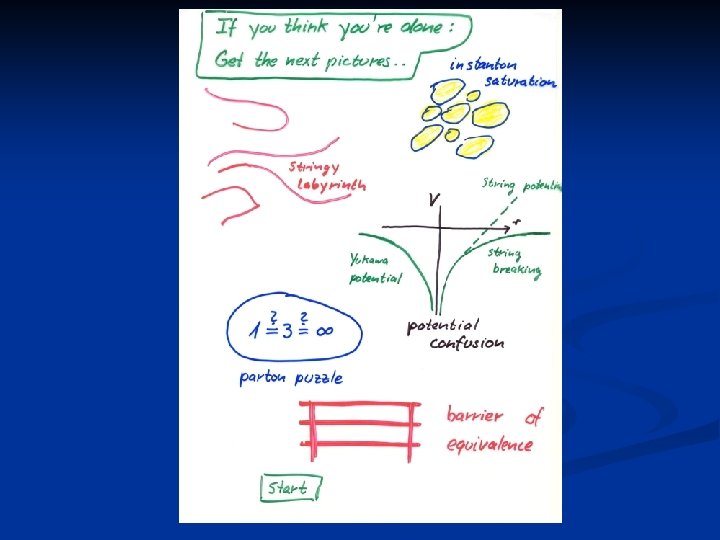
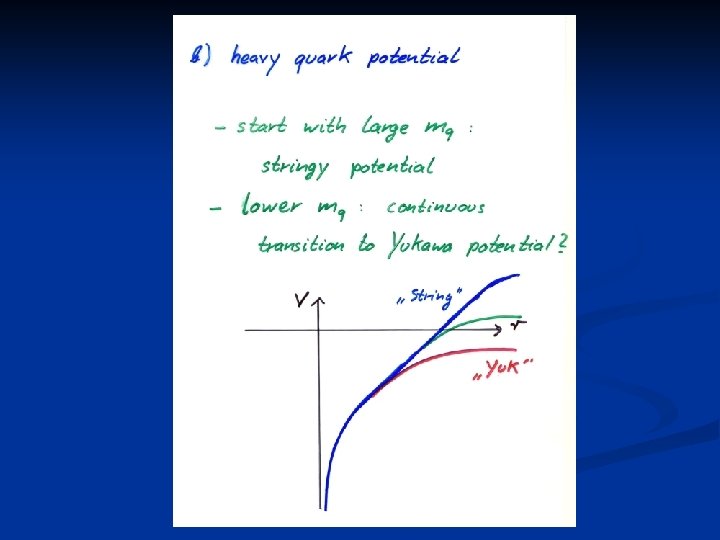
Lattice tests a) Continuity - - Add “fundamental” scalar octets and start in perturbative Higgs phase ( large negative mass term ). Remove scalars continuously by increasing the mass term to large positive values Phase transition or analytical crossover ?

Challenges Instanton computation of U(φ, χ) (improve by nonperturbative flow equation ) n Check continuity between Higgs and confinement description by lattice simulation n Explicit construction of a local diquark operator with transformation Wv (nonvanishing expectation value ) n

end