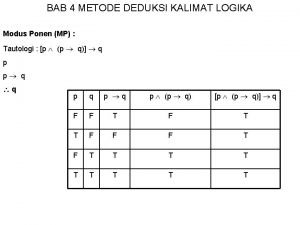
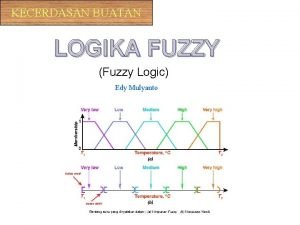
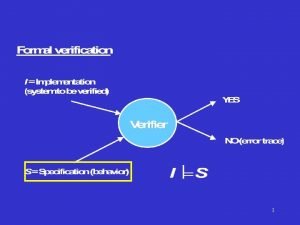
Logika U ovoj lekciji Uvod u logiku Wumpus

Logika

U ovoj lekciji • Uvod u logiku • Wumpus svijet • Primjeri Udžbenik • Poglavlja 7, 8, 9 i 10

Logika kao alat Kako možemo formalizovati naše znanje o okruženju tako da: • Možemo rezonovati. • Možemo izvoditi zaključke. • Možemo dokazivati. • Možemo planirati akcije. • Možemo razumijeti i objašnjavati.

Baze znanja Inference Engine Domain-independent knowledge Knowledge Base Domain-specific content • Knowledge base = skup rečenica formalnog jezika. • Deklarativni pristup izgradnji agenta ili drugog sistema: – Reći mu ono što mora da zna – Alternativa je učenje (u kasnijim lekcijama). • Odgovori moraju da slijede iz KB. • Agenti ili sistemi mogu se posmatrati na nivou znanja, tj. šta znaju, bez obzira kako su implementirani. • Ili na implementacionom nivou, tj. strukture podataka u KB i algoritmi koji manipulišu njima.

Predstavljamo vam THE WUMPUS

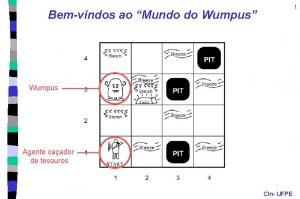
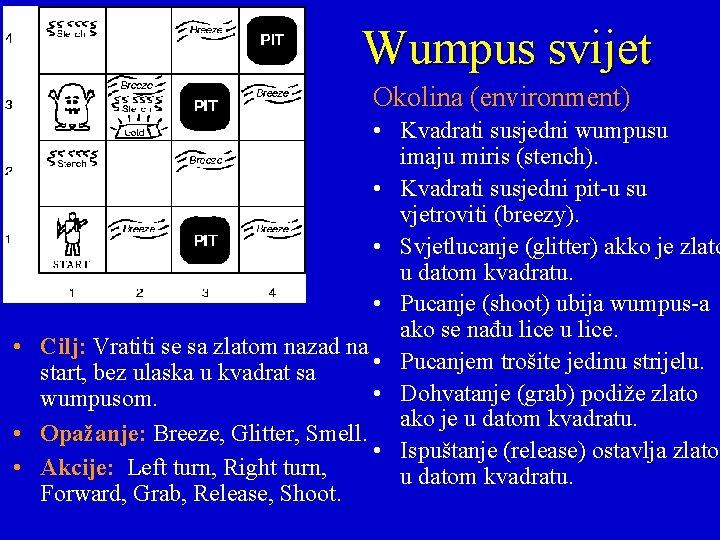
Wumpus svijet Okolina (environment) • Kvadrati susjedni wumpusu imaju miris (stench). • Kvadrati susjedni pit-u su vjetroviti (breezy). • Svjetlucanje (glitter) akko je zlato u datom kvadratu. • Pucanje (shoot) ubija wumpus-a ako se nađu lice. • Cilj: Vratiti se sa zlatom nazad na • Pucanjem trošite jedinu strijelu. start, bez ulaska u kvadrat sa • Dohvatanje (grab) podiže zlato wumpusom. ako je u datom kvadratu. • Opažanje: Breeze, Glitter, Smell. • Ispuštanje (release) ostavlja zlato • Akcije: Left turn, Right turn, u datom kvadratu. Forward, Grab, Release, Shoot.

Wumpus svijet - osobine • Da li je svijet deterministički? Da --- izlazi tačno zadati (outcomes exactly specified). • Da li je svijet potpuno dostupan (fully accessible)? Ne --- samo lokalna percepcija kvadrata u kome se nalazimo. • Da li je svijet statičan? Da --- Wumpus i Pits se ne pomjeraju. • Da li je svijet diskretan? Da.

Istraživanje Wumpus svijeta A

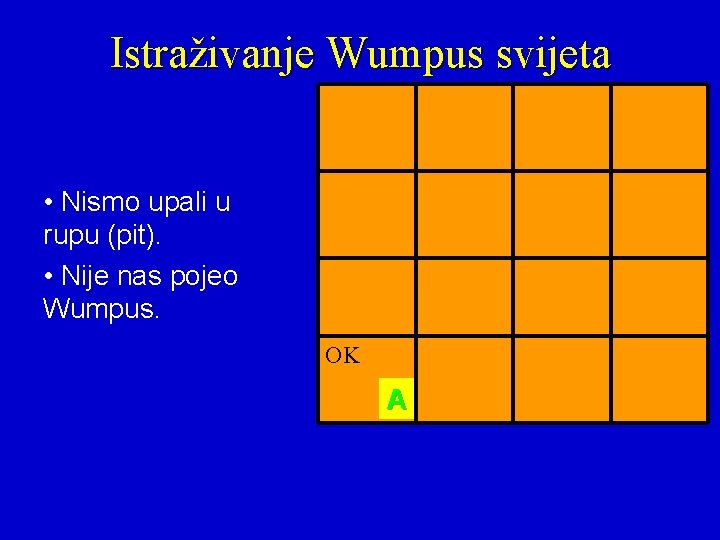
Istraživanje Wumpus svijeta • Nismo upali u rupu (pit). • Nije nas pojeo Wumpus. OK A

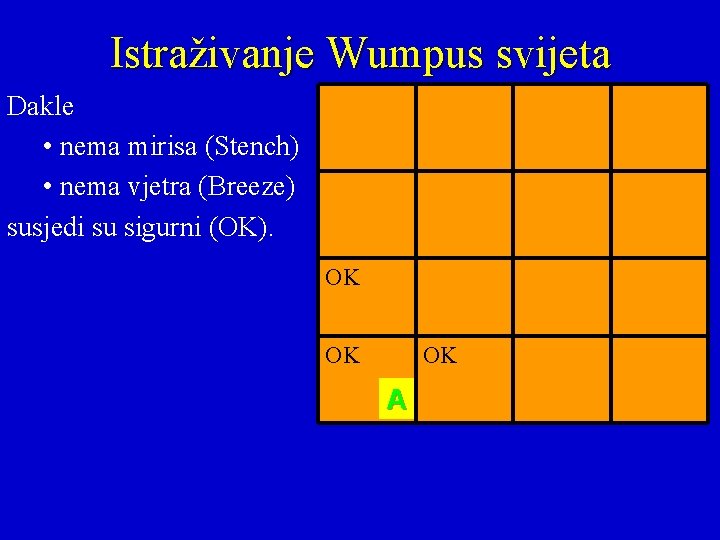
Istraživanje Wumpus svijeta Dakle • nema mirisa (Stench) • nema vjetra (Breeze) susjedi su sigurni (OK). OK OK OK A

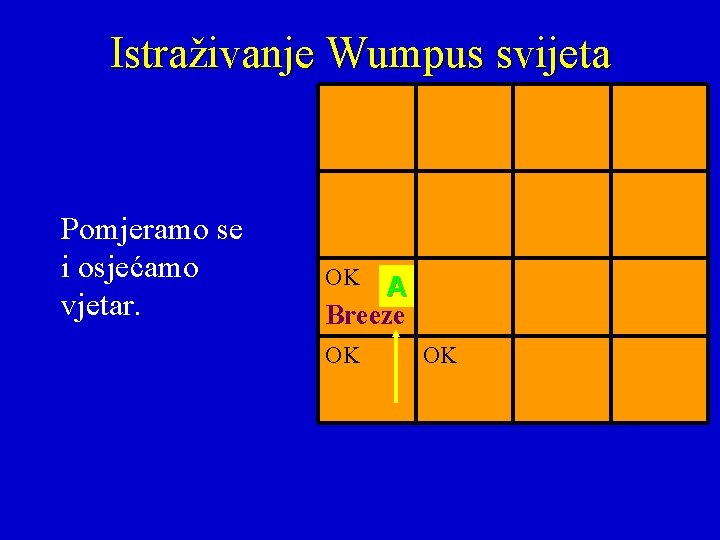
Istraživanje Wumpus svijeta Pomjeramo se i osjećamo vjetar. OK A Breeze OK OK

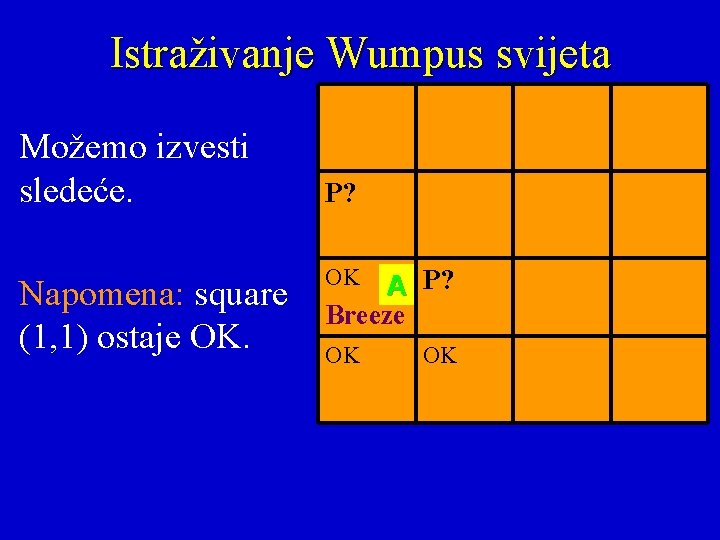
Istraživanje Wumpus svijeta Možemo izvesti sledeće. Napomena: square (1, 1) ostaje OK. P? OK A P? Breeze OK OK

Istraživanje Wumpus svijeta Krećemo se i osjećamo miris! P? OK Šta možemo zaključiti? P? Breeze OK OK A Stench

Istraživanje Wumpus svijeta Ali, može li u kvadratu (2, 2) zaista biti ili Wumpus ili pit? P? OK P? Breeze W? OK NE ! OK A W? Stench I šta je sa drugim P? i W? kvadratima

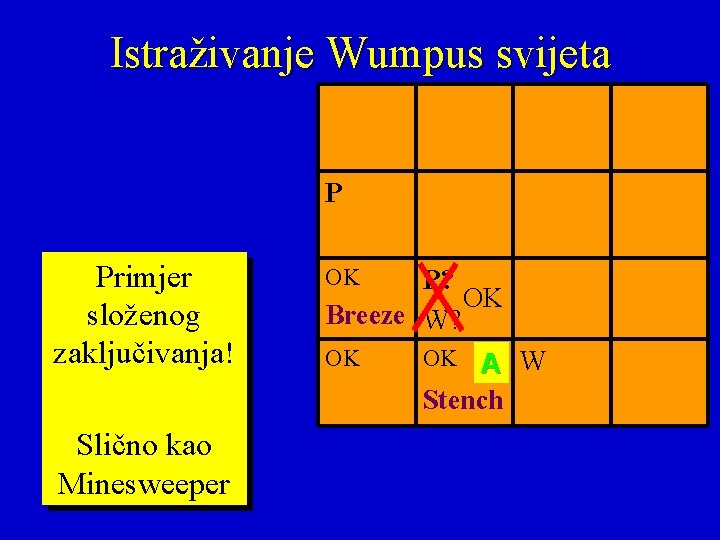
Istraživanje Wumpus svijeta P Primjer složenog zaključivanja! OK P? OK Breeze W? OK OK A W Stench Slično kao Minesweeper

Istraživanje Wumpus svijeta P OK OK OK A OK Breeze OK OK Stench W

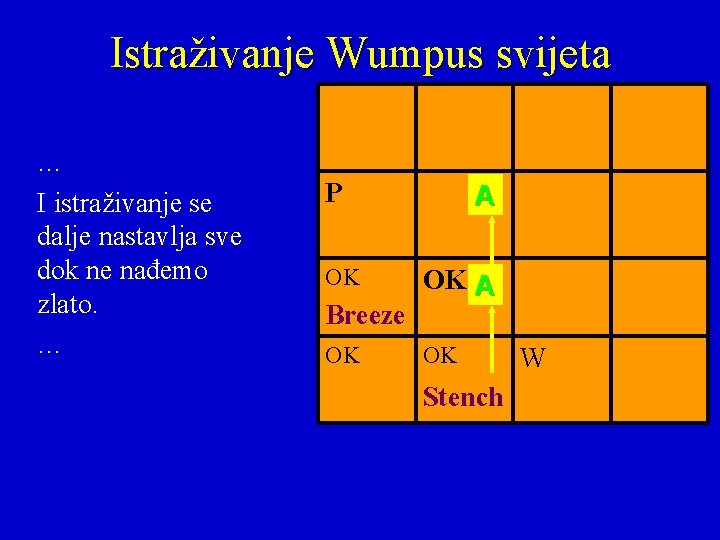
Istraživanje Wumpus svijeta … I istraživanje se dalje nastavlja sve dok ne nađemo zlato. … P OK Breeze OK A OK Stench W

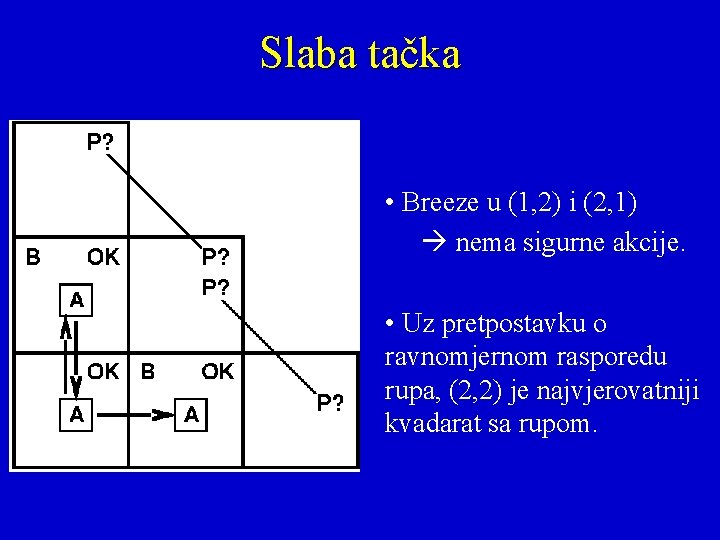
Slaba tačka • Breeze u (1, 2) i (2, 1) nema sigurne akcije. • Uz pretpostavku o ravnomjernom rasporedu rupa, (2, 2) je najvjerovatniji kvadarat sa rupom.

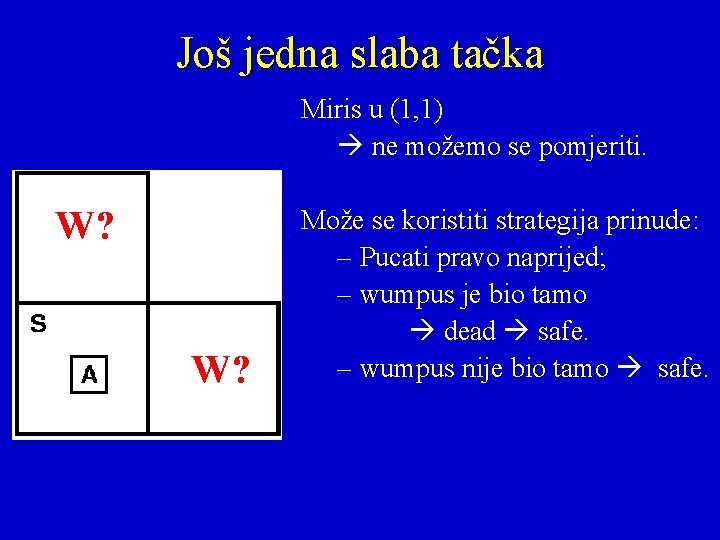
Još jedna slaba tačka Miris u (1, 1) ne možemo se pomjeriti. W? W? Može se koristiti strategija prinude: – Pucati pravo naprijed; – wumpus je bio tamo dead safe. – wumpus nije bio tamo safe.

Logika uopšteno • Logike su formalni jezici za reprezentaciju informacija tako da se mogu izvlačiti zaključci. • Sintaksa definiše rečenice jezika • Semantika definiše ``značenje'' rečenica; tj. definiše istinitost rečenice u svijetu. • Na primjer, u jeziku aritmetike – x + 2 y je rečenica. – x + y > nije rečenica. – x + 2 y je true ako je broj x+2 ne manji od broja y. – x + 2 y je true u svijetu u kojem je x = 7, y =1. – x + 2 y je false u svijetu u kojem je x = 0, y= 6.

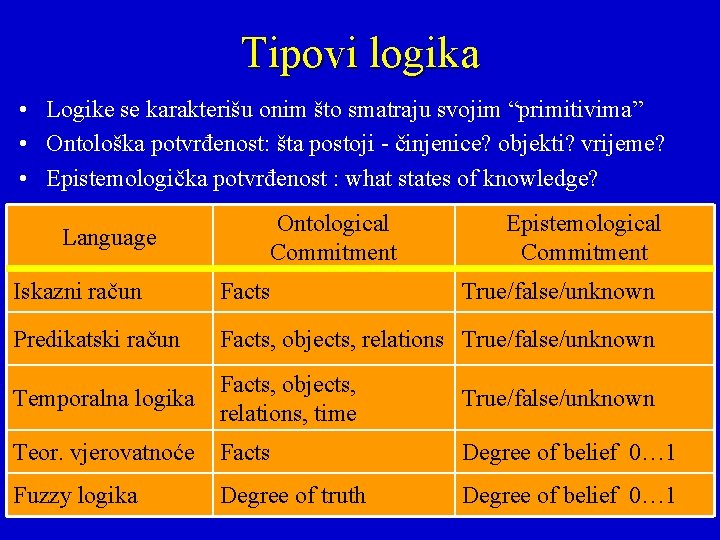
Tipovi logika • Logike se karakterišu onim što smatraju svojim “primitivima” • Ontološka potvrđenost: šta postoji - činjenice? objekti? vrijeme? • Epistemologička potvrđenost : what states of knowledge? Language Ontological Commitment Epistemological Commitment Iskazni račun Facts True/false/unknown Predikatski račun Facts, objects, relations True/false/unknown Temporalna logika Facts, objects, relations, time True/false/unknown Teor. vjerovatnoće Facts Degree of belief 0… 1 Fuzzy logika Degree of truth Degree of belief 0… 1

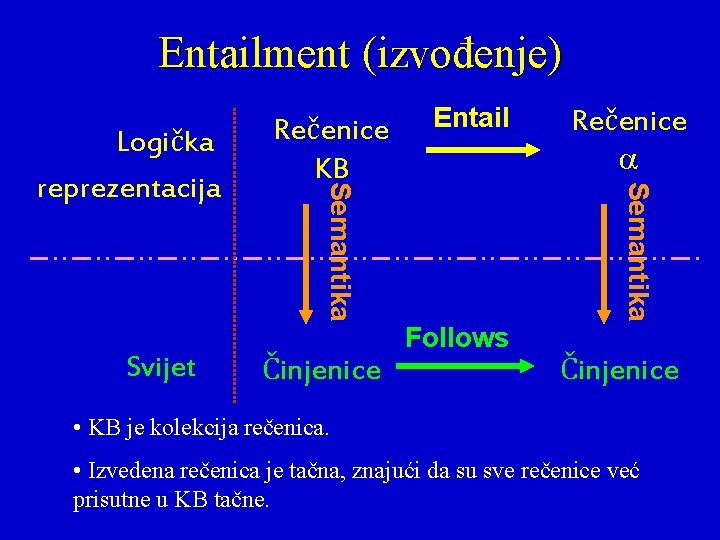
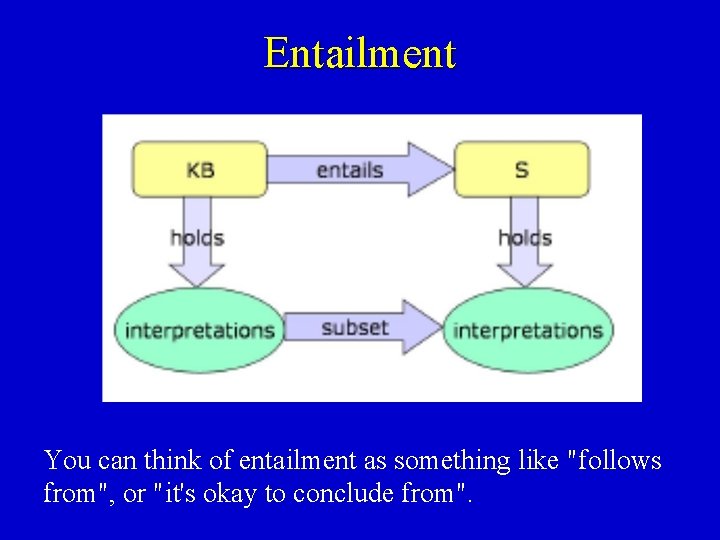
Entailment (izvođenje) Činjenice Entail Follows Rečenice Semantika Svijet Semantika Logička reprezentacija Rečenice KB Činjenice • KB je kolekcija rečenica. • Izvedena rečenica je tačna, znajući da su sve rečenice već prisutne u KB tačne.

Entailment You can think of entailment as something like "follows from", or "it's okay to conclude from".

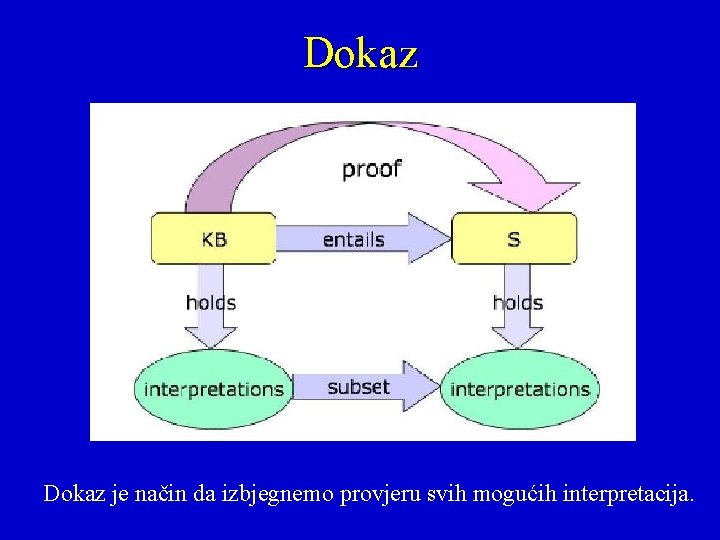
Dokaz je način da izbjegnemo provjeru svih mogućih interpretacija.

Zaključivanje (inference) • KB je kolekcija rečenica. Iz baze znanja KB izvodimo (entails) rečenicu ako je tačna kad je i KB tačna (tj. sve rečenice iz KB su tačne). • Procedura zaključivanja (dokazivanja) i može uraditi dvije stvari: – Za datu KB, generisati novu rečenicu za koju se tvrdi da se može zaključiti iz KB (to be entailed by KB). – Za datu KB i , javiti da li je izvedena (entailed) iz KB. • Procedura zaključivanja (dokazivanja) je potpuna (sound) ako daje samo izvedene (entailed) rečenice tj. svako S koje možemo dokazati procedurom zaključivanja iz KB je “entailed” iz KB • Procedura zaključivanja je kompletna (complete) ako se svaka izvedena (entailed) rečenica može generisati procedurom zaključivanja tj. svako S koje je “entailed” iz KB može se izvesti procedurom dokazivanja iz KB

Sintaksa iskaznog računa: BNF Sentence Atomic. Sentence | Complex. Sentence Atomic. Sentence TRUE | FALSE | P | Q | R Complex. Sentnece ( Sentence ) | Sentence Connective Sentence | Sentence Connective | | |

Iskazni račun: sintaksa • Iskazni račun je najprostija logika. • Logičke konstante TRUE i FALSE su rečenice. • Iskazni simboli P 1, P 2, itd. su rečenice. • Simboli P 1 i negirani simboli P 1 su literali. • • • Ako je S rečenica, S je rečenica (NOT). Ako su S 1 i S 2 rečenice, S 1 S 2 je rečenica (Kojunkcija - AND). Ako su S 1 i S 2 rečenice, S 1 S 2 je rečenica (Disjunkcija - OR). Ako su S 1 i S 2 rečenice, S 1 S 2 je rečenica (Implikacija). Ako su S 1 i S 2 rečenice, S 1 S 2 je rečenica (Ekvivalencija).

Prioritet Od najvišeg ka najnižem: zagrade ( rečenica ) NOT AND OR Implikacija Ekvivalencija

Iskazni račun: semantika Implikacija: P Q “Ako je P True, tada je Q True; inače, ne možemo da tvrdimo ništa o istinitosti Q. ” Po ovoj definiciji sledeće tvrđenje je tačno (Pigs fly) (Everyone_gets_an_A) Kako je “Pigs_Fly” False, tvrđenje je tačno bez obzira na istinitost rečenice “Everyone_gets_an_A”. [Ispravno zaključivanje u našoj interpretaciji gdje svinje zaista ne lete. ]

Iskazni račun: semantika Većina rečenica je ponekad tačna. P Q Neke rečenice su uvijek tačne. Model za P Q P P Neke rečenice nikad nisu tačne (nezadovoljive). P P

Iskazni račun: semantika Implikacija: P Q “Ako je P True, tada je i Q is True; u suprotnom, ništa ne tvrdimo o istinitosti Q. ” (Ili: P Q je ekvivalentno sa Q) Po ovoj definiciji, sledeće tvrđenje je tačno (true) Pigs_fly Everyone_gets_an_A Kako je “Pigs_Fly” False, tvrđenje je tačno bez obzira na istinitost “Everyone_gets_an_A”. [Da li je? Correct inference only when “Pigs_Fly” is known to be false. ]

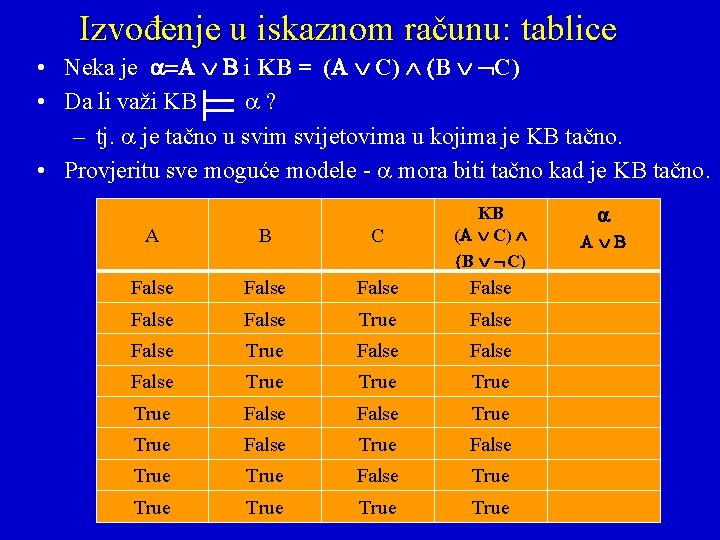
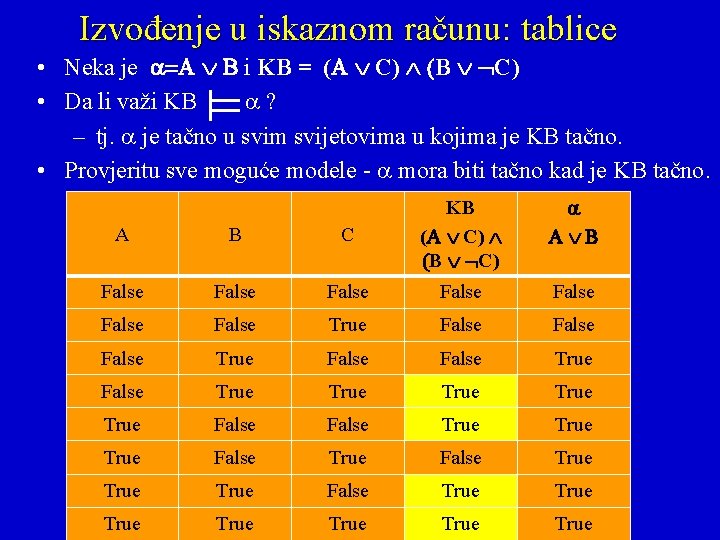
Izvođenje u iskaznom računu: tablice • Neka je i KB = ( C) B C) • Da li važi KB ? – tj. je tačno u svim svijetovima u kojima je KB tačno. • Provjeritu sve moguće modele - mora biti tačno kad je KB tačno. A B C False False True False True True True KB ( C) B C)

Izvođenje u iskaznom računu: tablice • Neka je i KB = ( C) B C) • Da li važi KB ? – tj. je tačno u svim svijetovima u kojima je KB tačno. • Provjeritu sve moguće modele - mora biti tačno kad je KB tačno. A B C KB ( C) B C) False False False True True False True False True True

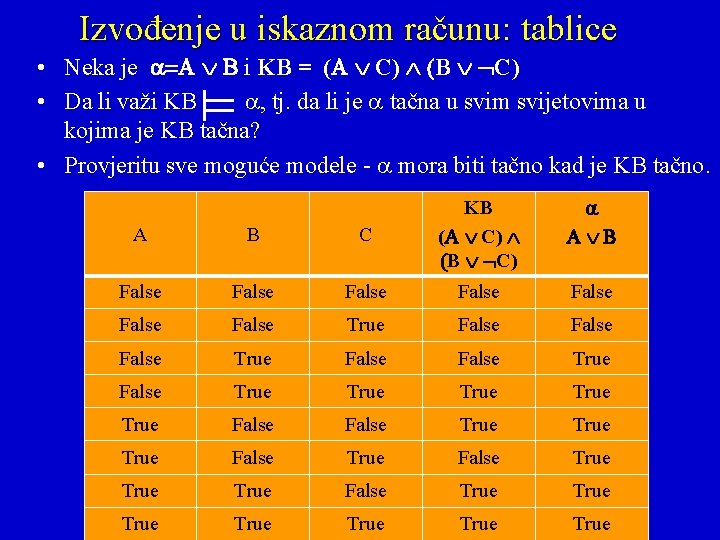
Izvođenje u iskaznom računu: tablice • Neka je i KB = ( C) B C) • Da li važi KB , tj. da li je tačna u svim svijetovima u kojima je KB tačna? • Provjeritu sve moguće modele - mora biti tačno kad je KB tačno. A B C KB ( C) B C) False False True False True False True True False True True True

Izvođenje u iskaznom računu: tablice • Neka je i KB = ( C) B C) • Da li važi KB ? – tj. je tačno u svim svijetovima u kojima je KB tačno. • Provjeritu sve moguće modele - mora biti tačno kad je KB tačno. A B C KB ( C) B C) False False True False True False True True False True True True

Izvođenje u iskaznom računu: tablice • Neka je i KB = ( C) B C) • Da li važi KB ? – tj. je tačno u svim svijetovima u kojima je KB tačno. • Provjeritu sve moguće modele - mora biti tačno kad je KB tačno. A B C KB ( C) B C) False False True False True False True True False True True True KB

Iskazni račun: metodi dokaza • Provjera modela (model checking) – Istinitosne tablice (sound and complete for propositional logic). • Primjena pravila izvođenja (inference rules) – Legitimno (sound) generisanje novih rečenica iz starih. – Dokaz = niz primjena pravila izvođenja. Mogu se koristiti pravila izvođenja kao operatori u standardnim algoritmima traženja.

Digresija: normalne forme Različiti pristupi izvođenju - upotreba sintaksnih operacija na rečenicama, često izraženim u standardizovanim formama • Konjunktivna normalna forma (CNF – univerzalna) Konjunkcija disjunkcije literala Na primjer, (A • Disjunktivna normalna forma (DNF – univerzalna) Disjunkcija konjunkcije literala Na primjer, • Hornovska forma (ograničena) Konjunkcija Hornovskih klauzula (sa najviše jednim pozitivnim literalom) Na primjer, C D Često se zapisuju kao skup implikacija B and C D) B

Pravila izvođenja Pravilo izvođenja je sound ako je zaključak tačan u svim slučajevima kada je tačna i premisa. _____ Premisa Zaključak (Conclusion)

Pravilo izvođenja: Modus Ponens ______ Premisa ______ Premisa Zaključak Modus Ponens Modus Tolens

Pravilo izvođenja : And - Eliminacija 1 2 … n ________ i Premisa Zaključak

Pravila izvođenja • And-Introduction 1, 2, …, n ________ 1 2 … n Premisa Zaključak • Dvostruka negacija _______ Premisa Zaključak

Dokazivanje - primjer

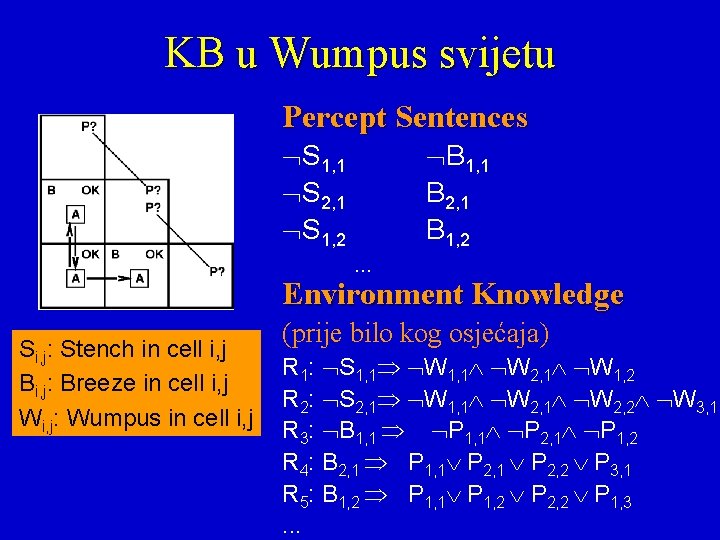
KB u Wumpus svijetu Percept Sentences S 1, 1 S 2, 1 S 1, 2 B 1, 1 B 2, 1 B 1, 2 … Environment Knowledge Si, j: Stench in cell i, j Bi, j: Breeze in cell i, j Wi, j: Wumpus in cell i, j (prije bilo kog osjećaja) R 1: S 1, 1 W 2, 1 W 1, 2 R 2: S 2, 1 W 1, 1 W 2, 2 W 3, 1 R 3: B 1, 1 P 2, 1 P 1, 2 R 4: B 2, 1 P 1, 1 P 2, 1 P 2, 2 P 3, 1 R 5: B 1, 2 P 1, 1 P 1, 2 P 2, 2 P 1, 3. . .

Zaključivanje u Wumpus svijetu Polazna KB Percept Sentences S 1, 1 S 2, 1 S 1, 2 B 1, 1 B 2, 1 B 1, 2 … Environment Knowledge R 1: S 1, 1 W 2, 1 W 1, 2 R 2: S 2, 1 W 1, 1 W 2, 2 W 3, 1 R 3: B 1, 1 P 2, 1 P 1, 2 R 4: B 2, 1 P 1, 1 P 2, 1 P 2, 2 P 3, 1 R 5: B 1, 2 P 1, 1 P 1, 2 P 2, 2 P 1, 3. . . Neka izvođenja: Primjena Modus Ponens na R 1 Dodaje u KB W 1, 1 W 2, 1 W 1, 2 Primjenon AND-Eliminacije Dodaje se u KB W 1, 1 W 2, 1 W 1, 2

Rezolucija ______ • Jedino pravilo dokazivanja - sound and complete proof system • Sve rečenice moraju biti u CNF

Iskazna logika - pregled • Logički agenti izvođenjem iz baze znanja dobijaju novu informaciju i donose odluke. • Osnovni koncepti logike: – Sintaksa: formalna struktura rečenica. – Semantika: istinitost rečenica u odnosu na model. – Entailment: neophodnost istinitosti jedne rečenice ako je data istinitost druge rečenica. – Izvođenje: izvođenje rečenica iz drugih rečenica. – Soundess: izvođenjem dobijamo samo entailed rečenice. – Kompletnost: izvođenjem dobijamo sve entailed rečenice. • Istinitosne tablice su sound and complete za iskazni račun. • U Wumpus svijetu, ovo je strašno dosadno.

Predikatski račun prvog reda (FOL – first order logic)

Predikatski račun • Iskazni račun ima ograničenu ontologiju: – Svijet se sastoji od činjenica. • Predikatski račun: – Objekti (kutije, ljudi, škole…); – Relacije (iznad, veći od…); – Svojstva (crveno, veliko, stinky, breeze…); – Funkcije (father of, best friend, next class…); – Kvantifikacija (svaki, postoji). • Može se izraziti sledeće: – Kvadrati susjedni Wumpus-u zaudaraju; – Kvadrati susjedni jami su vjetroviti.

Sintaksa Konstante Wumpus, 2, UIUC, PMF. . . Predikati Brother, >. . . Funkcije Sqrt, Left. Leg. Of. . . Veznici Promjenljive x, y, a, b. . . Kvantifikatori Jednakost = Legitiman izraz predikatskog računa naziva se formulom ili rečenicom (well-formed formula (wff)).

BNF za sintaksu

Simboli konstanti • Simboli, na primjer, Jean, Wumpus, Arrow, George. WBush, Jacques. Chirac, Marko. • Svaki simbol konstante imenuje tačno jedan objekat u univerzumu koji posmatramo, ali: – Nemaju svi objekti simbolička imena; – Neki objekti mogu imati više simboličkih imena. • Uobičajeno se označavaju velikim početnim slovom.

Promjenljive • Za predstavljanje objekata ili svojstava objekata bez eksplicitnog imenovanja objekta. • Uobičajeno malim slovima. • Na primjer: –x – father – square

Predikatski (relacioni) simboli • Predikatski simbol se koristi za predstavljanje relacija u univezumu od interesa. • Predicate(term 1, term 2, …) je ili TRUE ili FALSE. • Rečnica “Voltaire je napisao Candide” u univezumu imena i napisanih djela može da se zapiše kao: Wrote(Voltaire, Candide) • Drugi primjer: Predavač (AI, Goran)

Funkcijski simboli • Specijalni slučaj predikata. • Na primjer, Father može predstavljati sve parove osoba u relaciji otac-sin ili otac-kćer: – Father(Jane) – Father(Tahar) – Father(x) Otac osobe Jane Otac Tahara Otac x-a

Atomične rečenice Atomic Sentence = predicate(term 1, …, termn) ili term 1 = term 2 Term = function (term 1, …, termn) ili konstanta ili promjenljiva Na primjer: Intructor(CS 448, Jean) Instructor(CS 448, Son(Jean. Jacques)) Instructor(CS 448, Son(x))

Složene rečenice prave se od atomičnih rečenica primjenom veznika: S S 1 S 2 S 1 S 2 Na primjer: Married (Bill, Hillary) Married (Hillary, Bill) >(1, 2) >(1, 2)

Semantika predikatskog računa • Simboli konstanti, promjenljive i veznici su kao u iskaznom računu • Šta su funkcije i predikati? • Jezik logike je baziran na teoriji skupova: – Skupovi – Relacije – Funkcije

Skupovi • Skup objekata definiše univerzum - “Universe of Discourse. ” • Objekte predstavljamo konstantnim simbolima. A B C D E • Na primjer, u svijetu blokova, univerzum je {A, B, C, D, E}.

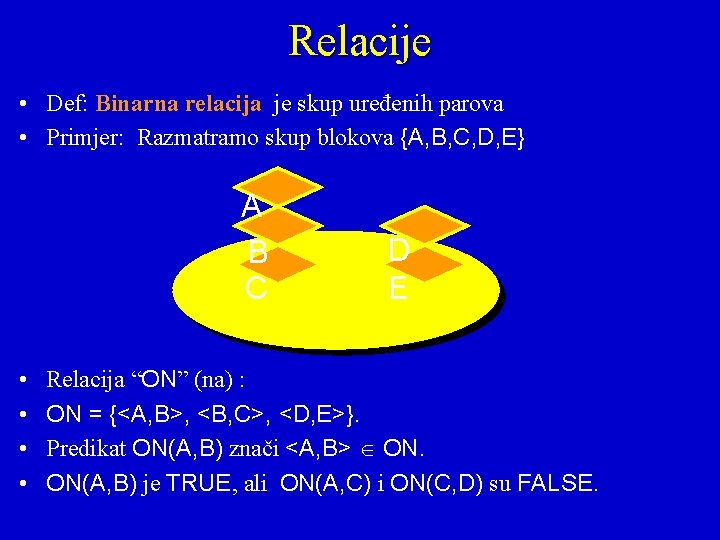
Relacije • Def: Binarna relacija je skup uređenih parova • Primjer: Razmatramo skup blokova {A, B, C, D, E} A B C • • D E Relacija “ON” (na) : ON = {<A, B>, <B, C>, <D, E>}. Predikat ON(A, B) znači <A, B> ON. ON(A, B) je TRUE, ali ON(A, C) i ON(C, D) su FALSE.

Relacije • Napomena: Binarna relacija nije uvijek konačan skup. • Primjer: “manje” < < = {<x, y> | x, y N z N, z 0 x+z = y }. Predikat: <(2, 3) je ekvivalentan sa <2, 3> <. A B C D E

Funkcije • Funkcija je binarna relacija takva da ne postoje 2 različita elementa sa jednakom drugom komponentom. • f je funkcija ako je <X, Y> f i <X, Z> f Y = Z • Ako je <X, Y> f : – X je argument f ; – Y vrijednost funkcije f u X ili slika argumenta X ; • Y = f(X)

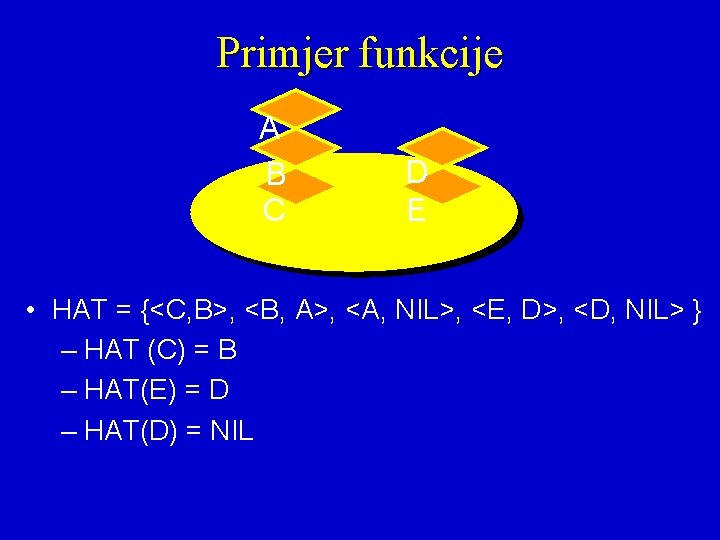
Primjer funkcije A B C D E • HAT = {<C, B>, <B, A>, <A, NIL>, <E, D>, <D, NIL> } – HAT (C) = B – HAT(E) = D – HAT(D) = NIL

Formalizacija znanja • Prvi korak je konceptualizacija, tj. reprezentacija objekata svijeta i njihovih odnosa: – Objekti – univerzum (U); a basis set, FBS); – Funkcije – osnovni skup funkcija (Functional d b basis set, RBS). – Relacije – osnovni skup realacija (Relational c e • Konceptualizacija je trojka < U of D, FBS, RBS >. • Svijet blokova: <{A, B, C, D, E}, {HAT, …}, {ON, …}>. • Drugi korak – izraziti konceptualizaciju primjenom predikatskog računa.

Univerzalni kvantifikator • <variable> <sentence> Za svaku instancu promjenljive, <sentence> je True. • Svako na UIUC je pametan: x At (x, UIUC) Smart(x) • x P je ekvivalentno konjunkciji instanciranja za P (tj. svih x-ova iz univerzuma). At (Jonathan, UIUC) Smart(Jonathan) At (Marc. Snir, UIUC) Smart(Marc. Snir) At (Bill. Clinton, UIUC) Smart(Bill. Clinton) At (George. WBush, UIUC) Smart(Georg. WBush) … • Univerzum može biti beskonačan.

Univerzalni kvantifikator, nastavak Tipično, je glavni veznik sa Uobičajena greška je upotreba kao glavnog veznika sa Šta je značenje sledeće rečenice? x At (x, UIUC) Smart(x) “Svako je na UIUC i svako je pametan. ”

Primjeri • “Birds Fly” x Bird (x) Fly(x) predikat

Primjeri • “Birds Fly” (sve ptice lete) x Bird (x) Fly(x) predikat • Šta je sa pingvinima? x Bird (x) Penguin(x) Fly(x) • “Ribe plivaju. ” x Fish (x) Swim(x)

Egzistencijalni kvantifikator • <variable> <sentence> Postoji instanca <variable> takva da je <sentence> true. • Neko iz Michigana je pametan: x At (x, Michigan) Smart(x) • x P je ekvivalentan disjunkciji instanciranja za P (tj. svih x-ova iz univerzuma). At (Rodrigo, Michigan) Smart(Rodrigo) At (Koditschek, Michigan) Smart(Koditschek) At (Gore, Michigan) Smart(Gore) At (Bush, Michigan) Smart(Bush) …

Egzistencijalni kvantifikator, nastavak Tipično, je glavni veznik sa . Uobičajena greška je upotreba kao glavnog veznika sa . x At (x, UIUC) Smart(x) je true ako postoji osoba koja nije na UIUC.

Primjeri • “Neko od studenata sa kursa CS 348 spava na času. ” x CS 348 Student (x) Sleeping(x) • Napomena: Možda ima više od jednog spavajućeg studenta, ali rečenica kaže da postoji bar jedan. • “Tačno jedan CS 348 student spava. ” x CS 348 Student (x) Sleeping(x) [ y (CS 348(y) Sleeping(y)) (x=y) ] • Ovo je naporno, pa se ponekad koristi skraćenica ! x tj. postoji tačno jedan.

Promjenljive moraju biti kvantifikovane • U well-formed formula (wff), sve promjenljive moraju biti u oblasti važenja nekog kvantifikatora. • Ovo su wff: x At (x, UIUC) Smart(x) x At (x, Michigan) Smart(x) • Nisu wff: At (x, UIUC) Smart(x) At (x, Michigan) Smart(x) • Povremeno, biće izraza u kojima promjenljive nisu kvantifikovane. Podrazumijevaće se univerzalni kvantifikator.

Osobine kvantifikatora • x y je isto što i y x (zašto? ). • x y je isto što i y x (zašto? ? ). • x y nije isto što i y x • Primjer – Hates predikat: Hates(x, y) je true ako x mrzi y – x y Hates(x, y) ''Postoji osoba koja mrzi svakog na svijetu. '' – y x Hates(x, y) ''Svaku osobu na svijetu mrzi bar jedna osoba. ''

Dualnost kvantifikatora Kvantifikatori se mogu izraziti jedan preko drugog. x Likes(x, Ice. Cream) • Svako voli sladoled. x Likes(x, Ice. Cream) [dualno] • Ne postoji niko ko ne voli sladoled. • Nobody dislikes ice cream. x Likes(x, Brussel. Sprouts) • Neko voli Briselske mladice (Brussel sprouts). x Likes(x, Brussel. Sprouts) • Nije tačno da svi ne vole mladice. [dualno]

Jednakost term 1 = term 2 je true pod datom interpretacijom (modelom) ako term 1 i term 2 referenciraju isti objekat Na primjer, definicija “rođaka prvog koljena” (RPK, sibling) preko predikata Parent x, y Sibling(x, y) [ (x=y) m, f (m=f) Parent(m, x) Parent(f, x) Parent(m, y) Parent(f, y)]

Malo vježbe Braća su RPK x, y Brother(x, y) Sibling(x, y) ``Sibling'' je refleksivna x, y Sibling(x, y) Sibling(y, x) Majka je ženski roditelj x, y Mother(x, y) (Female(x) Parent(x, y)) Brat/sestra od strica/tetke/ujaka - First. Cousin x, y First. Cousin(x, y) p, ps Parent (p, x) Sibling(ps, p) Parent(ps, y)

Malo teže pitanje • U svakom gradu postoji šinter kojeg je ujeo svaki gradski pas • “Every city has a dogcatcher who has been bitten by every dog in town” Predikati – City(x) – Dogcatcher(x, y) – Lives. In(x, y) – Bit(x, y) • x City (x) y Dogcatcher(x, y) ( z (Dog(z) Lives. In(x, z) Bit(y, z))

Logike višeg reda • U predikatskom računu, kvantifikujemo objekte, a predikati i funkcije su nad objektima. • U logikama višeg reda, kvantifikujemo predikate i funkcije. • Primjer: – “Dva objekta su jednaka ako su svi predikati primjenjeni nad njima ekvivalentni. ” – x, y (x=y) ( p p(x) p(y)) – Dvije funkcije su jednake ako imaju iste vrijednosti za sve argumente. – f, g (f=g) ( x f(x) = g(x) ) • Ovo nije dozvoljeno u predikatskom računu. • Logike višeg reda su izražajnije, ali u njima ne znamo efektivno da izvodimo zaključke i neodlučive su.

Baze znanja, aksiome i definicje • Baza znanja (knowledge base, KB) sadrži skup rečenica za koje se pretpostavlja da su tačne (TRUE). – Moraju biti konzistentne. • Inicijalni skup rečenica nazivamo aksiomama. • Iako je primamljivo definisati minimalni skup aksioma, to nije neophodno. • Aksiome oblika x, y P(x, y) … nazivamo definicijama. – Na primjer, definicija predikata Grandparent: g, c Grandparent (g, c) p Parent(g, p) Parent(p, c) • Monotonost dodavanja izvedenih rečenica u KB.

Wumpus svijet: agent primjenom FOL • KB počinje aksiomama i definicijama o wumpus svijetu. • Kako agent opaža i djela u vremenu, moramo uvesti pojam vremena u bazi znanja. • Pretpostavimo da agent u wumpus svijetu koristi FOL KB i opaža smell i breeze (ali ne i glitter) u trenutku t=5: • Možemo tvrditi sledeće (dodati u KB): Tell(KB, Percept([Smell, Breeze, None], 5))

Wumpus svijet: agent primjenom FOL • Možemo upitati KB koju akciju da odradimo: Ask(KB, a Action(a, 5)) • FOL sistem bi trebalo da izvede da li se može zaključiti neka akcija za t=5. • Odgovor: Da, {a/Shoot} supstitucija • Za datu rečenicu S i supstituciju , S označava rezultat primjene na S: – S = Bigger(x, y) – = {x/Cow, y/Lamb} – S = Bigger(Cow, Lamb) • Ask(KB, S) vraća neku ili sve takve da KB S

Izvođenje “sakrivenih” svojstava • “Kvadrati blizu rupe (pit) su vjetroviti (breezy). ” • Dijagnostičko pravilo – izvodimo uzrok iz efekta y Breezy(y) [ x Pit(x) Adjacent(x, y)] • Uzročno pravilo – izvodimo efekat iz uzroka x, y Pit(x) Adjacent(x, y) Breezy(y) • Nijedan od ovih nije kompletan – na primjer, dijagnostičko pravilo nam ne govori da kada nije vjetrovito, tada u susjedstvu nema rupe. • Definicija Breezy predikata: y Breezy(y) [ x Pit(x) Adjacent(x, y)]

Kako čuvati promjene • Činjenice važe u situacijama, a ne vječno. Na primjer, Holding(Gold, Now) ili Holding(Gold). • Situacioni račun jedan način predstavljanja promjena u FOL: – Dodati situacioni argument svakom “nevječnom” predikatu – Na primjer, Now u Holding(Gold, Now) označava situaciju • Situacije povezujemo funkcijom Result – Result(a, s) je situacija koja je rezultat akcije a u s. Više o situacionom računu u lekcijama o planiranju

Izvođenje (inference) Izvođenje je proces donošenja zaključaka iz premisa. Premise: 1. Pada snijeg ili pada kiša. 2. Ne pada kiša. Zaključak (conclusion): Pada kiša.

Validnost i zadovoljivost • Rečenica je validna, valjana ili tautologija ako je tačna u svim mogućim svjetovima (interpretacijama ili modelima). – Primjer: P P – U iskaznom računu, tablica se koristi za ispitivanje validnosti, svi redovi su TRUE • Rečenica je zadovoljiva (satisfiable) satisfiable ako postoji svijet (model. interpretacija) u kojem je tačna. – Primjer: P Q – U iskaznom računu, tablica se koristi za ispitivanje zadovoljivosti - bar jedan red je TRUE. • Rečenica je nezadovoljiva (unsatisfiable) unsatisfiable ako je netačna u svim mogućim svjetovima. – Primjer: P P – U iskaznom računu, tablica se koristi za ispitivanje zadovoljivosti – svi redovi su FALSE.

Pravila izvođenja • Sounds inference: Naći tako da KB . • Proces dokazivanja je traženje, operatori su pravila izvođenja. • Sva pravila izvođenja iskaznog računa važe i u FOL. Modus Ponens (MP): And Elimination (AE): primjer: Fish(George) Swims(George) Fish(George) Swims(George) Tired Hungry Tired Hungry

Pravila izvođenja And Introduction (AI): Modus Tolens: Relaxed Thirsty Snows Rains Snows

Supstitucije Za datu rečenicu i supstituciju , rezultat primjene supstitucije na označavamo sa Subst( , ). Primjer: = {x/Sam, y/Pam} = Likes(x, y) Subst({x/Sam, y/Pam}, Likes(x, y)) = Likes(Sam, Pam)

Izvođenje i univerzalni kvantifikator Universal Elimination (UE): x Subst({x/ }, ) substitution list [ mora biti “ground” term (term bez promjenljivih). ] Primjer Neka je naš univerzum {Rodrigo, Sharon, David, Jonathan} x At (x, UIUC) OK(x) At(Rodrigo, UIUC) OK(Rodrigo)

Izvođenje i egzistencijalni kvant. Existential Elimination: Subst({ /k}, ) gdje je k nova (Skolemova) konstanta. Primjer Iz x Teaches(x, CS 348) možemo izvesti da Teaches(Porky. Pig, CS 348) ako se simbol Porky. Pig nije već pojavljivao.

Primjer prostog dokaza • Premise: – Bob je bizon (buffalo) – Pat je svinja (pig) – Bizoni su brži (Faster) od svinja • Dokaži da “Bob je brži od Pat”. 1. Buffalo(Bob) 2. Pig(Pat) 3. x, y Buffalo(x) Pig(y) Faster(x, y) 4. Buffalo(Bob) Pig(Pat) AI 1, 2 5. Buffalo(Bob) Pig(Pat) Faster(Bob, Pat) UE 3, {x/Bob, y/Pat} 6. Faster(Bob, Pat) MP 4 & 5

Traženje sa primitivnim pravilima • Operatori su pravila izvođenja. • Stanja su skupovi rečenica. • Test cilja je da li stanje sadrži upit - rečenicu koju tražimo. • Problemi: faktor grananja je ogroman, posebno za UE. • Ideja: naći supstituciju koja će “poklopiti” premise sa nekim poznatim činjenicama. Samo jedno, mnogo moćnije pravilo izvođenja.

Unifikacija Supstitucija unificira atomične rečenice p i q ako Subst( , p)= Subst( , q) (može i oznaka p =q ). p q Knows(John, x) Knows(John, Jane) { x/Jane } Knows(John, x) Knows(y, Amy) { y/John, x/Amy } Knows(John, x) Knows(y, Mother(y)) { y/John, x/Mother(John) } Ideja: Unificirati premise sa poznatim činjenicama, primjena unifikatora na zaključak. Na primjer, ako znamo i q i Knows(John, x) Likes(John, x), možemo izvesti i: Likes(John, Jane) Likes(John, Amy) Likes(John, Mother(John))

Još malo o supstituciji Supstitucija je skup parova promjenljiva/term = { v 1/term 1, v 2/term 2, … } tako da: – Svaka promjenljiva se pojavljuje najviše jednom i – Termi koji odgovaraju promjenljivim ne smiju sadržati promjenljive koje su već upotrebljene [ na primjer, ne možemo imati supstituciju { x/f(y), y/f(x) } ]. Kada unificiramo izraze i , skupovi imena promjenljivih u i moraju biti disjunktni. – UNIFY(Loves (John, x), Loves (x, Jane)) ! Nema unifikatora – UNIFY(Loves (John, x), Loves (y, Jane)) ! Unifikator je = {x/Jane, y/John}

Osobine supstitucije 1. Svaka promjenljiva je asocirana sa najviše jednim izrazom. 2. Ne postoji promjenljiva unutar asociranog izraza koja se pojavljuje unutar bilo kog asociranog izraza (nema lijeve strane koja se pojavljuje kao desna strana(: U = {X/a, Y/f(X), Z/Y} nije pravilna supstitucija.

Unifikacija rečenica Skup izraza {S 1, S 2, …. Sn} se može unifikovati ako postoji supstitucija koja će izraze učiniti identičnim: S 1[U] = S 2 [U] =… = Sn [U] Primjer: U = {X/a, Y/b, Z/c} unificira izraze p(a, Y, Z) i p(X, b, Z) i p(a, Y, c)

Unifikatori nisu jedinstveni! • Dva izraza se mogu unificirati na više načina: S 1 = p(X, Y, Y) i S 2 = p(a, Z, Z) se mogu unificirati sa U 1={X/a, Y/Z} i U 2={X/a, Y/b, Z/b} S 1[ U 1] = S 2[ U 1] = p(a, Z, Z) S 1[ U 2] = S 2[ U 2] = p(a, b, b)

Relacija poretka za unifikatore • Neki unifikatori su opštiji od drugih: U 1 je opštiji od U 2 ako postoji unifikator U 3 takav da je U 1 U 3 = U 2 Primjer: U 1 = {X/f(Y), Z/W, R/c} je opštiji od U 2 = {X/f(a), Z/b, R/c} jer U 3 = {Y/a, W/b} U 1 U 3 ={X/f(Y), Z/W, R/c}{Y/a, W/b} = U 2 • Unifikatori formiraju parcijalno uređen skup

Najopštiji unifikator (MGU) • Za svaki skup rečenica postoji najopštiji unifikator (most general unifier - mgu) koji je jedinstven do na preimenovanje promjenljivih Primjer: za S 1 = p(X, Y, f(Z)) i S 2 = p(a, W, R) U={X/a, Y/W, R/f(Z)} je mgu, kao i U={X/a, W/Y, R/f(Z)} • Za rezoluciju, želimo da nađemo mgu literala: konstantu, promjenljivu ili n-arnu funkciju.

Najopštiji unifikator - MGU • Supstitucija je opštija od ako postoji supstitucija takva da je =. – Na primjer, = { z/ F(w) } je opštija od = { z/F(C) } jer za = { w/C } važi =. • Najopštiji (most general unifier) za i je supstitcija takva da za svaki unifikator za i , postoji supstitucija = = ( ). • Neformalno, MGU zadaje najmanje ograničenja na termove (sadrži najviše promjenljivih). • MGU je jedinstven do na redosled promjenljivih i promjenu imena promjenljivih u termu.

Izračunavanje MGU (1) function Unify_lists(x, y, U) returns a substitution inputs: x, y lists; U substitution if U = failure then return failure else if empty(x) and empty(y) then return U else if empty(x) or empty(y) then return failure else V : = Unify_elts(head(x), head(y), U); return Unify_lists(V[tail(x)], V[tail(y)], V) end

Izračunavanje MGU (2) function Unify_elts(a, b, U) returns substitution if Variable? (a) then return Unify_Var(a, b, U) else if Variable? (b) then return Unify_Var(b, a, U) else if Op(a) ~= Op(b) then return failure else return Unify_lists(Args(a), Args(b), U)

Izračunavanje MGU (3) function Unify_Var(v, x, U) returns substitution inputs: v individual variable; x expression; U substitution if Occur-Check(v, x) then return failure else return U. {v / x }

Osnovne funkcije empty, head i tail su funkcije za rad sa listom Variable? (e) je true akko je e individualna promjenljiva Op(e) je operatorski dio izraza e: Op(f(X, h(Y, a))) je f Args(e) je lista argumenata izraza e: Args(f(X, h(Y, a))) je lista (X, h(Y, a)) sa 2 elementa Occur-Check(v, e) je true akko se v pojavljuje u e

Primjer (1) Naći MGU za p(f(X, g(a, Y)) i p(f(X, Z). 1. Mgu se poziva na p i p, vraća {} 2. Mgu se poziva rekurzivno sa f(X, g(a, Y)) i f(X, Z) 3. Mgu se poziva na f i f, vraća {} 4. Mgu se poziva na X i X, vraća {} 5. Mgu se poziva na g(a, Y) i Z; kako je Z promjenljiva, vraća (preko Mguvar) {Z/g(a, Y)} poslije provjere da Z nije u g(a, Y).

Primjer (2) 6. {Z/g(a, Y)} je kreiran sa prethodnom (praznom) supstitucijom 7. Cijela supstitucija se primjenjuje na oba izraza, dovodeći do f(X, g(a, Y)) 8. Kako je i = 3, Mgu vraća {Z/g(a, Y)}, koji primjenjuje na izraze na najvišem nivou. Sve ostale provjere pokazuju jednakost. Rezultat je: p(f(X, g(a, Y))

Generalizovani Modus Ponens (GMP) p 1’, p 2’, …, pn’, (p 1 p 2 … pn q) q gdje pi’ = pi za svako i pi i q atomične rečenice Univerzalno kvantifik. promjenljive Na primjer p 1’ = Faster (Bob, Pat) p 2’ = Faster (Pat, Steve) Faster (x, y) Faster (y, z) Faster (x, z) Unificiramo p 1’ i p 2’ sa premisom primjenom = { x/Bob, y/Pat, z/Steve } Primjenimo supstituciju na zaključak q = Faster(Bob, Steve)

GMP Inference Engine • Primjenjujemo samo jedno pravilo - Generalizovani Modus Ponens. • Svaka rečenica u KB mora biti u kanonskom obliku – Atomična rečenica, ili – Pravilo p 1 p 2 … pn q gdje su pi i q atomične rečenice. • Ovo su Hornovske rečenice. Druge rečenice se mogu konvertovati u Hornovske rečenice primjenom eliminacije konjunkcije i egzistencijalnog kvantifikatora. • Podrazumijeva se da su sve promjenljive univerzalno kvantifikovane. • Prethodni dokaz je sada samo jedan korak.

Forward chaining Olančavanje unaprijed – forward chaining Kada se nova činjenica P dodaje u KB: Za svako pravilo u KB takvo da se P unificira sa premisom, i ako su ostale premise poznate, tada dodaj zaključak u KB i nastavi sa olančavanjem. Forward chaining je data-driven, tj. zaključujemo svojstva i kategorije iz opažanja.

Forward Chaining primjer • Bijela boja: činjenice • Žuta boja: Rezultat primjene implikacije. Buffalo(x) Pig(y) Faster(x, y) Pig(y) Slug(z) Faster(y, z) Faster(x, y) Faster(y, z) Faster(x, z) Buffalo(Bob) [ Unificira sa 1 -a ] Pig(Pat) [ Unificira sa 1 -b, GMP primjena ] [Unificira sa 2 -a ] 6. Faster(Bob, Pat) [ Unificira sa 3 -a, 3 -b ] 7. Slug(Steve) [Unificira sa 2 -b, GMP primjena ] 8. Faster(Pat, Steve) [ Unificira sa 3 -b i sa, GMP primjena] 9. Faster (Bob, Steve) 10. … 1. 2. 3. 4. 5.

Backward chaining p 1 p 2 … pn q • Kada odgovaramo na upit q : ako ima poklapanje q' koje znamo, vrati unifikatore; za svaku implikaciju (pravilo) čija konsekventa q' odgovara q, pokušajte da dokažete svaku premisu implikacije backward chaining. • Komplikuje čuvanje unifikatora • Još složenije je izbjegavanje beskonačnih petlji • Dvije verzije: (1) nađi bilo koje rješenje, (2) nađi sva rješenja. • Backward chaining je osnova za “logičko programiranje, ” na primjer Prolog.

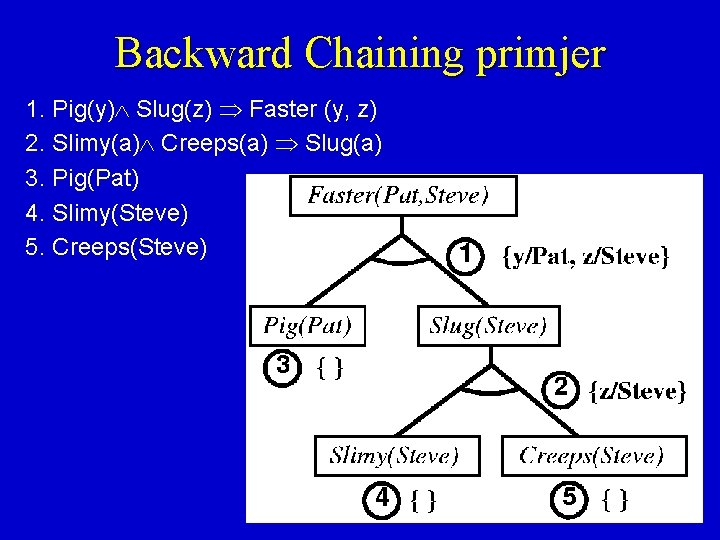
Backward Chaining primjer 1. Pig(y) Slug(z) Faster (y, z) 2. Slimy(a) Creeps(a) Slug(a) 3. Pig(Pat) 4. Slimy(Steve) 5. Creeps(Steve)

Soundness & kompletnost • Procedura izvođenja je sound ako je zaključak tačan u svim slučajevima kada su premise tačne. • Lako se dokazuje da je (GMP) sound. • Kompletnost: Ako iz KB logički slijedi , da li GMP izvodi ? Ph. D(x) Highly. Qualified(x) Ph. D(x) Early. Earnings(x) Highly. Qualified(x) Rich(x) Early. Earnings(x) Rich(x) Trebalo bi da izvedemo Rich(Me) [ili Rich(Kiki)], ali ne možemo jer Ph. D(x) Early. Earnings(x) nije Hornovska rečenica. • Otuda, GMP NIJE kompletan!

Dokazivanje pobijanjem • Dato je – KB (kolekcija tačnih rečenica), – tvrđenje P, želimo da dokažemo da je P TRUE. • Dokaz svođenjem na kontradikciju (pobijanje refutation): – Pretpostavimo da je P FALSE (tj. P je TRUE). – Dokazati da dolazi do kontradikcije. • Kompletan pristup pobijanju može se dobiti primjenom samo jednog pravila: rezolucije.

Rezolucija kao pravilo izvođenja • Ideja: Ako je true ili je true i je false ili je true Tada ili mora biti true • Osnovno pravilo rezolucije iz iskaznog računa: • Može se izraziti implikacijom , • Rezolucija je generalizacija Modus Ponens-a , je ekvivalentno sa TRUE , TRUE

Generalizovana rezolucija za FOL (sa promjenljivim) Ako se pj može unificirati sa qk, tada se može primjenti rezolucija: p 1 … pj … p m q 1 … qk … qn Subst( , (p 1 … pj-1 pj+1 … pm q 1 … qk-1 qk+1 … qn)) where = Unify (pj, qk) • Primjer: KB: Supstitucija: Zaključak: Rich(x) Unhappy(x) Rich(Me) = { x/Me } Unhappy(Me)

Forma klauzula • Želimo uniformnu reprezentaciju logičkih tvrđenja, da bi mogli koristiti jednostavnu proceduru dokazivanja. • Forma klauzula izražava sve logičke iskaze koristeći literale (atomične rečenice ili njihove negacije) i klauzule (disjunkcije literala). • Primjer: a => b ~a / b b / ~a ~(~a / ~b)

Konverzija u formu klauzula • Svaki skup rečenica može se konvertovati u formu kaluzula. • 8 koraka za konverziju: 1. Zamijeniti implikacije 2. Distribuirati negacije 3. Standardizovati promjenljive 4. Zamijeniti egzistencijalni kvantifikator 5. Ukloniti univerzalne kvantifikatore 6. Distribuirati disjunkcije 7. Zamijeniti operatore 8. Preimenovati promjenljive

1. Zamjena implikacija Svaka rečenica oblika: j => postaje ~j / na svim nivioma formule )~ označava negaciju) 2. Distribucija negacije Ponavljati sledeće radnje: ~~ postaje ~ j / postaje ~j / ~ ~ j / postaje ~j / ~ ~ X j postaje X ~j ~ X j postaje X ~j

3. Standardizacija promjenljivih Preimenovanje promjenljivih da bi osigurali da svaki kvantifikator ima svoju jedinstvenu promjenljivu. Primjer: ( X p(X)) / ( X q(X)) postaje ( X p(X)) / ( Y q(Y)) 4. Zamjena egzist. kvant. Posmatramo: ( Y X p(X, Y)) Identitet X-a zavisi od vrijednosti Y. Možemo zamijeniti X funkcijom čiji je argument Y: ( Y p(g(Y), Y)) gdje je g Skolemova funkcija

Skolemizacija • Zamjenjujemo svako pojavljivanje promjenljive pod egzistencijalnim kvantifikatorom Skolemovom funkcijom. • Argumenti funkcije su univerzalno kvantifikovane promjenljive koje su pod opsegom univerzalnih kvantifikatora čiji opseg uključuje opseg egzistencijalnog kvantifikatora kojeg eliminišemo. • Skolemova funkcija mora biti nova, tj. ne može biti funkcija koja je već prisutna u drugim rečenicima. • Ako egzstencijalni kvantifikator nije u opsegu univerzalnog kvantifikatora, koristimo Skolemovu funkciju bez argumenata, tj. konstantu.

Primjeri skolemizacije 1. X p(X) postaje p(g) 2. Y X p(X, Y) postaje Y p(g(Y), Y) 3. X Y p(X, Y) postaje Y p(g, Y) 4. Y X (((q(X) / p(X, Y)) / Z W(r(W))) postaje Y (((q(f(Y)) / p(f(Y), Y)) / Z (r(g(Y, Z))) gdje su f i g Skolemove funkcije.

5. Uklanjanje univerzalnih kvant. Uklanjamo sve i pretpostavljamo da su sve promjenljive univerzalno kvantifikovane. X Y Z q(h(Y)) / p(h(Y), X) / r(X, Z) postaje q(h(Y)) / p(h(Y), X) / r(X, Z) 6. Distribuiramo disjunkcije Napišemo formulu kao konjunktivnu normalnu formu: j / / postaje (j / / j /

7. Zamjena operatora • Zamjenjujemo konjunkciju S 1 / S 2 / …. / Sn skupom klauzula S 1 , S 2 , …, Sn • Konvertujemo svaki Si u skup literala (tj. eliminišemo simbole “ /” i zapisujemo ga u obliku klauzula(. Primjer: (p(X) / q(Y)) / (p(X) / ~r(X, Y)) postaje )2 klauzule): {p(X), q(Y)} {p(X), ~r(X, Y)}

8. Preimenovanje promjenljivih Mijenjamo imena promjenljivih tako da se ime promjenljive pojavljuje najviše u jednoj klauzuli: Primjer: {p(X), q(Y)} i {p(X), ~r(X, Y)} postaje {p(X), q(Y)} i {p(Z), ~r(Z, W)} Ovo možemo uraditi jer: X Y(p(X) / q(Y)) / (p(X) / ~r(X, Y)) je ekvivalentno sa X Y(p(X) / q(Y)) / Z W(p(Z) / ~r(Z, W))

Primjer cijele konverzije (3) 7. {~p(X), ~p(Y)), p(f(X, Y))}, {~p(X) , q(X, g(X)))}, {~p(X), ~p(g(X))} 8. {~p(X 1), ~p(Y 1)), p(f(X 1, Y 1))}, {~p(X 2) , q(X 2, g(X 2)))}, {~p(X 3), ~p(g(X 3))}

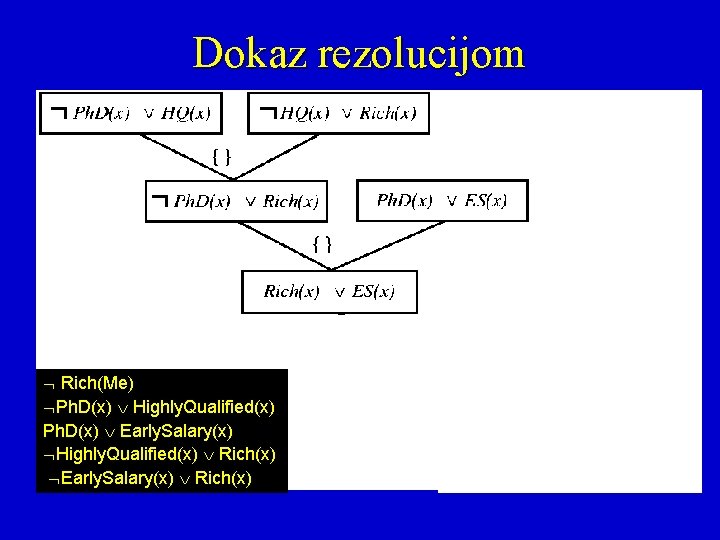
Dokaz rezolucijom p 1 … pj … p m q 1 … qk … qn Subst( , (p 1 … pj-1 pj+1 … pm q 1 … qk-1 qk+1 … qn)) • Da bi dokazali : – Negirati . – Konvertovati u CNF. – Dodati CNF u KB. – Izvesti kontradikciju primjenom rezolucije (kontradikcija je kada se izvede prazna klauzula). • Da bi dokazali Rich(Me), dodati Rich(Me) u CNF KB, i tada: Ph. D(x) Highly. Qualified(x) Ph. D(x) Early. Salary(x) Highly. Qualified(x) Rich(x) Early. Salary(x) Rich(x)

Dokaz rezolucijom Rich(Me) Ph. D(x) Highly. Qualified(x) Ph. D(x) Early. Salary(x) Highly. Qualified(x) Rich(x) Early. Salary(x) Rich(x)

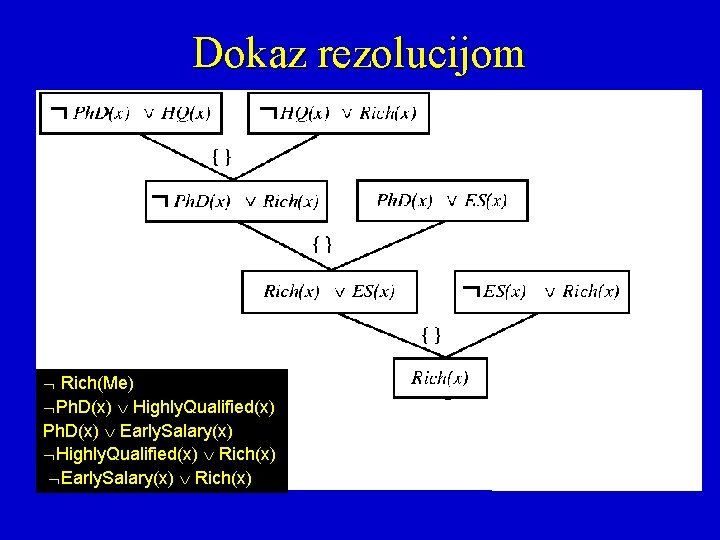
Dokaz rezolucijom Rich(Me) Ph. D(x) Highly. Qualified(x) Ph. D(x) Early. Salary(x) Highly. Qualified(x) Rich(x) Early. Salary(x) Rich(x)

Dokaz rezolucijom Rich(Me) Ph. D(x) Highly. Qualified(x) Ph. D(x) Early. Salary(x) Highly. Qualified(x) Rich(x) Early. Salary(x) Rich(x)

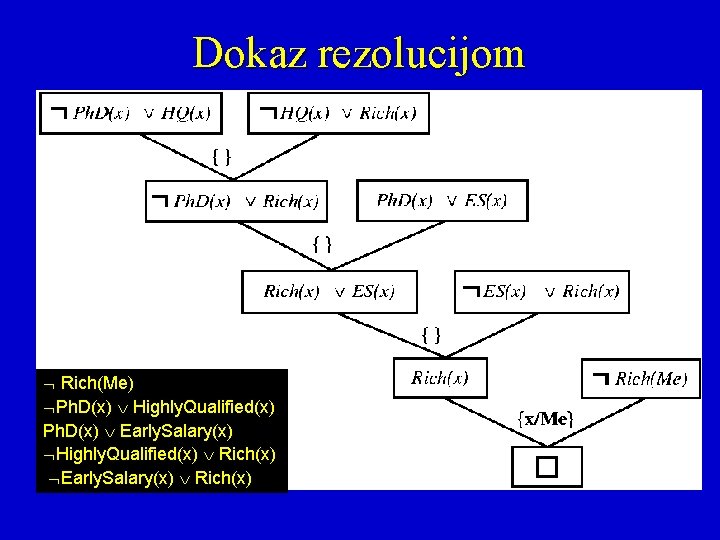
Dokaz rezolucijom Rich(Me) Ph. D(x) Highly. Qualified(x) Ph. D(x) Early. Salary(x) Highly. Qualified(x) Rich(x) Early. Salary(x) Rich(x)

Forward i backward rezolucija • Forward dedukcija prvo dokazati p 1, p 2, … , pn pa onda zaključiti q pokušati dostići cilj počevši od pravila • Backward dedukcija da bi dokazali q, probati sa p 1, p 2, … , pn radi od cilja unazad ka polaznim pravilima • Usmjerena rezolucija se može koristiti in forward, backward, ili pomiješano. Koja je najbolja, zavisi od faktora grananja.

Forward dedukcija 1. {~m(X), p(X)} 2. {m(a)} 3. {~p(Z)} 4. {p(a)} 5. { } KB KB KB 1, 2 3, 4 m(X) => p(X) m(a) p(Z) =>� p(a) {} Backward dedukcija 1. {p(X), ~m(X)} 2. {m(a)} 3. {~p(Z)} 4. {~m(Z)} 5. { } K K KB 1, 3 2, 4 p(X) <= m(X) m(a) <= p(Z) ~m(Z) {}

Forward rezonovanje: primjer Originalna KB 1. insect(X) => animal(X) 2. mammal(X) => animal(X) 3. ant(X) => insect(X) 4. bee(X) => insect(X) 5. spider(X) => insect(X) 5. lion(X) => mammal(X) 6. tiger(X) => mammal(X) 7. zebra(X) => mammal(X) Izvođenje 8. zebra(zeke) given 9. ~animal(zeke) concl. 10. mammal(zeke). 7, 8 11. animal(zeke) 2, 10 12 {} 9, 11

Backward rezonovanje: primjer Originalna KB 1. insect(X) => animal(X) 2. mammal(X) => animal(X) 3. ant(X) => insect(X) 4. bee(X) => insect(X) 5. spider(X) => insect(X) 5. lion(X) => mammal(X) 6. tiger(X) => mammal(X) 7. zebra(X) => mammal(X) Izvođenje 8. zebra(zeke) given 9. ~animal(zeke) concl. 10. ~insect(zeke). 1, 9 11. ~mammal(zeke) 2, 9 12. ~ant(zeke) 3, 10 13. ~bee(zeke) 4, 10 14. ~spider(zeke) 5, 10 15. ~lion(zeke) 6, 11 16. ~tiger(zeke) 7, 11 17. ~zebra(zeke) 8, 11 18. {}

Forward i Backward rezolucija • Problem određivanja da li je nabolji forward ili backward smjer (ili neka kombinacija) je NPkompletan. p => s 1 p => s 2 … p => sn ~sn p forward: n+1 steps backward: 2 steps s 1 => p s 2 => p … sn => p sn ~p forward: 2 steps backward: n+1 steps

True-or-False pitanja • All birds fly. • No bird swims • Pete is a bird • Does Pete Fly? Baza znanja 1. Bird(x) Flies(x) 2. Bird(y) Swims(y) 3. Bird(Pete) Upit 4. Flies ( Pete) Primjena rezolucije 5. Swims(Pete) 2, 3 6. Bird(Pete) 1, 4 7. { } 3, 6

Odlučivost Koliko je teško odrediti da li iz KB logički slijedi ? • Iskazni račun (logika nultog reda) je odlučiva (decidable): – U konačnom vremenu možemo odrediti može li ili ne logički slijediti iz KB. • Logike drugog reda se neodlučive (undecidable): – Ne možemo u konačnom vremenu odrediti da li iz KB logički slijedi . • Predikatski račun (FOL) je poluodlučiva (semi-decidable): – Ako iz KB logički slijedi ili , tada se dokaz može naći u konačnom vremenu. – Ali, ako iz KB logički ne slijede ni , tada proces dokazivanja može trajati beskonačno.

Rezolucija • Rezolucija je sound. • Rezolucija sa pobijanjem (resolution refutation) je kompletna. • Rezolucija (i bilo koja druga procedura dokazivanja) je, u najboljem slučaju, polu-odlučiva. – Napomena: provjera konzistentnosti baze znanja je takođe polu-odlučiva