1 Modalna i vremenska temporalna logika Modalna logika

1

Modalna i vremenska (temporalna) logika Modalna logika - proširenje klasične logike "modalitetima" istinitosti (subjektivnim konceptima), kao što su npr. "što mora biti istinito" i "što može biti istinito. Npr. : p = atomički propopzicijski simbol Neka je: p = F (neisitinit) u sadašnjem svijetu (stanju stvari). Tada: (moguće p) = T (nužno p) = F ako postoji neki drugi svijet (neka druga situacija, neki drugi scenarij, neka druga baza znanja) u kojoj je p = T. jer (nužno p) = T samo akko je p istinit u svim svjetovima. U klasičnu propozicijsku i predikatnu logiku dodaju se modalni operatori. 2

Semantika mogućih svjetova (Saul Kripke, 1971) (kontekst modalne logike) Kripke struktura M = (S, R, L) S = skup stanja: R = relacija dostupnosti: L = označavanje: skup mogućih svjetova (stanja). R S S između svjetova (stanja). interpretacija primitivnih (nemodalnih) formula u svakom svijetu (stanju); p, q, …. Atomi, koji su T ili F u pojedinom svijetu (stanju) Npr. izrazi neke modalne logike su istiniti (T) za stanje s: (possibly p) = T za stanje s akko p = T u s, ili nekom stanju dostupnom iz s. (necessary p) = T za stanje s akko p = T u s i svim stanjima dostupnim iz s. Analogno i formalno jednako modelu automata (stroju stanja). U Kripke strukturi oznake na čvorovima grafa (kod automata oznake su na lukovima). 3

Kasifikacija modalne logike Prema tipu modalnosti razlikujemo logike: Aletička logika Deontička logika: Epistemička logika: Vremenska logika: . . . potrebitost, mogućnost obligatornost (nužnost), dozvoljivost znanje, vjerovanje uvijek, konačno, što_je_bilo, što_je_sad, što_će_biti Vremenska logika (TL) - višestruki pogledi (1): TL propozicijska: Klasična propozicijska logika proširena vremenskim operatorima. Najviša razina apstrakcije u rasuđivanju. TL predikatna prvoga reda (varijable, funkcije, predikati, kvantifikatori): Različiti tipovi TL prvoga reda interpretirana-neinterpretirana (pretpostavlja ili ne strukturu), globalne i lokalne varijable, kvantifikacija preko vremenskih operatora ili ne. 4

Vremenska logika (TL) - višestruki pogledi (2): Globalna ili modularna: Endogena i egzogena. Rasuđivanje o kompletnom sustavu ili ne. TL linearnog vremena: U svakom trenutku postoji samo jedan budući trenutak (jedna vremenska crta). TL s grananjem vremena: U svakom trenutku može postojati više različitih budućih vremenskih crta. Diskretno ili kontinuirano vrijeme. U računarstvu uobičajeno diskretno vrijeme (sekvence stanja). Prošlo i buduće vrijeme. Izvorno TL obuhvaća oba vremena. U digitalnim sustavima uobičajeni su samo operatori budućeg vremena. Odabiremo: propozicijska, globalna, grananje, buduće vrijeme 5

Kripke struktura = model = kontekst = implementacija I (Vremenska ili temporalna) struktura M = ( S, R, L) gdje je : S: skup stanja R S×S: totalna binarna relacija (svako stanje je obuhvaćeno), t. j. s S ( t S | (s, t) R ) L: funkcija označavanja stanja: S 2 AP AP: skup atomičkih propozicijskih simbola L daje interpretaciju svih simbola iz skupa AP za stanje s. 6

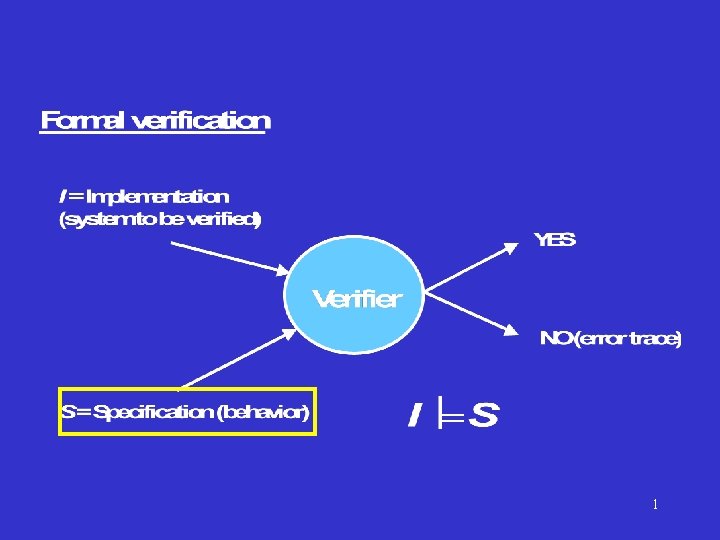
Kripke struktura M se može promatrati kao beskonačno stablo (“odmota” se počevši od promatranog stanja s 0 ): si sk Vremenska logika s grananjem Computation Tree Logic - CTL 7

=T =T =T 8

CTL vremenski operatori u radu sustava: Operators: Quantifiers: PAZI: Uvijek u paru !! 9

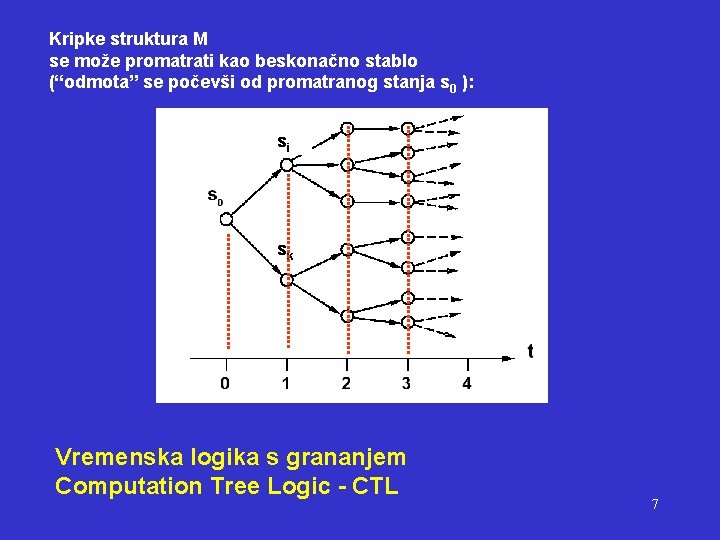
Za model M i stanje S, formula može imati slijedeću semantiku: p = true s (EF p) = True s (AF p) = True 10

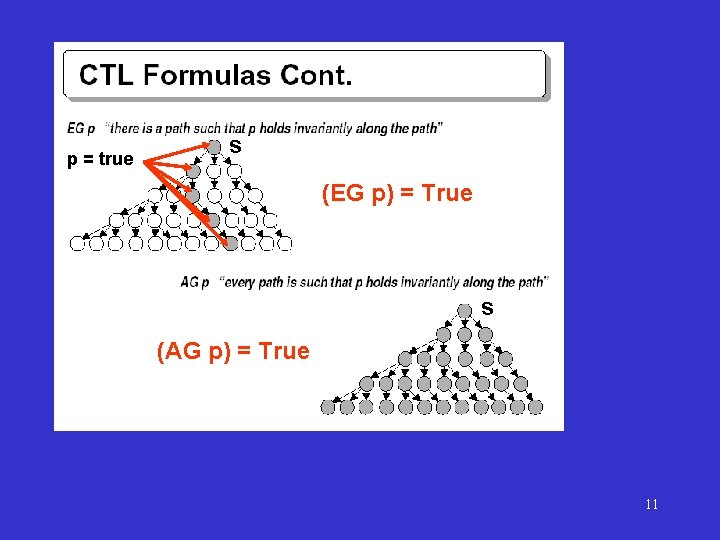
p = true s (EG p) = True s (AG p) = True 11

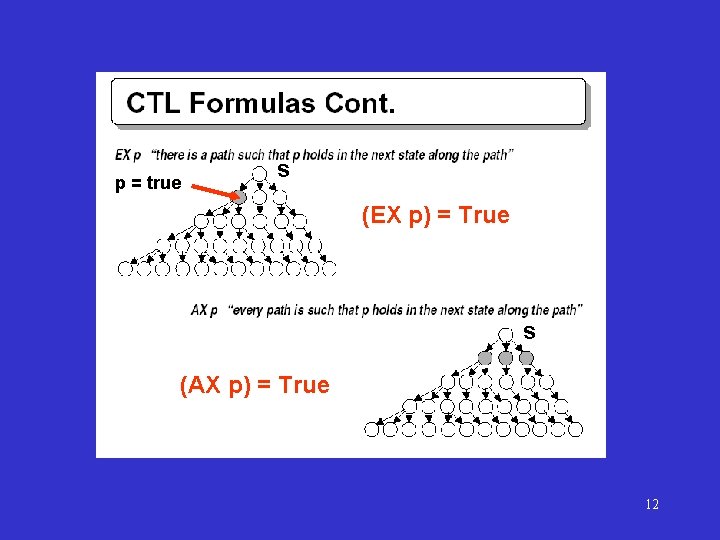
p = true s (EX p) = True s (AX p) = True 12

p = true s [E(p U q)] = True q = true Here p may or [A(p may not be true U q)] = True s 13

CTL sintaksa AU, EU - binarni operatori ostali - unarni operatori Neke dobro definirane CTL formule: AG (q EG r) EG p E (p U q) A (p U EFp) AG (p A [p U ( p A [ p U q] ) Neke krivo definirane formule CTL formule: FG p ; F i G slijede iza E ili A EF (r U q) ; U se može upariti samo sa A ili E ; Ex. : EF E(r U q), EF A(r U q) AF [(r U q) (p U r)] ; ispravan oblik je A( U ) ; F se ne može ovdje miješati ; može biti samo unutar ili ; Ex: A [(p q) U ( r q)] 14

CTL semantika M = (S, R, L) - model sustava (Kripke struktura) M, s formula vrem. Logike je istinita u modelu M za stanje s M, s formula vrem. logike nije istinita u modelu M za stanje s 1. M, s p istinita akko p L(s) (p je propozicijski atomički simbol) 2. M, s ( 1 2 ) akko M, s 1 i M, s 2 3. M, s ( 1 2 ) akko M, s 1 ili M, s 2 4. M, s ( 1 2 ) (implikacija) akko M, s 1 ili M, s 2 5. M, s AX akko za sve si takve da s si vrijedi M, si (u svakom slijedećem stanju vrijedi ) 15

6. M, s EX ako za neki si takav da s si , vrijedi M, si (u nekom slijedećem stanju vrijedi ) 7. M, s AG akko za sve putove s 1 s 2 s 3 …, gdje s = s 1 i svaki si duž puta , vrijedi M, si (za sve putove koji započinju u s, obilježje vrijedi globalno duž puta) 8. M, s EG akko postoji put s 1 s 2 s 3 …, gdje s = s 1 i za svaki si duž puta, vrijedi M, si (postoji put koji započinje u s, takav da obilježje vrijedi globalno duž puta) 9. M, s AF akko za sve putove s 1 s 2 s 3 …, gdje s = s 1 , postoji neki si duž puta takav da vrijedi M, si (za sve putove koji započinju u s, postoji neko buduće stanje u kojem vrijedi 16 obilježje )

10. M, s EF akko postoji put s 1 s 2 s 3 …, gdje s = s 1, i za neki si duž puta vrijedi M, si (postoji put koji započinje u s takav da obilježje vrijedi u nekom budućem stanju) 11. M, s A( 1 U 2) akko za sve putove s 1 s 2 s 3 …, gdje s = s 1, taj put zadovoljava ( 1 U 2). 1 je kontinuirano istinita dok se ne pojavi ( 2 = True) nekom stanju. 12. M, s E( 1 U 2) akko postoji put s 1 s 2 s 3 …, gdje je s = s 1, i taj put zadovoljava ( 1 U 2). 1 je kontinuirano istinita dok se ne pojavi ( 2 = true) u nekom stanju. 17

11. i 12. : 1 može biti istinit ili ne u i nakon stanja u kojem 2 = True (semantika "until" je različita od prirodnog jezika). 2 može biti istinit i prije početnog stanja s. Za 7. do 12. : Skup budućih stanja uključuje i sadašnje stanje (konvencija). Posljedica: p EF p (ako p vrijedi sada, EF p također vrijedi) (AG p) p q A(p U q) Ove formule su istinite u svakom stanju svakog modela. 18

Primjeri preslikavanja prirodnog jezika u CTL 1. Moguće je doći u stanje gdje start=T i ready=F. EF (start ready) 2. Za svako stanje, ako se postavi zahtjev (za nekim resursom) biti će sigurno (ne možda) konačno prihvaćen (kad-tad). AG ( zahtjev AF prihvaćen) 3. U svakom slučaju, određeni proces će konačno biti stalno zaustavljen AF (AG zaustavljen) 4. Iz svakog stanja moguće je doći do stanja "restart”. AG (EF restart) 5. Na putu prema gore, dizalo na drugom katu neće promijeniti smjer gibanja, ako postoji putnik koji želi na peti kat. AG[ ( kat=2 smjer=gore pritisnuta_tipka_5) A (smjer=gore U kat=5) ] 19

6. Dizalo može ostati stalno stajati na trećem katu sa zatvorenim vratima. AG [ (kat=3 stoji vrata=zatvoreno) EG (kat=3 stoji vrata=zatvoreno) ] 7. Kadgod in = 1, nakon dva takta uvijek out = 1 AG (in AX AX out) 8. Uvijek vrijedi: ako se pojavi "send" onda konačno "receive” postaje istinit, te do tog trenutka "send" mora ostati istinit AG (send A(send U receive)) (Napomena: pogledaj vis-user. ps !) 20

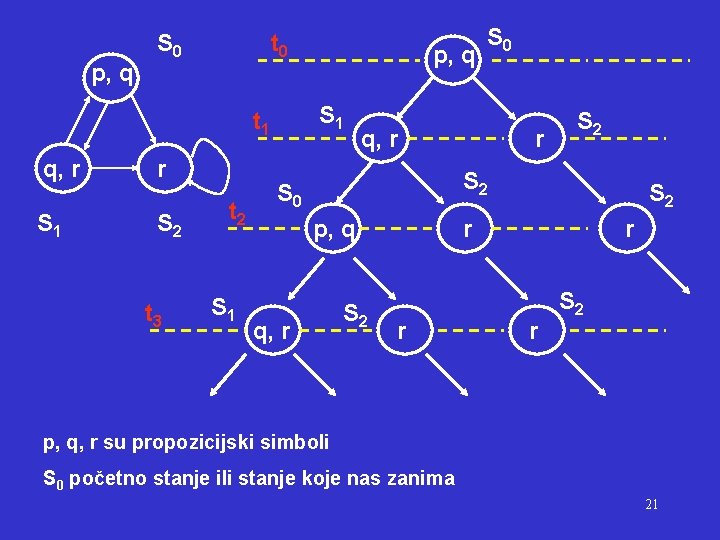
p, q S 0 t 0 S 1 t 1 q, r r S 1 S 2 t 3 t 2 S 1 p, q S 0 q, r r S 2 S 0 p, q q, r S 2 r r S 2 p, q, r su propozicijski simboli S 0 početno stanje ili stanje koje nas zanima 21

Ove formule su istinite za stanje s 0 (za ostala stanja drugačije) M, s 0 (p q) ; atomi p i q su istiniti u stanju s 0 M, s 0 r ; atom r nije istinit u stanju s 0 M, s 0 EX (q r) ; postoji put gdje je za slijedeće stanje vrijedi (q r) M, s 0 AX (q r) ; postoji jedan put na kojem ne vrijedi za slijdedeće stanje (q r) M, s 0 EF (p r) ; nema puta sa stanjem za koje vrijed (p r) M, s 0 AF r ; duž svih putova možemo dosegnuti stanje za koje vrijedii r M, s 0 E [(p q) U r] ; postoji put iz s 0 na kojem u svim stanjima (p q) = True, dok r=True (Npr. do s 2) M, s 0 A [p U r] ; na svim putovima vrijedi [p U r] 22

CTL ekvivalencije (1) AF = EG = AG = AX = AF = EG EG AF EF EX EX A (True U ) = EG E (True U ) [ A [True U ]] EG je nedjeljiv, ; de Morgan ; X je vlastiti dual t. j. E G nije ispravna CTL formula Ponekad notacija: A[p U q] E[p U q] Poterbno izračunati samo = = [p AU q] [ p EU q] EX, EG, EU = adekvatni skup (adequate set) Postoji više adekvatnih skupova. 23

EX, EG, EU – postupci izračunavanja EX – moramo naći postupak izračunavanja stanja iz kojega u jednom koraku dolazimo do stanja (sljedbenika) u kojem vrijedi Za EG i EU postoje rekurzije: EG = EX EG vrijedi sada (u sadašnjem stanju) i mora vrijediti duž jednog puta počevši od nekog u jednom koraku dostupnog slijedećeg stanja E[ U ] = ( EX E( U )) vrijedi sada (u sadašnjem stanju i tada je formula zadovoljena) ili vrijedi sada i za jedno slijedeće stanje vrijedi jednaka formula t. j. E( U ) 24

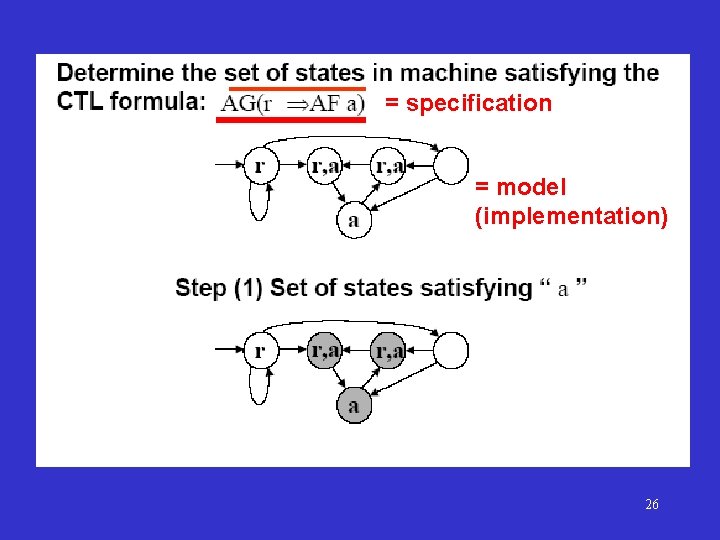
CTL PROVJERA MODELA (CTL model checking) Za danu Kripke strukturu (usmjereni označeni graf) i određen skup početnih stanja S 0 , provjeri da CTL formula zadovoljava za ta stanja: Formalno: M, S 0 , t. j. s 0 S 0 M, s 0 Potrebno je pronaći sva stanja koja zadovoljavaju CTL formulu , i ispitati da li je željeni podskup S 0 uključen. CTL provjera modela povlači manipulaciju skupovima stanja. 25

= specification = model (implementation) 26

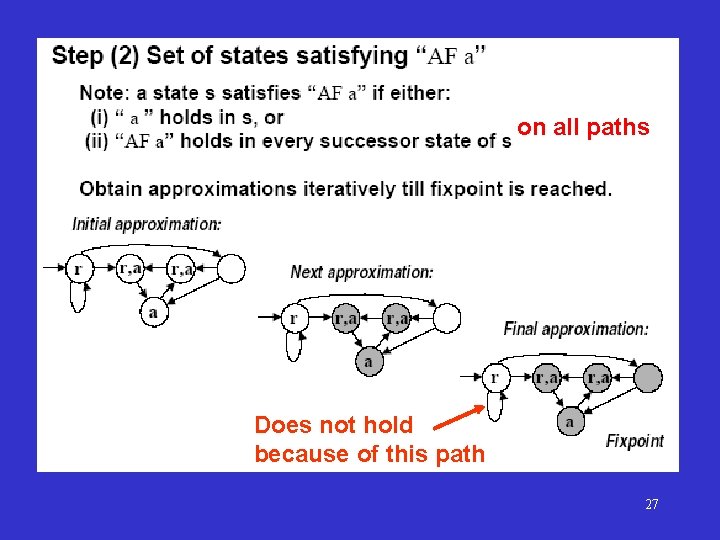
on all paths Does not hold because of this path 27

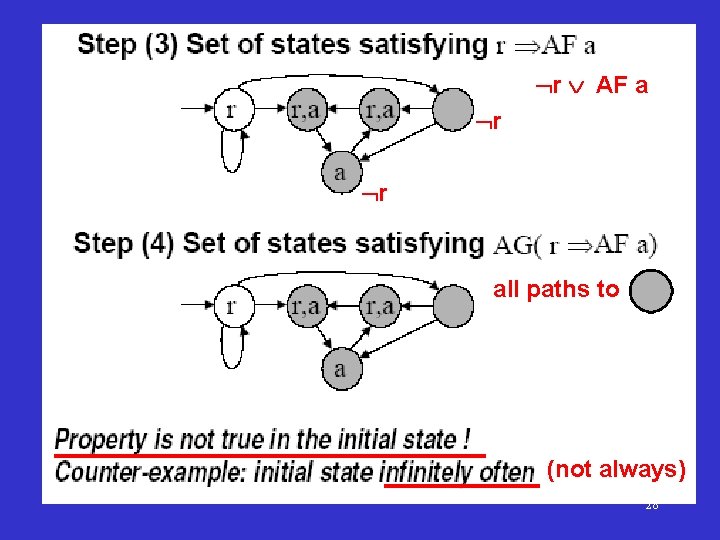
r AF a r r all paths to (not always) 28

Specifikacija ponašanja sustava CTL formalizmom 1. Obilježje sigurnosti (engl. safety) "Nešto loše se neće dogoditi. " Primjer raskršća: "Uvijek vrijedi da sporedna cesta ili glavna cesta imaju crveno svjetlo na semaforu. " AG ( cntl. farm_light = red cntl. highway_light = red ) Neuspjeh ove specifikacije pokazuje se s nekom konačnom sekvencom stanja. 29

Specifikacija ponašanja sustava CTL formalizmom 2. Obilježje životnosti (engl. liveness) "Nešto dobro će se konačno dogoditi. " Primjer raskršća: "Ako se pojavi auto na sporednoj cesti, on će konačno dobiti zeleno svjetlo na semaforu. " AG (farm_car AF cntl. farm_light = green) Neuspjeh ove specifikacije pokazuje se s nekom beskonačnom sekvencom stanja. 30

OGRANIČENJE pravednosti (izglednosti), fairness (1) Verifikacija M, s može dati negativan rezultat jer je u analizi uključeno i nerealno (teoretsko moguće ali u stvarnosti se ne pojavljuje) ponašanje modela M. Npr. Pretpostavljamo komunikacijski protokol u kojem stvarno ne postoji mogućnost da se neka poruka beskonačno puta ponovo šalje a da se nikad ne primi. Očekujemo da se ipak jednom u budućnosti primi (nakon konačnog broja bezuspješnih pokušaja). Npr. Međusobna isključivost dva procesa P 1 i P 2 pristupu zajedničkom resursu. Ako dozvolimo da proces P 1 ostane u svom kritičnom dijelu beskonačno dugo, P 2 nikad neće dobiti resurs. Želimo stoga maknuti tu beskonačnu petlju (put) i pretpostaviti da proces P 1 može ostati u kritičnom dijelu po volji konačno dugo, ali ne beskonačno dugo (zauvijek). 31

OGRANIČENJE pravednosti (izglednosti), fairness (2) Modelu M namećemo ponašanje ograničenjem pravednosti , kao dodatnom CTL formulom (specifikacija S ostaje). : !(stanje_P 1 = krit_sekcija) P 1 ne smije biti stalno u svom kritičnom dijelu, t. j. za svako stanje uvijek mora postojati neko buduće stanje u kojem P 1 nije u kritičnom dijelu. Formalna deefinicija: F = { 1, 2, …, n} n ograničenja pravednosti (CTL formule). Put s 0 s 1 … je pravedan u odnosu na taj skup ako za svaki i postoji: sk i t. j. svaki i je istinit beskonačno često duž puta izračunavanja. (ne može se dogoditi da i na nekom putu ne bude nikad istinit) s 0 s 1 ( =T) s 2 s 3 s 4 ( =T) s 5 … ( =T). . . Složen i opasan alat (zahtijeva oprez u korištenju). 32

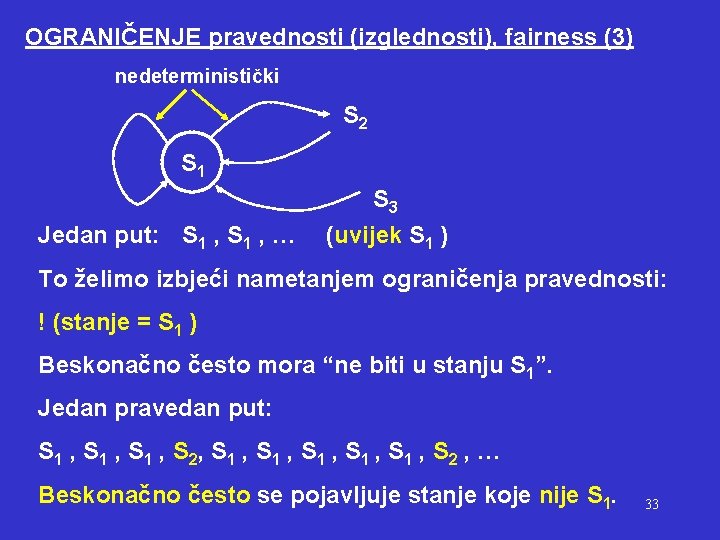
OGRANIČENJE pravednosti (izglednosti), fairness (3) nedeterministički S 2 S 1 S 3 Jedan put: S 1 , … (uvijek S 1 ) To želimo izbjeći nametanjem ograničenja pravednosti: ! (stanje = S 1 ) Beskonačno često mora “ne biti u stanju S 1”. Jedan pravedan put: S 1 , S 2, S 1 , S 1 , S 2 , … Beskonačno često se pojavljuje stanje koje nije S 1. 33

34

CTL PROVJERA MODELA - IZRAČUN SKUPOVA STANJA Za danu Kripke strukturu (usmjereni označeni graf) i određen skup početnih stanja S 0 , provjeri da je CTL formula zadovoljena za ta stanja: Formalno: M, S 0 , t. j. s 0 S 0 M, s 0 Uobičajen pristup: Potrebno je pronaći sva stanja koja zadovoljavaju CTL formulu , i ispitati da li je željeni podskup S 0 uključen. Problem: efikasan postupak izračunavanja stanja 35

EX, EG, EU – postupci izračunavanja EX – moramo naći postupak izračunavanja stanja iz kojega u jednom koraku dolazimo do stanja (sljedbenika) u kojem vrijedi Za EG i EU postoje rekurzije: EG = EX EG vrijedi sada (u sadašnjem stanju) i mora vrijediti duž jednog puta počevši od nekog u jednom koraku dostupnog slijedećeg stanja E[ U ] = ( EX E( U )) vrijedi sada (u sadašnjem stanju i tada je formula zadovoljena) ili vrijedi sada i za jedno slijedeće stanje vrijedi jednaka formula t. j. E( U ) 36

37

38

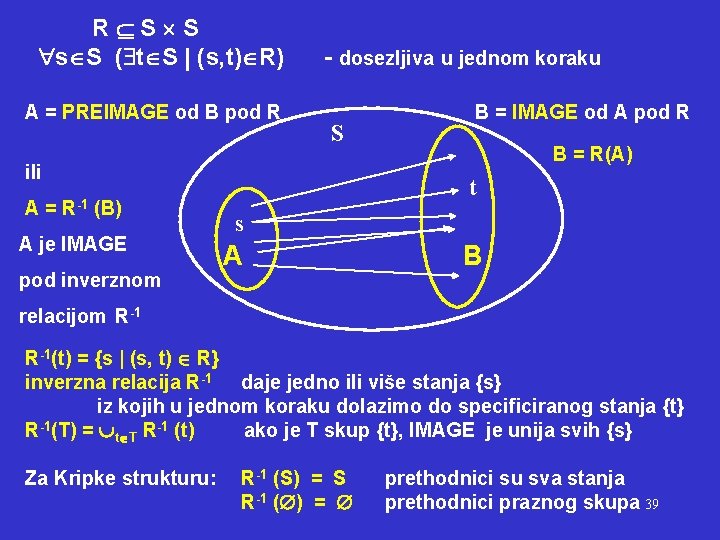
R S S s S ( t S | (s, t) R) A = PREIMAGE od B pod R - dosezljiva u jednom koraku S ili A = R-1 (B) A je IMAGE pod inverznom B = IMAGE od A pod R B = R(A) t s A B relacijom R-1(t) = {s | (s, t) R} inverzna relacija R-1 daje jedno ili više stanja {s} iz kojih u jednom koraku dolazimo do specificiranog stanja {t} R-1(T) = t T R-1 (t) ako je T skup {t}, IMAGE je unija svih {s} Za Kripke strukturu: R-1 (S) = S R-1 ( ) = prethodnici su sva stanja prethodnici praznog skupa 39

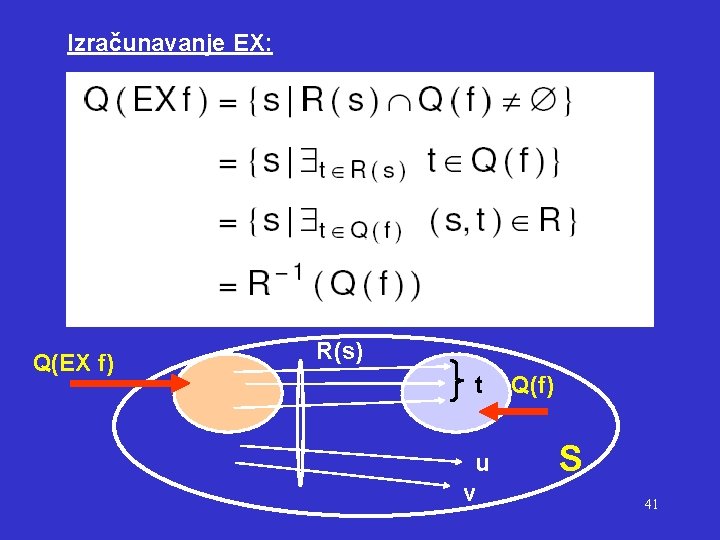
CTL operatori i skupovi stanja (logičke operacije zamijenjujemo operacijama sa skupovima) Model M = ( S, R, L ) EX, EG, EU - adekvatan skup R( s ) = { t S | ( s, t ) R} R(s) = sljedbenici stanja s (skup t-ova) Q( false ) = Q( true ) = S Q( p ) = { s | p L ( s ) } skup stanja s u kojima vrijedi p = True Q( ¬ f ) = S - Q( f ) sva stanja u S osim onih u kojima f = True Q( f g ) = Q( f ) Q( g ) skup dobiven presjekom skupova Q( EX f ) = { s | R ( s ) Q( f ) } stanja koja imaju sljedbenike u Q(f) ( R(s) daje sve sljedbenike) Q( EG f ) = Q(f ) Q( EX EG f ) stanja Q(f) u kojima je f = True i stanja za koja vrijedi Q( EG f) nakon jednog koraka (EX) Q[ E( f U g)] = Q( g ) Q( f ) Q( EX E( f U g)) stanja u kojima je g = True, ili stanja u kojima je f = True i nakon jednog koraka (EX) vrijedi E(f U g) 40

Izračunavanje EX: Q(EX f) R(s) t u v Q(f) S 41

Fiksna (čvrsta) točka (engl. Fix-point, Fixed-point) - 1 Monotone funkcije Definicije: S: F: P(S) - skup stanja - funkcija na svim podskupovima u S, P(S) = 2 S ("power set") 1. F je monotona akko X Y implicira (povlači) za sve podskupove X i Y u S. F(X) F(Y) 2. Podskup X od skupa S je fiksna točka akko: F(X)=X 42

Fiksna (čvrsta) točka (engl. Fix-point, Fixed-point) - 2 Primjer 1: Neka je S={s 0, s 1}, te neka je F(Y)=Y {s 0} za sve podskupove Y od S. Neka je Y' također bilo koji poskup od S. Svaki Y Y' , implicira Y {s 0} Y' {s 0}, te je F monotona. Fiksne točke su svi podskupovi od S koji sadrže s 0 , jer u tom slučaju F(Y) ne dodaje ništa novo (s 0 = s 0 ). Podskup { } nije fix-point, jer F({ }) = { } {s 0 } = {s 0 } Podskup {s 0} je najmanji fix-point, jer F({s 0}) = {s 0}. Podskup {s 1} nije fix-point jer F({s 1})= {s 1} {s 0} = {s 0, s 1} Skup {s 0, s 1} je najveći fix-point, jer F({s 0, s 1})={s 0, s 1} {s 0}={s 0, s 1}. Monotone funkcije uvijek imaju najmanji i najveći fix-point. 43

Fiksna (čvrsta) točka (engl. Fix-point, Fixed-point) - 3 Primjer 2: Funkcija: G(Y) = ako [Y = {s 0}] tada {s 1} inače {s 0} na skupu S={s 0, s 1} nije monotona, jer (za sve podskupove Y): G({}) = {s 0 } G({s 0}) = {s 1} G({s 1 }) = {s 0 } G({s 0, s 1} = {s 0} G(Y) nema nijedan fix-point. Monotone funkcije nad skupovima stanja u Kripke strukturi: Q(EG f) = Q(f) Q( EX EG f ) Q(E(f U g)) = Q(g) Q(f) Q( EX E( f U g)) 44

Fiksna (čvrsta) točka (engl. Fix-point, Fixed-point) - 4 Knaster-Tarski teorem Označimo: skup S = {s 0, s 1, …, sn} sa n+1 elementom, X je neki podskup od S. Fi : F primijenjena i-puta, t. j. : F(F(… F(X))) Npr. Neka je F(Y)=Y {s 0} F 2(Y) = F(F(Y)) = [Y {s 0}] {s 0} = Y {s 0} = F(Y), te je F 2 = F Za ovaj primjer vrijedi: Fi = F za za sve i 1 Teorem: Ako je F: P(S) monotona, tada Fn+1( ) je najmanji fix-point od F. Fn+1(S) je najveći fix-point od F. 45

Dokaz da je Fn+1( ) najmanji fix-point od F Fix - 5 Ako monotona: F( ), povlači F( ) F(F( )), odn. F 1( ) F 2( ). Indukcijom slijedi: F 1( ) F 2( ) … Fi( ) za sve i 1 Neka: Tvrdimo: i=n+1 jedan od gornjih Fk( ) je fix-point, t. j. Fk( )= Kad F 1( ) nebi bio fix-point onda bi F 1( ) morao sadržavati najmanje 1 element (jer samo u tom slučaju F( )). Indukcijom ostali, npr, F 2( ) bi morao sadržavati bar 2 elementa, jer bi morao biti veći od F 1( ). Svaki daljnji bi morao imati barem jedan element više od prethodnika. Kad Fn+1( ) nebi bio fix-point, F(Fn+1( )) bi morao imati n+1+1 element, što je nemoguće jer S ima samo n+1 elemenata. Slijedi: F(Fn+1( )) = Fn+1( ), t. j. Fn+1( ) je fix-point 46

Još treba dokazati da je to najmanji fix-point. Fix - 6 Neka je X neki drugi fix-point od F. Moramo pokazati da je Fn+1( ) X. Kako je X, to slijedi F( ) F(X) = X (jer je funkcija monotona) Dakle: F( ) X. Indukcijom Fi( ) X za sve i 0, pa i za i = n + 1, slijedi Fn+1( ) X Dokaz za najveći fix-point analogno uz zamjenu: sa sa S "veći" sa "manji" Teorem daje ujedno i algoritam izračunavanja i garantira završetak: Najmanj. I fix-point: iterativna primjena F na prazan skup , dok rezultat ne postane invarijantan na tu primjenu F. Najveća gornja granica broja iteracija: n+1 (za S sa n+1 elementom). 47

Izračunavanje EG: Izračunavanje fiksne (1) (čvrste) točke za monotone funkcije: Ako je S skup stanja, a F funkcija na svim podskupovima u S, podskup Z od skupa S je fiksna (čvrsta točka) akko Z Q(EG f) = F(Z) 48

Izračunavanje EG: Q(EG f): (2) ZEG = FEG (ZEG) = Qf R-1(ZEG) 2 S EG (CTL f) { k : = 0; Zk : = S; do { Zk+1 : = Q(f) R-1 (Zk ); If Zk+1 = Zk return Zk ; k++ ; } forever; } S Q(f) Fix Budući da R-1(S) = S, bolje je započeti sa Zk = Q(f) 49

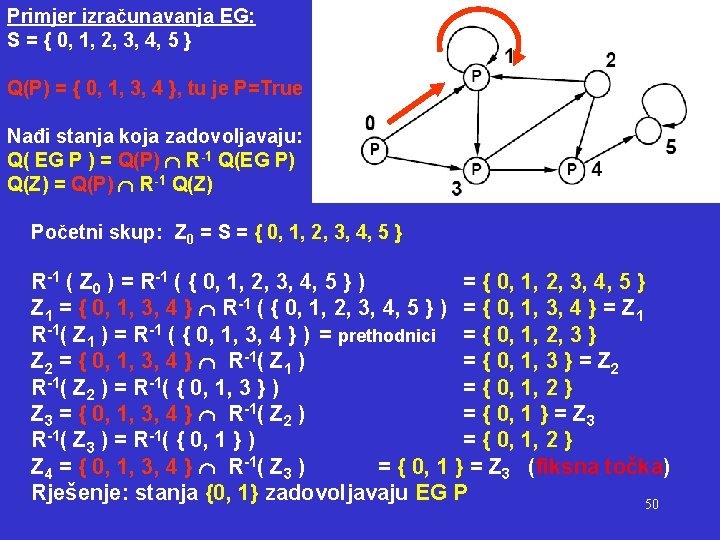
Primjer izračunavanja EG: S = { 0, 1, 2, 3, 4, 5 } Q(P) = { 0, 1, 3, 4 }, tu je P=True Nađi stanja koja zadovoljavaju: Q( EG P ) = Q(P) R-1 Q(EG P) Q(Z) = Q(P) R-1 Q(Z) Početni skup: Z 0 = S = { 0, 1, 2, 3, 4, 5 } R-1 ( Z 0 ) = R-1 ( { 0, 1, 2, 3, 4, 5 } ) = { 0, 1, 2, 3, 4, 5 } Z 1 = { 0, 1, 3, 4 } R-1 ( { 0, 1, 2, 3, 4, 5 } ) = { 0, 1, 3, 4 } = Z 1 R-1( Z 1 ) = R-1 ( { 0, 1, 3, 4 } ) = prethodnici = { 0, 1, 2, 3 } Z 2 = { 0, 1, 3, 4 } R-1( Z 1 ) = { 0, 1, 3 } = Z 2 R-1( Z 2 ) = R-1( { 0, 1, 3 } ) = { 0, 1, 2 } Z 3 = { 0, 1, 3, 4 } R-1( Z 2 ) = { 0, 1 } = Z 3 R-1( Z 3 ) = R-1( { 0, 1 } ) = { 0, 1, 2 } Z 4 = { 0, 1, 3, 4 } R-1( Z 3 ) = { 0, 1 } = Z 3 (fiksna točka) Rješenje: stanja {0, 1} zadovoljavaju EG P 50

Izračunavanje EU: (1) Q[ E(f U g)] Izračunavanje fiksne (čvrste) točke za monotone funkcije: Ako je S skup stanja, a F funkcija na svim podskupovima u S, podskup Z od skupa S je fiksna (čvrsta točka) akko Z Q[ E(f U g) ] = = F(Z) F ( Q[ E(f U g)] ) 51

Izračunavanje EU: Q(f EU g): ZEU = FEU(ZEG) (2) = Qg Qf R-1(ZEU) 2 S EU (CTL f, CTL g) { k : = 0; Zk : = ; do { Zk+1 : = Q(g) Q(f) R-1 (Zk ); If Zk+1 = Zk return Zk ; k++ ; } forever; } Q(g) Budući da R-1( ) = , bolje započeti sa Zk = Q(g) S Fix 52