LOGIKA PERNYATAAN Logika Gambaran Umum Logika Logika Pernyataan

LOGIKA & PERNYATAAN

Logika Gambaran Umum Logika : - Logika Pernyataan membicarakan tentang pernyataan tunggal dan kata hubungnya sehingga didapat kalimat majemuk yang berupa kalimat deklaratif. - Logika Predikat menelaah variabel dalam suatu kalimat, kuantifikasi dan validitas sebuah argumen.

Lanjut …………. . - Logika Hubungan mempelajari hubungan antara pernyataan, relasi simetri, refleksif, antisimtris, dll. - Logika himpunan membicarakan tentang unsur-unsur himpunan dan hukum-hukum yang berlaku di dalamnya. - Logika Samar merupakan pertengahan dari dua nilai biner yaitu ya-tidak, nol-satu, benarsalah.

PERNYATAAN (PROPOSISI) Pernyataan/ Kalimat Deklaratif/ Proposisi adalah kalimat yang bernilai benar atau salah tetapi tidak keduanya. Contoh : Yogyakarta adalah kota pelajar 2+2=4 Semua manusia adalah fana 4 adalah bilangan prima 5 x 12=90 (Benar). (Salah).

Lanjt ……… Tidak semua kalimat berupa proposisi Contoh : Dimanakah letak pulau bali? . Pandaikah dia? . Andi lebih tinggi daripada Tina. 3 x-2 y=5 x+4. x+y=2.

Penghubung Kalimat dan Tabel Kebenaran Satu atau lebih proposisi dapat dikombinasikan untuk menghasilkan proposisi baru lewat penggunaan operator logika.

Lanjut ………. Dalam menggabungkan proposisi atomik menjadi sebuah proposisi majemuk, diperlukan sebuah kata penghubung/perangkai kalimat ü DAN ü ATAU ü BUKAN ü JIKA DAN HANYA JIKA

5 Penghubung dalam Logika

Contoh Penggunaan kata penghubung

Contoh Lanjut……………. . p menyatakan kalimat “ Mawar adalah nama bunga” q menyatakan kalimat “ Apel adalah nama buah” Maka kalimat “ Mawar adalah nama bunga dan Apel adalah nama buah “ simbol p q

Lanjut ………… p: hari ini hari minggu q: hari ini libur nyatakan kalimat dibawah ini dengan simbol logika : a. Hari ini tidak hari minggu tetapi libur b. Hari ini tidak hari minggu dan tidak libur c. Tidak benar bahwa hari ini hari minggu dan libur

Penyelesaian a. Kata “tetapi” mempunyai arti yang sama dengan dan sehingga kalimat (a) bisa ditulis sebagai : ¬p q b. ¬p ¬q c. ¬(p q)

Tabel Kebenaran Tabel kebenaran adalah tabel nilai yang mendefinisikan nilai kebenaran keseluruhan kalimat berdasarkan nilai kebenaran masing kalimat penyusunnya.

Negasi (Ingkaran) Negasi suatu pernyataan P adalah pernyataan baru yang bernilai salah jika P benar dan bernilai benar jika P bernilai salah. notasi negasi P adalah ∼P

Contoh Misal : P adl “x lebih kecil dari 5” , negasinya adl : 1. Tidak ( lah benar ) x lebih kecil dari 5 2. x tidak lebih kecil dari 5 3. x lebih besar atau sama dengan 5

Konjungsi dari dua pernyataan p dan q ditulis p∧q (dibaca p and q) adalah suatu pernyataan yang bernilai benar jika kedua komponennya, yaitu p dan q, bernilai benar, dan akan bernilai salah jika salah satu komponennya bernilai salah.

Lanjut………. Tabel Kebenaran Konjungsi

Lanjut …… Contoh 1 : “ Yogyakarta Ibukota Provinsi DIY dan 112 habis dibagi 2”, dalam logika dianggap suatu pernyataan yang sah. (Apakah termasuk kalimat konjungsi? ) Contoh 2: 1. p = Ali dan Budi duduk dikelas 2 Konjungsi 2. q = Ali dan Budi Bersaudara

Disjungsi (inklusif) dari dua pernyataan p atau q ditulis p∨q (dibaca p atau q) adalah suatu pernyataan yang bernilai benar jika salah satu komponennya, yaitu p atau q, bernilai benar, dan ber nilai salah jika kedua komponennya bernilai salah

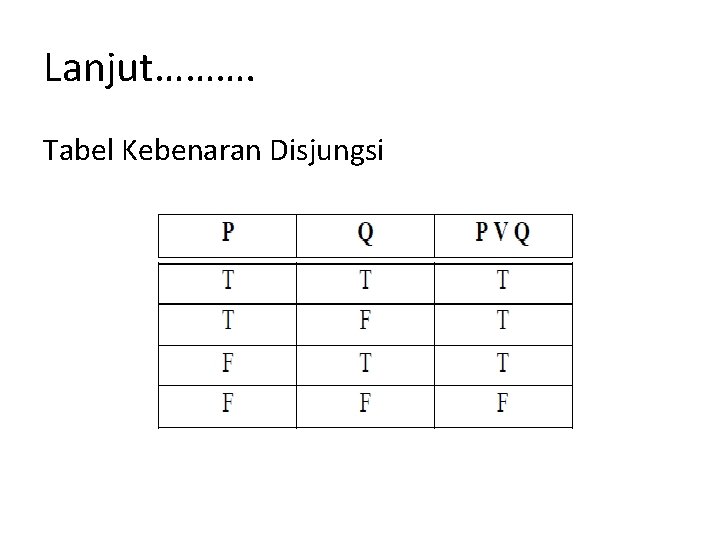
Lanjut………. Tabel Kebenaran Disjungsi

Disjungsi Mempunyai 2 arti yaitu : 1. INKLUSIF OR yaitu jika “p benar atau q benar atau keadanya “True” 2. EKSLUSIF OR yaitu jika “p benar atau q benar tetapi tidak keduanya.

Implikasi - Implikasi dua pernyataan p dan q adalah p q yang dibaca : Jika p maka q. q jika p P adalah syarat cukup untuk q q adalah syarat perlu untuk p

Lanjut …………. Tabel Kebenaran Implikasi

Lanjut ……. Contoh : p : Pak Ali adalah seorang haji. q : Pak Ali adalah seorang muslim. p q : Jika Pak Ali adalah seorang haji maka pastilah dia seorang muslim.

p : Hari hujan. q : Adi membawa payung. Benar atau salahkah pernyataan berikut? – Hari benar-benar hujan dan Adi benar-benar membawa payung. – Hari benar-benar hujan tetapi Adi tidak membawa payung. – Hari tidak hujan tetapi Adi membawa payung. – Hari tidak hujan dan Adi tidak membawa payung.

TERIMA KASIH