Inference for the mean vector Univariate Inference Let








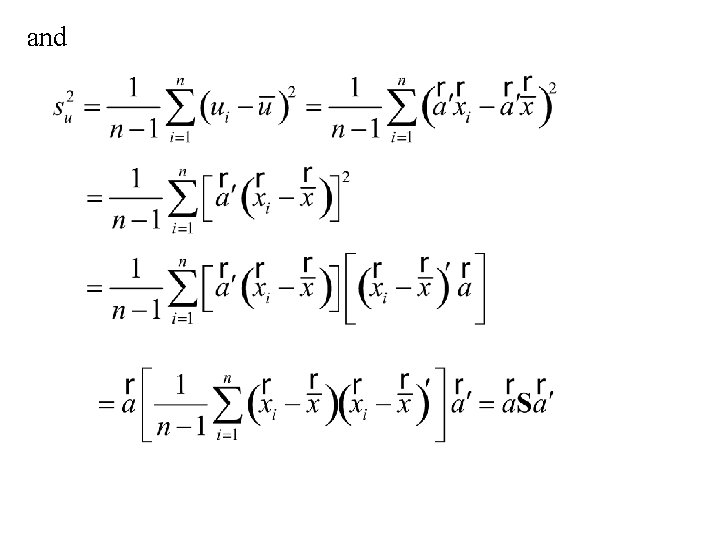
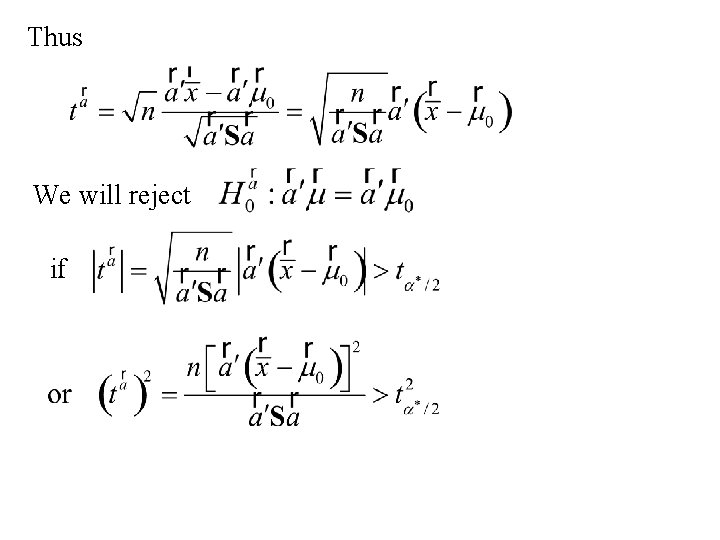

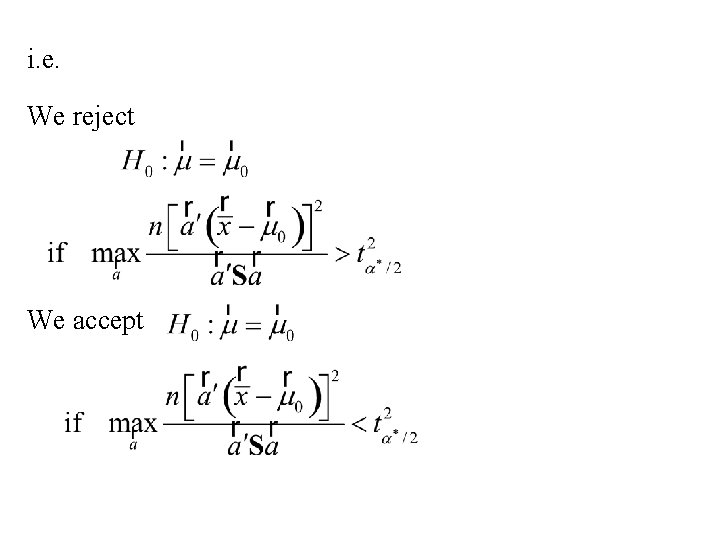

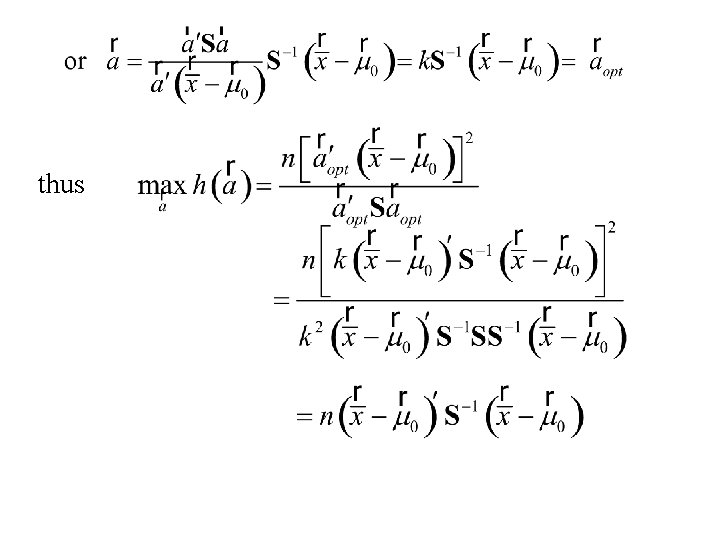


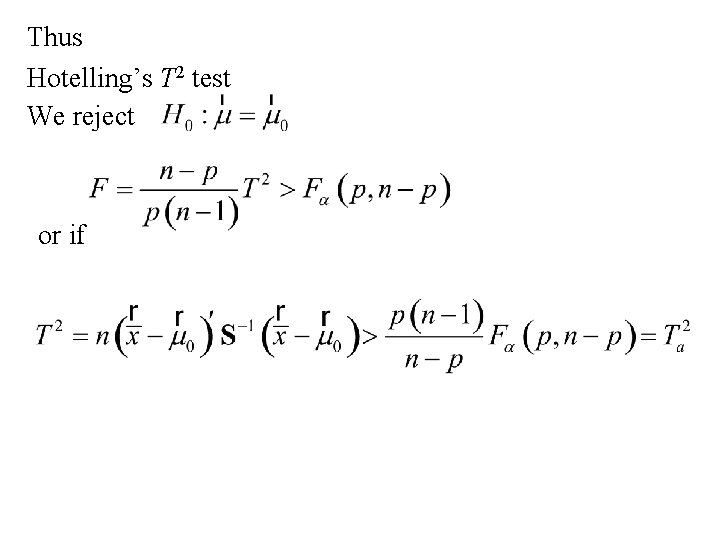







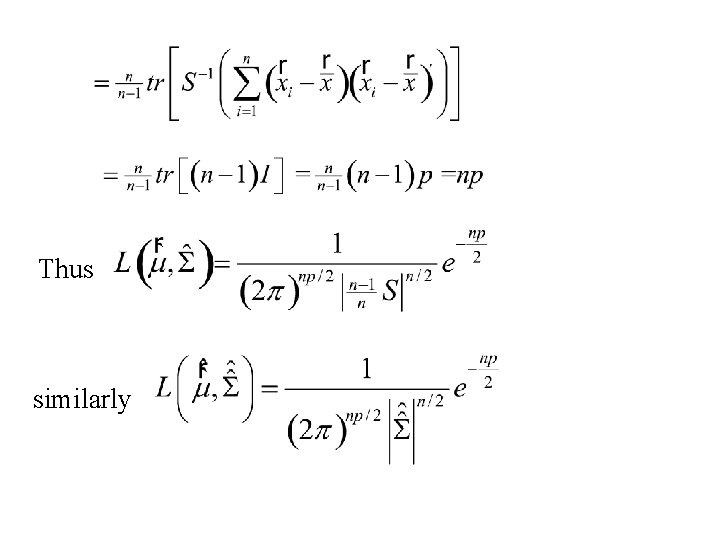

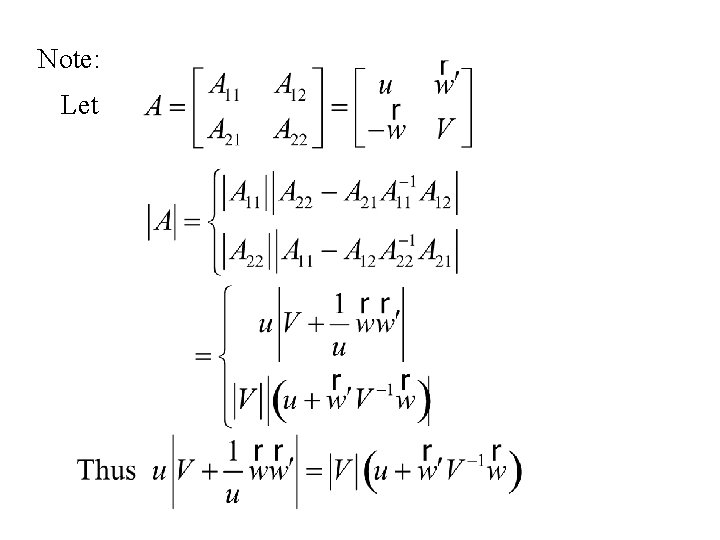

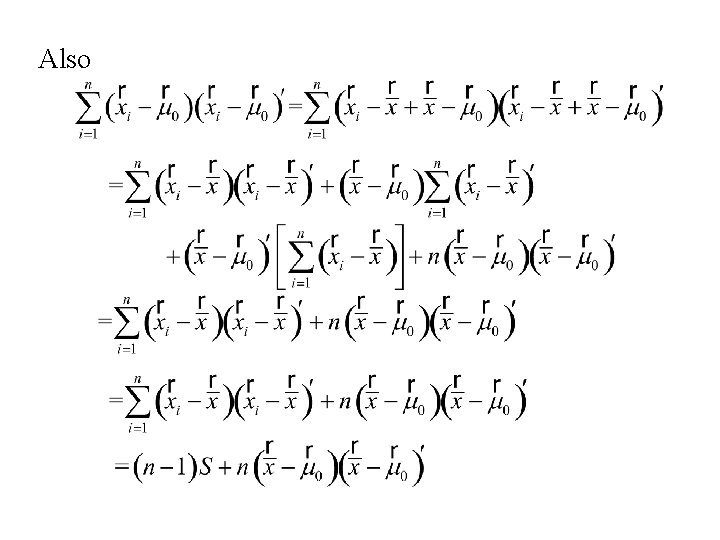
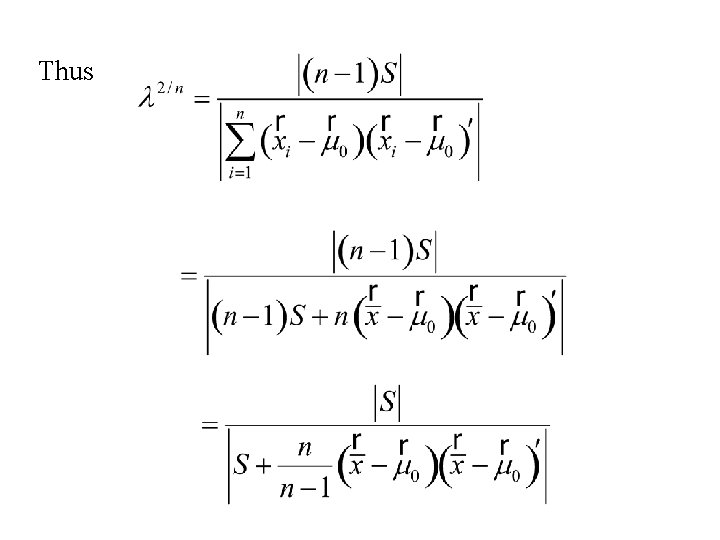
































![Computer security: p 1: Valid users p 2: Imposters P[2|1] = P[identifying a valid Computer security: p 1: Valid users p 2: Imposters P[2|1] = P[identifying a valid](https://slidetodoc.com/presentation_image_h2/43c9d4b2294c8a24f7cddea5049f0f8f/image-76.jpg)






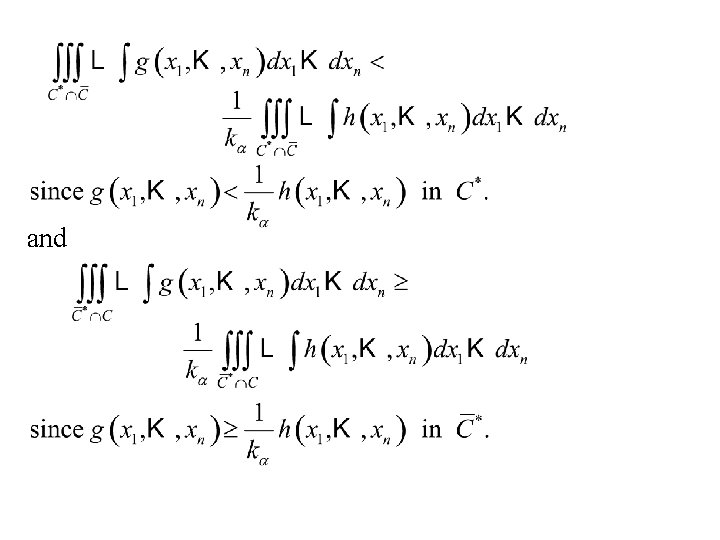









- Slides: 94

Inference for the mean vector

Univariate Inference Let x 1, x 2, … , xn denote a sample of n from the normal distribution with mean m and variance s 2. Suppose we want to test H 0: m = m 0 vs HA : m ≠ m 0 The appropriate test is the t test: The test statistic: Reject H 0 if |t| > ta/2

The multivariate Test Let denote a sample of n from the p-variate normal distribution with mean vector and covariance matrix S. Suppose we want to test

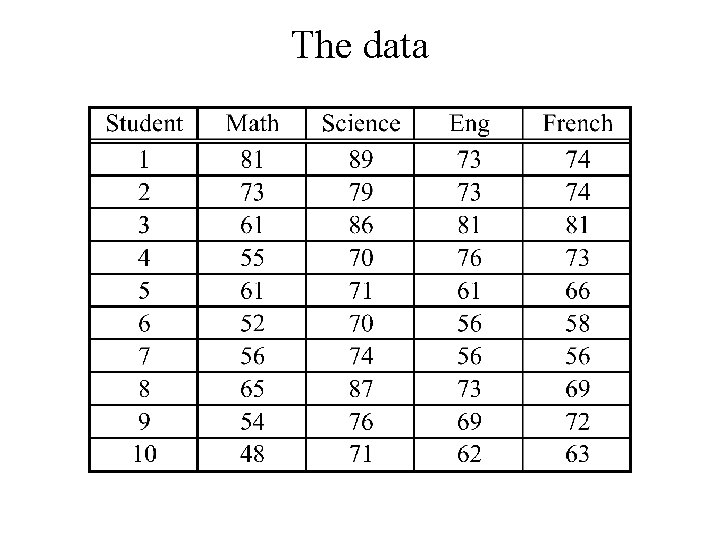
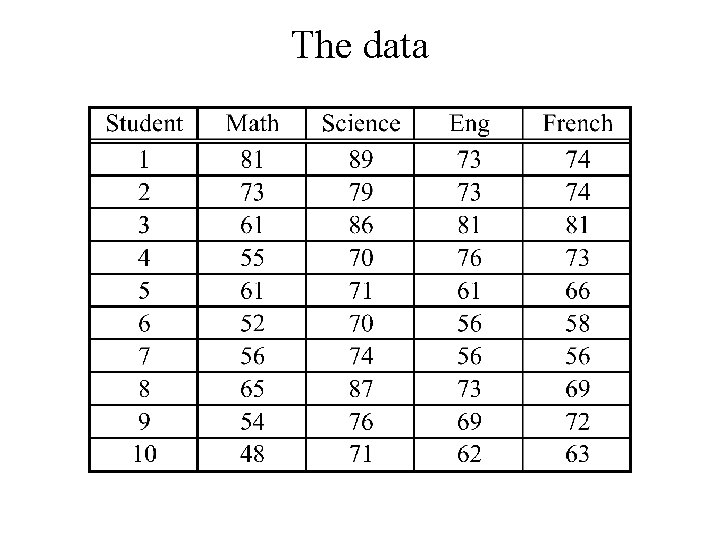
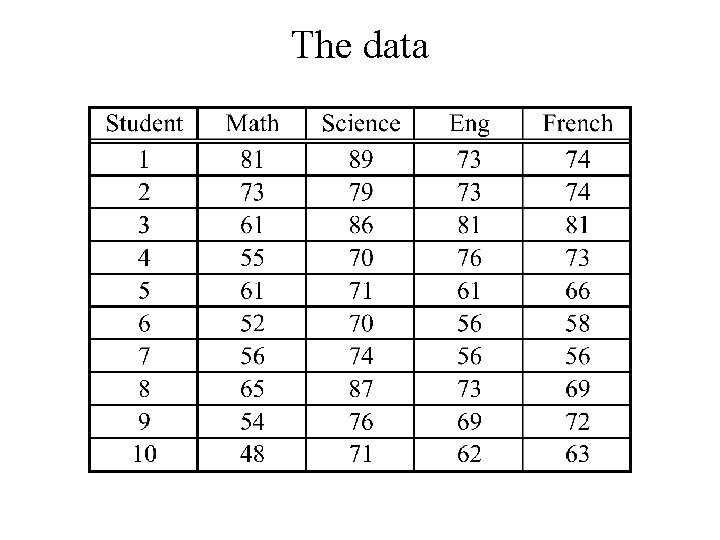
Example For n = 10 students we measure scores on – Math proficiency test (x 1), – Science proficiency test (x 2), – English proficiency test (x 3) and – French proficiency test (x 4) The average score for each of the tests in previous years was 60. Has this changed?

The data

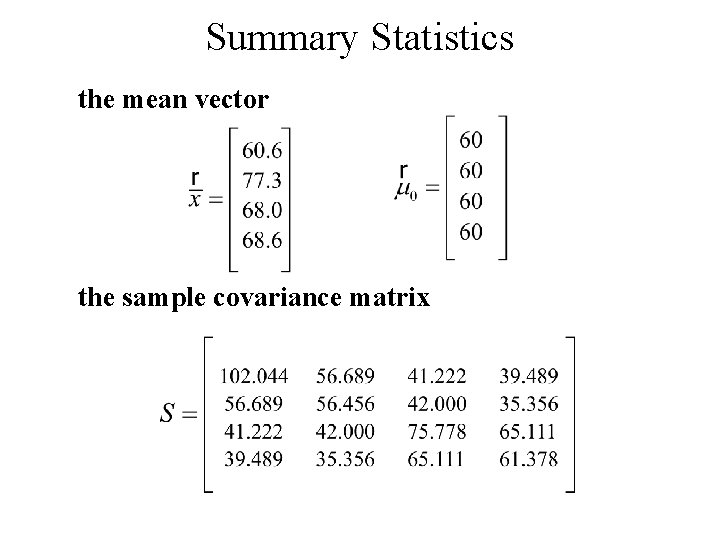
Summary Statistics the mean vector the sample covariance matrix

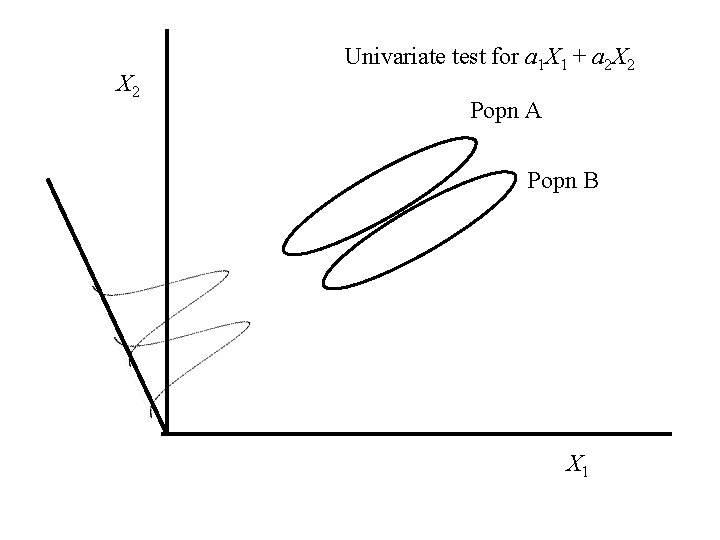
Roy’s Union- Intersection Principle This is a general procedure for developing a multivariate test from the corresponding univariate test. 1. Convert the multivariate problem to a univariate problem by considering an arbitrary linear combination of the observation vector.

2. 3. 4. 5. 6. Perform the test for the arbitrary linear combination of the observation vector. Repeat this for all possible choices of Reject the multivariate hypothesis if H 0 is rejected for any one of the choices for Accept the multivariate hypothesis if H 0 is accepted for all of the choices for Set the type I error rate for the individual tests so that the type I error rate for the multivariate test is a.

Application of Roy’s principle to the following situation Let denote a sample of n from the p-variate normal distribution with mean vector and covariance matrix S. Suppose we want to test Then u 1, …. un is a sample of n from the normal distribution with mean and variance.

to test we would use the test statistic:
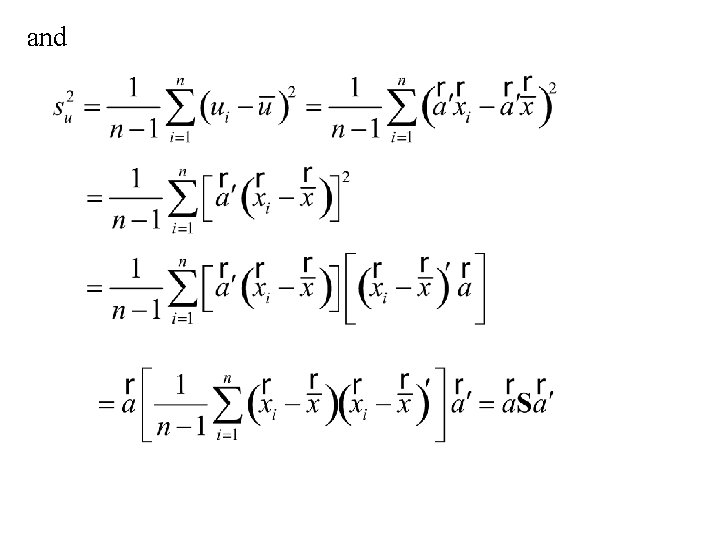
and
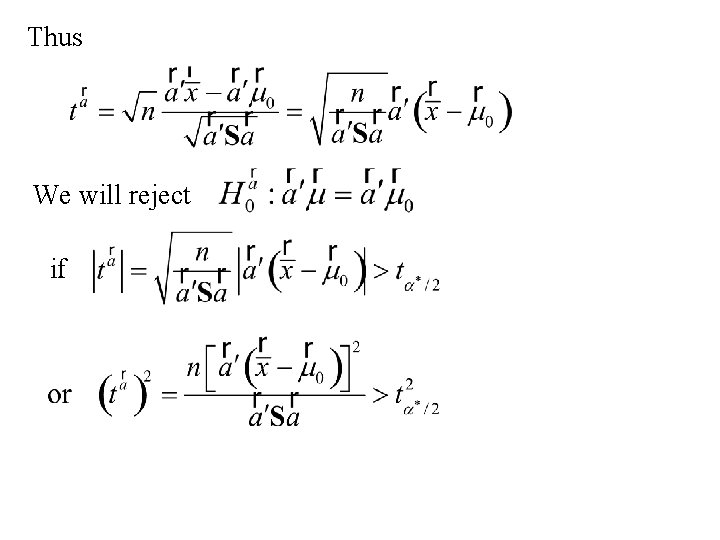
Thus We will reject if

Using Roy’s Union- Intersection principle: We will reject We accept
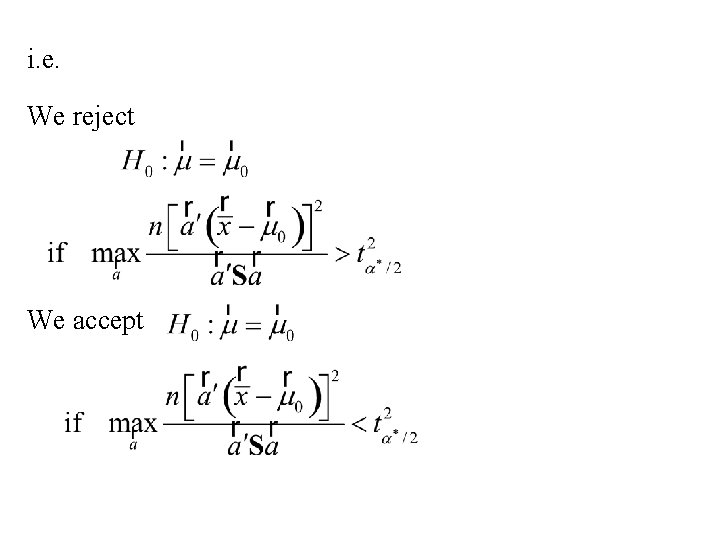
i. e. We reject We accept

Consider the problem of finding: where
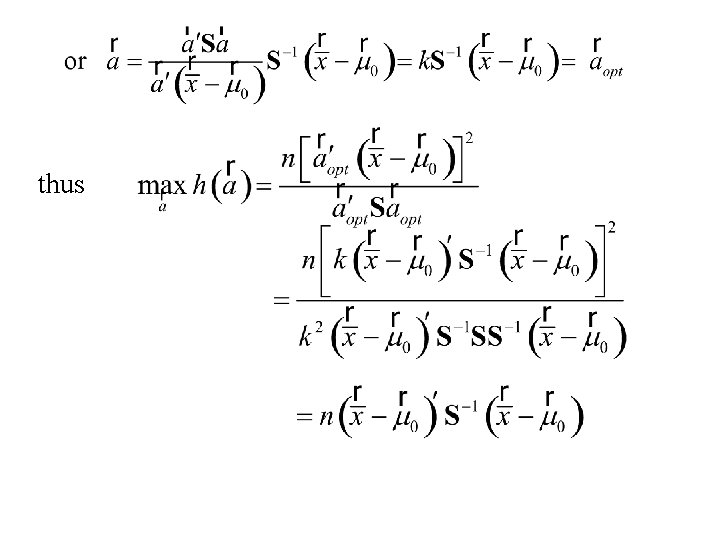
thus

Thus Roy’s Union- Intersection principle states: We reject We accept is called Hotelling’s T 2 statistic

Choosing the critical value for Hotelling’s T 2 statistic We reject , we need to find the sampling distribution of T 2 when H 0 is true. It turns out that if H 0 is true than has an F distribution with n 1 = p and n 2 = n - p
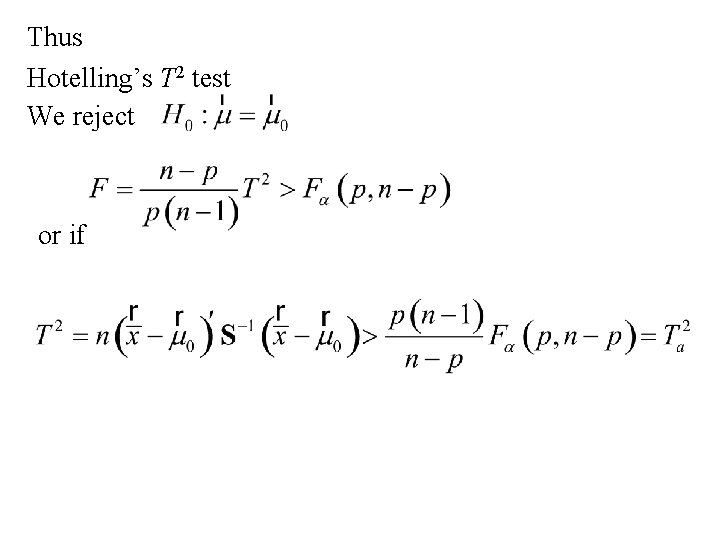
Thus Hotelling’s T 2 test We reject or if

Another derivation of Hotelling’s T 2 statistic Another method of developing statistical tests is the Likelihood ratio method. Suppose that the data vector, , has joint density Suppose that the parameter vector, , belongs to the set W. Let w denote a subset of W. Finally we want to test

The Likelihood ratio test rejects H 0 if

The situation Let denote a sample of n from the p-variate normal distribution with mean vector and covariance matrix S. Suppose we want to test

The Likelihood function is: and the Log-likelihood function is:

the Maximum Likelihood estimators of are and

the Maximum Likelihood estimators of when H 0 is true are: and

The Likelihood function is: now
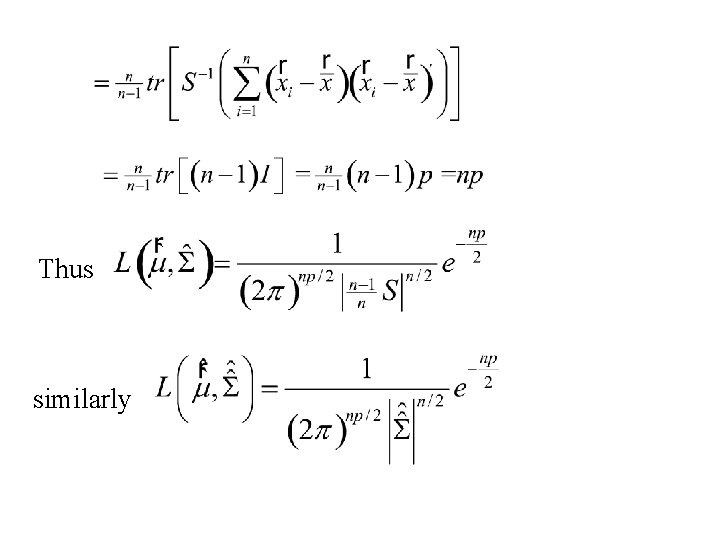
Thus similarly

and
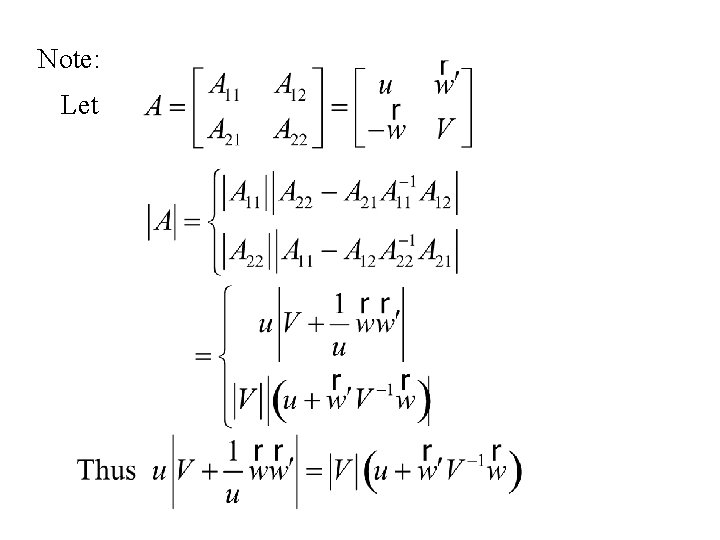
Note: Let

and Now and
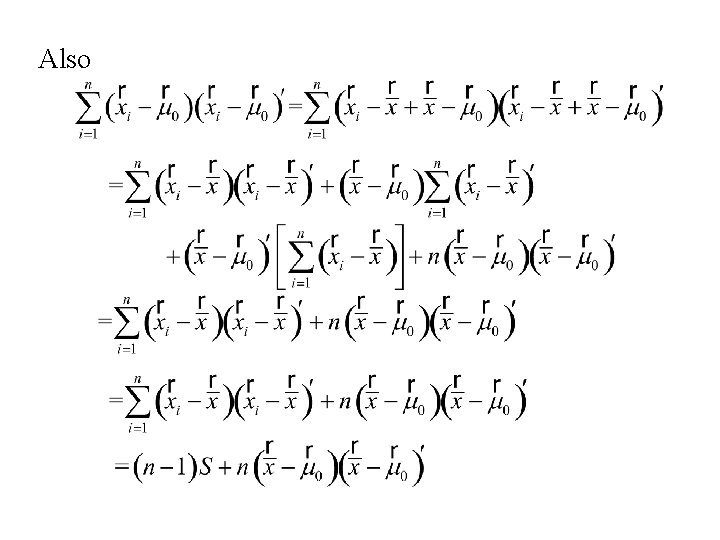
Also
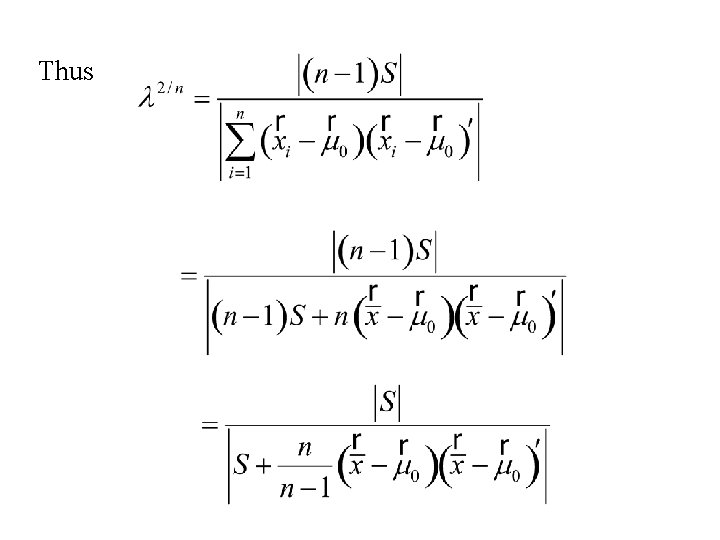
Thus

Thus using

Then Thus to reject H 0 if l < la This is the same as Hotelling’s T 2 test if

Example For n = 10 students we measure scores on – Math proficiency test (x 1), – Science proficiency test (x 2), – English proficiency test (x 3) and – French proficiency test (x 4) The average score for each of the tests in previous years was 60. Has this changed?

The data

Summary Statistics

Inference for the mean vector

Univariate Inference Let x 1, x 2, … , xn denote a sample of n from the normal distribution with mean m and variance s 2. Suppose we want to test H 0: m = m 0 vs HA : m ≠ m 0 The appropriate test is the t test: The test statistic: Reject H 0 if |t| > ta/2

Hotelling’s T 2 statistic and test We reject

Example For n = 10 students we measure scores on – Math proficiency test (x 1), – Science proficiency test (x 2), – English proficiency test (x 3) and – French proficiency test (x 4) The average score for each of the tests in previous years was 60. Has this changed?

The data

Summary Statistics

The two sample problem

Univariate Inference Let x 1, x 2, … , xn denote a sample of n from the normal distribution with mean mx and variance s 2. Let y 1, y 2, … , ym denote a sample of n from the normal distribution with mean my and variance s 2. Suppose we want to test H 0: mx = my vs HA : mx ≠ my

The appropriate test is the t test: The test statistic: Reject H 0 if |t| > ta/2 d. f. = n + m -2

The multivariate Test Let denote a sample of n from the p-variate normal distribution with mean vector and covariance matrix S. Let denote a sample of m from the p-variate normal distribution with mean vector and covariance matrix S. Suppose we want to test

Hotelling’s T 2 statistic for the two sample problem if H 0 is true than has an F distribution with n 1 = p and n 2 = n +m – p - 1

Thus Hotelling’s T 2 test We reject

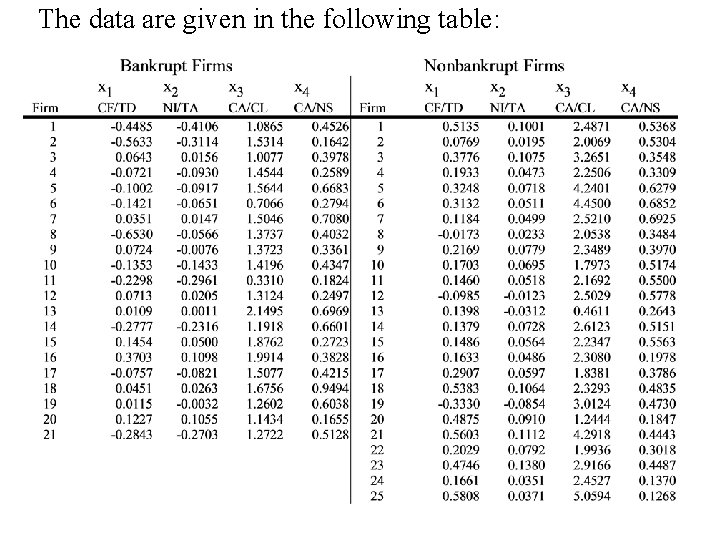
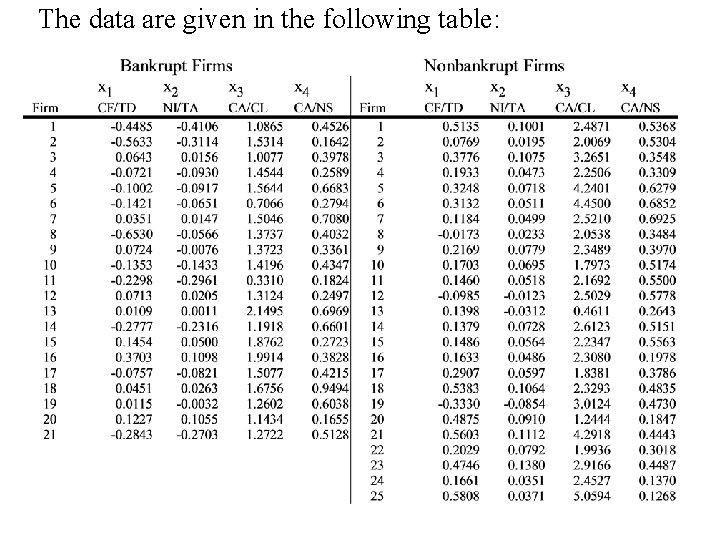
Example 2 Annual financial data are collected for firms approximately 2 years prior to bankruptcy and for financially sound firms at about the same point in time. The data on the four variables • x 1 = CF/TD = (cash flow)/(total debt), • x 2 = NI/TA = (net income)/(Total assets), • x 3 = CA/CL = (current assets)/(current liabilties, and • x 4 = CA/NS = (current assets)/(net sales) are given in the following table.

The data are given in the following table:

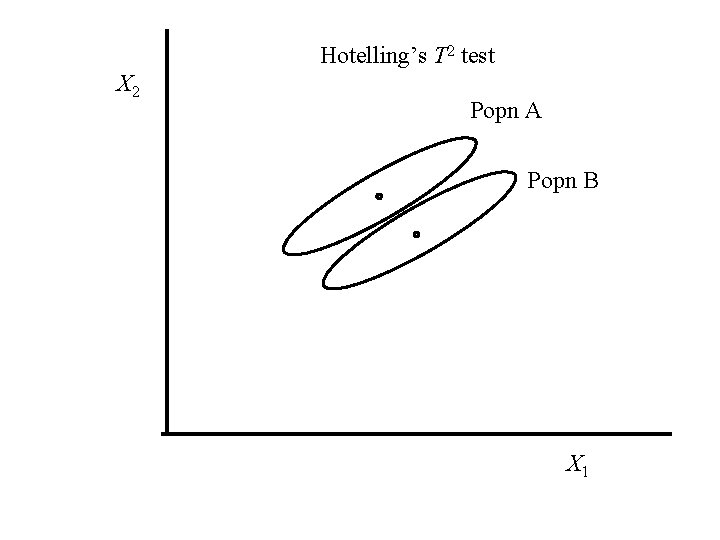
Hotelling’s T 2 test A graphical explanation

Hotelling’s T 2 statistic for the two sample problem

is the test statistic for testing:

Hotelling’s T 2 test X 2 Popn A Popn B X 1

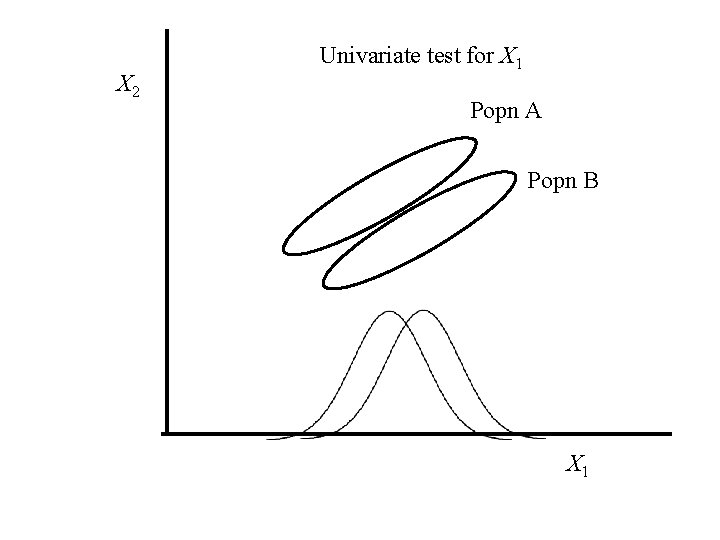
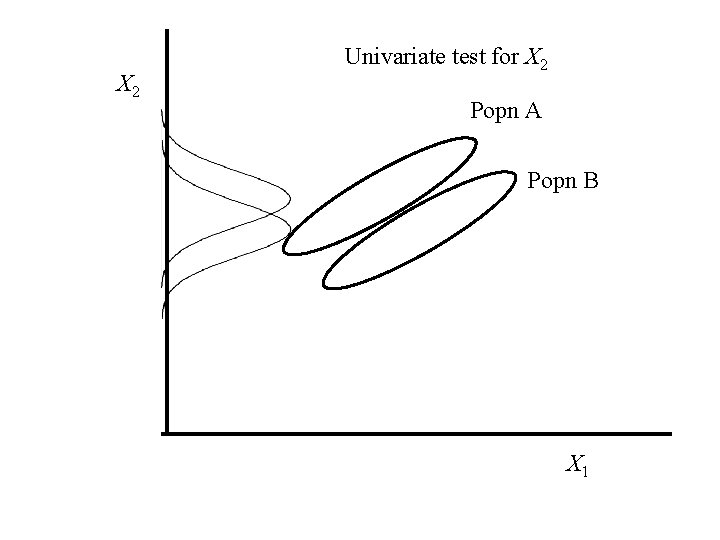
X 2 Univariate test for X 1 Popn A Popn B X 1

X 2 Univariate test for X 2 Popn A Popn B X 1

X 2 Univariate test for a 1 X 1 + a 2 X 2 Popn A Popn B X 1

Mahalanobis distance A graphical explanation

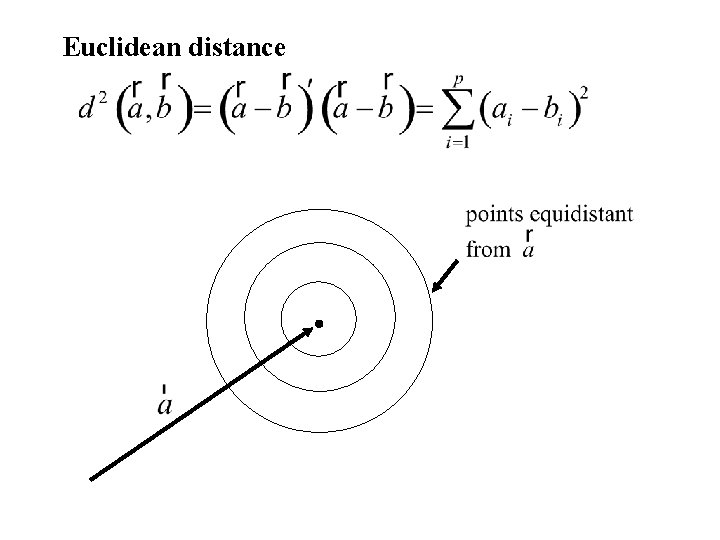
Euclidean distance

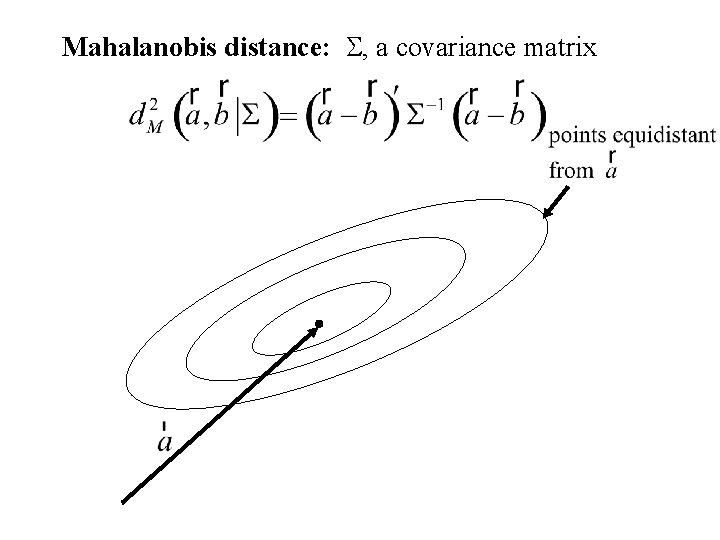
Mahalanobis distance: S, a covariance matrix

Hotelling’s T 2 statistic for the two sample problem

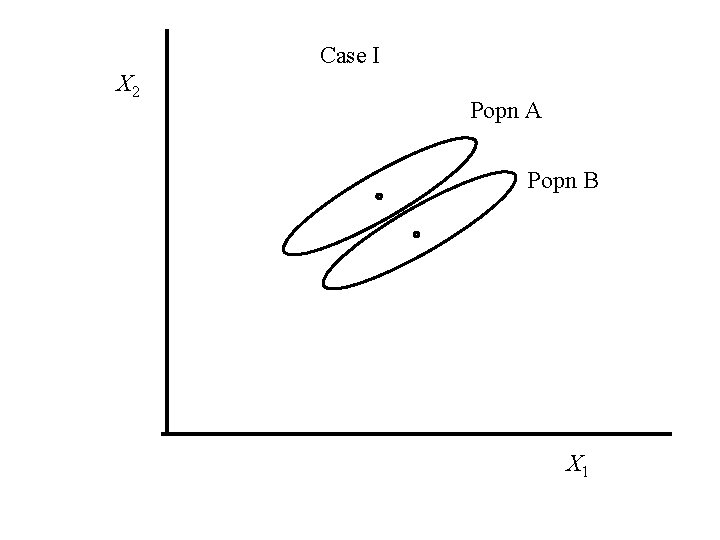
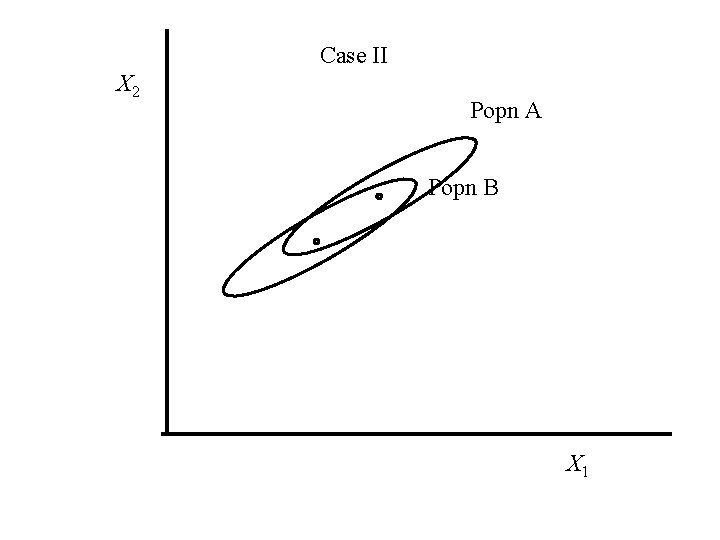
Case I X 2 Popn A Popn B X 1

Case II X 2 Popn A Popn B X 1

In Case I the Mahalanobis distance between the mean vectors is larger than in Case II, even though the Euclidean distance is smaller. In Case I there is more separation between the two bivariate normal distributions

Discrimination and Classification

Discrimination Situation: We have two or more populations p 1, p 2, etc (possibly p-variate normal). The populations are known (or we have data from each population) We have data for a new case (population unknown) and we want to identify the which population for which the new case is a member.

Examples

The Basic Problem Suppose that the data from a new case x 1, … , xp has joint density function either : p 1: f(x 1, … , xn) or p 2: g(x 1, … , xn) We want to make the decision to D 1: Classify the case in p 1 (f is the correct distribution) or D 2: Classify the case in p 2 (g is the correct distribution)

The Two Types of Errors 1. Misclassifying the case in p 1 when it actually lies in p 2. Let P[1|2] = P[D 1|p 2] = probability of this type of error 2. Misclassifying the case in p 2 when it actually lies in p 1. Let P[2|1] = P[D 2|p 1] = probability of this type of error This is similar Type I and Type II errors in hypothesis testing.

Note: A discrimination scheme is defined by splitting p – dimensional space into two regions. 1. C 1 = the region were we make the decision D 1. (the decision to classify the case in p 1) 2. C 2 = the region were we make the decision D 2. (the decision to classify the case in p 2)

There can be several approaches to determining the regions C 1 and C 2. All concerned with taking into account the probabilities of misclassification P[2|1] and P[1|2] 1. Set up the regions C 1 and C 2 so that one of the probabilities of misclassification , P[2|1] say, is at some low acceptable value a. Accept the level of the other probability of misclassification P[1|2] = b.

2. Set up the regions C 1 and C 2 so that the total probability of misclassification: P[Misclassification] = P[1] P[2|1] + P[2]P[1|2] is minimized P[1] = P[the case belongs to p 1] P[2] = P[the case belongs to p 2]

3. Set up the regions C 1 and C 2 so that the total expected cost of misclassification: E[Cost of Misclassification] = c 2|1 P[1] P[2|1] + c 1|2 P[2]P[1|2] is minimized P[1] = P[the case belongs to p 1] P[2] = P[the case belongs to p 2] c 2|1= the cost of misclassifying the case in p 2 when the case belongs to p 1. c 1|2= the cost of misclassifying the case in p 1 when the case belongs to p 2.

4. Set up the regions C 1 and C 2 The two types of error are equal: P[2|1] = P[1|2]
![Computer security p 1 Valid users p 2 Imposters P21 Pidentifying a valid Computer security: p 1: Valid users p 2: Imposters P[2|1] = P[identifying a valid](https://slidetodoc.com/presentation_image_h2/43c9d4b2294c8a24f7cddea5049f0f8f/image-76.jpg)
Computer security: p 1: Valid users p 2: Imposters P[2|1] = P[identifying a valid user as an imposter] P[1|2] = P[identifying an imposter as a valid user ] P[1] = P[valid user] P[2] = P[imposter] c 2|1= the cost of identifying the user as an imposter when the user is a valid user. c 1|2= the cost of identifying the user as a valid user when the user is an imposter.

This problem can be viewed as an Hypothesis testing problem H 0: p 1 is the correct population HA: p 2 is the correct population P[2|1] = a P[1|2] = b Power = 1 - b

The Neymann-Pearson Lemma Suppose that the data x 1, … , xn has joint density function f(x 1, … , xn ; q) where q is either q 1 or q 2. Let g(x 1, … , xn) = f(x 1, … , xn ; q 1) and h(x 1, … , xn) = f(x 1, … , xn ; q 2) We want to test H 0: q = q 1 (g is the correct distribution) against HA: q = q 2 (h is the correct distribution)

The Neymann-Pearson Lemma states that the Uniformly Most Powerful (UMP) test of size a is to reject H 0 if: and accept H 0 if: where ka is chosen so that the test is of size a.

Proof: Let C be the critical region of any test of size We want to show that Note: a. Let

hence and Thus

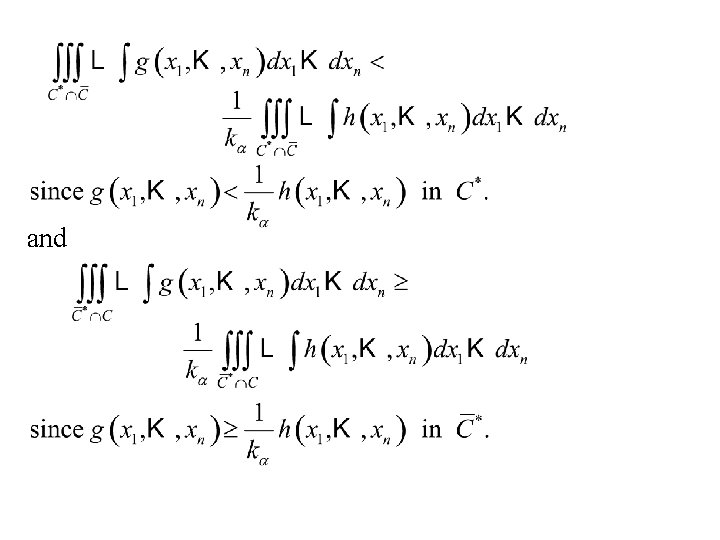
and

Thus and when we add the common quantity Q. E. D. to both sides.

Fishers Linear Discriminant Function. Suppose that x 1, … , xp is either data from a p-variate Normal distribution with mean vector: The covariance matrix S is the same for both populations p 1 and p 2.

The Neymann-Pearson Lemma states that we should classify into populations p 1 and p 2 using: That is make the decision D 1 : population is p 1 if l ≥ ka

or or and Finally we make the decision D 1 : population is p 1 if where

The function Is called Fisher’s linear discriminant function

In the case where the populations are unknown but estimated from data Fisher’s linear discriminant function




Example 2 Annual financial data are collected for firms approximately 2 years prior to bankruptcy and for financially sound firms at about the same point in time. The data on the four variables • x 1 = CF/TD = (cash flow)/(total debt), • x 2 = NI/TA = (net income)/(Total assets), • x 3 = CA/CL = (current assets)/(current liabilties, and • x 4 = CA/NS = (current assets)/(net sales) are given in the following table.

The data are given in the following table:
 John 10:22-28
John 10:22-28 Univariate statistical tests
Univariate statistical tests Univariat dan bivariat
Univariat dan bivariat Univariate verfahren
Univariate verfahren Univariate analysis spss
Univariate analysis spss Univariate eda
Univariate eda Bivariate transformation of random variables
Bivariate transformation of random variables Normal equation logistic regression
Normal equation logistic regression Univariate anova
Univariate anova Experimental research design types
Experimental research design types Univariate vs multivariate
Univariate vs multivariate Univariate analysis excel
Univariate analysis excel What are i and j in vectors
What are i and j in vectors Cosenos directores de un vector
Cosenos directores de un vector Why is vector resolution the opposite of vector addition
Why is vector resolution the opposite of vector addition Define position vector with example
Define position vector with example Let's let them object to another one
Let's let them object to another one Go to my house
Go to my house Let him who has ears to hear
Let him who has ears to hear What does inferance mean
What does inferance mean Matriks kovarian adalah
Matriks kovarian adalah Let t(x y) mean that students like cuisine y
Let t(x y) mean that students like cuisine y Formuö
Formuö Typiska novell drag
Typiska novell drag Nationell inriktning för artificiell intelligens
Nationell inriktning för artificiell intelligens Ekologiskt fotavtryck
Ekologiskt fotavtryck Shingelfrisyren
Shingelfrisyren En lathund för arbete med kontinuitetshantering
En lathund för arbete med kontinuitetshantering Kassaregister ideell förening
Kassaregister ideell förening Vilotidsbok
Vilotidsbok Anatomi organ reproduksi
Anatomi organ reproduksi Förklara densitet för barn
Förklara densitet för barn Datorkunskap för nybörjare
Datorkunskap för nybörjare Stig kerman
Stig kerman Mall för debattartikel
Mall för debattartikel Delegerande ledarskap
Delegerande ledarskap Nyckelkompetenser för livslångt lärande
Nyckelkompetenser för livslångt lärande Påbyggnader för flakfordon
Påbyggnader för flakfordon Kraft per area
Kraft per area Offentlig förvaltning
Offentlig förvaltning Jag har nigit för nymånens skära text
Jag har nigit för nymånens skära text Presentera för publik crossboss
Presentera för publik crossboss Teckenspråk minoritetsspråk argument
Teckenspråk minoritetsspråk argument Vem räknas som jude
Vem räknas som jude Klassificeringsstruktur för kommunala verksamheter
Klassificeringsstruktur för kommunala verksamheter Fimbrietratt
Fimbrietratt Claes martinsson
Claes martinsson Centrum för kunskap och säkerhet
Centrum för kunskap och säkerhet Lågenergihus nyproduktion
Lågenergihus nyproduktion Mat för unga idrottare
Mat för unga idrottare Verktyg för automatisering av utbetalningar
Verktyg för automatisering av utbetalningar Rutin för avvikelsehantering
Rutin för avvikelsehantering Smärtskolan kunskap för livet
Smärtskolan kunskap för livet Ministerstyre för och nackdelar
Ministerstyre för och nackdelar Tack för att ni har lyssnat
Tack för att ni har lyssnat Vad är referatmarkeringar
Vad är referatmarkeringar Redogör för vad psykologi är
Redogör för vad psykologi är Borstål, egenskaper
Borstål, egenskaper Tack för att ni har lyssnat
Tack för att ni har lyssnat Borra hål för knoppar
Borra hål för knoppar Orubbliga rättigheter
Orubbliga rättigheter Formula varians
Formula varians Tack för att ni har lyssnat
Tack för att ni har lyssnat Rita perspektiv
Rita perspektiv Verksamhetsanalys exempel
Verksamhetsanalys exempel Tobinskatten för och nackdelar
Tobinskatten för och nackdelar Toppslätskivling dos
Toppslätskivling dos Gibbs reflekterande cykel
Gibbs reflekterande cykel Egg för emanuel
Egg för emanuel Elektronik för barn
Elektronik för barn Plagg i gamla rom
Plagg i gamla rom Strategi för svensk viltförvaltning
Strategi för svensk viltförvaltning Kung dog 1611
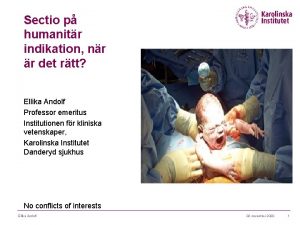
Kung dog 1611 Humanitr
Humanitr Ro i rom pax
Ro i rom pax Tack för att ni lyssnade
Tack för att ni lyssnade Enheter för massa
Enheter för massa Form dikt
Form dikt Inköpsprocessen steg för steg
Inköpsprocessen steg för steg Fuktmätningar i betong enlig rbk
Fuktmätningar i betong enlig rbk Etik och ledarskap etisk kod för chefer
Etik och ledarskap etisk kod för chefer Hur stor skarns är det för ett barn att få cancer
Hur stor skarns är det för ett barn att få cancer Myndigheten för delaktighet
Myndigheten för delaktighet Trög för kemist
Trög för kemist Tillitsbaserad ledning
Tillitsbaserad ledning Läkarutlåtande för livränta
Läkarutlåtande för livränta Karttecken
Karttecken Ramsa geometriska former
Ramsa geometriska former Texter för hinduer tantra
Texter för hinduer tantra Mitos steg
Mitos steg Bris för vuxna
Bris för vuxna Big brother rösta
Big brother rösta Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Lp html
Lp html Bổ thể
Bổ thể