Vector and Vector Resolution Scalar Vector Vectors Vector

Vector and Vector Resolution

Scalar

Vector

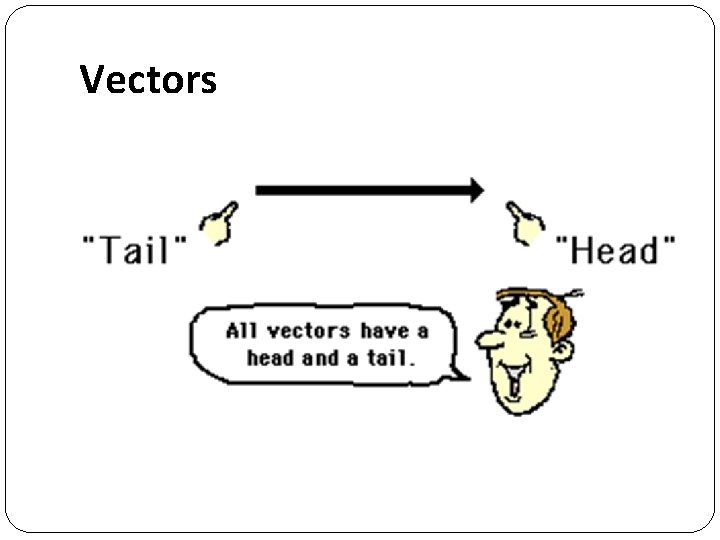
Vectors

Vector Addition • VECTOR ADDITION – If 2 similar vectors point in the SAME direction, add them. • Example: A man walks 54. 5 meters east, then another 30 meters east. Calculate his displacement relative to where he started.

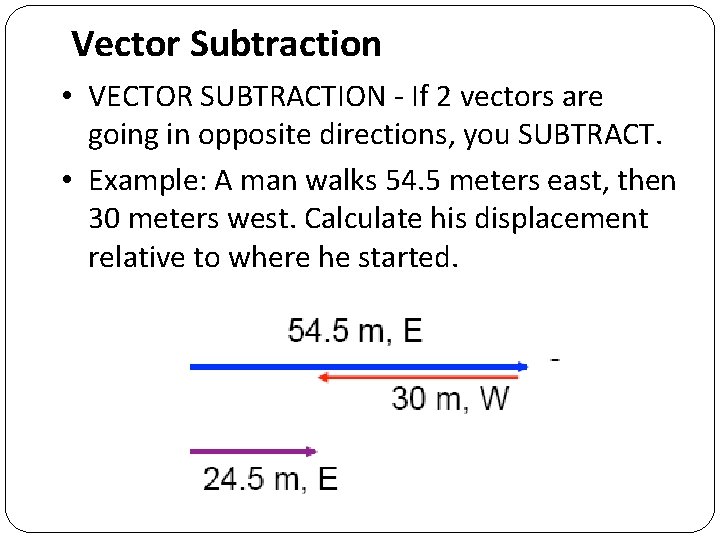
Vector Subtraction • VECTOR SUBTRACTION - If 2 vectors are going in opposite directions, you SUBTRACT. • Example: A man walks 54. 5 meters east, then 30 meters west. Calculate his displacement relative to where he started.

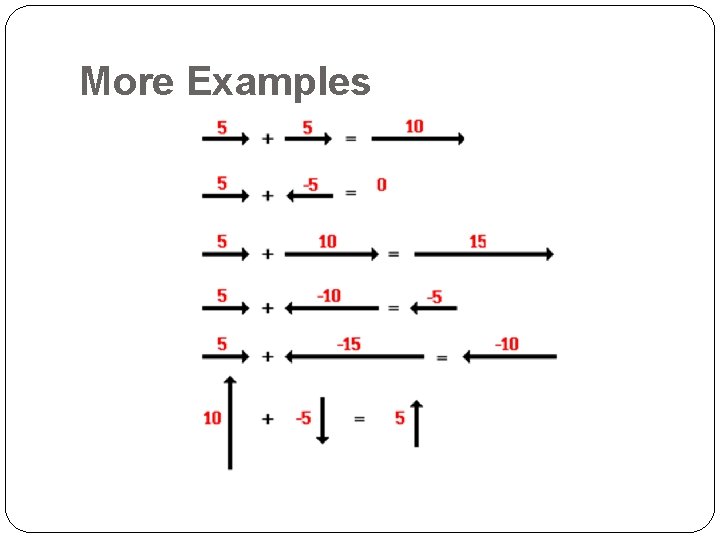
More Examples

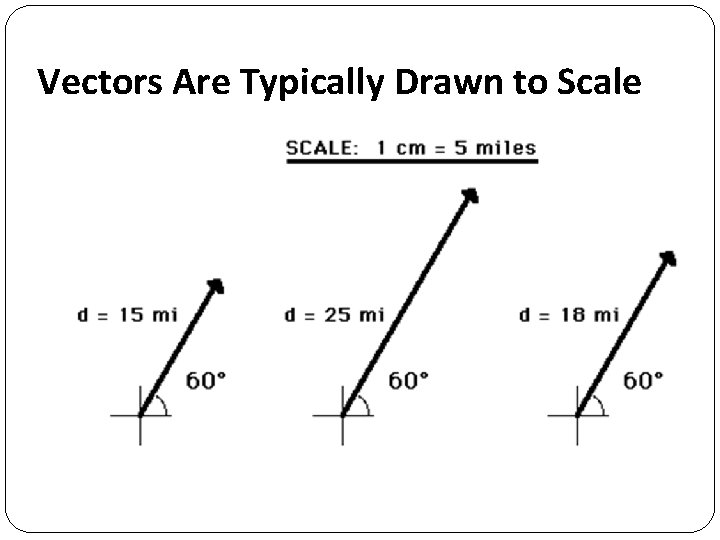
Vectors Are Typically Drawn to Scale

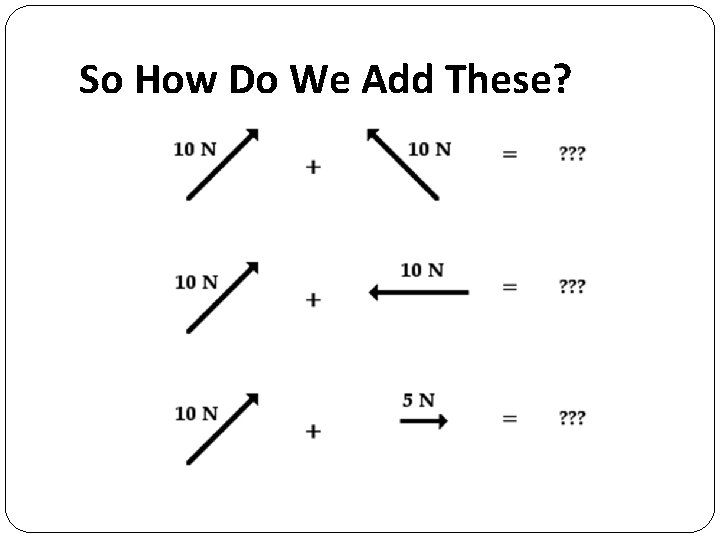
So How Do We Add These?

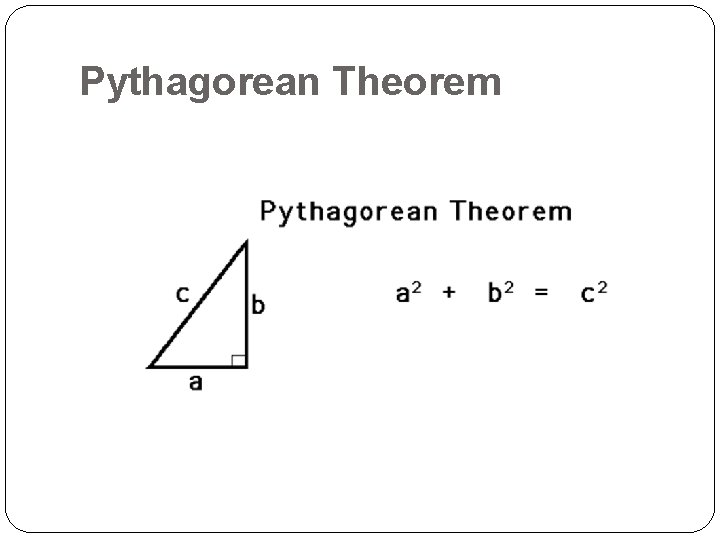
Pythagorean Theorem

Example

Resultant and Components �Resultant - The “result” from adding or subtracting vectors. �Components- The legs of the triangle or the parts that make up the resultant.

Adding Vectors that are at different angles �Head to Tail Method – easiest method to use to add vectors; always add vectors “head to tail” �Parallelogram Method- another way to add vectors �Graphical Method- another way to add vectors; involves drawing to scale and measuring

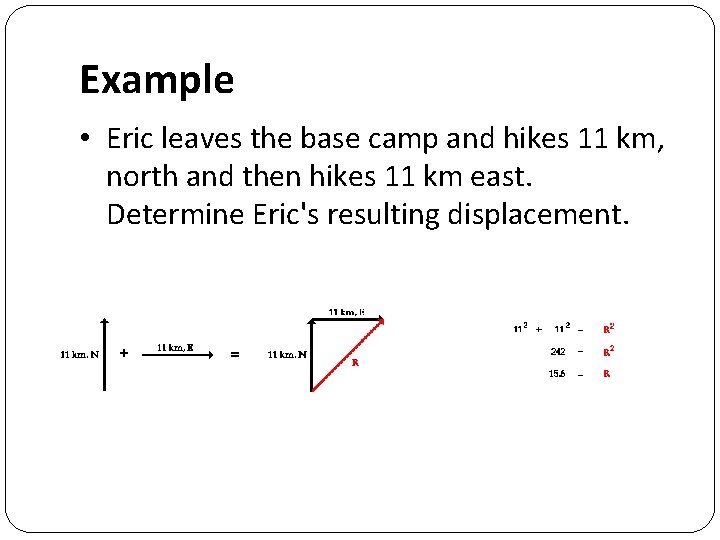
Example • Eric leaves the base camp and hikes 11 km, north and then hikes 11 km east. Determine Eric's resulting displacement.

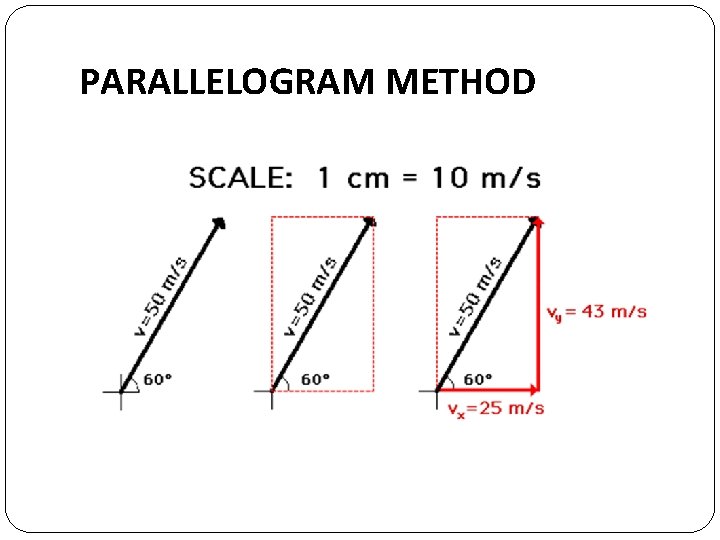
PARALLELOGRAM METHOD

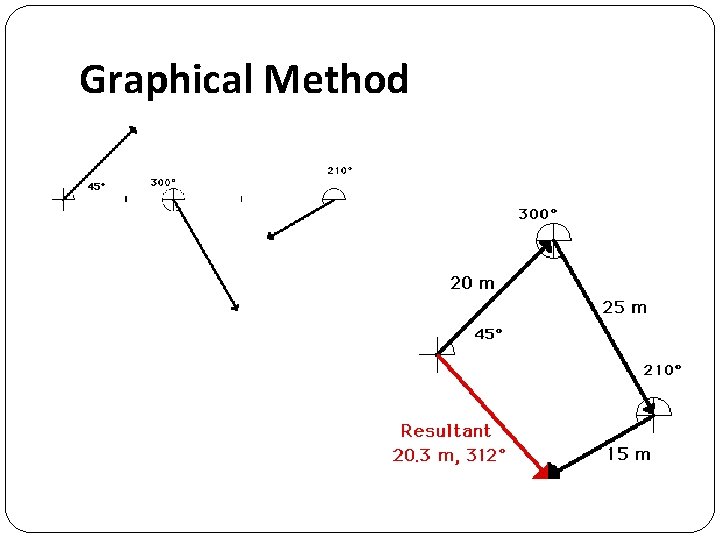
Graphical Method

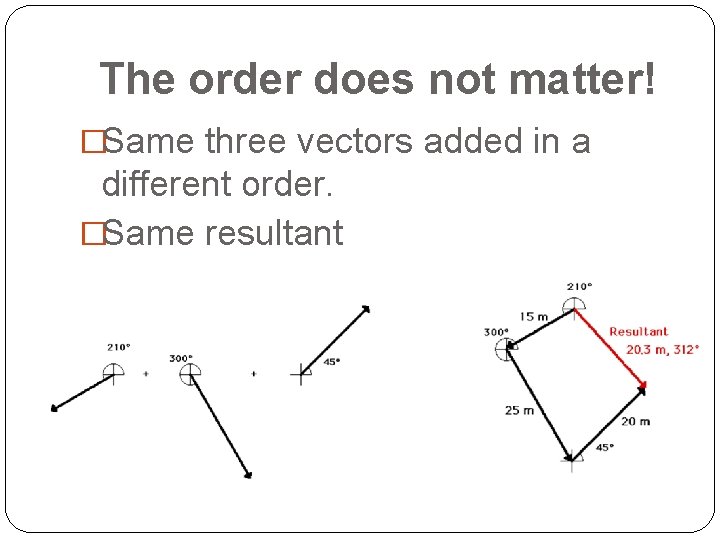
The order does not matter! �Same three vectors added in a different order. �Same resultant

Animation

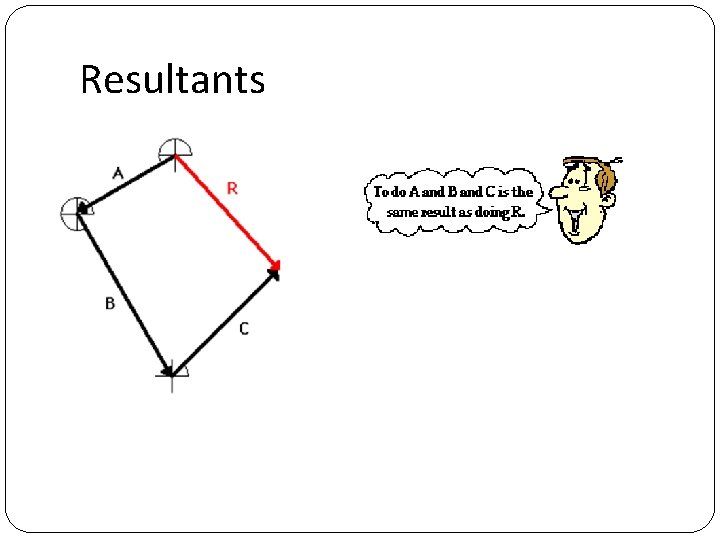
Resultants

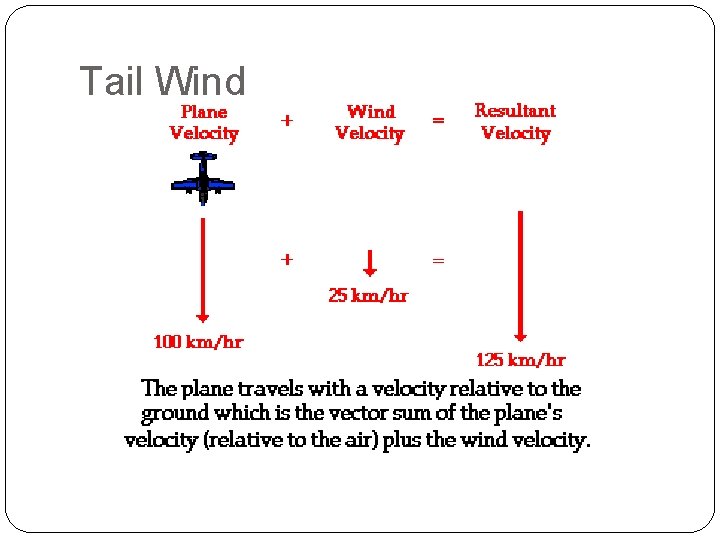
Tail Wind

Head Wind

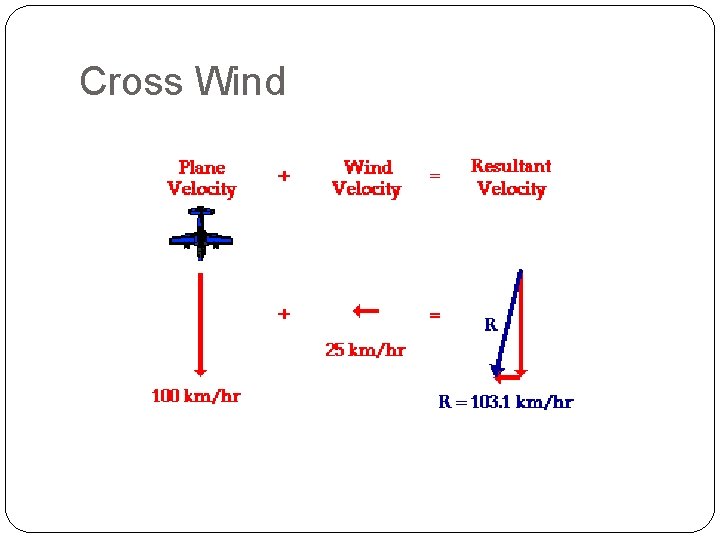
Cross Wind

To calculate velocity • • • (100 km/hr)2 + (25 km/hr)2 = R 2 10000 km 2/hr 2 + 625 km 2/hr 2 = R 2 10625 km 2/hr 2 = R 2 SQRT(10 625 km 2/hr 2) = R 103. 1 km/hr = R

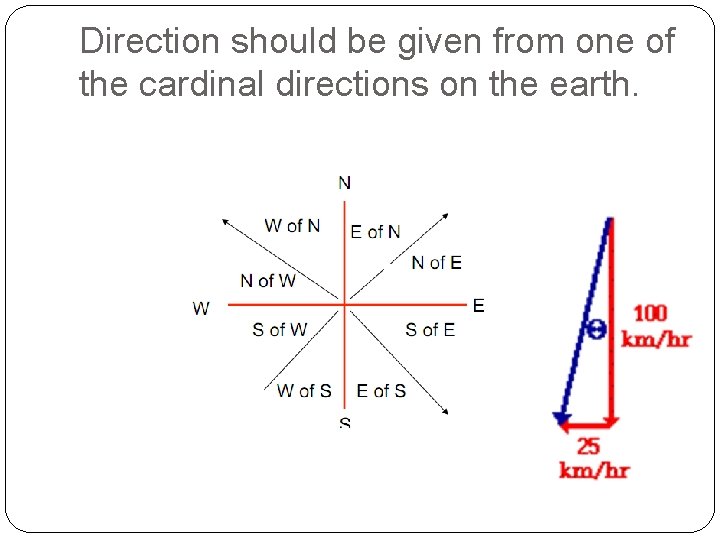
Vectors include direction! �Therefore anytime we are dealing with a direction we must give direction. If it is not due north, south, east, or west, an angle must also be given. • • tan q= (opposite/adjacent) tan q= (25/100) q = inverse tan (25/100) q = 14. 0 degrees

Direction should be given from one of the cardinal directions on the earth.

Animation

Example • A boat moves with a velocity of 15 m/s, N in a river which flows with a velocity of 8. 0 m/s, west. Calculate the boat's resultant velocity with respect to due north.

Sometimes we need to find the components of a vector �Vector resolution is the process of breaking down one vector into its parts called components. �Components are two vectors added together which give the resultant. �When asked or necessary, you will need to find the values of both components. �These are generally given from a cardinal direction on the earth (N, S, E, W) or horizontal or vertical.

Example • A plane moves with a velocity of 63. 5 m/s at 32 degrees South of East. Calculate the plane's horizontal and vertical velocity components.