Inference for the mean vector Univariate Inference Let







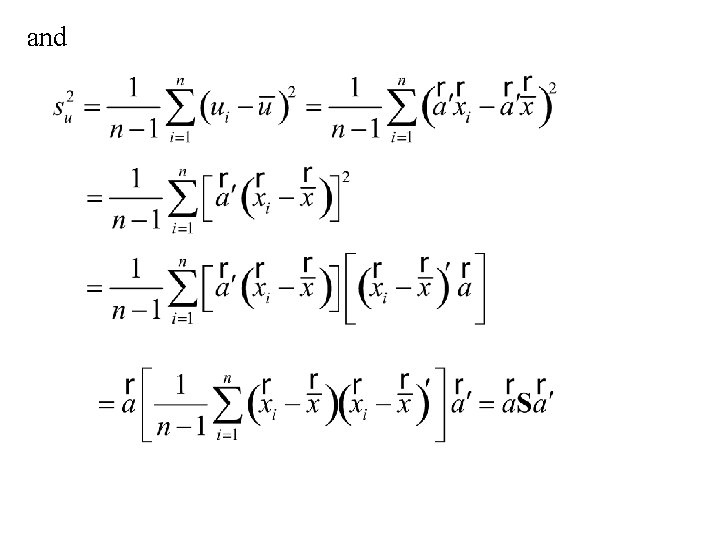
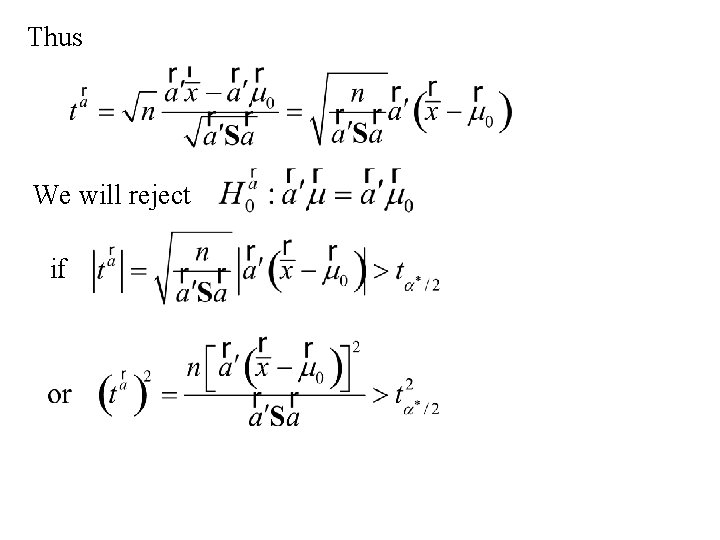

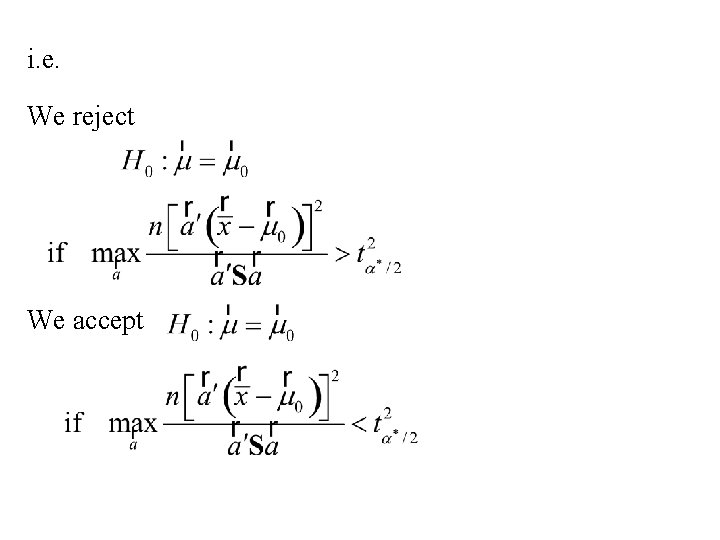

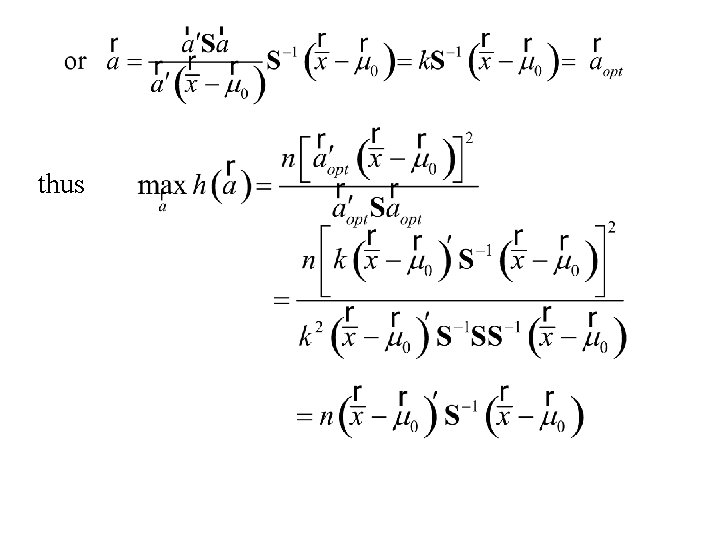


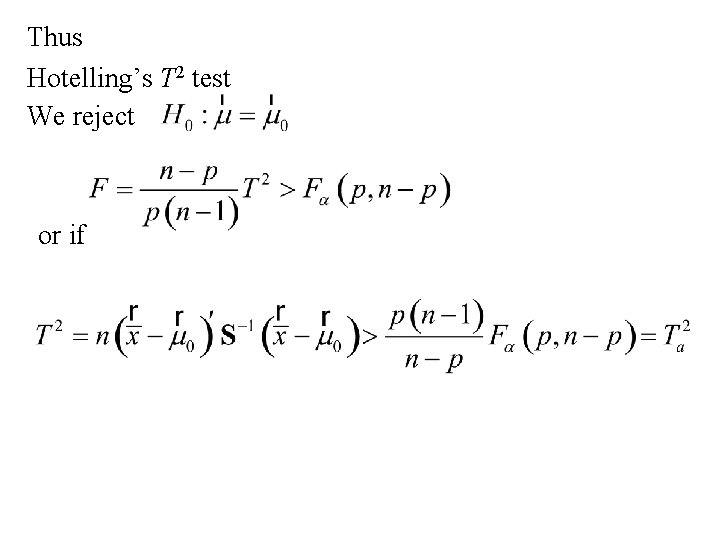







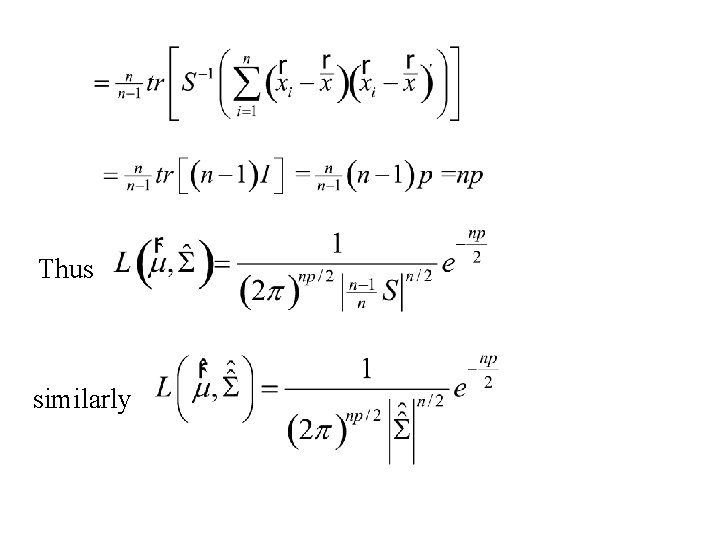

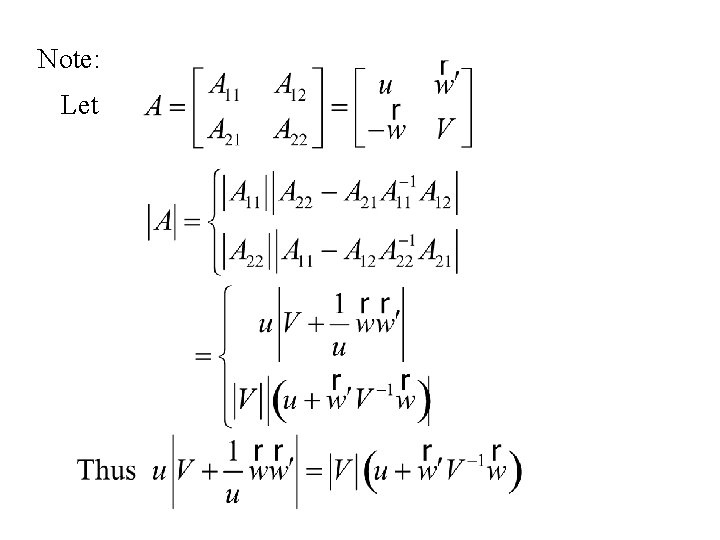

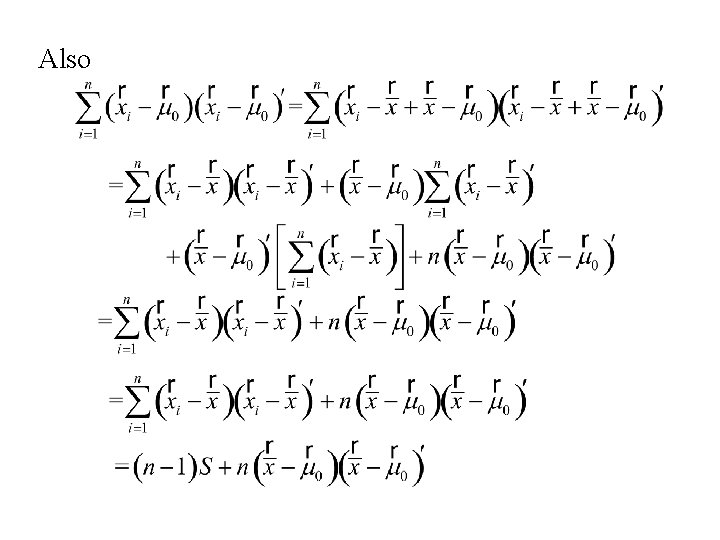
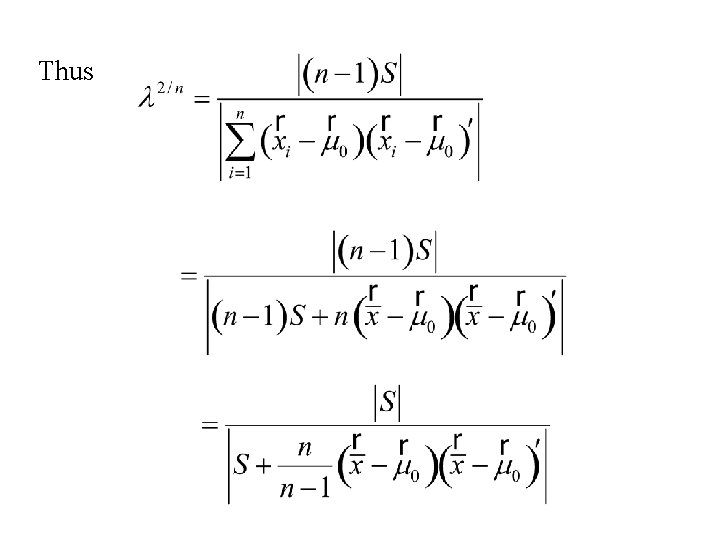






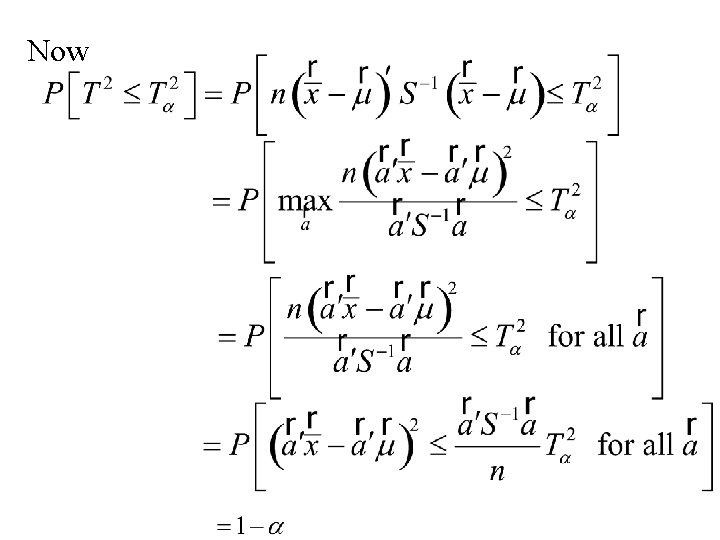









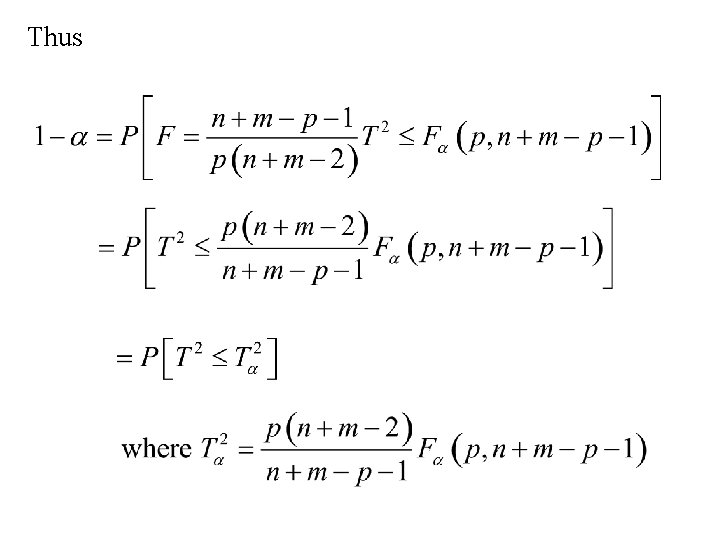
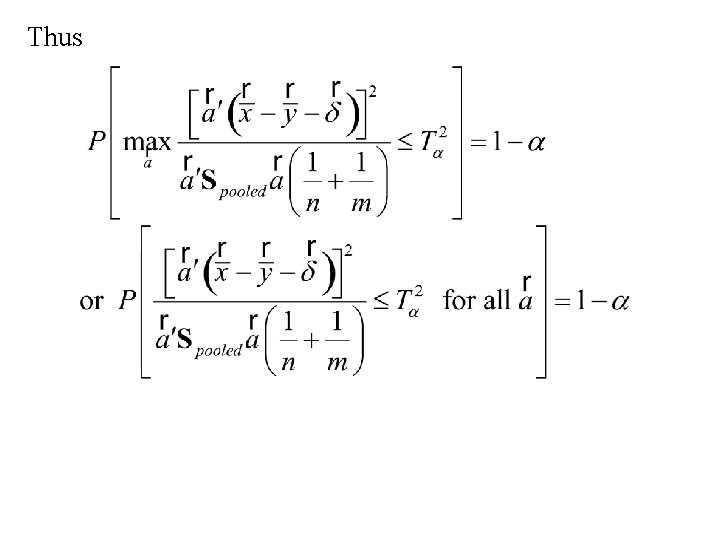
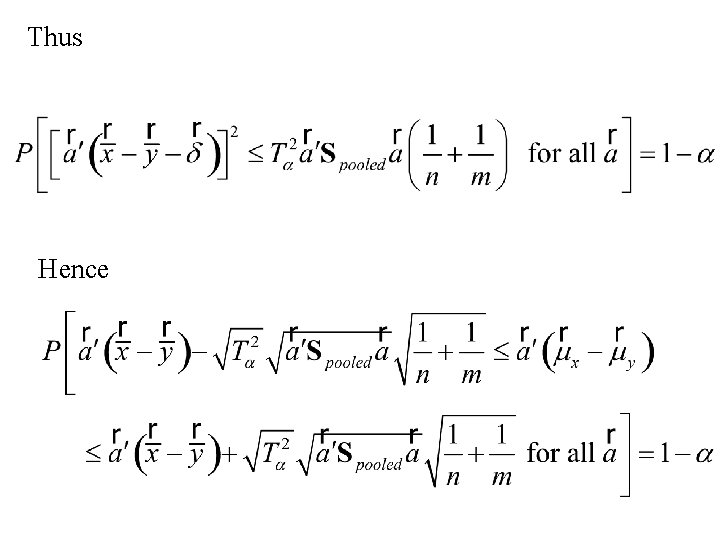







- Slides: 63

Inference for the mean vector

Univariate Inference Let x 1, x 2, … , xn denote a sample of n from the normal distribution with mean m and variance s 2. Suppose we want to test H 0: m = m 0 vs HA : m ≠ m 0 The appropriate test is the t test: The test statistic: Reject H 0 if |t| > ta/2

The multivariate Test Let denote a sample of n from the p-variate normal distribution with mean vector and covariance matrix S. Suppose we want to test

Roy’s Union- Intersection Principle This is a general procedure for developing a multivariate test from the corresponding univariate test. 1. Convert the multivariate problem to a univariate problem by considering an arbitrary linear combination of the observation vector.

2. 3. 4. 5. 6. Perform the test for the arbitrary linear combination of the observation vector. Repeat this for all possible choices of Reject the multivariate hypothesis if H 0 is rejected for any one of the choices for Accept the multivariate hypothesis if H 0 is accepted for all of the choices for Set the type I error rate for the individual tests so that the type I error rate for the multivariate test is a.

Application of Roy’s principle to the following situation Let denote a sample of n from the p-variate normal distribution with mean vector and covariance matrix S. Suppose we want to test Then u 1, …. un is a sample of n from the normal distribution with mean and variance.

to test we would use the test statistic:
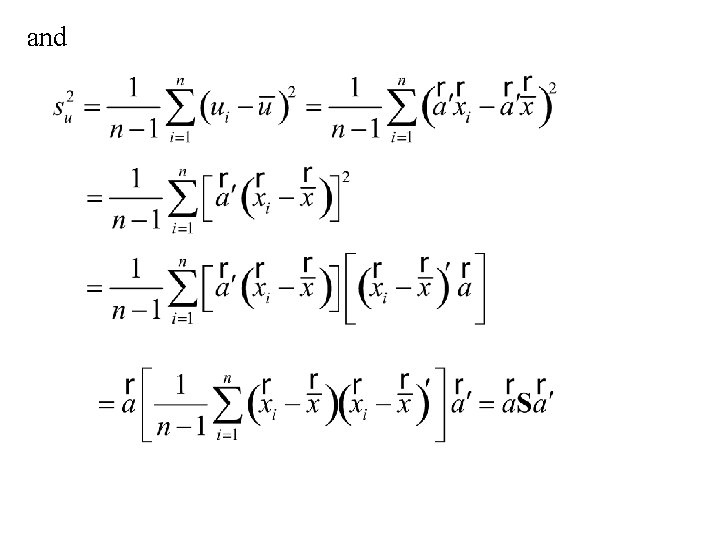
and
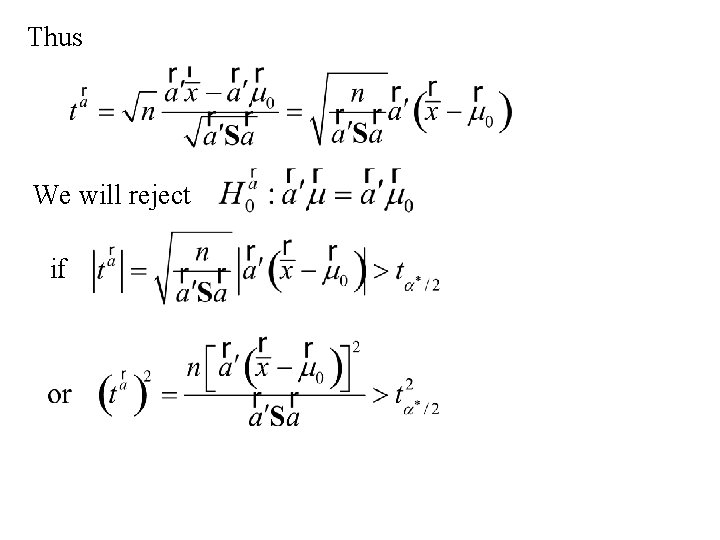
Thus We will reject if

Using Roy’s Union- Intersection principle: We will reject We accept
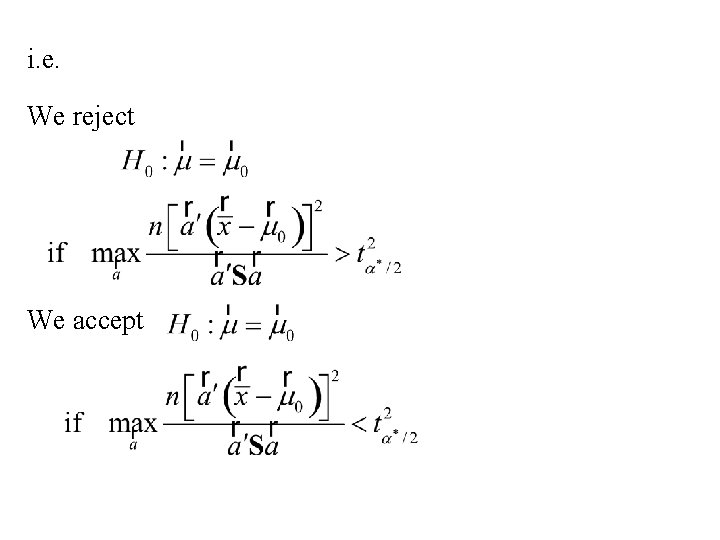
i. e. We reject We accept

Consider the problem of finding: where
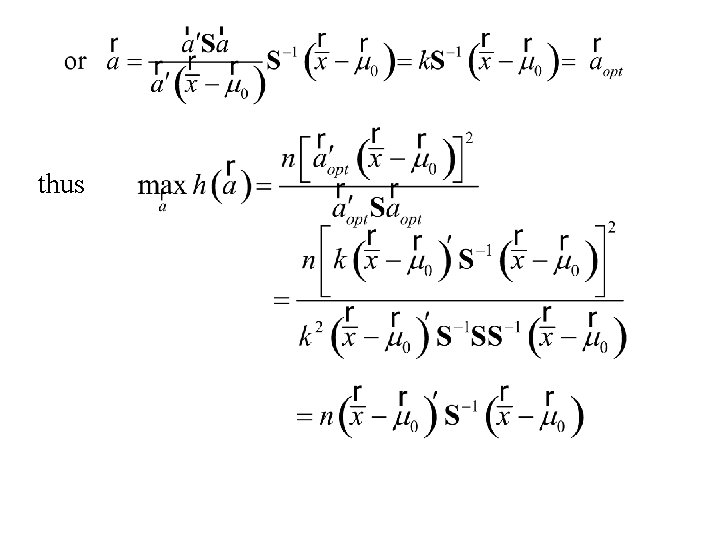
thus

Thus Roy’s Union- Intersection principle states: We reject We accept is called Hotelling’s T 2 statistic

Choosing the critical value for Hotelling’s T 2 statistic We reject , we need to find the sampling distribution of T 2 when H 0 is true. It turns out that if H 0 is true than has an F distribution with n 1 = p and n 2 = n - p
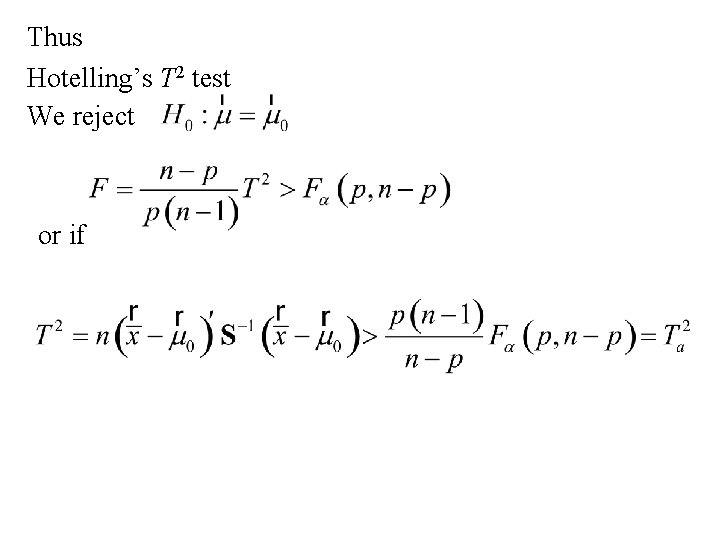
Thus Hotelling’s T 2 test We reject or if

Another derivation of Hotelling’s T 2 statistic Another method of developing statistical tests is the Likelihood ratio method. Suppose that the data vector, , has joint density Suppose that the parameter vector, , belongs to the set W. Let w denote a subset of W. Finally we want to test

The Likelihood ratio test rejects H 0 if

The situation Let denote a sample of n from the p-variate normal distribution with mean vector and covariance matrix S. Suppose we want to test

The Likelihood function is: and the Log-likelihood function is:

the Maximum Likelihood estimators of are and

the Maximum Likelihood estimators of when H 0 is true are: and

The Likelihood function is: now
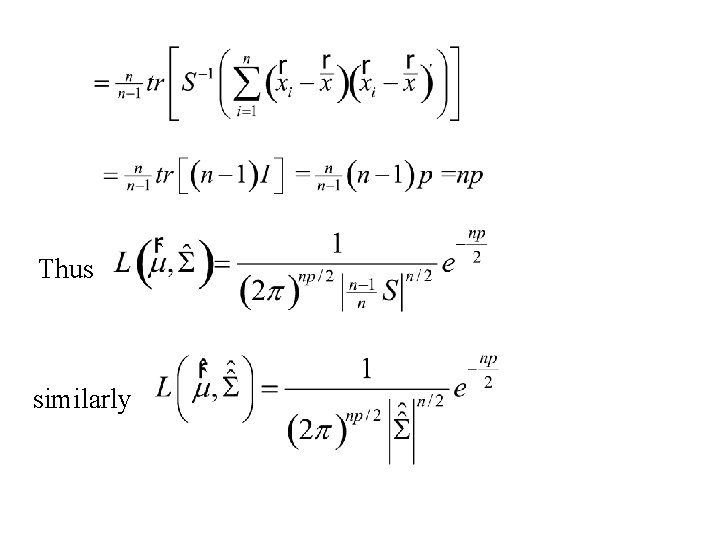
Thus similarly

and
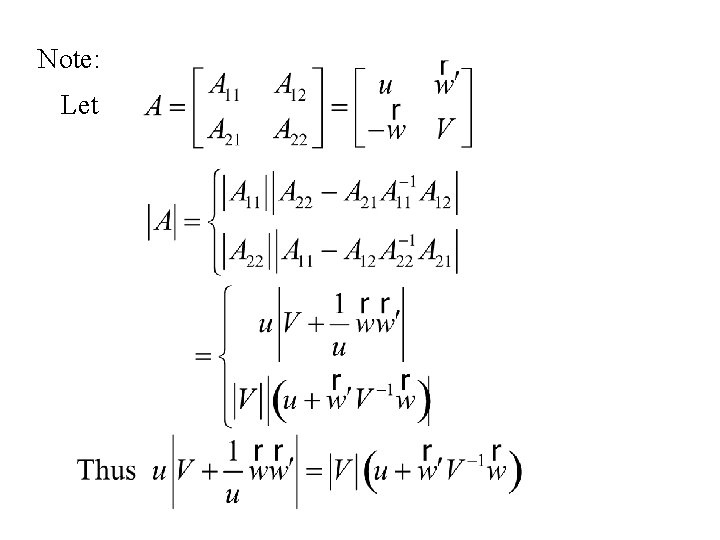
Note: Let

and Now and
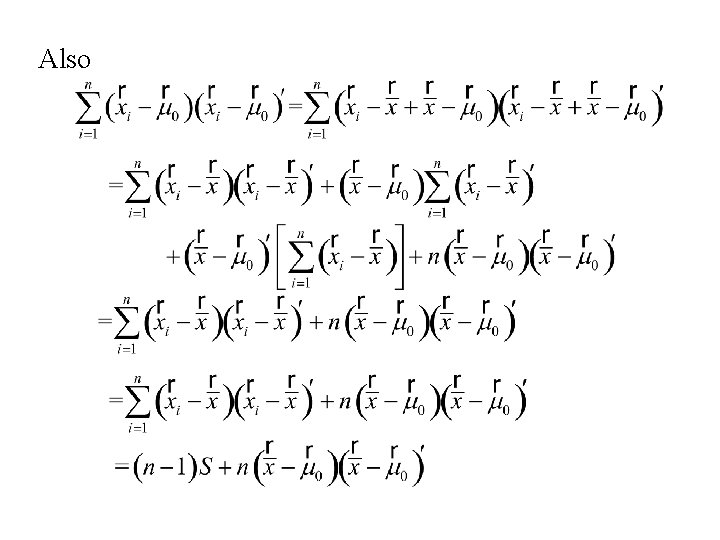
Also
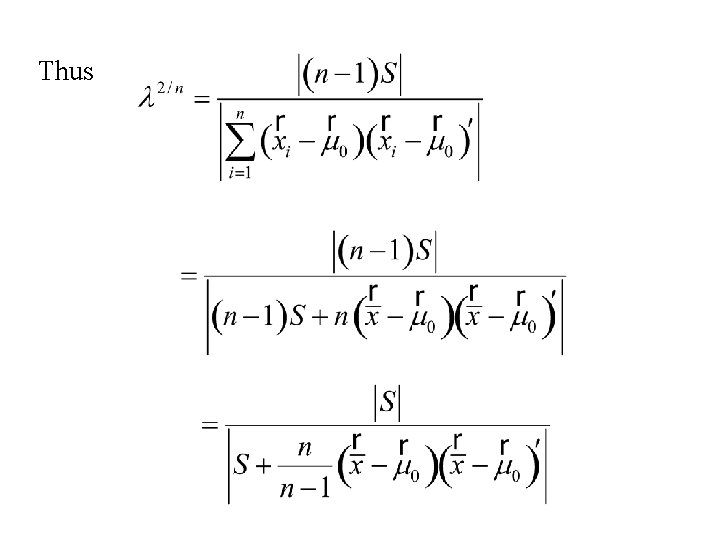
Thus

Thus using

Then Thus to reject H 0 if l < la This is the same as Hotelling’s T 2 test if

Example For n = 10 students we measure scores on – Math proficiency test (x 1), – Science proficiency test (x 2), – English proficiency test (x 3) and – French proficiency test (x 4) The average score for each of the tests in previous years was 60. Has this changed?

The data

Summary Statistics

Simultaneous Inference for means Recall (Using Roy’s Union Intersection Principle)
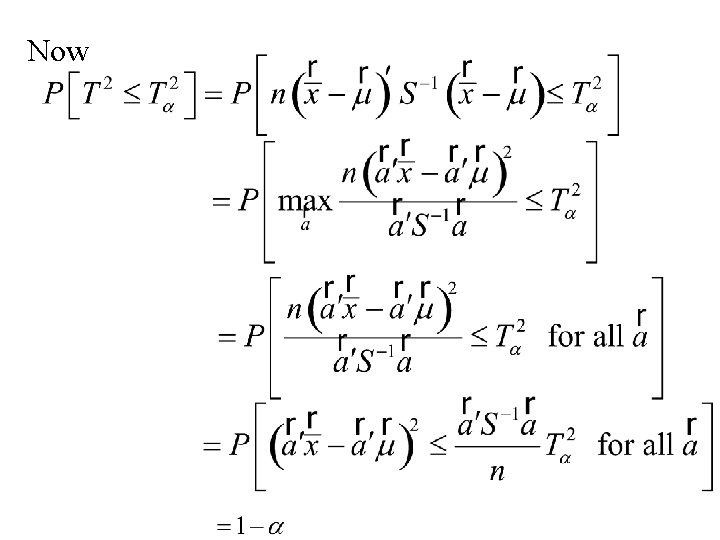
Now

Thus and the set of intervals Form a set of (1 – a)100 % simultaneous confidence intervals for

Recall Thus the set of (1 – a)100 % simultaneous confidence intervals for

The two sample problem

Univariate Inference Let x 1, x 2, … , xn denote a sample of n from the normal distribution with mean mx and variance s 2. Let y 1, y 2, … , ym denote a sample of n from the normal distribution with mean my and variance s 2. Suppose we want to test H 0: mx = my vs HA : mx ≠ my

The appropriate test is the t test: The test statistic: Reject H 0 if |t| > ta/2 d. f. = n + m -2

The multivariate Test Let denote a sample of n from the p-variate normal distribution with mean vector and covariance matrix S. Let denote a sample of m from the p-variate normal distribution with mean vector and covariance matrix S. Suppose we want to test

Hotelling’s T 2 statistic for the two sample problem if H 0 is true than has an F distribution with n 1 = p and n 2 = n +m – p - 1

Thus Hotelling’s T 2 test We reject

Simultaneous inference for the two-sample problem • Hotelling’s T 2 statistic can be shown to have been derived by Roy’s Union-Intersection principle
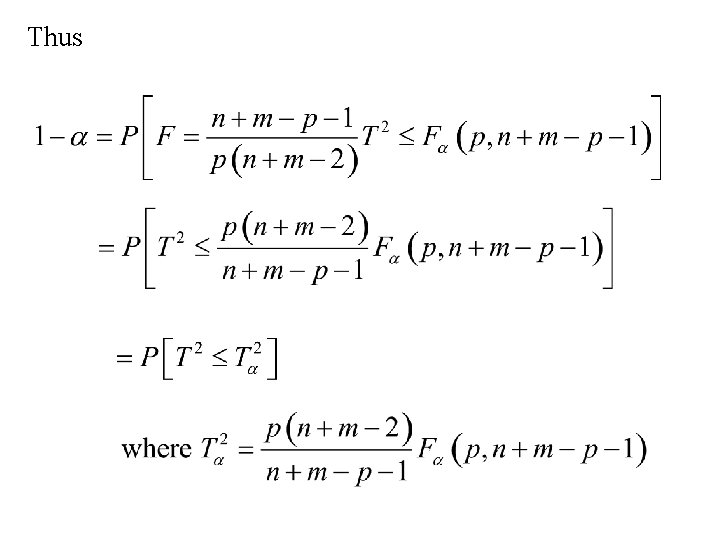
Thus
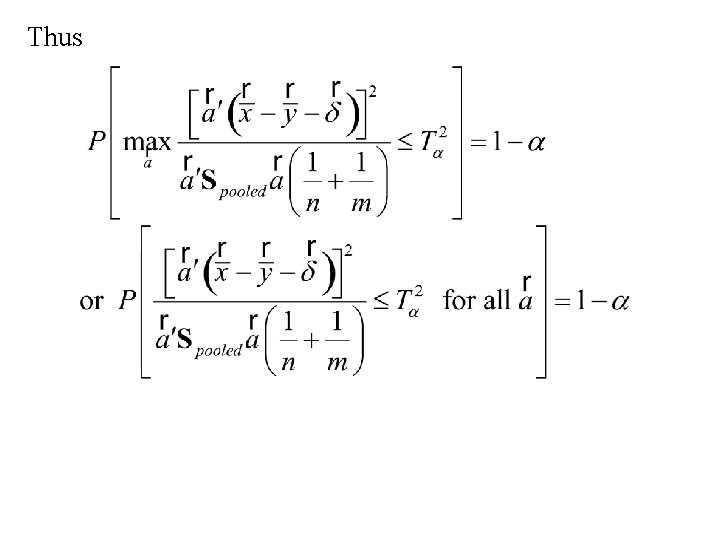
Thus
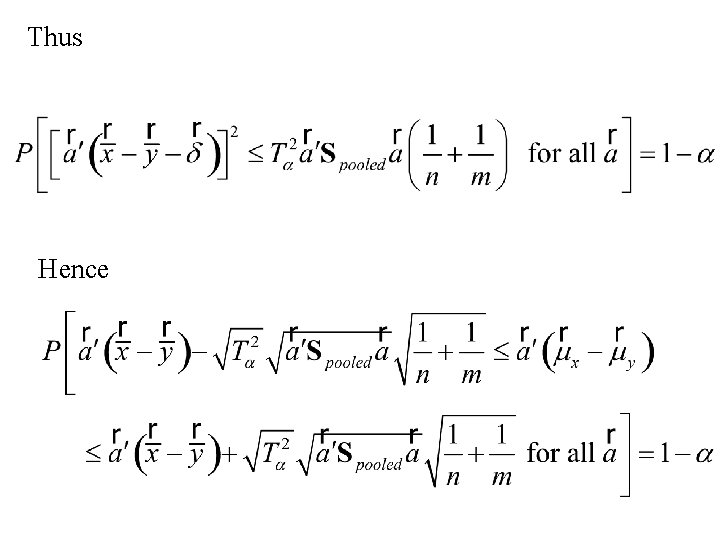
Thus Hence

Thus form 1 – a simultaneous confidence intervals for

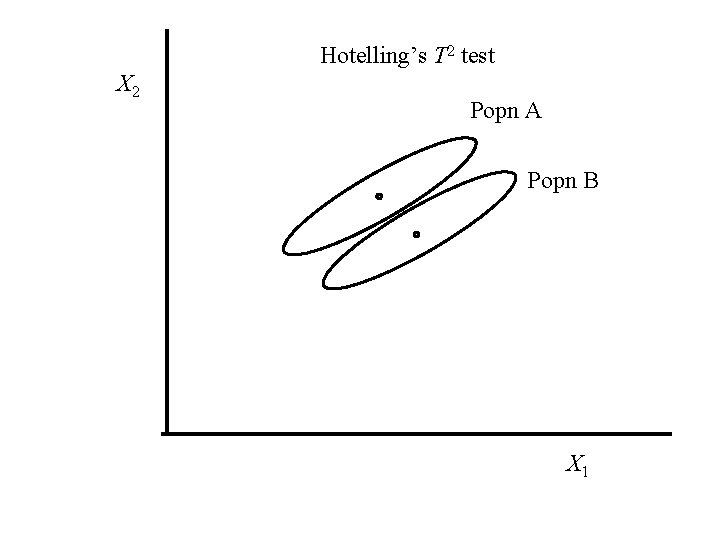
Hotelling’s T 2 test A graphical explanation

Hotelling’s T 2 statistic for the two sample problem

is the test statistic for testing:

Hotelling’s T 2 test X 2 Popn A Popn B X 1

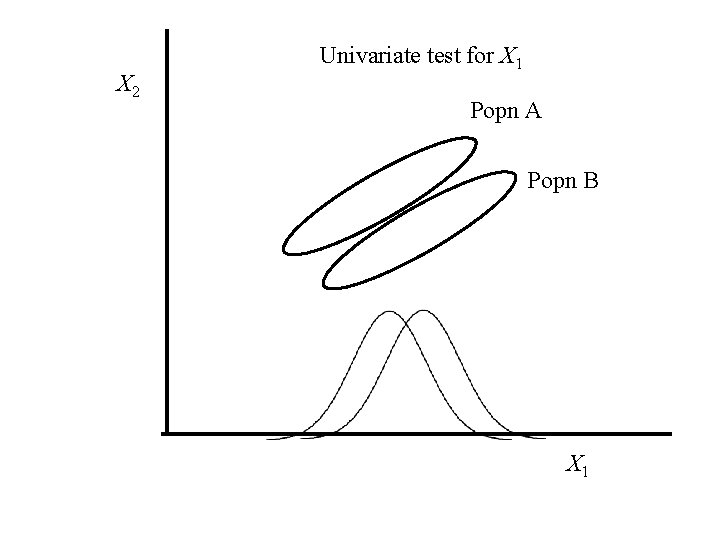
X 2 Univariate test for X 1 Popn A Popn B X 1

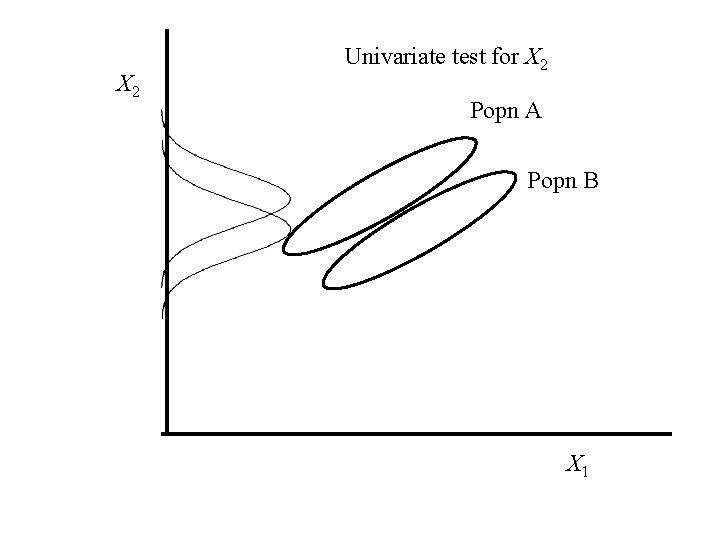
X 2 Univariate test for X 2 Popn A Popn B X 1

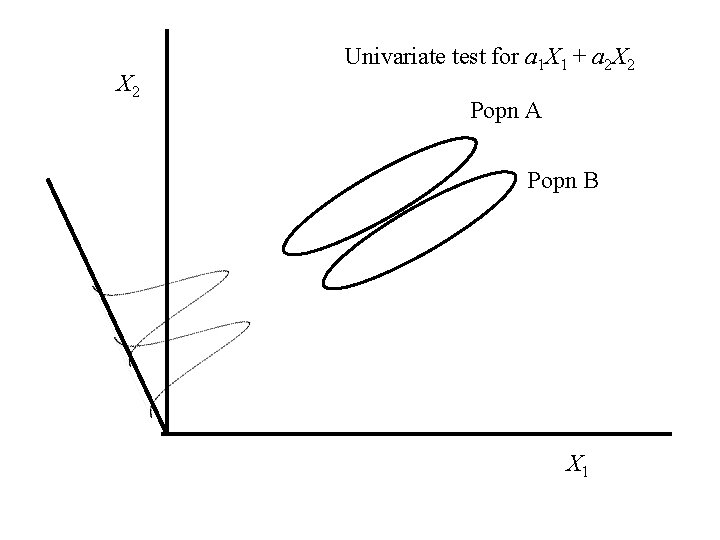
X 2 Univariate test for a 1 X 1 + a 2 X 2 Popn A Popn B X 1

Mahalanobis distance A graphical explanation

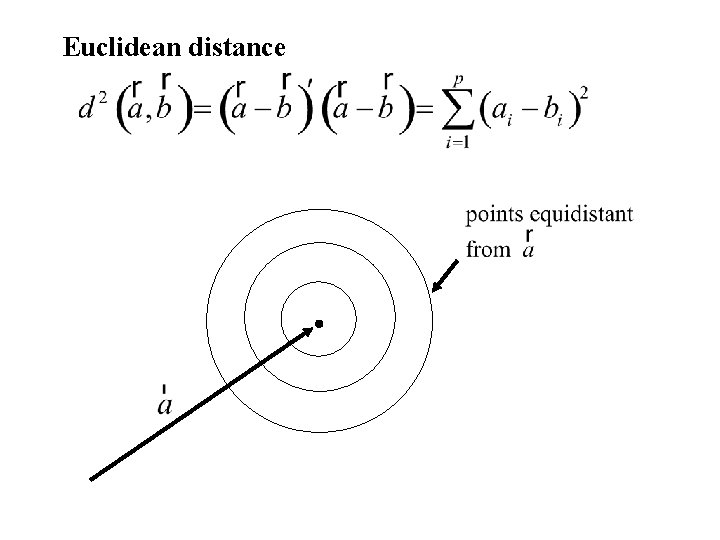
Euclidean distance

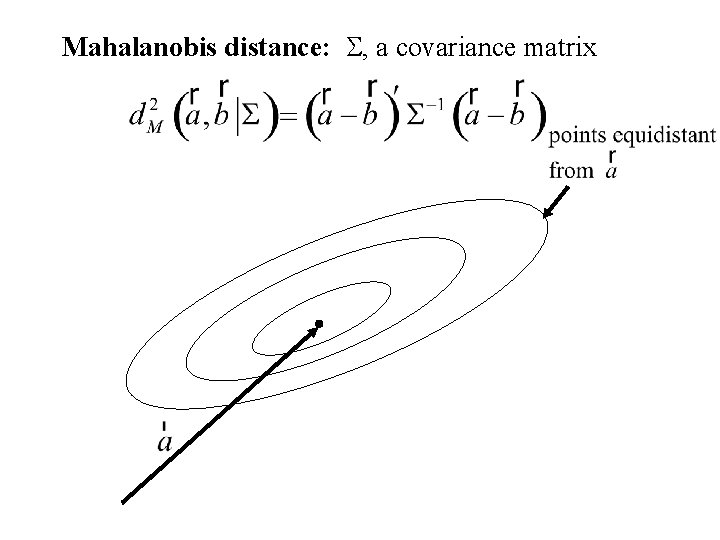
Mahalanobis distance: S, a covariance matrix

Hotelling’s T 2 statistic for the two sample problem

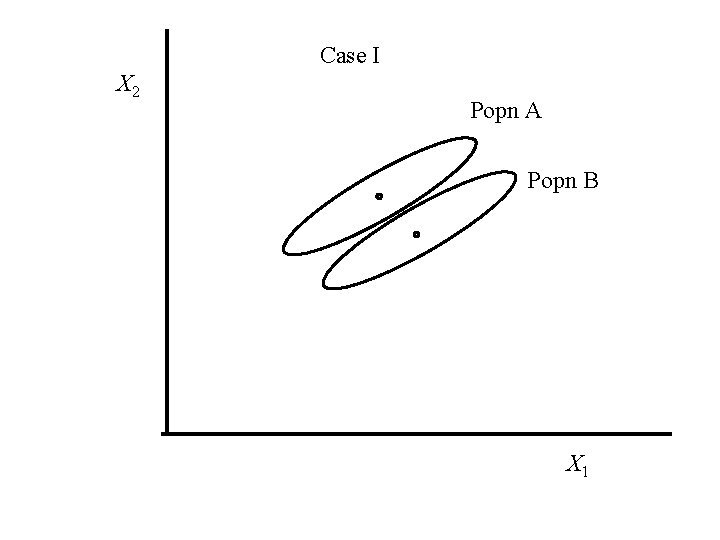
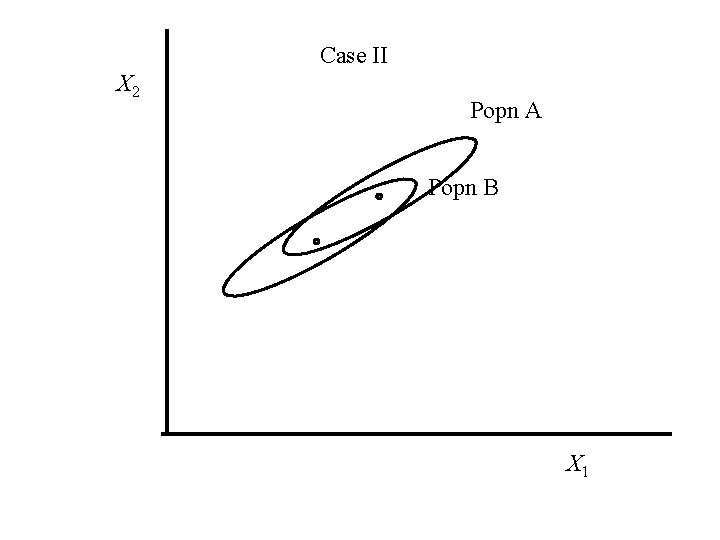
Case I X 2 Popn A Popn B X 1

Case II X 2 Popn A Popn B X 1

In Case I the Mahalanobis distance between the mean vectors is larger than in Case II, even though the Euclidean distance is smaller. In Case I there is more separation between the two bivariate normal distributions
 Let me let me let me
Let me let me let me Univariate analysis tests
Univariate analysis tests Analisis univariat dan bivariat
Analisis univariat dan bivariat Univariate verfahren
Univariate verfahren Univariate analysis spss
Univariate analysis spss Univariate eda
Univariate eda O g n
O g n Univariate vs multivariate logistic regression
Univariate vs multivariate logistic regression Univariate anova
Univariate anova Univariate descriptive design
Univariate descriptive design Univariate vs multivariate
Univariate vs multivariate Univariate analysis excel
Univariate analysis excel Vector directed line segment
Vector directed line segment Vector resultante
Vector resultante How is vector resolution the opposite of vector addition
How is vector resolution the opposite of vector addition Position vector define
Position vector define Let's let them object to another one
Let's let them object to another one Let's go to my house
Let's go to my house He who has ears let him hear
He who has ears let him hear What does inference mean
What does inference mean Contoh soal distribusi normal multivariat
Contoh soal distribusi normal multivariat Let t(x y) mean that student x likes dish y
Let t(x y) mean that student x likes dish y Kontinuitetshantering
Kontinuitetshantering Typiska novell drag
Typiska novell drag Tack för att ni lyssnade bild
Tack för att ni lyssnade bild Vad står k.r.å.k.a.n för
Vad står k.r.å.k.a.n för Shingelfrisyren
Shingelfrisyren En lathund för arbete med kontinuitetshantering
En lathund för arbete med kontinuitetshantering Särskild löneskatt för pensionskostnader
Särskild löneskatt för pensionskostnader Personlig tidbok fylla i
Personlig tidbok fylla i Sura för anatom
Sura för anatom Densitet vatten
Densitet vatten Datorkunskap för nybörjare
Datorkunskap för nybörjare Stig kerman
Stig kerman Debattartikel mall
Debattartikel mall Magnetsjukhus
Magnetsjukhus Nyckelkompetenser för livslångt lärande
Nyckelkompetenser för livslångt lärande Påbyggnader för flakfordon
Påbyggnader för flakfordon Vätsketryck formel
Vätsketryck formel Svenskt ramverk för digital samverkan
Svenskt ramverk för digital samverkan Lyckans minut erik lindorm analys
Lyckans minut erik lindorm analys Presentera för publik crossboss
Presentera för publik crossboss Vad är ett minoritetsspråk
Vad är ett minoritetsspråk Kanaans land
Kanaans land Treserva lathund
Treserva lathund Epiteltyper
Epiteltyper Claes martinsson
Claes martinsson Centrum för kunskap och säkerhet
Centrum för kunskap och säkerhet Verifikationsplan
Verifikationsplan Bra mat för unga idrottare
Bra mat för unga idrottare Verktyg för automatisering av utbetalningar
Verktyg för automatisering av utbetalningar Rutin för avvikelsehantering
Rutin för avvikelsehantering Smärtskolan kunskap för livet
Smärtskolan kunskap för livet Ministerstyre för och nackdelar
Ministerstyre för och nackdelar Tack för att ni har lyssnat
Tack för att ni har lyssnat Referat mall
Referat mall Redogör för vad psykologi är
Redogör för vad psykologi är Borstål, egenskaper
Borstål, egenskaper Tack för att ni har lyssnat
Tack för att ni har lyssnat Borra hål för knoppar
Borra hål för knoppar Vilken grundregel finns det för tronföljden i sverige?
Vilken grundregel finns det för tronföljden i sverige? Standardavvikelse formel
Standardavvikelse formel Tack för att ni har lyssnat
Tack för att ni har lyssnat Steg för steg rita
Steg för steg rita






















































































