Classifying Quadrilaterals GEOMETRY LESSON 6 1 For help

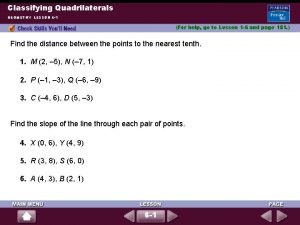
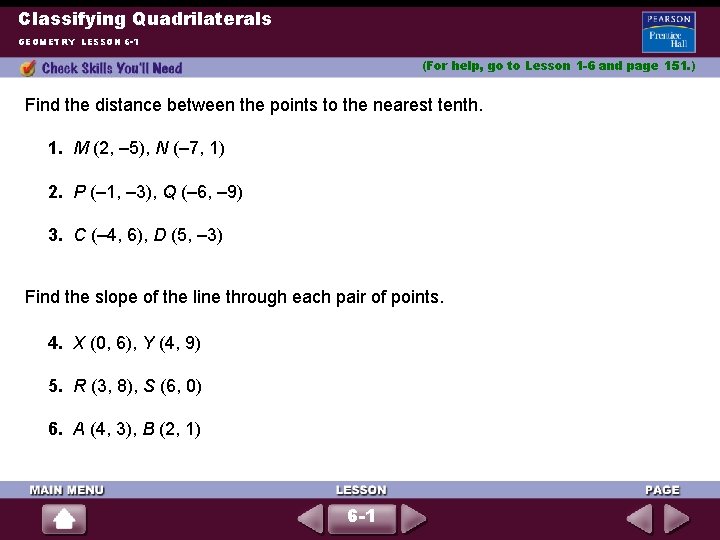
Classifying Quadrilaterals GEOMETRY LESSON 6 -1 (For help, go to Lesson 1 -6 and page 151. ) Find the distance between the points to the nearest tenth. 1. M (2, – 5), N (– 7, 1) 2. P (– 1, – 3), Q (– 6, – 9) 3. C (– 4, 6), D (5, – 3) Find the slope of the line through each pair of points. 4. X (0, 6), Y (4, 9) 5. R (3, 8), S (6, 0) 6. A (4, 3), B (2, 1) 6 -1

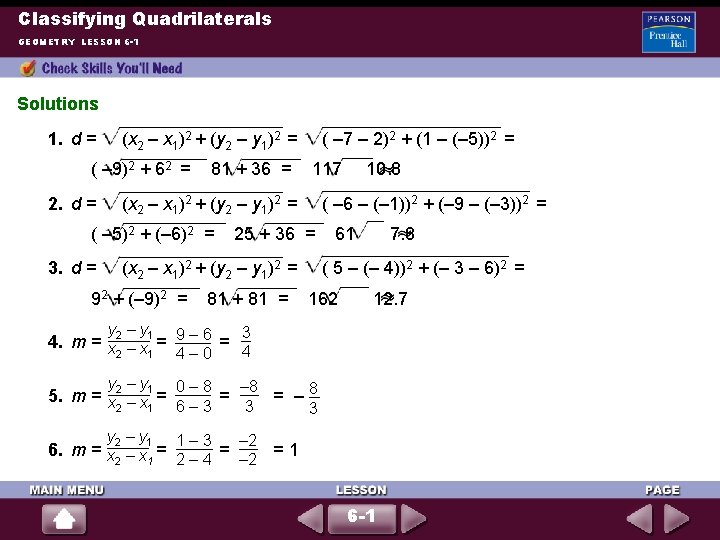
Classifying Quadrilaterals GEOMETRY LESSON 6 -1 Solutions 1. d = (x 2 – x 1)2 + (y 2 – y 1)2 = ( – 9)2 + 62 = 2. d = 81 + 36 = 117 (x 2 – x 1)2 + (y 2 – y 1)2 = ( – 5)2 + (– 6)2 = 3. d = ( – 7 – 2)2 + (1 – (– 5))2 = ( – 6 – (– 1))2 + (– 9 – (– 3))2 = 25 + 36 = (x 2 – x 1)2 + (y 2 – y 1)2 = 92 + (– 9)2 = 81 + 81 = 10. 8 61 7. 8 ( 5 – (– 4))2 + (– 3 – 6)2 = 162 12. 7 y 2 – y 1 9 – 6 3 4. m = x – x = = 4 2 1 4– 0 y 2 – y 1 0– 8 5. m = x – x = = 6– 3 3 2 1 = – 8 3 y 2 – y 1 1 – 3 – 2 6. m = x 2 – x 1 = 2 – 4 = – 2 = 1 6 -1

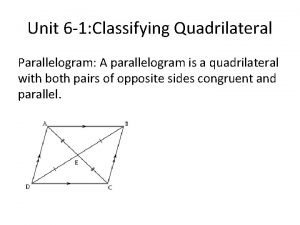
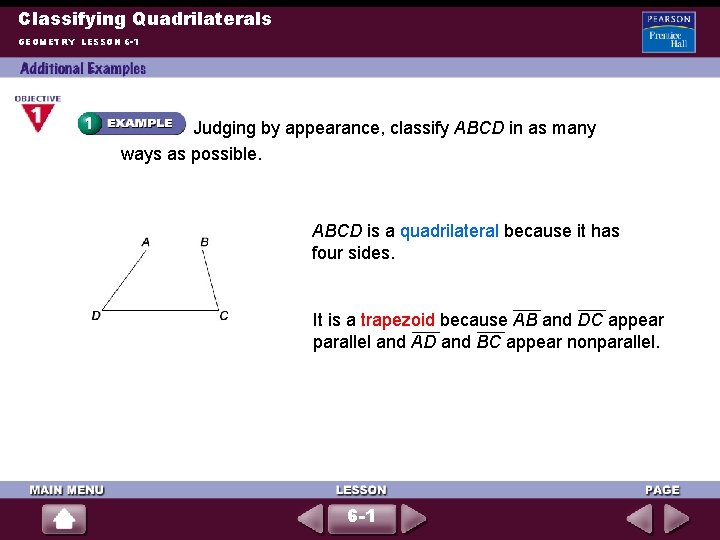
Classifying Quadrilaterals GEOMETRY LESSON 6 -1 Judging by appearance, classify ABCD in as many ways as possible. ABCD is a quadrilateral because it has four sides. It is a trapezoid because AB and DC appear parallel and AD and BC appear nonparallel. 6 -1

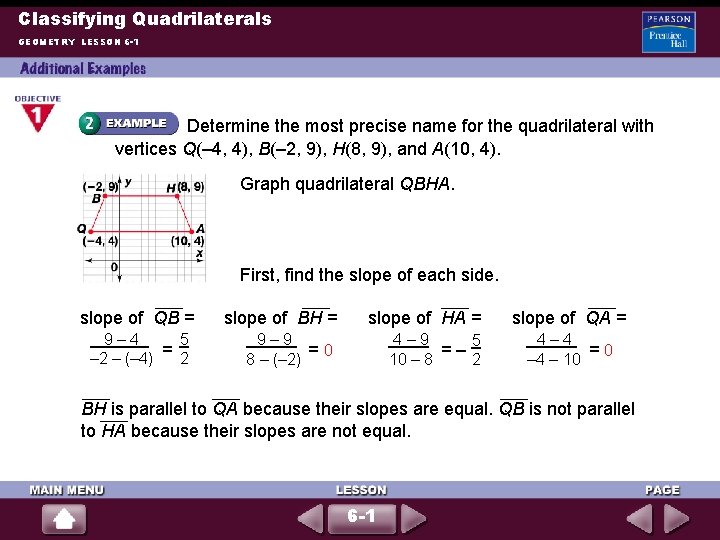
Classifying Quadrilaterals GEOMETRY LESSON 6 -1 Determine the most precise name for the quadrilateral with vertices Q(– 4, 4), B(– 2, 9), H(8, 9), and A(10, 4). Graph quadrilateral QBHA. First, find the slope of each side. slope of QB = 9– 4 5 = – 2 – (– 4) 2 slope of BH = slope of HA = 9– 9 =0 8 – (– 2) 4– 9 5 = – 10 – 8 2 slope of QA = 4– 4 =0 – 4 – 10 BH is parallel to QA because their slopes are equal. QB is not parallel to HA because their slopes are not equal. 6 -1

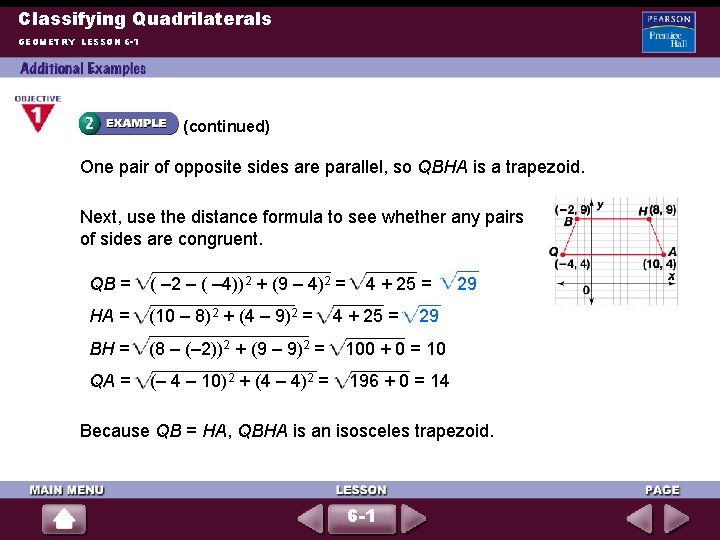
Classifying Quadrilaterals GEOMETRY LESSON 6 -1 (continued) One pair of opposite sides are parallel, so QBHA is a trapezoid. Next, use the distance formula to see whether any pairs of sides are congruent. QB = ( – 2 – ( – 4))2 + (9 – 4)2 = 4 + 25 = HA = (10 – 8)2 + (4 – 9)2 = BH = (8 – (– 2))2 + (9 – 9)2 = 100 + 0 = 10 QA = (– 4 – 10)2 + (4 – 4)2 = 196 + 0 = 14 4 + 25 = 29 29 Because QB = HA, QBHA is an isosceles trapezoid. 6 -1

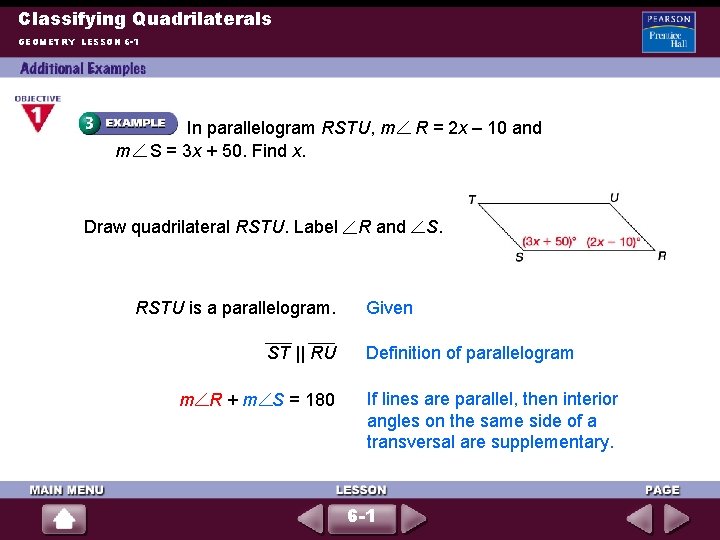
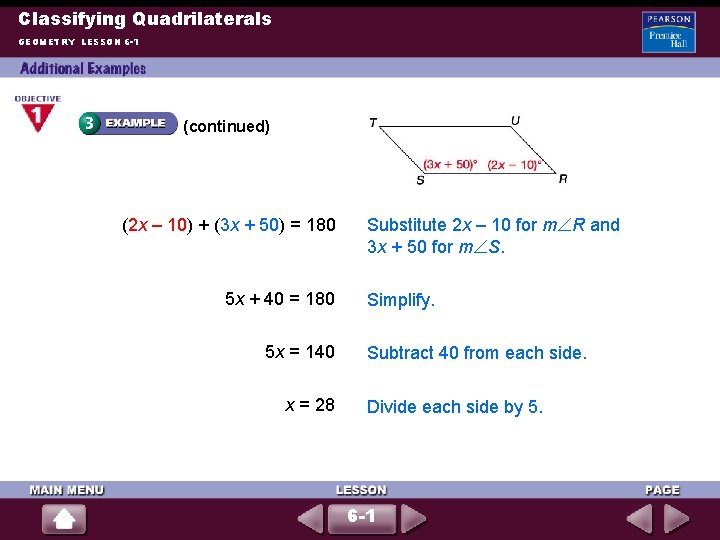
Classifying Quadrilaterals GEOMETRY LESSON 6 -1 m In parallelogram RSTU, m S = 3 x + 50. Find x. Draw quadrilateral RSTU. Label RSTU is a parallelogram. ST || RU m R + m S = 180 R and R = 2 x – 10 and S. Given Definition of parallelogram If lines are parallel, then interior angles on the same side of a transversal are supplementary. 6 -1

Classifying Quadrilaterals GEOMETRY LESSON 6 -1 (continued) (2 x – 10) + (3 x + 50) = 180 5 x + 40 = 180 5 x = 140 x = 28 Substitute 2 x – 10 for m R and 3 x + 50 for m S. Simplify. Subtract 40 from each side. Divide each side by 5. 6 -1

Classifying Quadrilaterals GEOMETRY LESSON 6 -1 Pages 290 -293 Exercises 1. , rectangle, rhombus, square 8. parallelogram 13. rhombus 9. rhombus 2. parallelogram 10. rectangle 3. trapezoid 11. kite 4. , rhombus 12. isosc. trapezoid 5. kite 6. trapezoid, isosc. trapezoid 7. rhombus 6 -1 14. kite

Classifying Quadrilaterals GEOMETRY LESSON 6 -1 15. trapezoid 17. quadrilateral 19. x = 11, y = 29; 13, 23, 23 20. x = 4, y = 4. 8; 4. 5, 6. 8, 6. 8 21. x = 2, y = 6; 2, 7, 7, 2 22. x = 1; 4, 4, 4, 9 16. rectangle 18. isos. trapezoid 23. x = 3, y =5; 15, 15, 15 24. x = 5, y = 4; 3, 3, 3, 3 25. 40, 140, 140; 11, 15, 32 6 -1

Classifying Quadrilaterals GEOMETRY LESSON 6 -1 26. 58, 122, 122; 6, 6, 6, 6 32. 29. 27. rectangle, square, trapezoid 30. 33. 28. Check students’ work 29 -34. Answers may vary. Samples are given. 31. Impossible; a trapezoid with one rt. must have another, since two sides are. 6 -1

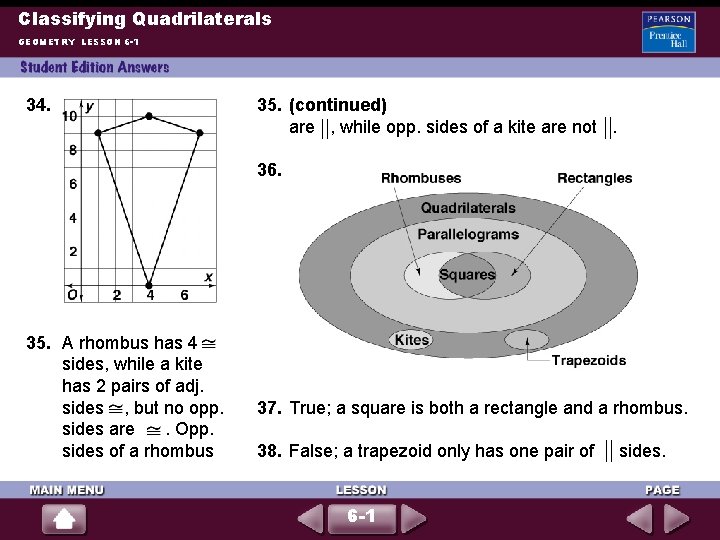
Classifying Quadrilaterals GEOMETRY LESSON 6 -1 34. 35. (continued) are , while opp. sides of a kite are not. 36. 35. A rhombus has 4 sides, while a kite has 2 pairs of adj. sides , but no opp. sides are. Opp. sides of a rhombus 37. True; a square is both a rectangle and a rhombus. 38. False; a trapezoid only has one pair of 6 -1 sides.

Classifying Quadrilaterals GEOMETRY LESSON 6 -1 39. False; a kite does not have opp. sides. 40. True; all squares are s. 41. False; kites are not s. 43. (continued) from the same cut. 50. A trapezoid has only one pair of sides. 44 -45. Check students’ work. 51 -54. Check students’ sketches. 46. some isos. trapezoids, some trapezoids. 51. rectangle, 52. rhombus, 47. 42. False; only rhombuses with rt. s are squares. 43. Rhombuses; all 4 sides are because they come , kite , rhombus, rectangle, square 48. rectangle, square 49. rhombus, square, kite, some trapezoids 6 -1 53. square, rhombus, 54. rhombus, , kite

Classifying Quadrilaterals GEOMETRY LESSON 6 -1 55. Answers may vary. Sample: a. 55. b. (continued) above, KL = LM and KN = NM, but KL =/ KN. 58. kite, , rhombus, trapezoid, isos. trapezoid 59. 56 -59. Explanations may vary. Samples are given. N can be anywhere on the y-axis except (0, 0), (0, 2), and (0, – 2). , rectangle, square, rhombus, kite, trapezoid 60. C 56. 57. , rectangle, trapezoid , kite, rhombus, trapezoid, isos. Trapezoid. b. For points N mentioned 6 -1 61. I 62. C 63. H

Classifying Quadrilaterals GEOMETRY LESSON 6 -1 64. [2] Slope of AB is – 3. The slope 2 of BC is 1, so AB and BC are not. Since one is not a right and a rectangle requires all 4 s to be right s , the figure could not be a rectangle. [1] incorrect slope OR failure to recognize the information 64. [1] (continued) provided by the slopes. 70. 12 mm 65. Yes; the sum of the lengths of any 2 sides is greater than the third side. 72. 90 71. 82 73. 58 74. y = – 3 x + 4 66. No; 5 + 7 > 20 67. No; 3 + 5 > 8 68. 28 mm 69. 16 mm 6 -1

Classifying Quadrilaterals GEOMETRY LESSON 6 -1 Judging by appearance, classify the quadrilaterals in Exercises 1 and 2 in as many ways as possible. 1. 2. quadrilateral, kite quadrilateral, parallelogram, rectangle, rhombus, square 3. What is the most precise name for the figure in Exercise 1? 4. What is the most precise name for the figure in Exercise 2? square kite 5. Find the values of the variables in the rhombus to the right. a = 60, x = 6, y = 2 6 -1

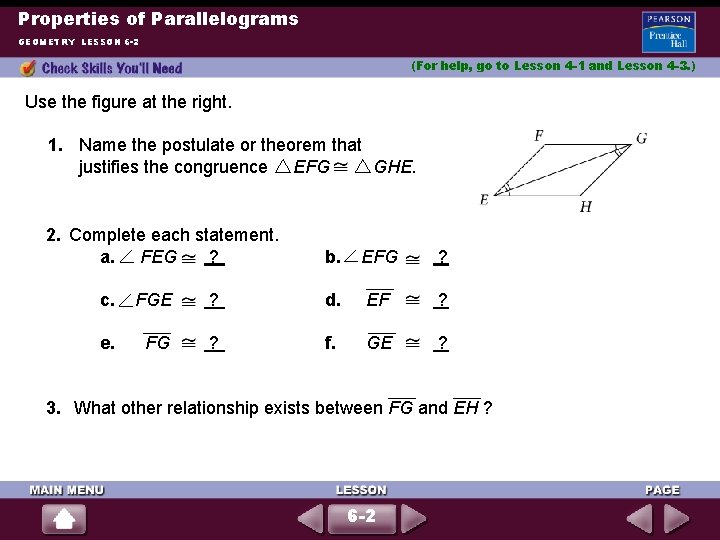
Properties of Parallelograms GEOMETRY LESSON 6 -2 (For help, go to Lesson 4 -1 and Lesson 4 -3. ) Use the figure at the right. 1. Name the postulate or theorem that GHE. justifies the congruence EFG 2. Complete each statement. a. FEG ? b. EFG ? c. FGE ? d. EF ? e. FG ? f. GE ? 3. What other relationship exists between FG and EH ? 6 -2

Properties of Parallelograms GEOMETRY LESSON 6 -2 Solutions 1. The triangles share the side EG, which is the included side between a pair of congruent corresponding angles. So, the triangles are congruent by the ASA Postulate. 2. a. In the triangle congruence statement EFG GHE, follow the order of the letters for the angles: FEG HGE b. In the triangle congruence statement, EFG GHE follow the GHE order of the letters for the angles: EFG c. In the triangle congruence statement, EFG GHE follow the order of the letters for the angles: FGE HEG 6 -2

Properties of Parallelograms GEOMETRY LESSON 6 -2 Solutions (continued) d. In the triangle congruence statement, EFG GHE use the position of the letters for the congruent segments: EF GH GHE use the e. In the triangle congruence statement, EFG position of the letters for the congruent segments: FG HE f. In the triangle congruence statement, EFG GHE use the position of the letters for the congruent segments: GE EG 3. Since the alternate interior angles are congruent, FG || EH. 6 -2

Properties of Parallelograms GEOMETRY LESSON 6 -2 Use KMOQ to find m O. Q and O are consecutive angles of KMOQ, so they are supplementary. m O + m Q = 180 m O + 35 = 180 m O = 145 Definition of supplementary angles Substitute 35 for m Q. Subtract 35 from each side. 6 -2

Properties of Parallelograms GEOMETRY LESSON 6 -2 Find the value of x in x + 15 = 135 – x 2 x + 15 = 135 ABCD. Then find m A. Opposite angles of a are congruent. Add x to each side. 2 x = 120 Subtract 15 from each side. x = 60 Divide each side by 2. Substitute 60 for x. m B = 60 + 15 = 75 m A + m B = 180 Consecutive angles of a parallelogram are supplementary. m A + 75 = 180 Substitute 75 for m B. m A = 105 Subtract 75 from each side. 6 -2

Properties of Parallelograms GEOMETRY LESSON 6 -2 Find the values of x and y in x = 7 y – 16 2 x + 5 = 5 y 2(7 y – 16) + 5 = 5 y 14 y – 32 + 5 = 5 y 14 y – 27 = 5 y – 27 = – 9 y KLMN. The diagonals of a parallelogram bisect each other. Substitute 7 y – 16 for x in the second equation to solve for y. Distribute. Simplify. Subtract 14 y from each side. 3=y Divide each side by – 9. x = 7(3) – 16 Substitute 3 for y in the first equation to solve for x. x=5 So x = 5 and y = 3. Simplify. 6 -2

Properties of Parallelograms GEOMETRY LESSON 6 -2 Theorem 6 -4 states If three (or more) parallel lines cut off congruent segments on one transversal, then they cut off congruent segments on every transversal. Explain how to divide a blank card into five equal rows using Theorem 6 -4 and a sheet of lined paper. Place a corner of the top of the card on the first line of the lined paper. Place any other corner on the sixth line. Mark the points where the lines intersect one side of the card. Mark the points where the lines intersect the opposite side of the card. Connect the marks on opposite sides using a straightedge. If you use the same-side bottom corner, the lines are parallel to the top of the card. If you use the opposite corner, the lines are parallel to the diagonal of the card. 6 -2

Properties of Parallelograms GEOMETRY LESSON 6 -2 Pages 297 -301 Exercises 1. 127 2. 67 10. 3; 10, 20 16. 6; m m 3. 76 11. 22; 18. 5, 23. 6 17. x = 6, y = 8 4. 124 12. 20 18. x = 5, y = 7 5. 100 13. 18 19. x = 7, y = 10 6. 118 14. 17 20. x = 6, y = 9 7. 3 4 21. x = 3, y = 4 8. 4 15. 12; m Q = m S = 36, m P = m R = 144 9. 4 6 -2 H = m J = 30, I = m K = 150 22. 12; 24

Properties of Parallelograms GEOMETRY LESSON 6 -2 23. Pick 4 equally spaced lines on the paper. Place the paper so that the first button is on the first line and the last button is on the fourth line. Draw a line between the first and last buttons. The remaining buttons should be placed where the drawn line crosses the 2 lines on the paper. 24. 3 33. 6. 75 25. 3 34. BC = AD = 14. 5 in. ; AB = CD = 9. 5 in. 26. 6 35. BC = AD = 33 cm; AB = CD = 13 cm 27. 6 28. 9 36. a. DC 29. 2. 25 b. AD c. 30. 2. 25 d. Reflexive 31. 4. 5 e. ASA f. CPCTC 32. 4. 5 6 -2

Properties of Parallelograms GEOMETRY LESSON 6 -2 37. a. Given 37. (continued) f. ASA h. CPCTC g. ASA i. CPCTC b. Def. of c. If 2 lines are , then alt. int. s are. 38. d. If 2 lines are , then alt. int. s are. e. Reflexive Prop. of. 6 -2

Properties of Parallelograms GEOMETRY LESSON 6 -2 39. 38, 32, 110 46. x = 109, y = 88, z = 76 53. (continued) measures. Consecutive s are suppl. , so their sum is 180. 40. 81, 28, 71 47. x = 25, y = 115 41. 95, 37 48. x = y = 6 42. The lines going across may not be since they are not marked as. 54. a. Answers may vary. Check students’ work. 49. x = 10, y = 4 50. x = 12, y = 4 43. 18, 162 51. x = 0, y = 5 44. 60 52. x = 9, y = 6 b. No; the corr. sides can be but the s may not be. 55. a. Given 45. x = 15, y = 45 53. The opp. s are so they have = 6 -2 , b. Def of a

Properties of Parallelograms GEOMETRY LESSON 6 -2 55. (continued) c. Opp. Sides of a are. d. Trans. Prop. of e. If 2 lines are to the same line, then they are to each other. f. If 2 lines are , then the corr. s are. g. Trans. Prop. of h. AAS i. CPCTC 56. Answers may vary. Sample: 1. LENS and NGTH are s. (Given) 2. 3. 4. ELS (Opp. s ENS (Vertical ENS and GTH of a are. ) s GNH are. ) ELS GTH (Trans. Prop. of ) 57. Answers may vary. Sample: In s LENS and NGTH, GT EH and EH LS by the def. of a. Therefore LS GT because if 2 lines are to the same line then they are to each other. 6 -2

Properties of Parallelograms GEOMETRY LESSON 6 -2 58. Answers may vary. Sample: 1. LENS and NGTH are s. (Given) 2. GTH 3. ENS GNH (Opp. GNH (Vertical 4. LEN is supp. to 5. ENS 6. E is suppl. to s of a are . ) s ENS (Cons. s in a GTH (Trans. Prop. of T. (Suppl. of . ) are suppl. ) ) s are suppl. ) 59. Answers may vary. Sample: In RSTW and XYTZ, X T because opp. s of a are. Then R Prop. of. 6 -2 R T and X by the Trans.

Properties of Parallelograms GEOMETRY LESSON 6 -2 60. In RSTW and XYTZ, XY TW and RS TW by the def. of a. Then XY RS because if 2 lines are to the same line, then they are to each other. 61. AB DC and AD BC by def. of. 2 3 and 1 4 because if 2 lines are , then alt. int. s are. 3 4 because if 2 s are each s , then they are to 2. By Def. of bisect, AC bisects DCB. 62. a. Given: 2 sides and the included of ABCD are to the corr. parts of WXYZ. Let A W, AB WX and 6 -2 62. a. (continued) AD WZ. Since opp. s of a are , A C and W Y. Thus C Y by the Trans. Prop. of. Similarly, opp. sides of a are , thus AB CD and WX ZY. Using the Trans. Prop. of , CD ZY. The same can be done to prove BC XY. Since consec. s of a are suppl. , A is suppl. to D, and W is s suppl. to Z. Suppls. of are , thus D Z. The same can be done to prove B X. Therefore, since all corr. s and sides are ,

Properties of Parallelograms GEOMETRY LESSON 6 -2 62. a. (continued) ABCD 69. 42 WXYZ. 70. rhombus b. No; opp. s and sides are not necessarily in a trapezoid. 71. parallelogram 63. 10 72. AC 64. 11 73. 49 65. 126 74. 131 66. 126 75. 49 67. 160 76. 131 68. 148 6 -2 DB

Properties of Parallelograms GEOMETRY LESSON 6 -2 Use parallelogram ABCD for Exercises 1– 5 1. If AB = 3 x + 11, BC = 2 x + 19, and CD = 7 x – 17, find x. 7 2. If m BAD = y and m ADC = 4 y – 70, find y. 50 3. If m ABC = 2 x + 100 and m ADC = 6 x + 84, find m BCD. 72 4. If m BCD = 80 and m CAD = 34, find m ACD. 46 5. If AP = 3 x, BP = y, CP = x + y, and DP = 6 x – 40, find x and y. x = 10, y = 20 6 -2

Proving that a Quadrilateral Is a Parallelogram GEOMETRY LESSON 6 -3 (For help, go to Lesson 1 -6 and 3 -6. ) Use the figure at the right for Exercises 1– 4. 1. Find the coordinates of the midpoints of AC and BD. What is the relationship between AC and BD ? 2. Find the slopes of BC and AD. How do they compare? 3. Are AB and DC parallel? Explain. 4. What type of figure is ABCD? 6 -3

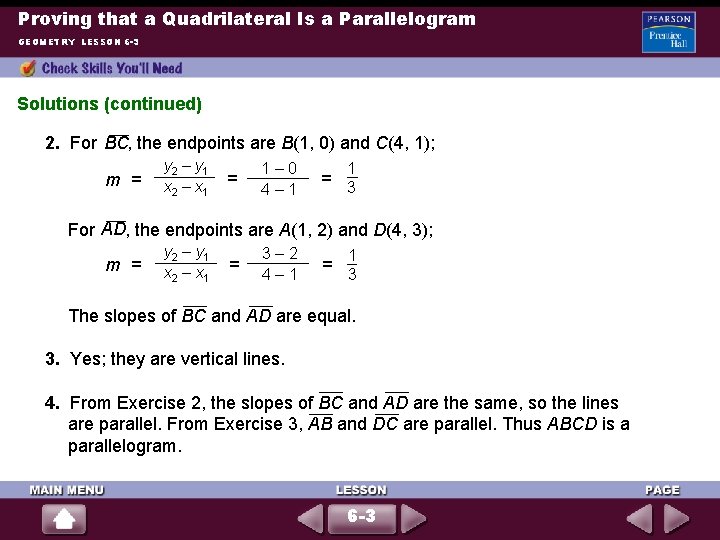
Proving that a Quadrilateral Is a Parallelogram GEOMETRY LESSON 6 -3 Solutions 1. For A(1, 2) and C(4, 1), x 1 + x 2 y 1 + y 2 , 2 2 = 1+4 , 2 2+1 2 = 5 3 , 2 2. or (2. 5, 1. 5). For B(1, 0) and D(4, 3), x 1 + x 2 y 1 + y 2 , 2 2 = 1+4 , 0+3 2 2 or (2. 5, 1. 5). They bisect one another. 6 -3 = 5 3 , 2 2

Proving that a Quadrilateral Is a Parallelogram GEOMETRY LESSON 6 -3 Solutions (continued) 2. For BC, the endpoints are B(1, 0) and C(4, 1); m = y 2 – y 1 x 2 – x 1 = 1– 0 4– 1 1 = 3 For AD, the endpoints are A(1, 2) and D(4, 3); m = y 2 – y 1 x 2 – x 1 = 3– 2 4– 1 = 1 3 The slopes of BC and AD are equal. 3. Yes; they are vertical lines. 4. From Exercise 2, the slopes of BC and AD are the same, so the lines are parallel. From Exercise 3, AB and DC are parallel. Thus ABCD is a parallelogram. 6 -3

Proving that a Quadrilateral Is a Parallelogram GEOMETRY LESSON 6 -3 Find values of x and y for which ABCD must be a parallelogram. If the diagonals of quadrilateral ABCD bisect each other, then ABCD is a parallelogram by Theorem 6 -5. Write and solve two equations to find values of x and y for which the diagonals bisect each other. 10 x – 24 = 8 x + 12 2 x – 24 = 12 2 x = 36 x = 18 Diagonals of parallelograms bisect each other. Collect the variable terms on one side. Solve. 2 y – 80 = y + 9 y – 80 = 9 y = 89 If x = 18 and y = 89, then ABCD is a parallelogram. 6 -3

Proving that a Quadrilateral Is a Parallelogram GEOMETRY LESSON 6 -3 Determine whether the quadrilateral is a parallelogram. Explain. a. All you know about the quadrilateral is that only one pair of opposite sides is congruent. Therefore, you cannot conclude that the quadrilateral is a parallelogram. b. The sum of the measures of the angles of a polygon is (n – 2)180, where n represents the number of sides, so the sum of the measures of the angles of a quadrilateral is (4 – 2)180 = 360. If x represents the measure of the unmarked angle, x + 75 + 105 + 75 = 360, so x = 105. Theorem 6 -8 states If both pairs of opposite angles of a quadrilateral are congruent, then the quadrilateral is a parallelogram. Because both pairs of opposite angles are congruent, the quadrilateral is a parallelogram by Theorem 6 -8. b. 6 -3

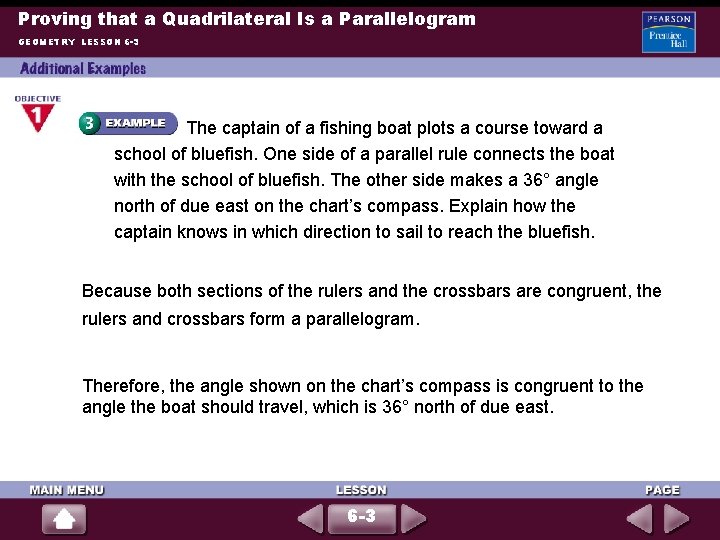
Proving that a Quadrilateral Is a Parallelogram GEOMETRY LESSON 6 -3 The captain of a fishing boat plots a course toward a school of bluefish. One side of a parallel rule connects the boat with the school of bluefish. The other side makes a 36° angle north of due east on the chart’s compass. Explain how the captain knows in which direction to sail to reach the bluefish. Because both sections of the rulers and the crossbars are congruent, the rulers and crossbars form a parallelogram. Therefore, the angle shown on the chart’s compass is congruent to the angle the boat should travel, which is 36° north of due east. 6 -3

Proving that a Quadrilateral Is a Parallelogram GEOMETRY LESSON 6 -3 Pages 307 -310 Exercises 1. 5 2. x = 3, y = 4 3. x = 1. 6, y =1 4. 5 3 5. 5 6. 13 7. Yes; both pairs of opp. sides are. 8. No; the quad. Could be kite. 13. Yes; both pairs of opp. sides are. 9. Yes; both pairs of opp. s are. 14. No; opp. sides are not. 10. No; the quad. could be a trapezoid. 15. No; the quad. could be a kite. 11. Yes; both pairs of opp. sides are because alt. int. s are. 16. It remains a because the shelves and connecting pieces remain. 12. Yes; one pair of opp sides are and. 6 -3

Proving that a Quadrilateral Is a Parallelogram GEOMETRY LESSON 6 -3 17. a. bisect b. XR c. XYR d. ASA e. alt. interior 18. Opp. sides of a quad. are if and only if the quad. is a 19. a. Distr. Prop. 22. Yes; a pair of opp. sides is and. b. Div. Prop. of Eq. c. AD BC, AB DC d. If same-side int. are suppl. , the lines are. e. Def. of 20. Yes; both pairs of opp. s are. 21. No; the figure could be a kite. 6 -3 s 23. No; the figure could be a trapezoid. 24. Yes; the both pairs of opp. sides are. 25. Yes; diag. bisect each other. 26. x = 15, y = 25 27. x = 3, y = 11

Proving that a Quadrilateral Is a Parallelogram GEOMETRY LESSON 6 -3 28. c = 8, a = 24 32. (4, 0) 29. k = 9, m = 23. 4 33. (6, 6) 30. Answers may vary. Sample: 34. (– 2, 4) 35. You can show a quad. is a if both opp. sides are , if both opp. s are , if opp. sides are , if diag. bisect each other, if all consecutive s are suppl. , if one pair of opp. sides are both and. 36. Answers vary. Sample: 1. TRS RTW (Given) 1 31. 6 2. RS TW, 3. SR WT 6 -3 SRT (If alt. int. WTR (CPCTC) s are , then lines are. )

Proving that a Quadrilateral Is a Parallelogram GEOMETRY LESSON 6 -3 36. (continued) 4. RSTW is a. (If one pair of opp. sides are and , then it is a. ) 37. Answers may vary. Sample: 1. AB CD, AC BD (Given) 2. ACDB is a. ) 39. C 40. F . (If opp. sides are , then it 3. M is the midpoint of BC. (The diag. of a bisect each other. ) 41. C 4. AM is a median. (Def. of a median) 38. G(– 4, 1), H(1, 3) 42. H 6 -3

Proving that a Quadrilateral Is a Parallelogram GEOMETRY LESSON 6 -3 43. [2] Statements 1. NRJ 2. NJ Reasons CPT CT 44. [4] a. 6 x = 7 x – 11; x = 11 (Given) (CPCTC) 3. NJ TC (Given) 4. JNTC is a. quad. are both and , then the quad. is a. ) (If opp. sides of a b. Yes; m ABC = m CDE = 66 c. Yes; BD FE and BF DE [3] one or more error in calculating x [2] one explanation is incorrect [1] proof missing steps [1] only part (a) answered 6 -3

Proving that a Quadrilateral Is a Parallelogram GEOMETRY LESSON 6 -3 50. If two lines and a transversal form corr. s , then the two lines are ; if two lines are , then a transversal forms corr. s. 45. a = 8, h = 30, k = 20 46. m = 9. 5, x = 15 47. e = 17, f = 11, c = 204 51. If the prod. of the slopes of two nonvertical lines is – 1, then they are ; if two nonvertical lines are , then the prod. of their slopes os – 1. 48. It is given that AD BC and DAB CBA. By the Reflexive Prop. of AB AB, thus DAB CBA by SAS, so AC BD by CPCTC. 49. If a quad. is a , then the diag. bisect each other; if the diag. of a quad. bisect each other, then it is a. 6 -3

Proving that a Quadrilateral Is a Parallelogram GEOMETRY LESSON 6 -3 Find the values of the variables for which GHIJ must be a parallelogram. 1. 2. a = 34, b = 26 x = 6, y = 0. 75 Determine whether the quadrilateral must be a parallelogram. Explain. 3. Yes; the diagonals bisect each other. 4. 5. Yes; one pair of opposite sides is both congruent and parallel. 6 -3 No; both pairs of opposite sides are not necessarily congruent.

Special Parallelograms GEOMETRY LESSON 6 -4 (For help, go to Lesson 6 -2. ) PACE is a parallelogram and m PAC = 109. Complete each of the following. 1. EC = ? 2. EP = ? 3. m CEP = ? 4. PR = ? 5. RE = ? 6. CP = ? 7. m EPA = ? 8. m ECA = ? 9. Draw a rhombus that is not a square. Draw a rectangle that is not a square. Explain why each is not a square. 6 -4

Special Parallelograms GEOMETRY LESSON 6 -4 Solutions 1. EC = AP = 4. 5 2. EP = AC = 7 3. m CEP = m PAC = 109 4. PR = CR = 4. 75 5. RE = AR = 3. 5 6. CP = 2 RC = 2(4. 75) = 9. 5 7. Since PACE is a parallelogram, AC || PE. By the same-side Interior Angles Theorem, PAC and EPA are supplementary. So, m EPA = 180 – m PAC = 180 – 109 = 71. 8. From Exercise 7, m EPA = 71. Since PACE is a parallelogram, opposite angles are congruent. So, m ECA = m EPA = 71. 9. Answers may vary. Samples given. The rhombus is not a square because it has no right s. The rectangle is not a square because all 4 sides aren’t. 6 -4

Special Parallelograms GEOMETRY LESSON 6 -4 Find the measures of the numbered angles in the rhombus. Theorem 6– 9 states that each diagonal of a rhombus bisects two angles of the rhombus, so m 1 = 78. Theorem 6 -10 states that the diagonals of a rhombus are perpendicular, so m 2 = 90. Because the four angles formed by the diagonals all must have measure 90, 3 and ABD must be complementary. Because m ABD = 78, m 3 = 90 – 78 = 12. Finally, because BC = DC, the Isosceles Triangle Theorem allows you to conclude 1 4. So m 4 = 78. 6 -4

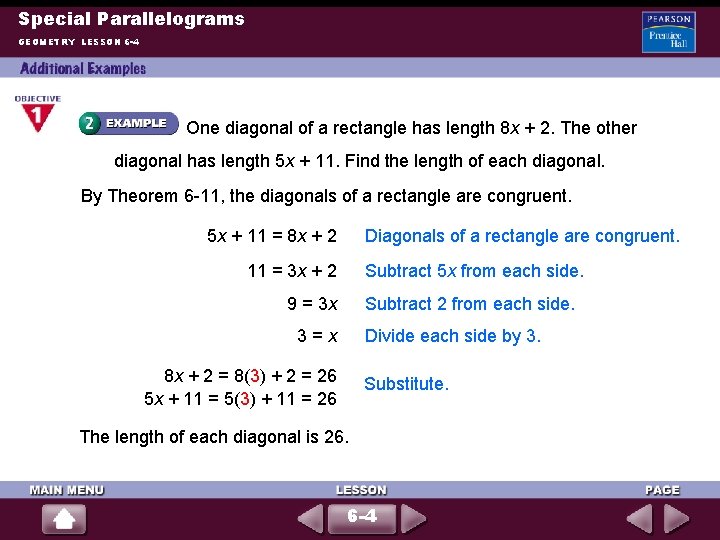
Special Parallelograms GEOMETRY LESSON 6 -4 One diagonal of a rectangle has length 8 x + 2. The other diagonal has length 5 x + 11. Find the length of each diagonal. By Theorem 6 -11, the diagonals of a rectangle are congruent. 5 x + 11 = 8 x + 2 Diagonals of a rectangle are congruent. 11 = 3 x + 2 Subtract 5 x from each side. 9 = 3 x Subtract 2 from each side. 3=x Divide each side by 3. 8 x + 2 = 8(3) + 2 = 26 5 x + 11 = 5(3) + 11 = 26 Substitute. The length of each diagonal is 26. 6 -4

Special Parallelograms GEOMETRY LESSON 6 -4 The diagonals of ABCD are perpendicular. AB = 16 cm and BC = 8 cm. Can ABCD be a parallelogram? Explain. Use indirect reasoning to show why ABCD cannot be a parallelogram. Suppose that ABCD is a parallelogram. Then, because its diagonals are perpendicular, ABCD must be a rhombus by Theorem 6 -12. But AB = 16 cm and BC = 8 cm. This contradicts the requirement that the sides of a rhombus are congruent. So ABCD cannot be a parallelogram. 6 -4

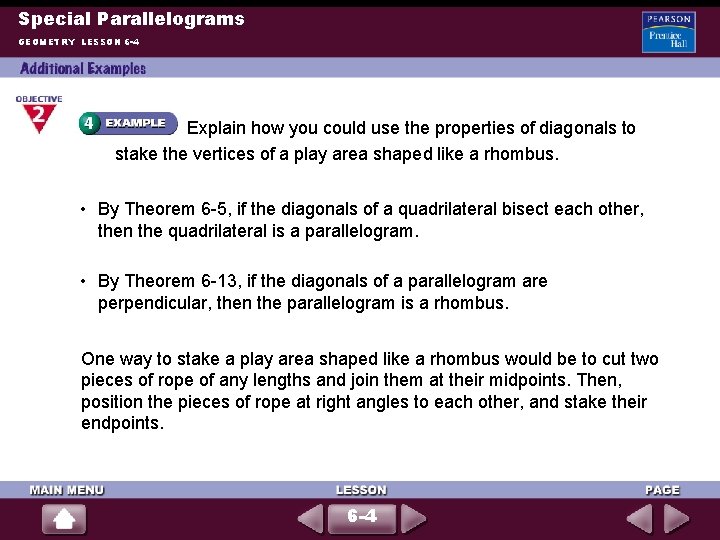
Special Parallelograms GEOMETRY LESSON 6 -4 Explain how you could use the properties of diagonals to stake the vertices of a play area shaped like a rhombus. • By Theorem 6 -5, if the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram. • By Theorem 6 -13, if the diagonals of a parallelogram are perpendicular, then the parallelogram is a rhombus. One way to stake a play area shaped like a rhombus would be to cut two pieces of rope of any lengths and join them at their midpoints. Then, position the pieces of rope at right angles to each other, and stake their endpoints. 6 -4

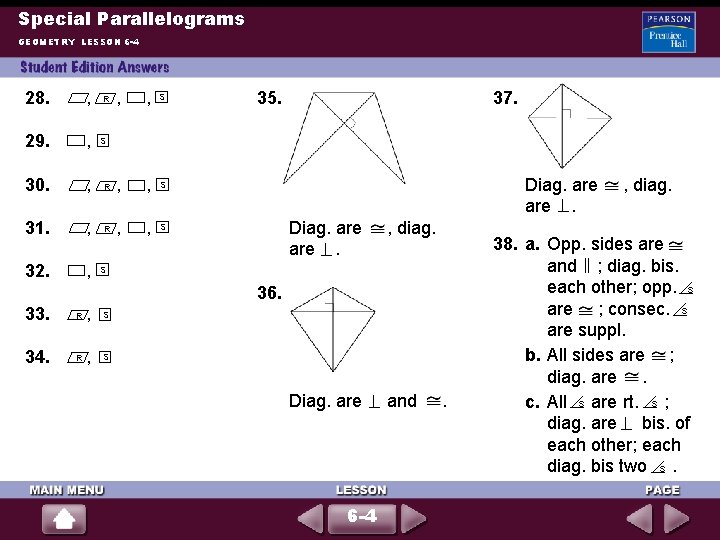
Special Parallelograms GEOMETRY LESSON 6 -4 Pages 315 -318 Exercises 1. 38, 38, 38 9. 90, 55, 90 2. 26, 128 10. 4; LN = MP = 4 3. 118, 31 11. 3; LN = MP= 7 16. (continued) then it would have to be a rectangle and have right s. 17. Yes; diag. in a mean it can be a rectangle with 2 opp. sides 2 cm long. 4. 33. 5, 113, 33. 5 12. 1; LN = MP = 4 5. 32, 90, 58, 32 13. 9; LN = MP = 67 6. 90, 60, 30 14. 5 ; LN = MP = 29 = 9 2 7. 55, 35, 55, 90 15. 5 ; LN = MP = 12 1 8. 60, 90, 30 16. Impossible; if the diag. of a are 3 3 3 2 2 6 -4 , 18. Impossible; in a , consecutive s must be supp. , so all s must be right s. This would make it a rectangle.

Special Parallelograms GEOMETRY LESSON 6 -4 19. Impossible; if the figure is a , then the opp. the bisected is also bisected, and the figure is a rhombus. But the sides are not. 20. Yes; the s are bisected so it could be a rhombus which is a. 21. Yes; the diag. are so it could be a square which is a . 22. The pairs of opp. sides of the frame remain , so the frame remains a. 23. After measuring the sides, she can measure the diag. If the diag. are , then the figure is a rectangle by Thm. 614. 24. Square; a square is both a rectangle and a rhombus, so its diag. have the same 6 -4 24. (continued) properties of both. 25 -34. Symbols may vary. Samples are given: parallelogram: rhombus: R rectangle: square: S 25. , S 26. , R , , S 27. , R , , S R

Special Parallelograms GEOMETRY LESSON 6 -4 28. , 29. , 30. , 31. , 32. , , , S R 35. 37. S Diag. are are. , diag. Diag. are and S 36. 33. R , S 34. R , S 6 -4 . , diag. 38. a. Opp. sides are and ; diag. bis. each other; opp. s are ; consec. s are suppl. b. All sides are ; diag. are. c. All s are rt. s ; diag. are bis. of each other; each diag. bis two s.

Special Parallelograms GEOMETRY LESSON 6 -4 39 -44. Answers may vary. Samples are given. 39. Draw diag. 1, and construct its midpt. Draw a line through the mdpt. Construct segments of length diag. 2 in opp. directions from mdpt. Then, bisect these segments. Connect these mdpts. with the endpts. of diag. 1. 40. Construct a rt. , and draw diag. 1 from its vertex. Construct the from the opp. end of diag. 1 to a side of the rt. . Repeat to other side. 41. Same as 39, but construct a line at the midpt. of diag. 1. 42. Same as 41 except make the diag. =. 43. Draw diag. 1. 6 -4 43. (continued) Construct a at a pt. different than the mdpt. Construct segments on the line of length diag. 2 in opp. directions from the pt. Then, bisect these segments. Connect these midpts. to the endpts. of diag. 1. 44. Draw an acute with the smaller diag. as a side. Construct the line to the other

Special Parallelograms GEOMETRY LESSON 6 -4 44. (continued) side through the nonvertex endpt. of the smaller diag. Draw an arc with compass set to the length of the larger diag. from the non-diag. side of the , passing through the line. Draw the larger diag. , and then draw the non- sides of the trapezoid. 45. Yes; since all right are , the opp. ares 45. (continued) and it is a. Since it has all right s , it is a rectangle. 48. 30 49. x = 5, y = 32, z = 7. 5 50. x = 7. 5, y = 3 46. Yes; 4 sides are , so the opp. sides are making it a. Since it has 4 sides it is also a rhombus. 47. Yes; a quad. with 4 sides is a and a with 4 sides and 4 right s is a square. s 6 -4 51 -53. Drawings may vary. Samples are given. 51. Square, rectangle, isosceles trapezoid, kite.

Special Parallelograms GEOMETRY LESSON 6 -4 51. (continued) 52. Rhombus, 53. For a < b: trapezoid, isosc. trapezoid (a > 1 b), , rhombus , 2 kite. , trapezoid, kite. For a > b: trapezoid, isos. trapezoid, , rhombus (a < 2 b), kite, rectangle, square (if a = 2 b) 6 -4

Special Parallelograms GEOMETRY LESSON 6 -4 53. (continued) 54. (continued) d. Reflexive Prop. of. e. ABC ADE f. CPCTC 54. a. Def. of a rhombus g. Add. Post. h. AEB and AED are rt. b. Diagonals of a bisect each other. i. c. AE j. Def. of AE suppl. rt. s Thm. 6 -4 s s . are 55. Answers may vary. Sample: only one diag. is needed. 56. Given ABCD with diag. AC. Let AC bisect BAD. Because ABC DAC, AB = DA by CPCTC. But since opp. sides of a are , AB = CD and BC = DA. So AB = BC = CD = DA, and ABCD is a rhombus. The new statement is true.

Special Parallelograms GEOMETRY LESSON 6 -4 57. 16, 16 58. 2, 2 59. 1, 1 60. 1, 1 61. 4. ABC ADC (ASA) 5. AB AD (CPCTC) 6. AB DC, AD 7. AB BC CD BC (Opp. sides of a AD (Trans. Prop. of 6 -4 are ) . ) 62. Answers may vary. Sample: The diagonals of a bisect each other so AE CE. Both AED and CED are right s because AC BD, and since DE DE by the Reflexive Prop. , AED CED by SAS. By CPCTC AD CD , and since opp. sides of a are , AB BC AD.

Special Parallelograms GEOMETRY LESSON 6 -4 62. (continued) So ABCD is a rhombus because it has 4 sides. 63. 6 -4

Special Parallelograms GEOMETRY LESSON 6 -4 64. D 67. Yes; both pairs of opp. sides are 65. I 68. No; there are not 2 necess. opp. sides that are both and. 66. [2] Since diag. of a rhombus bisect each other, QS = 9 cm. Also, since all sides are , RS = 9 cm. So QRS is an equilateral and each interior is 180 or 60º. 3 69. Yes; the diag. bisect each other. 70. 6 71. 16 QTS is also an 72. 5 equilateral , so its s are 60º. By add. (m PST + m PSR = m RST), m RST = 60 + 60 or 120. 73. RQ 74. RP 75. ST [1] no work shown OR a response that is only partially correct 76. 89 6 -4 .

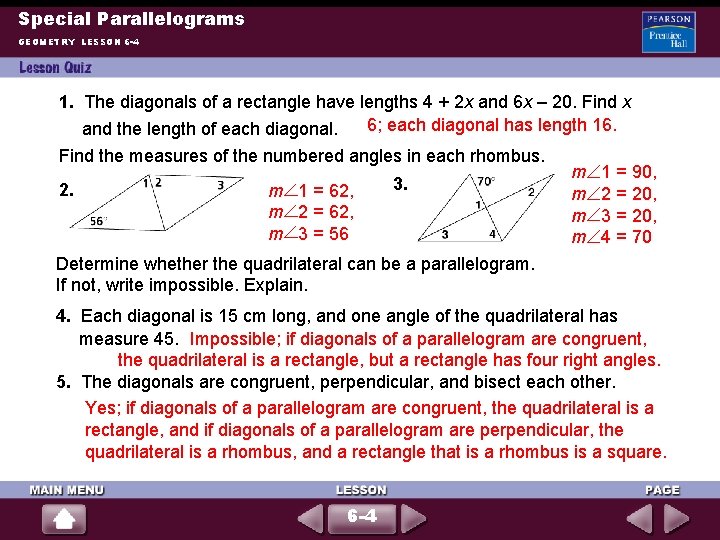
Special Parallelograms GEOMETRY LESSON 6 -4 1. The diagonals of a rectangle have lengths 4 + 2 x and 6 x – 20. Find x 6; each diagonal has length 16. and the length of each diagonal. Find the measures of the numbered angles in each rhombus. 2. m 1 = 62, m 2 = 62, m 3 = 56 3. m m 1 = 90, 2 = 20, 3 = 20, 4 = 70 Determine whether the quadrilateral can be a parallelogram. If not, write impossible. Explain. 4. Each diagonal is 15 cm long, and one angle of the quadrilateral has measure 45. Impossible; if diagonals of a parallelogram are congruent, the quadrilateral is a rectangle, but a rectangle has four right angles. 5. The diagonals are congruent, perpendicular, and bisect each other. Yes; if diagonals of a parallelogram are congruent, the quadrilateral is a rectangle, and if diagonals of a parallelogram are perpendicular, the quadrilateral is a rhombus, and a rectangle that is a rhombus is a square. 6 -4

Trapezoids and Kites GEOMETRY LESSON 6 -5 (For help, go to Lesson 6 -1. ) Find the values of the variables. Then find the lengths of the sides. 1. 3. 2. 6 -5

Trapezoids and Kites GEOMETRY LESSON 6 -5 (For help, go to Lesson 6 -1. ) Solutions 1. a – 1. 4 = 2 a – 7. Solve for a to get a = 5. 6. Substitute 5. 6 for a in the expression a – 1. 4: 5. 6 – 1. 4 = 4. 2. The lengths of the sides are 4. 5, 4. 2, and 4. 5. 2. 4 y + 6 = 7 y – 3. Solve for y to get y = 3. Substitute 3 for y in the expression 4 y + 6: 4(3) + 6 = 18. Substitute 3 for y in the expression 5 y + 1. 4: 5(3) + 1. 4 = 16. 4. The lengths of the sides are 18, 4. 8, 18, and 16. 4. 3. n = 3 m and n + 6 = 7 m – 14. Substitute 3 m for n in n + 6 = 7 m – 14: 3 m + 6 = 7 m – 14. Solve for m to get m = 5. Substitute 5 for m in n = 3 m to get n = 15. Substitute 5 for m in 7 m – 14: 7(5) – 14 = 21. The lengths of the sides are 15, 21, and 21. 6 -5

Trapezoids and Kites GEOMETRY LESSON 6 -5 XYZW is an isosceles trapezoid, and m X = 156. Find m Y, m Z, and m W. m X + m W = 180 156 + m W = 180 m W = 24 Two angles that share a leg of a trapezoid are supplementary. Substitute. Subtract 156 from each side. Because the base angles of an isosceles trapezoid are congruent, m Y = m X = 156 and m Z = m W = 24. 6 -5

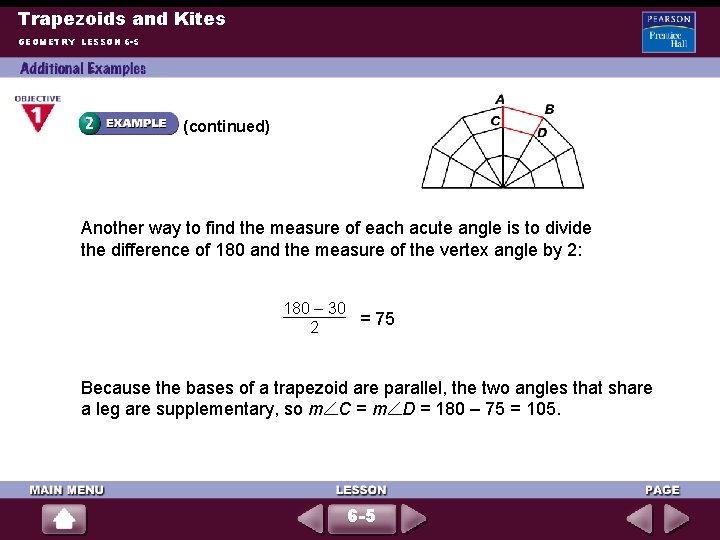
Trapezoids and Kites GEOMETRY LESSON 6 -5 Half of a spider’s web is shown below, formed by layers of congruent isosceles trapezoids. Find the measures of the angles in ABDC. Trapezoid ABDC is part of an isosceles triangle whose vertex angle is at the center of the spider web. Because there are 6 adjacent congruent vertex angles at the center of the web, together forming a straight angle, each vertex angle measures 180 , or 30. 6 By the Triangle Angle-Sum Theorem, m A + m B + 30 = 180, so m A + m B = 150. Because ABDC is part of an isosceles triangle, m A = m B, so 2 m A = 150 and m A = m B = 75. 6 -5

Trapezoids and Kites GEOMETRY LESSON 6 -5 (continued) Another way to find the measure of each acute angle is to divide the difference of 180 and the measure of the vertex angle by 2: 180 – 30 = 75 2 Because the bases of a trapezoid are parallel, the two angles that share a leg are supplementary, so m C = m D = 180 – 75 = 105. 6 -5

Trapezoids and Kites GEOMETRY LESSON 6 -5 Find m 1, m 2, and m 3 in the kite. m 2 = 90 RU = RS m 1 = 72 m 3 + m RDU + 72 = 180 m RDU = 90 m 3 + 90 + 72 = 180 m 3 + 162 = 180 m 3 = 18 Diagonals of a kite are perpendicular. Definition of a kite Isosceles Triangle Theorem Triangle Angle–Sum Theorem Diagonals of a kite are perpendicular. Substitute. Simplify. Subtract 162 from each side. 6 -5

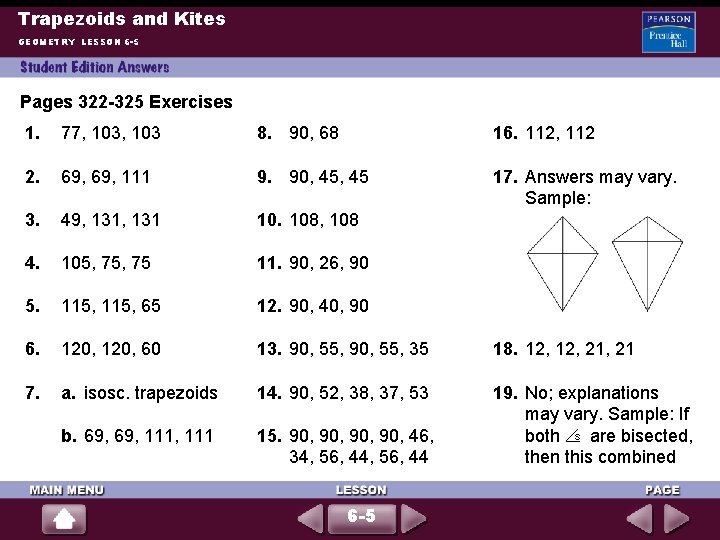
Trapezoids and Kites GEOMETRY LESSON 6 -5 Pages 322 -325 Exercises 1. 77, 103 8. 90, 68 16. 112, 112 2. 69, 111 9. 90, 45 17. Answers may vary. Sample: 3. 49, 131 10. 108, 108 4. 105, 75 11. 90, 26, 90 5. 115, 65 12. 90, 40, 90 6. 120, 60 13. 90, 55, 35 18. 12, 21, 21 7. a. isosc. trapezoids 14. 90, 52, 38, 37, 53 b. 69, 111, 111 15. 90, 90, 46, 34, 56, 44 19. No; explanations may vary. Sample: If both s are bisected, then this combined 6 -5

Trapezoids and Kites GEOMETRY LESSON 6 -5 19. (continued) with KM KM by the Reflexive Prop. means KLM KNM by SAS. So by CPCTC, opp. s L and N are , so it is not an isos. trapezoid. 24. 4 25. 1 26. 1. ABCD is an isos. trapezoid, AB DC. (Given) 2. Draw AE DC. (Two points determine a line. ) 3. AD EC (Def. of a trapezoid) 20. 12 4. AECD is a 21. 15 5. 22. 15 6. DC AE (Opp. sides of a 23. 3 7. AB AE (Trans. Prop. of C . (Def. of a 1 (Corr. 6 -5 s are ). ) are ) . )

Trapezoids and Kites GEOMETRY LESSON 6 -5 26. (continued) 8. AEB is an isosc. 9. B 1 (Base . (Def. of an isosc. s of an isosc. ) are 30. Isosc. trapezoid; all the large rt. s appear to be. . ) 31. 112, 68 10. 11. 12. B C (Trans. Prop. of B and BAD are suppl. , are suppl. (Same side int. BAD CDA (Suppl. of ) s C and CDA are suppl. ) s are . ) 32. Yes, the be obtuse. s can 33. Yes, the be obtuse, as well as one other. 27. 28 s are 34. Yes; if 2 rt. s , they are suppl. The other 2 are also suppl. 28. x = 35, y = 30 29. x = 18, y = 108 6 -5 s

Trapezoids and Kits GEOMETRY LESSON 6 -5 35. No; if two consecutive s are suppl. , then another pair must be also because one pair of opp. s is. Therefore, the opp. s would be , which means the figure would be a and not a kite. s must 36. Yes; the be 45° or 135° each. 37. No; if two consecutive s 37. (continued) compl. , then the kite would be concave. 38. Rhombuses and squares would be kites since opp. sides can be also. 39. D is any point on BN such that ND =/ BN and D is below N. were 6 -5 40. 1. AB CD, and AD CD (Given) 2. BD BD (Refl. Prop. of 3. ABD (SSS) 4. A C (CPCTC) ) CBD 41. Answers may vary. Sample: Draw TA and RP

Trapezoids and Kites GEOMETRY LESSON 6 -5 41. (continued) 1. isosc. trapezoid TRAP (Given) 42. Draw BI as described, then draw BT and BP. 2. TA RP (Diag. of an isosc. trap. are. ) 1. TR 2. 3. TR PA (Given) 4. RA RA (Refl. Prop. of ) R A (Base trap. are. ) 3. RB 5. TRA PAR (SSS) 4. 6. RTA APR (CPCTC) 5. BT 6. 6 -5 PA (Given) s of isosc. AB (Def. of bisector) TRB RBT PAB (SAS) BP (CPCTC) ABP (CPCTC)

Trapezoids and Kites GEOMETRY LESSON 6 -5 42. 7. (continued) TBI PBI s are (Compl. of 8. BI 43 -44. Check students’ justifications. Samples are given. . ) BI (Refl. Prop. of ) 9. TBI PBI (SAS) 10. BIT BIP (CPCTC) 11. 12. BIT and ( suppl. TI 43. It is one half the sum of the lengths of the bases; draw a diag. of the trap. to form 2. The s bases B and b of the trap. are each a base of a. Then the segment joining the midpts. of the non- sides is the sum of the midsegments of the. BIP are rt. s. s are rt. s. ) This sum is PI (CPCTC) 1 2 B+ s 1 2 b– 1 2 (B + b). 44. It is one half the difference of the lengths of the bases; from Ex. 43, the length of the segment joining 13. BI is bis. of TP. (Def. of bis. ) 6 -5

Trapezoids and Kites GEOMETRY LESSON 6 -5 49. D 44. (continued) the midpts. of the non- sides is 1 (B + b). The middle part of this 2 segment joins the midpts. of the diags. Each outer segment measures 1 B. So the length of 2 the segment connecting the midpts. of the diags. is 1 (B – b). 50. [2] HRW and 2 HBW [1]incorrect diagram OR no work shown 45. B 46. I 51. 126 47. C 52. 27 48. C 53. 27 6 -5

Trapezoids and Kites GEOMETRY LESSON 6 -5 54. a. 4 b. 5 c. 5 55. a. 3 b. 30 c. 30 56. SAS 6 -5

Trapezoids and Kites GEOMETRY LESSON 6 -5 Use isosceles trapezoid ABCD for Exercises 1 and 2. 1. If m A = 45, find m B, m C, and m D. m B = 45, m C = m D = 135 2. If AC = 3 x – 16 and BD = 10 x – 86, find x. 10 Use kite GHIJ for Exercises 3– 6. 3. Find m 90 4. Find m 9 5. Find m 81 6. Find m 40 1. 2. 3. 4. 6 -5

Placing Figures in the Coordinate Plane GEOMETRY LESSON 6 -6 (For help, go to Lesson 6 -1. ) Draw a quadrilateral with the given vertices. Then determine the most precise name for each quadrilateral. 1. H(– 5, 0), E(– 3, 2), A(3, 2), T(5, 0) 2. S(0, 0), A(4, 0), N(3, 2), D(– 1, 2) 3. R(0, 0), A(5, 5), I(8, 4), N(7, 1) 4. W(– 3, 0), I(0, 3), N(3, 0), D(0, – 3) 6 -6

Placing Figures in the Coordinate Plane GEOMETRY LESSON 6 -6 Solutions 1. The slope of EA and the slope of HT are both 0, so EA || HT. Since EH and AT are not parallel, HEAT is a trapezoid. HE = 8 and TA = 8. The legs of the trapezoid are congruent, so HEAT is an isosceles trapezoid. 2. DN and SA are both horizontal, so their slopes are both 0. Since their slopes are the same, DN || SA. The slope of DS and the slope of NA are both – 2 = – 2, so DS || NA. 1 Since both pairs of opposite sides are parallel, the quadrilateral is a parallelogram. 6 -6

Placing Figures in the Coordinate Plane GEOMETRY LESSON 6 -6 Solutions (continued) 3. RA AI IN NR = = 50, 10, and 50 Since two pairs of adjacent sides are congruent, the quadrilateral is a kite. 4. WI = IN = ND = DW = 18. The slope of IN and the slope of DW are 3 both – 3 = – 1. The slope of WI and the slope of ND are both = 1. Since 3 3 the product of 1 and – 1 is – 1 WI IN, IN ND, ND DW, and DW WI. Since all sides are congruent and all angles are right angles, the quadrilateral is a square. 6 -6

Placing Figures in the Coordinate Plane GEOMETRY LESSON 6 -6 Use the properties of parallelogram OCBA to find the missing coordinates. Do not use any new variables. The vertex O is the origin with coordinates O(0, 0). Because point A is p units to the left of point O, point B is also p units to the left of point C because OCBA is a parallelogram. So the first coordinate of point B is –p – x. Because AB || CO and CO is horizontal, AB is also horizontal. So point B has the same second coordinate, q, as point A. The missing coordinates are O(0, 0) and B(–p – x, q). 6 -6

Placing Figures in the Coordinate Plane GEOMETRY LESSON 6 -6 Show that TWVU is a parallelogram by proving both pairs of opposite sides congruent. If both pairs of opposite sides of a quadrilateral are congruent, then the quadrilateral is a parallelogram by Theorem 6 -8. You can prove that TWVU is a parallelogram by showing that TW = VU and WV = TU. Use the Distance Formula. 6 -6

Placing Figures in the Coordinate Plane GEOMETRY LESSON 6 -6 (continued) Use the coordinates T(a, b), W(a + c, b + d), V(c + e, d), and U(e, 0) that you found in Example 2. TW = (a + c – a)2 + (b + d – b)2 = c 2 + d 2 VU = (c + e – e)2 + (d – 0)2 = WV = ((a + c) – (c + e))2 + (b + d – d)2 = TU = (a – e)2 + (b – 0)2 = c 2 + d 2 (a – e)2 + b 2 Because TW = VU and WV = TU, TWVU is a parallelogram. 6 -6

Placing Figures in the Coordinate Plane GEOMETRY LESSON 6 -6 Pages 328 -330 Exercises 1. W(0, h); Z(b, 0) 9. (–b, 0); undefined 2. W(a, a); Z(a, 0) 10. a , b ; – b 3. 4. W(–b, b); Z(–b, –b) W(0, b); Z(a, 0) 2 11. ––r 12. 2 a ; t – 2 2 – b , c ; 0 2 5. W(–r, 0); Z(0, –t) 13. a. (2 a, 0) 6. W(–b, c); Z(0, c) b. (0, 2 b) 7. 8. b, h ; – h 2 2 b a, a ; undefined 2 t r 13. (continued) e. b 2 + a 2 f. b 2 + a 2 g. MA = MB = MC 14– 19. Answers may vary. Samples are given. 14. A, C, H, F c. (a, b) 15. B, D, H, F d. b 2 + a 2 16. A, B, F, E 6 -6

Placing Figures in the Coordinate Plane GEOMETRY LESSON 6 -6 17. A, C, G, E 25. W(– 2 b, 2 c); Z(0, 2 c) 18. A, C, F, E 26. a. Diag. of a rhombus are. 27. (continued) sides are. 28. (c – a, b) 19. A, D, G, F 20. W(0, 2 h); Z(2 b, 0) b. Diag. of a that is not a rhombus are not. 29. (a, 0) 30. (–b, 0) 21. W(2 a, 2 a); Z(2 a, 0) 22. W(– 2 b, 2 b); Z(– 2 b, – 2 b) 27. Answers may vary. Sample: r = 3, t = 2; slopes are 2 and – 2 ; 3 23. W(0, b); Z(2 a, 0) 24. Z(0, – 2 t); W(– 2 r, 0) 31. a. 3 all lengths are 13; the opp. sides have the same slope, so they are. The 4 6 -6 b. (–b, 0), (0, b), (b, 0), (0, –b)

Placing Figures in the Coordinate Plane GEOMETRY LESSON 6 -6 31. (continued) c. b 2 32. (continued) b. 34. Step 1: (0, 0) Step 2: (a, 0) d. 1, – 1 e. Yes, because the product of the slopes is – 1. c. b 2 + 4 c 2 d. b 2 + 4 c 2 32. a. Step 3: Since m 1 + m 2 + 90 = 180, 1 and 2 must be compl. 3 and 2 are the acute s of a rt. . e. the lengths are =. Step 4: (–b, 0) 33. Step 5: (–b, a) Step 6: Using the formula for slope, the 6 -6

Placing Figures in the Coordinate Plane GEOMETRY LESSON 6 -6 34. (continued) slope for 1 = b 40. C a and the slope for 2 = – a. Mult. the b slopes, b • – a = – 1. a b 41. [2] (b, a); the diag. of a rectangle bisect each other. 35. B [1] no conclusion given 36. F 42. 62, 118; 2. 5 37. C 43. (3, 2) 38. C 44. (– 3, – 4) 39. A 45. a. Reflexive b. AAS 6 -6

Placing Figures in the Coordinate Plane GEOMETRY LESSON 6 -6 Find the missing coordinates of each figure. 1. parallelogram M (b, c + a) 2. rhombus M(2 a, 0), D(a, –b) 3. rectangle A(0, b), D(a, 0) Find the coordinates of the midpoint and the slope. 4. OM in Exercise 1 midpoint: slope: c + a b b c+a , ; 2 2 5. AD in Exercise 2 6. AD in Exercise 3 midpoint: (a, 0); midpoint: slope: undefined slope: – a 6 -6 b a b , ; 2 2

Proofs Using Coordinate Geometry GEOMETRY LESSON 6 -7 (For help, go to Lesson 6 -6. ) 1. Graph the rhombus with vertices A(2, 2), B(7, 2), C(4, – 2), and D(– 1, – 2). Then, connect the midpoints of consecutive sides to form a quadrilateral. What do you notice about the quadrilateral? Give the coordinates of B without using any new variables. 2. rectangle 3. isosceles triangle 6 -7

Proofs Using Coordinate Geometry GEOMETRY LESSON 6 -7 Solutions 1. The coordinates of the midpoints are ( 9 , 2), (11 , 0), ( 1 3 , – 2), and ( 2 , 0). 2 2 2 rise The slope ( run ) of the two longer segments is 2 , or 1, and the slope of the 4 2 – 2 two shorter segments is 1 , or – 2. Since the slopes of opposite sides are equal, opposite sides are parallel. The quadrilateral is a parallelogram. Also, 1 since (– 2) = – 1, adjacent sides are perpendicular to one another. Thus, the 2 parallelogram is a rectangle. 6 -7

Proofs Using Coordinate Geometry GEOMETRY LESSON 6 -7 Solutions (continued) 2. The coordinates of B are (a, c). 3. Since BO AO the coordinates of B are (–a, 0). 6 -7

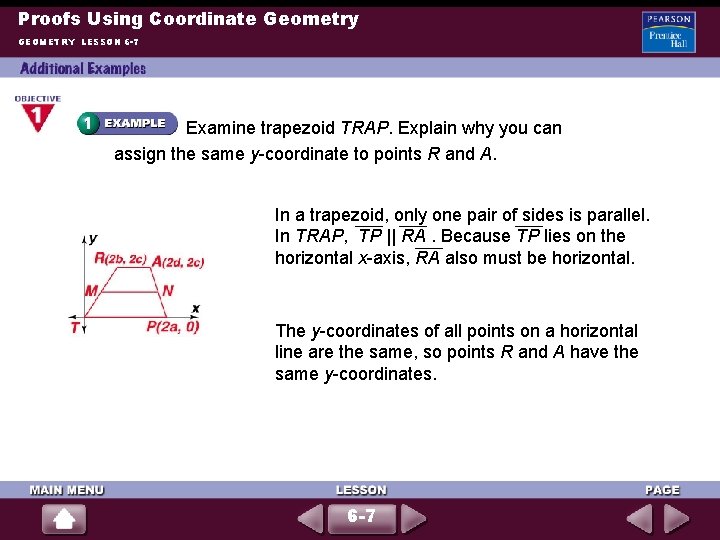
Proofs Using Coordinate Geometry GEOMETRY LESSON 6 -7 Examine trapezoid TRAP. Explain why you can assign the same y-coordinate to points R and A. In a trapezoid, only one pair of sides is parallel. In TRAP, TP || RA. Because TP lies on the horizontal x-axis, RA also must be horizontal. The y-coordinates of all points on a horizontal line are the same, so points R and A have the same y-coordinates. 6 -7

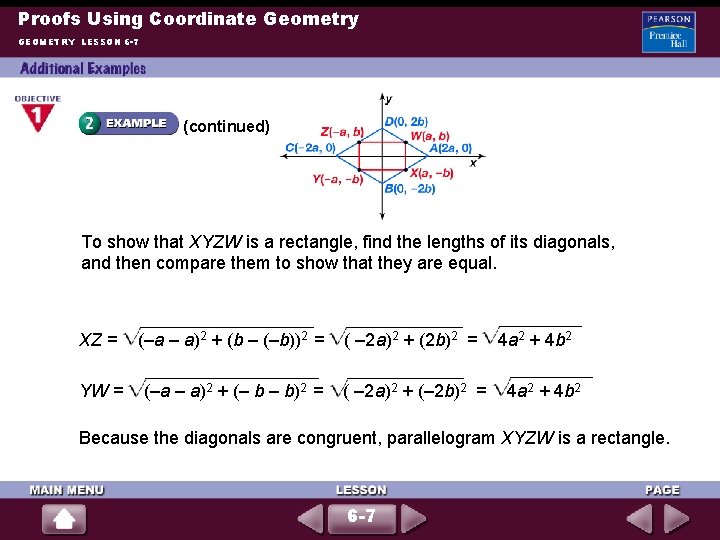
Proofs Using Coordinate Geometry GEOMETRY LESSON 6 -7 Use coordinate geometry to prove that the quadrilateral formed by connecting the midpoints of rhombus ABCD is a rectangle. The quadrilateral XYZW formed by connecting the midpoints of ABCD is shown below. From Lesson 6 -6, you know that XYZW is a parallelogram. If the diagonals of a parallelogram are congruent, then the parallelogram is a rectangle by Theorem 6 -14. 6 -7

Proofs Using Coordinate Geometry GEOMETRY LESSON 6 -7 (continued) To show that XYZW is a rectangle, find the lengths of its diagonals, and then compare them to show that they are equal. XZ = (–a – a)2 + (b – (–b))2 = ( – 2 a)2 + (2 b)2 = YW = (–a – a)2 + (– b – b)2 = ( – 2 a)2 + (– 2 b)2 = 4 a 2 + 4 b 2 Because the diagonals are congruent, parallelogram XYZW is a rectangle. 6 -7

Proofs Using Coordinate Geometry GEOMETRY LESSON 6 -7 Pages 333 -337 Exercises 1. a. W a , b ; 2. a. origin c+e d , 2 2 b. x-axis 2 Z 2 b. W(a, b); Z(c + e, d) c. W(2 a, 2 b); Z(2 c + 2 e, 2 d) d. c; it uses multiples of 2 to name the coordinates of W and Z. 4. (continued) c. multiples of 2 d. M c. 2 e. N d. coordinates f. Midpoint 3. a. y-axis g. Distance b. Distance 5. a. isos. 4. a. rt. b. x-axis b. legs c. y-axis 6 -7

Proofs Using Coordinate Geometry GEOMETRY LESSON 6 -7 5. (continued) d. midpts. e. 6. sides 8. a. D(–a – b, c), E(0, 2 c), F(a + b, c), G(0, 0) a+b i. – c a+b f. slopes b. (a + b)2 + c 2 j. sides g. the Distance Formula c. (a + b)2 + c 2 k. DEFG d. (a + b)2 + c 2 a. e. (a + b)2 + c 2 b. (a, b) f. c a+b c. the same point a 2 + b 2 g. b. 2 9. a. (a, b) (b + a)2 + c 2 b. (a + b)2 + c 2 7. 8. (continued) h. – c a 2 + b 2 6 -7 10. Answers may vary. Sample: The

Proofs Using Coordinate Geometry GEOMETRY LESSON 6 -7 10. (continued) Midsegment Thm. ; the segment connecting the midpts. of 2 sides of the is to the 3 rd side and half its length; you can use the Midpoint Formula and the Distance Formula to prove the statement directly. 11. (continued) c. (– 2 b, 2 c) 12– 24. Answers may vary. Samples are given. d. L(b, a + c), M(b, c), N(–b, c), K(–b, a + c) 12. yes; Dist. Formula e. 0 13. yes; same slope f. vertical lines 14. yes; prod. of slopes = – 1 g. 15. no; may not have intersection pt. h. 11. a. 16. no; may need measures b. midpts. 6 -7

Proofs Using Coordinate Geometry GEOMETRY LESSON 6 -7 17. no; may need measures 23. yes; slope of AB = slope of BC 18. yes; prod. of slopes of sides of A = – 1 24. yes; Dist. Formula, AB = BC = CD = AD 19. yes; Dist. Formula 25. 1, 4, 7 20. yes; Dist. Formula, 2 sides = 26. 0, 2, 4, 6, 8 21. no; may need measures 22. yes; intersection pt. for all 3 segments 27. – 0. 8, 0. 4, 1. 6, 2. 8, 4, 5. 2, 6. 4, 7. 6, 8. 8 28. – 1. 76, – 1. 52, – 1. 28, . . . , 9. 52, 9. 76 29. – 2 + 12 , – 2 + 2 12 , n n – 2 + 3 12 , . . , n – 2 +(n – 1) 12 n 30. (0, 7. 5), (3, 10), (6, 12. 5) 31. – 1, 6 2 , 1, 8 1 , 3 3 (3, 10), 5, 112 , 3 7, 13 1 3 32. (– 1. 8, 6), (– 0. 6, 7), 6 -7

Proofs Using Coordinate Geometry GEOMETRY LESSON 6 -7 35. Assume b > a. a + b – a , 32. (continued) (0. 6, 8), (1. 8, 9), (3, 10), (4. 2, 11), (5. 4, 12), (6. 6, 13), (7. 8, 14) a+2 b–a , . . , n a + (n – 1) b – a 33. (– 2. 76, 5. 2), (– 2. 52, 5. 4), (– 2. 28, 5. 6), . . . , (8. 52, 14. 6), (8. 76, 14. 8) 34. n 36. Assume b ≥ a, d ≥ c. a+ b–a , c+ d–c – 3, + 12 , 5 + 10 , n n – 3 + 2 12 , 5 + 2 10 n n n , n a+2 b–a , c+2 d–c n , . . . , a + (n – 1) b – a , c + (n – 1) d – c n – 3 + (n – 1) n 12 10 , 5 + (n – 1) n n n 37. a. The s with bases d and b, and heights c and a, respectively, have the same area. They 6 -7

Proofs Using Coordinate Geometry GEOMETRY LESSON 6 -7 37. a. (continued) share the small right with base d and height c, and the remaining areas are s with base c and height (b – d). So 1 ad = 1 bc. 2 38. (continued) other s and follow the same steps. Where the two lines meet connecting the centroids of the 4 s is the centroid of the quad. 2 Mult. both sides by 2 gives ad = bc. 39. a. L(b, d), M(b + c, d), N(c, 0) d x; b+c BN: y = 2 d (x – c); 2 b – c d CL: y = b – 2 c (x – 2 c) b. AM: y = b. The diagram shows that a = c , b d since both represent the slope of the top segment of the. So by (a), ad = bc. c. P 2(b + c) , 2 d 38. Divide the quad. into 2 s. Find the centroid for each and connect them. Now divide the quad. into 2 3 3 d. Pt. P satisfies the eqs. for AM 6 -7

Proofs Using Coordinate Geometry GEOMETRY LESSON 6 -7 39. d. (continued) and CL. e. AM = AP = 40. (continued) b. Let a pt. on line p be (x, y). Then the eq. of p is (b + c)2 + d 2 ; 2(b + c) 3 2 or y = 2 d 2= 3 b (x – a). c y– 0 =b x–a c c. x = 0 (b + c)22 + d 2 = 2 d. When x = 0, y = b (x – a) = 3 2 (b + c)2 + d 2 = 3 c b ab (–a) = –. So p and q c c intersect at 0, – ab. c e. a c 2 AM 3 The other 2 distances are found similarly 40. a. b f. Let a pt. on line r be (x, y). c Then the eq. of r is y – 0 = a x–b 6 -7 c

Proofs Using Coordinate Geometry GEOMETRY LESSON 6 -7 40. f. (continued) or y = a (x – b). 41. (continued) c. Let the eq. for c g. – ab = a (0 – b) c c h. 0, – ab c and for 2 1 be y = b x a a be y = – x and the b origin be the int. point. 41. a. Horiz. lines have slope 0, and vert. lines have undef. slope. Neither could be mult. to get – 1. b. Assume the lines do not intersect. Then they have the same slope, say m. Then m • m = m 2 = – 1, which is impossible. So the lines must intersect. 6 -7

Proofs Using Coordinate Geometry GEOMETRY LESSON 6 -7 44. [2] a. 7 + a = 3; a = – 1; 41. c. (continued) Define C(a, b), A(0, 0), and 2 – 3 + b = 4; b = 11; 2 2 B a, a. Using the Distance b Formula, AC = BA = (a, b) = (– 1, 11) a 2 + b 2 , 4 a 2 + a 2 , and b. b 2 CB = b + a. (7 – (– 1))2 + (– 3 – 11)2 = 260 = 2 ≈ 16. 12 b Then AC 2 + BA 2 = CB 2, and m A = 90 by the Conv. of the Pythagorean Thm. So 1 2. 65 [1] minor computational error OR no work shown 42. A 43. G 6 -7

Proofs Using Coordinate Geometry GEOMETRY LESSON 6 -7 45. [4] a-b. Sample: 46. (–a, b) 47. a. If the sum of the s of a polygon is 360°, then the polygon is a quad. b. If a polygon is a quad. , then the sum of its s is 360°. c. AP = (b – a)2 + c 2 = RQ PQ = PQ AQ = a = RP APQ RQP by SSS [3] minor computational error 48. a. If x =/ 51, then 2 x =/ 102. b. If 2 x =/ 102, then x =/ 51. 49. a. If a =/ 5, then a 2 =/ 25. [2] parts (a) and (b) correct b. If a 2 =/ 25, then a =/ 5. [1] one part correct 6 -7

Proofs Using Coordinate Geometry GEOMETRY LESSON 6 -7 50. a. If b ≥ – 4, then b is not neg. b. If b is not neg. , then b ≥ – 4. 51. a. If c ≤ 0, then c is not pos. 54. LM NK, LN NL by the Refl. Prop. of , and LNK NLM by all rt. s are. So LNK NLM by SAS, and K M by CPCTC. b. If c is not pos. , then c ≤ 0. 52. A C, AD CD and ADB CDB so by ASA ADB CDB and by CPCTC AB CB. 53. HE FG, EF GH, and HF HF by the Refl. Prop. of , so HEF FGH by SSS. Then CPCTC 1 2. 6 -7

Proofs Using Coordinate Geometry GEOMETRY LESSON 6 -7 Use the diagram for Exercises 1– 5. 1. Point M is the midpoint of AC. Find its coordinates. (a + c, d ) 2. Point N is the midpoint of BC. Find its coordinates. (b + c, d ) 3. Explain how you know that MN || AB. Both have slope 0, so they are parallel. 4. Show that MN = 1 AB. 2 The Distance Formula finds MN = b – a and AB = 2 b – 2 a. 5. What theorem do Exercises 1– 4 prove? Triangle Midsegment Theorem 6 -7

Quadrilaterals GEOMETRY CHAPTER 6 Page 342. 1. 3. 4. (continued) b. (0, 0), (3, 0), (4, 3), (1, 3) trapezoid c. (0, 0), (5, 3), (0, 3) 2. parallelogram 4. Answers may vary. Sample: d. (0, 0), (5, 0), (4, 3), (1, 3) 5. 6 in. 6. 9 cm kite a. (0, 0), (3, 3), (0, 3) 6 -A 7. Check students’ work

Quadrilaterals GEOMETRY CHAPTER 6 8. x = 100, y = 50, z = 40 9. x = 57, y = 57, z = 66 10. x = 6, y = 5 11. x = 36, y = 108, z = 72 13. (continued) then the quad. is a. 16. (continued) kite has no opp. sides. 14. Yes; if both pairs of opp. sides of a quad. are , then the quad. is a. 17. x = 2, y = 1 18. 90, 30 19. 50, 130 12. No; both diag. must bisect each other. 15. Yes; if both pairs of opp. s in a quad. are , the quad is a. 13. Yes; if one pair of opp. sides of a quad. is and , 16. Answers may vary. Sample: A square has 4 sides and a 6 -A 20. S(–a, –b), T(–a, b); (–a, 0); no slope 21. x-coordinates may vary. Sample: S(0, 0), T(b + c, d); b+c , d 2 2 ; b +d c

Quadrilaterals GEOMETRY CHAPTER 6 22. 20 ft 23. a. a 2 b. a 2 c. AC 6 -A