Projective Geometry Projective Geometry Projective Geometry Projective Geometry

Projective Geometry

Projective Geometry

Projective Geometry

Projective Geometry

Projective Geometry

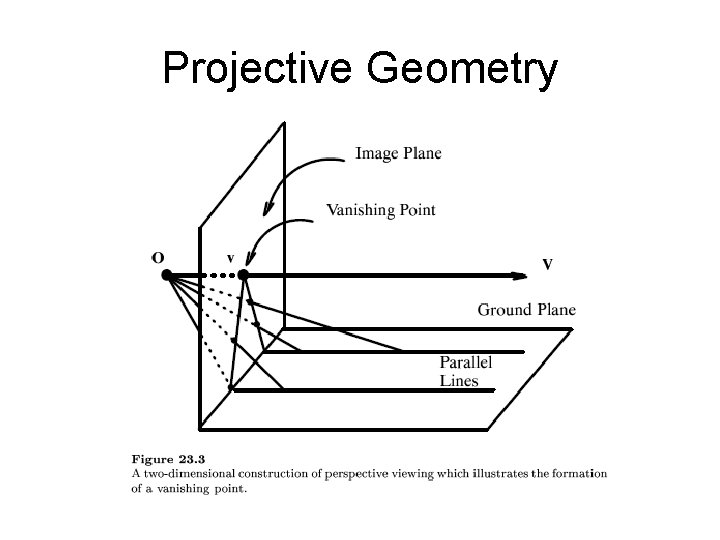
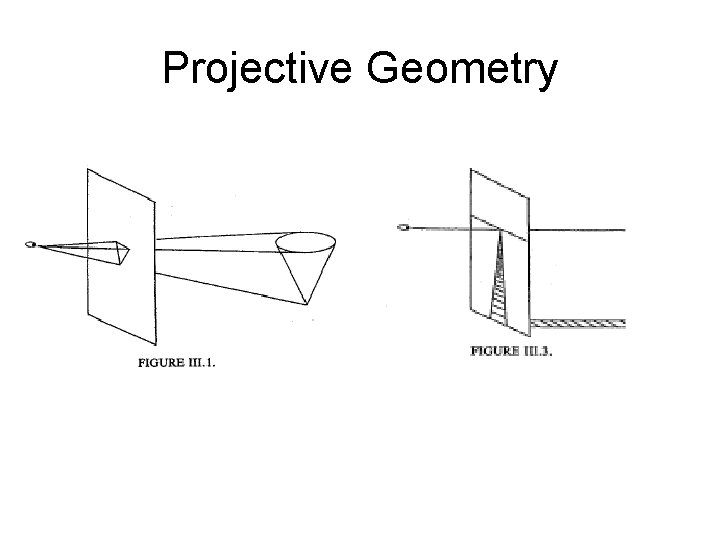
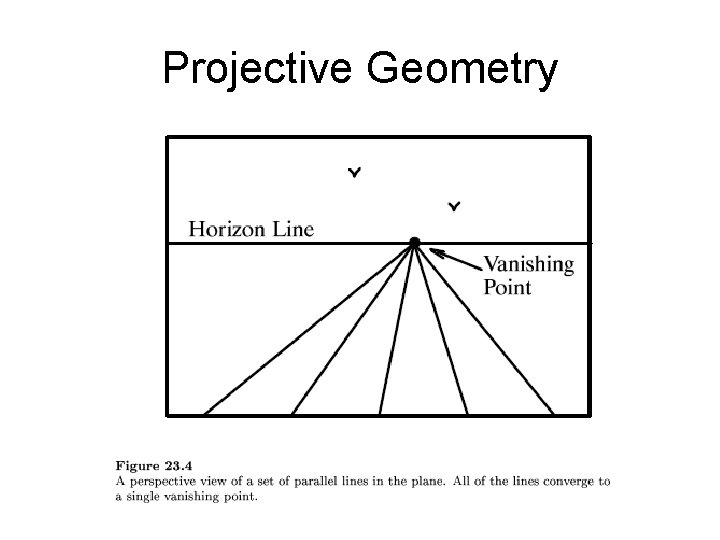
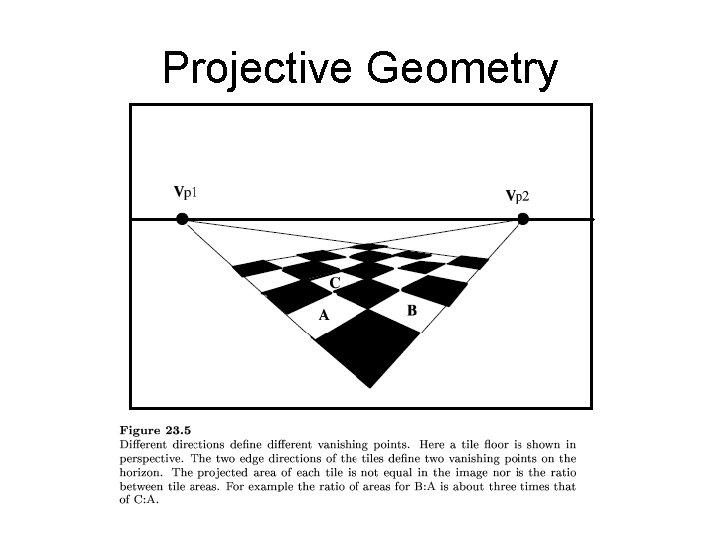
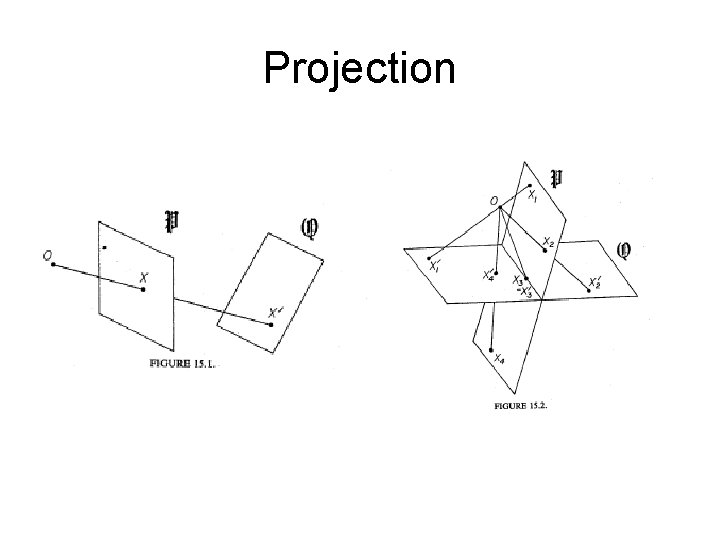
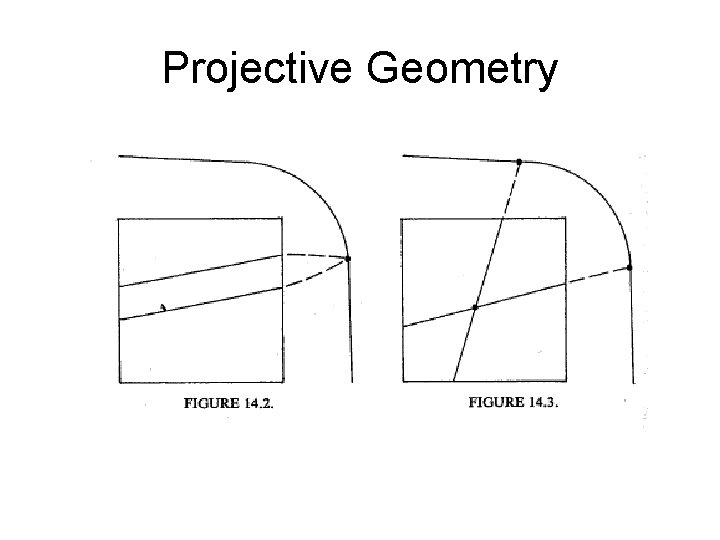
Projection

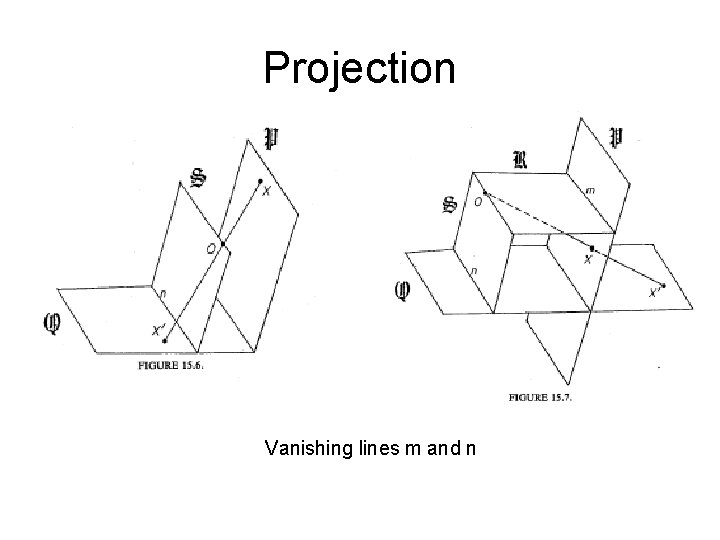
Projection Vanishing lines m and n

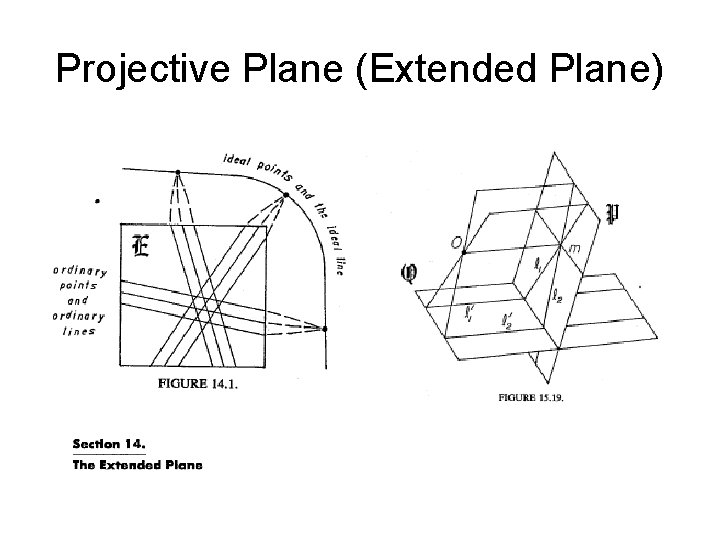
Projective Plane (Extended Plane)

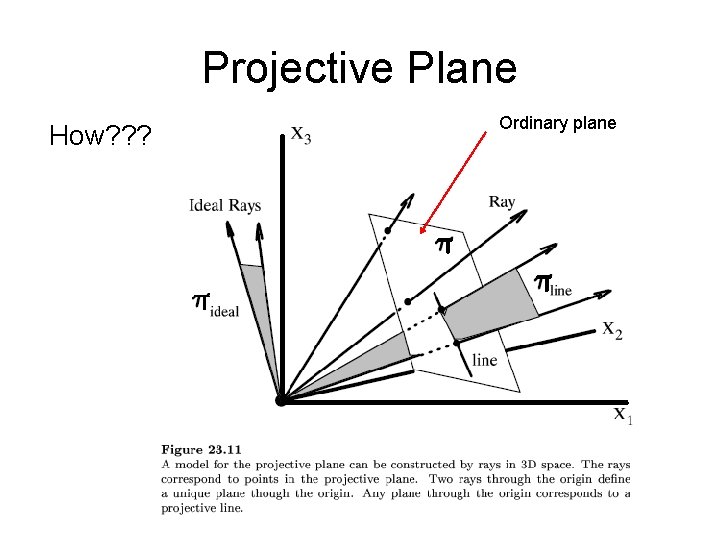
Projective Plane How? ? ? Ordinary plane

Point Representation A point in the projective plane is represented as a ray in R 3

Projective Geometry

Homogeneous coordinates Homogeneous representation of 2 D points and lines The point x lies on the line l if and only if Note that scale is unimportant for incidence relation equivalence class of vectors, any vector is representative Set of all equivalence classes in R 3 (0, 0, 0)T forms P 2 Homogeneous coordinates Inhomogeneous coordinates but only 2 DOF

Projective Geometry

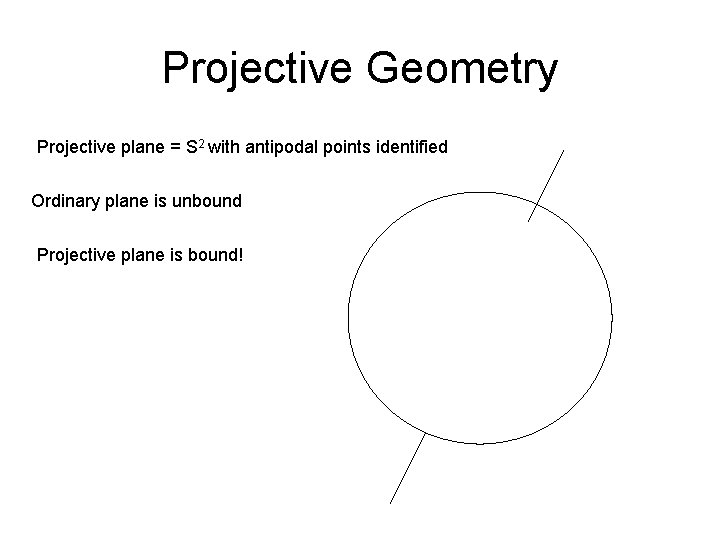
Projective Geometry Projective plane = S 2 with antipodal points identified Ordinary plane is unbound Projective plane is bound!

Projective Geometry

Projective Geometry

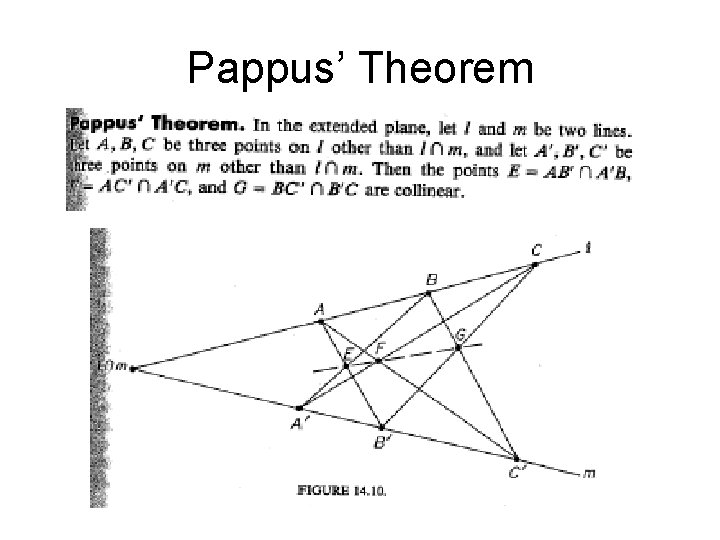
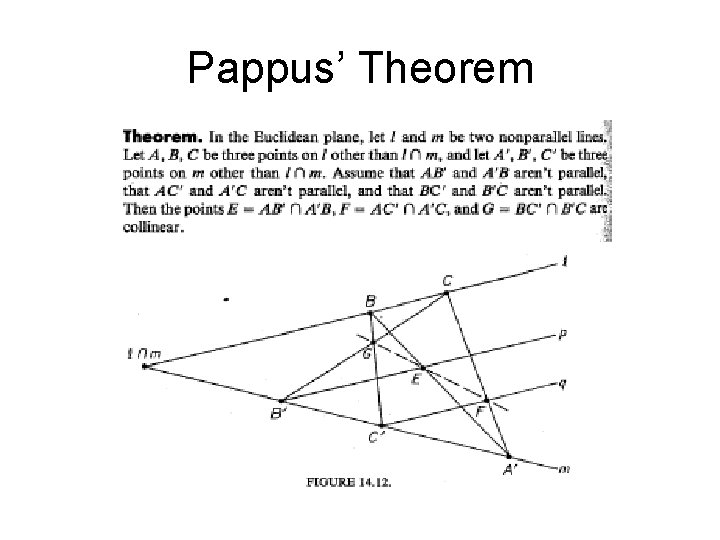
Pappus’ Theorem

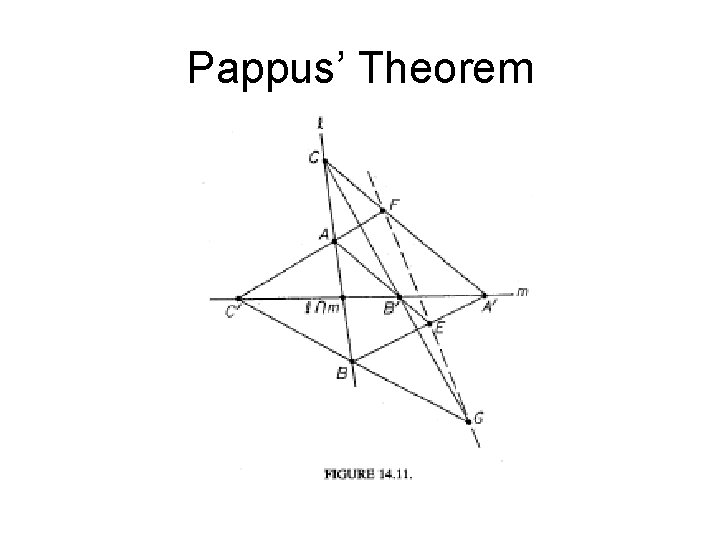
Pappus’ Theorem

Pappus’ Theorem

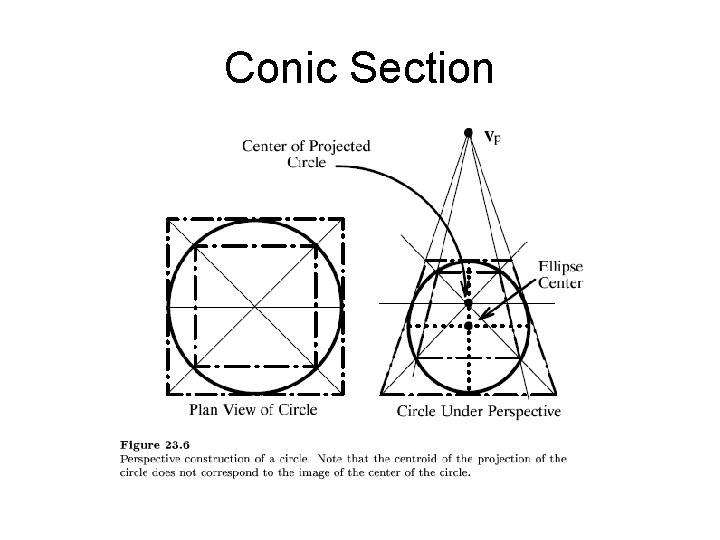
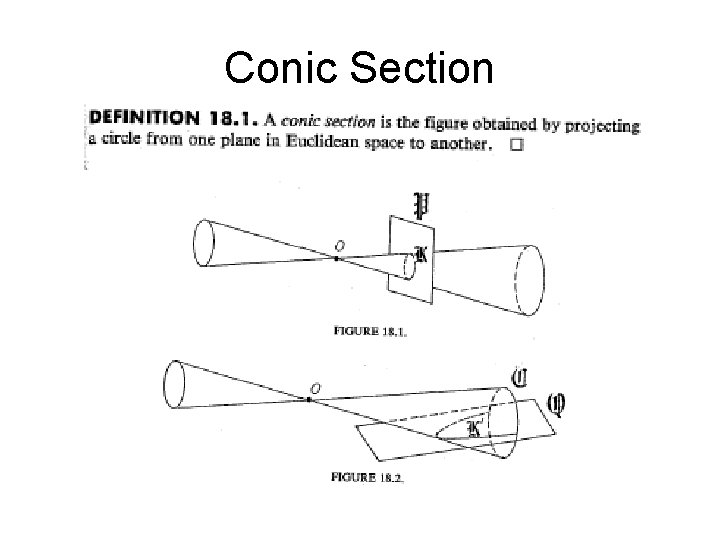
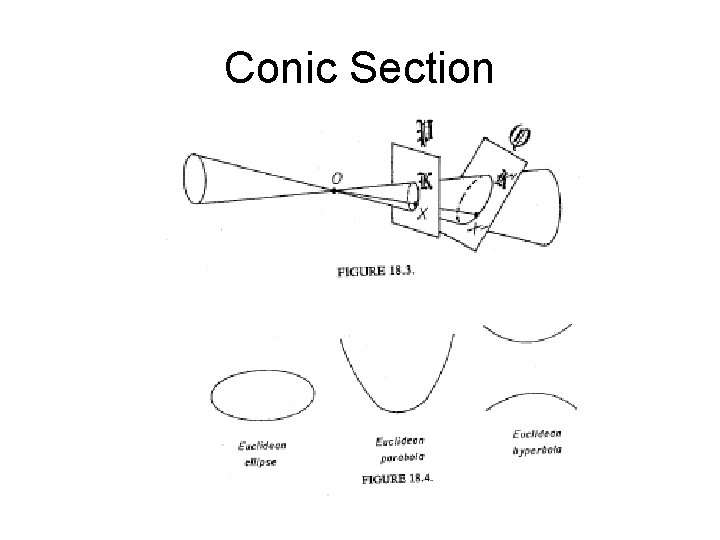
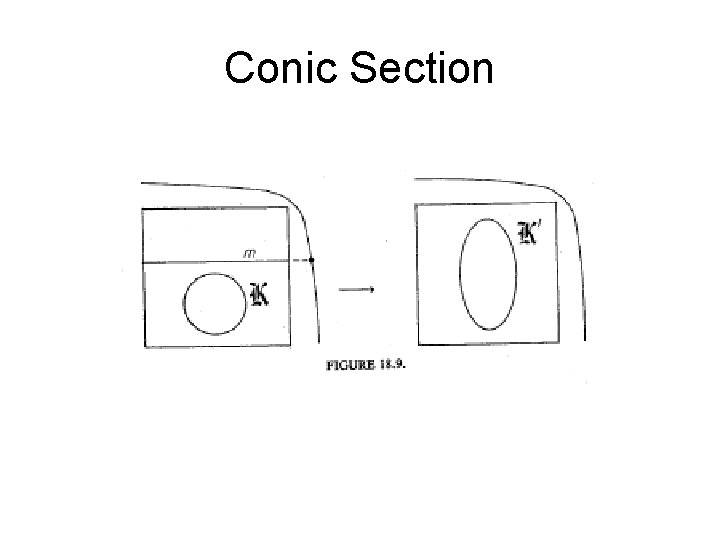
Conic Section

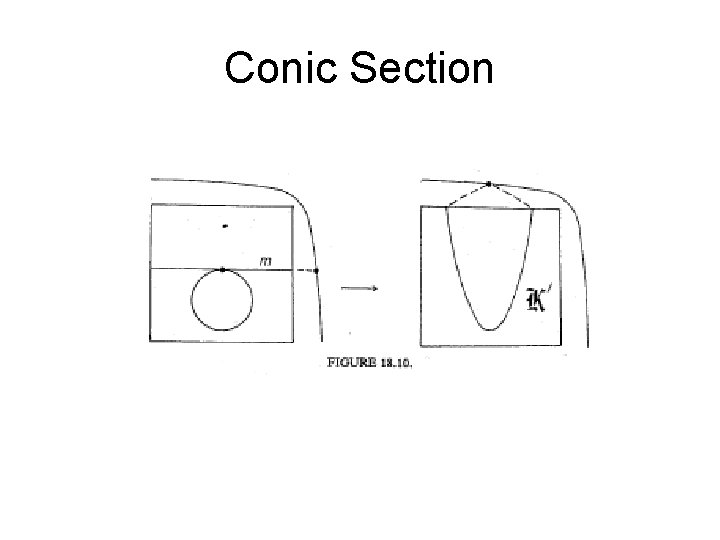
Conic Section

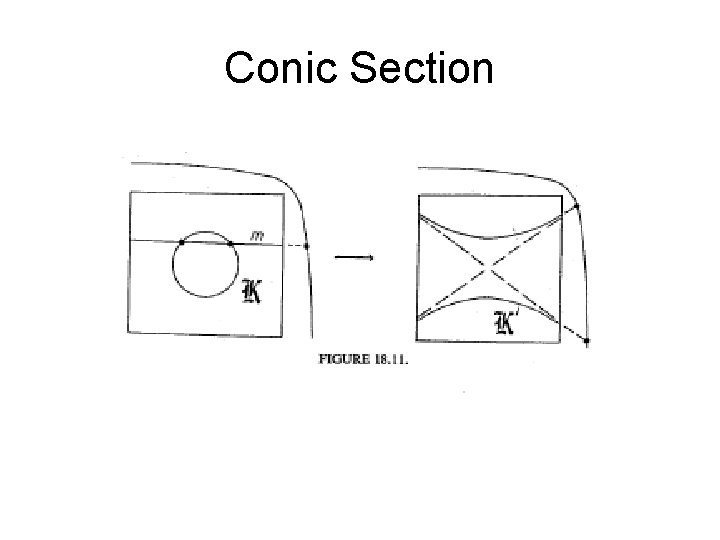
Conic Section

Conic Section

Conic Section

Conic Section

Conic Section

Conic Section

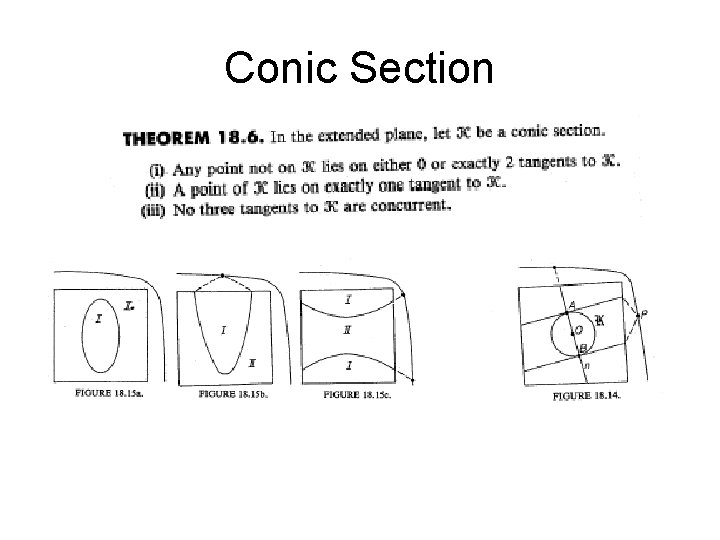
Form of Conics

Transformation • Projective • Affine • Similarity : incidence, tangency : plane at infinity, parallelism : absolute conics

Circular Point Circular points

Euclidean Transformation Any transformation of the projective plane which leaves the circular points fixed is a Euclidean transformation, and Any Euclidean transformation leaves the circular points fixed. A Euclidean transformation is of the form:

Euclidean Transformation

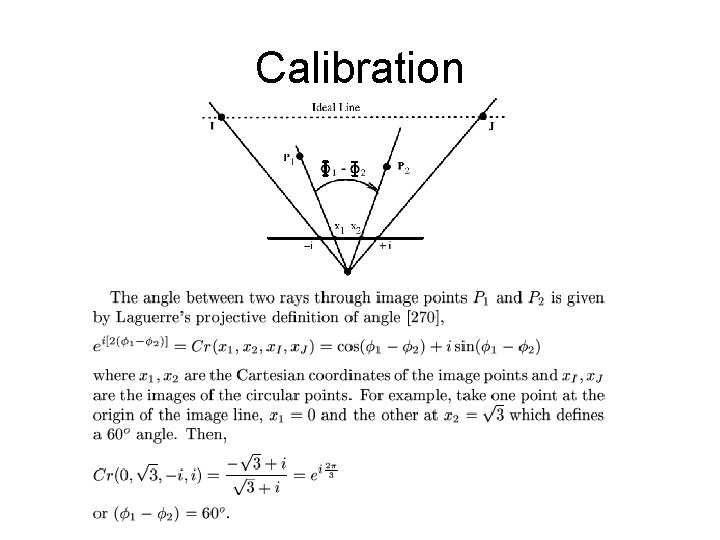
Calibration

Calibration Use circular point as a ruler…

Calibration

Today • Cross ratio • More on circular points and absolute conics • Camera model and Zhang’s calibration • Another calibration method

Transformation • Let X and X’ be written in homogeneous coordinates, when X’=PX • P is a projective transformation when…. . • P is an affine transformation when…. . • P is a similarity transformation when…. .

Transformation Projective Affine Similarity Euclidean

Matrix Representation

Invariance • Mathematician loves invariance ! • Fixed point theorem • Eigenvector

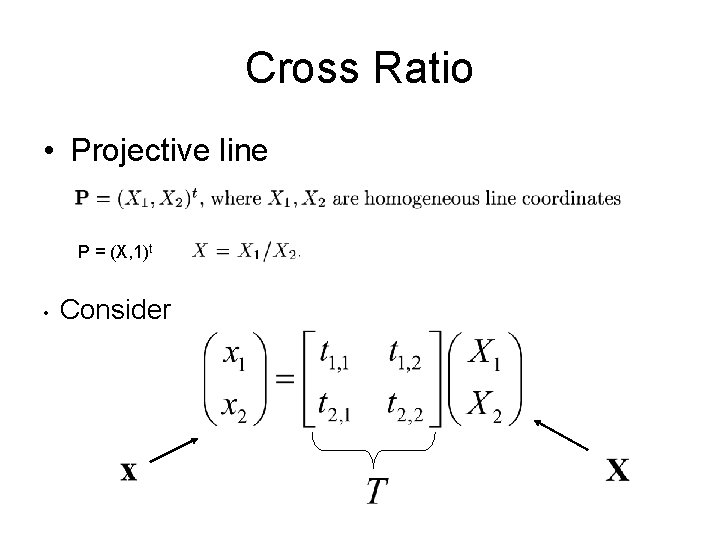
Cross Ratio • Projective line P = (X, 1)t • Consider

Cross Ratio

Cross Ratio Consider determinants: Rewritting So we have Consider

Cross Ratio How do we eliminate |T| and the coefficients The idea is to use the ratio. Consider and The remaining coefficients can be eliminated by using the fourth point

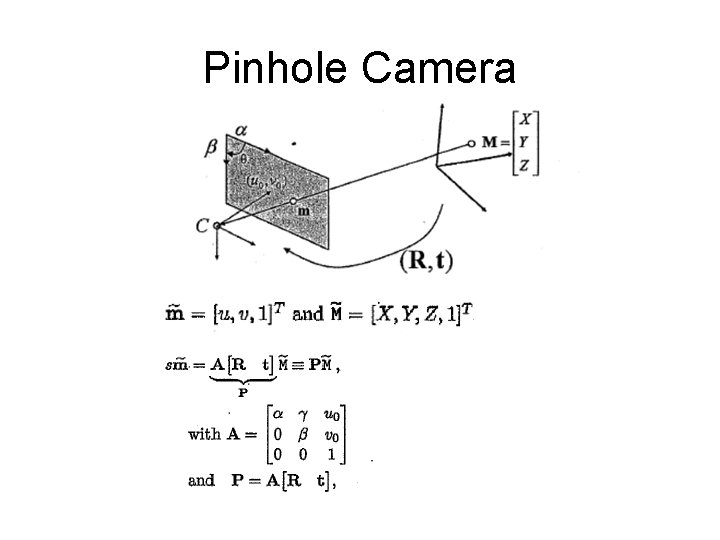
Pinhole Camera

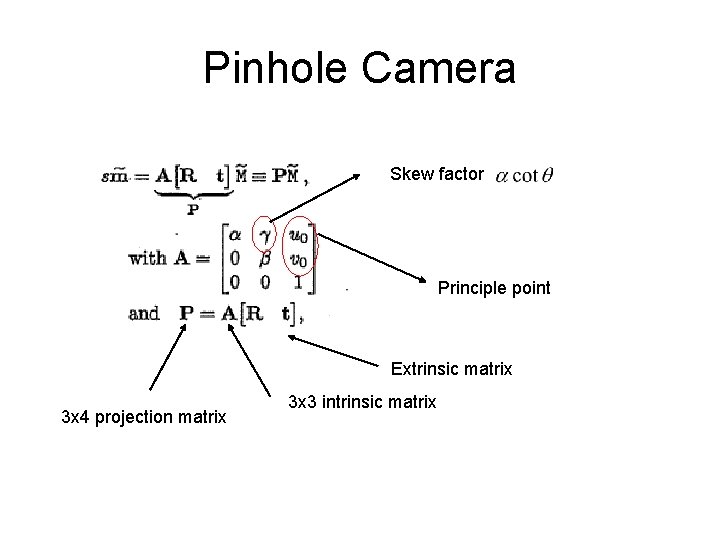
Pinhole Camera Skew factor Principle point Extrinsic matrix 3 x 4 projection matrix 3 x 3 intrinsic matrix

Pinhole Camera

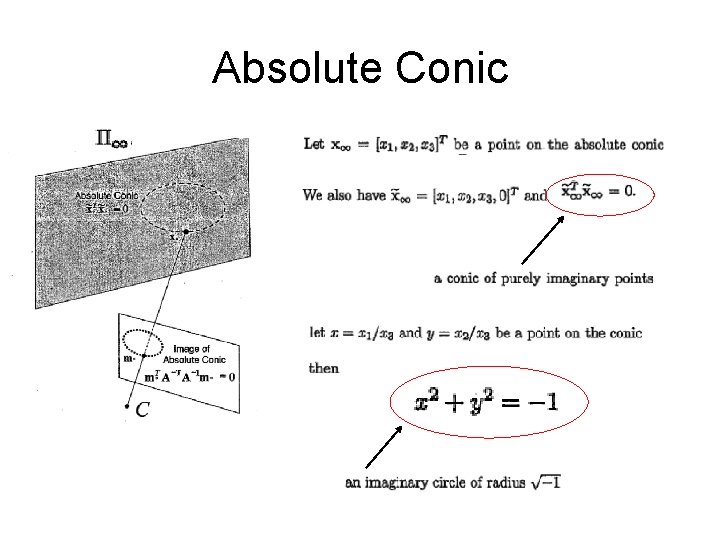
Absolute Conic

Absolute Conic

Absolute Conic Important: absolute conic is invariant to any rigid transformation That is, We can write and obtain and

Absolute Conic Now consider the image of the absolute conic It is defined by

Typical Calibration 1. Estimate the camera projection matrix from correspondence between scene points and image points (Zhang p. 12) 2. Recover intrinsic and extrinsic parameters

Typical Calibration P[3][4], B[3][3], b[3]

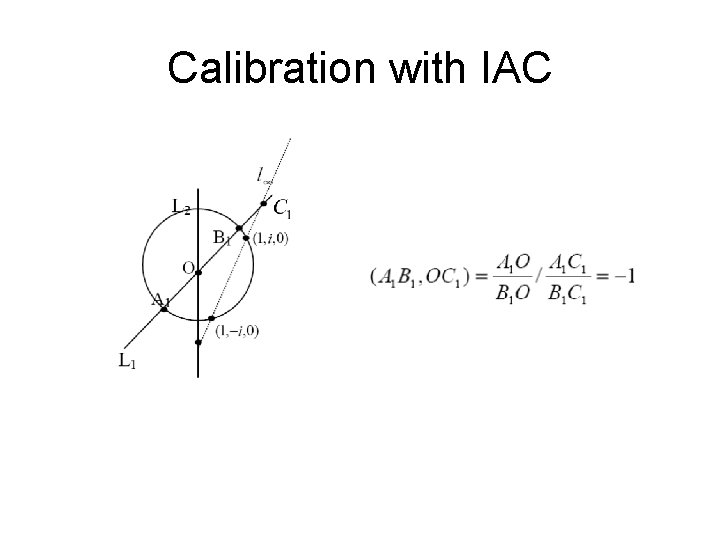
Calibration with IAC Can we calibrate without correspondence? (British Machine Vision)

Calibration with IAC

Calibration with IAC From Zhang’s, the image of the absolute conic is the conic Let’s assume that the model plane is on the X-Y plane of the world coordinate system, so we have:

Calibration with IAC It is sufficient to consider model plane in homogeneous coordinates Points on the model plane with t=0 form the line at infinity We know that the circular points I = (1, i, 0, 0)T and J = (1, -i, 0, 0)T must satisfy Let the image of I and J be denoted by

Calibration with IAC Consider the circle in the model plane with center (Ox, Oy, 1) and radius r. This circle intersects the line at infinity when or Any circle (any center, any radius) intersects line at infinity in the two circular points The image of the circle should intersect the image of the line at infinity (vanishing line) in the image of the two circular points

Calibration with IAC

Calibration with IAC