Projective cameras Motivation Elements of Projective Geometry Projective

Projective cameras • Motivation • Elements of Projective Geometry • Projective structure from motion Planches : – http: //www. di. ens. fr/~ponce/geomvis/lect 3. ppt – http: //www. di. ens. fr/~ponce/geomvis/lect 3. pdf

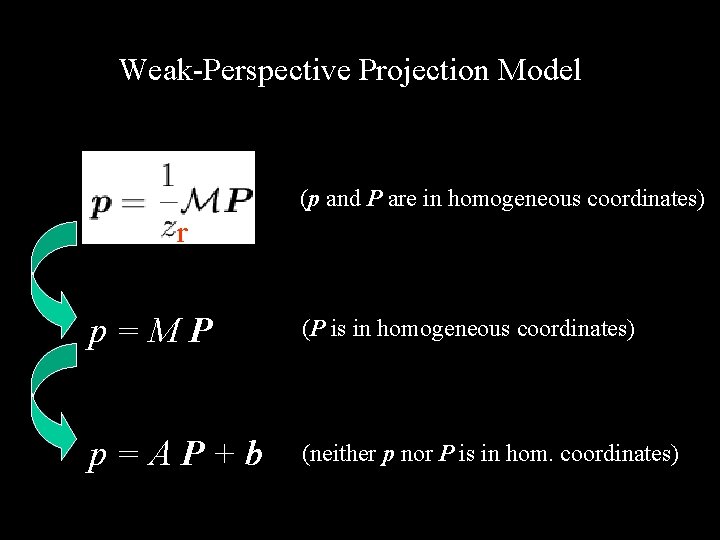
Weak-Perspective Projection Model (p and P are in homogeneous coordinates) r p=MP (P is in homogeneous coordinates) p=AP+b (neither p nor P is in hom. coordinates)

Affine Spaces: (Semi-Formal) Definition

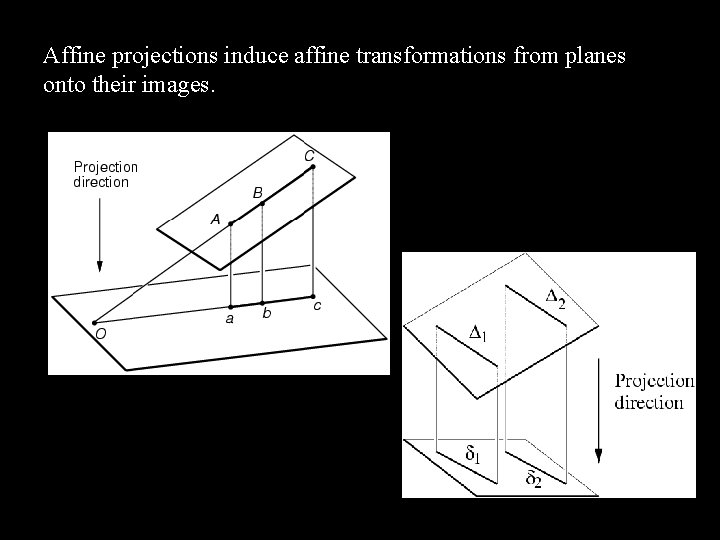
Affine projections induce affine transformations from planes onto their images.

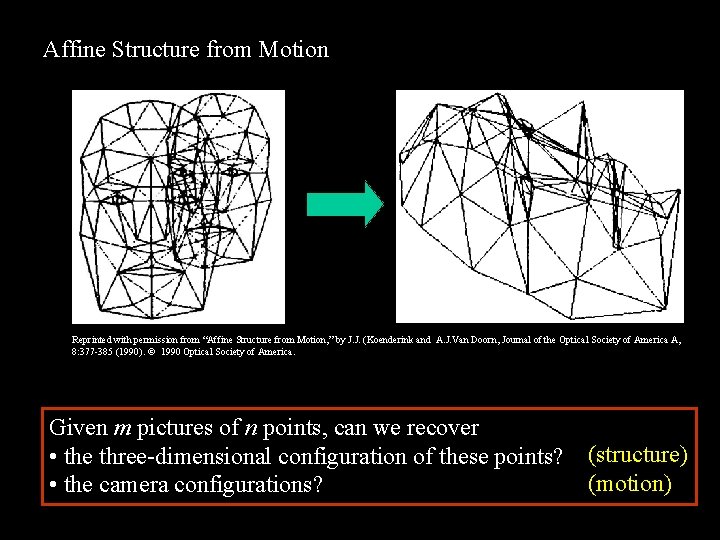
Affine Structure from Motion Reprinted with permission from “Affine Structure from Motion, ” by J. J. (Koenderink and A. J. Van Doorn, Journal of the Optical Society of America A, 8: 377 -385 (1990). 1990 Optical Society of America. Given m pictures of n points, can we recover • the three-dimensional configuration of these points? • the camera configurations? (structure) (motion)

Geometric affine scene reconstruction from two images (Koenderink and Van Doorn, 1991).

The Projective Structure-from-Motion Problem Given m perspective images of n fixed points P we can write j Problem: estimate the m 3 x 4 matrices M iand the n positions P j from the mn correspondences p. ij 2 mn equations in 11 m+3 n unknowns Overconstrained problem, that can be solved using (non-linear) least squares!

The Projective Ambiguity of Projective SFM When the intrinsic and extrinsic parameters are unknown If M i and P are solutions, j So are M’ and P’ where i j and Q is an arbitrary non-singular 4 x 4 matrix. Q is a projective transformation.

Projective Spaces: (Semi-Formal) Definition

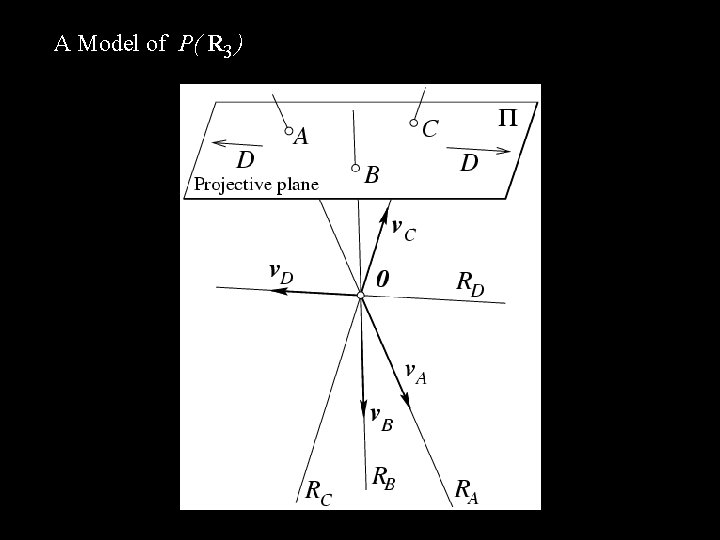
A Model of P( R 3 )

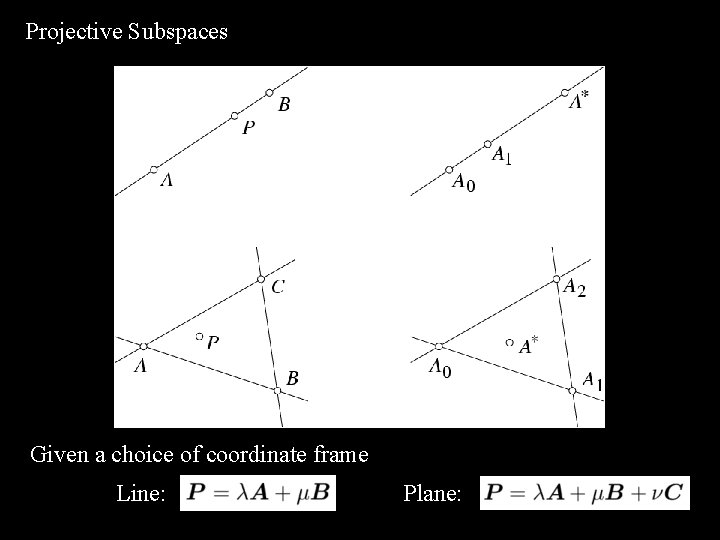
Projective Subspaces and Projective Coordinates

Projective Subspaces and Projective Coordinates P Projective coordinates

Projective Subspaces Given a choice of coordinate frame Line: Plane:

When do m+1 points define a p-dimensional subspace Y of an n-dimensional projective space X equipped with some coordinate frame? Rank ( D ) = p+1, where Writing that all minors of size (p+1)x(p+1) of D are equal to zero gives the equations of Y.

Hyperplanes and duality Consider n+1 points P 0, … , Pn-1, P in a projective space X of dimension n. They lie in the same hyperplane when Det(D)=0. This can be rewritten as u 0 x 0+u 1 x 1+…+unxn = 0, or T P = 0, where = (u 0, u 1, …, un)T. Hyperplanes form a dual projective space X* of X, and any theorem that holds for points in X holds for hyperplanes in X*. What is the dual of a straight line?

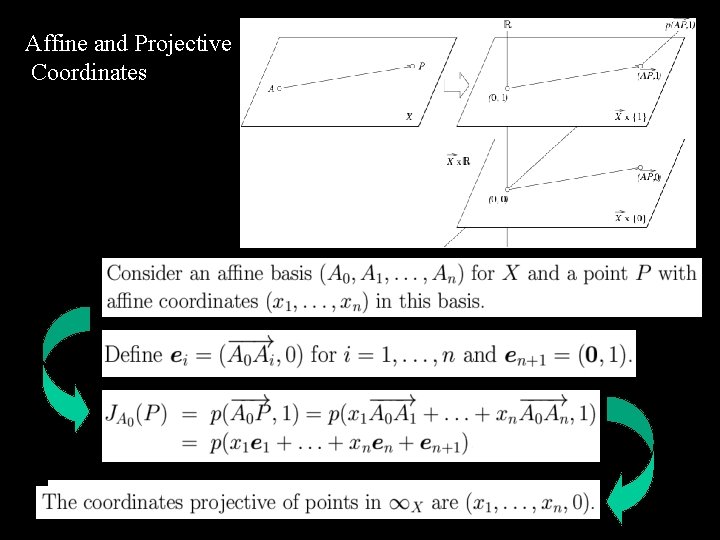
Affine and Projective Spaces

Affine and Projective Coordinates

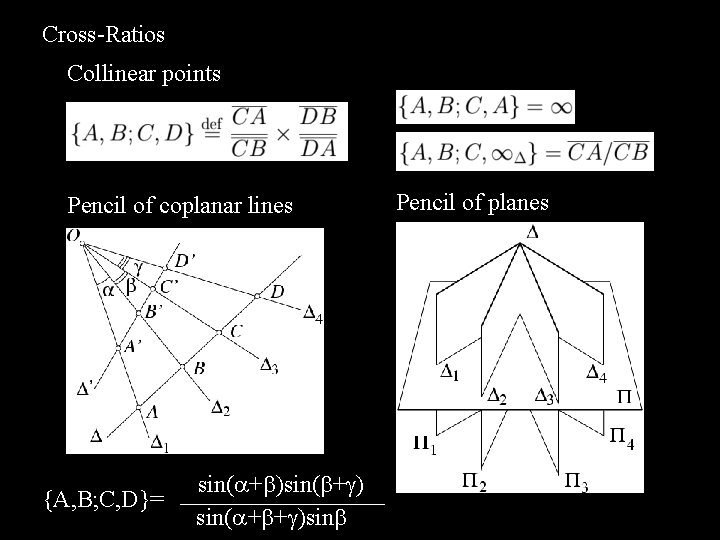
Cross-Ratios Collinear points Pencil of coplanar lines {A, B; C, D}= sin( + ) sin( + + )sin Pencil of planes

Cross-Ratios and Projective Coordinates Along a line equipped with the basis In a plane equipped with the basis In 3 -space equipped with the basis *

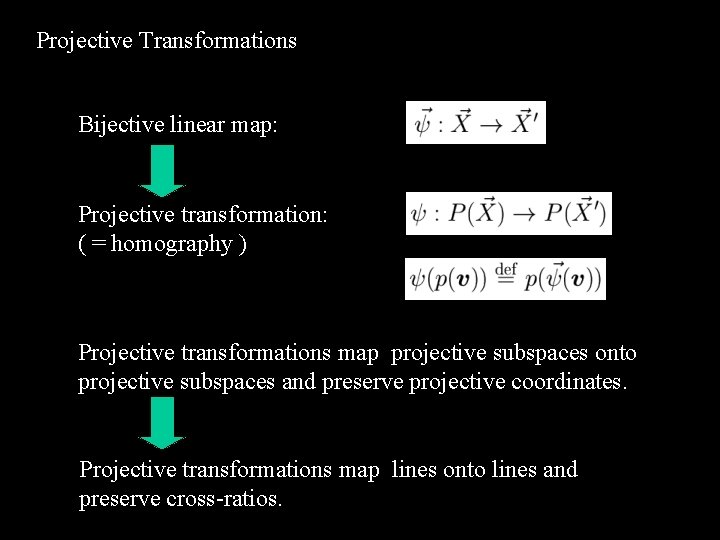
Projective Transformations Bijective linear map: Projective transformation: ( = homography ) Projective transformations map projective subspaces onto projective subspaces and preserve projective coordinates. Projective transformations map lines onto lines and preserve cross-ratios.

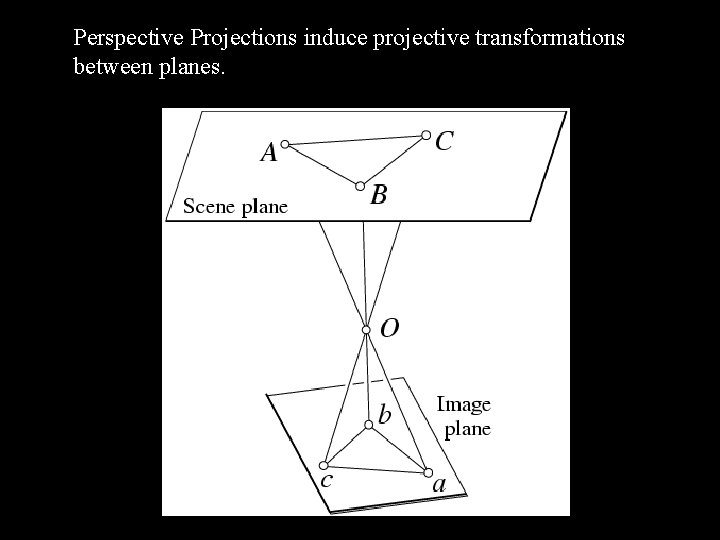
Perspective Projections induce projective transformations between planes.

Projective Shape Two point sets S and S’ in some projective space X are projectively equivalent when there exists a projective transformation y: X X such that S’ = y ( S ). Projective structure from motion = projective shape recovery. = recovery of the corresponding motion equivalence classes.

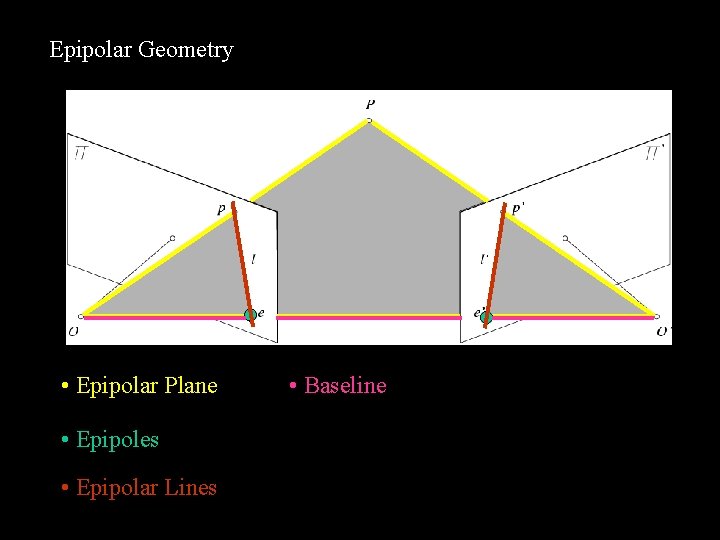
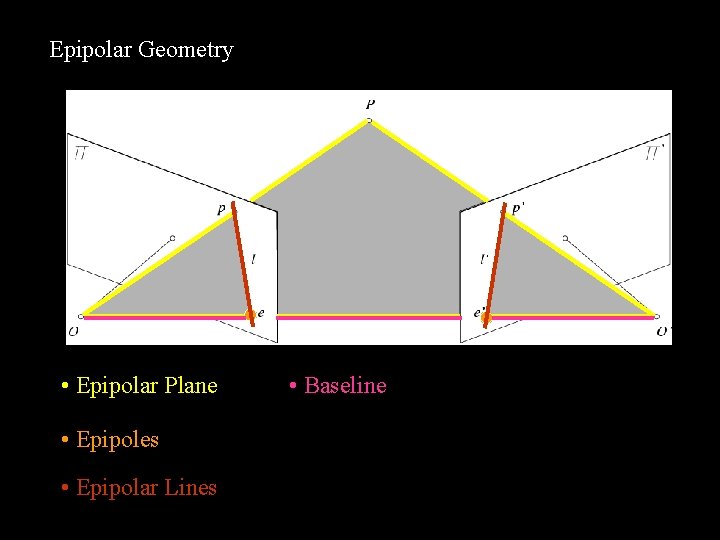
Epipolar Geometry • Epipolar Plane • Epipoles • Epipolar Lines • Baseline

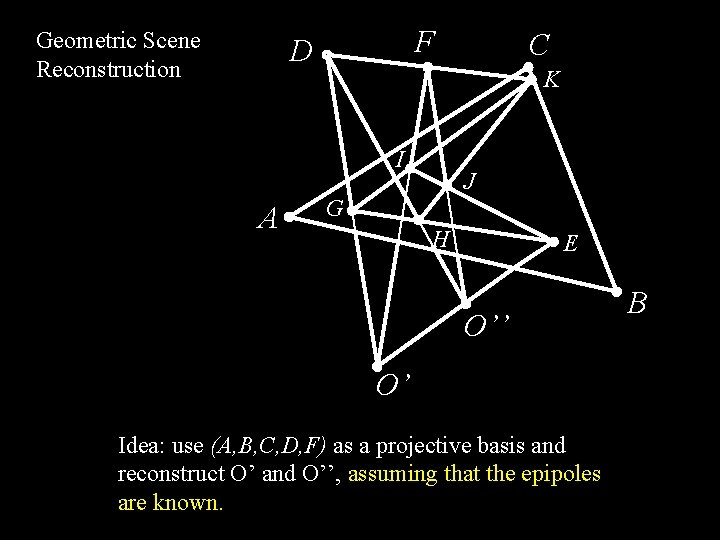
Geometric Scene Reconstruction F D K I A C J G H E O’’ O’ Idea: use (A, B, C, D, F) as a projective basis and reconstruct O’ and O’’, assuming that the epipoles are known. B

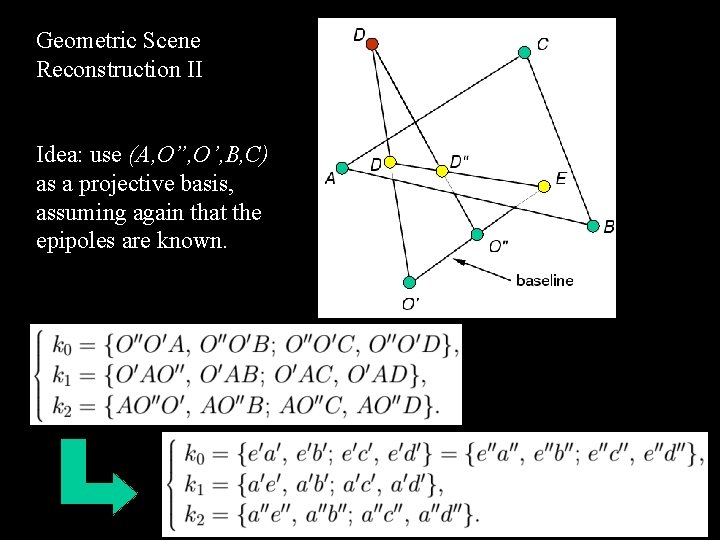
Geometric Scene Reconstruction II Idea: use (A, O”, O’, B, C) as a projective basis, assuming again that the epipoles are known.

Multi-View Geometry • Epipolar Geometry • The Essential Matrix • The Fundamental Matrix

Epipolar Geometry • Epipolar Plane • Epipoles • Epipolar Lines • Baseline

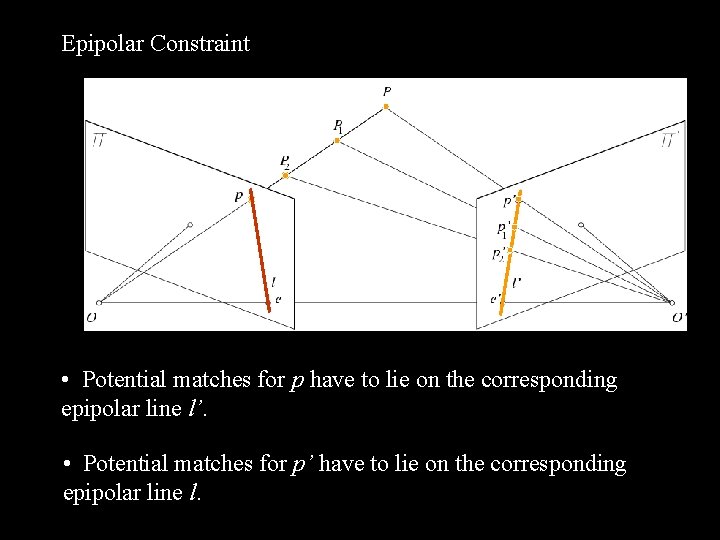
Epipolar Constraint • Potential matches for p have to lie on the corresponding epipolar line l’. • Potential matches for p’ have to lie on the corresponding epipolar line l.

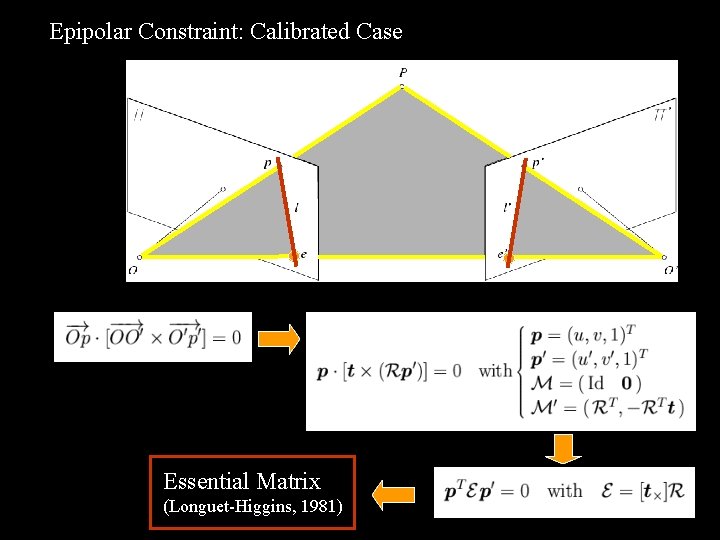
Epipolar Constraint: Calibrated Case Essential Matrix (Longuet-Higgins, 1981)

Properties of the Essential Matrix • E p’ is the epipolar line associated with p’. • E Tp is the epipolar line associated with p. T • E e’=0 and E e=0. • E is singular. • E has two equal non-zero singular values (Huang and Faugeras, 1989).

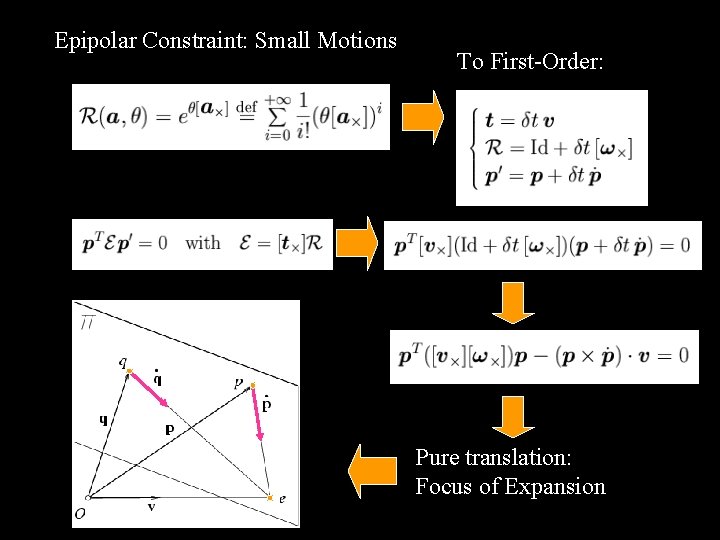
Epipolar Constraint: Small Motions To First-Order: Pure translation: Focus of Expansion

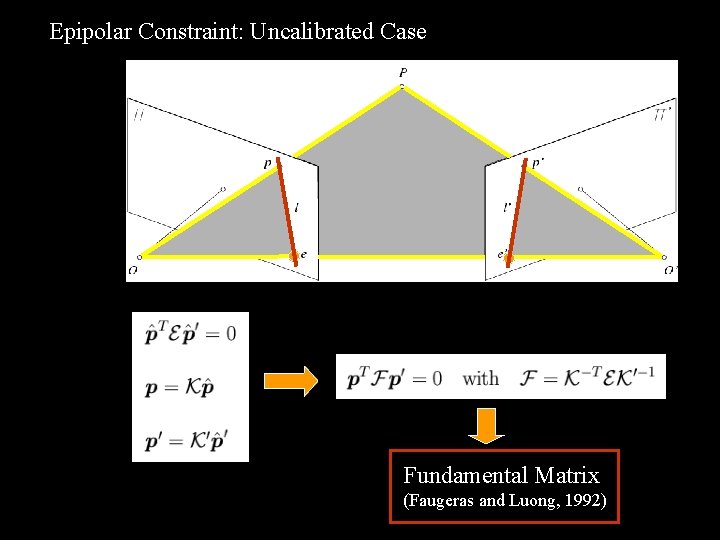
Epipolar Constraint: Uncalibrated Case Fundamental Matrix (Faugeras and Luong, 1992)

Properties of the Fundamental Matrix • F p’ is the epipolar line associated with p’. • F Tp is the epipolar line associated with p. T • F e’=0 and F e=0. • F is singular.

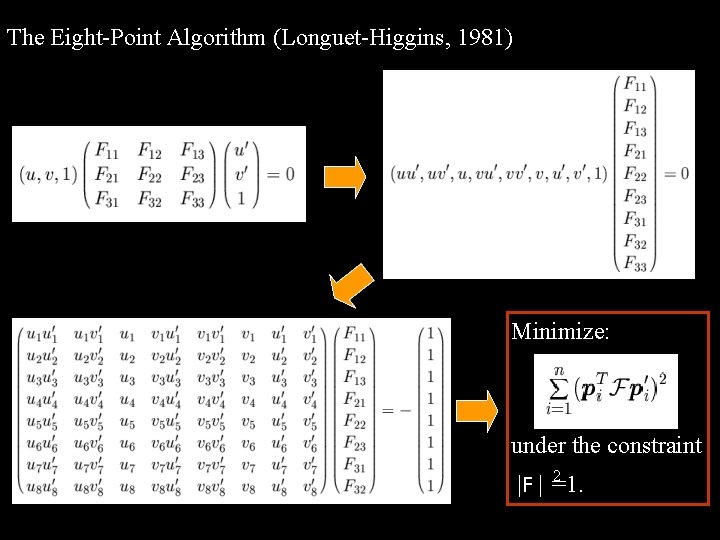
The Eight-Point Algorithm (Longuet-Higgins, 1981) Minimize: under the constraint 2 |F | =1.

Non-Linear Least-Squares Approach (Luong et al. , 1993) Minimize with respect to the coefficients of F , using an appropriate rank-2 parameterization.

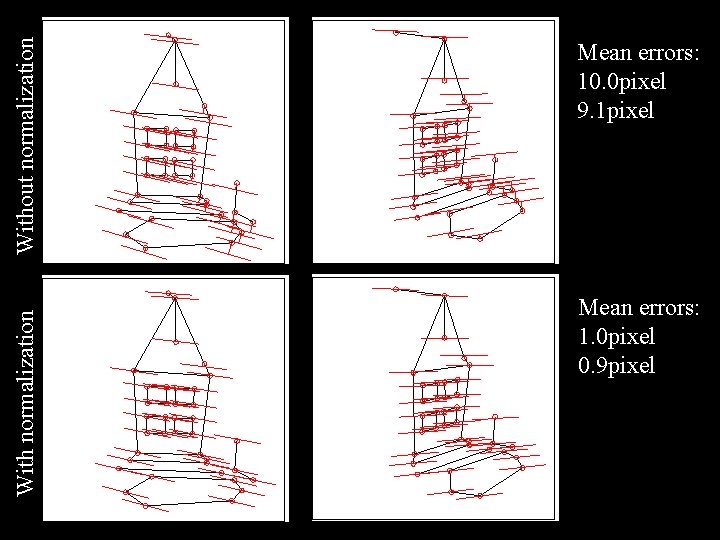
The Normalized Eight-Point Algorithm (Hartley, 1995) • Center the image data at the origin, and scale it so the mean squared distance between the origin and the data points is 2 pixels: q = T p , q’ = T’ p’. i i • Use the eight-point algorithm to compute F from the points q i and q’i. • Enforce the rank-2 constraint. • Output T TF T’.

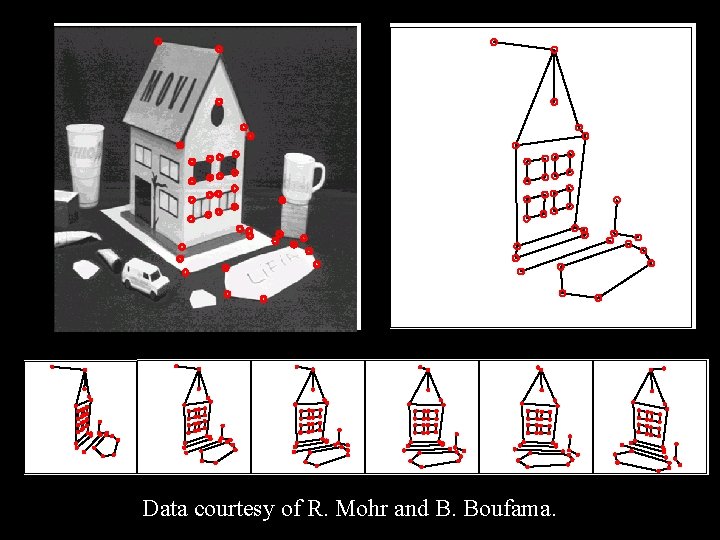
Data courtesy of R. Mohr and B. Boufama.

Without normalization With normalization Mean errors: 10. 0 pixel 9. 1 pixel Mean errors: 1. 0 pixel 0. 9 pixel

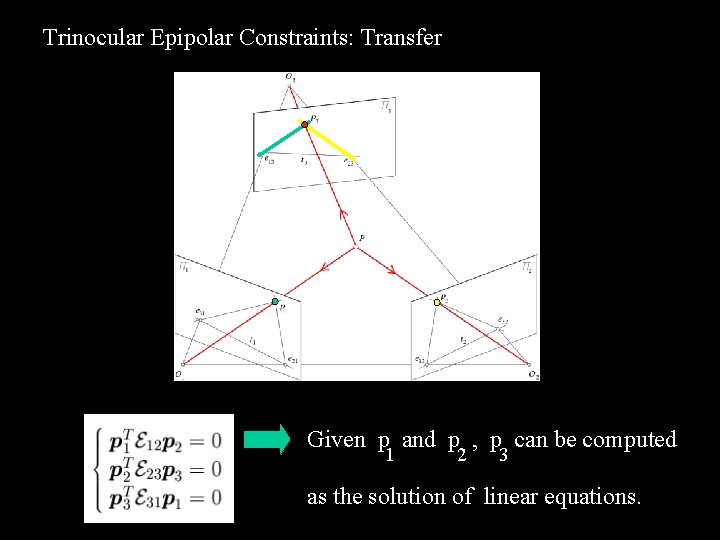
Trinocular Epipolar Constraints These constraints are not independent!

Trinocular Epipolar Constraints: Transfer Given p and p , p can be computed 1 2 3 as the solution of linear equations.

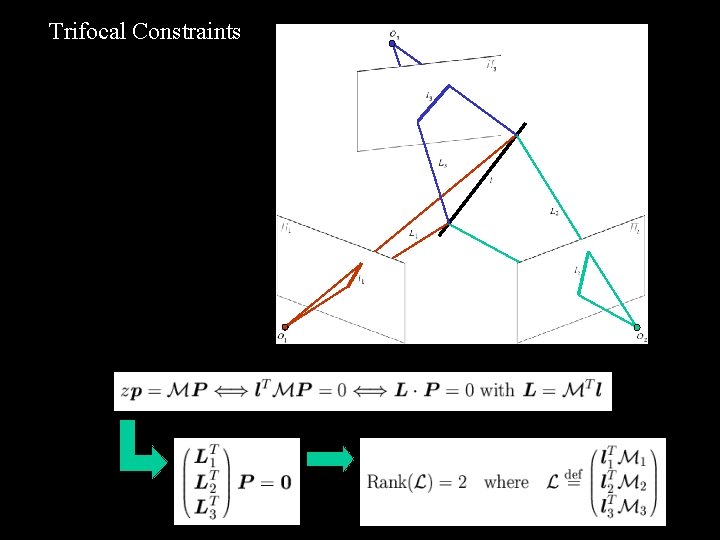
Trifocal Constraints

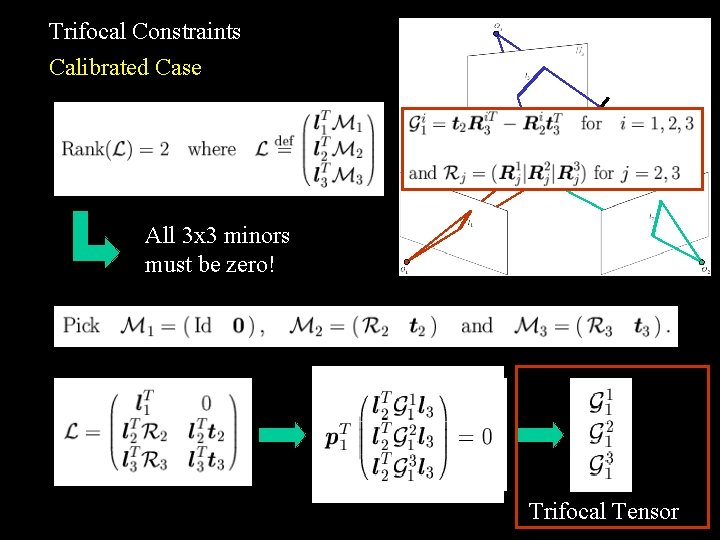
Trifocal Constraints Calibrated Case All 3 x 3 minors must be zero! Trifocal Tensor

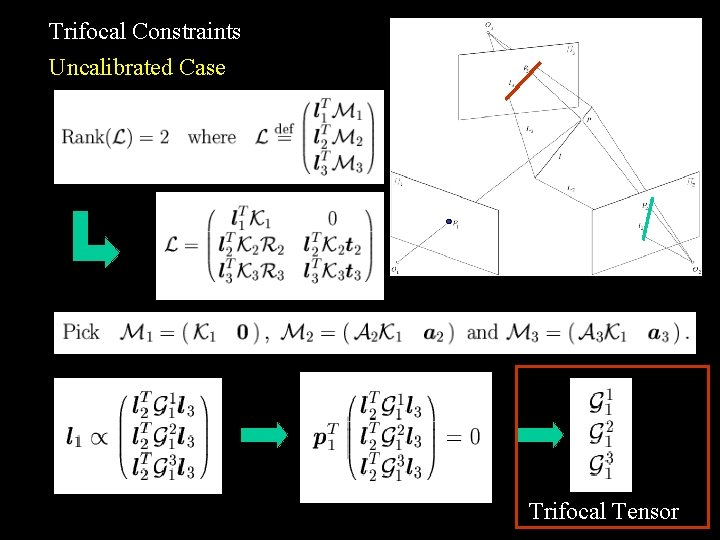
Trifocal Constraints Uncalibrated Case Trifocal Tensor

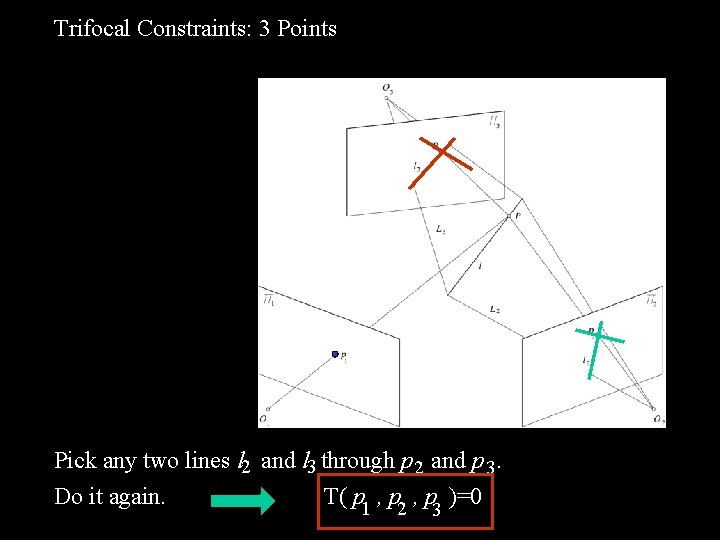
Trifocal Constraints: 3 Points Pick any two lines l 2 and l 3 through p 2 and p 3. Do it again. T( p 1 , p 2 , p )=0 3

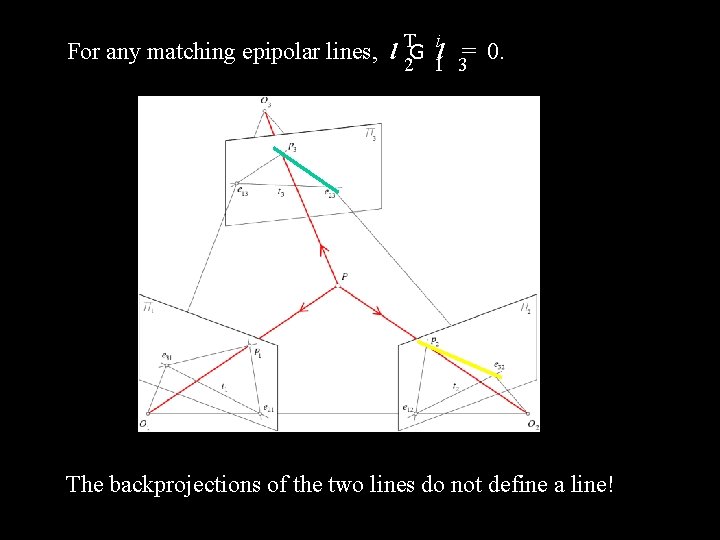
Properties of the Trifocal Tensor T i • For any matching epipolar lines, l 2 G 1 l 3= 0. • The matrices G i are singular. 1 • They satisfy 8 independent constraints in the uncalibrated case (Faugeras and Mourrain, 1995). Estimating the Trifocal Tensor • Ignore the non-linear constraints and use linear least-squares a posteriori. • Impose the constraints a posteriori.

T i For any matching epipolar lines, l 2 G 1 l 3= 0. The backprojections of the two lines do not define a line!

Multiple Views (Faugeras and Mourrain, 1995)

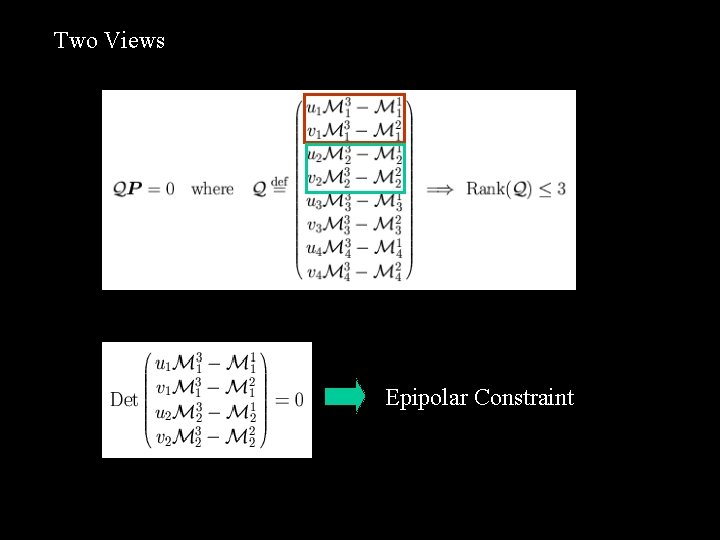
Two Views Epipolar Constraint

Three Views Trifocal Constraint

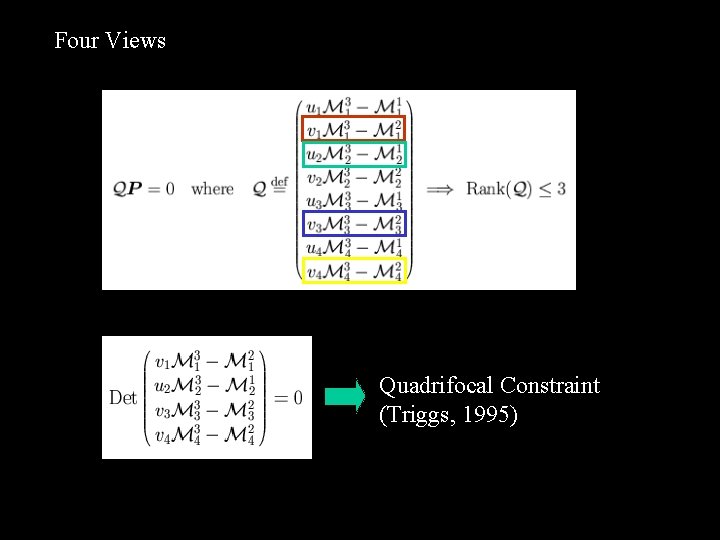
Four Views Quadrifocal Constraint (Triggs, 1995)

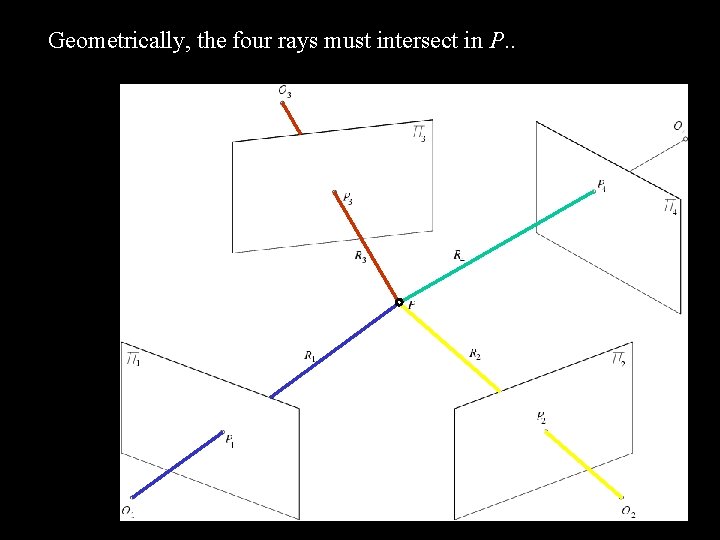
Geometrically, the four rays must intersect in P. .

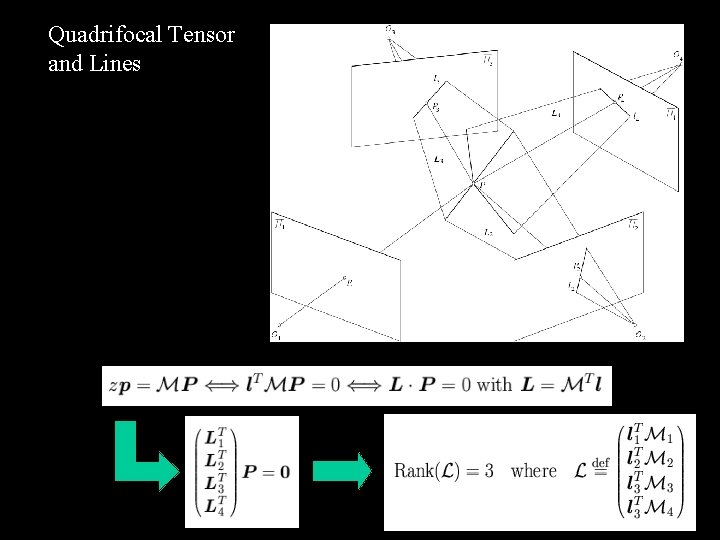
Quadrifocal Tensor and Lines

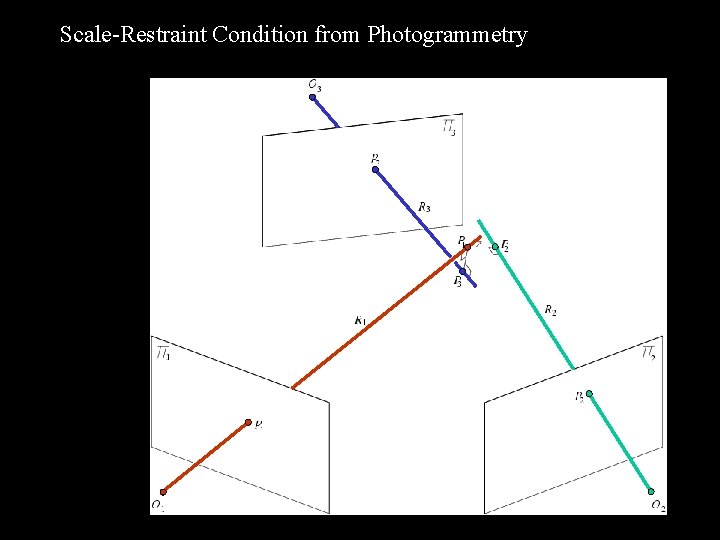
Scale-Restraint Condition from Photogrammetry