Projective geometry Ames Room Slides from Steve Seitz

Projective geometry Ames Room Slides from Steve Seitz and Daniel De. Menthon

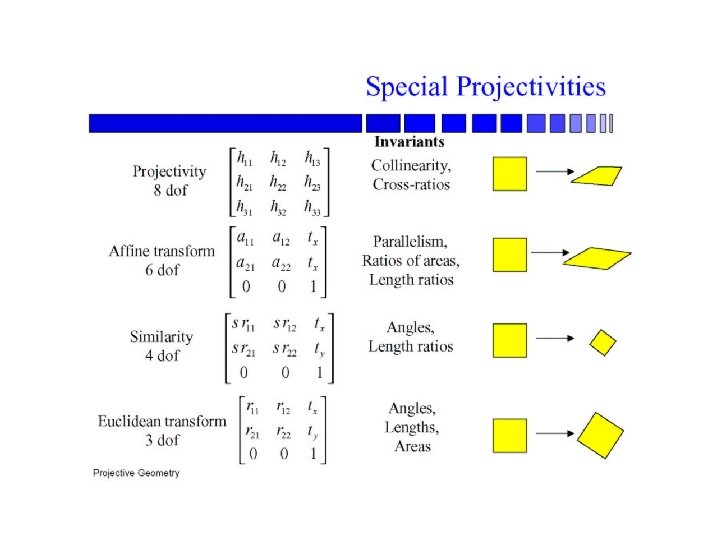
Projective geometry—what’s it good for? Uses of projective geometry • • Drawing Measurements Mathematics for projection Undistorting images Focus of expansion Camera pose estimation, match move Object recognition

Applications of projective geometry Vermeer’s Music Lesson

Measurements on planes 4 3 2 1 1 2 Approach: unwarp then measure What kind of warp is this? 3 4

Image rectification p’ p To unwarp (rectify) an image • solve for homography H given p and p’ • solve equations of the form: wp’ = Hp – linear in unknowns: w and coefficients of H – H is defined up to an arbitrary scale factor – how many points are necessary to solve for H?

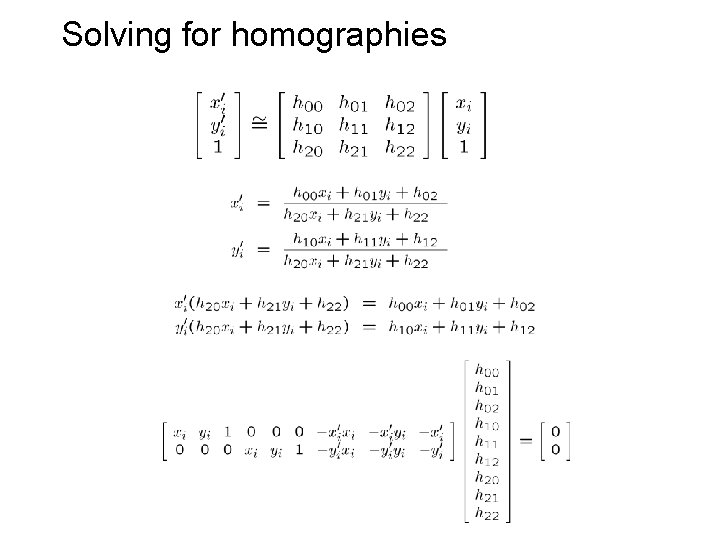
Solving for homographies

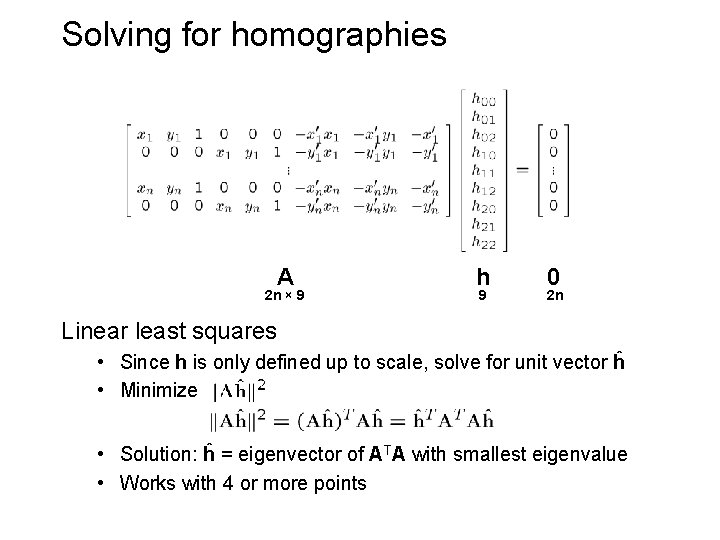
Solving for homographies A 2 n × 9 h 9 0 2 n Linear least squares • Since h is only defined up to scale, solve for unit vector ĥ • Minimize • Solution: ĥ = eigenvector of ATA with smallest eigenvalue • Works with 4 or more points

The projective plane Why do we need homogeneous coordinates? • represent points at infinity, homographies, perspective projection, multi-view relationships What is the geometric intuition? • a point in the image is a ray in projective space y (x, y, 1) (0, 0, 0) z x (sx, sy, s) image plane • Each point (x, y) on the plane is represented by a ray (sx, sy, s) – all points on the ray are equivalent: (x, y, 1) (sx, sy, s)

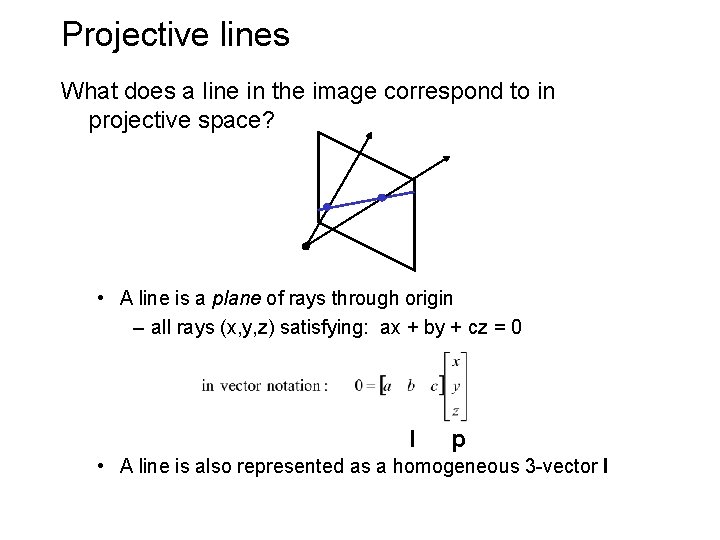
Projective lines What does a line in the image correspond to in projective space? • A line is a plane of rays through origin – all rays (x, y, z) satisfying: ax + by + cz = 0 l p • A line is also represented as a homogeneous 3 -vector l

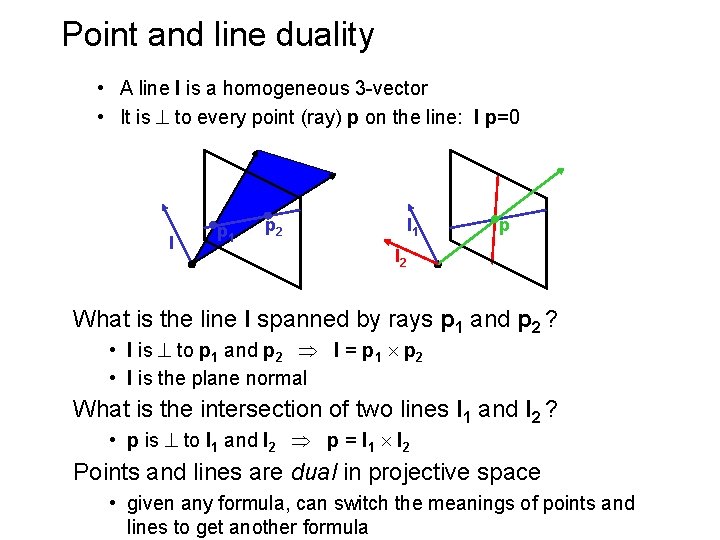
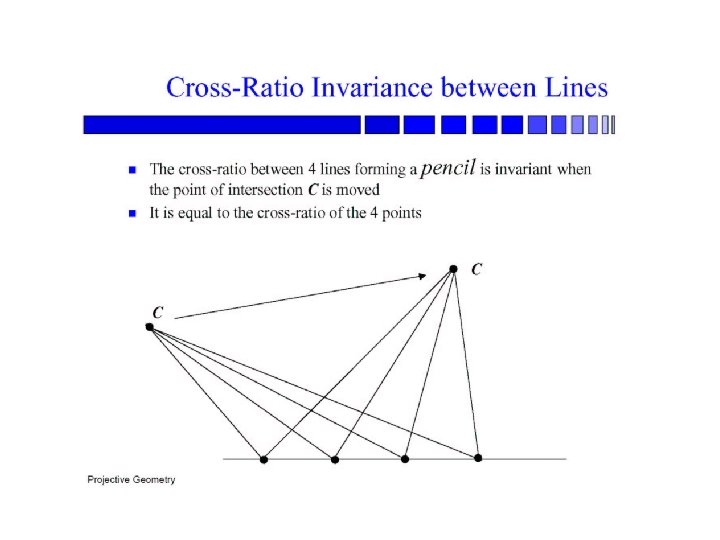
Point and line duality • A line l is a homogeneous 3 -vector • It is to every point (ray) p on the line: l p=0 l p 1 p 2 l 1 p l 2 What is the line l spanned by rays p 1 and p 2 ? • l is to p 1 and p 2 l = p 1 p 2 • l is the plane normal What is the intersection of two lines l 1 and l 2 ? • p is to l 1 and l 2 p = l 1 l 2 Points and lines are dual in projective space • given any formula, can switch the meanings of points and lines to get another formula

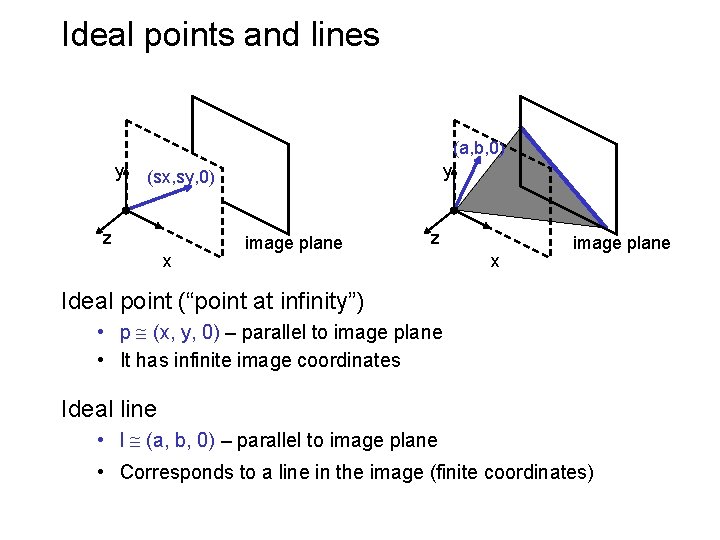
Ideal points and lines (a, b, 0) y y (sx, sy, 0) z x image plane Ideal point (“point at infinity”) • p (x, y, 0) – parallel to image plane • It has infinite image coordinates Ideal line • l (a, b, 0) – parallel to image plane • Corresponds to a line in the image (finite coordinates)

Homographies of points and lines Computed by 3 x 3 matrix multiplication • To transform a point: p’ = Hp • To transform a line: lp=0 l’p’=0 – 0 = lp = l. H-1 Hp = l. H-1 p’ l’ = l. H-1 – lines are transformed by postmultiplication of H-1

3 D to 2 D: “perspective” projection Matrix Projection: What is not preserved under perspective projection? What IS preserved?

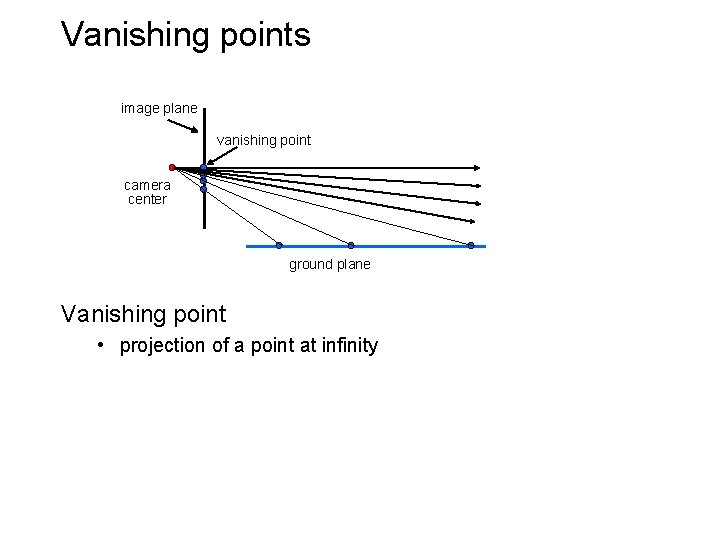
Vanishing points image plane vanishing point camera center ground plane Vanishing point • projection of a point at infinity

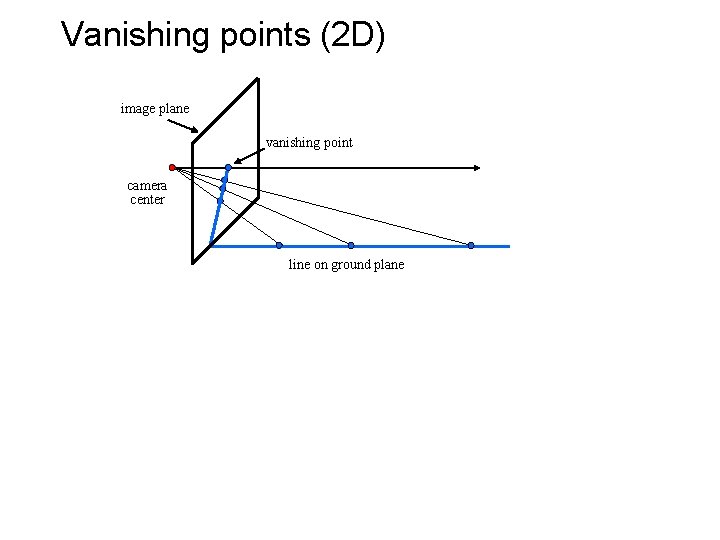
Vanishing points (2 D) image plane vanishing point camera center line on ground plane

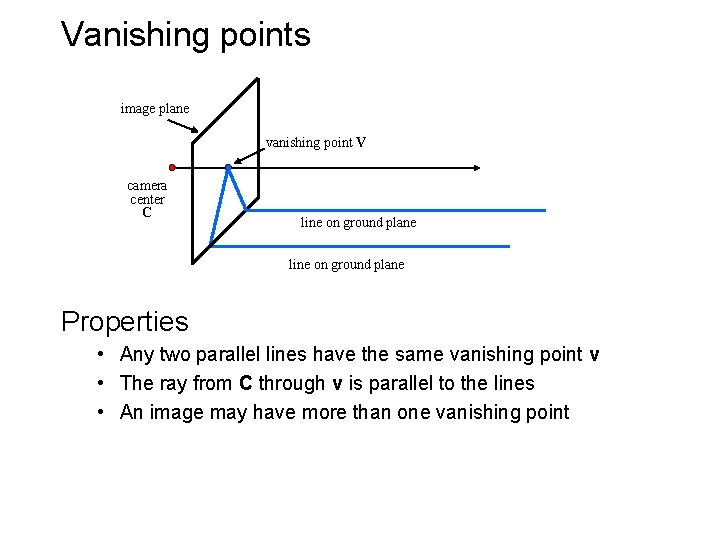
Vanishing points image plane vanishing point V camera center C line on ground plane Properties • Any two parallel lines have the same vanishing point v • The ray from C through v is parallel to the lines • An image may have more than one vanishing point

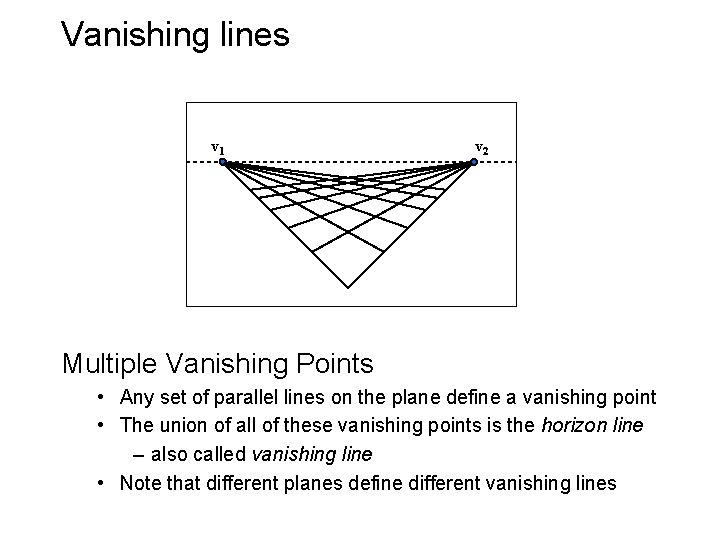
Vanishing lines v 1 v 2 Multiple Vanishing Points • Any set of parallel lines on the plane define a vanishing point • The union of all of these vanishing points is the horizon line – also called vanishing line • Note that different planes define different vanishing lines

Vanishing lines Multiple Vanishing Points • Any set of parallel lines on the plane define a vanishing point • The union of all of these vanishing points is the horizon line – also called vanishing line • Note that different planes define different vanishing lines

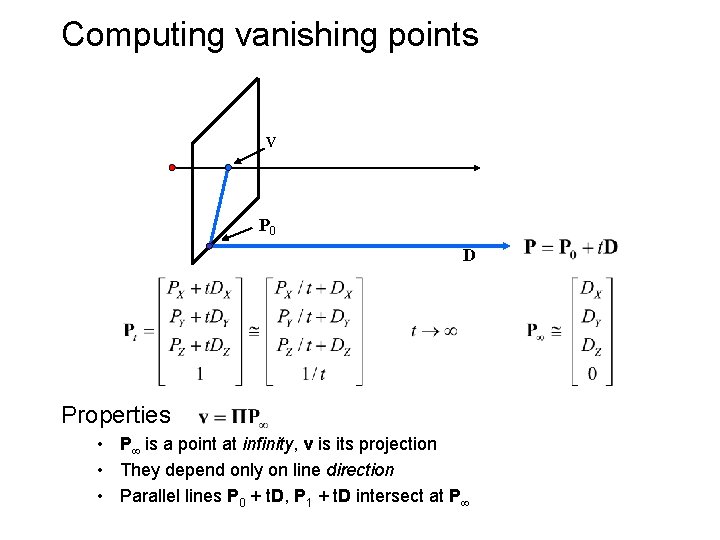
Computing vanishing points V P 0 D Properties • P is a point at infinity, v is its projection • They depend only on line direction • Parallel lines P 0 + t. D, P 1 + t. D intersect at P

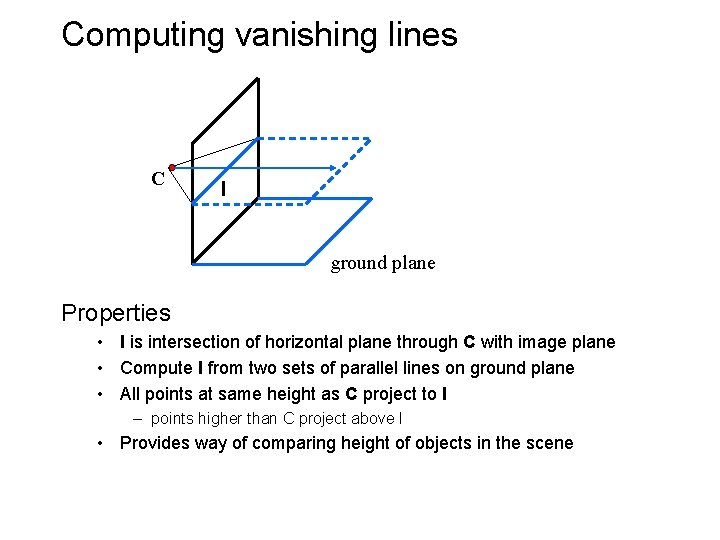
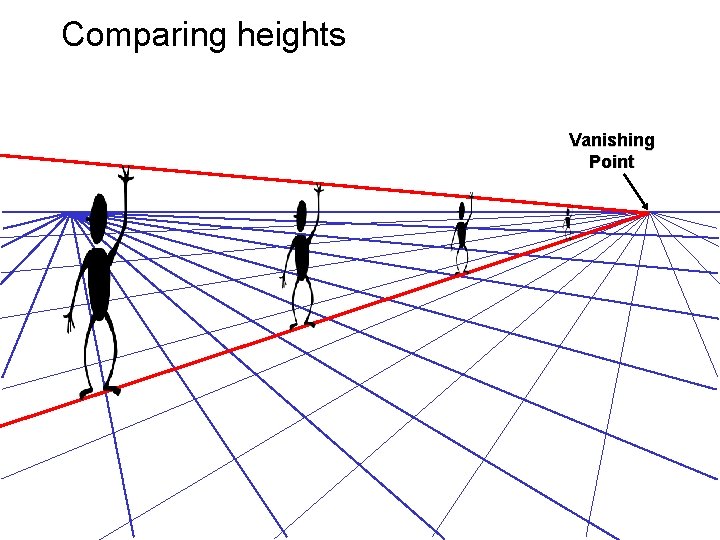
Computing vanishing lines C l ground plane Properties • l is intersection of horizontal plane through C with image plane • Compute l from two sets of parallel lines on ground plane • All points at same height as C project to l – points higher than C project above l • Provides way of comparing height of objects in the scene

Fun with vanishing points

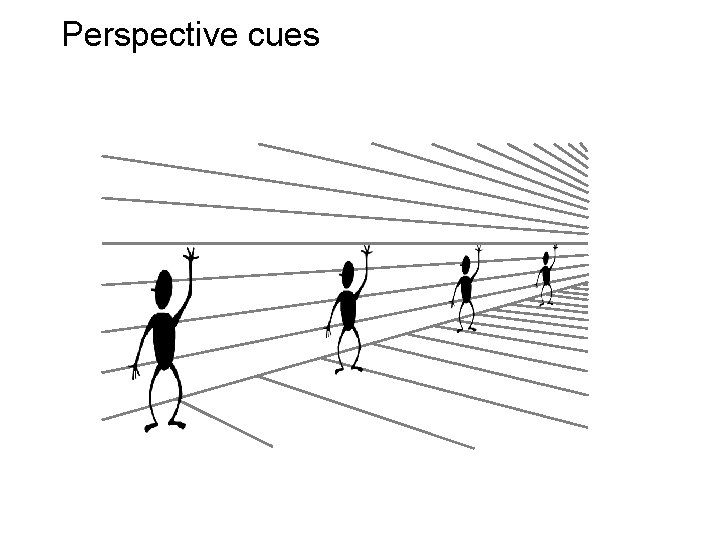
Perspective cues

Perspective cues

Perspective cues

Comparing heights Vanishing Point

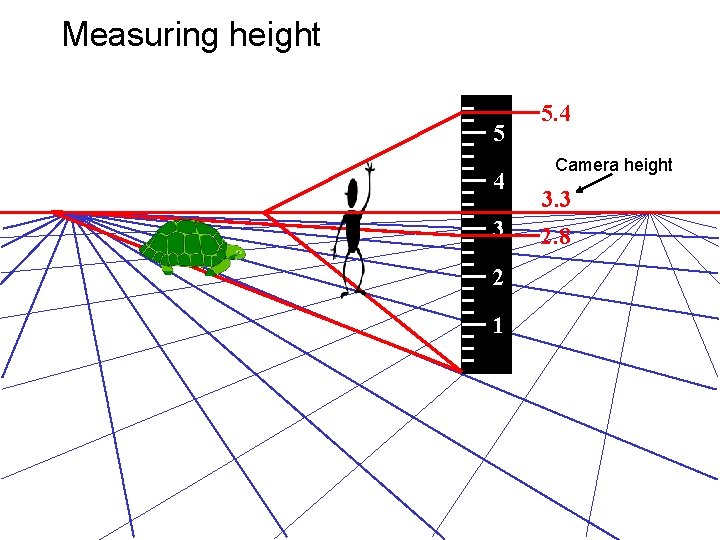
Measuring height 5 4 3 2 1 5. 4 Camera height 3. 3 2. 8

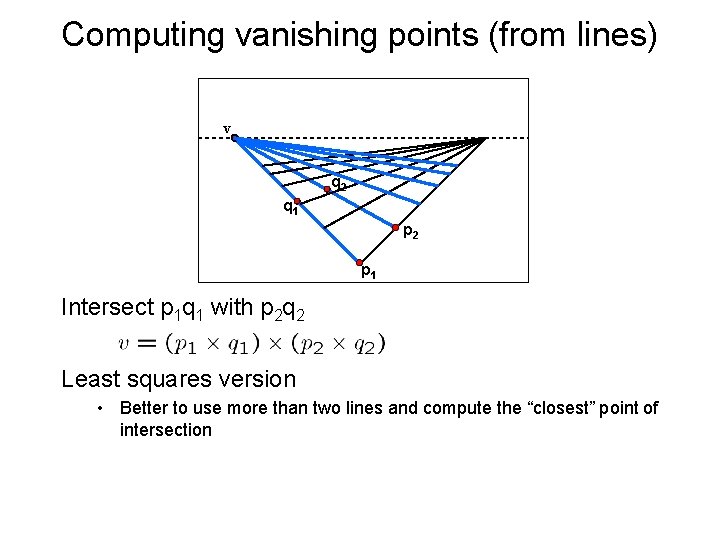
Computing vanishing points (from lines) v q 2 q 1 p 2 p 1 Intersect p 1 q 1 with p 2 q 2 Least squares version • Better to use more than two lines and compute the “closest” point of intersection

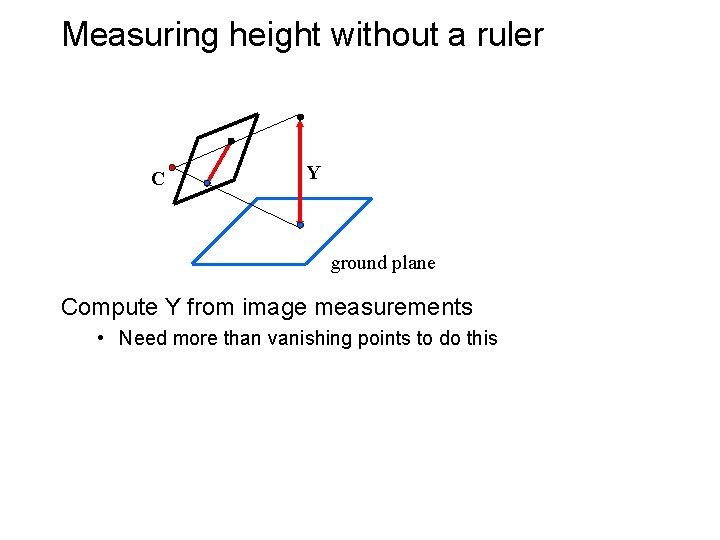
Measuring height without a ruler C Y ground plane Compute Y from image measurements • Need more than vanishing points to do this

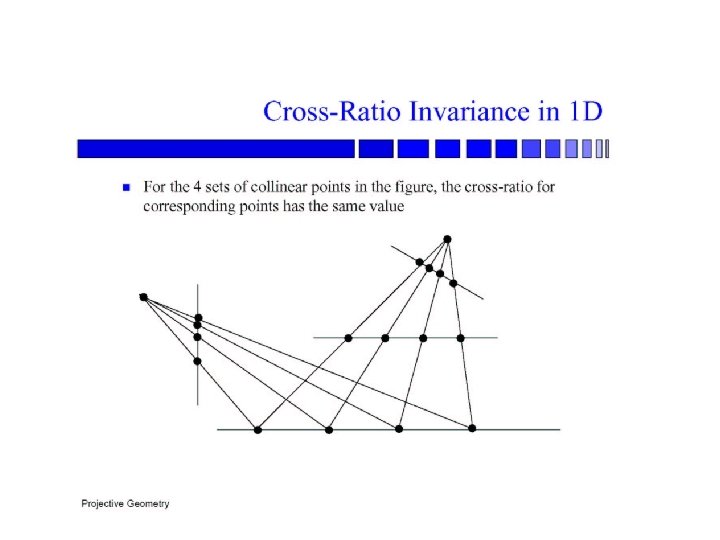
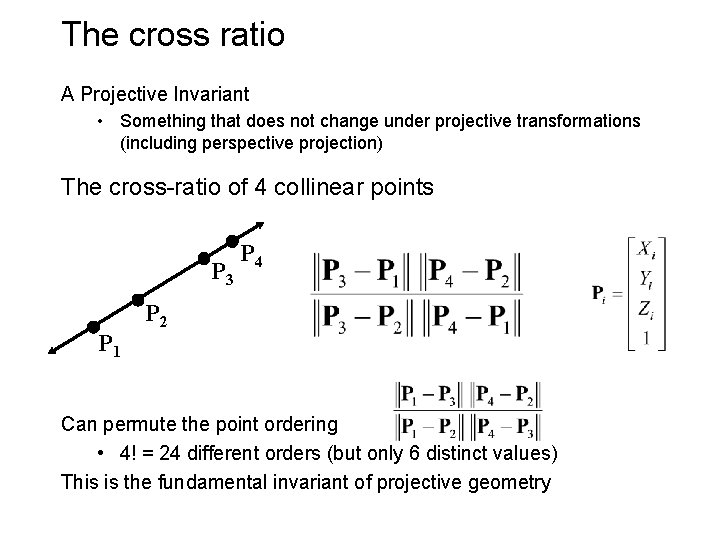
The cross ratio A Projective Invariant • Something that does not change under projective transformations (including perspective projection) The cross-ratio of 4 collinear points P 3 P 1 P 4 P 2 Can permute the point ordering • 4! = 24 different orders (but only 6 distinct values) This is the fundamental invariant of projective geometry

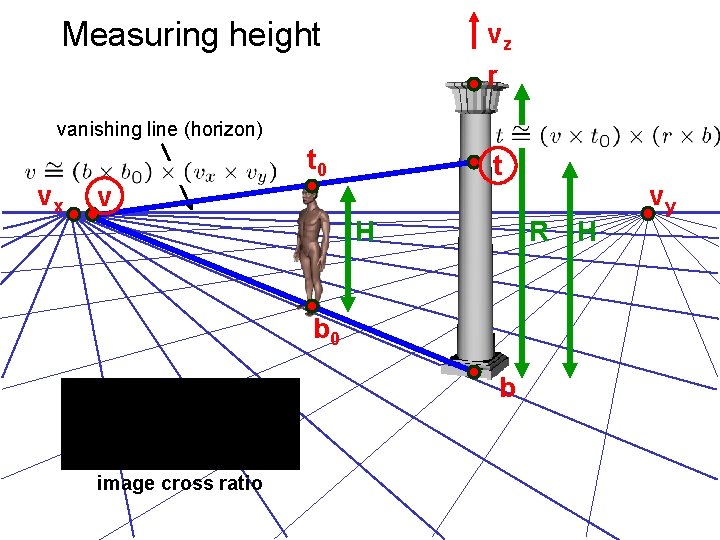
Measuring height scene cross ratio T (top of object) R (reference point) t C v. Z r b H R B image cross ratio (bottom of object) ground plane scene points represented as image points as

Measuring height vz r vanishing line (horizon) vx t 0 t v H R H b 0 b image cross ratio vy

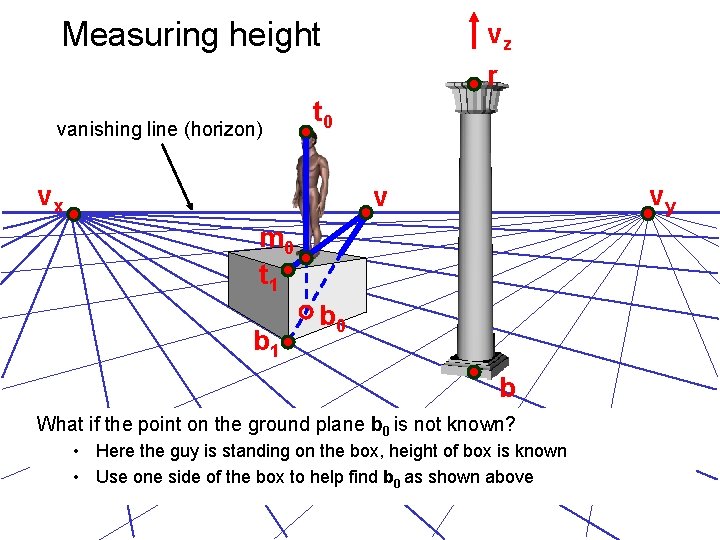
Measuring height vanishing line (horizon) vz r t 0 vx vy v m 0 t 1 b 0 b What if the point on the ground plane b 0 is not known? • Here the guy is standing on the box, height of box is known • Use one side of the box to help find b 0 as shown above

3 D projective geometry These concepts generalize naturally to 3 D • Homogeneous coordinates – Projective 3 D points have four coords: P = (X, Y, Z, W) • Duality – A plane N is also represented by a 4 -vector – Points and planes are dual in 3 D: N P=0 • Projective transformations – Represented by 4 x 4 matrices T: P’ = TP, N’ = N T-1