Multiple View Geometry Projective Geometry Transformations of 2

Multiple View Geometry Projective Geometry & Transformations of 2 D Vladimir Nedović Intelligent Systems Lab Amsterdam (ISLA) Informatics Institute, University of Amsterdam Kruislaan 403, 1098 SJ Amsterdam, The Netherlands vnedovic@science. uva. nl 18 -01 -2008

Outline Intro to projective geometry The 2 D projective plane Projective transformations Hierarchy of transformations Projective geometry of 1 D Recovery of affine & metric properties from images More properties of conics

Intro to Projective Geometry Projective transformation: any mapping of points in the plane that preserves straight lines Projective space: an extension of a Euclidean space in which two lines always meet in a point parallel lines meet at inf. => no parallelism in proj. space coordinates in Euclidean R 2 x = x/1 y = y/1 homogeneous coordinates in P 2 (x, y) = (x, y, 1) = (kx, ky, k) (x, y, 0) = (x/0, y/0, 0) = (∞, ∞, 0) k≠ 0 points at infinity

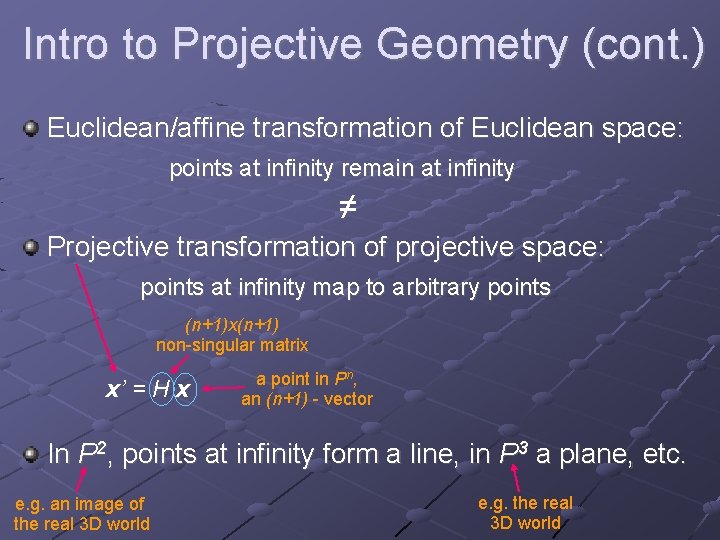
Intro to Projective Geometry (cont. ) Euclidean/affine transformation of Euclidean space: points at infinity remain at infinity ≠ Projective transformation of projective space: points at infinity map to arbitrary points (n+1)x(n+1) non-singular matrix x’ = H x a point in Pn, an (n+1) - vector In P 2, points at infinity form a line, in P 3 a plane, etc. e. g. an image of the real 3 D world e. g. the real 3 D world

The 2 D projective plane Line l in the plane: ax + by + c = 0 – equiv. to in slope-intercept notation – thus a line could be represented by a vector (a, b, c)T Lines and points represented by homogeneous vectors (a, b, c)T = k(a, b, c)T k≠ 0 (x, y)T = k(x, y)T A point x lies on line l iff ax + by + c = (x, y, 1)(a, b, c)T = x. Tl = 0

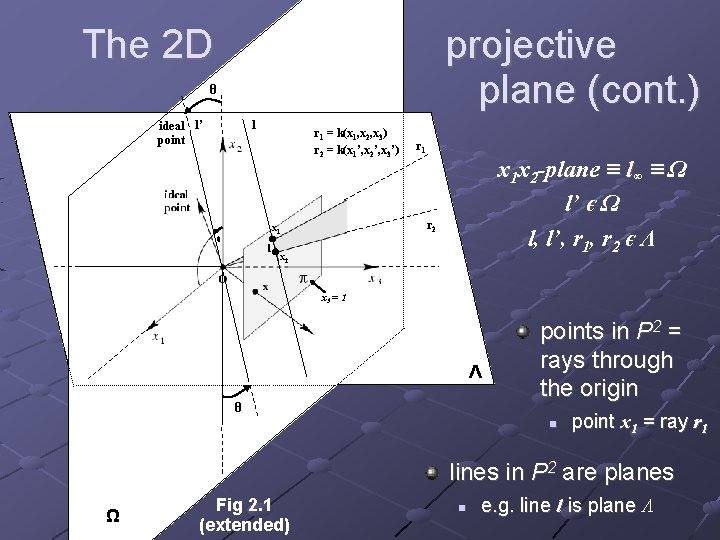
The 2 D projective plane (cont. ) The intersection of two lines l and l’ is the point: x = l x l’ The line through two points x and x’ can be analogously written as l = x x x’ duality principle Set of all points at infinity (= ideal points) in P 2 (e. g. (x 1, x 2, 0)T) lies on the line at infinity l∞ = (0, 0, 1)T P 2 = set of rays in R 3 through the origin (see Ch. 1) vectors k(x 1, x 2, x 3)T for diff. k form a single ray (a point in P 2) lines in P 2 are planes in R 3

The 2 D projective plane (cont. ) θ ideal l’ point l r 1 = k(x 1, x 2, x 3) r 2 = k(x 1’, x 2’, x 3’) x 1 x 2 -plane ≡ l∞ ≡ Ω l’ є Ω l, l’, r 1, r 2 є Λ r 2 x 1 θ r 1 x 2 x 3 = 1 Λ θ points in P 2 = rays through the origin point x 1 = ray r 1 lines in P 2 are planes Ω Fig 2. 1 (extended) e. g. line l is plane Λ

The 2 D projective plane (cont. ) Duality principle for 2 D projective geometry – for every theorem there is a dual one, obtained by interchanging the roles of points and lines A curve in Euclidean space corresponds to a conic in projective space – defined using points: x. TCx = 0 C is a homog. representation, only the ratios of elements matter – defined using (tangent) lines: l. TC-1 l = 0 via the equation of a conic tangent at x: l = Cx C-1 only if C non-singular, otherwise C* if C not of full rank, the conic is degenerate

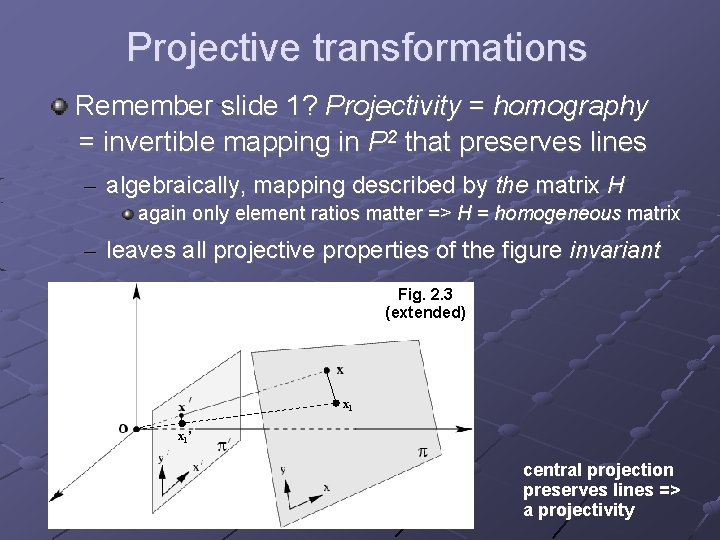
Projective transformations Remember slide 1? Projectivity = homography = invertible mapping in P 2 that preserves lines – algebraically, mapping described by the matrix H again only element ratios matter => H = homogeneous matrix – leaves all projective properties of the figure invariant Fig. 2. 3 (extended) x 1’ central projection preserves lines => a projectivity

Projective transformations (cont. ) Effect of central projection (e. g. distorted shape) is described by H => inverse transformation leads back to the original (via H-1) H can be calculated from 4 point correspondences (i. e. 8 linear equations) between the original (e. g. the 3 D world) and the projection (e. g. the image) Points transform according to H, but lines transform according to H-1: l’T= l. TH-1 For a conic, the transformation is C’ = H-TCH-1

A hierarchy of transformations Projective transformations form a group, PL(3) – characterized by invertible 3 x 3 matrices In terms of increased specialization: 1. Isometry 2. Similarity 3. Affine 4. Projective Can be described algebraically (i. e. via the transform matrix) or in terms of invariants similarity affine projective

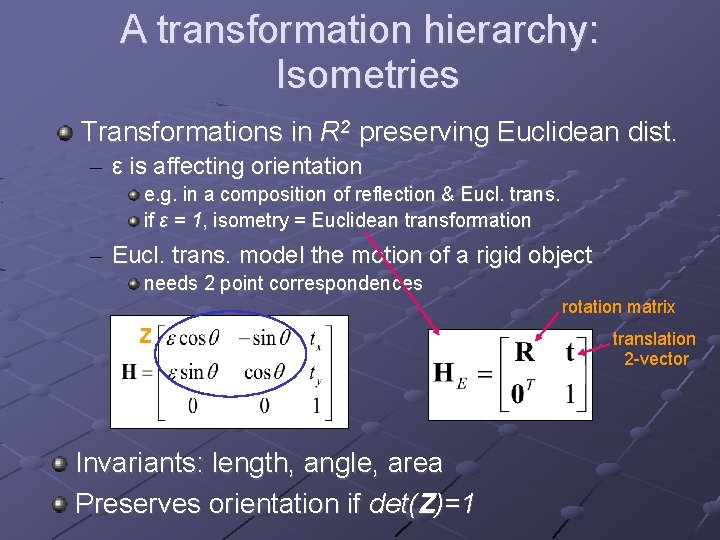
A transformation hierarchy: Isometries Transformations in R 2 preserving Euclidean dist. – ε is affecting orientation e. g. in a composition of reflection & Eucl. trans. if ε = 1, isometry = Euclidean transformation – Eucl. trans. model the motion of a rigid object needs 2 point correspondences rotation matrix Z Invariants: length, angle, area Preserves orientation if det(Z)=1 translation 2 -vector

A transformation hierarchy: Similarity I. e. isometry + isotropic scaling – – also called equi-form, since it preserves shape in its planar form, needs 2 point correspondences If isometry does not include reflection, matrix is scaling factor Invariants: angles, parallel lines, ratio of lengths (not length itself!), ratio of areas Metric structure: something defined up to a similarity

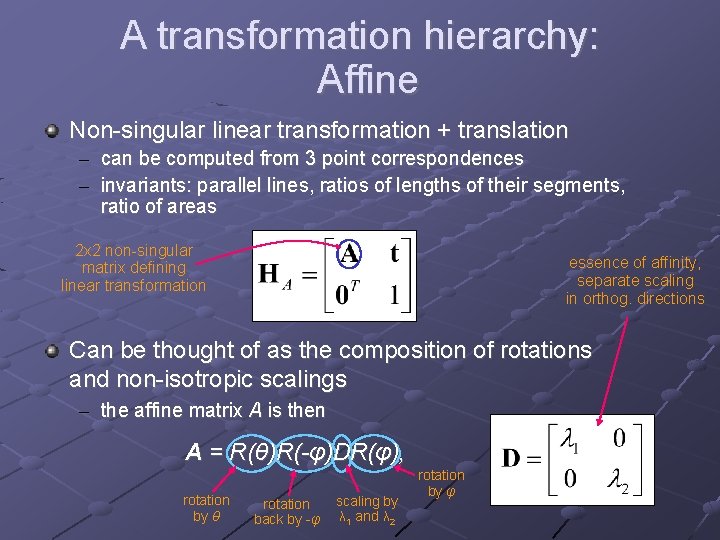
A transformation hierarchy: Affine Non-singular linear transformation + translation – can be computed from 3 point correspondences – invariants: parallel lines, ratios of lengths of their segments, ratio of areas 2 x 2 non-singular matrix defining linear transformation essence of affinity, separate scaling in orthog. directions Can be thought of as the composition of rotations and non-isotropic scalings – the affine matrix A is then A = R(θ)R(-φ)DR(φ), rotation by θ rotation back by -φ scaling by λ 1 and λ 2 rotation by φ

A transformation hierarchy: Projective Most general linear trans. of homog. coords. – – i. e. the one that only preserves straight lines affine was as general, but in inhomogeneous coords. requires 4 point correspondences the block form of the matrix is v = (v 1, v 2)T (not null as with affine => non-linear effects) Invariants: cross-ratio of 4 collinear points (i. e. the ratio of ratios of line segments)

Comparison of transformations Affine are between similarities and projectivities: – angles not preserved => shapes skewed – but effect homogeneous over the entire plane – orientation of transformed line depends only on orientation, not on planar position of source – ideal points remain at infinity Projectivities: – – – area scaling varies with position orientation of trans. line depends on both orientation & position ideal points map to finite points (thus vanishing points modeled) Projectivity can be decomposed into a chain of more specific transformations: A = s. RK + tv. T, det(K) = 1

Projective geometry of 1 D Very similar to 2 D – proj. trans. of the plane implies a 1 D proj. trans. of every line in the plane Proj. trans. for a line is a 2 x 2 homog. matrix – thus 3 point correspondences required Cross ratio is the basic projective invariant in 1 D Dual to collinear points are concurrent lines, also having a P 1 geometry signed distance from one to another (if each is a finite point, and homog. coord. is 1)

Recovery of affine & metric properties from images Recover metric properties (i. e. up to a similarity) 1. by using 4 points to completely remove projective distortion 2. by identifying line at infinity l∞ and two circular points (i. e. their images) Affine is the most general trans. for which l∞ remains a fixed line – but point-wise correspondence achieved only if the point is an eigenvector of A Once l∞ is identified in the image, affine measurements can be made in the original – e. g. parallel lines can be identified, length ratios computed, etc.

Recovery of affine & metric properties from images (cont. ) But identified l∞ can also be transformed to l∞ = (0, 0, 1)T with a suitable proj. matrix – – such a matrix could be this matrix can then be applied to all points, and affine measurements made in the recovered image Figure 2. 12

Recovery of affine & metric properties from images (cont. ) Beside the line at infinity, the two circular points are fixed under similarity – – i. e. a pair of complex conjugates every circle intersects l∞ at these Metric rectification is possible if circular points are transformed into their canonical positions – applying the transformation to the entire image results in a similarity The degenerate line conic is dual to circ. points – – once it is identified, Euclidean angles and length rations can be measured direct metric rectification also possible

Properties of conics Some point x and some conic C define a line l = Cx (i. e. a polar of x w. r. t. C) – the line intersects the conic at 2 points -> the tangents at these points intersect at x The conic induces a map between points & lines of P 2 – – a projective invariant (involves only intersection & tangency) called correlation, represented by a 3 x 3 matrix A: l = Ax For two points x and y, if x is on the polar of y, then y is on the polar of x Any conic is projectively equiv. to one with a diagonal matrix – classification based on diag. elements – hyperbola, ellipse & parabola from Eucl. geom. projectively equiv. to a circle (still valid in affine geom. )

The End !