Projective geometry Ames Room Readings Mundy J L

Projective geometry Ames Room Readings • Mundy, J. L. and Zisserman, A. , Geometric Invariance in Computer Vision, Appendix: Projective Geometry for Machine Vision, MIT Press, Cambridge, MA, 1992, (read 23. 1 - 23. 5, 23. 10) – available online: http: //www. cs. cmu. edu/~ph/869/papers/zisser-mundy. pdf CSE 576, Spring 2008 Projective Geometry 1

Projective geometry—what’s it good for? Uses of projective geometry • • Drawing Measurements Mathematics for projection Undistorting images Focus of expansion Camera pose estimation, match move Object recognition CSE 576, Spring 2008 Projective Geometry 2

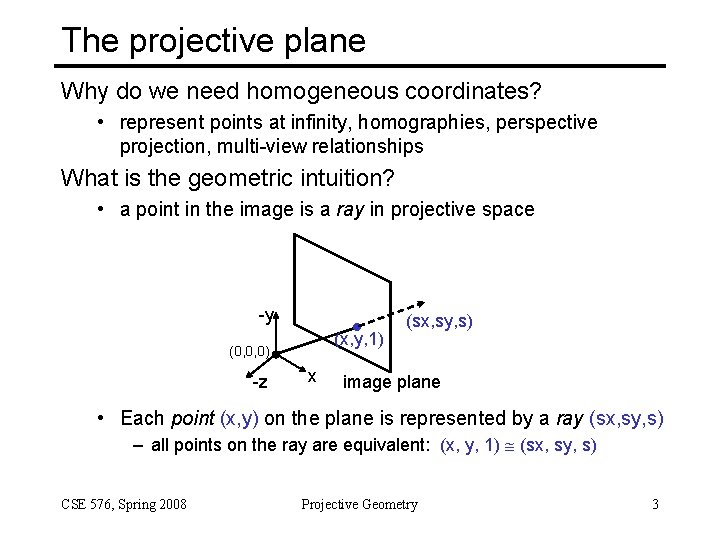
The projective plane Why do we need homogeneous coordinates? • represent points at infinity, homographies, perspective projection, multi-view relationships What is the geometric intuition? • a point in the image is a ray in projective space -y (x, y, 1) (0, 0, 0) -z x (sx, sy, s) image plane • Each point (x, y) on the plane is represented by a ray (sx, sy, s) – all points on the ray are equivalent: (x, y, 1) (sx, sy, s) CSE 576, Spring 2008 Projective Geometry 3

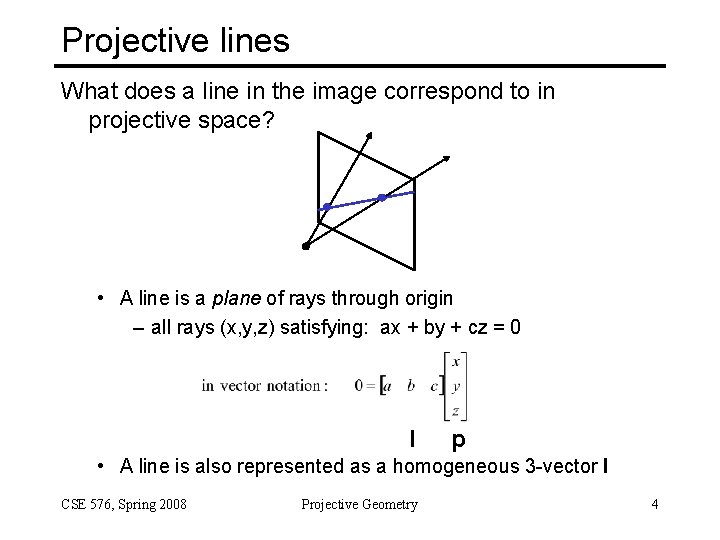
Projective lines What does a line in the image correspond to in projective space? • A line is a plane of rays through origin – all rays (x, y, z) satisfying: ax + by + cz = 0 l p • A line is also represented as a homogeneous 3 -vector l CSE 576, Spring 2008 Projective Geometry 4

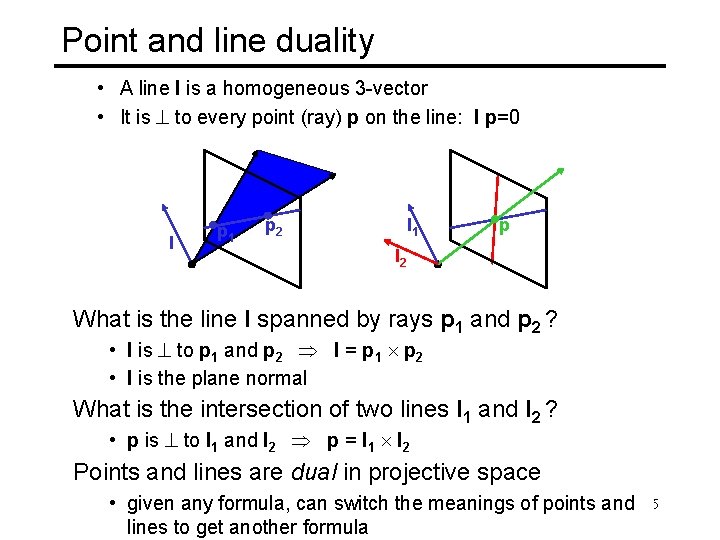
Point and line duality • A line l is a homogeneous 3 -vector • It is to every point (ray) p on the line: l p=0 l p 1 p 2 l 1 p l 2 What is the line l spanned by rays p 1 and p 2 ? • l is to p 1 and p 2 l = p 1 p 2 • l is the plane normal What is the intersection of two lines l 1 and l 2 ? • p is to l 1 and l 2 p = l 1 l 2 Points and lines are dual in projective space CSE 576, • Spring 2008 any given Projective Geometry formula, can switch the meanings of points and lines to get another formula 5

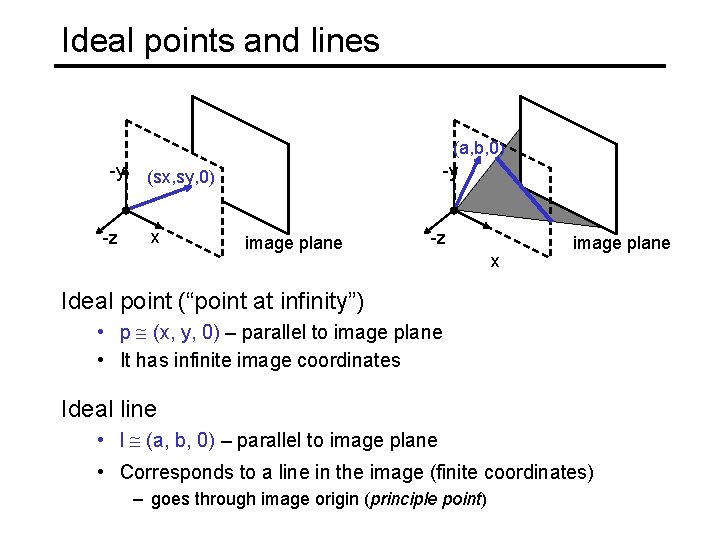
Ideal points and lines -y -z (a, b, 0) -y (sx, sy, 0) x image plane -z x image plane Ideal point (“point at infinity”) • p (x, y, 0) – parallel to image plane • It has infinite image coordinates Ideal line • l (a, b, 0) – parallel to image plane • Corresponds to a line in the image (finite coordinates) – goes CSE 576, Spring 2008 through image. Projective origin Geometry (principle point) 6

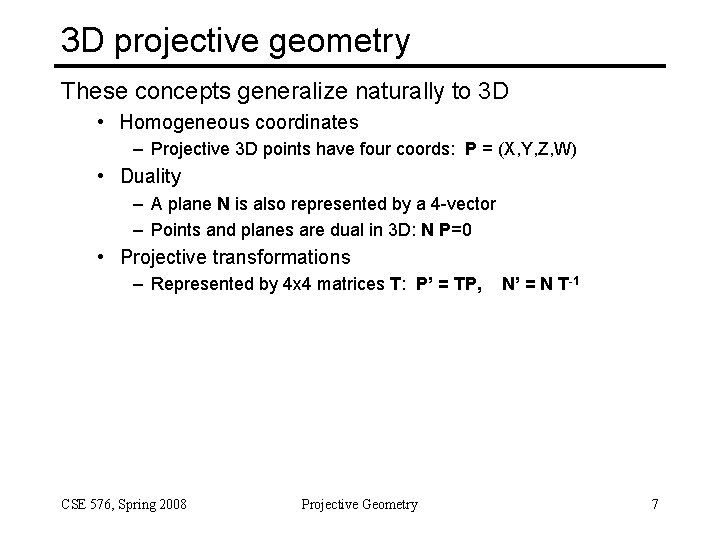
3 D projective geometry These concepts generalize naturally to 3 D • Homogeneous coordinates – Projective 3 D points have four coords: P = (X, Y, Z, W) • Duality – A plane N is also represented by a 4 -vector – Points and planes are dual in 3 D: N P=0 • Projective transformations – Represented by 4 x 4 matrices T: P’ = TP, CSE 576, Spring 2008 Projective Geometry N’ = N T-1 7

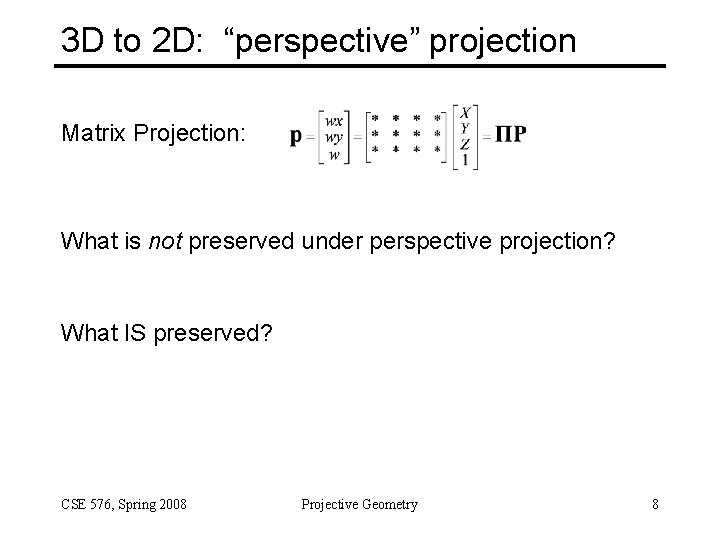
3 D to 2 D: “perspective” projection Matrix Projection: What is not preserved under perspective projection? What IS preserved? CSE 576, Spring 2008 Projective Geometry 8

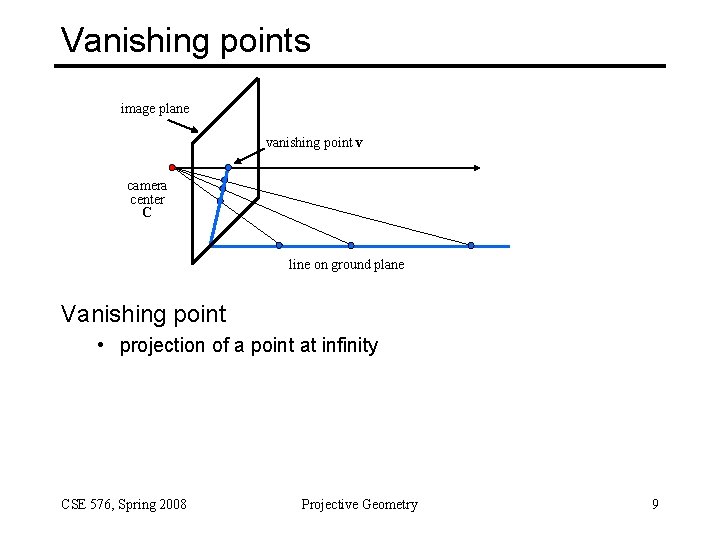
Vanishing points image plane vanishing point v camera center C line on ground plane Vanishing point • projection of a point at infinity CSE 576, Spring 2008 Projective Geometry 9

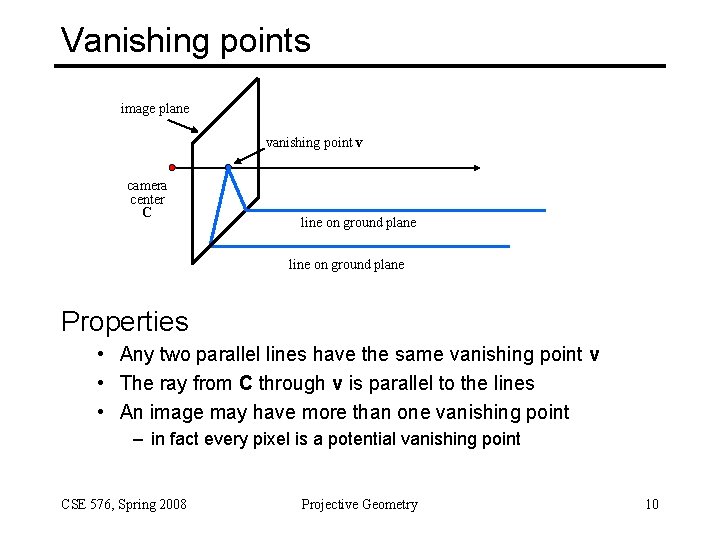
Vanishing points image plane vanishing point v camera center C line on ground plane Properties • Any two parallel lines have the same vanishing point v • The ray from C through v is parallel to the lines • An image may have more than one vanishing point – in fact every pixel is a potential vanishing point CSE 576, Spring 2008 Projective Geometry 10

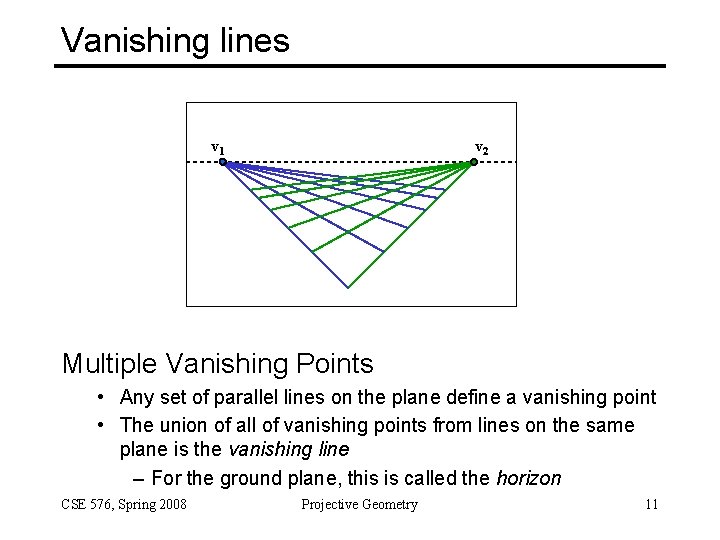
Vanishing lines v 1 v 2 Multiple Vanishing Points • Any set of parallel lines on the plane define a vanishing point • The union of all of vanishing points from lines on the same plane is the vanishing line – For the ground plane, this is called the horizon CSE 576, Spring 2008 Projective Geometry 11

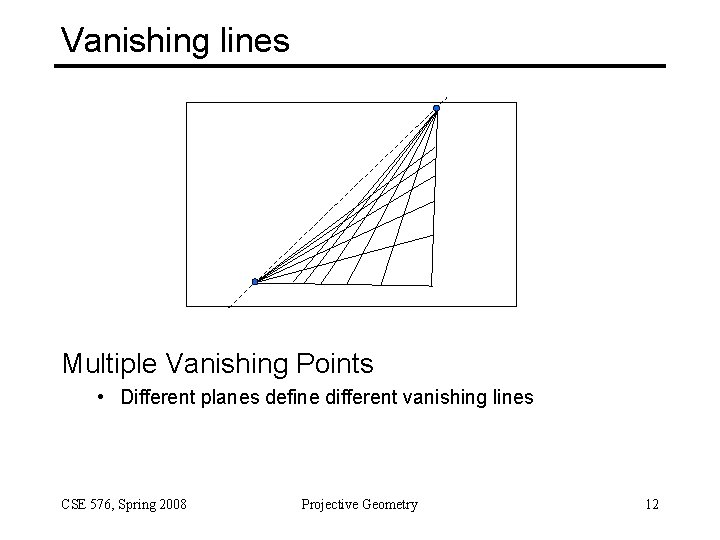
Vanishing lines Multiple Vanishing Points • Different planes define different vanishing lines CSE 576, Spring 2008 Projective Geometry 12

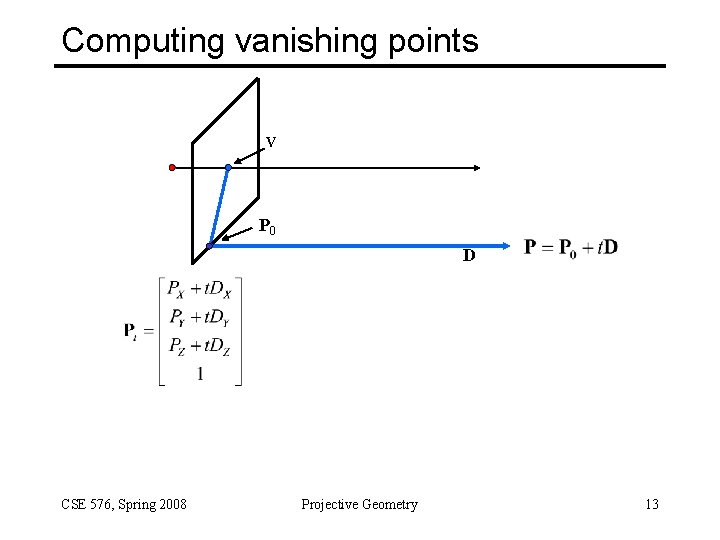
Computing vanishing points V P 0 D CSE 576, Spring 2008 Projective Geometry 13

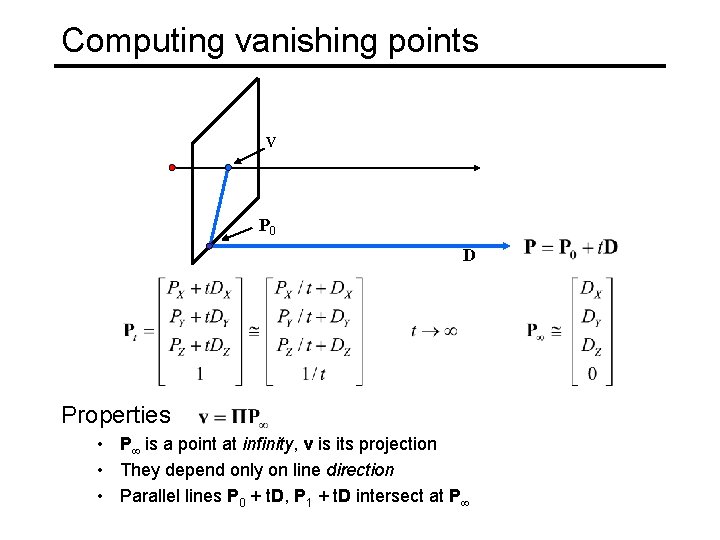
Computing vanishing points V P 0 D Properties • P is a point at infinity, v is its projection • They depend only on line direction • Parallel lines P 0 + t. D, PProjective at P 1 + t. D intersect CSE 576, Spring 2008 Geometry 14

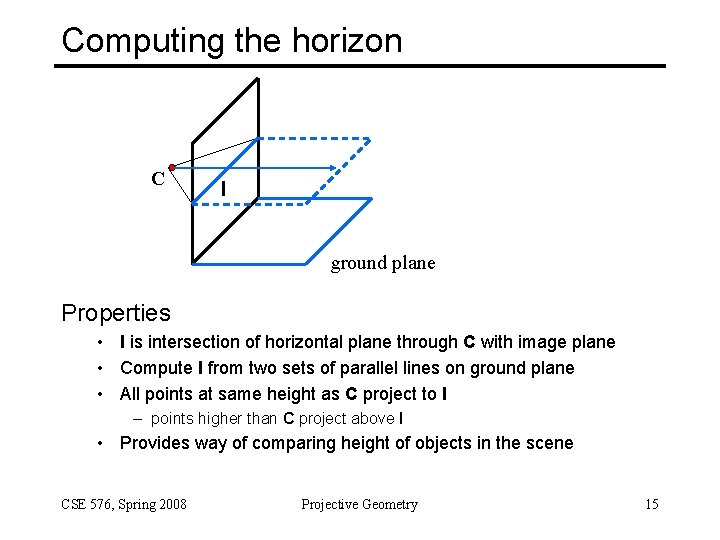
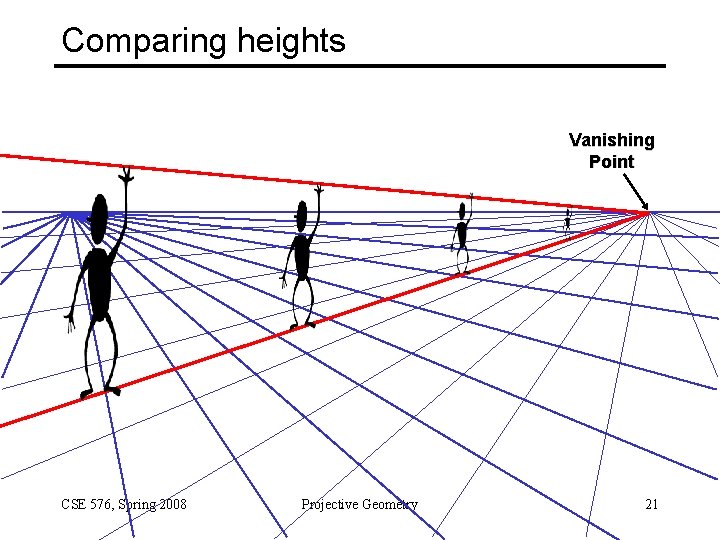
Computing the horizon C l ground plane Properties • l is intersection of horizontal plane through C with image plane • Compute l from two sets of parallel lines on ground plane • All points at same height as C project to l – points higher than C project above l • Provides way of comparing height of objects in the scene CSE 576, Spring 2008 Projective Geometry 15

CSE 576, Spring 2008 Projective Geometry 16

Fun with vanishing points CSE 576, Spring 2008 Projective Geometry 17

Perspective cues CSE 576, Spring 2008 Projective Geometry 18

Perspective cues CSE 576, Spring 2008 Projective Geometry 19

Perspective cues CSE 576, Spring 2008 Projective Geometry 20

Comparing heights Vanishing Point CSE 576, Spring 2008 Projective Geometry 21

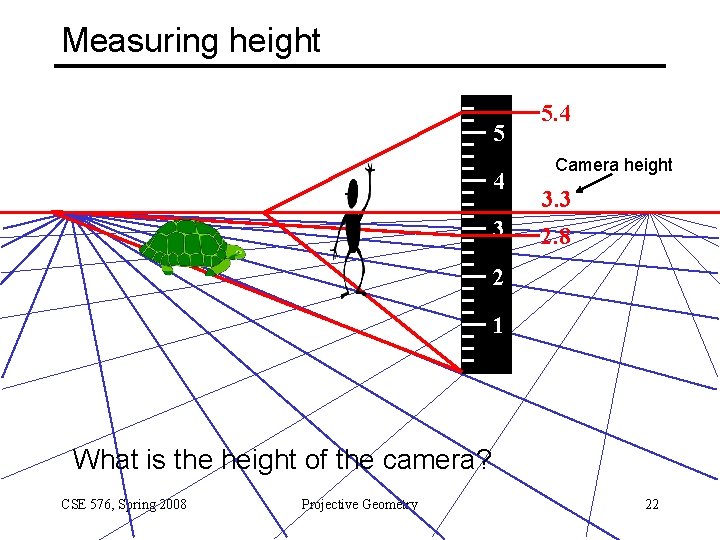
Measuring height 5 4 3 5. 4 Camera height 3. 3 2. 8 2 1 What is the height of the camera? CSE 576, Spring 2008 Projective Geometry 22

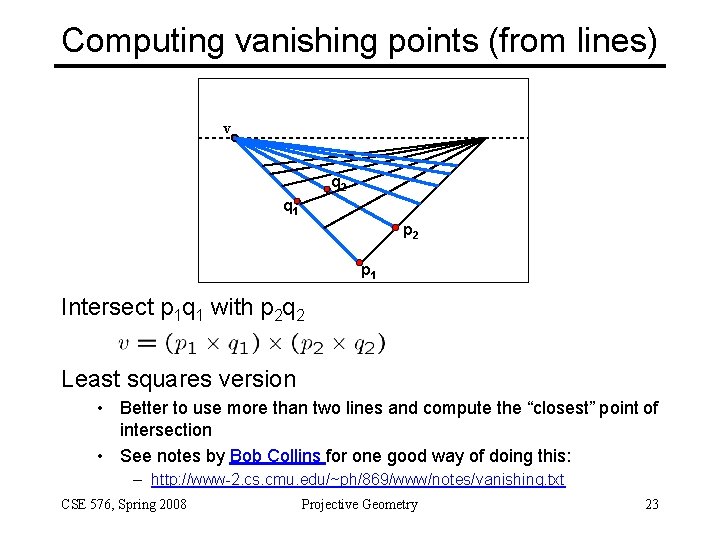
Computing vanishing points (from lines) v q 2 q 1 p 2 p 1 Intersect p 1 q 1 with p 2 q 2 Least squares version • Better to use more than two lines and compute the “closest” point of intersection • See notes by Bob Collins for one good way of doing this: – http: //www-2. cs. cmu. edu/~ph/869/www/notes/vanishing. txt CSE 576, Spring 2008 Projective Geometry 23

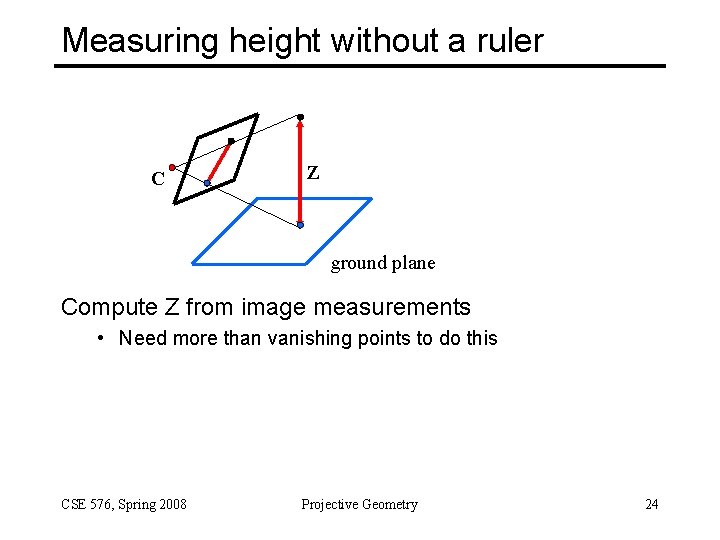
Measuring height without a ruler C Z ground plane Compute Z from image measurements • Need more than vanishing points to do this CSE 576, Spring 2008 Projective Geometry 24

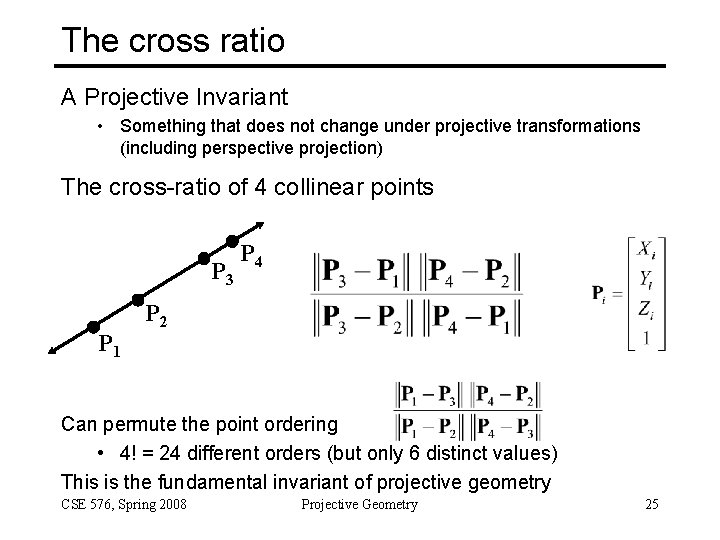
The cross ratio A Projective Invariant • Something that does not change under projective transformations (including perspective projection) The cross-ratio of 4 collinear points P 3 P 1 P 4 P 2 Can permute the point ordering • 4! = 24 different orders (but only 6 distinct values) This is the fundamental invariant of projective geometry CSE 576, Spring 2008 Projective Geometry 25

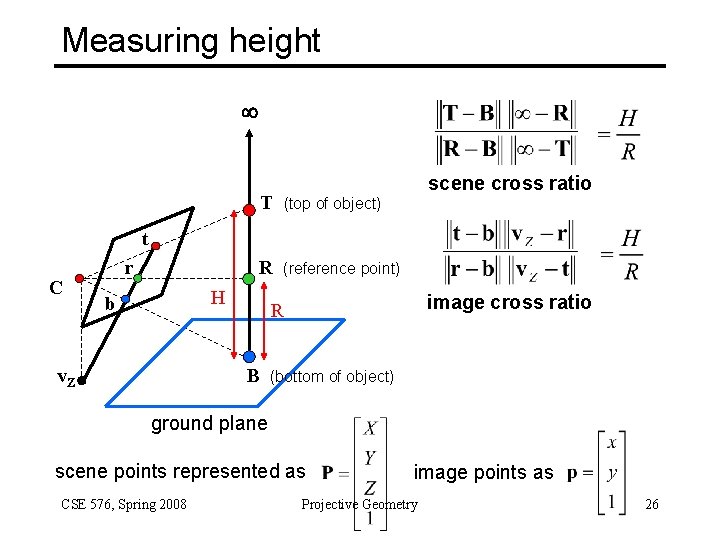
Measuring height scene cross ratio T (top of object) R (reference point) t C r H b B v. Z image cross ratio R (bottom of object) ground plane scene points represented as CSE 576, Spring 2008 image points as Projective Geometry 26

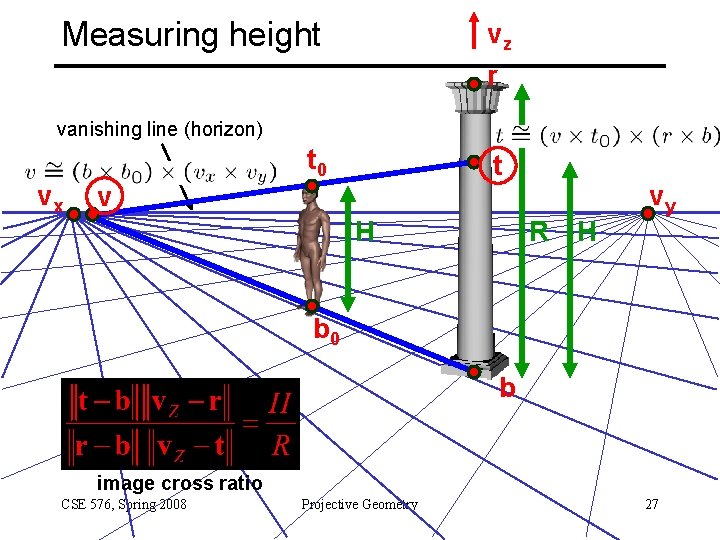
Measuring height vz r vanishing line (horizon) vx t 0 t v H R H vy b 0 b image cross ratio CSE 576, Spring 2008 Projective Geometry 27

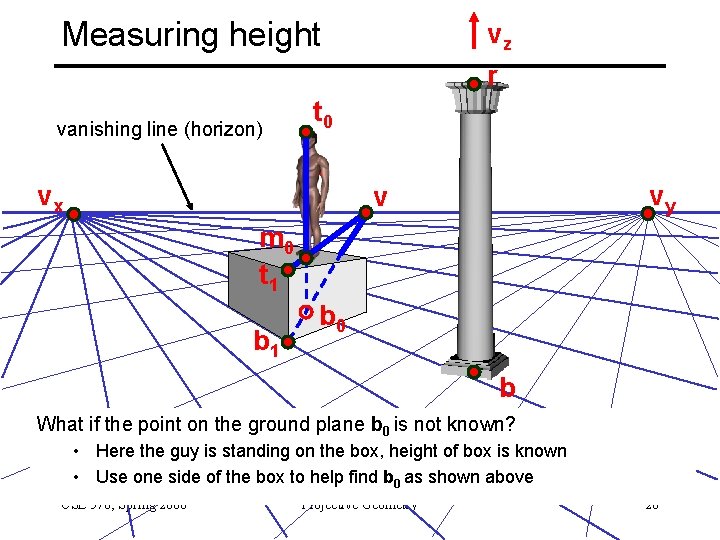
Measuring height vanishing line (horizon) vz r t 0 vx vy v m 0 t 1 b 0 b What if the point on the ground plane b 0 is not known? • Here the guy is standing on the box, height of box is known • Use one side of the box to help find b 0 as shown above CSE 576, Spring 2008 Projective Geometry 28

Computing (X, Y, Z) coordinates CSE 576, Spring 2008 Projective Geometry 29

3 D Modeling from a photograph CSE 576, Spring 2008 Projective Geometry 30

Camera calibration Goal: estimate the camera parameters • Version 1: solve for projection matrix • Version 2: solve for camera parameters separately – intrinsics (focal length, principle point, pixel size) – extrinsics (rotation angles, translation) – radial distortion CSE 576, Spring 2008 Projective Geometry 31

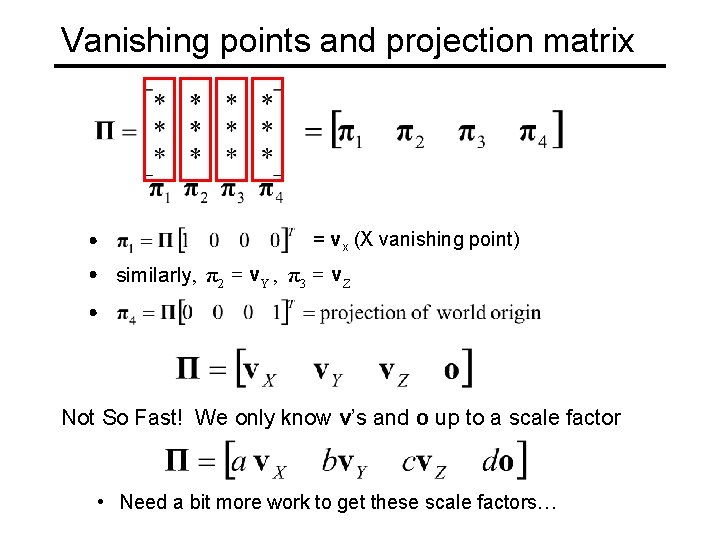
Vanishing points and projection matrix = vx (X vanishing point) similarly, π 2 = v Y , π 3 = v Z Not So Fast! We only know v’s and o up to a scale factor • Spring Need 2008 a bit CSE 576, more work. Projective to get. Geometry these scale factors… 32

Finding the scale factors… Let’s assume that the camera is reasonable • Square pixels • Image plane parallel to sensor plane • Principal point in the center of the image CSE 576, Spring 2008 Projective Geometry 33

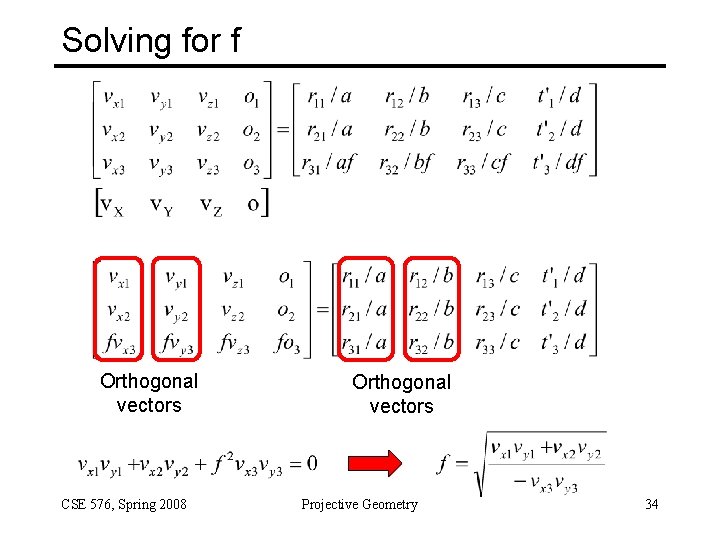
Solving for f Orthogonal vectors CSE 576, Spring 2008 Orthogonal vectors Projective Geometry 34

Solving for a, b, and c Norm = 1/a Solve for a, b, c • Divide the first two rows by f, now that it is known • Now just find the norms of the first three columns • Once we know a, b, and c, that also determines R How about d? • Need a reference point in the scene CSE 576, Spring 2008 Projective Geometry 35

Solving for d Suppose we have one reference height H • E. g. , we known that (0, 0, H) gets mapped to (u, v) Finally, we can solve for t CSE 576, Spring 2008 Projective Geometry 36

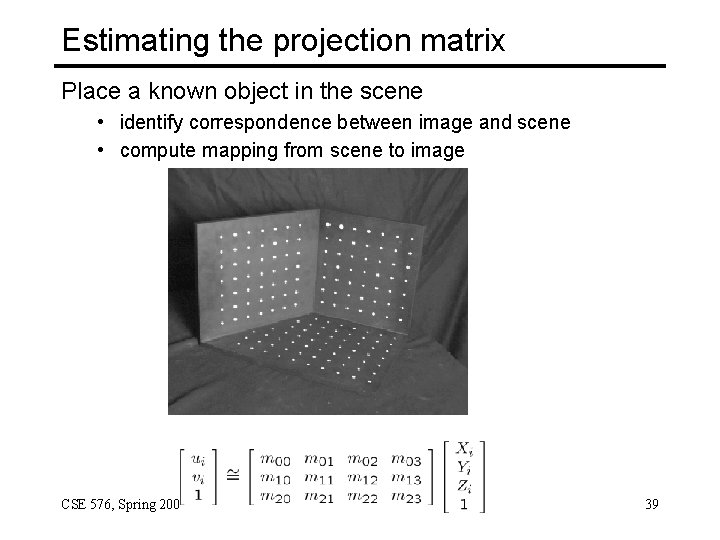
Calibration using a reference object Place a known object in the scene • identify correspondence between image and scene • compute mapping from scene to image Issues • must know geometry very accurately CSE 576, Projective Geometry • Spring must 2008 know 3 D->2 D correspondence 37

Chromaglyphs Courtesy of Bruce Culbertson, HP Labs http: //www. hpl. hp. com/personal/Bruce_Culbertson/ibr 98/chromagl. htm CSE 576, Spring 2008 Projective Geometry 38

Estimating the projection matrix Place a known object in the scene • identify correspondence between image and scene • compute mapping from scene to image CSE 576, Spring 2008 Projective Geometry 39

Direct linear calibration CSE 576, Spring 2008 Projective Geometry 40

Direct linear calibration Can solve for mij by linear least squares • use eigenvector trick that we used for homographies CSE 576, Spring 2008 Projective Geometry 41

Direct linear calibration Advantage: • Very simple to formulate and solve Disadvantages: • • Doesn’t tell you the camera parameters Doesn’t model radial distortion Hard to impose constraints (e. g. , known focal length) Doesn’t minimize the right error function For these reasons, nonlinear methods are preferred • Define error function E between projected 3 D points and image positions – E is nonlinear function of intrinsics, extrinsics, radial distortion • Minimize E using nonlinear optimization techniques – e. g. , variants of Newton’s method (e. g. , Levenberg Marquart) CSE 576, Spring 2008 Projective Geometry 42

Alternative: multi-plane calibration Images courtesy Jean-Yves Bouguet, Intel Corp. Advantage • • • Only requires a plane Don’t have to know positions/orientations Good code available online! – Intel’s Open. CV library: http: //www. intel. com/research/mrl/research/opencv/ – Matlab version by Jean-Yves Bouget: http: //www. vision. caltech. edu/bouguetj/calib_doc/index. html CSE 576, Spring 2008 Projective Geometry 43 – Zhengyou Zhang’s web site: http: //research. microsoft. com/~zhang/Calib/

Some Related Techniques Image-Based Modeling and Photo Editing • Mok et al. , SIGGRAPH 2001 • http: //graphics. csail. mit. edu/ibedit/ Single View Modeling of Free-Form Scenes • Zhang et al. , CVPR 2001 • http: //grail. cs. washington. edu/projects/svm/ Tour Into The Picture • Anjyo et al. , SIGGRAPH 1997 • http: //koigakubo. hitachi. co. jp/little/DL_Tip. E. html CSE 576, Spring 2008 Projective Geometry 44