Basic Geometry Terms Points In geometry we use

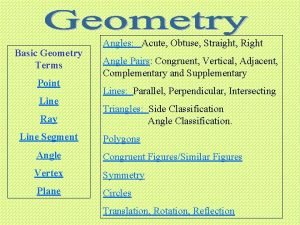
Basic Geometry Terms

Points In geometry, we use points to specify exact locations. They are generally denoted by a number or letter. Because points specify a single, exact location, they are zero-dimensional. In other words, points have no length, width, or height. It may be helpful to think of a point as a miniscule “dot” on a piece of paper.

Lines in geometry may be thought of as a “straight” line that can be drawn on paper with a pencil and ruler. However, instead of this line being bounded by the dimensions of the paper, a line extends infinitely in both directions. A line is one -dimensional, having length, but no width or height. Lines are uniquely determined by two points.

Line Segments Consider the task of drawing a “straight” line on a piece of paper (as we’ve done when thinking about lines). What you’ve actually done is create a line segment. Because our piece of paper has defined dimensions and we cannot draw a line infinitely in any direction, we have constructed a segment that begins somewhere and ends somewhere. Note that the notation for lines and line segments differ because a line segment has a defined length, whereas a line does not.

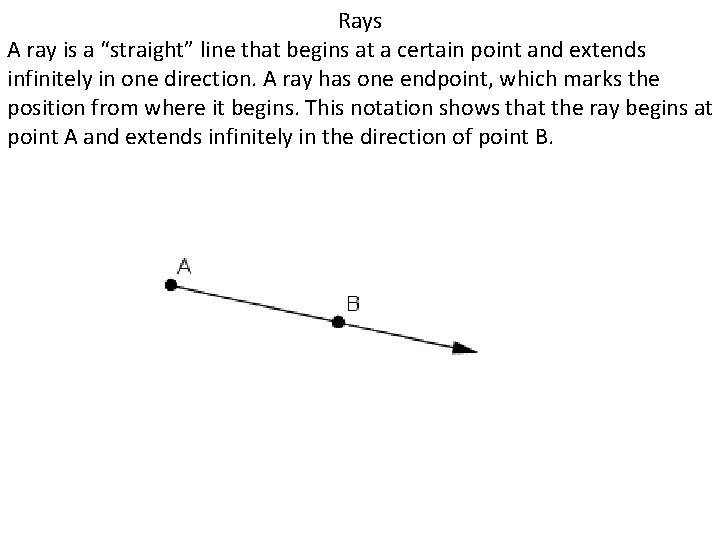
Rays A ray is a “straight” line that begins at a certain point and extends infinitely in one direction. A ray has one endpoint, which marks the position from where it begins. This notation shows that the ray begins at point A and extends infinitely in the direction of point B.

Endpoints mark the beginning or end of a line segment or ray. Line segments have two endpoints, giving them defined lengths, whereas rays only have one endpoint, so the length of a ray cannot be measured. Midpoints The midpoint of a line segment marks the point at which the segment is divided into two equal segments. In other words, the lengths of the segments from either endpoint to the midpoint are equal. Note that neither lines nor rays can have midpoints because they extend infinitely in at least one direction. It would be impossible to find the middle of a line or ray that never ends!

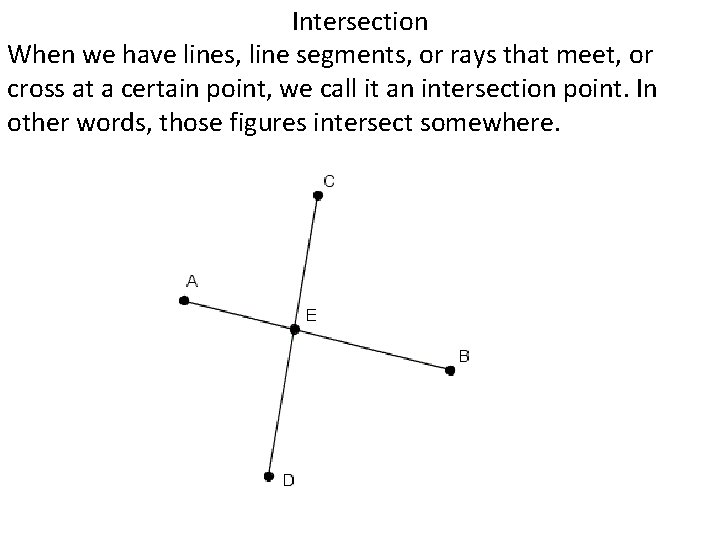
Intersection When we have lines, line segments, or rays that meet, or cross at a certain point, we call it an intersection point. In other words, those figures intersect somewhere.

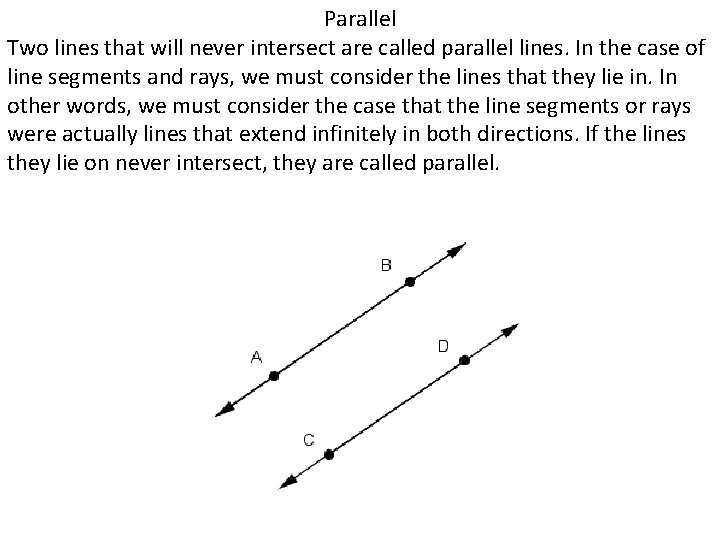
Parallel Two lines that will never intersect are called parallel lines. In the case of line segments and rays, we must consider the lines that they lie in. In other words, we must consider the case that the line segments or rays were actually lines that extend infinitely in both directions. If the lines they lie on never intersect, they are called parallel.

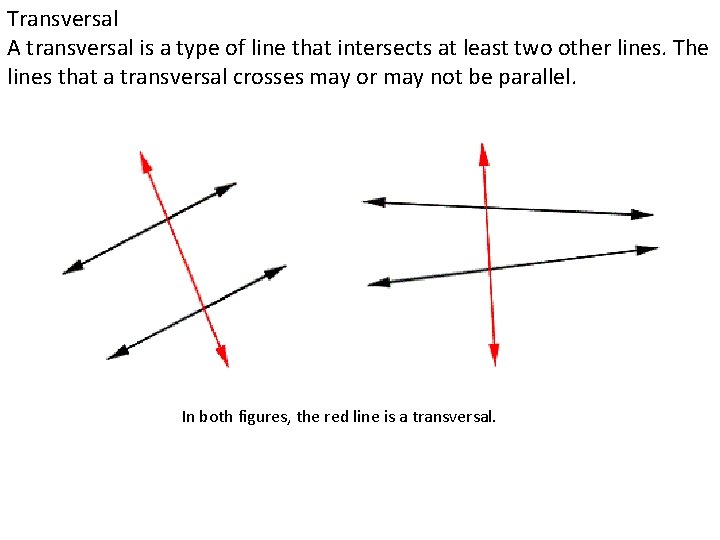
Transversal A transversal is a type of line that intersects at least two other lines. The lines that a transversal crosses may or may not be parallel. In both figures, the red line is a transversal.

Planes A plane can be thought of as a two-dimensional flat surface, having length and width, but no height. A plane extends indefinitely on all sides and is composed of an infinite number of points and lines. One way to think about a plane is as a sheet of paper with infinite length and width. Space is the set of all possible points on an infinite number of planes. Thus, space covers all three dimensions – length, width, and height.

Angles

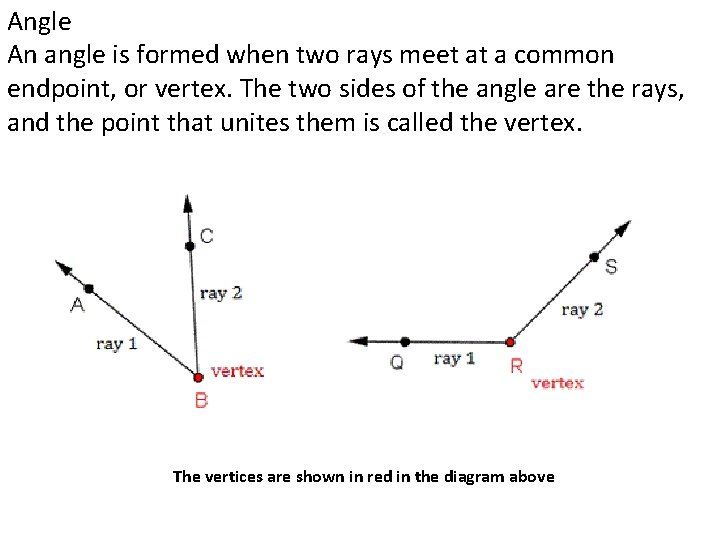
Angle An angle is formed when two rays meet at a common endpoint, or vertex. The two sides of the angle are the rays, and the point that unites them is called the vertex. The vertices are shown in red in the diagram above

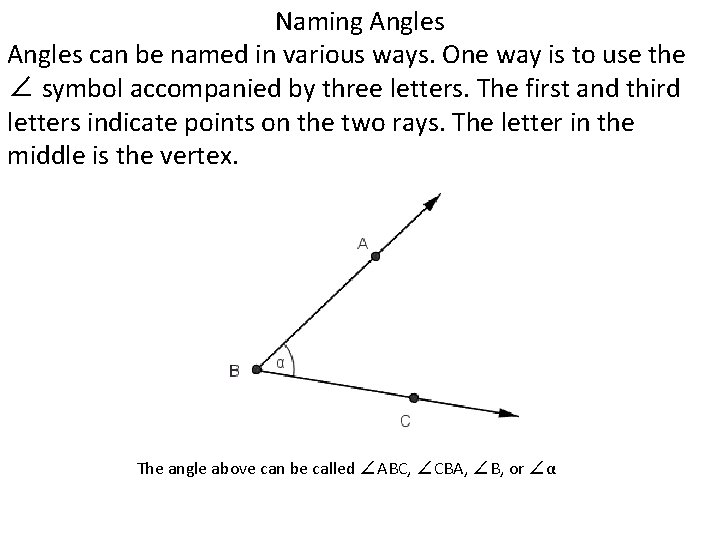
Naming Angles can be named in various ways. One way is to use the ∠ symbol accompanied by three letters. The first and third letters indicate points on the two rays. The letter in the middle is the vertex. The angle above can be called ∠ABC, ∠CBA, ∠B, or ∠α

Classifications of Angles can be measured in degrees or radians. For the time being, we will strictly talk about angles in terms of their degree measure. The symbol for degrees is °. Angles can measure from 0° up to 360°. Angles with no measure are called zero angles, while angles of 360° are full rotations. For our study of geometry, we will primarily focus on three important classifications of angles: • Acute • Obtuse • Right

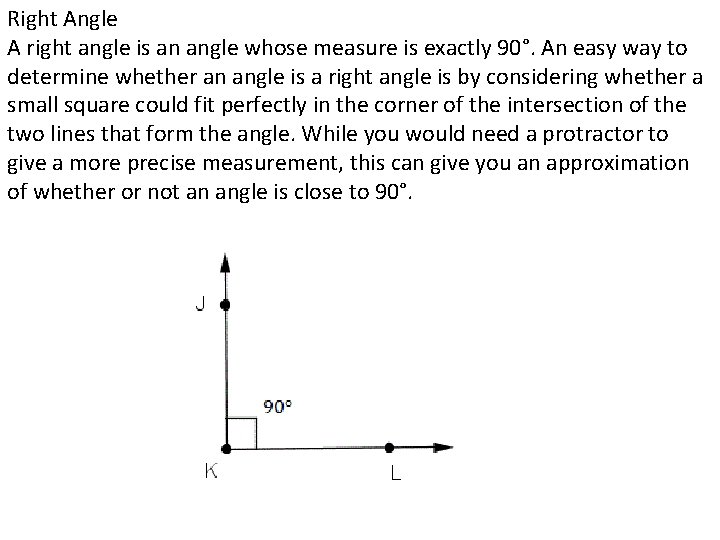
Right Angle A right angle is an angle whose measure is exactly 90°. An easy way to determine whether an angle is a right angle is by considering whether a small square could fit perfectly in the corner of the intersection of the two lines that form the angle. While you would need a protractor to give a more precise measurement, this can give you an approximation of whether or not an angle is close to 90°.

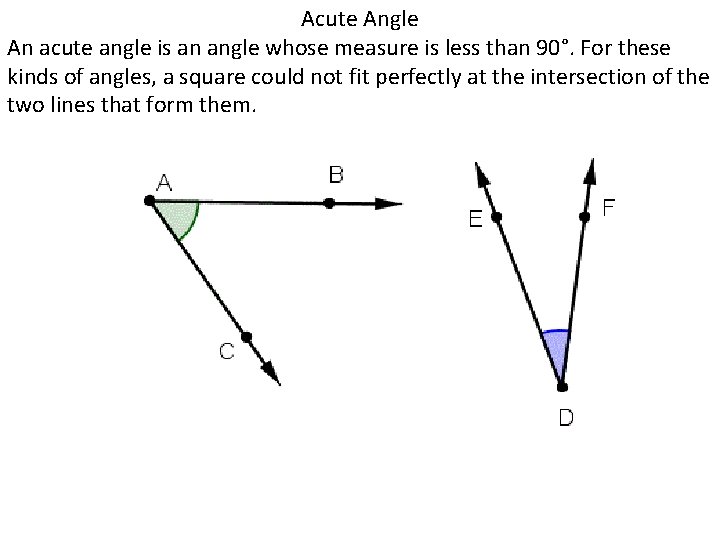
Acute Angle An acute angle is an angle whose measure is less than 90°. For these kinds of angles, a square could not fit perfectly at the intersection of the two lines that form them.

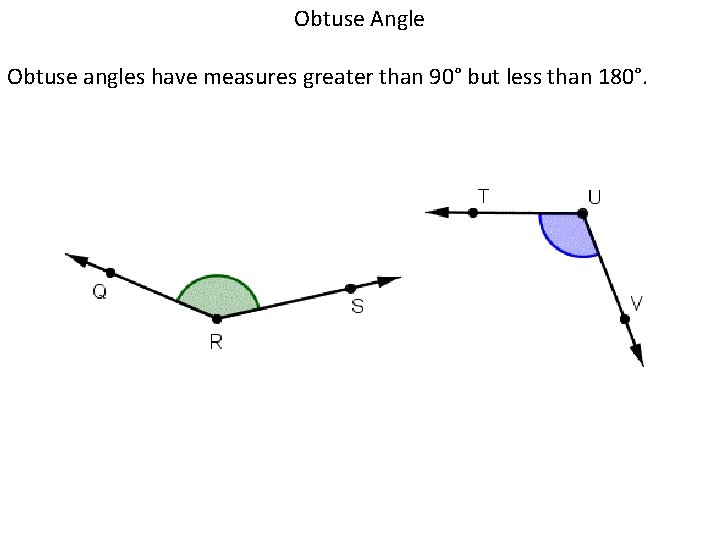
Obtuse Angle Obtuse angles have measures greater than 90° but less than 180°.

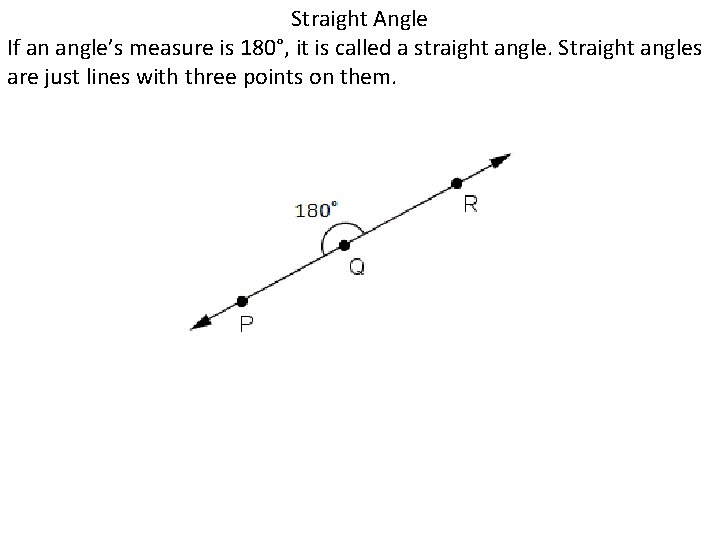
Straight Angle If an angle’s measure is 180°, it is called a straight angle. Straight angles are just lines with three points on them.

Pairs of Angles

Complementary Angles Two angles are complementary angles if their degree measurements add up to 90°. That is, if we attach both angles and fit them side by side (by putting the vertices and one side on top of each other), they will form a right angle. We can also say that one of the angles is the complement of the other. Complementary angles are angles whose sum is 90°

Supplementary Angles Another special pair of angles is called supplementary angles. One angle is said to be the supplement of the other if the sum of their degree measurements is 180°. In other words, if we put the angles side by side, the result would be a straight line. Supplementary angles are angles whose sum is 180°

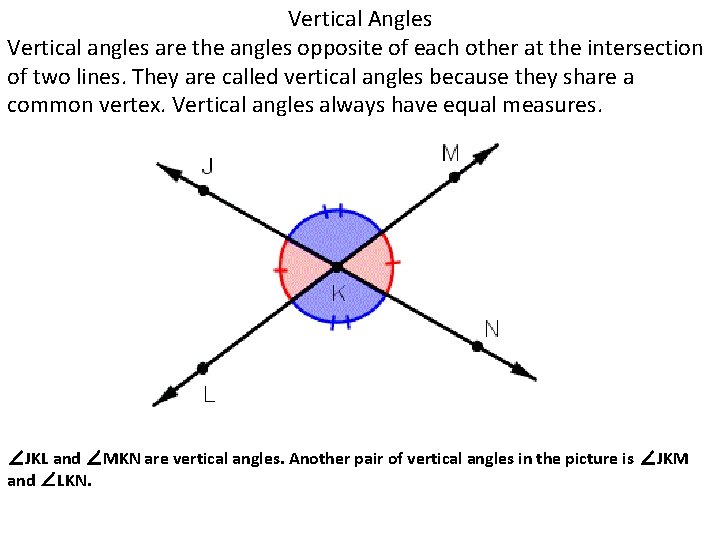
Vertical Angles Vertical angles are the angles opposite of each other at the intersection of two lines. They are called vertical angles because they share a common vertex. Vertical angles always have equal measures. ∠JKL and ∠MKN are vertical angles. Another pair of vertical angles in the picture is ∠JKM and ∠LKN.

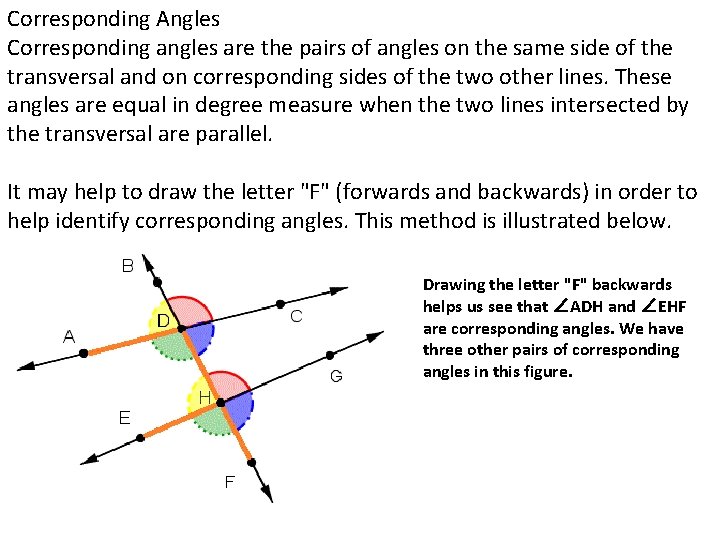
Corresponding Angles Corresponding angles are the pairs of angles on the same side of the transversal and on corresponding sides of the two other lines. These angles are equal in degree measure when the two lines intersected by the transversal are parallel. It may help to draw the letter "F" (forwards and backwards) in order to help identify corresponding angles. This method is illustrated below. Drawing the letter "F" backwards helps us see that ∠ADH and ∠EHF are corresponding angles. We have three other pairs of corresponding angles in this figure.

Triangles

Acute Triangle A triangle whose three angles are acute is called an acute triangle. That is, if all three angles of a triangle are less than 90°, then it is an acute triangle. Every angle in these triangles is acute.

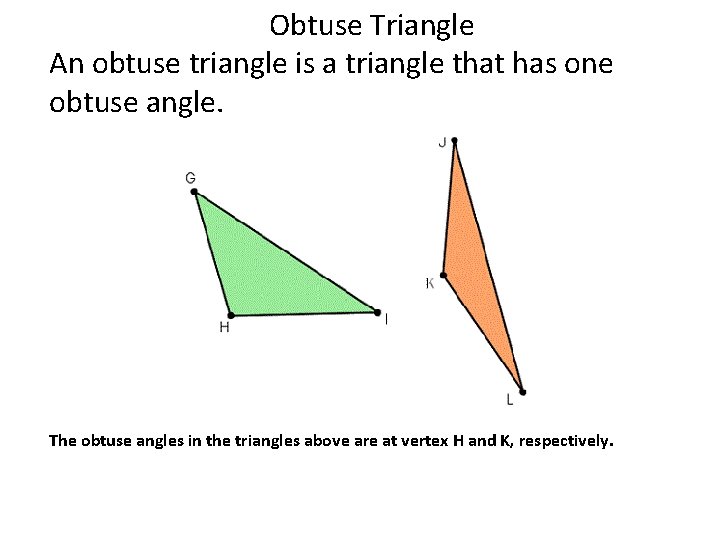
Obtuse Triangle An obtuse triangle is a triangle that has one obtuse angle. The obtuse angles in the triangles above are at vertex H and K, respectively.

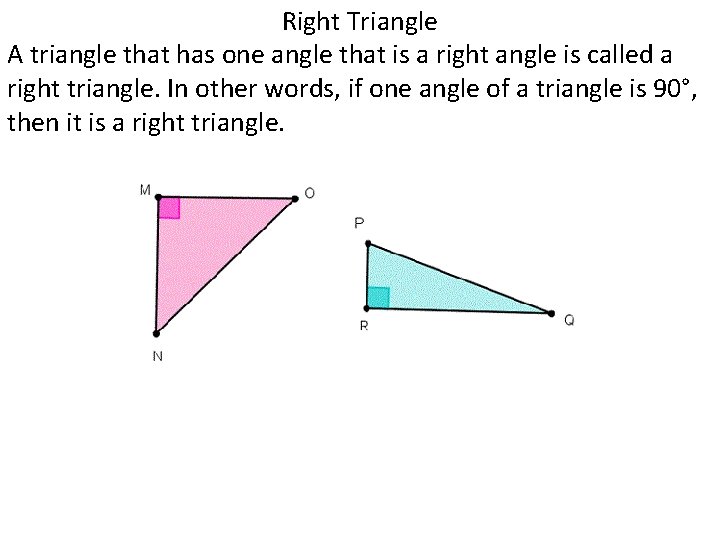
Right Triangle A triangle that has one angle that is a right angle is called a right triangle. In other words, if one angle of a triangle is 90°, then it is a right triangle.

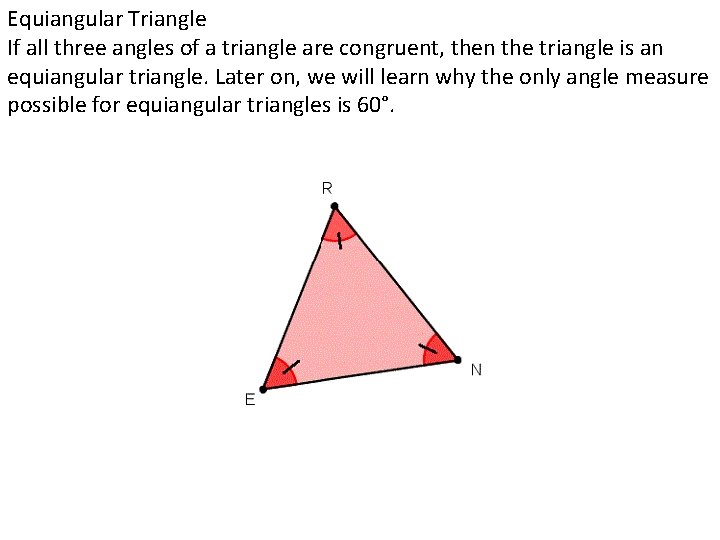
Equiangular Triangle If all three angles of a triangle are congruent, then the triangle is an equiangular triangle. Later on, we will learn why the only angle measure possible for equiangular triangles is 60°.

Classifying Triangles by Sides The sum of the measures of the interior angles of a triangle is 180.

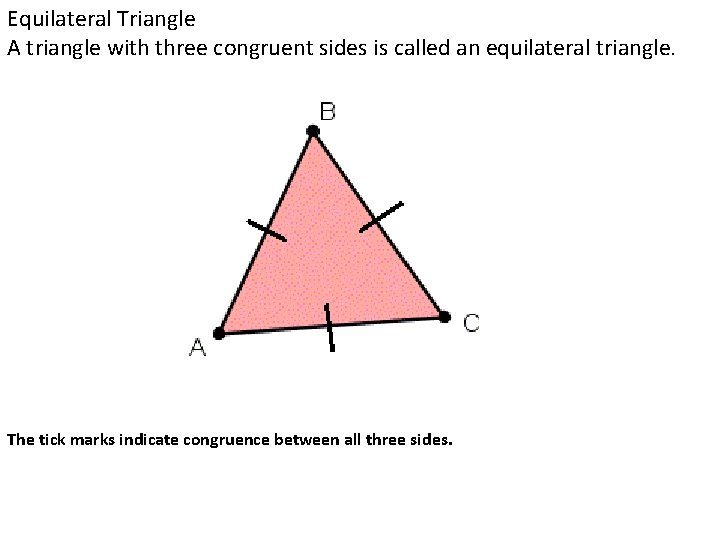
Equilateral Triangle A triangle with three congruent sides is called an equilateral triangle. The tick marks indicate congruence between all three sides.

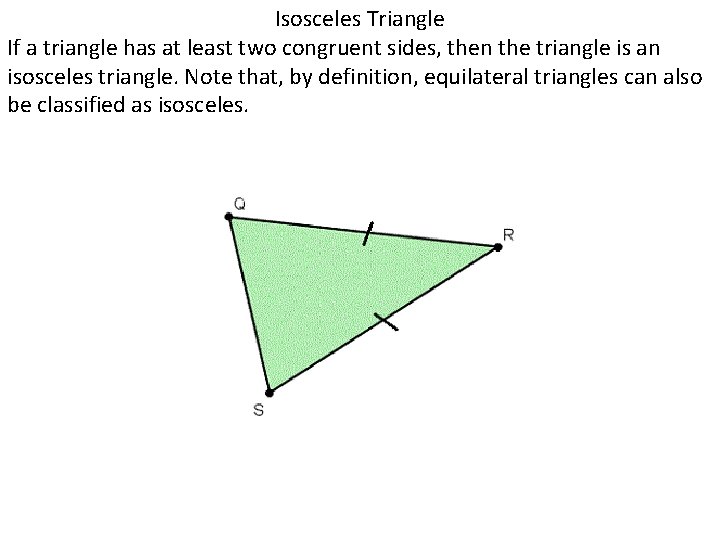
Isosceles Triangle If a triangle has at least two congruent sides, then the triangle is an isosceles triangle. Note that, by definition, equilateral triangles can also be classified as isosceles.

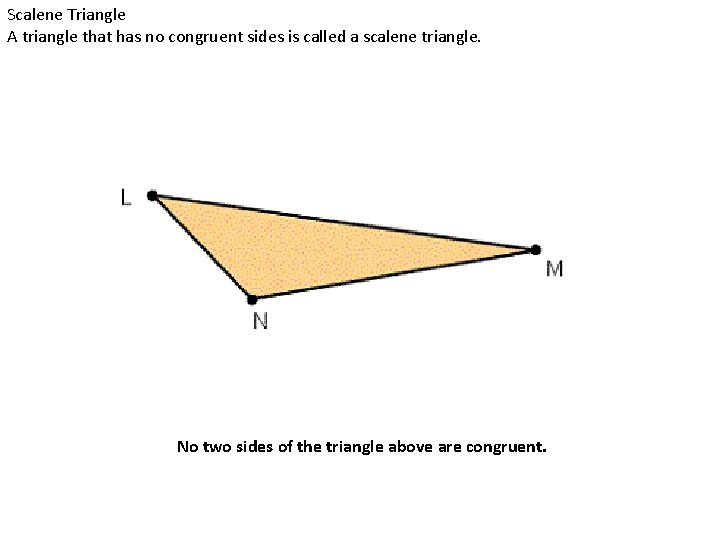
Scalene Triangle A triangle that has no congruent sides is called a scalene triangle. No two sides of the triangle above are congruent.