Projective geometry ECE 847 Digital Image Processing Stan

Projective geometry ECE 847: Digital Image Processing Stan Birchfield Clemson University

Lines almost • A line in 2 D is described by two parameters: ^ slope y-intercept • But vertical lines? • Only two parameters are sufficient, but requires nonlinear formulation:

Lines • A better parameterization can represent all lines: • Here the line is represented by 3 parameters: • But nonzero scalar multiple does not change the equation: • So we have only 2 degrees of freedom • To make this work, we have to introduce a non-intuitive definition: • I. e. , the vector u and its scalar multiple are the same

Lines • While we are at it, let us put the point into a vector, too: • Which leads to the beautiful expression: • Nonzero scalar multiple also does not change the point: • So we introduce an analogous non-intuitive definition:

Example • Ques: What does the vector [4, 6, 2]T represent? • Ans: It depends. – If the vector is a 2 D point, then the point is (4/2, 6/2) = (2, 3) -- divide by 3 rd coordinate – If the vector is a 2 D line, then the line is 4 x + 6 y + 2 = 0, or 2 x + 3 y + 1 = 0 • Points and lines are represented in the same way. Context determines which.

Lines • Ques. : Is the point p on the line u? • Ans: Check whether p. Tu = 0 • Ques. : Which line passes through two points p 1 and p 2? • Ans. : Compute u = p 1 x p 2 • Ques. : Which points lies at the intersection of two lines? • Ans. : Compute p = u 1 x u 2

Euclidean transformation • 2 D Euclidean transformation: • is more conveniently represented as • Again, we use 3 numbers to represent 2 D point (These are homogeneous coordinates)

Perspective projection • Nonlinear perspective projection • can be replaced by linear equation • where (x, y, w)T are homogeneous coordinates of (u, v, 1)T:

Recap • Homogeneous coordinates of 2 D point (x, y)T are p=(wx, wy, w)T where w ≠ 0 • We have seen three reasons for homogeneous coordinates: – simple representation of points and lines, no special cases – simple representation of Euclidean transformation – simple representation of perspective projection

Q&A • Questions: – Is there a unifying theory to explain homogeneous coordinates? – How can they be extended to 3 D? – Are they useful for anything else? • Answers: – Projective geometry – Useful for planar warping, 3 D reconstruction, image mosaicking, camera calibration, etc.

Euclidean Projective • Start with 2 D Euclidean point (x, y) • To convert to Projective, – Append 1 to the coordinates: p=(x, y, 1) – Declare equivalence class: p=ap, a≠ 0 • To convert back to Euclidean, – Divide by last coordinate: (u, v, w) (u/w, v/w) x=u/w, y=v/w

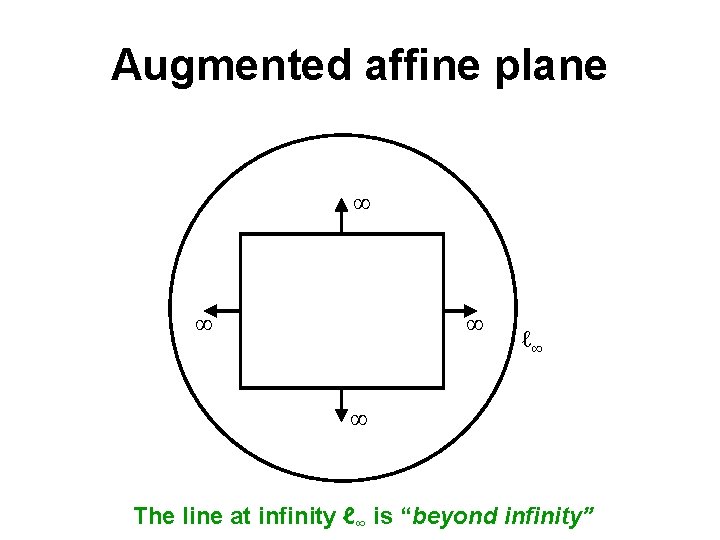
Ideal points • What if last coordinate is zero? (u, v, 0) • Cannot divide by zero • Projective plane contains more points than the Euclidean plane: – All Euclidean planes, plus – Points at infinity (a. k. a. ideal points) • All ideal points lie on ideal line: (0, 0, 1)

Are ideal points special? • In pure projective geometry, there is no distinction between real points and ideal points – Transformations will often convert one to another – We will freely make use of this, and often ignore the distinction • However, distinction is necessary to convert back to Euclidean – Distinction will be made when we need to interpret results

Geometries • Every geometry has – transformations – invariants

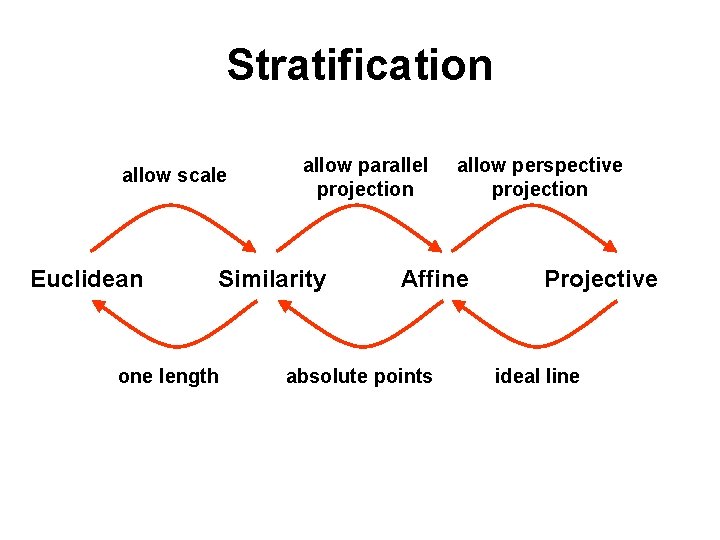
Stratification of geometries • • Euclidean similarity affine projective

Stratification allow scale Euclidean allow parallel projection Similarity one length allow perspective projection Affine absolute points Projective ideal line

Cross ratio

Ray space

Unit hemisphere

Augmented affine plane ∞ ∞ ∞ ℓ∞ ∞ The line at infinity ℓ∞ is “beyond infinity”

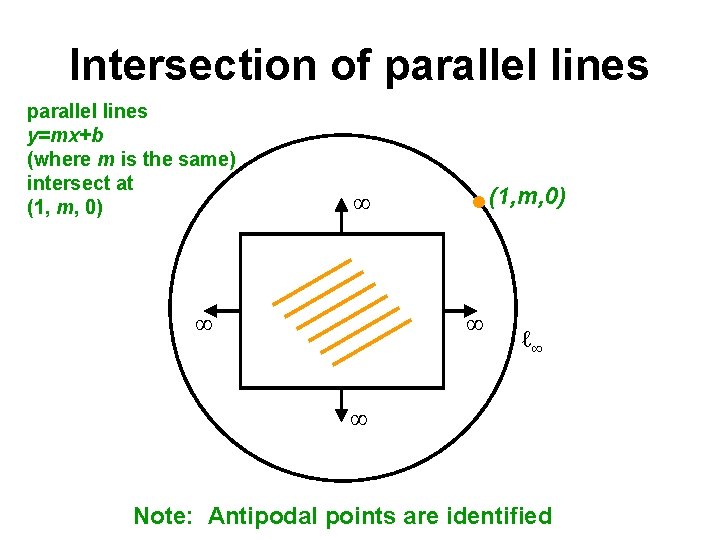
Intersection of parallel lines y=mx+b (where m is the same) intersect at (1, m, 0) ∞ ∞ ∞ ℓ∞ ∞ Note: Antipodal points are identified

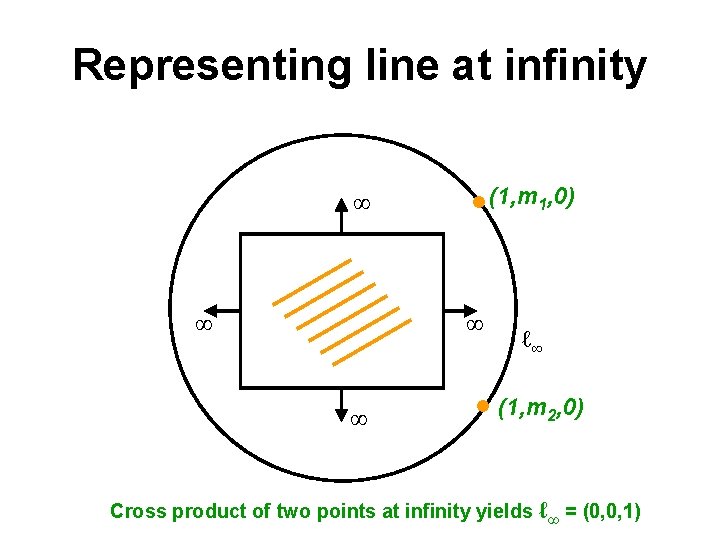
Representing line at infinity (1, m 1, 0) ∞ ∞ ℓ∞ (1, m 2, 0) Cross product of two points at infinity yields ℓ∞ = (0, 0, 1)

The strange world beyond infinity The line at infinity ℓ∞ = (0, 0, 1) ax+by+c=0 This means 1 = 0 !

Line transformations • If point transforms according to p’ = Ap • How does line transform? u’ = A-Tu

Conics • Take picture of circle ellipse • No distinction between types of conic sections in projective geometry

3 D Projective • Points and planes • Plucker coordinates for lines

Image formation • 3 D world point is (X, Y, Z, W)T • 2 D image point is (x, y, w)T • Therefore, perspective projection is a 3 x 4 matrix P

Perspective projection • Camera calibration matrix K

Homography • Simple case is projection from plane to plane – – Can be either world plane to image plane, or image plane to another image plane, or world plane to another world plane, etc. • 3 x 3 matrix is a projective transformation • Called a homography

Euclidean homography • Needs K

Essential and fundamental matrices

Relationship b/w FM and H • Fundamental matrix and homography

How to compute homography • Direct Linear Transform

Normalization • Important